Partitioning and quantifying regulatory mechanisms acting on within-host malaria using the effective propagation number

Abstract

Immune clearance and resource limitation (via red blood cell depletion) shape the peaks and troughs of malaria parasitaemia, which in turn affect disease severity and transmission. Quantitatively partitioning the relative roles of these effects through time is challenging. Using data from rodent malaria we estimate the effective propagation number, which shows that the relative importance of contrasting within-host control mechanisms fluctuates through time and is sensitive to the inoculating parasite dose. Furthermore, the capacity of innate responses to restrict initial parasite growth saturates with parasite dose, and experimentally enhanced innate immunity can affect parasite density indirectly via resource depletion. Our statistical approach offers a tool to improve targeting of drugs or vaccines for human therapy by revealing the dynamics and interactions of within-host regulatory mechanisms.

In the bloodstream phase of many malaria species, including those infecting humans, infected red blood cells (RBCs) burst in synchrony, releasing merozoites that must locate and infect a new RBC rapidly or else they die (1). Twenty-four to seventy-two hours later (depending on the Plasmodium species) the next generation of merozoites bursts out. The cycle repeats itself until the host dies or clears the infection (Fig. S1). Clearance of infection requires various complex immunological and physiological processes, the relative roles and timing of which have proven difficult to quantify (2-4). We propose a straightforward statistical approach to the problem. Building on the analogy between cell-to-cell propagation and host-to-host transmission (5), we borrow a model from between-host disease population ecology (6) to show how cell-to-cell transmission of malaria can be estimated using standard experimental data from rodent malaria (the modeling framework is readily extended to suitably-detailed data on human malaria, discussed below). If I_t is the number of infected RBCs at time t, and S_t is the number of uninfected RBCs, then the expected number of infected RBCs observed at time t+1 will be E[I_t+1] = P_E,t S_t I_t where E[] denotes the expectation and P_E,t is the effective propagation number of the infection at t. This number can be thought of as the product of merozoite burst size, contact rates between merozoites and uninfected RBCs, and invasion probability given that a contact has occurred. This quantity is analogous to the transmission coefficient in canonical models of between-host infection dynamics (7). The effective propagation number will vary through time as a function of variation in the availability of susceptible RBCs and efficacy of immune mechanisms. Taking the log on both sides of the relationship above, we can write

$$log(\mathrm{E}[(I_{t+1})])=log(P_{E,t})+log(I_t)+log(S_t).$$ 1

Applying regression techniques to [1] enables estimation of P_E,t, whenever time-series of I and S are available. While of critical interest in its own right, P_E is also important because of its relation to the within-host basic (R₀) and time-varying effective (R_E) reproductive ratios. For blood phase malaria, these two dimensionless quantities are defined as the number of newly infected cells that would arise from the merozoites that burst from a single infected cell in an otherwise uninfected bloodstream, and the average number of new infected cells per infected cell in a previously infected bloodstream, respectively (8). From our estimates of P_E,t, we can directly quantify the effective reproductive ratio, as R_E,t = P_E,t S_t. When R_E >1, within-host parasite density will increase. When R_E <1, parasite density will decrease. The maximum upper bound on R_E (and R₀) is the burst size, or number of merozoites emerging from a single infected RBC, and is attained if invasion probability on contact is 1, and crowding and immune effects are absent.

A variety of immune and non-immune factors determine the magnitude of P_E and thus R_E. The relative importance of these factors will vary during the course of an infection because of time-dependent variation in RBC availability/susceptibility and the density of immune effectors (9, 10). A standard approach to quantifying this variation is to test data against mathematical models that incorporate a series of differential equations chosen to reflect processes involving explicitly defined interacting populations of cells and effectors, as a function of time and/or pathogen titer (3, 5, 11-18). Focusing on P_E allows us to side-step many complex unknowns required for this approach, not least the arbitrary choice of specific functional forms for key relationships such as immune killing (14, 19), and the need to wrestle with parameter identifiability issues (12, 18, 20).

To illustrate our data-driven approach, we use data on the rodent malaria Plasmodium chabaudi in laboratory mice. Infected RBCs burst every 24 hours in this species, releasing on average 6 merozoites (21). Applying [1] therefore requires daily estimates of numbers of infected and uninfected RBCs. Here we analyse experimental work on CD4+ T-cell depleted mice (22), intact mice infected at a range of starting parasite densities (23), and mice treated with a neutralizing antibody that acts to up-regulate immunity (24), all infected with the AS clone of P. chabaudi (see Figs S2-S4 and (25) for details). Framing our analysis in ecological terms (4, 14) we contrast bottom-up processes (analogous to resource availability for free-living organisms) with top-down mechanisms (analogous to control by natural enemies). There are two widely recognized bottom-up controls in malaria dynamics (3, 4, 11-13, 26-28): the availability of susceptible cells and age-dependent variation in susceptibility of these cells. For example, younger RBCs (reticulocytes, less than four days old) are less susceptible to P. chabaudi AS infection than are normocytes (29). Both RBC availability and age-distribution are shaped by infected cell density (since parasites destroy RBCs) and RBC supply (erythropoiesis and/or splenic retention of uninfected RBCs (30)). Top-down regulatory mechanisms include innate and adaptive immunity provided by effectors ranging from macrophages to strain-specific antibodies (9).

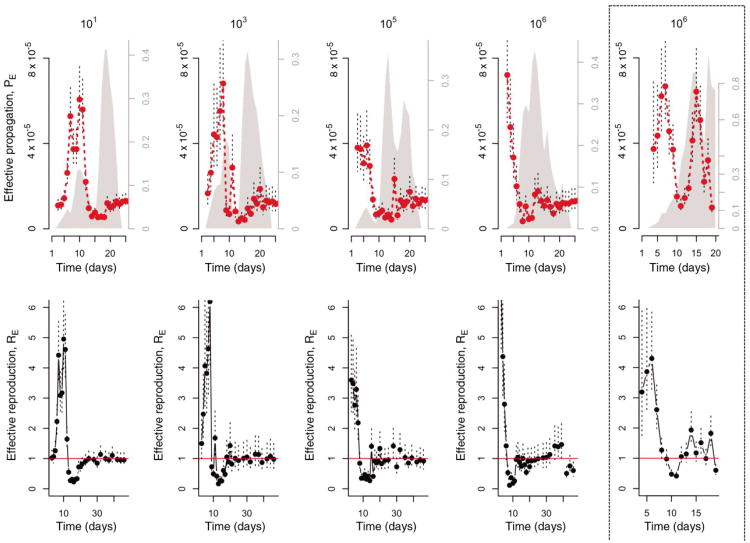
We first estimate the time-varying quantities defined above. In both CD4+ T-cell depleted and intact mice, the effective propagation number (P_E,t) fluctuates considerably over the course of the infection (Fig. 1). This combined with the fluctuations in susceptible RBC supply leads to variation in the effective reproductive ratio (R_E,t), typically ranging from 4-6 early in the infection to less than 1 later on. The effect of treatments on P_E,t and R_E,t reveals three broad determinants of within-host malaria dynamics in rodents, detailed below.

Figure 1. Within-host effective propagation.

The red line is the estimate of effective propagation for 5 or 10 intact AS infected mice with different inocula sizes (1-4^th columns to the left) and 5 CD4+ T-cell depleted AS infected mice (far right, dashed enclosure). The size of the inocula is indicated by the title of each column (10¹, 10³, 10⁵, 10⁶, CD4+ T-cell depleted mice inocula sizes are comparable to the largest levels used in intact mice); standard errors from the regression are shown as dashed vertical lines. Grey polygons show mean approximate proportion of RBCs aged 1-3 days, based on RBC-change reconstruction (right-hand axis). The bottom row shows the corresponding R_E, up to day 50 for intact mice; P_E changes little over the later days.

Dose dependence of early innate immunity

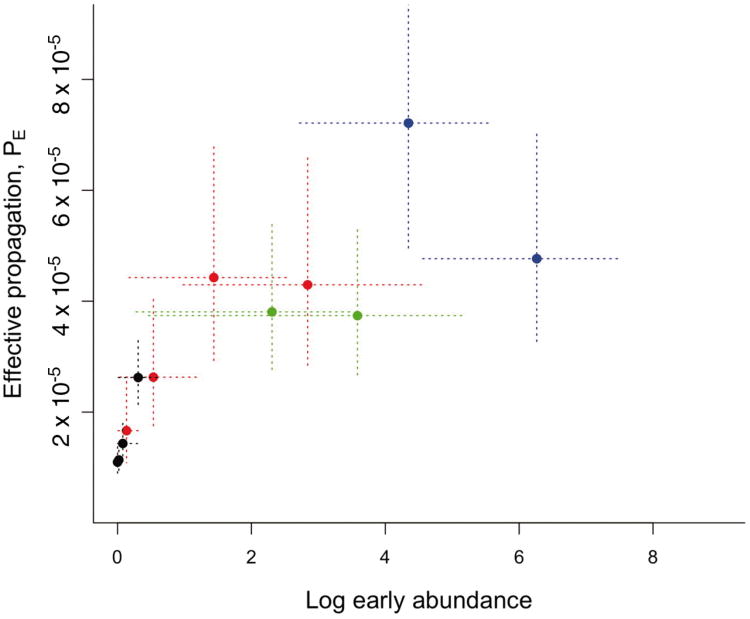
Comparing the dynamics of P_E across inoculum sizes in intact mice (Fig. 1) reveals a surprising and conspicuous dose-dependence in the early propagation of the parasite: higher starting numbers of parasites resulted in substantially higher effective propagation numbers early in infections (Fig. 2). This curve resembles the type II functional response classically described for predator-prey systems: if the immune response has a ‘predator’ handling time associated with each ‘prey’ caught (i.e., infected RBCs or free merozoites killed) (e.g. (31)), the prey per-capita death rate will decline as a function of prey numbers. This interpretation is also compatible with innate immunity modeled as drawing on a limited pool of effectors (32). Thus, early host defenses (active within 1-4 days and thus likely to reflect an arm of innate immunity (9)) can retain R_E near 1 for small numbers of parasites (Fig. 1), but if numbers of parasites are above a threshold, this control is overwhelmed. In fact, the upper limit of the range of burst sizes reported for the AS clone (6, (21)) is close to the maximum estimate of R_E observed at high doses (Fig. 1), suggesting that for sufficiently high inocula, there is negligible loss of parasites to immunity in the early phase. More effective control at low doses might contribute to the dose-dependence of pre-patency observed in human malaria infections during neurosyphilis treatments (33). However, detecting dose-dependence of innate immune efficacy in human hosts is likely to be complicated, since evidence from both neurosyphilis treatments (2, 3) and vaccine trials (10) points to considerable patient to patient variability in innate immunity.

Figure 2. Decelerating control.

Effective propagation over the first 2-4 days (with the last day set when P_E,t starts to decay sharply, see Figure 1) for 4 different starting inoculation sizes (10¹ in black (n=10 mice, 3 days), 10³ in red (n=5, 4 days), 10⁵ in green (n=5, 2 days), 10⁶ in blue (n=5, 2 days)) indicates a decelerating function of density suggestive of a handling-time type-effect for innate immunity; vertical lines are standard errors from the regression defining P_E,t; horizontal lines are 95% quantiles for abundance of parasites observed on that day.

Impact of RBC age structure

If adaptive immunity can be assumed to be very impaired in CD4+ T-cell depleted mice (9), temporal fluctuations in P_E will primarily reflect the action of RBC availability, age structure and/or innate immunity. The age structure of RBCs can be inferred via the change in RBC numbers due to processes other than infection of individual cells (25)(Fig. S5). Significant shifts towards younger age classes occur over the course of the infection: from <5% reticulocytes in uninfected mice to as much as 80% in CD4+ T-cell depleted and 40% in intact infected mice (Fig. 1; proportion occupied by grey polygons increases with time). This replacement of normocytes by reticulocytes is associated with a reduction in P_E reflecting reduced average susceptibility of circulating RBCs. We can build on the regression equation defined in [1] to fit two age-specific propagation parameters (P_E1, P_E2, which respectively account for effective propagation in normocytes and reticulocytes) to the time-series of immune depleted mice (25). Incorporation of these parameters significantly improves the fit to the temporal pattern of effective propagation compared to a model lacking age structure (Fig. S7) (LR=11.53, p<0.01, df=1). This provides direct empirical evidence of the importance of RBC age-structure to control of malaria parasites in immune depleted mice. Indeed, the joint effect of RBC depletion and skewed age structure results in a 3-fold reduction of the effective reproductive ratio (Table S1), which suggests that the many host-dependent mechanisms of RBC reduction that are evident in both rodent and human malaria (30) may reflect an evolutionary adaptation.

Impact of adaptive immunity

Using the two RBC age-specific parameters estimated from immune depleted mice (P_E1, P_E2), we can predict the pattern of effective propagation through time that would be observed if all fluctuations in P_E,t were due to bottom-up controls only, and compare this with the observed time-series in intact mice to reveal the relative importance of top-down and bottom-up factors through time (Fig. S8, S9). Our approach reveals that this is also highly dependent on initial parasite dose. For mice inoculated with high doses, dynamics for the first approximately 10 days are adequately explained by RBC availability and age structure, but after that the effective propagation number is consistently and substantially over-predicted by the bottom-up model (Fig. S9). This indicates that potent top-down controls are established after about a week. Mice infected with low parasite density have an additional early over-prediction of P_E,t because the bottom-up only model does not capture the ability of early innate immunity to control propagation from low densities (Fig. 2, S8, S9). We can extend the model to incorporate early immunity (Fig. 2) by defining early parasite survival to be a function of parasite density that increases towards a plateau, and fitting this to time-series of intact mice (25)(Fig. S10). A combined model of bottom-up and early innate controls can precisely predict the early propagation numbers and course of infection, but not the later propagation numbers (Fig. S9). The failures of prediction from this simple model reflect the action of adaptive immunity. Conversely, successes of this restricted model highlight the interval of time over which failure to account for resource limitation as a mechanism of malaria control could impair inference about immunity (Fig. S8).

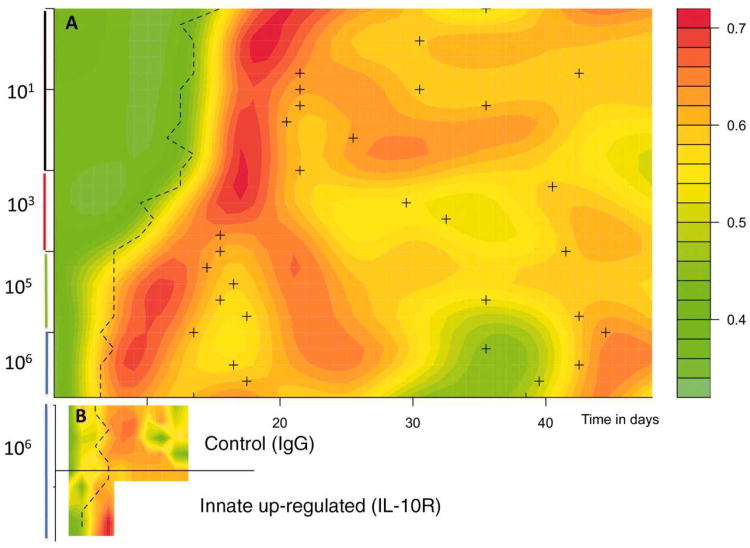
The discrepancy between observed and predicted P_Es allows us to calculate the efficacy of immune clearance via the proportion of infected cells p_t that must be killed to obtain the observed number of parasitized cells while accounting for RBC limitation (25). To visualize changes in immune efficacy (parasite kill rates) we plot the smoothed surface of this fraction through time, ranking mice by early parasite density (Fig. 3A). Immune efficacy peaks around 0.85, indicating that at its maximum efficacy, adaptive immunity removes on the order of 85% of parasites per day, resulting in a 13-fold reduction in the effective reproductive ratio (Table S1). From an applied point of view, this quantification might represent a useful yardstick against which the efficacy of immunity elicited by candidate vaccines or new drugs could be measured. The peak efficacy was similar in all mice, irrespective of inoculating dose, but the timing of the peak varied. Mice receiving higher doses experienced an earlier peak in parasitaemia (Fig. 3A, dashed line) and an earlier increase in immune efficacy (as early as day 8 vs. as late as day 20 for the lowest dose, Fig. 3A). Declines in immune efficacy occur after initial parasitaemia is controlled, with kill rates approximately halved (Fig. 3A). This decline, which might reflect down-regulation of immunity (under host or parasite control), depletion of the immune effector pool, and/or antigen escape, allows re-emergence of parasitaemia in some mice (Fig. S3). The pattern of decline is complex and dose-dependent (Fig. 3A). Higher starting densities result in a rapid dip in immune efficacy following the initial peak. Subsequently, in response to recrudescence (Fig. S3, peaking at around 15 days, Fig. S11), immune efficacy increases and then decays again (around day 35). By contrast, mice infected with intermediate starting densities experience slower declines in immunity. Feedbacks inherent in activation of adaptive immunity may partly underlie this variability (34, 35): if conditions at the peak of infection are such that few susceptible RBCs are available, control may be achieved by relatively less sustained immune killing, with the result that immune memory is retained less well (36) for higher inoculum sizes.

Figure 3. Visualizing efficacy of immunity.

in A) intact mice for different starting inoculum sizes (y axis labels); and B) intact mice and intact mice treated with IL-10R, which up-regulates innate immunity (y axis labels to the right). Surfaces show smoothed proportion of infected cells killed, p_t, against time in days (x axis) with mice ranked via their early densities within each category (rows, y axis); dashed thick line indicates the timing of the first major peak of infection; and for A) the crosses indicate secondary peaks, generally following dips in immune efficacy. In A) higher early densities experience an earlier increase in mortality of infected cells but this effect decays, then increases, finally dipping significantly around the 35^th day associated with a resurgence of parasites. In B) mice treated with IL-10R experience an earlier peak in immune efficacy. However, treated mice generally died by day 9.

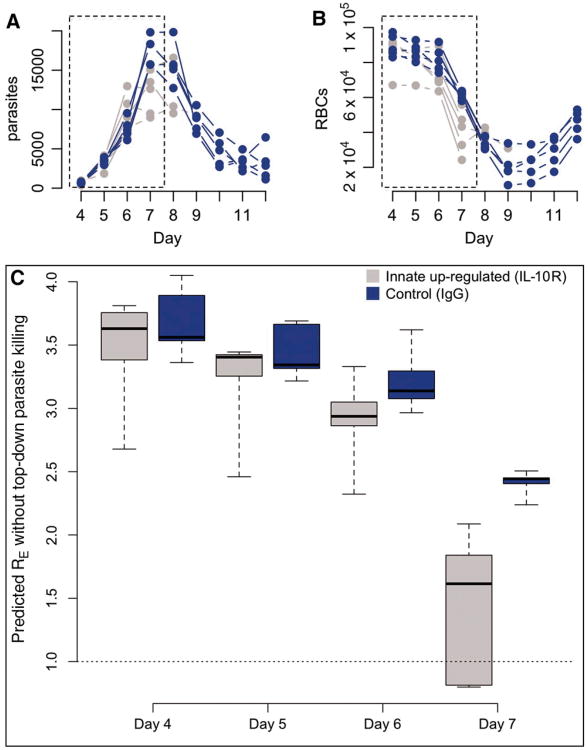
To further illustrate how the time series approach can provide new insights from manipulative immunological experiments, we calculated surfaces of immune efficacy for control and anti-interleukin 10 receptor (anti-IL-10R) treated mice (Fig. 3B). Treated mice experience a slightly earlier increase in immune efficacy, in keeping with the accelerated innate response generated by blockade of the potent modulatory cytokine IL-10 (24). This slight difference in the timing of peak immune efficacy between anti-IL-10R treated and untreated mice results in rather different maximum parasite densities (Fig. 4A). Two factors may explain this. First, because malaria within-host kinetics are so dynamic, a small impact at the right time may have a large consequence several time steps later. Second, anti-IL-10R-treated mice experience earlier anemia (Fig. 4A), perhaps attributable to increased bystander killing, suppression of erythropoesis and/or retention of uninfected RBCs by the spleen (some of which are likely repercussions of increased TNF-α production (30)). Consequently, there is a decline in the effective reproductive ratio in treated mice, beyond the reduction due to direct killing of infected cells (Fig. 4). Therefore, this immune manipulation generates an apparent increase in immune efficacy (in the sense that the effective propagation number is reduced) that is mediated via a resource depletion mechanism. Low levels of IL-10 have been implicated in severe anemia in human malaria (37), suggesting similar mechanisms could be operating. An intriguing corollary is that substantial bystander killing (whereby more than 4 uninfected cells may be killed for every infected cell killed during rodent malaria (4)), rather than being an unintended side-effect of immune activity, may in part be an evolutionary adaptation for using top-down mechanisms to enhance bottom-up controls.

Figure 4. Top-down controls acting via bottom-up effects.

Time-series (×10^-2 per μl) of parasites (A) and RBCs (B) for mice treated with IL-10-R (grey, n=4) and controls (blue, n=4), and the corresponding estimate of the effective reproductive ratio, R_E on days 4-7 (C) that would be observed in the absence of immune killing of infected cells obtained by combining RBC age-specific estimates of P_E obtained from CD4+ T cell-depleted mice with the RBC dynamics and age-structure indicated by these time-series. Dotted regions in A and B show the time period plotted in C. In IL-10R treated mice, this predicted R_E drops precipitously simply due to RBC depletion (B); and this anemia is not due to parasite levels, which remain comparable in controls and treated mice (A). This indicates that immune-mediated killing of uninfected RBCs is a key mechanism of control.

Discussion

Anti-parasite effects of RBC resource limitation (e.g., via suppression of erythropoesis, or the action of protective RBC polymorphisms that reduce susceptibility) are indicated by a range of studies on human malaria (38, 39). A key merit of the effective propagation number is that it provides a straightforward way of controlling for effects of target cell availability on within-host replication, thus revealing the relative and absolute strength of mechanisms that drive within-host dynamics (e.g., killing of infected cells, or heterogeneities among target cells in transmission characteristics), and their variation through time. The method also yields a direct quantification of fluctuations in the within-host effective reproduction number, R_E, thus identifying key points for interventions – e.g., when parasite effective reproduction is so low that any additional challenge to growth may result in clearance of the infection (8), with potential relevance for applications towards human health. Finally, our application of the methodology to the P. chabaudi case study shows that the method can reveal previously-overlooked aspects of control in mouse malaria, producing new hypotheses for the regulation of human malaria. Interestingly, the diminishing impact of innate immunity with increased dose may be the selective pressure responsible for the evolution of the large burst size of liver schizonts (and, as a consequence, the long incubation period in the liver), which is compatible with estimates of 10⁵ - 10⁶ merozoites released following a single infective bite (40) and robustly over the threshold of innate immune escape discovered here (Fig. 2).

Previous work on malaria has fitted more mechanistically detailed dynamic models to time-series data on uninfected and infected cells (3, 4, 11-14, 26, 41). Our simpler statistical method confirms conclusions from this work (e.g., roles for age-structure of RBCs (12, 13) and clearance of uninfected RBCs (11)) but also identifies dynamical features not previously detected (e.g., dose-dependence in the impact of innate immunity and complex time-dependence in the efficacy of adaptive immunity). Our method also sidesteps much of the difficulty involved in fitting such models and provides empirical insights into the shapes that functional forms in more mechanistic models should reflect (such as the dose-dependent saturation of the early innate control (Fig 2), or the response surface of adaptive immunity (Fig 3)). As shown (Fig. 3B, 4), our approach enables detailed interpretations of existing experimental data (e.g., time-series following knock-downs of immune factors (42, 43), induced erythropoeisis or blood transfusions (41, 44), etc.). Given time-series of susceptible and infected RBCs, estimates of time-varying effective propagation are directly accessible to anyone with basic statistical knowledge. This should ultimately open the way for a complete characterization of the roles of direct and indirect top-down and bottom-up mechanisms involved in the regulation of parasite densities (Fig. S12, Table S1) in the context of both single and mixed infections, and how this in turn impacts transmission and disease severity.

The underlying process of bursting infected RBCs and invasion of uninfected RBCs is common to blood-phase malaria across animal taxa. The methods we introduce will consequently be generally applicable. The strength of the mouse data we have used is the finely resolved measures of uninfected and infected red blood cells. We are unaware of any experimental time series in human patients in which these parameters were directly measured but our analyses suggest that future longitudinal studies of individual patients that undertake the simple assays required to directly assess RBC densities in addition to parasite densities will lead to considerable insights into the factors regulating human malaria.