Optimizing the Analysis of Adherence Interventions Using Logistic Generalized Estimating Equations

Abstract

Interventions aimed at improving HIV medication adherence could be dismissed as ineffective due to statistical methods that are not sufficiently sensitive. Cross-sectional techniques such as t tests are common to the field, but potentially inaccurate due to increased risk of chance findings and invalid assumptions of normal distribution. In a secondary analysis of a randomized controlled trial, two approaches using logistic generalized estimating equations (GEE)—planned contrasts and growth curves—were examined for evaluating percent adherence data. Results of the logistic GEE approaches were compared to classical analysis of variance (ANOVA). Robust and bootstrapped estimation was used to obtain empirical standard error estimates. Logistic GEE with either planned contrasts or growth curves in combination with robust standard error estimates was superior to classical ANOVA for detecting intervention effects. The choice of longitudinal model led to key differences in inference. Implications and recommendations for applied researchers are discussed.

Introduction

Inappropriate statistical analyses can result in the failure to detect an effective intervention or to incorrectly support an ineffective intervention. Both false negatives and false positives undermine the validity of the results [1, 2]. A commonly cited statistical problem with randomized controlled trials (RCTs) is the excessive use of cross-sectional significance tests (e.g., Student’s t) at every time point to compare group differences [3, 4]. The prevalence of cross-sectional testing in RCT reports is understandable given its ease, but this approach is accompanied by two methodological hazards: (a) inflation of Type I error and (b) failure to account for measurements taken at different time points as coming from the same individual.

Statistical analysis is fundamentally about quantifying signal-to-noise ratio, and the treatment of error is different when data are longitudinal, as in the case of RCTs. Outcomes measured across time often are correlated, which must be considered in the calculation of standard errors [5]. Failure to model noise (i.e., error) correctly can lead to erroneous findings. An array of alternatives is available for analyzing longitudinal data, including multilevel models such as generalized estimating equations (GEE) and generalized linear mixed regression (GLMM), but these are under-utilized [6]. In the context of RCT research, techniques for longitudinal data analysis may be the most appropriate because they permit the estimation of treatment effects (i.e., group differences) across multiple time-points within a single statistical model. Such an approach minimizes the accumulation of Type I error from multiple endpoint comparisons. Furthermore, true multilevel regression techniques that model the correlation of measurements within the same subjects permit inference using valid standard errors.

In the present study, the issue of statistical model selection is addressed in the context of adherence to antiretroviral (ARV) therapy, a relatively nascent area of RCT research with particularly challenging outcome variables. Although medication adherence is critical for successful treatment of HIV, non-adherence is widespread. Adherence is most commonly measured as a percentage of prescribed doses taken in a specified period, ranging from the past 3 to 30 days [7]. However, adherence data are often highly skewed or multi-modal, with high frequencies of individuals reporting either zero or perfect adherence. Consequently, continuous measures of adherence may be ill-suited to statistical models with strong assumptions of normally distributed data.

A common alternative to measuring adherence continuously is to categorize adherence at cut-points presumably associated with viral suppression, such as 95 or 100% adherence. Dichotomous variables have minimal distributional requirements since there are only two possible outcomes (e.g., adherent and non-adherent). However, the disadvantage of dichotomization is that information is discarded, resulting in lower statistical power and increased likelihood of Type II error [8]. A more principled alternative to dichotomization is to utilize statistical methods that are capable of analyzing percentage data. Although logistic regression is most commonly used to analyze dichotomous variables, it can also accommodate any fractional outcome bounded between 0 and 1. The application of logistic regression in this manner is not widespread, but has practical advantages since the assumptions of a logistic model more closely reflect the nature of fractional data. Consequently, estimates of standard error would, in principle, be more trustworthy when analyzing medication adherence data using a logistic approach.

Additional means of obtaining accurate standard error estimates include well-established techniques such as “robust” variance corrections [9] and bootstrapping [10] that can be applied to obtain empirical standard error estimates, valid even if the assumptions of the statistical model are not entirely met. Notably, both dichotomous [11] and fractional data [12] are inherently heteroskedastic, meaning that variance of the outcome is tied to the values of the predictors. This can result in inflated standard error estimates in both linear and logistic regression models, leading to reduced statistical power for detecting a treatment effect. Recent quantitative work by Papke and Wooldridge [12] suggests that the combination of logistic GEE and robust standard error correction may be the most accurate approach for analyzing fractional data in longitudinal studies. Both GEE and robust standard error estimation are available in commercial statistical packages including SPSS, SAS, and Stata.

The literature on ARV adherence offers a case example of the importance of statistical methodology and model selection. A recent meta-analysis of 18 behavioral interventions for medication adherence among HIV patients reported an odds ratio of 1.50 (P < 0.01) for achieving 95% adherence across studies [13], corresponding with a small effect size [14]. Given that effects appear to be generally small, choosing the most sensitive techniques for detecting effects may be particularly important for this area of research.

Simoni and colleagues’ [13] meta-analysis provides a window into the methods commonly used for evaluating medication adherence. Of the eighteen RCTs they reviewed, thirteen (72%) examined adherence as a continuous outcome and five (28%) used a dichotomous outcome. With respect to studies that focused on continuous adherence, eight (62%) utilized two-sample tests to evaluate group differences at follow-up, three (23%) used repeated measures analysis of variance (ANOVA), and two (15%) used GEE. Only three (38%) of the studies using two-sample methods used non-parametric tests, such as the Wilcoxon signed-ranks or Mann–Whitney U, with relaxed assumptions of normality [15-17]. The reliance on parametric two-sample tests in the medication adherence literature may be highly problematic due to alpha inflation through multiple testing and incorrect assumptions of normality. Across the 18 RCTs reviewed, eight (44%) yielded null effects at post-intervention assessment, pointing to the need for maximizing statistical sensitivity when analyzing adherence data.

The objective of the present study is to identify the most sensitive technique for characterizing treatment effects for percent adherence data. We compare three statistical approaches to assessing intervention effectiveness: (1) classical ANOVA, (2) logistic GEE with planned contrasts and (3) logistic GEE with growth curves. Illustrative data come from the Promoting Adherence for Life (PAL) project, a 2 × 2 factorial RCT that evaluated the effect of a peer and pager support on compliance to ARV medication regimens [18].

We first perform classical ANOVAs to evaluate the interventions separately at each follow-up, consistent with an approach commonly utilized in the literature. These results assume the dependent variable is normally distributed and are provided for reference. We improve upon the classical ANOVA by relaxing the assumption of normal distribution and combining the separate statistical models at each time point into a unified model using logistic GEE. We perform two sets of GEE analyses: (1) a planned contrast model where the intervention effects at each follow-up were evaluated in relation to baseline via dummy variables and (2) a growth curve model to provide a full-fledged longitudinal test of interventions. We estimate all logistic GEE models with robust standard errors as recommended when analyzing fractional data [12, 19]. Standard errors are re-estimated using bootstrap estimation to gauge the effect of an alternate standard error correction.

It was hypothesized that logistic GEE using growth curves would be more sensitive than classical ANOVA by combining information from all time points to estimate the intervention effect. We hypothesized that the GEE model with categorical contrasts would be less sensitive than the longitudinal approach since each contrast would only leverage information from two time points (i.e., half of the data) to assess the treatment effect. We conclude with a discussion of the strengths and weaknesses of each statistical technique, reporting issues associated with each model, and the implications for medication adherence intervention research.

Method

Procedures

This is a secondary analysis of data collected as part of an NIH-supported RCT conducted in an outpatient HIV clinic to evaluate the effectiveness of peer support and pager support on ARV medication adherence. The sample consisted of 224 patients recruited from the adult HIV primary care outpatient clinic at Harborview Medical Center, a public institution serving mainly indigent, ethnic minority individuals in Seattle, Washington. A full description of the peer and pager support treatments is detailed in a previous report [18].

Measures

Medication Adherence

Past three-day dose ARV adherence was assessed using a modified version of the Adult AIDS Clinical Trial Group Instrument [20]. For each medication, separate questions assessed the number of doses missed yesterday, the day before yesterday, and three days ago. Prescribed regimen was ascertained by referencing the three days prior to the assessment date with information from patient medical charts. From these data, we determined the three-day dose adherence across all ARV medications, calculated as the fraction of doses taken (doses prescribed – doses missed) over the total number of doses prescribed during the period.

Statistical Analyses

All statistical analyses were performed in the Stata 11 statistical software [21]. Exploratory analyses were conducted to examine the distribution of the adherence data, including the magnitude of skew and kurtosis and the presence of multiple modes and floor/ceiling effects. These descriptive analyses provided information on any departure from normal distribution that could have a bearing on classical ANOVA. Bivariate correlations were calculated between measurements at baseline, 3, 6, and 9 months to assess how adherence outcomes were associated across time.

All analyses excluded the interaction effect between peer and pager support. This approach maximizes the statistical power for detecting intervention effects when analyzing a factorial trial [22], but assumes that the effectiveness of each intervention does not change when combined. To verify that the peer and pager support interventions did not have an interactive effect, full factorial GEE analyses incorporating all peer support × pager support interactions were conducted using robust estimation. These preliminary GEE models were replicated using both a planned contrast and growth curve specification. Wald tests indicated that the additional interaction effects were collectively non-significant (P’s > 0.05) in both models (data not shown) so they were excluded from all analyses.

Classical Analysis of Variance

Between-subject ANOVA provides a statistical test of whether the means of two or more groups are equivalent. It is a generalization of the t test that can accommodate multiple grouping factors. In contrast to full-fledged longitudinal techniques such as GEE, the dependent variable in a between-subject ANOVA is limited to a single time point. In classical ANOVA models, the dependent variable is assumed to have a normal distribution. Each adherence outcome was analyzed with four separate two-factor ANOVA models to assess treatment effects at baseline, 3, 6, and 9 months. For these analyses, the adherence outcome at each follow-up was regressed on both peer support and pager support treatment. The treatments were evaluated by the main effects of peer support and pager support. These main effects were reported as un-standardized betas, interpreted directly as percent adherence (0.01 = 1%).

Logistic Generalized Estimating Equations

GEE [23] is a multilevel regression technique that adjusts standard errors to account for correlated data, such as the correlation of repeated measurements in a longitudinal study. A “working correlation” structure is specified a priori and defines the hypothesized relationship between repeated observations on a subject. Regression parameters in GEE are first estimated through a generalized linear regression that initially ignores whether the data are longitudinal. Next, the standard error estimates are adjusted according to the hypothesized correlation between different time points of the outcome. This adjustment updates the standard errors in the analysis to account for repeated observations within the same subject. The adherence outcome was analyzed using a logit link function, which accounted for the floor and ceiling effects at 0 and 1, respectively.

A first-order autoregressive correlation structure (AR-1) was chosen for the main GEE models. This assumption is appropriate in the context of balanced longitudinal data when measurements closer in time are more correlated than measurements further apart in time. Balanced data occurs when subjects are assessed at the same intervals, which is typical of RCTs. In a first-order autoregressive structure, the correlation of the outcome between any two points in time is a mathematical power of their distance in time. For example, adherence measurements a single time point apart would be correlated by r¹ (i.e., r raised to the power of one), adherence measurements two time points apart would be correlated by r² (i.e., r raised to the power of two), and so forth.

In planned contrast analyses, time was categorized into three contrasts of baseline versus 3, 6, and 9 months. The interventions were evaluated by the peer support × time (Month 3 vs. 0, 6 vs. 0, 9 vs. 0) and pager support × time (Month 3 vs. 0, 6 vs. 0, 9 vs. 0) interactions. Wald tests of all peer support × time and pager support × time interactions provided an omnibus test of each intervention. The interaction effects were reported as odds ratios, interpreted as the odds of perfect versus zero adherence (1 vs. 0).

A piecewise linear approach [24] was used for the growth curve analysis. This analysis allowed for unique slopes of adherence between (1) baseline and post-intervention and (2) post-intervention to 9-month follow up. This specification was the consistent with the design of the RCT, structured with a 3-month intervention phase followed by 6 months of follow-up. For each outcome, adherence at all time points was regressed on peer support, pager support, time, peer support × time, and pager support × time. Time was divided into two linear parameters, one corresponding with the entire study interval (Month 0, 3, 6, 9 = 0, 1, 2, 3) and a “deflection” term (Month 0, 3, 6, 9 = 0, 0, 1, 2) that allowed the slope after post-intervention to change. In combination, these parameters are interpreted as the slope (i.e., rate of change) from Month 0 to 3 and the increase or decrease in slope from Month 6 to 9. The interventions were evaluated by the peer support × time (Month 0–3; Month 3–9) and pager support × time (Month 0–3; Month 3–9) interactions. Wald tests of all peer support × time and pager support × time interactions provided an omnibus test of each intervention.

Empirical Standard Errors

Robust [25, 26] and bootstrapped [10] standard errors were calculated for all logistic GEE models to derive standard error estimates resistant to departures from model assumptions, including heteroskedasticity and the correlation of data from different time points. Bootstrapping is an alternate data-driven and computationally intensive simulation method that involves randomly sampling observations with replacement from the original dataset. Consequently, the sample is treated as if it were the population. The effect of sampling with replacement is that one observation may be represented more than once while another may be left out. As a result, the bootstrap dataset is equal in size to the original but not necessarily identical. Bootstrapping involves three steps: (a) creating a random sample with replacement from the original data, (b) calculating the statistic of interest using the generated data, and (c) repeating the process a minimum of 1,000 times [10]. This iterative procedure approximates the sampling distribution of a desired statistic (e.g., regression coefficient), and can be used to adjust estimates of standard error for violations of parametric assumptions, such as normal distribution or equal variance of the outcome across groups.

In the present study, all analyses were replicated with both the Huber-White correction and bootstrap simulation to calculate adjusted standard error estimates for each analysis. Bootstrapping was performed with 10,000 iterations to provide a conservative margin above the minimal number recommended by Efron and Tibshirani [10]. The P values and standard errors from the (1) unadjusted models were compared to estimates from the (2) robust and (3) bootstrapped models to assess relative sensitivity.

Results

Preliminary Analyses

Missing Data

Across the four assessment points, 67% of participants had complete data, 18% missed a single assessment, and 15% missed two or more assessments. Differences in retention were evaluated to identify potential bias in the findings due to greater drop out in certain treatment groups. Retention did not differ significantly by study condition at any assessment point, indicating that differential attrition did not occur. Collectively, these results suggest that missing data occurred randomly and did not bias the statistical evaluation of the interventions.

Although GEE can accommodate data containing missing values without dropping participants, ANOVA cannot. Therefore, to retain participants with missed assessments across all analyses, multiple imputation was performed using the multivariate normal method [27]. This method has been shown to perform well even when used to impute non-normally distributed variables [28]. All analyses were replicated across the same imputed datasets, with the final results calculated as a pooled average of the ten analyses using Rubin’s rules [29]. This insured that the sample was consistent across analyses and that differences between results were not artifacts of missing data.

Adherence Outcomes

Bivariate correlations, means, standard deviations, skew, and kurtosis statistics across assessment points for medication adherence are provided in Table 1. Average adherence over the three-day windows was 85%. An examination of the means and standard deviations indicated that medication adherence eroded over time from 91% at baseline to 82% at 9 months. The distribution for continuous adherence was multi-modal with the highest concentrations of adherence data at 0 and 100%. Kurtosis statistics for adherence were positive (i.e., leptokurtotic) and ranged from 5 to 11 across time points, reflecting a high probability of extreme values, a pattern consistent with previous investigations [30]. Adherence assessed closer in time (e.g., baseline and 3 months) was more highly correlated than when separated by one or two assessments (e.g., baseline and 9 months), indicating a decay in correlation across greater intervals.

Table 1.

Pearson correlations among month 0, 3, 6, and 9 adherence outcome with means, standard deviations, skew, and kurtosis statistics

	Month 3	Month 6	Month 9	M	SD	Skew	Kurtosis
Month 0	0.30	0.24	0.05	0.91	0.19	−2.80	11.43
Month 3		0.32	0.26	0.88	0.26	−2.38	7.95
Month 6			0.36	0.79	0.34	−1.45	3.56
Month 9				0.82	0.31	−1.76	4.87

Note: All pairwise correlations significant at P < 0.05 except for the correlation between month 0 and 9

The statistical sensitivity of classical ANOVA and logistic GEE with planned contrasts or growth curves was evaluated by comparing estimated intervention effects, standard errors, and P values from each method. The classical ANOVA models at each time point served as reference analyses. All logistic GEE models were replicated with robust standard errors and bootstrap correction to derive corrected estimates of standard error.

Sensitivity Analyses

Beta coefficients/odds ratios, standard errors and significance levels for the peer and pager support interventions estimated from classical ANOVA and logistic GEE are reported in Tables 2 and 3. The pager support intervention was not associated with statistically significant effects in any of the models and is not described in detail.

Table 2.

Effect of peer support intervention on past 3-day medication adherence

		Unadjusted
	B	SE	P
Classical ANOVA
Month 0	−0.03	0.03	0.28
Month 3	0.06	0.04	0.11
Month 6	−0.09	0.05	0.06^
Month 9	−0.03	0.05	0.51
		Unadjusted		Robust		Bootstrapped
	OR	SE	P	SE	P	SE	P
Logistic GEE (Planned contrasts)
Peer support × Month 3 versus 0	2.58	1.35	0.07^	0.99	0.01*	1.02	0.02*
Peer support × Month 6 versus 0	0.83	0.46	0.74	0.32	0.64	0.33	0.65
Peer support × Month 9 versus 0	1.17	0.69	0.79	0.51	0.72	0.53	0.73
Logistic GEE (Growth curves)
Peer support × Month 0–3	2.00	1.01	0.17	0.69	0.04*	0.71	0.05*
Peer support × Month 3–9	0.37	0.24	0.12	0.16	0.03*	0.17	0.03^

Note: B un-standardized beta, OR odds ratio, SE standard error, P P value;

^{^}P ≤ 0.10;

^*P ≤ 0.05

Table 3.

Effect of pager support intervention on past 3-day medication adherence

		Unadjusted
	B	SE	P
Classical ANOVA
Month 0	−0.03	0.03	0.27
Month 3	0.03	0.04	0.46
Month 6	−0.06	0.05	0.22
Month 9	0.02	0.05	0.64
		Unadjusted		Robust		Bootstrapped
	OR	SE	P	SE	P	SE	P
Logistic GEE (Planned contrasts)
Pager support × Month 3 versus 0	1.98	1.06	0.20	0.81	0.09^	0.83	0.10^
Pager support × Month 6 versus 0	1.01	0.56	0.99	0.39	0.99	0.40	0.99
Pager support × Month 9 versus 0	1.66	1.00	0.40	0.74	0.26	0.76	0.27
Logistic GEE (Growth curves)
Pager support × Month 0–3	1.64	0.84	0.34	0.59	0.18	0.61	0.19
Pager support × Month 3–9	0.59	0.38	0.42	0.27	0.26	0.28	0.27

Note: B un-standardized beta, OR odds ratio, SE standard error, P P value;

^{^}P ≤ 0.10

Classical ANOVA

In the classical ANOVA model, baseline medication adherence did not differ significantly between the peer support and standard of care groups (Beta = −0.03, 95% CI −0.08–0.02, P = 0.28). Peer support was not associated with any cross-sectional difference in medication adherence at 3 months (Beta = 0.06, 95% CI −0.01–0.13, P = 0.1) or 9 months (Beta = −0.03, 95% CI −0.13–0.06, P = 0.51). At 6 months, peer support was associated with marginally lower adherence (Beta = 0.06, 95% CI −0.08–0.02, P = 0.28). Across time-points, the cross-sectional intervention effect estimated by ANOVA varied between −0.09 and 0.06, with standard errors comparable in size to the beta coefficients, suggesting that peer support when analyzed in this fashion had a net effect of zero on medication adherence.

Logistic GEE

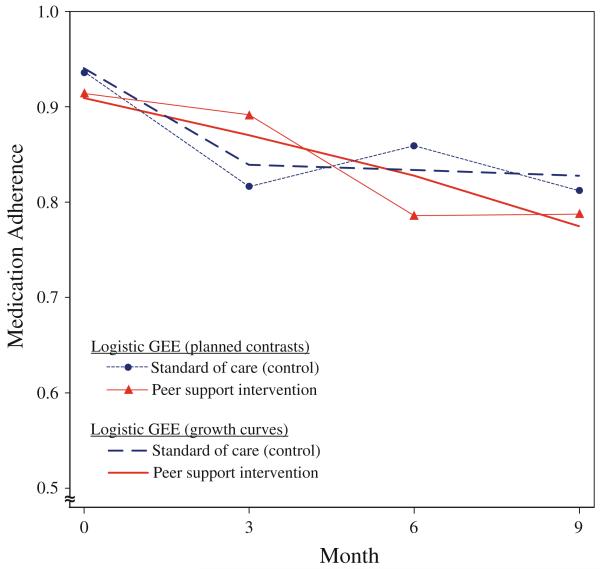
To facilitate interpretation, model-estimated medication adherence for the peer support and standard of care groups is plotted in Fig. 1 for the contrast and growth curve models. In the contrast models, adherence in the standard of care group dropped from 0.94 at baseline to 0.81 at 3 months, rebounded to 0.86 at 6 months, and dropped again to 0.81 at 9 months. For peer support, adherence from baseline to 3 months was stable at 0.91 and 0.89, respectively, and dropped to 0.78 at 6 and 9 months.

Fig. 1.

Predicted medication adherence for peer support intervention and standard of care by logistic GEE model

In the unadjusted logistic GEE model with contrasts, the omnibus peer support × time effect indicated a marginally significant association between peer support and change in adherence over time, F(3,1000) = 2.48, P = 0.06. Peer support was associated with a marginally smaller drop in adherence (OR 2.58, 95% CI 0.92–7.23, P = 0.07) from baseline to 3 months. Peer support was not associated with any difference in medication adherence at 6 months (OR 0.83, 95% CI 0.28–2.47, P = 0.74), or 9 months (OR 1.17, 95% CI 0.37–3.74, P = 0.79) compared with baseline. In the robust model, the omnibus peer support × time effect indicated a statistically significant association between peersupport and change in adherence over time, F(3,1000) = 3.70, P = 0.01. The smaller drop in medication adherence associated with peer support at 3 months compared with baseline reached statistical significance (P = 0.01). Robust standard error adjustment was associated with smaller standard errors across all other points.

In the logistic GEE models with growth curves, adherence in the standard of care group dropped from 0.94 at baseline to 0.84 at 3 months and remained stable at 0.83 at 6 and 9 months. For peer support, adherence dropped from 0.91 to 0.87 at 3 months and continued dropping to 0.83 at 6 months and 0.77 at 9 months. In the unadjusted models, the omnibus peer support × time effect was non-significant, F(2,1000) = 1.24, P = 0.29. The erosion rate of adherence was not significantly different between standard of care and peer support from baseline to 3 months (OR 2.00, 95% CI 0.74–5.39, P = 0.17) or from 3 to 9 months (OR 0.37, 95% CI 0.11–1.30, P = 0.12). In the robust model, the omnibus peer support × time effect indicated a marginally-significant association between peer support and change in adherence over time, F(2,878.5) = 2.62, P = 0.07. The erosion rate of medication adherence from baseline to 3 months was significantly lower in the peer support group (P = 0.04). Additionally, the robust model indicated that while adherence stabilized after 3 months in the standard of care group, it continued to erode in the peer support group, a difference that was statistically significant (P = 0.03).

Across all models, bootstrapped estimates were close or identical to the robust estimates. Robust and bootstrap standard error adjustment resulted in comparable estimates of standard error and statistical significance for both the peer and pager support interventions.

Discussion

This study compared three statistical approaches to assessing interventions for improving adherence to ARV medication: (1) classical ANOVA, (2) logistic GEE with planned contrasts, and (3) logistic GEE with growth curves. The objective was to identify the most sensitive method for detecting intervention effects when evaluating adherence as a percentage of doses taken. One aspect of statistical methodology included the broad selection of statistical model (e.g., ANOVA vs. GEE) and whether medication adherence was modeled appropriately as a fractional outcome in a logistic analysis. A second aspect was the manner in which the chosen model was parameterized, such as a GEE analysis with planned contrasts or growth curves. The strength of our comparison was the use of real data, which demonstrated how differences in statistical methodology can lead to markedly different conclusions regarding intervention effectiveness. Although there was consensus among the two logistic GEE approaches with respect to adherence, inference regarding the long-term effect of peer support diverged across statistical methods.

In the classical ANOVA models, the cross-sectional effect of peer support fluctuated between −9 and +6% with a single difference reaching only marginal significance, a pattern suggestive of a null intervention effect. If inference were based solely on a classical ANOVA model, the conclusion would be that the peer and pager support interventions did not change adherence.

We improved upon the classical ANOVA by analyzing medication adherence as a fractional outcome in a unified logistic GEE analysis using planned contrasts, an approach analogous to repeated measures ANOVA. In these analyses, baseline levels of the outcome were incorporated into the dependent variable and robust estimation was utilized. In the logistic GEE analysis with planned contrasts, the overall effect of peer support, but not pager support, was statistically significant. Specifically, peer support was associated with a smaller drop in adherence from baseline to 3 months compared with standard of care (−2 vs. −12%). However, the non-significant results at 6 and 9 months indicated that the short-term benefits at post-intervention were not maintained at follow-up.

Finally, we performed a full-fledged longitudinal analysis in logistic GEE analysis using growth curves. These models leveraged data from all time points to estimate the intervention effects. We incorporated flexibility into this longitudinal analysis by allowing the effect of peer and pager support to change after the intervention was completed. In the logistic growth curve analysis, peer support was associated with a smaller drop in adherence from baseline to 3 months compared with standard of care (−4 vs. −10%). However, this pattern reversed during the follow-up period such that adherence in the peer support group continued dropping, but stabilized in the standard of care group (−10 vs. −1%), a difference that was statistically significant.

In contrasting classical ANOVA with logistic GEE using planned contrasts or growth curves it is important to recognize that each model evaluated intervention effectiveness in a different way. In the classical ANOVA, a positive intervention effect was defined as higher adherence than standard of care at each time point. By this definition, the classical ANOVA approach found no evidence cross-sectionally that either the peer or pager support interventions were effective.

The most illustrative findings comes from the respective logistic GEE analyses. In both the planned contrasts and growth curve models, intervention effectiveness was defined as slower erosion in adherence than standard of care. In the planned contrast model, change in adherence was examined in a piecemeal manner by comparing each time point with baseline. Although this definition of adherence had lower statistical power, the estimated adherence at each time point exactly reflected the data. In the growth curve model, change in adherence was examined across the entire 9-month study period, an approach with higher statistical power that averaged across multiple time points.

Our comparison demonstrated that the type of longitudinal model can have a dramatic effect on inference, with the results from GEE using planned contrasts versus growth curves having different interpretations. The superimposed plot of the two models revealed that the growth curve analysis was less representative of adherence at follow-up. The protective effect of peer support, up until 3 months, was supported in both logistic GEE models. However, the growth curve model implies that once peer support was removed, adherence among those who previously received the intervention degraded while those receiving the standard of care were stable. In comparison, the contrast model indicates that adherence stabilized in the peer support group with no such iatrogenic effect after the intervention was completed. The logistic GEE model with growth curves illustrated that a well-intentioned, a priori longitudinal analysis can average over data in unexpected ways, potentially leading to mistaken conclusions.

Collectively, logistic GEE with planned contrasts and growth curves identified intervention effects that were missed by a classical ANOVA approach. Specifically, these models converged upon a post-intervention effect of peer support that was not detected by the ANOVA. Although logistic GEE with growth curves did not accurately predict adherence after post-intervention, this shortcoming was not a general problem with logistic GEE, but rather a specific problem with assuming linear change in adherence over time. The discrepancy between the growth curve model and the pattern of adherence over time highlights the importance of careful model-checking [5] to verify that the assumed shape of a growth curve fits the data. Our results indicated that the combination of logistic GEE with robust standard error adjustment was the most sensitive approach for evaluating medication adherence. There is an extensive quantitative literature dating back decades supporting the validity of robust standard error adjustment [9]. Furthermore, the convergence of the bootstrapped analyses with the robust analyses increases confidence regarding the validity of the results.

In principle, a fully longitudinal approach like the growth curve model used in the present study would be the preferred analysis for several reasons. First, statistical power is maximized because data across all time points are leveraged in the estimation of intervention effectiveness. Although some statistical sensitivity is “lost” by testing the intervention in a single way rather than multiple ways, this is offset by the gain in sensitivity by consolidating all of the data into a single more powerful test. Second, because the intervention effect is not subdivided, the risk of chance findings from numerous statistical comparisons is reduced. However, since the assumptions of a particular longitudinal model can influence the substantive findings, the predictions made by the statistical model should always be compared against the data to ensure validity of the analysis. If necessary, alternative models can be presented to inform interpretation. For example, had logistic GEE with growth curves been chosen as the a priori analysis, a post hoc statistical analysis using GEE with categorical contrasts could temper interpretation regarding the long-term effect of peer support following the intervention.

Theoretically and practically, GEE is an attractive option for evaluating adherence data. On a theoretical level, longitudinal regression maximizes statistical power by adjusting standard errors and P values for correlated outcomes, while the addition of robust estimation accounts for characteristics of fractional data that lead to inefficient estimates of standard error. On a practical level, logistic GEE does not require specialized software and is available in major menu-based commercial statistical packages including SPSS, SAS, and Stata, making it accessible to non-statisticians. The basic code for running logistic GEE in these three statistical packages is provided as an Electronic supplement to this article. This syntax illustrates logistic GEE with both the planned contrast and piecewise growth curve specifications.

It is important to consider the limitations of this study when interpreting the findings. First, because the statistical models defined the intervention effect differently, the standard errors were not directly comparable between models. Therefore, our sensitivity analysis placed emphasis on P values for assessing statistical sensitivity. Although the reliance on P values and null hypothesis testing for inference is frequently criticized [31], it was utilized as a tool for comparison since it is the convention in both the psychological and biomedical literature. Second, we focused on only some of the possible longitudinal models for analyzing medication adherence as a percent variable. All of the GEE models could be estimated using a GLMM approach using random effects [24], also known as hierarchical generalized linear modeling. In principle, the results from GLMM should be similar if not identical if modeled with the same specifications as a comparable GEE model. Differences in results would be due to the mathematical underpinnings of the statistical models and vagaries of estimation. However, follow-up research to examine the use of GLMM in the context of fractional adherence outcomes would be useful since the literature to date has focused on GEE.

Despite these limitations, it is possible to make some specific recommendations. We showed that the choice of statistical method could mean the difference between evaluating an intervention as effective, ineffective, or even iatrogenic. Given the urgent need to identify effective interventions in areas such as medication adherence, it is crucial that researchers take advantage of not only the most sensitive methodology available, but also the most accurate. Logistic GEE in tandem with robust standard error estimates can maximize statistical power when assessing medication adherence as a percentage outcome. However, statistical results depend as much on the way the model is used as the model itself. Predictions made by all a priori statistical models should be carefully checked against both the data and alternative statistical models to insure that conclusions are not idiosyncratic to a single model with a particular set of statistical assumptions.