Mechanisms of Coordination in Distributed Neural Circuits: Decoding and Integration of Coordinating Information

Abstract

We describe the synaptic connections through which information required to coordinate limb movements reaches the modular microcircuits that control individual limbs on different abdominal segments of the crayfish, Pacifastacus leniusculus. In each segmental ganglion, a local commissural interneuron, ComInt 1, integrates information about other limbs and transmits it to one microcircuit. Five types of nonspiking local interneurons are components of each microcircuit's pattern-generating kernel (Smarandache-Wellmann et al., 2013). We demonstrate here, using paired microelectrode recordings, that the pathway through which information reaches this kernel is an electrical synapse between ComInt 1 and one of these five types, an IRSh interneuron. Using single-electrode voltage clamp, we show that brief changes of ComInt 1's membrane potential affect the timing of its microcircuit's motor output. Changing ComInt 1's membrane potential also changes the phase, duration, and strengths of bursts of spikes in its microcircuit's motor neurons and corresponding changes in its efferent coordinating neurons that project to other ganglia. These effects on coordinating neurons cause changes in the phases of motor output from other microcircuits in those distant ganglia. ComInt 1s function as hub neurons in the intersegmental circuit that synchronizes distributed microcircuits. The synapse between each ComInt 1 and its microcircuit's IRSh neuron completes a five synapse pathway in which analog information is encoded as a digital signal by efference-copy neurons and decoded from digital to analog form by ComInt 1. The synaptic organization of this pathway provides a cellular explanation of this nervous system's key dynamic properties.

Introduction

Mechanistic explanations of natural behaviors begin with concrete knowledge of the nervous system's component neurons and their synaptic organization. With this foundation, we can address questions about the system's dynamics and its modulation in different contexts (Callaway and Marder, 2012). Coordinated movements of different limbs that enable effective locomotion in arthropods and terrestrial vertebrates are driven by distributed microcircuits that control individual limbs or joints. These distributed microcircuits are synchronized by coordinating circuits that entrain them so that their activity is coherent. In tetrapods and insects, pathways that organize locomotion have been well described at the systems level (Stein, 2008; Berkowitz, 2010; Büschges et al., 2011; Daun-Gruhn and Tóth, 2011; Büschges, 2012; Bicanski et al., 2013), but the details of their cellular and synaptic organization are still incompletely known or understood.

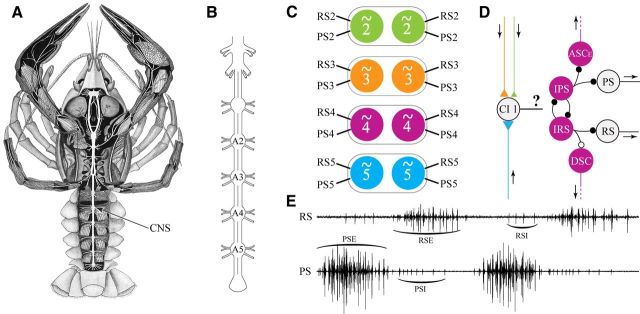
During forward swimming, many decapod crustaceans generate thrust by periodic beating of four or five pairs of limbs called swimmerets on different abdominal segments. The neural circuits that control these movements occur as pairs, one microcircuit per limb (see Fig. 1C), distributed bilaterally in different segmental ganglia of the CNS (see Fig. 1A,B). Each microcircuit includes the sensory and motor neurons that innervate one swimmeret, two coordinating neurons (Smarandache et al., 2009), a set of nonspiking interneurons that form the kernel of each microcircuit's pattern generator (see Fig. 1D,E), and a bilateral local commissural interneuron, ComInt 1 (Mulloney and Hall, 2003), which is a hub neuron synchronizing the microcircuit's output (Gutierrez et al., 2013).

Figure 1.

Organization of the neural circuits that control crayfish swimmerets. A, The crayfish CNS exposed from the dorsal side of the animal (after Keim, 1915). B, Diagram of the CNS, depicting the posterior ventral nerve cord (thoracic ganglia T4 and T5, and abdominal ganglia A1–A6). Labels indicate the four ganglia that innervate swimmerets (A2, A3, A4, and A5). C, Each of these four ganglia contains a pair of bilaterally symmetrical neural microcircuits (∼2, ∼3, ∼4, and ∼5) that innervate the pair of swimmerets on that segment of the abdomen. Anterior and posterior branches of the nerve to each swimmeret contain the axons of PS and RS motor neurons that innervate swimmeret muscles. The different colors will be used in later figures to identify the segment in which a neuron originated or from which spikes were recorded. D, Diagram of the pattern-generating circuit within each microcircuit that produces alternating bursts of impulses in PS and RS branches of the N1 that projects from the microcircuit to one swimmeret. Large circles represent an identified neuron or group of functionally similar neurons. Small black circles represent inhibitory chemical synapses. Colored triangles represent excitatory chemical synapses; larger triangles represent stronger synapses. Arrows indicate the direction of orthodromic impulse propagation. The question mark (?) labels the connection from ComInt 1 (CI 1) to the local circuit that is the focus of this paper. E, Two cycles of motor output recorded from PS and RS branches of the nerve to one swimmeret. Brackets label four bursts of impulses in different sets of motor axons: PSEs, RSEs, PSIs, and RSIs.

Although periods of their movements can change 10-fold, beating swimmerets maintain a stable phase difference because their microcircuits are linked by an intersegmental coordinating circuit that adjusts the timing and strength of each microcircuit's output and so maintains the posterior-to-anterior metachronal progression needed for effective thrust (Zhang et al., unpublished observation). We have identified intersegmental coordinating neurons that originate in each microcircuit (see Fig. 1D) (Namba and Mulloney, 1999; Smarandache et al., 2009) and learned what information these neurons encode (Mulloney et al., 2006). In this paper, we describe how this coordinating information is decoded and integrated into the ongoing activity of the microcircuit that controls each limb.

Axons of these coordinating neurons synapse in other segmental ganglia onto commissural interneurons called ComInt 1 (Mulloney and Hall, 2007a). ComInt 1s decode the information transmitted to them and use it to affect the timing and strength of their own microcircuit's motor output (Smarandache et al., 2009). To discover how ComInt 1 does so, we used paired microelectrode recordings to test for direct synaptic connections between ComInt 1 and different interneurons in the microcircuit's pattern-generating kernel. We found an electrical synapse between ComInt 1 and just one type of these pattern-generating neurons (Smarandache-Wellmann et al., 2013). We used single-electrode voltage clamp to describe how the membrane potential of an individual ComInt 1 affects the output from its own microcircuit and the phases of output from microcircuits in other segments. Finally, we use this description to explain these local and distant effects of ComInt 1 on the system's motor output.

Materials and Methods

Crayfish, Pacifastacus leniusculus, of both sexes were anesthetized by chilling on ice and then exsanguinated by transfusion with cold saline. The last two thoracic ganglia and the entire abdominal nerve cord, parts of the CNS (see Fig. 1A,B), were removed to a dish lined with transparent Sylgard (Dow-Corning) and pinned out linearly dorsal-side up with stainless steel pins. To permit insertion of microelectrodes, the sheath was removed from the dorsal side of each ganglion using iridectomy scissors.

Normal saline contained 5.4 mm KCl, 2.6 mm MgCl₂, 13.5 mm CaCl₂, and 195 mm NaCl and was buffered with 10 mm Tris base and 4.7 mm maleic acid at pH 7.4. If a preparation was not spontaneously active, stable expression of the swimmeret motor pattern was elicited by bath application of carbachol (RBI, Sigma; 1.5–3 μmin different preparations) dissolved in normal saline (Mulloney, 1997).

Electrophysiological recordings.

In addition to motor, sensory, and coordinating neurons, each microcircuit includes unilateral nonspiking interneurons, IPS and IRS (Fig. 1D) (Smarandache-Wellmann et al., 2013), and a bilateral local commissural interneuron, ComInt 1 (Mulloney and Hall, 2003). There are four functional groups of motor neurons: ∼35 power-stroke excitors (PSEs), ∼35 return-stroke excitors (RSEs), two power-stroke inhibitors (PSIs), and three return-stroke inhibitors (RSIs) (Mulloney and Hall, 1990, 2000). Axons of these motor neurons project to the limb through one nerve, N1, that in this species promptly divides into a posterior power-stroke branch (PS) that contains PSE and PSI axons and an anterior return-stroke branch (RS) that contains RSE and RSI axons (Fig. 1E). To record spikes from PS and RS branches of each ganglion's N1, we placed stainless-steel pin-electrodes in contact with the appropriate branches of N1 and insulated each electrode from the bathing saline with a small amount of Vaseline petroleum jelly.

The coordinating neurons that originate in each microcircuit, ascending coordinating neuron (ASC_E) and descending coordinating neuron (DSC) (Namba and Mulloney, 1999; Smarandache et al., 2009), encode detailed information about each cycle of motor output as efference copies and conduct it to targets in other ganglia. ASC_E and DSC neurons project their axons from the ganglion's lateral neuropils (LNs) dorsally through the minuscule tract (MnT) toward the midline before entering the interganglionic connectives (Namba and Mulloney, 1999; Mulloney and Hall, 2003). Action potentials in these axons were recorded extracellularly with a suction electrode placed on the MnT as it crossed dorsal to the lateral giant axon. Because of the details of the anatomy of these coordinating neurons and the swimmeret system, spikes recorded with suction electrodes positioned carefully on an MnT could confidently be attributed to individual coordinating axons originating in the swimmeret microcircuit just below it (Smarandache et al., 2009).

Extracellular recordings were amplified and filtered using A-M Systems Model 1700 amplifiers. Signals from both extracellular and intracellular recordings were digitized using a Digidata 1322A or 1440A digitizer and pClamp software (Molecular Devices) and recorded as computer files for later analysis.

Intracellular recordings.

In abdominal ganglia A2-A5 (Fig. 1B,C), there is an anatomically localized microcircuit of neurons within each LN whose function is to drive one swimmeret's alternating power-stroke and return-stroke movements (Mulloney and Smarandache-Wellmann, 2012). The IPS and IRS interneurons form a local pattern-generating circuit (Fig. 1D) that organizes the microcircuit's motor output (Fig. 1E) (Smarandache-Wellmann et al., 2013). Through an unknown pathway, the ComInt 1 neuron integrates and transmits coordinating information to this pattern-generating circuit (Fig. 1D). To discover how ComInt 1 is connected to other neurons in its own microcircuit, we made paired microelectrode recordings from processes of identified neurons within the same LN.

This paper reports results from 183 paired microelectrode experiments. Individual neurons were penetrated with a sharp microelectrode in one of a ganglion's LNs (Skinner, 1985; Mulloney et al., 2003) and tentatively identified by physiological criteria. These identifications were later tested by filling each neuron and observing its anatomy. Only results from experiments where anatomy confirmed the physiological identification have been included in this paper.

Microelectrode recordings were made using npi SEC 05 amplifiers (npi electronic). Neurons were voltage-clamped using the npi amplifier's discontinuous single-electrode voltage-clamp mode (dSEVC). Current injections were made using the discontinuous current-clamp mode. During paired discontinuous current-clamp mode or dSEVC recordings, the switching-clocks of the two amplifiers were synchronized to minimize crosstalk, and a grounded metal shield was inserted between the two electrodes to further reduce artifactual noise. The settling of the electrode voltage between each current pulse was monitored continuously on a dedicated oscilloscope. To permit high sampling rates, these microelectrodes were coated with Sylgard 186, and the level of the perfusion solution above the ganglion was kept low. We usually attained switching frequencies >25 kHz.

Microelectrodes contained either 1% Dextran Texas Red (dTR; Dextran Texas Red MW 3000 fixable; Invitrogen) or 5% Neurobiotin (NB; Vector Labs) dissolved in a solution of 1 m K acetate + 0.1 m KCl, and had tip resistances of 30–50 megohms. During the experiment, each neuron was filled by injecting either dTR or NB using +1 nA current pulses, 250-ms-long at 2 Hz. At the end of the experiment, the preparation was fixed overnight in 4% paraformaldehyde in PBS. Preparations that contained only a dTR-filled neuron were then rinsed with PBS four times for 10 min each, pinned out dorsal-side up, and cleared in an ascending ethanol series to methyl salicylate.

Preparations that contained an NB-filled neuron were first washed 3 times for 10 min in 0.1 m glycine after fixation, then dehydrated and rehydrated in an ascending and descending ethanol series (25%, 50%, 70%, 80%, 95%, and 100%). This was followed by six 30 min washes in 0.3% Triton X-100 in PBS and an overnight incubation in streptavidin conjugated to Alexa Fluor 488 (Invitrogen) in 0.3% Triton X-100 in PBS in the dark on a rotator at 2–4°C. The tissue was rinsed with PBS four times for 15 min each and sent through the ascending ethanol series to methyl salicylate.

Imaging.

Cleared whole mounts were mounted in methyl salicylate in a Permanox dish with a coverslip base. A small, thick section of glass was placed on top of the nerve cord to prevent movement during imaging. The filled neuron's structure was examined in the cleared whole mount under an Olympus FLUOVIEW confocal microscope (Olympus America) equipped with krypton (488 nm) and argon (568 nm) lasers using an Olympus 20× 0.7 NA UPlanApo lens. Step size was 0.75 μm. Images were adjusted in Fluoview software and converted to 24-bit TIF images, then exported to Adobe Photoshop for further adjustment of brightness, contrast, and sharpness.

Imaging of the dye-coupled whole mounts.

These preparations were dehydrated, cleared, and imaged as described above (see Fig. 4). However, the field of view of the Olympus 20× 0.7 NA UPlanApo lens was not sufficient to encompass the entire ganglion. To remedy this, four overlapping images were taken of the four quadrants of the ganglion. The image stacks were then opened in Fluoview, where a full flattened image of each quadrant was created, as well as several smaller, flattened sections depicting various planes of the image stack. All the resulting images were converted to 24-bit TIF images and exported to Photoshop. Once in Photoshop, the full flattened image was used as the base image, and the extraction tool was used on the smaller sections to compensate for the summated background. The images of the four quadrants were then adjusted individually to the same degree of brightness, contrast, and sharpness, and placed into a new file where they were aligned precisely and merged into a single image of the whole ganglion. Overlapping portions of the image were not summated; rather, the best image quadrant was selected as the foremost layer, and the other three images filled out the remaining quadrants of the ganglion. Sharp lines that delineated the edge of each quadrant's image were erased before merging the images.

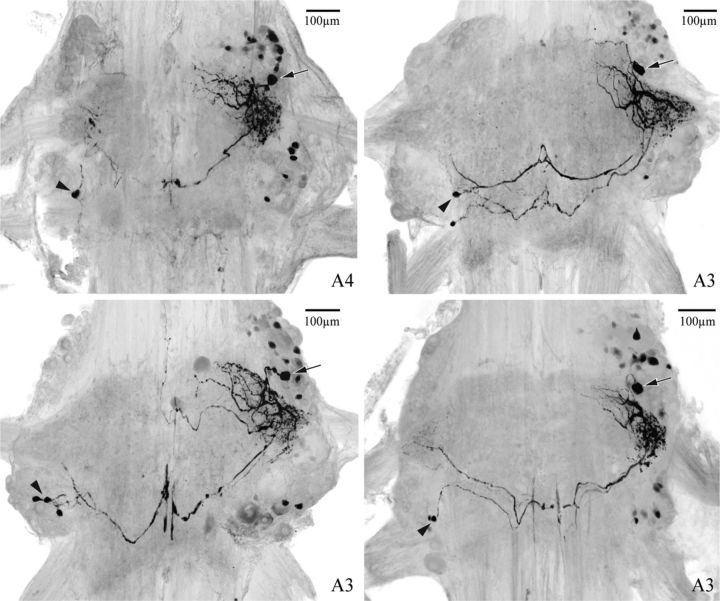
Figure 4.

Neurobiotin fills of four different IRSh neurons in abdominal ganglia A3 or A4 visualized with streptavidin Alexa Fluor 488, viewed as whole mounts from the dorsal side with anterior at the top. In each whole mount, in addition to the IRSh neuron into which NB had been injected, the ComInt 1 neuron that projected to the same LN is also visible. Arrows indicate the soma of IRSh neurons; arrowheads indicate the somas of ComInt 1 neurons. In each ganglion, the cell bodies of a few other neurons weakly dye-coupled to IRSh are also visible.

Measuring strengths of bursts of spikes.

In different cycles of motor output, the strengths of bursts of spikes in PS and RS motor neurons (the numbers of motor neurons recruited and the numbers of spikes each neuron fired) can vary. To quantify these changes, we squared each measured voltage to rectify the extracellular recording, then smoothed it using an FFT with a triangular kernel, and restored the smoothed recording using an inverse FFT. By plotting this smoothed recording and defining a threshold above the noise, we isolated each burst, calculated its area, and saved the list of areas and times at which each burst began. The area associated with a burst increased as the numbers and sizes of spikes within it increased (Mulloney, 2005).

Measuring parameters of the motor patterns.

The start and stop times of bursts of spikes in extracellular recordings were measured using Dataview (http://www.st-andrews.ac.uk/∼wjh/) and used to describe the structure of the periodic motor pattern. The period of each cycle was the interval from the start of one PS burst to the start of the next PS burst. The latency of an event occurring during a cycle was measured as the time interval between the start of the event and the start of the preceding PS burst that marked the start of the cycle. The phases of these events were then defined as the ratio of these latencies to that cycle's period. Therefore, phase could range from 0 to 1.0.

Generating phase-response curves (PRCs).

To describe changes in cycle periods caused by voltage-pulses applied at different phases in the cycle, we measured the periods of the four cycles that immediately preceded the start of the pulse and the period of the cycle in which the pulse occurred. For voltage-step i in cycle j, the mean of these four preceding periods, X̄_ij, made a good predictor of the expected period after the start of the stimulus. For each stimulus, we calculated the normalized period difference, Dif_ij, between each experimental period, X_ij, and the mean period just preceding it, X̄_ij, as Dif_ij = (X_ij − X̄_ij)/X̄_ij. This definition of Dif_ij, is common among biologists and consistent with our prior work but opposite in sign to that common in mathematics (Canavier, 2006; Izhikevich, 2007). The phase of each stimulus was calculated as the time from the start of that cycle to the start of the voltage step, divided by the cycle period, X_ij, Plotting these Dif_ij, as functions of the phase of the stimulus gives the PRC (Netoff et al., 2012).

We fitted a “locally weighted estimate” curve to each PRC using the “robust loess” function in MATLAB (MathWorks). This function takes into account that phase values were irregularly spaced. To avoid errors in the calculation of these curves near their ends, we took advantage of the periodic property of the motor pattern (Fig. 1E) by extending the range of the data from 1.0 to 1.25 by copying the points from 0.0 to 0.25, and from −0.75 to 0.0 with points from 0.75 to 1.0. Then we fitted over the range −0.75 to 1.25, and plotted the fitted curve between 0 and 1.0.

Statistical analysis.

To test the probability that a parameter measured under different conditions during an individual experiment did not change, we calculated single-factor ANOVA (Zar, 1996) using the routines in SigmaPlot 11.2 (SysStat). To test the probability that a parameter measured under different conditions did not change in a group of similar experiments, we calculated repeated-measures (RM) ANOVA (Zar, 1996) using SigmaPlot. The results of these statistical tests are reported as probabilities (p), sample sizes (n), F statistic, and power (α = 0.05). Probabilities <0.05 that different samples came from the same population were taken to be evidence that the samples were different. When an ANOVA found probable differences, we used either Holm–Sidak tests or Dunnett's test to identify those pairs of measurements that probably were different. To assess the degree to which two variables changed together, Pearson correlation coefficients were calculated using the routines in SigmaPlot.

Results

When the CNS expresses the normal swimmeret motor pattern, each swimmeret microcircuit generates periodic bursts of spikes in its different motor neurons (Fig. 1E). Two coordinating neurons in each microcircuit, ASC_E and DSC, encode detailed information about this motor output as efference copies (Namba and Mulloney, 1999; Mulloney and Smarandache-Wellmann, 2012). Each ASC_E neuron encodes information about PSE bursts (Mulloney et al., 2006) and conducts this information to targets in more anterior ganglia. Each DSC neuron encodes information about RSE bursts and conducts it to targets in more posterior ganglia (Tschuluun et al., 2001; Smarandache et al., 2009). The information that ASC_E and DSC neurons encode is necessary and sufficient to coordinate the output of microcircuits in different ganglia (Namba and Mulloney, 1999; Tschuluun et al., 2001).

In their target ganglia, ASC_E and DSC axons synapse near the midline onto ComInt 1, a nonspiking commissural interneuron (Figs. 1D and 2Ai). Each ComInt 1 integrates postsynaptic potentials (PSPs) from each passing ASC_E and DSC axon and transmits the result to the microcircuit in one of the ganglion's LNs (Smarandache et al., 2009).

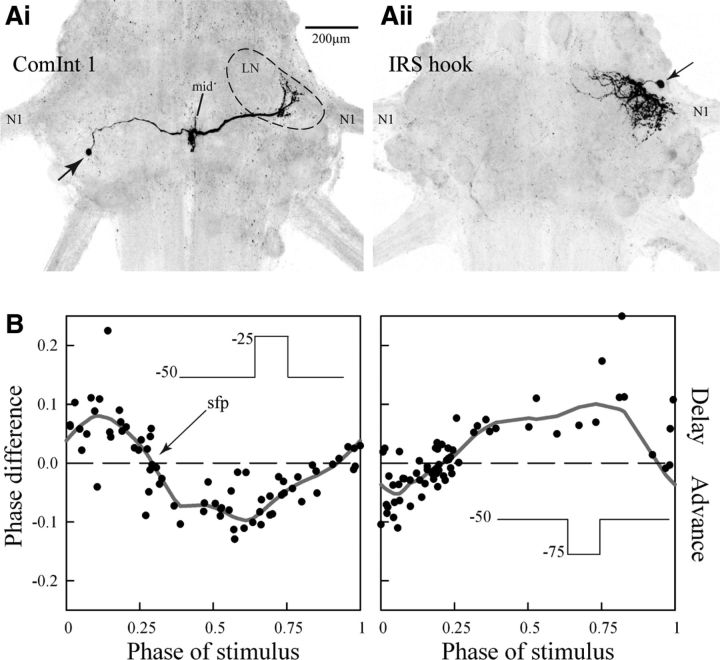
Figure 2.

A, Whole-mount preparations of two abdominal ganglia, seen from the dorsal side. The left ganglion (Ai) contains a ComInt 1 neuron filled with a fluorescent marker. The neuron's cell body is at the left (arrow), its branches that receive synaptic connections from ASC_E and DSC axons lie at the midline (mid), and its output synapses with the local pattern-generating neurons lie in the right LN (dashed outline), near the base of the nerve (N1) that innervates the right swimmeret. In each ganglion, ComInt 1s occur as a bilaterally symmetrical pair. The right ganglion (Aii) contains an IRSh filled with a fluorescent marker. This neuron's cell body (arrow) lies laterally in the ganglion, anterior to the base of N1. Its processes are restricted to the anterior regions of the right LN. B, Phase response curves that show how timing of the motor output from one microcircuit changed when depolarizing (left) or hyperpolarizing (right) steps were imposed on a voltage-clamped ComInt 1 neuron at different points in the periodic cycle of motor output (compare Fig. 1E). Voltage steps are 250 ms long. Sfp, Stable fixed point. The dotted horizontal lines indicate no difference in the output.

The membrane potential of a ComInt 1 affects the timing of PS bursts

Depolarizing a ComInt 1 neuron excites PSE and RSI units but inhibits RSE and PSI units in the microcircuit to which the ComInt 1 projects (Mulloney and Hall, 2003). Hyperpolarizing the same neuron has reciprocal effects; PSE and RSI units are inhibited, but RSE and PSI units are excited (Mulloney and Hall, 2003). These effects are graded with the strength of the injected currents.

PRCs show that transient changes in a ComInt 1 neuron's membrane potential imposed by single-electrode voltage-clamp (dSEVC) at the midline, near the neuron's synaptic inputs, affect the timing of its microcircuit's periodic output (Fig. 2B, left). Depolarizations (25 mV steps from −50 mV, 250 ms long) starting early in a cycle, when PSE neurons were firing, delayed the next PSE burst, but the same stimuli arriving later in the cycle advanced the next PSE burst. Stimuli of opposite sign (−25 mV from −50 mV) had opposite effects on the microcircuit's output (Fig. 2B, right); hyperpolarizations early in the cycle advanced the next burst of PSE spikes, whereas the same stimuli arriving later in the cycle delayed the next PSE burst. These results demonstrate that dSEVC can control ComInt 1's membrane potential at its output connections with neurons in the microcircuit's local pattern-generating circuit. The phase dependence of these effects is strong evidence that periodic depolarizations of ComInt 1 by the bursts of excitatory PSPs caused by bursts of spikes in ASC_E and DSC axons (Smarandache et al., 2009) can entrain and synchronize the activity of swimmeret microcircuits in different segments (Schwemmer and Lewis, 2012; Zhang and Lewis, 2013). The zero-crossing with the negative slope marked by the arrow in Figure 2B is a stable fixed point because stimuli arriving at phases earlier in the cycle delay the next PS burst, whereas stimuli arriving at later phases advance the next PS burst. This fixed point falls near a phase of 0.25, the normal phase difference between swimmerets on neighboring segments (Mulloney and Smarandache-Wellmann, 2012).

ComInt 1s synapse with IRS neurons through an electrical synapse

The local pattern-generating circuit that organizes the periodic firing of PS and RS motor neurons (Fig. 1D) includes two classes of identified nonspiking local neurons: IPS neurons and IRS neurons (Smarandache-Wellmann et al., 2013). Bursts of spikes in PSE and RSE motor neurons are driven by periodic synaptic inhibition by IPS or IRS neurons (Mulloney, 2003). When the system is active, the membrane potentials of these inhibitory interneurons oscillate periodically (Smarandache-Wellmann et al., 2013), which affects their graded release of transmitter at synapses onto motor neurons. The timing of these oscillations of potential in different microcircuits is synchronized to the same period by the information transmitted through ComInt 1 neurons (Smarandache et al., 2009), but the synaptic connections through which this synchronization is achieved are unknown. To learn how coordinating information reaches the local pattern-generating circuit, we made paired intracellular microelectrode recordings from ComInt 1s and other neurons in the microcircuit to which the ComInt 1 projected. We tested each pair of neurons for evidence of a synaptic connection by injecting current pulses into one neuron while recording changes in membrane potential in the other.

In each of three experiments where we recorded simultaneously from a ComInt 1 and an IRS neuron, we saw clear evidence of a synaptic connection. These three IRS neurons belonged to the “IRS hook” type, IRSh (Fig. 3Ai), which are distinguished from other IRS neurons by their distinctive shapes (Smarandache-Wellmann et al., 2013). Both depolarizing and hyperpolarizing currents injected into the ComInt 1 caused changes in the IRSh membrane potential (Fig. 3Aii). These postsynaptic changes were seemingly attenuated versions of the potential changes in the presynaptic ComInt 1, which suggests the synapse includes an electrical component. The same currents injected into the IRSh neuron also caused changes in the membrane potential of ComInt 1 (Fig. 3Aiii), consistent with an electrical synapse between these neurons. The coupling coefficients (ratios of postsynaptic to presynaptic voltage changes) were similar in both directions: 0.030 ± 0.023 and 0.022 ± 0.014 (mean ± SD, n = 3).

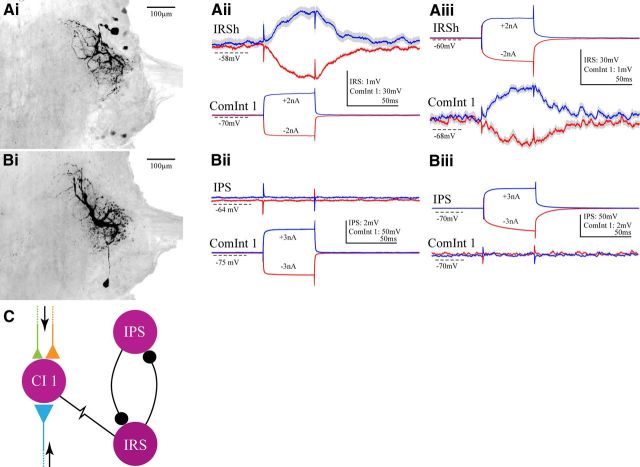
Figure 3.

The ComInt 1 neuron that projects to each LN synapses only with an IRSh neuron in the pattern-generating circuit (Fig. 1D), not with an IPS neuron. Ai, A whole mount, viewed from the dorsal side, showing one IRSh neuron filled with a fluorescent marker. Aii, Simultaneous intracellular recordings from a ComInt 1 neuron and an IRSh neuron in the same microcircuit made while the system was inactive. Both depolarizing (blue) and hyperpolarizing (red) 50 ms current steps injected into ComInt 1 cause a simultaneous change in IRS's membrane potential. Aiii, Similarly, depolarizing and hyperpolarizing currents in the IRSh neuron cause simultaneous changes in ComInt 1's membrane potential. Recordings are averages of multiple sweeps. The gray outlines represent the 95% confidence limits of the averaged sweeps. Bi, A whole mount, viewed from the dorsal side, showing one IPS neuron filled with a fluorescent marker. Bii, Simultaneous intracellular recordings from a ComInt 1 neuron and an IPS neuron in the same microcircuit. Neither depolarizing (blue) nor hyperpolarizing (red) the ComInt 1 caused a postsynaptic potential in the IPS neuron. Biii, Similarly, neither depolarizing nor hyperpolarizing the IPS neuron caused a postsynaptic response in the ComInt 1 neuron. Recordings are averages of multiple sweeps. C, A diagram of the synaptic circuit through which information conducted by coordinating neurons to synapses onto a ComInt 1 is transmitted to the IRSh neuron in the pattern-generating circuit. ComInt 1 makes an electrical synapse (resistor symbol) with an IRSh neuron in the local circuit. The colors symbolize the segments from which coordinating axons originate (Fig. 1).

Direct synaptic connections between crayfish neurons recorded at room temperature have brief synaptic delays, between 2.0 and 3.5 ms at chemical synapses (Sherff and Mulloney, 1996; Namba et al., 1997; Nakagawa and Mulloney, 2001) and faster at electrical synapses (Edwards et al., 1998; Antonsen and Edwards, 2003). With a microelectrode in ComInt 1 near the ganglion's midline and a second in IRSh within the LN (Fig. 2), the delay between the onset of a presynaptic depolarization of ComInt 1 and the postsynaptic response by IRSh was 2.16 ± 0.76 ms (mean ± SD) and for a presynaptic hyperpolarization 2.22 ± 0.63 ms. The mean delay in the other direction, between the onset of a depolarization of IRSh and the postsynaptic response by ComInt 1, was 2.8 ± 0.79 ms and for a hyperpolarization of IRSh was 2.42 ± 0.69 ms (n = 3 experiments).

Neurons connected by electrical synapses are often also dye-coupled, so we looked for this phenomenon here. In 9 of 10 experiments where an IRSh neuron was filled with NB, we saw clearly that the ComInt 1 neuron projecting to the same LN was also filled (Fig. 4 shows four examples), consistent with the presence of an electrical synapse connecting these neurons. In contrast, the other type of IRS neuron, “IRS no hook” (IRSn) (Smarandache-Wellmann et al., 2013), does not appear to be connected to ComInt 1 by this type of synapse. Eight of 10 fills of IRSn neurons showed no evidence of dye coupling to ComInt 1. In the many preparations where ComInt 1 itself was filled with NB, we did not see any evidence that IRSh or other unilateral local interneurons were also filled, so dye-coupling here is apparently directionally selective (Antonsen and Edwards, 2003).

Depolarizing a ComInt 1 neuron excites the microcircuit's PSE motor neurons, which suggests that ComInt 1 might inhibit IPS neurons. IPS neurons can be distinguished from IRS neurons both physiologically (IPS neurons inhibit PSE and RSI motor neurons but IRS neurons inhibit RSE and PSI motor neurons) and anatomically (Fig. 3Ai,Bi); IPS neurons have cell bodies posterior to the base of N1, whereas IRS neurons have cell bodies anterior to the base of N1 (Smarandache-Wellmann et al., 2013). In 10 experiments where we recorded simultaneously from a ComInt 1 neuron and an IPS neuron, we saw no evidence of a direct synaptic connection between them (Fig. 3B). In this example, neither depolarization nor hyperpolarization of ComInt 1 caused a measurable change in the membrane potential of the IPS neuron. Depolarization of the IPS neuron did nothing to the ComInt 1 neuron's potential. We conclude that ComInt 1 neurons do not synapse directly with IPS neurons.

In summary, the ComInt 1 that projects to the microcircuit in each LN makes an electrical synapse with the IRSh neuron in that microcircuit's pattern-generating kernel (Fig. 3C), but not with the IPS neurons in the same circuit.

ComInt 1's membrane potential affects motor output from its home microcircuit

Under normal conditions, ComInt 1's membrane potential depolarizes during part of each cycle (Fig. 5A). Despite ComInt 1's extended anatomy (Figs. 2Ai and 4), dSEVC with an electrode in its major processes effectively prevents oscillations of its membrane potential (Fig. 5A) and allows controlled changes in its potential within the LN (Smarandache et al., 2009). The voltage-clamped condition can be viewed as an average potential with all periodic information removed. At the location of the microelectrode, the dSEVC system accurately measures these changes, but at sites more remote from the electrode the clamped potentials will be attenuated by the neuron's passive properties. Acknowledging this imperfect “space clamp,” dSEVC is an effective tool for controlling the potentials of nonspiking neurons like ComInt 1 (Figs. 2B and 5A). In these Results, we use “clamp” to mean control at the recording site, with the understanding that space-clamp was imperfect.

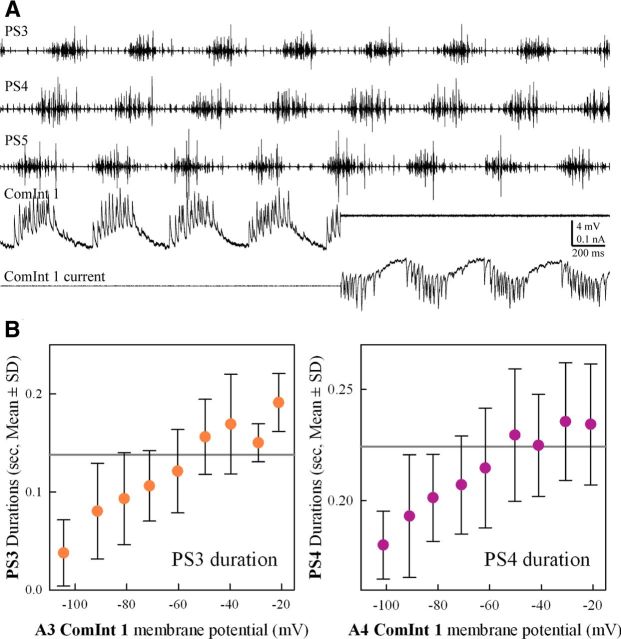
Figure 5.

Changes in the membrane potential of a ComInt 1 affected the durations of bursts of impulses in PS motor neurons in the same microcircuit. A, Simultaneous extracellular recordings of seven cycles of motor output from ganglia A3, A4, and A5 (PS3, PS4, and PS5) and an intracellular recording of membrane potential and membrane current from a ComInt 1 in A4. At the beginning of the fourth cycle, the intracellular recording was switched to voltage-clamp mode. This recording was from ComInt 1's terminals in the lateral neuropil. B, Plots of the durations of PS bursts (mean ± SD) recorded from one microcircuit in ganglia A3 (left) or A4 (right) while the membrane potential of the ComInt 1 neuron that projected to that microcircuit was clamped at different potentials. The horizontal gray lines indicate the mean durations of PS3 or PS4 in these experiments when ComInt 1 was not voltage-clamped.

Because perturbations of a ComInt 1's membrane potential in active preparations affected the timing of PS bursts (Fig. 2B), we examined the influence of ComInt 1's membrane potential on three other parameters of its microcircuit's motor output. In 13 preparations that were expressing continuous, stable motor patterns, we clamped a ComInt 1 neuron at a series of potentials from ∼−100 to −20 mV and recorded a continuous series of PS bursts at each potential. Of these, 13 preparations (four in which a ComInt 1 in ganglion A3 and six in which a ComInt 1 in A4 were successfully clamped at six or more potentials) were analyzed in detail. The remaining three experiments had recorded fewer different potentials.

Clamping ComInt 1's potential did not disrupt the synchronization of local circuits in different segments, nor did it affect the period of their output. using repeated-measures RM-ANOVA to separate the effects of membrane potential from variations in individual preparations, we found little effect on the motor pattern's period. The mean periods of the A3 preparations were similar at seven potentials between −27 mV and −90 mV (RM-ANOVA: p = 0.833, n = 4, F = 0.488, power = 0.05) and were the same as the unclamped control condition. The mean periods of the A4 preparations were similar at six potentials between −34 mV and −87 mV (range, 0.465–0.455 ms), but the mean period of the −87 mV series did differ from the mean period, 0.468 ms, expressed during the unclamped control condition (RM-ANOVA p = 0.003, n = 6, F = 4.753, power = 0.869). However, the 13 ms difference between these two mean periods is not biologically significant.

In contrast to the period of their bursts, the durations of bursts of spikes in PSE neurons changed systematically with ComInt 1's membrane potential in the same microcircuit (Fig. 5B). The durations of PSE bursts increased as ComInt 1 was depolarized above rest and decreased as it was hyperpolarized. In the same sets of experiments whose periods had been analyzed, RM-ANOVA of PSE burst durations and ComInt 1 membrane potential confirmed that ComInt 1's potential affected duration (for A3: p = 0.015, n = 4 experiments, F = 3.362, power = 0.714; for A4: p < 0.001, n = 6 experiments, F = 9.527, power = 1.0).

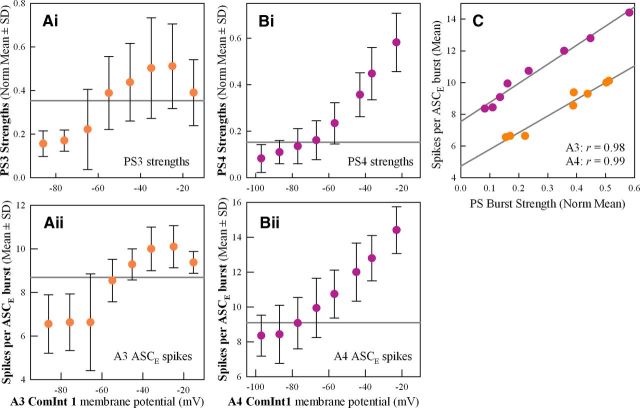
The strengths of PSE bursts also changed systematically with ComInt 1's membrane potential (Fig. 6Ai,Bi). The motor innervation of a swimmeret responds to increasing excitation by increasing the numbers of spikes each neuron fires per cycle and by recruiting more motor neurons according to a size principle (Davis, 1971). By changes in “strength,” we mean changes in the numbers of motor neurons recruited during a burst and the numbers of spikes fired by each recruited neuron. In four experiments (two from the A3 group and two from the A4 group), chosen because firing of the ASC_E neuron in the same microcircuit had also been recorded simultaneously, the strengths of PSE bursts increased as ComInt 1 was depolarized and decreased as the cell was hyperpolarized. For each experiment, ANOVA of PSE strengths and ComInt 1 potential confirmed that burst strengths differed with potential (p < 0.001 that they did not change, n = 4 experiments, F ≥ 6.397, power = 1.0).

Figure 6.

Changes in the membrane potential of a microcircuit's ComInt 1 affected both the strengths of its PS bursts and the numbers of spikes per burst in its ASC_E neuron. Ai, Bi, Here, two pairs of plots show changes in the mean normalized strengths of PS bursts recorded when a ComInt 1 in ganglion A3 or A4 was clamped at different potentials. In each plot, the horizontal gray line marks the mean strength measured when ComInt 1 was not voltage-clamped. Aii, Bii, The numbers of spikes per burst in ASC_E neurons in ganglion A3 or A4 changed systematically with their ComInt 1's membrane potential. C, The numbers of spikes per ASC_E burst were strongly correlated with the strengths of the simultaneous PS bursts at each ComInt 1 membrane potential. r, Pearson correlation coefficients.

Changes in PSE burst strengths are accompanied by changes in numbers of spikes in ASC_E bursts

During spontaneous fluctuations in excitation of the system, the numbers of spikes per ASC_E burst closely track changes in the strengths of bursts in PSE motor neurons (Mulloney et al., 2006). Similarly, in these experiments, as the strengths of PSE bursts responded to changes in ComInt 1's membrane potential, the numbers of spikes per burst in the ASC_E neuron originating in the same microcircuit also changed (Fig. 6Aii,Bii). Strengths of PSE bursts and numbers of ASC_E spikes covaried when ComInt 1 was clamped either in ganglion A3 or in A4 (Fig. 6C).

The numbers of spikes per burst in ASC_E and DSC coordinating axons affect the strength and timing of output from microcircuits in other ganglia (Mulloney and Hall, 2007a,b). Having observed that changes in ComInt 1's membrane potential affected ASC_E's firing (Fig. 6), we examined the effects of an individual ComInt 1's membrane potential on the output of microcircuits in other segments.

ComInt 1's membrane potential affects the phase of output from microcircuits in other segments

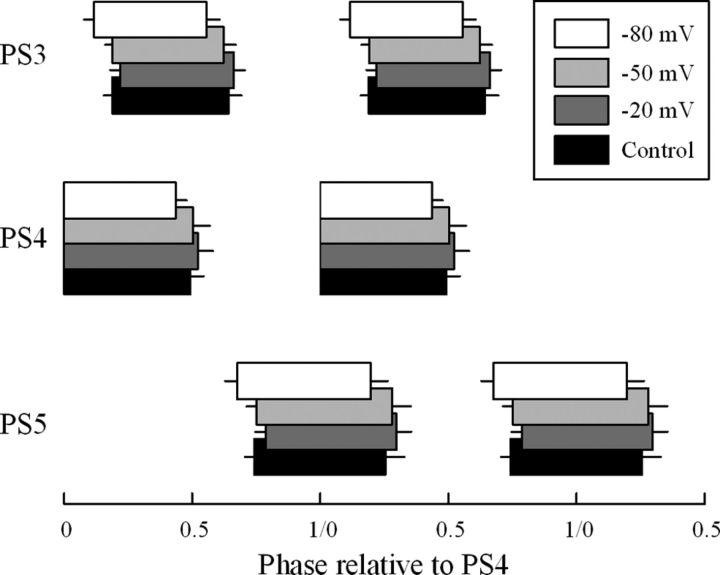
Although the anatomy of a ComInt 1 is restricted to one ganglion and its direct output is limited to one microcircuit (Mulloney and Hall, 2003), clamping a ComInt 1's membrane potential did affect the phases of activity in other microcircuits of both anterior and posterior ganglia (Fig. 7). For the phases of PS3 and PS5 in the group of six A4 experiments, p < 0.001 that they remained the same as the A4 ComInt 1's potential changed (RM-ANOVA n = 6, F ≥ 7.92, power ≥ 0.996). The example in Figure 7 compares the mean phases and durations of PSE bursts in ganglia A3, A4, and A5 recorded in the unclamped (control) condition with those recorded when ComInt 1 was clamped at three different potentials. When ComInt 1 in A4 was clamped at −50 mV, near its resting potential, the phases of PS bursts in all three ganglia were similar to the unclamped controls. When it was clamped at −20 mV, the phases of PS3 and PS5 bursts were delayed. When it was clamped at −80 mV, phases of PS3 and PS5 bursts were advanced. Clamping a ComInt 1 in A3 had similar effects on phases of PS4 and PS5 (RM-ANOVA p ≤ 0.007, n = 4 experiments, F ≥ 3.952, power ≥ 0.825).

Figure 7.

Boxplots that illustrate parameters of the system's motor output recorded simultaneously from ganglia A3, A4, and A5 (PS3, PS4, and PS5) while the potential of the ComInt 1 in an A4 microcircuit was clamped at −20, −50, or −80 mV. This figure illustrates four sequences of two bursts each during two cycles, using the start of the PS4 bursts to define the start of each cycle. Each PS4 box shows the mean PS4 duty cycle (duration/period) + SD. The other boxes begin at the mean phases (− SD), and show mean duty cycles (+ SD) of the other PS recordings. Control, the unclamped control condition.

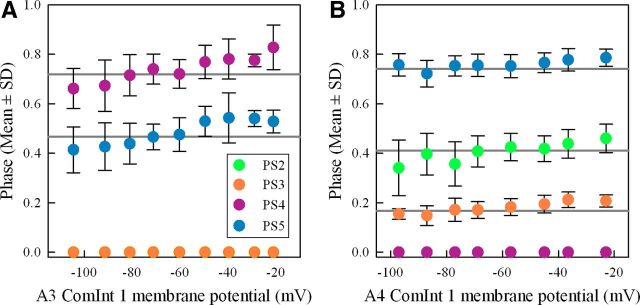
The patterns of these intersegmental changes and their dependence on ComInt 1's potential are best seen in plots of the phases of PS bursts versus ComInt 1's membrane potential (Fig. 8), where phase is defined in cycles that start with each PS burst in the ComInt 1's home microcircuit (as in Fig. 7). In both A3 and the A4 examples (Fig. 8A,B), the mean phases of PS bursts in other ganglia decreased in proportion to ComInt 1's hyperpolarization and increased in proportion to its depolarization. The phases of PS4 and PS5 bursts in Figure 8A differed significantly from their control values as ComInt 1's potential in A3 changed (Dunnett's test: p < 0.001, n = 10 potentials, F ≥ 8.276, power = 1.0). The phases of PS2, PS3, and PS5 bursts in Figure 8B also differed from their control values as ComInt 1's potential in A4 changed (Dunnett's test: p < 0.001, n = 9 potentials, F ≥ 5.905, power = 0.99).

Figure 8.

Changes in the membrane potential of a ComInt 1 in one microcircuit affected the phases of motor output from microcircuits in other segments. In each plot, the horizontal gray lines indicate the means recorded when ComInt 1 was not clamped. Colors indicate the segments in which the different recordings were made (compare Fig. 1C). A, Plots of the phases of PS4 and PS5 bursts within cycles of PS3 firing when a ComInt 1 in ganglion A3 was clamped at different potentials. The phase of PS3 is zero. B, Plots of phases of PS2, PS3, and PS5 bursts within cycles of PS4 firing when a ComInt 1 in A4 was clamped at different potentials. Here, the phase of PS4 is zero.

In contrast to these effects on the phases of PSE bursts in other ganglia, ComInt 1's potential had no influence on their durations. In the group of six A4 experiments, neither PS3's nor PS5's durations changed (RM-ANOVA for PS3: p = 0.142, n = 6, F = 1.776, power = 0.25; for PS5: p = 0.736, n = 5, F = 0.558, power = 0.05). In the group of four A3 experiments, neither PS4's nor PS5's durations changed (RM-ANOVA for PS4: p = 0.590, n = 4, F = 0.809, power = 0.05; for PS5: p = 0.192, n = 4, F = 1.593, power = 0.195). Given ComInt 1's marked influence on the durations of PSE bursts in its home microcircuit (Fig. 5), this absence of effects on durations in other microcircuits is noteworthy.

Discussion

Properties of the ComInt 1–IRS synapse

The physiological properties of the connection between these two neurons are evidence of an electrical synapse both because it is reciprocal (Fig. 3A) and because of the dye-coupling to ComInt 1 we detected when an IRSh was filled with NB (Fig. 4). It is not out of the question that this connection also has a chemical component (Coleman et al., 1995), but the dye-coupling is evidence of gap junctions between these neurons, and an electrical synapse is the most straightforward conclusion. Discovery of this synapse between a microcircuit's ComInt 1 and IRSh interneuron allows us to explain several features of the microcircuit's performance.

The synaptic organization and dynamics of a swimmeret microcircuit

The components of each microcircuit (motor neurons, coordinating neurons, pattern-generating interneurons, and commissural neurons) are organized by a set of synaptic connections that establish the temporal structure of the microcircuit's motor output (Fig. 1E). The kernel of the microcircuit's pattern-generating circuit is formed by reciprocal inhibitory synapses between IPS and IRS neurons (Fig. 9). This reciprocal inhibition will generate alternating oscillations of the IPS and IRS neurons' membrane potentials (Perkel and Mulloney, 1974; Wang and Rinzel, 1992; Skinner et al., 1994; Zhang and Lewis, 2013). Oscillations of these potentials cause periodic changes in transmitter release from their graded inhibitory synapses onto different motor neurons (Fig. 9). These periodic changes in inhibition cause alternating bursts of spikes in different functional groups of motor neurons (Mulloney, 2003; Tschuluun et al., 2009).

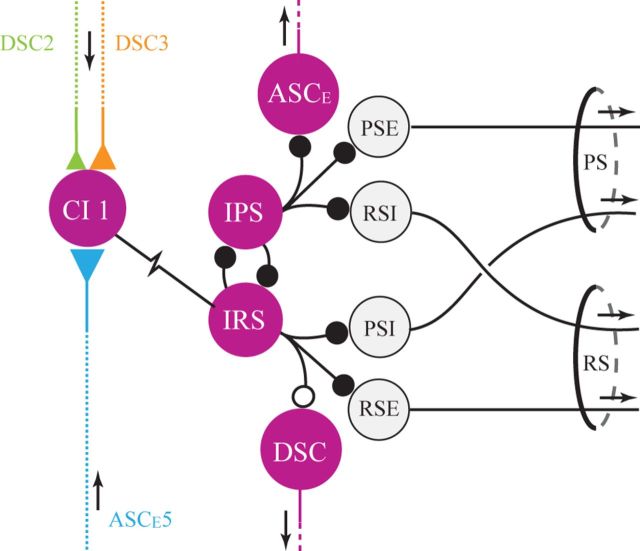
Figure 9.

Structure of a swimmeret microcircuit (here in ganglion A4). The resistor symbol connecting ComInt 1 (CI 1) and the IRS neuron is the pathway through which coordinating information from other ganglia reaches the microcircuit's pattern-generating kernel, the reciprocal inhibition of IPS and IRS interneurons. Large circles represent an identified neuron or group of functionally similar neurons. Small black circles represent inhibitory chemical synapses. Colored triangles represent excitatory chemical synapses; larger triangles represent stronger synapses. Arrows indicate the direction of orthodromic impulse propagation.

Depolarizing a ComInt 1 excites PS neurons but inhibits RS neurons in the same microcircuit (Mulloney and Hall, 2003). The trisynaptic pathway from ComInt 1 to IRSh to IPS to PSE motor neurons explains why these differential changes occur (Fig. 9). PSE neurons are directly inhibited by graded transmission from IPS neurons (Mulloney, 2003). Depolarizing ComInt 1 depolarizes the IRSh neuron and so increases its inhibition of RSE motor neurons, which weakens RSE bursts. IPS neurons are also inhibited by IRS neurons. Depolarizing ComInt 1 also increases inhibition of IPS neurons and thus weakens their periodic inhibition of PSE motor neurons, so PSE bursts grow stronger.

Each ComInt 1 integrates EPSPs transmitted from periodic bursts of spikes in ASC_E and DSC axons converging from other ganglia (Smarandache et al., 2009). These integrated EPSPs act as periodic perturbations that entrain the microcircuit's output to the same period as its neighboring microcircuits and to a particular phase relative to their output (Kopell and Ermentrout, 1988; Schwemmer and Lewis, 2012). This phase is apparent as the PRC's stable fixed point near 0.25 (Fig. 2B), the same phase difference as the posterior-to-anterior phase lag between movements of swimmerets on neighboring segments (Mulloney and Smarandache-Wellmann, 2012; Zhang et al., unpublished observation).

Coordination of distributed microcircuits by the intersegmental circuit

ComInt 1s are nonspiking local neurons whose anatomy is limited to a single ganglion and whose output is restricted to just half of that ganglion (Figs. 2Ai and 4). It is puzzling, then, that a ComInt 1's membrane potential can affect the phase of motor output from microcircuits in other ganglia (Figs. 7 and 8). The solution to this puzzle follows from the system's phase-responses to excitation of ASC_E and DSC neurons (Mulloney and Hall, 2007a), and from ComInt 1's electrical synapse with the IRSh neuron. In each microcircuit, ASC_E and DSC neurons fire bursts of spikes that encode information about each cycle of motor output (Mulloney and Hall, 2007b). Adding spikes in a normally timed ASC_E or DSC burst causes a phase delay in the axon's target ganglion; subtracting spikes causes a phase advance (Mulloney and Hall, 2007a). Depolarizing ComInt 1 depolarizes IRSh, too (Figs. 3 and 9), which through IRSh's synapse onto IPS (Fig. 9), we postulate weakens inhibition of ASC_E. Therefore, when a ComInt 1 is depolarized, the ASC_E neuron in its microcircuit fires more spikes per burst (Fig. 6), and the phases of PSE bursts in more anterior ganglia are delayed (Figs. 7 and 8). Similarly, because the ComInt 1–IRS synapse is electrical, hyperpolarizing ComInt 1 also hyperpolarizes IRS. We postulate that this reduces IRSh's inhibition of IPS and so increases IPS's inhibition of ASC_E (Fig. 9). Therefore, ASC_E fires fewer spikes per burst (Fig. 6), and the phases of PSE bursts in more anterior ganglia are advanced.

In contrast to its phases, the period of the system's output did not respond significantly to step changes in a ComInt 1's membrane potential. Two factors probably contribute to this stability: all microcircuits were uniformly excited by bath-applied carbachol (Tschuluun et al., 2009), and each microcircuit still received periodic entraining input from three others (Smarandache et al., 2009). Changes in the potential of one ComInt 1 affected the strength of its microcircuit's output (Fig. 6) enough to alter its neighbors' phases (Figs. 7 and 8), but not enough to override the entrainment caused by convergent excitation from the other microcircuits in the system.

ComInt 1s as integrative nodes, and as hub neurons

The information encoded by ASC_E and DSC neurons is both necessary and sufficient to establish and maintain intersegmental synchronization and the posterior-to-anterior phase lags that enable effective swimmeret movements (Namba and Mulloney, 1999; Tschuluun et al., 2001). ASC_E and DSC axons encode different information and conduct it in different directions (Fig. 9), so it is surprising that, as they traverse each ganglion, they synapse onto the same target neuron, ComInt 1 (Fig. 9). This convergence allows information from both anterior and posterior microcircuits to be integrated before it affects the dynamics of this microcircuit's pattern-generating kernel.

ComInt 1 neurons may be viewed as hub neurons that link local circuits into a larger structure identified by its common period and stable phase differences (Gutierrez and Marder, 2013; Gutierrez et al., 2013). Like the hub neurons in Gutierrez's theoretical circuits, ComInt 1s integrate chemical synaptic input from more than one other microcircuit, are electrically coupled to a microcircuit, and influence the phases of oscillations in the system of microcircuits. The electrical synapse between each ComInt 1 and IRSh allows a continuously varying modulation of the local pattern-generating circuit through a wide range of ComInt 1's potentials (Figs. 5B and 6). This suggests that modulation of a ComInt 1's membrane potential by factors other than EPSPs from coordinating axons would affect both the strength of the local circuit's motor output and the phase of this output within the coordinated activity of the system.

Other distributed motor systems may use the same principles

The problem of coordinating segmentally distributed motor circuits that drive locomotion is common at least to vertebrates, annelids, and arthropods. Different classes of animals vary in the degree to which descending or proprioceptive inputs are necessary for canonical coordination (Puhl and Mesce, 2010; Mullins et al., 2011; Berni et al., 2012; Puhl et al., 2012; Büschges and Borgmann, 2013; Bicanski et al., 2013), but all have central intersegmental coordinating circuits that contribute to synchronization of motor output from modular segmental motor circuits (Kiehn, 2006; Büschges et al., 2011; Eklof-Ljunggren et al., 2012; Wiggin et al., 2012). Proprioceptive feedback directly affects each cycle of local motor output and, through the coordinating circuit, the phases and strengths of output from circuits in other segments. The patterns of intersegmental connections between these distributed circuits are still largely unmapped, but we think it likely that hub neurons that integrate weighted inputs from multiple segments and transmit strong entraining signals to each segmental circuit, like ComInt 1, will prove to be a common solution.

Some forms of motor behaviors (e.g., respiration in vertebrates and heartbeat in leech) use a different strategy. A controlling circuit located in the brainstem (Feldman, 2010; Gariépy et al., 2012) or in a few anterior ganglia (García et al., 2008) sets the period, but the phases of movements in each cycle are determined by differences in strengths of synapses made by axons descending onto segmental motor neurons (Norris et al., 2011; Wright and Calabrese, 2011). There is no cycle-by-cycle interaction between different segments.

Analog and digital information in the coordinated system

Encoding, decoding, and integration of information at various points in this circuit seem to use different mechanisms appropriate for local and long-distance communication. In each microcircuit, ASC_E and DSC axons fire conventional propagating spikes that encode information as digital signals: bursts that vary both in duration and in numbers of spikes proportional to variation in motor bursts (Mulloney et al., 2006). EPSPs in ComInt 1 caused by ASC_E and DSC spikes are integrated as an analog signal, a ragged compound PSP whose size and duration are functions of the numbers and timing of the presynaptic spikes. The IRS and IPS neurons that generate PS-RS alternation use graded inhibitory chemical synapses (Mulloney, 2003), which can have high rates of information transfer (DiCaprio, 2004). Thus, encoding information for export is accomplished by spiking neurons controlled by graded inhibition, whereas decoding information from multiple distant sources is accomplished by nonspiking hub neurons that transform a burst of presynaptic spikes into a complex analog PSP. These decoded signals entrain the oscillations of each microcircuit and synchronize the system.