IMAGING GENETICS VIA SPARSE CANONICAL CORRELATION ANALYSIS

Abstract

The collection of brain images from populations of subjects who have been genotyped with genome-wide scans makes it feasible to search for genetic effects on the brain. Even so, multivariate methods are sorely needed that can search both images and the genome for relationships, making use of the correlation structure of both datasets. Here we investigate the use of sparse canonical correlation analysis (CCA) to home in on sets of genetic variants that explain variance in a set of images. We extend recent work on penalized matrix decomposition to account for the correlations in both datasets. Such methods show promise in imaging genetics as they exploit the natural covariance in the datasets. They also avoid an astronomically heavy statistical correction for searching the whole genome and the entire image for promising associations.

1. INTRODUCTION

The last few years have seen an unprecedented surge in data acquisition in fields ranging from signal processing to biology and medicine. This ability to acquire massive amounts of data has opened the door to qualitatively different approaches to science as well, often using high-dimensional datasets from more than one modality. One example is the convergence of biomedical imaging and genomics in the nascent field of imaging genetics [1]. The basic idea is to identify genetic variants that can best capture and explain phenotypic variations in brain function and structure. To be more concrete, two sets of data are observed, p genotypes and q neuroimaging phenotypes, on n samples. Both p and q may be small or large and there has been prior testing for effects in various scenarios. In [2], Joyner et al. studied a dataset with small q, four brain size measures, and small p, 11 single nucleotide polymorphisms (SNPs). In [3], Potkin et al. considered small q, the mean BOLD signal from fMRI, and large p, 317,503 SNPs. Filippini et al. explored the combination of large q, 29,812 voxels, and small p, a single SNP [4]. Finally, Stein et al. in [5] took on the most challenging scenario of large q, 31,622 voxels, and large p, 448,293 SNPs. Thus, on the same set of imaged subjects, high-dimensional genetic data is also collected, e.g. hundreds of thousands of SNP genotypes. In some cases, well defined regions of interest (ROIs) are already known, but in other cases they are not. Similarly, in some cases, candidate genes may or may not be available. In this scenario, one wishes to simultaneously identify ROIs and a parsimonious set of genetic loci that are associated with each other.

The last case in particular presents not only intriguing possibilities but also computational and statistical challenges. Indeed, the simplest strategy is to perform pq univariate regressions between all possible voxels and SNPs [5] and adjust for multiple comparisons. While such an approach is straightforward, it also completely ignores the correlation structure among the SNPs and voxels. It also lacks power, as an astronomical correction must be made for the number of tests performed. Given the correlation structure a multivariate approach is called for. To address these shortcomings, in this paper we present a sparse canonical correlation analysis (CCA) method to identify joint signals in a pair of high-dimensional data sets, namely diffusion tensor images (DTI) and SNP measurements. The goal in classical CCA is to determine a coordinate system that maximizes the cross-correlation between two data sets [6]. In other words we seek the linear transformation of two data sets such that the linear forms are maximally correlated. We anticipate, however, that relatively few DTI voxels will contain signals that are correlated with again relatively few SNPs. Despite the fact that both data live in very high dimensional spaces, DTI voxels number in the tens of thousands and SNPs number in the hundreds of thousands, the relevant signal often resides in a low dimensional manifold. Indeed penalized methods such as the LASSO [7] have been very successful in recovering meaningful parsimonious models from high dimensional data. Building on this idea, Witten et al. introduced a penalized matrix decomposition (PMD) on the sample cross-covariance matrix in [8] aimed at introducing sparsity into the linear combinations. In related work, Vounou et al. introduced sparse Reduced Rank Regression (sRRR) [9, 10] as another multivariate alternative. Indeed, the PMD is a special case of the sRRR when relevant covariance matrices are taken to be identity matrices. Nonetheless, despite having a more general framework, the algorithms presented in [9, 10] make the same simplifying assumptions made in PMD. We also note that under the diagonal covariance assumption such decompositions are equivalent to a partial least squares regression [11]. In this work we extend the PMD model to account for correlation structure in both data sets.

2. METHODS

2.1. Simulation Experiment

Suppose we have 100 subjects for whom 1,000 SNPs have been typed, X ∈ ℝ^100×1,000, and on which a 100 × 100 image has been taken, 𝒴 ∈ ℝ^{100×100×100} (here we introduce the ideas for a set of 2D images but they hold in any dimension without loss of generality). Let Y ∈ ℝ^100×10,000 denote the matricization of 𝒴 along its first mode. The data sets are generated as follows. Let β ∈ ℝ^1,000 be sparse with

$${\beta }_i=\{\begin{array}{cc}2\hfill & i\in \{192,438,623,786,780\}\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

The images are also similarly sparse.

$$y_{\text{ij}}=\{\begin{array}{cc}{\sum }_{j\prime }{x}_{ij\prime }{\beta }_{j\prime }\hfill & (i,j)\in R\subset {\{1,\dots ,100\}}^2\hfill \\ 0\hfill & \text{otherwise,}\hfill \end{array}$$

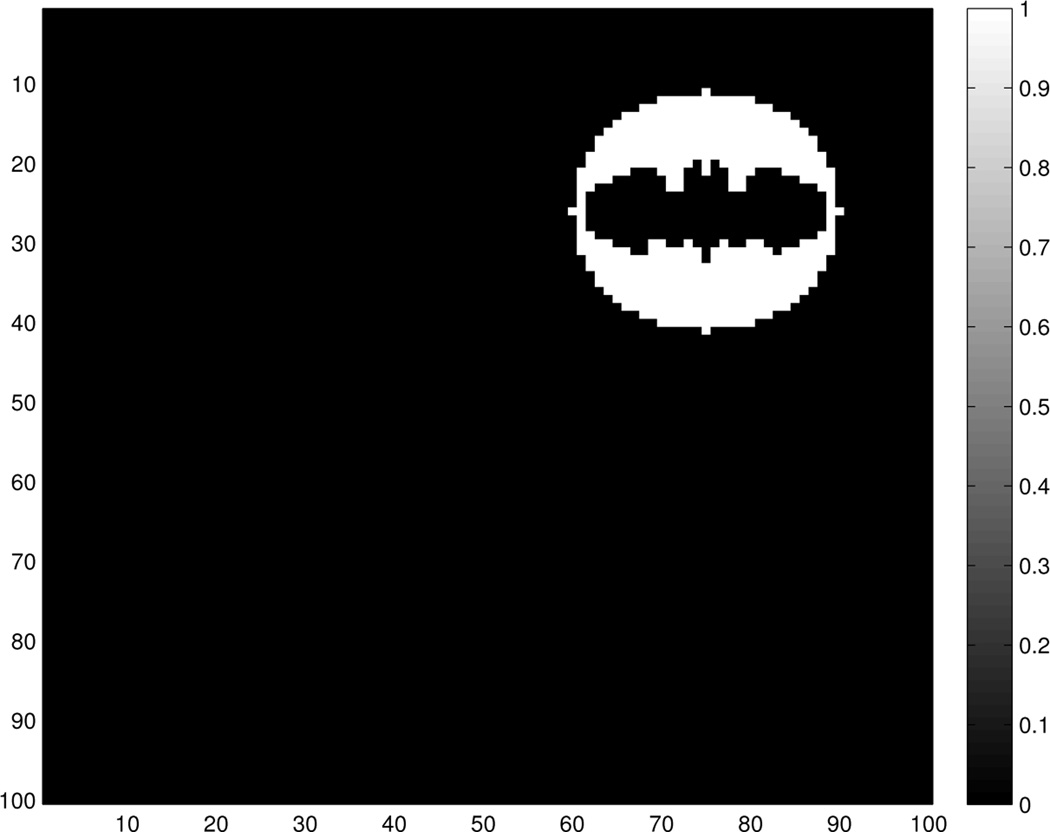
where R denotes the ROI. The ROI for this problem is shown in Figure 1. Finally, we do not observe 𝒴 but rather a noisy version of it 𝒵.

$$z_{\text{ijk}}=y_{\text{ijk}}+\sigma {\epsilon }_{\text{ijk}},$$

where ε_ijk are i.i.d. standard normal and σ = 10. An example of the observed image data for a subject is shown in Figure 2.

Fig. 1.

Region of Interest (ROI) for a simulated example problem, with a coherent signal in the image. Pixels that belong to the ROI have value of 1. Pixels outside the ROI have value of 0.

Fig. 2.

An example of the observed image data: 𝒵(1, :, :) which corresponds to the observed image of the first subject.

2.2. Sparse Canonical Correlation Analysis

Let X ∈ ℝ^n×p denote the SNP data matrix and Y ∈ ℝ^n×q denote the matrix of vectorized DTI fractional anisotropy (FA) scores. Classical CCA solves the following optimization problem

$$\underset{\mathbf{a},\mathbf{b}}{\text{max}}{\mathbf{a}}^{\top }{\mathbf{X}}^{\top }\mathbf{Y}\mathbf{b}$$

subject to the constraints a^⊤X^⊤Xa = 1 and b^⊤Y^⊤Yb = 1. The matrices X^⊤Y,X^⊤X; and Y^⊤Y are estimates of the cross-covariance and covariance matrices respectively. PMD introduces a LASSO penalty and assumes the covariance matrices are identity matrices, i.e., PMD solves the optimization problem

$$\underset{\mathbf{a},\mathbf{b}}{\text{max }}{\mathbf{a}}^{\top }{\mathbf{X}}^{\top }\mathbf{Y}\mathbf{b}-{\lambda }_a{\Vert \mathbf{a}\Vert }_1-{\lambda }_b{\Vert \mathbf{b}\Vert }_1$$

subject to the constraints a^⊤a ≤ 1 and b^⊤b ≤ 1. Note that the equality constraints have been relaxed to inequality constraints to make the feasible sets convex. The parameters λ_a ≥ 0 and λ_b ≥ 0 tune the degree of sparsity in a and b. Since the objective function is biconvex, namely it is convex in a with b fixed and vice versa, PMD iteratively minimizes with respect to a holding b fixed, and vice versa until convergence. The update for a is given by

$$\widehat{\mathbf{a}}=\underset{\mathbf{a}}{\text{arg min}}\frac{1}{2}{\Vert {\mathbf{X}}^{\top }\mathbf{Y}\mathbf{b}-\mathbf{a}\Vert }_2^2+\lambda {\Vert \mathbf{a}\Vert }_1$$

$${\mathbf{a}}^{*}=\{\begin{array}{cc}\frac{\widehat{\mathbf{a}}}{{\Vert \widehat{\mathbf{a}}\Vert }_2}\hfill & \text{if}{\Vert \widehat{\mathbf{a}}\Vert }_2>0.\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

The update for b is similar. To weaken the identity covariance assumption we minimize the same objective function but alter the constraints to a^⊤ Σ̃_xa ≤ 1 and b^⊤ Σ̃_yb ≤ 1, where Σ̃_x and Σ̃_y are estimated covariance matrices. Again the problem is amenable to block relaxation, namely iteratively minimizing with respect to a holding b fixed and vice versa. Consider optimizing with respect to a first. We can rewrite the problem as

$$\text{max }{\mathbf{a}}^{\top }{\mathbf{X}}^{\top }\mathbf{Y}\mathbf{b}-\lambda {\Vert \mathbf{a}\Vert }_1$$

subject a^⊤Σ̃_xa ≤ 1. A little convex calculus shows that the updates are given by

$$\widehat{\mathbf{a}}=\underset{\mathbf{a}}{\text{arg min}}\frac{1}{2}{\Vert {\tilde{\mathbf{\Sigma }}}_x^{-1/2}{\mathbf{X}}^{\top }\mathbf{Y}\mathbf{b}-{\tilde{\mathbf{\Sigma }}}_x^{-1/2}\mathbf{a}\Vert }_2^2+\lambda {\Vert \mathbf{a}\Vert }_1.$$ (1)

and

$${\mathbf{a}}^{*}=\{\begin{array}{ll}\frac{\widehat{\mathbf{a}}}{{\Vert {\tilde{\mathbf{\Sigma }}}_x\widehat{\mathbf{a}}\Vert }_2}\hfill & \text{if}{\Vert {\tilde{\mathbf{\Sigma }}}_x\widehat{\mathbf{a}}\Vert }_2>0.\hfill \\ 0\hfill & \text{o.w}.\hfill \end{array}$$ (2)

Thus, the update occurs in two stages. We first solve a LASSO penalized regression problem in (1) where the response variable is ${\tilde{\mathbf{\Sigma }}}_x^{-1/2}{\mathbf{X}}^{\top }\mathbf{Y}\mathbf{b}$ and the design matrix is ${\tilde{\mathbf{\Sigma }}}_x^{-1/2}$. Then if the solution of (1) is non-zero we normalize the solution so that ‖Σ̃_xa*‖₂ = 1. If the solution to (1) is zero, the final solution a* is zero. Note that if we take Σ̃_x and Σ̃_y to be identity matrices, we recover the algorithm employed in prior work [8, 9, 10].

We note that the choice of covariance estimator is critical. Indeed the sample covariance is well recognized as a poor estimator of the population covariance in the small n, large p regime considered here. This problem even plagues the classical CCA problem as well when p is close to n. This has been addressed by applying a ridge estimate of the covariance matrices, namely [12, 13]. Ledoit and Wolf introduced a well-conditioned and consistent linear estimator of the sample covariance in [14] and a considerably more complicated nonlinear one in [15]. Here we employ Ledoit and Wolf’s simple linear estimator.

$${\tilde{\mathbf{\Sigma }}}_x=\lambda m_x\mathbf{I}+(1-\lambda ){\mathbf{S}}_x,$$

where S_x is the sample covariance, mx is the average eigenvalue of S_x, and λ ∈ [0, 1] is a convex mixing coefficient that shrinks the sample covariance towards m_xI as λ approaches 1. Ledoit and Wolf derive a value for λ to ensure that Σ̃_x is a consistent estimator of the true covariance Σ_x.

We apply both PMD and our extension of it on the simulated data described above. As a proof of concept - to see if we could recover the generative sparse model - we hand picked the regularization parameters λ_a and λ_b to see if there was a pair of values for which we could recover the true set of SNPs. In particular, we are interested in how many relevant SNPs were missed when sufficient regularization was applied to drop all irrelevant SNPs from the model. In practice, we would choose the regularization parameters with either a measure of complexity such as the BIC or by a data driven method such as cross-validation.

3. RESULTS

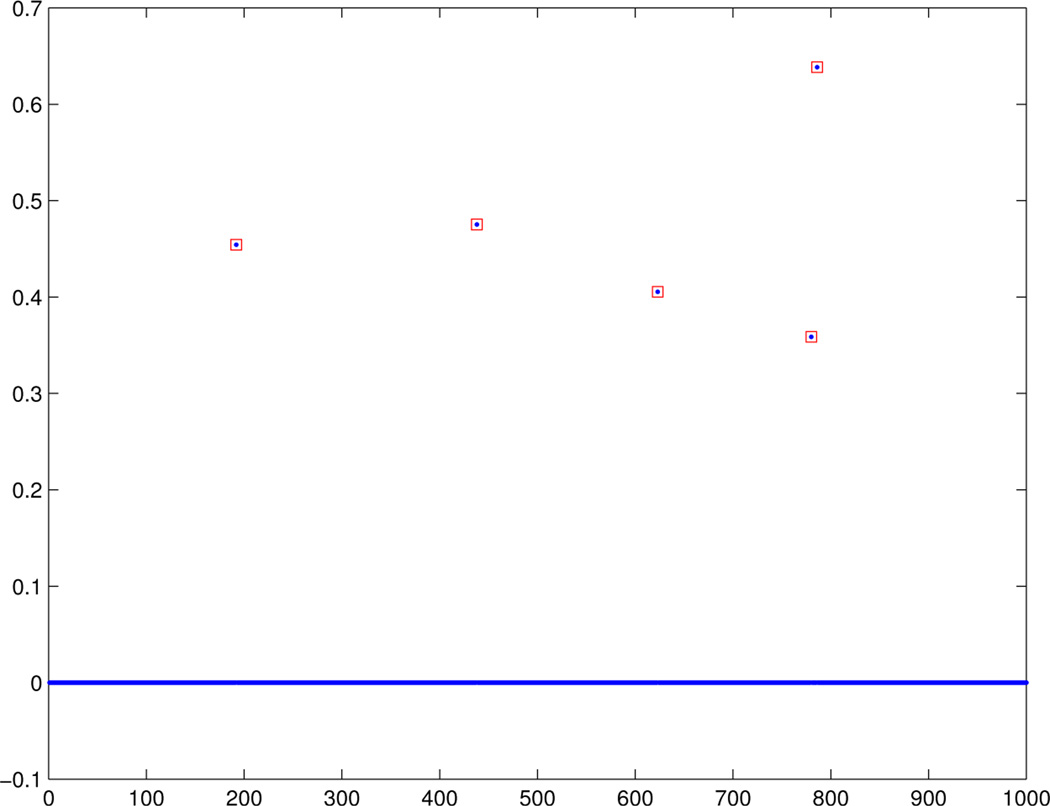
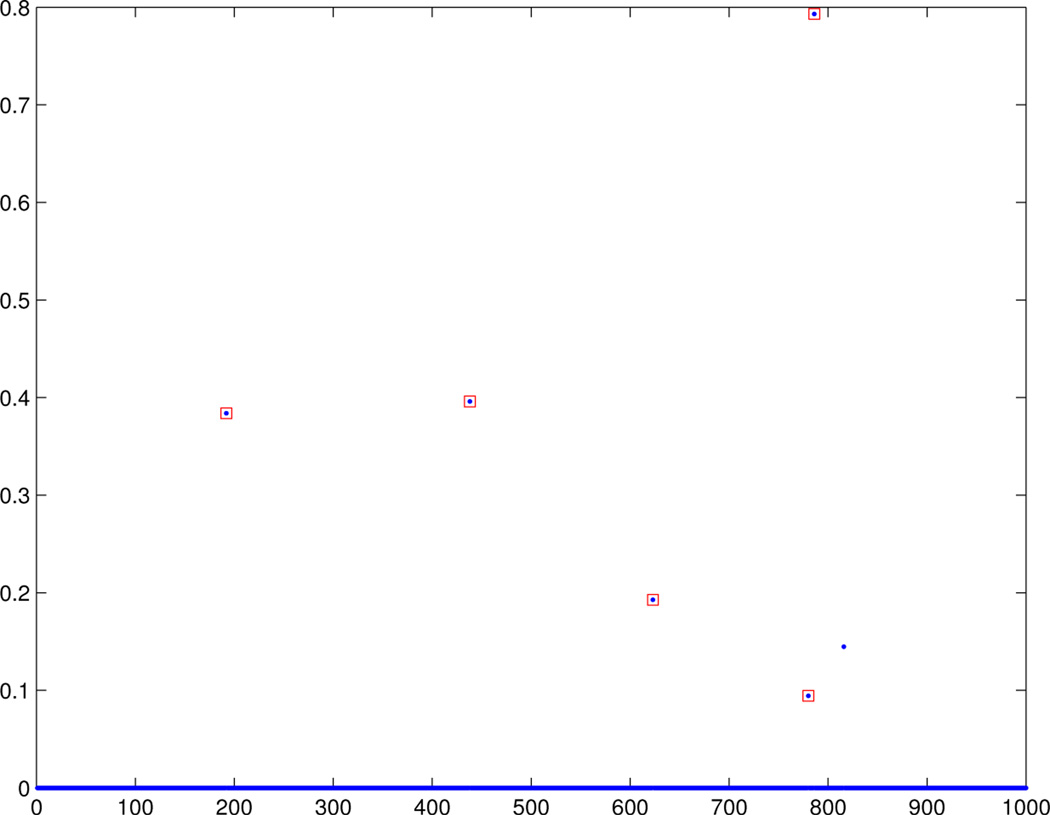
Figures 3 and 4 show the estimated canonical correlation vectors b and a unfolded when the non-trivial covariance estimate is used. We see that there is a regularization parameter that recovers the correct support. Figure 5 shows estimated a obtained via PMD using hand picked regularization parameters. PMD selected the same set of voxels and for space considerations, the results are not shown. Nonetheless, interestingly, the selected SNPs are different. Choosing a smaller λ_a will indeed include the missed SNP, but the cost is that false positives will also be included.

Fig. 3.

With non-trivial covariance estimate: The unfolded vector b that summarizes Y.

Fig. 4.

With non-trivial covariance estimate: The estimated sparse vector a that summarizes X. The SNP loci annotated in red denote the loci used to generate the data.

Fig. 5.

PMD: The estimated sparse vector a that summarizes X. The SNP loci annotated in red denote the loci used to generate the data.

4. DISCUSSION

In this paper we build on previous penalized multivariate methods for finding sparse structure in pairs of related data sets by showing how to incorporate correlation information. Our simulation example shows that our method is capable of recovering true latent sparse structure and that the solutions obtained when accounting for correlation structure can differ from multivariate approaches that assume identity covariances. Using non-trivial covariance estimates, however, makes the optimization problem harder. To that end we are working on developing more efficient algorithms that can work with non-trivial covariance matrices. Additionally, we are currently investigating our methods on real data.