AUTOMATIC QUANTIFICATION OF TREE-IN-BUD PATTERNS FROM CT SCANS

Abstract

In this paper, we present a fully automatic method to quantify Tree-in-Bud (TIB) patterns for respiratory tract infections. The proposed quantification method is based on our previous effort to detect and track TIB patterns with a computer assisted detection (CAD) system [9]. In addition to accurately identifying TIB on CT, quantifying TIB is important for measuring the volume of affected lung as a potantial marker of disease severity. This quantification can be challenging due to the complex shape of TIB and high intensity variation contributing mixed features. Our proposed quantification method is based on a local scale concept such that TIB regions detected via the CAD system are quantified adaptively, and volume percentages of the quantified regions are compared to visual scoring of participating radiologists. We conducted the experiments with a data set of 94 chest CTs (laboratory confirmed 39 viral bronchiolitis caused by human parainfluenza (HPIV), 34 nontuberculous mycobacterial (NTM), and 21 normal control). Experimental results show that the proposed quantification system is well suited to the CAD system for detecting TIB patterns. Correlations of observer-CAD agreements are reported as (R² = 0.824, p < 0.01) and (R² = 0.801, p < 0.01) for HPIV and NTM cases, respectively.

1. INTRODUCTION

Abnormal nodular branching opacities in CT scans are termed in the radiology literature as tree-in-bud (TIB) opacities. Fig. 1(a) and (b) show typical TIB patterns in a chest computed tomography (CT). These subtle opacity differences represent pulmonary disease in the small airways, most often due to infectious or non-infectious bron-chiolitis. Previously, we have developed a CAD system for accurate detection of this complex pattern. As an extension of our previous work [9], we study another challenging issue of this pattern: quantification. Indeed, precise quantification and measurement of the TIB abnormality using CAD is uniquely challenging due to the complex shape characteristics and high intensity variation of TIB patterns. Regarding these difficulties, we propose an automatic adaptive quantification method based on a local scale approach in order to bring local information of TIB regions into quantification framework and compute the volume affected by TIB existence more accurately.

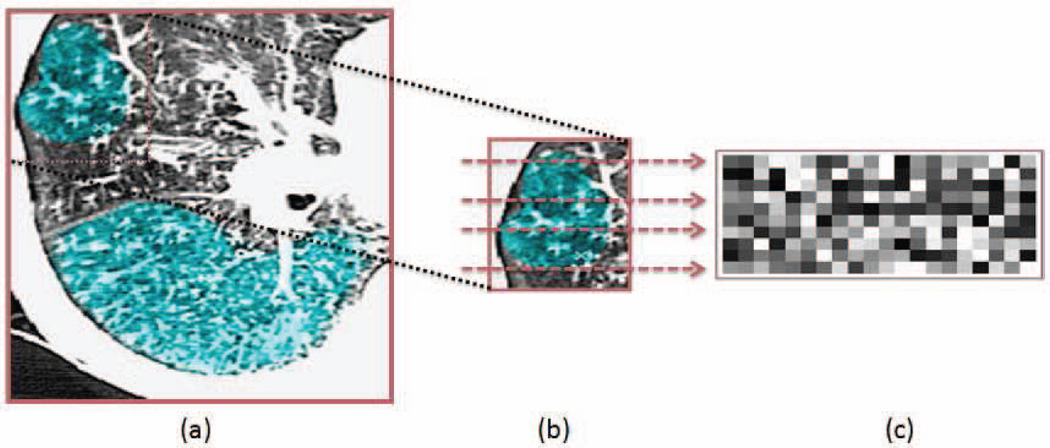
Fig. 1.

a. A single axial CT slice with a significant amount of TIB patterns (blue regions). b. Zoomed (a) with selected rows for intensity analysis. c. Intensity profiles from the selected rows (from (b)) of a TIB region.

The rest of the paper is organized as follows: Section 2 explains the methods of the proposed quantification system and gives a brief summary of our previously presented CAD system for detecting TIB patterns. Section 3 presents the feasibility of the proposed quantification method within the CAD system by evaluating the detection and quantification performances both qualitatively and quantitatively. We end the paper with conclusion and discussion in Section 4.

2. METHODS

2.1. Detection of TIB patterns through a CAD system

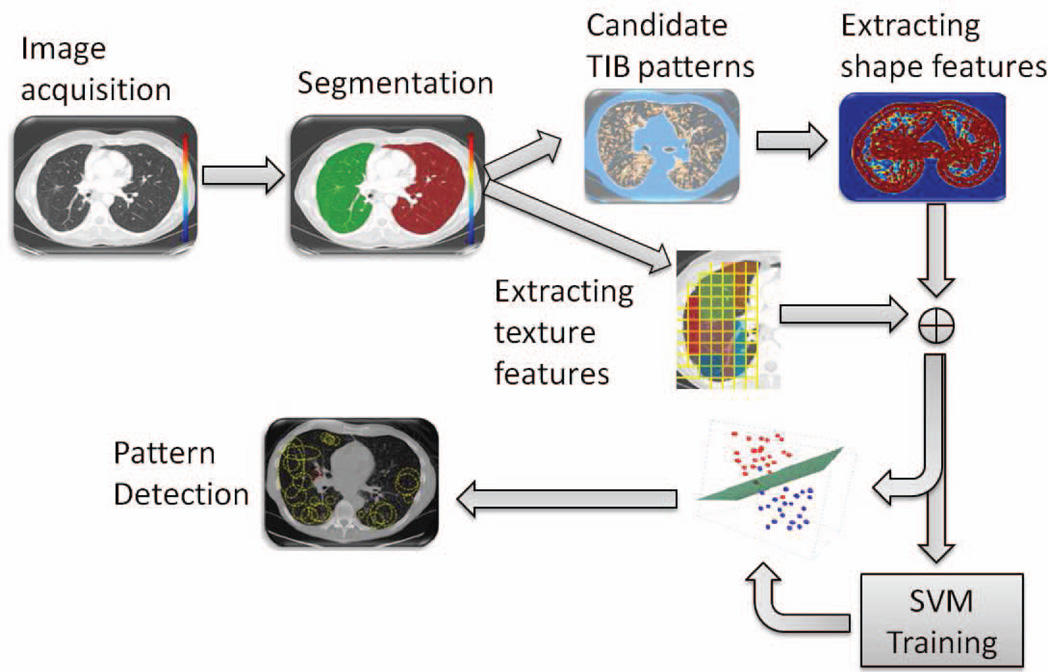
To fully appreciate how the proposed quantification system is designed, we summarize the detection component of the CAD system in this section. The detection method is illustrated in Fig. 2. After lungs were segmented from CT images using clinically accepted and validated fuzzy connectedness image segmentation algorithm [10], we defined candidate TIB regions in the segmented lungs based on the local scale (i.e., size) information of the images. Small scale valued patterns were selected as candidate regions and then for each local region enclosing candidate patterns, we extracted the texture and shape features. This process reduces the number of regions from which features were extracted. Similar to the feature extraction step in most of the CAD studies, the lung regions were divided into equal size blocks (9 × 9 pixels) and each block was used to extract predefined feature sets. For this step, we extracted 8 local shape features, including the Willmore energy and local shape features such as mean curvature, Gaussian curvature, shape index, elongation, shear, compactness, and distortion [9]. Moreover, we also extracted 18 texture (GLCM) features [11] from each block and combined these features with local shape features extracted previously (a total of 26 features for each local region). Extracted features are summarized in Table 1. Finally, we classified the extracted features through support vector classification (SVM), which we trained the classifier in training and adapt its parameters, respectively. The whole data set was randomly divided into training and test sets. Parameters of the SVM classifiers were learned based on the CT scans pertaining to the training set. SVM regression was based on pixel-wise classification [7]. For any given image in the test step, the set of feature vectors were fed into the SVM classifiers to classify different types of tissue patterns (i.e., TIB and normal).

Fig. 2.

The flowchart of the proposed CAD system.

Table 1.

Features used for detection of the TIB patterns. Assume κ₁ and κ₂ indicate eigenvalues of the local Hessian matrix (H_e) for any given local patch ℒ, K and H indicate Gaussian and mean curvature respectively, dA is the induced area metrics on Σ, and ds is length metric on ∂Σ.

Extracted features	Definition
Willmore Energy	∫Σ |H|2 dA − ∫∂Σ |K|ds
Shape index	$\mathit{\text{SI}}=\frac{2}{\pi }\mathit{\text{arctan}}(\frac{{\kappa }_1+{\kappa }_2}{{\kappa }_1-{\kappa }_2})\in [-1,1]$
Gaussian curvature	K = κ1κ2
Mean curvature	H = (κ1 + κ2) / 2
Elongation	κ2 / κ1 with κ2 ≤ κ1
Distortion	|κ1 − κ2|
Shear	(κ1 − κ2)2 / 4
Compactness	$1/(4\pi \sqrt{{\kappa }_1{\kappa }_2})$
Grey level	autocorrelation, contrast, entropy,
Co-Occurrence	variance, dissimilarity, homogeneity,
Matrix (GLCM) based	cluster shade, energy, max probability,
texture features	sum of averages, difference of variance,
	sum of squares of variance, mutual information,
	sum of variance,sum of entropy
	difference of entropy, normalized inverse,
	cluster prominence, difference moment.

2.2. Scale based quantification

Among local scale based approaches, the ball-scale (b-scale) method has been shown to be very useful in explicitly representing objects contained in the images [9, 10]. The main idea in b-scale encoding is to determine the size of local structures at every voxel as the radius of the largest ball centered at the voxel within which intensities were homogeneous under a pre-specified region-homogeneity criterion. We briefly explained below how b-scale scene is computed:

In the 2D digital space (Z², ν), a scene 𝒞 = (C, f) is represented by a pair where C is a rectangular array of voxels, ν = (ν₁, ν₂) indicates the size of the voxels, and f is a function that assigns to every voxel an image intensity value. A ball B_k,ν (c) of radius k ≥ 0 centered at a voxel c ∈ C in 𝒞 is defined by

$$B_{k,\nu }(c)=\left\{e\in C|\sqrt{{\displaystyle \sum _{i=1}^n\frac{{\nu }_i^2{(c_i-e_i)}^2}{{\mathit{\text{min}}}_j[{\nu }_j^2]}}}\le k\right\}.$$ (1)

The fraction of object is denoted by FO_k,ν (c) and indicates the fraction of the ball boundary occupied by a region which is sufficiently homogeneous with c. FO_k,ν(c) was defined as

$${\mathit{\text{FO}}}_{k,\nu }(c)=\frac{{\displaystyle {\sum }_{e\in B_{k,\nu }(c)-B_{k-1,\nu }(c)}{W}_{\psi }(|f(c)-f(e)|)}}{|B_{k,\nu }(c)-B_{k-1,\nu }(c)|}$$ (2)

where |B_k,ν (c) − B_k−1,ν(c)| is the number of voxels in B_k,ν (c) − B_k−1,ν (c) and W_ψ is a homogeneity function [10]. In all experiments, we used a zero-mean un-normalized Gaussian function for W_ψ. The size of the local structure was estimated using appearance information of the grey-level images, i.e., region-homogeneity criterion, b-scale scenes contain rough geometric information. A detailed description of W_ψ and FO_k,ν is presented in [10].

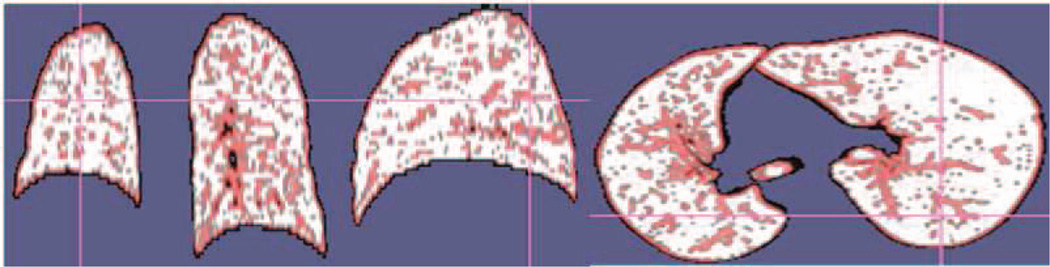
We observed from a sample TIB region shown in Fig. 1(b) and (c) that TIB patterns were localized only in the vicinity of small homogeneous regions, and their boundaries have high curvatures due to the nature of its complex shape. These observations (i.e., size and high intensity variation) provided useful information: in the feature extraction process, we only extracted features if and only if at least “one” small b-scale pattern exists in the local regions. That is, we thresholded b-scale scenes specifically so only the smallest b-scale patterns remained in the scene [9]. Fig. 3 shows smallest b-scale patterns left on the segmented lungs after thresholding. Each pattern, with its local surrounding region (i.e., 9×9 pixels), is considered a candidate TIB region and features are extracted from these regions [9].

Fig. 3.

Candidate TIB voxels are obtained by thresholding b-scale scenes.

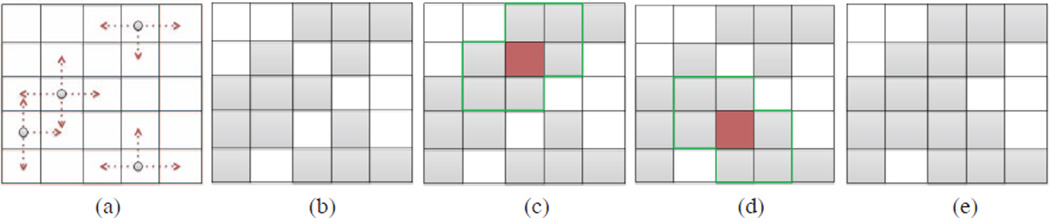
In return, we used a similar scale based approach for the quantification. For any local region ℒ_i (i.e., block), if the region was classified as a region with TIB patterns through SVM, then we checked the corresponding b-scale region ℬ_i of ℒ_i. Next, we identified smallest valued scales in the scene by thresholding (Fig.4(a)). For each b-scale pattern remained after thresholding, we labelled 4-neighbours of those patterns as TIB patterns (see Fig.4(b)). Although the connected component algorithm correctly labels pixels throughout the most of the region, some pixel may remain mislabelled (Fig.4(c) and (d)). Pixels were determined to be mislabelled if all surrounding pixels are classified as TIB and the pixel was labelled as non-TIB, since the probability of this occurrence is usually very low. This determination procedure was based on the observations on the characteristics of shape and intensity profiles of TIB patterns described previously in Fig. 1 (b) and (c). Hence, in order to label those regions correctly, we applied an additional step for identifying mislabelled pixels by considering the 4-neighbours of each unlabelled pixel, and refine the pixel classification respectively (Fig.4(e)).

Fig. 4.

(a) smallest b-scale patterns. (b) Connected-components of each pattern is labelled. (c and d) Possible mislabelled pixels are shown. (e) Refinement of labelled regions.

2.3. Visual grading scheme

To analyze existence and dispersion of abnormality, as well as normality of subjects, a visual grading system was adapted. Each lung was divided into three zones (for a bilateral total of six) as shown in Fig. 5A. Zone 1 included the apex to the carina. Zone 2 extended from the tracheal carina to the left atrium’s junction with inferior pulmonary veins. Zone 3 included the remainder of the lungs below the level of the inferior pulmonary veins atrial junction. A severity score (0 to 5) was assigned to each zone based on the percentage of the zone occupied as listed in Fig. 5B. Consensus visual scores from participating radiologists having more than ten years of specialized experience (DMJ and AW) on a scale of 0–5 over the entire lung volume. These visual scores were recorded and compared with computer scores (of the proposed CAD system). Following the same visual scoring scheme, another participating radiologist (OA), who was blinded to the consensus visual scores previously obtained, was involved in the visual grading process to provide information on inter-observer variability.

Fig. 5.

(A) Lungs are divided into three zones (left). Rough anatomical locations separating zones are shown in coronal (middle) and axial CT slices (right), respectively. (B) Visual Grading Scheme.

3. RESULTS

3.1. Data

With Institutional Review Board (IRB) approval, 39 CTs of human parainfluenza virus (HPIV) infection, 34 CTs of nontuberculous mycobacterial (NTM) infection, and 21 normal lung CTs were collected for these experiments. These infections were confirmed from laboratory data at our institution from nasopharyngeal washings (NPW) and/or bronchioalveolar lavage (BAL). All patients were imaged at our institution using a 64-detector row Philips Brilliance or a 320-detector row Toshiba Aquilion CT scanner. The non-contrasted chest CT studies were performed at end-inspiration with 1.0 or 2.0 collimation obtained at 10 or 20 mm intervals from the base of the neck to upper abdomen with a tube voltage of 120 kV and a current of 200–320 mA depending on the subject’s weight. Imaging data were constructed to 512×512 matrices with slice thickness of 5 mm. The in-plane resolution was affected by patients’ size and varied from 0.62 mm to 0.82 mm. For the HPIV infected subjects and normal subjects, one CT scan was collected per patient, for a total of 39 and 21 scans respectively (no multiple-scans from subjects). However, baseline and follow-up scans (two scans) were obtained from the 17 subjects infected with NTM virus, for a total of 34 CT scans, at different time points in order to measure disease progression.

3.2. Quantitative and qualitative evaluations

We compared the consensus reading of two expert observers (AW and DJM) to another expert observer (OA), who was blinded to the consensus scores. We used Pearson product-moment correlation coefficients to determine inter-observer agreement over each zone, left, right, and all lung volumes. An overall correlation coefficient of R² = 0.77 (p < 0.01) for all subjects indicates a good agreement on the existence of TIB patterns. This agreement may decrease to R² = 0.6 (p < 0.01) if a conventional region labelling is used instead of a scale based quantification method.

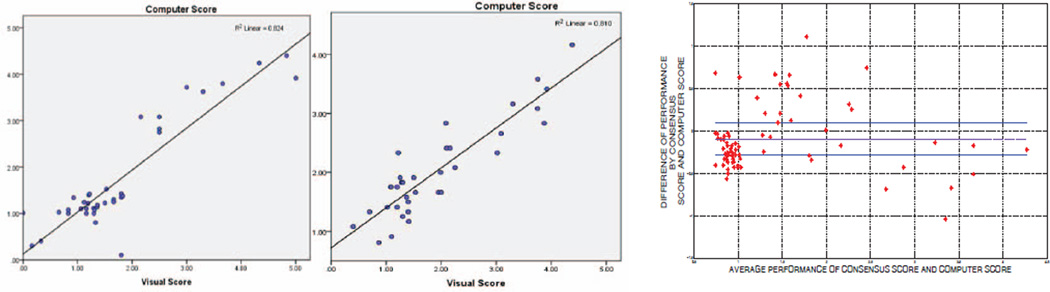
A computer score was calculated by averaging the volume occupied by the labelled TIB regions computed from the scale based quantification algorithm. Calculated computer score was then normalized to fit the visual grading scheme. Linear regression model was fitted to all subjects’ scores both from computer and the consensus scores. Scatter-plots of the linear regression model and the computer-observer agreement correlation are shown in Fig. 6 (left and middle). Furthermore, in the Bland-Altman plot shown in Fig. 6(right), the difference of the computer performance and consensus scoring performance was plotted against the average of the performances. It is clear from these plots that visual and quantitative assessments correlate well as indicated by the Pearson product-moment correlation of R² = 0.824 (p < 0.01) and R² = 0.81 (p < 0.01) for HPIV and NTM subjects, respectively.

Fig. 6.

Visual grading versus computer evaluation for HPIV subjects (left figure) and NTM subjects (middle figure). Bland-Altman scatter-plot for all HPIV and NTM quantification is drawn together for analysis of variability between CAD system and consensus reading by interpreters (right figure).

4. DISCUSSION AND CONCLUSION

In this study, we propose a local-scale based method for quantifying TIB pattern from CT scans by integrating quantification algorithms with the CAD system. This study shows high correlations between CAD and visual grading scores, suggesting that CAD-based quantification of TIB is a viable technique for assessing infectious disease of the lungs. Further studies aim to include detection and quantification of other pulmonary patterns on CT.