KERNEL-BASED MULTI-TASK JOINT SPARSE CLASSIFICATION FOR ALZHEIMER’S DISEASE

Abstract

Multi-modality imaging provides complementary information for diagnosis of neurodegenerative disorders such as Alzheimer’s disease (AD) and its prodrome, mild cognitive impairment (MCI). In this paper, we propose a kernel-based multi-task sparse representation model to combine the strengths of MRI and PET imaging features for improved classification of AD. Sparse representation based classification seeks to represent the testing data with a sparse linear combination of training data. Here, our approach allows information from different imaging modalities to be used for enforcing class level joint sparsity via multi-task learning. Thus the common most representative classes in the training samples for all modalities are jointly selected to reconstruct the testing sample. We further improve the discriminatory power by extending the framework to the reproducing kernel Hilbert space (RKHS) so that nonlinearity in the features can be captured for better classification. Experiments on Alzheimer’s Disease Neuroimaging Initiative database shows that our proposed method can achieve 93.3% and 78.9% accuracy for classification of AD and MCI from healthy controls, respectively, demonstrating promising performance in AD study.

1. INTRODUCTION

As a worldwide prevalent neurodegenerative disorder, Alzheimer’s disease (AD) is a common type of dementia that affects elderly people. Accurate diagnosis of AD and its prodrome, mild cognitive impairment (MCI), is crucial for possible treatment. Currently, various biomarkers have been investigated for early diagnosis of AD, including brain atrophy measured by magnetic resonance imaging (MRI), hypometabolism measured by positron emission tomography (PET), and biological/genetic biomarkers measured in cerebrospinal fluid (CSF).

Multi-modality imaging provides complementary information for diagnosis of AD. Considerable research efforts have been directed to combine information from different imaging modalities to improve diagnosis of AD [1, 2]. For example, Zhang et al. [1] proposed a multi-kernel method to improve diagnosis performance by weighted combination of kernels for 3 modalities: MRI, PET, and CSF. Grid-search was used to find the optimal weights for each modality kernel. The mixed kernel was finally fed into a standard SVM for classification between AD/MCI patients and normal controls. Despite these efforts, the efficient utilization and combination of information from different imaging modalities remains a challenging problem.

Motivated by multi-task sparse representation and classification for visual objects in [3], we propose a multi-task sparse representation framework to combine the strengths of MRI and PET imaging features for better classification of AD. Our framework is inspired by sparse representation-based classification (SRC), which has been applied to face recognition with good performance [4]. SRC assumes that, if sufficient training samples are available from each class, it is possible to represent each testing sample by a linear combination of a sparse subset of the training samples. The class label of the testing sample is assigned as the class with the minimum representation residual over all classes.

The use of l₁-norm regularization can further enhance the robustness to occlusion and illustration changes [4]. To combine features of two imaging modalities for classification, a simple solution is to apply SRC to features from each imaging modality independently, and then combine the classification results for making final classification. However, this approach ignores the correlation of the different imaging modalities. A multi-task learning scheme can be used to capture the cross-task relations when the tasks to be learned share some latent factors. This is especially important when the number of training samples is small - transferring some knowledge between tasks will help improve the classification performance.

In our framework, SRC using each modality is considered as one task. A multi-task learning scheme is applied to concurrently compute the sparse representations associated with features from two imaging modalities, i.e., MRI and PET. Joint sparsity is imposed across different tasks on the representation coefficients via a l_2,1-norm penalty [5]. Thus, multi-task sparse representation models can be simultaneously estimated with proper regularization on the parameters across all the models. This will increase the robustness and accuracy in determining a common class of training samples that are most related to the testing sample. We further improve the discriminant power of the features by using a nonlinear kernel. That is, we extend the multi-task SRC framework to the reproducing kernel Hilbert space (RKHS) as in [3]. The kernel-based multi-task SRC (KMT-SRC) can thus model the nonlinearity of the feature space for greater separability and more accurate classification of AD.

We evaluated our method with the baseline MRI and PET imaging data from Alzheimer’s Disease Neuroimaging Initiative (ADNI) database. Experimental results indicate that the proposed KMT-SRC method, which combines both the kernel-based method and the multi-task SRC method, can achieve better performance on AD and MCI classification, compared to the traditional SRC methods. The organization of the paper is as follows. Section 2 presents the proposed method in detail. Then experimental results are presented in Section 3. Finally, conclusions are provided in Section 4.

2. METHOD

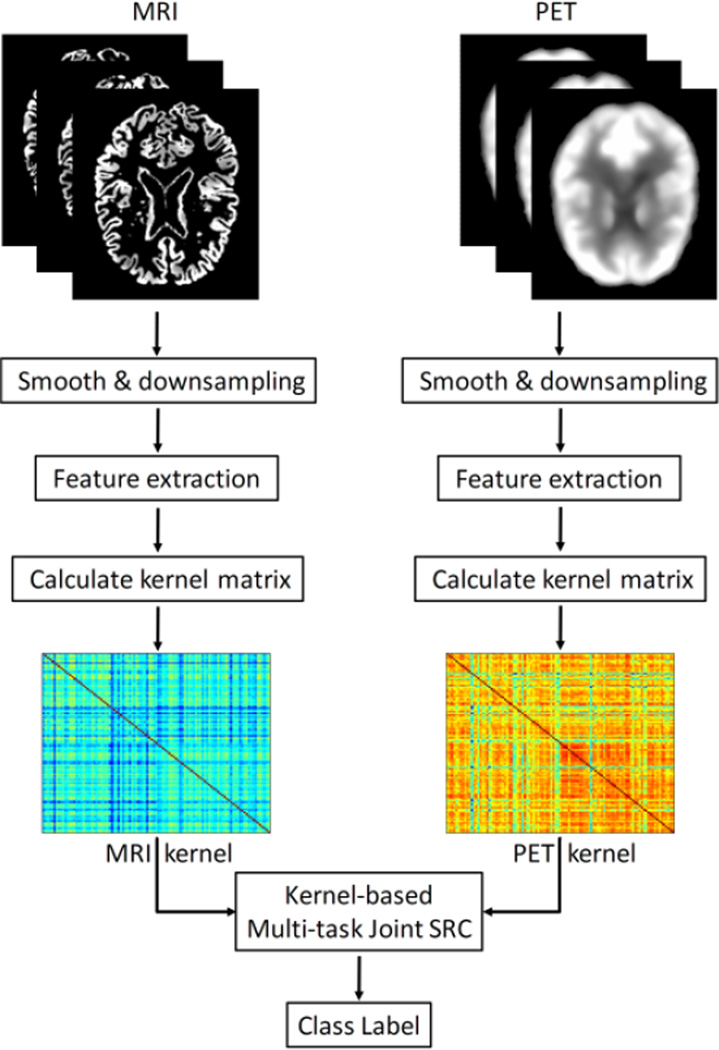
In this paper, we propose using a kernel-based multi-task sparse representation method to combine different modality neuroimaging features for AD and MCI classification. Here, classification problems using features from different modalities are regarded as different tasks. The proposed classification algorithm is summarized in the schematic shown in Fig. 1. We evaluated the proposed classification algorithm with both baseline MRI and PET images in the ADNI database.

Fig. 1.

Schematic illustration of the proposed kernel-based multi-task sparse classification pipeline.

2.1. Image preprocessing and feature extraction

First, all MRI and PET images were pre-processed. MR brain images were skull-stripped [6] and cerebellum-removed after intensity inhomogeneity correction. Then each brain image was segmented into three different tissue types: grey matter (GM), white matter (WM), and cerebrospinal fluid (CSF). The tissue density of each tissue type was captured in a stereotaxic space by mass-preserving deformable spatial normalization [7]. The PET images were rigidly aligned to their respective MRI images. For consistency, all images were resampled to size 256× 256×256 and resolution 1×1×1 mm³. The tissue density maps and PET images were further smoothed using a Gaussian kernel (with unit standard deviation) to improve signal to noise ratio. Note that only the GM density map was used in this study because pathologies associated with AD are known to be manifested as GM changes. The voxel values of the GM density maps and the PET intensity images were used as features for classification.

2.2. Multi-task sparse representation-based classification (MT-SRC)

Sparse representation-based classification (SRC) has been recently demonstrated effective for robust multi-class classification. It exploits the discriminative nature of sparse representation for effective classification. The l₁-norm penalization is used to select a small subset of training samples to best represent a testing sample. The objective function can be formulated as follows [4]:

$$\mathit{\alpha ̂}={\text{argmin}}_{\mathit{\alpha }}{\Vert \mathit{\alpha }\Vert }_1,\text{subject to}{\Vert \mathit{A}\mathit{\alpha }-\mathit{y}\Vert }_2^2\le \epsilon ,$$ (1)

where A = [A₁, …, A_c, …, A_C] represents the training samples from C classes, with each column representing a feature vector of one training sample; α = [α₁, …, α_c, …, α_C] represents the coefficient vector corresponding to all training samples; y represents the feature vector of the testing sample; and ε > 0 is the tolerance error. Given the optimal estimated α̂, the class label of y is assigned as the class with the minimum residual over all classes, e.g.,

$$l(\mathit{y})={\text{argmin}}_c{\Vert {\mathit{A}}_c{\mathit{\alpha ̂}}_c-\mathit{y}\Vert }_2^2.$$ (2)

The above SRC model is defined only for single-modality features. Recently, it has been shown that combining complementary features from different modalities helps improve classification accuracy. In this respect, multi-task learning has received a lot of attention. This method takes explicit consideration of relations between tasks for improved classification. In this paper, a multi-task sparse representation framework is proposed to combine features from different imaging modalities. More specifically, we impose class-level sparsity to allow multiple imaging modalities to help jointly select the training samples of a common class to represent a testing sample. This can be realized through a regularization framework [5], where the joint sparsity regularization will favor learning a common subset of features for all tasks. For a training dataset with C classes (i.e., C = 2 in our study) and each sample with M different modalities, the multi-task sparse representation can be formulated as follows:

$$\mathit{Û}={\text{argmin}}_{\mathit{U}}(\frac{1}{2}\sum _{m=1}^M{\Vert {\mathit{A}}^m{\mathit{U}}^m-{\mathit{y}}^m\Vert }_2^2+\lambda \sum _{c=1}^C{\Vert {\mathit{U}}_c\Vert }_2),{\mathit{A}}^m=[{\mathit{A}}_1^m,\dots ,{\mathit{A}}_c^m,\dots ,{\mathit{A}}_C^m],{\mathit{U}}^m=[{\mathit{U}}_1^m,\dots ,{\mathit{U}}_c^m,\dots ,{\mathit{U}}_C^m],{\mathit{U}}_c=[{\mathit{U}}_c^1,\dots {\mathit{U}}_c^m,\dots ,{\mathit{U}}_c^M],\mathit{U}=[{\mathit{U}}^1,\dots ,{\mathit{U}}^m,\dots ,{\mathit{U}}^M].$$ (3)

where the l₂-norm is imposed on U_c for combining the strength of all the atoms within class c, and the l₁-norm applied across the l₂-norm of the U_c is used for promoting sparsity to allow just the common class to be involved in joint sparsity representation. As a result, the testing sample y will be reconstructed by the common most representative classes in the training samples for all tasks. Given the estimated optimal coefficient matrix Û, the class label for the testing sample is set as the class with the lowest residual accumulated over all M tasks:

$$l(\mathit{y}=[{\mathit{y}}^1,\dots ,{\mathit{y}}^m,\dots ,{\mathit{y}}^M])={\text{argmin}}_c\sum _{m=1}^M{\Vert {\mathit{A}}_c^m{\mathit{Û}}_c^m-{\mathit{y}}^m\Vert }_2^2.$$ (4)

2.3. Kernel-based Multi-task sparse representation-based classification (KMT-SRC)

Kernel methods have the ability to capture the nonlinear relationships between features in a high dimensional space. It has been shown that the kernel-based sparse representation method can further improve the recognition accuracy [8]. Accordingly, we further extend our framework to work in the reproducing kernel Hilbert space (RKHS). Given a nonlinear mapping function ψ for mapping the feature A^m in the original space to the high dimensional feature space as ψ(A^m), in the new RKHS the objective function of MT-SRC in Equation (3) can be rewritten as:

$$\mathit{Û}={\text{argmin}}_{\mathit{U}}(\frac{1}{2}\sum _{m=1}^M{\Vert \psi ({\mathit{A}}^m){\mathit{U}}^m-\psi ({\mathit{y}}^m)\Vert }_2^2+\lambda \sum _{c=1}^C{\Vert {\mathit{U}}_c\Vert }_2)={\text{argmin}}_{\mathit{U}}(\frac{1}{2}\sum _{m=1}^M{\Vert \sum _{c=1}^C\psi ({\mathit{A}}_c^m){\mathit{U}}_c^m-\psi ({\mathit{y}}^m)\Vert }_2^2+\lambda \sum _{c=1}^C{\Vert {\mathit{U}}_c\Vert }_2,)$$ (5)

where $\psi ({\mathit{A}}_c^m)=[\psi ({\mathit{A}}_{c,1}^m),\dots ,\psi ({\mathit{A}}_{c,n_c}^m)]$, and ${\mathit{A}}_c^m$ represents the n_c columns of A^m associated with n_c samples in the c-th class. According to [3], Equation (5) can be kernelized. Assuming kernel function η, so $\eta ({\mathit{A}}_c^m,{\mathit{A}}_c^m)=\psi {({\mathit{A}}_c^m)}^T\psi ({\mathit{A}}_c^m)$ and $\eta ({\mathit{A}}_c^m,{\mathit{y}}^m)=\psi {({\mathit{A}}_c^m)}^T\psi ({\mathit{y}}^m)$ according to the kernel theory. With the optimal reconstruction coefficient matrix Û estimated, the classification decision is made by

$$l(\mathit{y})={\text{argmin}}_c\sum _{m=1}^M{\Vert \psi ({\mathit{A}}_c^m){\mathit{Û}}_c^m-\psi ({\mathit{y}}^m)\Vert }_2^2={\text{argmin}}_c\sum _{m=1}^M(-2\eta ({\mathit{A}}_c^m,{\mathit{y}}^m){\mathit{Û}}_c^m+{({\mathit{Û}}_c^m)}^T\eta ({\mathit{A}}_c^m,{\mathit{A}}_c^m){\mathit{Û}}_c^m).$$ (6)

In this paper, the Gaussian radial basis function kernel is adopted for η, with $\eta ({\mathit{A}}_c^m(i),{\mathit{A}}_c^m(j))=\text{exp}(-k{\Vert {\mathit{A}}_c^m(i)-{\mathit{A}}_c^m(j)\Vert }_2^2/\mu )$. ${\mathit{A}}_c^m(i)$ is the i-th sample in the m-th modality of class c. μ is set as the mean value of the pairwise Euclidean distances between the feature vectors over all the training samples. To better adapt to the different datasets, we allow k ∈ [0.01,100] for tuning the parameter μ.

3. RESULTS

We evaluated the effectiveness of the proposed classification algorithm based on the baseline MRI and PET images obtained from the ADNI.

3.1. Subjects

Table 1 shows the demographic information of the population studied in this work, where MMSE and CDR are the acronyms of Mini-Mental State Examination and Clinical Dementia Rating, respectively. 202 subjects are studied in total, including 52 healthy control (HC) subjects, 99 MCI patients, and 51 AD patients. The voxel values of the GM density maps and the PET intensity image are utilized as classification features. To reduce computation cost, we down-sampled all GM tissue density maps and PET intensity images to size 64×64×64.

Table 1.

Demographic information of the studied population (from the ADNI dataset). The values shown here are the means (standard deviations).

Diagnosis	Age	Education	MMSE	CDR
HC (n=52)	75.3(5.2)	15.8(3.2)	29.0(1.2)	0.0(0.0)
MCI(n=99)	75.3(7.0)	15.9(2.9)	27.1(1.7)	0.5(0.0)
AD (n=51)	75.2(7.4)	14.7(3.6)	23.8(2.0)	0.7(0.3)

3.2. Experimental Setup

In the following experiments, 10-fold cross-validation was performed to evaluate the performance of different classification methods in terms of accuracy, sensitivity and specificity. The population of images was randomly partitioned into 10 equal size subpopulations. Of the 10 subpopulations, a single subpopulation was retained as the testing data for evaluating the classification accuracy, and the remaining 9 subpopulations were used as training data. Note that, for parameter tuning, the training data was further partitioned for another training and validation subpopulations. It is also based on a 10-fold cross-validation procedure. We compared the proposed method with sparse representation-based classification (SRC) applied on each single modality, kernel-based SRC (KSRC) applied on each single modality, and Multi-task based SRC (MT-SRC). For all these methods, their respective optimal regularization parameter λ was obtained through cross-validation using grid search.

3.3. Experimental Results

The classification results for AD vs. HC and MCI vs. HC are shown in Tables 2 and 3, respectively. As can be seen from the tables, the KSRC consistently achieves better performance than SRC for both AD classification and MCI classification. MT-SRC also consistently achieves better result than SRC. Our method, by embedding the kernel-based method into the multi-task sparse representation framework, yields significant improvement on both AD classification and MCI classification, in terms of accuracy, sensitivity, specificity, and Area under the ROC curve (AUC), compared with all other methods. The classification accuracy is 93.3% and 78.9% for AD classification and MCI classification, respectively. These are comparable to 93.2% and 76.4% reported in [1], which uses multi-kernel SVM to combine 3 modalities (MRI+PET+CSF), while our method uses only 2 imaging modalities (MRI+PET). That is, we could obtain similar or even better performance with a smaller number of imaging modalities. When we use the same modalities (MRI+PET), taking the AD vs. HC classification for example, the classification accuracy is 93.3%, which is significantly better than the accuracy result of 90.6% reported in [1]. Note that for most methods the specificity values are significantly lower than the sensitivity values in MCI vs. HC classification experiment. This is due to the imbalanced number of subjects between the two groups, i.e., the number of MCI subjects is almost twice of that of HC subjects. The same situation occurred in [1]. On the other hand, the AD classification experiment with matched number of subjects gives relatively high and balanced sensitivity and specificity values, with the proposed method still superior to all other methods.

Table 2.

Results for AD vs. HC classification. (ACC=Accuracy, SEN=Sensitivity, SPE=Specificity, AUC=Area under ROC).

Methods	ACC %	SEN %	SPE %	AUC
SRC-MRI	83.7	78.3	89.1	0.917
SRC-PET	84.7	80.3	89.1	0.927
KSRC-MRI	84.7	86.3	83.1	0.935
KSRC-PET	86.2	80.0	92.6	0.940
MT-SRC	86.3	80.4	92.4	0.941
Proposed	93.3	90.0	96.6	0.970

Table 3.

Results for MCI vs. HC classification. (ACC=Accuracy, SEN=Sensitivity, SPE=Specificity, AUC=Area under ROC).

Methods	ACC %	SEN %	SPE %	AUC
SRC-MRI	71.4	79.4	55.4	0.741
SRC-PET	72.1	80.0	56.9	0.748
KSRC-MRI	74.3	81.7	60.3	0.756
KSRC-PET	75.0	82.2	60.9	0.763
MT-SRC	74.9	83.3	60.0	0.769
Proposed	78.9	85.6	66.3	0.807

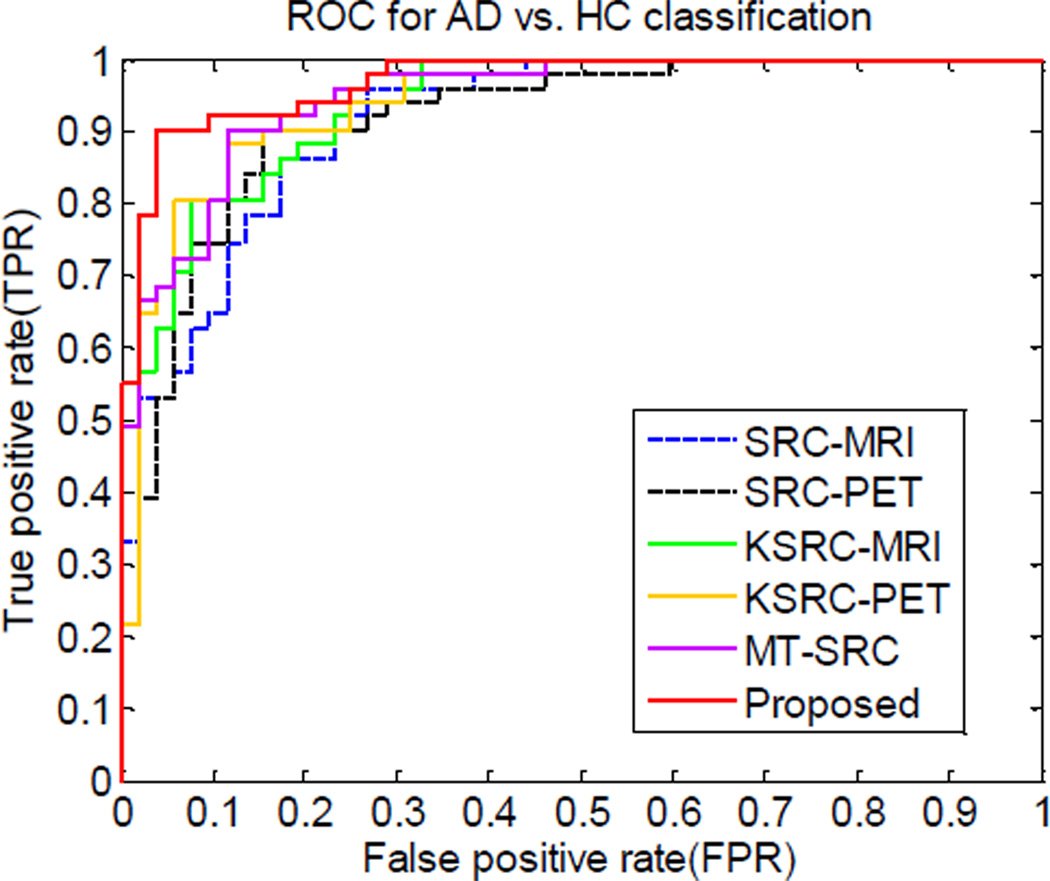
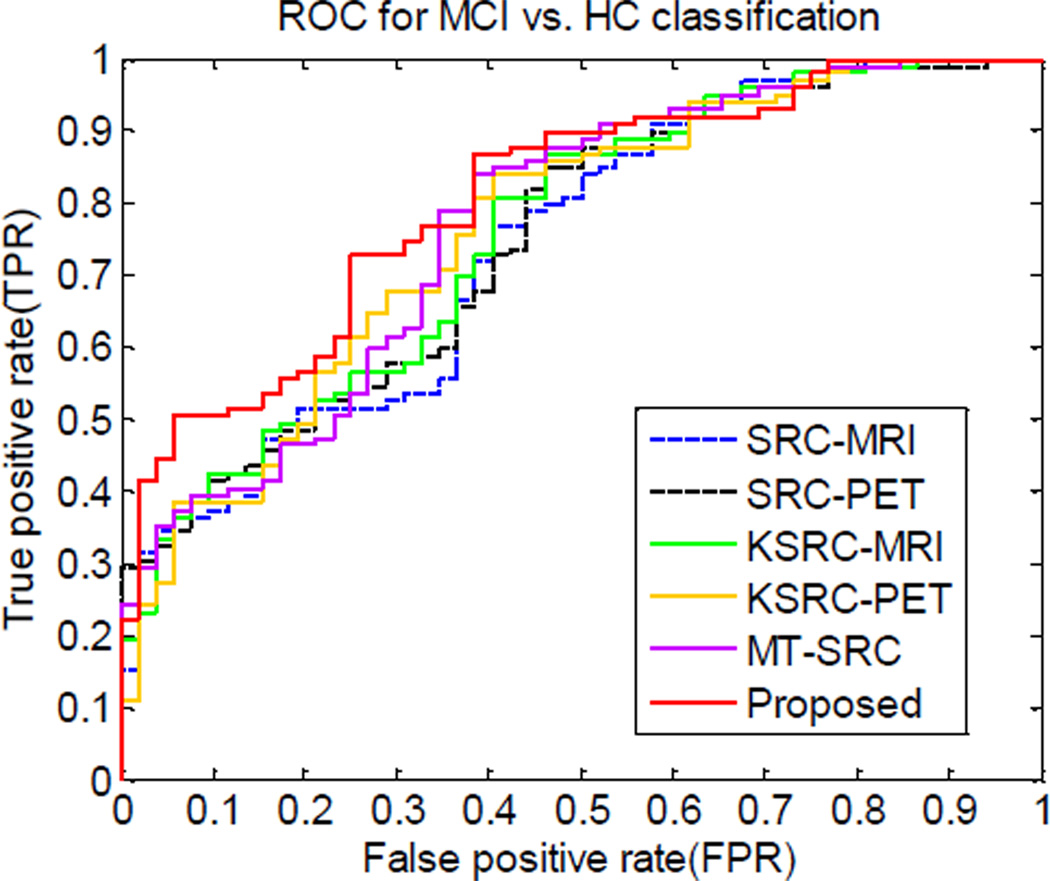
The AUC values of different methods are presented in Table 2 and Table 3 for AD classification and MCI classification experiments, respectively. The corresponding ROC curves of the different methods for AD classification and MCI classification are illustrated in Fig. 2 and Fig. 3. From Fig. 2, it can be observed that both KSRC and MT-SRC are superior to SRC. Our proposed method performed better than all other methods, with AUC of 0.970, which agrees with the results in Table 2. Similar conclusion can also be drawn from the ROC curves in MCI classification (Fig. 3). The proposed method is superior to all other methods, with AUC of 0.807.

Fig. 2.

ROC curves for the different methods in AD vs. HC classification.

Fig. 3.

ROC curves for the different methods in MCI vs. HC classification.

4. CONCLUSION

We have presented a kernel-based multi-task sparse representation method to combine multi-modality imaging data for AD and MCI classification. By embedding the kernel-based method in the multi-task sparse representation framework, it greatly improves the feature separability in high dimensional space. And the multi-task sparse representation framework further helps jointly select the representative training samples in the same class to represent the testing sample image over different modality features via a class-level sparsity term. The strengths of features from different imaging modalities are thus effectively combined. Experimental results using the ADNI database showed that the proposed method achieves greater accuracy in both AD classification and MCI classification.