ACCELERATING CARDIOVASCULAR IMAGING BY EXPLOITING REGIONAL LOW-RANK STRUCTURE VIA GROUP SPARSITY

Abstract

Sparse sampling of (k, t)-space has proved useful for cardiac MRI. This paper builds on previous work on using partial separability (PS) and spatial-spectral sparsity for high-quality image reconstruction from highly undersampled (k, t)-space data. This new method uses a more flexible control over the PS-induced low-rank constraint via group-sparse regularization. A novel algorithm is also described to solve the corresponding (1,2)-norm regularized inverse problem. Reconstruction results from simulated cardiovascular imaging data are presented to demonstrate the performance of the proposed method.

1. INTRODUCTION

Real-time cardiovascular magnetic resonance imaging (MRI) has many potential applications. However, imaging speed is still a major issue, especially for higher-dimensional imaging such as whole-heart 3D dynamic imaging. Earlier efforts to increase imaging speed primarily focused on fast-scanning pulse sequences and parallel imaging. A new class of methods based on sparse sampling of (k, t)-space has also emerged with the potential to further accelerate cardiovascular MRI. Demonstrated approaches to sparse sampling for cardiac MRI include specialized sampling and modeling methods [1], (r, f)-space packing methods [2, 3], low-rank modeling methods [4–8], compressed sensing (CS) methods [9–11], joint low-rank modeling and CS methods [12, 13], and most recently, (r, f)-space group sparsity methods [14].

This paper presents further development of fast cardiac imaging using sparse sampling of (k, t)-space, wherein we exploit the specific low-rank structure of cardiac images. Within the framework of the partial separability (PS) model [5], we impose a novel spatially-varying rank constraint on the spatial components via group-sparse regularization. This imaging model assigns varying model orders (i.e., effective ranks) to different spatial regions of the image so that a higher model order can be used over the cardiac region than over the rest of the image. This provides flexible control over the low-rank constraint. The proposed method can be further integrated with fast scanning pulse sequences and parallel imaging to provide even higher acceleration of cardiovascular MRI.

The remainder of this paper is organized as follows: Section 2 describes the proposed method in detail, specifically the data acquisition procedure, the imaging model, and the algorithm to solve the resulting inverse problem; Section 3 presents representative reconstruction results from simulations using a numerical cardiovascular phantom; and Section 4 contains the conclusion of the paper.

2. THE PROPOSED METHOD

2.1. Data Acquisition

We will focus on Fourier-encoded MRI, in which the measured signal d(k, t) from a dynamic image I(r, t) can be expressed as

$$d(\mathbf{k},t)={\int }_{-\infty }^{\infty }I(\mathbf{r},t)e^{-i2\pi \mathbf{k}·\mathbf{r}}d\mathbf{r}.$$ (1)

We use a typical PS model-motivated sparse sampling strategy to cover (k, t)-space [4–6], although other sampling strategies may also be appropriate. The strategy employed in this paper interleaves two sampling schemes. One scheme densely samples a region of (k, t)-space which has limited k-space extent (i.e., samples in high temporal resolution but low spatial resolution); the other scheme sparsely samples the “full” (k, t)-space with greater k-space extent, (i.e., samples with high spatial resolution but low temporal resolution). Fig. 1 illustrates this sampling strategy. This strategy is useful for PS model-based imaging because it allows direct estimation of the temporal subspace of I(r, t) from the densely sampled data. This temporal subspace can then be used to constrain image reconstruction from the sparsely sampled data.

Fig. 1.

A typical (k, t)-space sparse sampling scheme for PS model-based imaging. The dense sampling set is marked by filled circles, and the sparse sampling set is marked by outlined circles.

2.2. Image Model

The PS image model represents I(r, t) as

$$I(\mathbf{r},t)=\sum _{\ell =1}^L{p}_{\ell }(\mathbf{r})q_{\ell }(t),$$ (2)

where p_ℓ(r) and q_ℓ (t) can be viewed as the ℓth set of spatial coefficients and the ℓth temporal basis function, respectively. The PS model implies a low-rank structure for I(r, t). Specifically, the matrix

$$\mathbf{C}=\left[\begin{array}{cccc}I({\mathbf{r}}_1,t_1)& I({\mathbf{r}}_1,t_2)& \dots & I({\mathbf{r}}_1,t_N)\\ I({\mathbf{r}}_2,t_1)& I({\mathbf{r}}_2,t_2)& \dots & I({\mathbf{r}}_2,t_N)\\ ⋮& ⋮& \ddots & ⋮\\ I({\mathbf{r}}_M,t_1)& I({\mathbf{r}}_M,t_2)& \dots & I({\mathbf{r}}_M,t_N)\end{array}\right]$$

has at most rank L [5]. This property yields the factorization C = PQ, where P_ij = p_j (r_i) and Q_ij = q_i(t_j).

In (2), a uniform rank is assumed over the entire image using a shared temporal subspace. However, cardiac and non-cardiac spatial regions are associated with different types of motion that can be expressed in different temporal subspaces. Specifically, we can partition the image function as

$$I(\mathbf{r},t)=\{\begin{array}{cc}{\sum }_{\ell =1}^K{p}_{\ell }(\mathbf{r})q_{\ell }^{(1)}(t),& \text{if}\mathbf{r}\notin \mathrm{\Omega }\\ {\sum }_{\ell =1}^L{p}_{\ell }(\mathbf{r})q_{\ell }^{(2)}(t),& \text{if}\mathbf{r}\in \mathrm{\Omega }\end{array},$$ (3)

where ${\{q_{\ell }^{(1)}(t)\}}_{\ell =1}^K$ and ${\{q_{\ell }^2(t)\}}_{\ell =1}^L$ span different temporal sub-spaces and Ω is the set of spatial locations within the cardiac region.

Employing the model in (3) during image reconstruction requires identifying temporal subspaces that correspond to different spatial regions given sparsely sampled (k, t)-space data, which may be difficult. On the other hand, our data acquisition scheme includes a dense subset of data with high temporal resolution, which can be arranged into the matrix

$$\mathbf{D}=\left[\begin{array}{cccc}d({\mathbf{k}}_1,t_1)& d({\mathbf{k}}_1,t_2)& \dots & d({\mathbf{k}}_1,t_N)\\ d({\mathbf{k}}_2,t_1)& d({\mathbf{k}}_2,t_2)& \dots & d({\mathbf{k}}_2,t_N)\\ ⋮& ⋮& \ddots & ⋮\\ d({\mathbf{k}}_Z,t_1)& d({\mathbf{k}}_Z,t_2)& \dots & d({\mathbf{k}}_Z,t_N)\end{array}\right]$$

with Z < M. The singular value decomposition (SVD) of D yields the matrix factorization UΣV^H. We can then use Q̂ = [v₁ v₂ … v_L]^H to estimate a temporal basis that is shared by all spatial regions. Therefore, instead of separating this temporal basis into disjoint sets, we assume overlapping temporal subspaces by using ${\widehat{q}}_{\ell }^{(1)}(t_n)={\widehat{q}}_{\ell }^{(2)}(t_n)={\widehat{\mathbf{Q}}}_{\ell n}$ for 1 ≤ ℓ ≤ K < L. Since the cardiac region has more high-order temporal components, we restrict the subspaces as

$$\text{span}({\{{\widehat{q}}_{\ell }^{(1)}(t)\}}_{\ell =1}^K)\subset \text{span}({\{{\widehat{q}}_{\ell }^{(2)}(t)\}}_{\ell =1}^L).$$ (4)

In other words, the cardiac region is represented within a space which has more degrees of freedom than the space of the non-cardiac region. A variable-rank imaging model is appropriate for cardiovascular imaging, as the non-cardiac spatial region is primarily associated with slow respiratory motion, whereas the cardiac spatial region is associated with both respiratory motion and the more rapid cardiac motion.

Although the model (4) is generally valid, it might be violated in some non-cardiac regions that exhibit high temporal activity (e.g., vasculature). In addition, strictly imposing this constraint requires accurate specification of the model orders K and L. In the interest of introducing flexibility to the regional model order selections, the proposed imaging model relaxes the assumption by allowing some areas of the non-cardiac region to take on effective model orders between K and L. This is achieved via the use of group-sparse regularization. Specifically, we consider the spatial coefficients ${\{p_{\ell }(\mathbf{r})\}}_{\ell =K+1}^L$ to be group sparse such that the majority of the non-cardiac region of the image has the effective rank K, and that the cardiac region has an effective rank between K + 1 and L. This group sparse model assumes that only a small number of predefined clusters or groups of ${\{p_{\ell }(\mathbf{r})\}}_{\ell =K+1}^L$ have nonzero energy.

Defining x_(i) as the ith group of a vector x, then x can be said to be group sparse when the set of 2-norms ${\{{\Vert {\mathbf{x}}_{(i)}\Vert }_2\}}_{i=1}^I$ is sparse. Sparsity of ${\{{\Vert {\mathbf{x}}_{(i)}\Vert }_2\}}_{i=1}^I$ is promoted by penalizing the 1-norm of the 2-norms, a mixed norm referred to as the (1,2)-norm: ${\Vert \mathbf{x}\Vert }_{1,2}={\sum }_{i=1}^I{\Vert {\mathbf{x}}_{(i)}\Vert }_2$. Unlike the signal sparsity assumption that is central to compressed sensing, there is no assumption of sparsity within any given group x_(i) itself. As such, the (1,2)-norm does not overly penalize small nonzero elements within groups. This provides an avenue to incorporate prior knowledge regarding the location of signal energy into the reconstruction process as a means of protecting subtle, but potentially important, features in those locations.

The group sparsity assumption reduces to the sparsity assumption when x_(i) = x_i (i.e., when each element of x is considered to be in its own group). Therefore, by grouping together spatial coefficients from the cardiac region, but placing non-cardiac spatial coefficients in individual groups, we can protect the cardiac region while promoting sparsity of the higher-order (i.e., ℓ > K) non-cardiac spatial coefficients.

The proposed imaging model imposes group sparsity of P by penalizing ||R{P}||_1,2, where R{P} concatenates the rightmost columns of P (i.e., p_K+1 through p_L), with (1,2)-norm grouping such that

$${\Vert R\{\mathbf{P}\}\Vert }_{1,2}=\sum _{\ell =K+1}^L\left(\sqrt{\sum _{m:{\mathbf{r}}_m\in \mathrm{\Omega }}{\mid {\mathbf{P}}_{m\ell }\mid }^2}+\sum _{m:{\mathbf{r}}_m\notin \mathrm{\Omega }}\mid {\mathbf{P}}_{m\ell }\mid \right).$$ (5)

This penalty promotes sparsity of {p_ℓ(r_m) : r_m ∉ Ω, ℓ > K} such that only a few non-cardiac image voxels have an effective rank above K. The corresponding cardiac spatial coefficients are penalized in groups to protect them from sparse regularization and to prevent noise amplification. This results in a spatially-varying PS model order.

2.3. Image Reconstruction

Denoting d as the measured data and 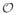{·} as the imaging operator which incorporates both the signal model in (1) and the sparse sampling operation, the proposed reconstruction problem is

$$\widehat{\mathbf{P}}=arg\underset{\mathbf{P}}{min}{\Vert \mathbf{d}-\mathcal{O}\{\mathbf{P}\widehat{\mathbf{Q}}\}\Vert }_2^2+{\lambda }_1{\Vert R\{\mathbf{P}\}\Vert }_{1,2}+{\lambda }_2{\Vert \text{vec}(\mathbf{P}\widehat{\mathbf{Q}}{\mathcal{F}}_t)\Vert }_1.$$ (6)

The additional regularization term ||vec(PQ̂ 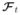)||₁ promotes sparsity of the spatial-spectral image 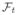{I(r, t)} as a means of further regularizing the solution [10–12]. The final reconstructed image Î(r, t) is obtained by Ĉ = P̂Q̂. Notice that when λ₁ = 0, the reconstruction problem (6) reduces to the ℓ₁-norm regularized PS model (referred to as the “PS-CS model”). If we further assumed L = min{M, N}, i.e., that Ĉ is full-rank, then we would obtain the basic (r, f)-space sparsity inverse problem (the “CS model”).

We propose to solve the convex optimization problem in (6) by using an additive half-quadratic minimization algorithm [15] with a continuation procedure [12], extended in the following to handle the (1,2)-norm regularization. For notational simplicity, we define the operators A{P} = {PQ̂} and $\mathrm{\Psi }\{\mathbf{P}\}={\left[\frac{{\lambda }_1}{\lambda }R{\{\mathbf{P}\}}^T\frac{{\lambda }_2}{\lambda }\text{vec}{(\mathbf{P}\widehat{\mathbf{Q}}{\mathcal{F}}_t)}^T\right]}^T$. We also generalize the regularization constraints from (6) as an alternative (1,2)-norm expression with groupings such that

$$\lambda {\Vert \mathrm{\Psi }\{\mathbf{P}\}\Vert }_{1,2}={\lambda }_1{\Vert R\{\mathbf{P}\}\Vert }_{1,2}+{\lambda }_2{\Vert \text{vec}(\mathbf{PQ}{\mathcal{F}}_t)\Vert }_1.$$

Using this simplified notation, (6) becomes

$$\widehat{\mathbf{P}}=arg\underset{\mathbf{P}}{min}{\Vert \mathbf{d}-A\{\mathbf{P}\}\Vert }_2^2+\lambda {\Vert \mathrm{\Psi }\{\mathbf{P}\}\Vert }_{1,2}.$$ (7)

We introduce the approximation ${\Vert \mathbf{x}\Vert }_{1,2}\approx {\sum }_{i=1}^I\phi [{\mathbf{x}}_{(i)},\alpha ]$, where

$$\begin{array}{l}\phi (\mathbf{y},\alpha )=\{\begin{array}{ll}{\Vert \mathbf{y}\Vert }_2^2/2\alpha ,\hfill & {\Vert \mathbf{y}\Vert }_2\le \alpha \hfill \\ {\Vert \mathbf{y}\Vert }_2-\alpha /2,\hfill & {\Vert \mathbf{y}\Vert }_2>\alpha \hfill \end{array}\\ =\underset{\mathbf{q}}{min}\frac{1}{2\alpha }{\Vert \mathbf{y}-\mathbf{q}\Vert }_2^2+{\Vert \mathbf{q}\Vert }_2.\end{array}$$

with α > 0. The resulting (1,2)-norm approximation is

$${\Vert \mathbf{x}\Vert }_{1,2}\approx \underset{\mathbf{g}}{min}\frac{1}{2\alpha }{\Vert \mathbf{x}-\mathbf{g}\Vert }_2^2+{\Vert \mathbf{g}\Vert }_{1,2}.$$ (8)

The value of φ(y, α) is reached when q is the projection of y onto the 2-norm ball of radius max{0, ||y||₂ − α}. Similarly, the approximation in (8) is achieved when g is the projection of x onto the (1,2)-norm ball of radius max{0, ||x||_1,2 − α}. As α → 0, we have φ[x_(i), α] → ||x_(i)||₂ and ${\sum }_{i=1}^I\phi [{\mathbf{x}}_{(i)},\alpha ]\to {\Vert \mathbf{x}\Vert }_{1,2}$.

Substituting (8) into (7), we have

$$\{\widehat{\mathbf{P}},\widehat{\mathbf{g}}\}=arg\underset{\{\mathbf{P},\mathbf{g}\}}{min}{\Vert \mathbf{d}-A\{\mathbf{P}\}\Vert }_2^2+\frac{\lambda }{2\alpha }{\Vert \mathrm{\Psi }\{\mathbf{P}\}-\mathbf{g}\Vert }_2^2+\lambda {\Vert \mathbf{g}\Vert }_{1,2},$$ (9)

We can solve (9) through alternating optimization of g and P.

At the nth iteration, we first fix P as the value obtained from the previous iteration (denoted as P̂⁽ⁿ⁻¹⁾). The minimization problem for g⁽ⁿ⁾ then has a cost function in the form of (8):

$${\widehat{\mathbf{g}}}^{(n)}=arg\underset{\mathbf{g}}{min}\frac{1}{2\alpha }{\Vert \mathrm{\Psi }\{{\widehat{\mathbf{P}}}^{(n-1)}\}-\mathbf{g}\Vert }_2^2+{\Vert \mathbf{g}\Vert }_{1,2}.$$ (10)

It follows that ĝ⁽ⁿ⁾ is then the projection of Ψ{P̂⁽ⁿ⁻¹⁾} onto the (1,2)-norm ball of radius max{0, ||Ψ{P̂⁽ⁿ⁻¹⁾}||_1,2 − α}. This projection is given by

$${\widehat{\mathbf{g}}}_{(i)}^{(n)}=\{\begin{array}{ll}\frac{max\{0,{\Vert {\mathbf{c}}_{(i)}\Vert }_2-\alpha \}}{{\Vert {\mathbf{c}}_{(i)}\Vert }_2}{\mathbf{c}}_{(i)},\hfill & \text{if}{\Vert {\mathbf{c}}_{(i)}\Vert }_2\ne 0\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$

where c = Ψ{P̂⁽ⁿ⁻¹⁾}.

With a fixed ĝ⁽ⁿ⁾, we then minimize (9) with respect to P, which is a quadratic optimization problem:

$${\widehat{\mathbf{P}}}^{(n)}=arg\underset{\mathbf{P}}{min}{\Vert \mathbf{d}-A\{\mathbf{P}\}\Vert }_2^2+\frac{\lambda }{2\alpha }{\Vert \mathrm{\Psi }\{\mathbf{P}\}-{\widehat{\mathbf{g}}}^{(n)}\Vert }_2^2.$$ (11)

The matrix P̂⁽ⁿ⁾ is then the solution to the linear system of equations

$$A^{\ast }A\{{\widehat{\mathbf{P}}}^{(n)}\}+\frac{\lambda }{2\alpha }{\mathrm{\Psi }}^{\ast }\mathrm{\Psi }\{{\widehat{\mathbf{P}}}^{(n)}\}=A^{\ast }\{\mathbf{d}\}+\frac{\lambda }{2\alpha }{\mathrm{\Psi }}^{\ast }\{{\widehat{\mathbf{g}}}^{(n)}\}.$$ (12)

When direct inversion of (12) is too large to compute, (11) can be efficiently solved using the conjugate gradient method with initial guess P̂⁽ⁿ⁻¹⁾.

Alternating optimization of (9) using the described procedure converges to

$$\widehat{\mathbf{P}}=arg\underset{\mathbf{P}}{min}{\Vert \mathbf{d}-A\{\mathbf{P}\}\Vert }_2^2+\lambda \sum _{i=1}^I\phi [\mathrm{\Psi }{\{\mathbf{P}\}}_{(i)},\alpha ].$$ (13)

The cost functions in (10), (11), and (13) are all convex. For a fixed α, alternating minimization converges towards the solution to (13) [15].

The solution (13) approximates the solution (7) with increasing accuracy as α → 0. Convergence generally requires fewer iterations for higher values of α [15], so we combine the above alternating minimization algorithm with a continuation procedure [12]. In this procedure, a large initial α is used to solve (13); this solution is used as an initial guess to solve (13) with a smaller value of α (e.g., reduced by a factor of 10). This process is repeated until α is small enough that (13) approximates (7) with high accuracy.

3. RESULTS AND DISCUSSION

We have evaluated the proposed imaging method using a realistic cardiac numerical phantom (C_gold) generated from real human MR data. We provide reconstruction examples using the proposed imaging method, the CS model, and the PS-CS model. The numerical phantom used for these simulations was created from retrospectively ECG- and respiratory-gated experimental data. Respiration was simulated using spatial deformations and temporal warping was used to vary both the respiratory and heart rates. The image sequence contains one 200 × 256 frame every 3 ms over a 30 s duration.

We conducted simulations by sparsely sampling (k, t)-space data from the numerical phantom. The sampling pattern was limited to a single (k, t)-space readout line every 3 ms (the effective T_R) to represent time-sequential sampling conditions, and sampling was interleaved between dense and sparse subsets. Q̂ was estimated from the SVD of the dense dataset. We considered both the noiseless case and the case with a blood-to-myocardium contrast-to-noise ratio (CNR) of 10. Three models were used for reconstruction: the CS model, the PS-CS model with L = 64, and the proposed method with K = 25 and L = 64. The cardiac region was manually identified. Regularization parameters were chosen for minimum NRMS reconstruction error ||C_gold − Ĉ||₂/||C_gold||₂ after a comprehensive sweep. All reconstructions have a framerate of 33 fps.

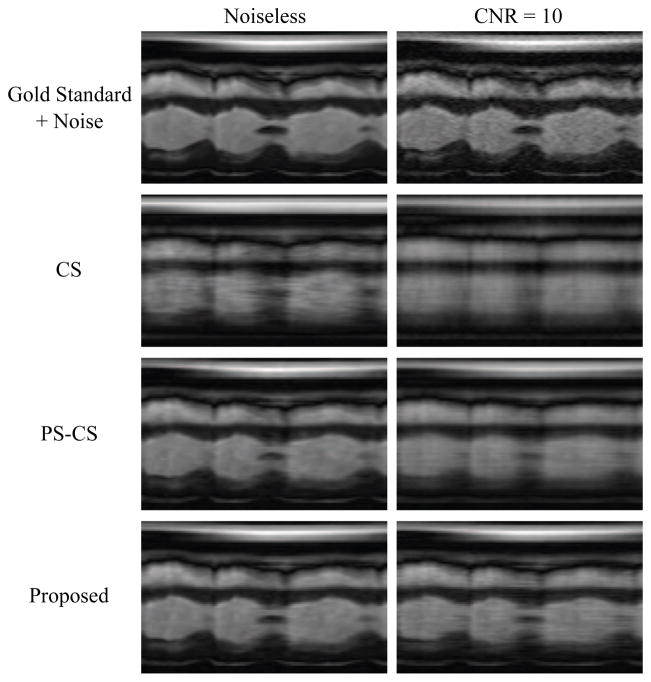
Fig. 2 depicts a 2D spatiotemporal slice from the gold standard image sequence (plus noise of the relevant variance) as well as reconstructions from the highly undersampled data. Reconstructions from the CS, PS-CS, and proposed methods are pictured. The resulting NRMS reconstruction errors are summarized in Table 1. Fig. 3 depicts normalized singular value curves of the cardiac region and the non-cardiac (“other”) region of the proposed reconstruction with CNR=10. The constraint in (5) successfully promoted sparsity of the non-cardiac spatial coefficients indexed above K, yielding the desired effective ranks of L for the cardiac region and K for the non-cardiac region.

Fig. 2.

Gold standard and reconstructions using multiple imaging methods at multiple contrast-to-noise ratios.

Table 1.

Normalized RMS reconstruction errors

	Noiseless	CNR = 10
CS	9.31%	10.87%
PS-CS	3.81%	7.60%
Proposed	3.28%	5.81%

Fig. 3.

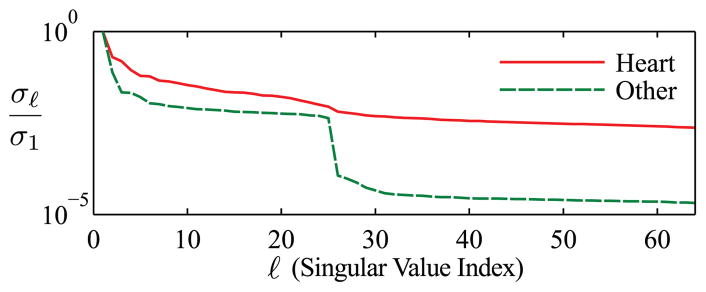
Normalized singular value curves from the cardiac and non-cardiac (“other”) regions of the proposed reconstruction with CNR=10. The proposed method successfully enforced the desired effective ranks.

Overall, the proposed method yields the most accurate reconstructions in the NRMS reconstruction error sense as well as providing the most faithful representation of the true cardiovascular dynamics at both noise levels. The improvement in reconstruction accuracy over the PS-CS method is modest in the noiseless case, but the improvement is more pronounced in the more realistic scenario involving noisy data. We attribute this improvement to the added control over the model which exploits the specific regional low-rank structure of cardiovascular images. In contrast, the CS and PS-CS models do not distinguish between the regions of the image and impose regionally unspecific model assumptions.

4. CONCLUSION

This paper presents an improved method for reconstruction of cardiac images from highly undersampled (k, t)-space data. The method uses a regional low-rank constraint enforced via group sparsity which allows more flexible control over the effective PS model order in different spatial regions of the image. The proposed method has been validated using simulated cardiac imaging data, yielding very encouraging results.