PROPER ORDERED MESHING OF COMPLEX SHAPES AND OPTIMAL GRAPH CUTS APPLIED TO ATRIAL-WALL SEGMENTATION FROM DE-MRI

Abstract

Segmentation of the left atrium wall from delayed enhancement MRI is challenging because of inconsistent contrast combined with noise and high variation in atrial shape and size. This paper presents a method for left-atrium wall segmentation by using a novel sophisticated mesh-generation strategy and graph cuts on a proper ordered graph. The mesh is part of a template/model that has an associated set of learned intensity features. When this mesh is overlaid onto a test image, it produces a set of costs on the graph vertices which eventually leads to an optimal segmentation. The novelty also lies in the construction of proper ordered graphs on complex shapes and for choosing among distinct classes of base shapes/meshes for automatic segmentation. We evaluate the proposed segmentation framework quantitatively on simulated and clinical cardiac MRI.

1. INTRODUCTION

In the context of imaging, delayed enhancement MRI (DE-MRI) produces contrast in myocardium and in regions of fibrosis and scarring, which are associated with risk factors and treatment of atrial fibrillation (AF). DE-MRI is therefore useful for evaluating the potential effectiveness of radio ablation therapy and for studying recovery. Automatic segmentation of the heart wall in this context is quite important; in a single clinic, hundreds of man hours are spent per month in manual segmentation.

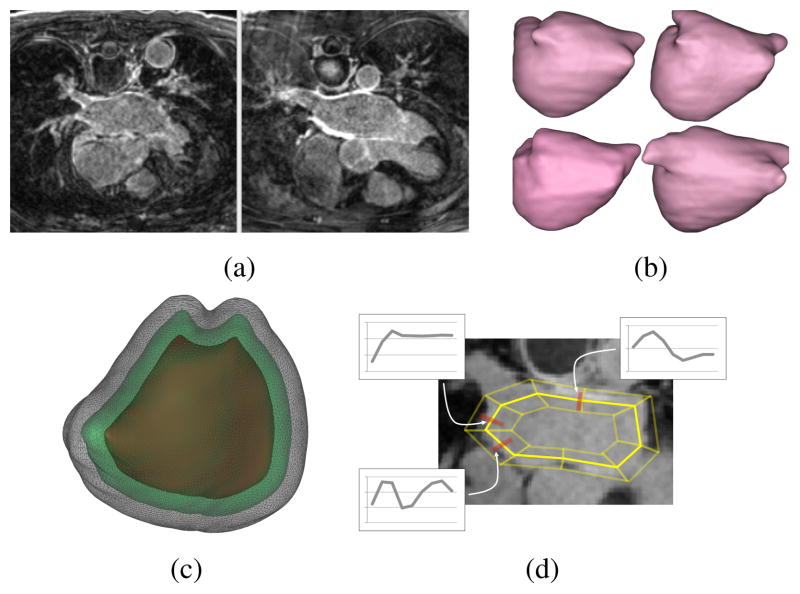
Automatic segmentation of the heart wall in DE-MRI is quite challenging, because of relatively low and inconsistent contrast, high level of unwanted texture and noise, and high variability of atrial shape. Figure 1(a) shows typical DE-MRI images of the left atrium (LA). Several conventional segmentation methods have been ineffective.

Fig. 1.

(a) MRI examples showing low contrast and uneven background. (b) Examples of average shapes, derived from k-means clustering on distance transforms of training images, around which the PO-meshes are constructed. (c) An example of several layers of PO-meshes for the LA. (d) A mock up of a simplified PO-mesh in 2D with examples of feature detectors learned from the training data (actually, PO-meshes for the LA have over 400,000 vertices)

Several papers address the problem of segmentation of blood pool in images from MRI angiography (MRI-A) protocols [1, 2]. These methods take advantage of the relatively homogeneous brightness of the blood pool in MRI-A, which is well suited for deformable models or registration-based approaches. However, high-quality properly-aligned blood-pool images are often not readily available from DE-MRI protocols. Further, the atrial wall is relatively thin in DE-MRI, confounding algorithms like template registration that often rely on coarse anatomical features. Deformable-surface methods that rely on gradient descent optimizations, including level sets, are unable to deal with the large variations in boundary contrast. Statistical models, such as active shape models, which rely on a low-dimensional subspace of learned models, have been proven to be too inflexible in dealing with the small and large-scale shape variability, and they also suffer from being trapped in local minima during optimization. While recent developments to address this problem (such as [3]) are promising, they rely on deformable models and/or image registration approaches. In our experience, they tend to get caught in local minima, and are not particularly reliable — a problem that we explicitly address in this paper.

The difficulty of optimizing shape or surface models in the presence of weak signal, high variability, and high noise, suggests that this problem would benefit from an optimization strategy that seeks global optima. Wu and Chen [4] described a strategy that represents a segmentation problem as a minimum s-t cut on a proper ordered graph, which is solved (globally) by a polynomial-time algorithm. Later, it was extended by Li et al. [5] to simultaneously segment multiple coupled surfaces, by incorporating offset constraints via the graph construction. The approach has demonstrated some success in several challenging segmentation problems [6, 7].

The standard proper ordered graph technique is not applicable on complex and irregular anatomical structures, particularly LA. The graph constructed from these structures results in “tangling” between columns. This does not comply with the underlying assumption of topological smoothness which breaks the graph-cut model. Thus, these proper ordered graph-cut methods require a careful construction of the underlying graph. We propose a new method for the construction of a proper ordered graph that avoids tangling. The construction is carried out by a nested set of triangular meshes through a set of prisms, which form columns of a proper order graph. The feature detectors on each node of the graph are also learned from the input data. Because of the variability in shape, we cluster the training examples into a small collection of shape templates. The algorithm automatically selects the best template for a particular test image based on the correlation. The evaluation has been carried out on a set of synthetic examples and LA DE-MRI images with hand segmentations as the ground truth.

2. METHODS

A graph is a pair of sets G = (V, E), which are vertices, {v_i}, and edges, {e_i,j = (v_i, v_j )}, respectively. For a proper ordered graph, the vertices are arranged logically as a collection of parallel columns that have the same number of vertices. The position of each vertex within the column is denoted by a superscript, e.g. $v_i^l$. The collection of vertices at the same position across all columns is called a layer. We let N be the number of columns and L be the number of vertices in each column (number of layers).

The construction of the derived directed graph is based on the method proposed by [8]. Here, the weight of each vertex in the innermost layer, the base layer, is given by $w_i^0=c_i^0$. Every vertex in this layer is connected by a directed edge to every other vertex with a cost +∞ in its adjacent columns. This makes the base layer strongly connected. For each vertex in layer l ∈ [1, L − 1], a weight of $w_i^l=c_i^l-c_i^{l-1}$ is assigned to each vertex. Again, a directed edge $e_{i,i}^{l,l-1}$ with a cost +∞ is connected from that vertex to the one below it.

A pair of directed edges $e_{i,j}^{l,l-\mathrm{\Delta }s}$ and $e_{j,i}^{l,l-\mathrm{\Delta }s}$ with costs +∞ go from a vertex $v_i^l$ to a vertex $v_j^{l-\mathrm{\Delta }s}$ and from $v_j^l$ to a vertex $v_i^{l-\mathrm{\Delta }s}$ making them an ordered pair. The Δs parameter controls the deviation in cuts between one column and its neighbors. To transform this graph into the s-t graph, G_st, two special nodes, called the source and the sink are added. The edges connecting each vertex to either the source or sink depend upon the sign of its weight. In case the weight on the vertex is negative, an edge with capacity equal to the absolute values of the weights of the corresponding vertex is directed from a source to that vertex; otherwise an edge is directed from that vertex to the sink. For simultaneous segmentation of multiple interacting surfaces, disjoint subgraphs are constructed as above and are connected with a series of directed edges defined by Δl and Δu parameters. These edges enforce the lower and upper inter surface constraints (described in [8]).

These edge capacities combined with the underlying topology of the graph determine the minimum s-t cut of the graph. The optimal surface is obtained by finding a minimum closed set Z^* in G^st [4]. Thus, a k^th surface in each sub graph is recovered by the intersection of the uppermost vertex of each layer in its respective sub graph and the minimum closed set Z^*. The computation of Z^* is done using minimum s-t cut algorithm, which produces global optima in polynomial time.

2.1. Building a Valid Proper Ordered Mesh

The previous section describes the graph topology based on a triangle structure within a layer, relying on vertex cost associated with image properties. To do so, we associate with each vertex $v_i^l$, a 3D position ${\overrightarrow{x}}_i^l$, which corresponds to a position in the image (volume). Here we describe how to assign 3D positions to mesh vertices and to triangulate each layer so that the layers form a nested set of watertight meshes in 3D. We call this set of vertices, their 3D positions, and the prismatic topology of the nested meshes, a proper ordered (PO) mesh.

For constructing the PO-mesh we use an extension of the dynamic-particle-system method proposed by Meyer et al. [9] for meshing implicit surfaces. We build this mesh using a template shape (described in the next section), which approximates very roughly the LA that we intend to segment. This template shape is represented as the zero level set of a signed distance transform in a volume. We first describe, very briefly how to build a mesh for the zero level set of this template.

Point or particles are distributed on an implicit surface by interactively minimizing a potential function. The potential function is defined pairwise between points and decreases monotonically with distance, $U_{i,j}^{l,l}=\mathrm{\Phi }(\mid {\overrightarrow{x}}_i^l-{\overrightarrow{x}}_j^l\mid )$, and thus particles repel each other. We denote the sum of this collection of repulsive potentials within each layer as . These particle systems have been shown to form consistent, nearly regular packings on complex surface [9]. Once points have been distributed on an implicit surface (with sufficient density), a Delaunay tetrahedralization scheme can be used to build a water-tight triangle mesh of the surface [10].

To build a nested set of surface meshes, we require a collection of offset surfaces, both inside and out, that not only inherent the topology of the base surface, but also represent valid, watertight 3D triangle meshes. This is essential, because the cuts, which mix vertices from different layers, must also form watertight triangle meshes. Thus, it results to bend the columns in order to avoid tangling of columns/triangles as the layers extend outward from the mean shape. For this, we introduce a collection of particle systems, one for each layer in the graph/mesh, and we couple these particles by an attractive force (Hooks law) between layers. Thus, there is an additional set of potentials of the form $U_{i,i}^{l,l+1}={\mid {\overrightarrow{x}}_i^l-{\overrightarrow{x}}_i^{l+1}\mid }^2$, and we denote the sum of the attractive forces of neighboring particles between layers as .

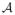To optimize a collection of particle systems for L layers, we perform gradient descent, using asynchronous updates, as in [9], on the total potential 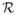+ β 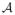. Figure 1(c) shows a nester 3-layered mesh for one of the LA templates.

The parameter β controls the relationship between attraction across layers and repulsion within layers and is tuned to prevent tangling. For this paper, we have used β = 10. The optimization requires an initial collection of particles. So, we place a particle at each point where the adjacent voxels have values on either side of the level set. This gives an average density of approximately one particle per unit surface area (in voxel units). The physical distance between layers must be inversely proportional to the particle density within layers, and this is a compromise between the tangling that results from large offsets and the extra computation associated with many thin layers. This corresponds to around 14,000 particles for heart images and 2000 particles for simulated images.

2.2. Learning Template Meshes and Feature Detectors

This section describes the construction of template shapes and the mechanism for computing costs on nodes from input images. Due to the high variability of shapes of LA, we rely on a training set of 32 DE-MRI images with LA segmentations. These training images provide (i) a way of constructing a collection of PO graphs, so that new images can be segmented as cuts through one of these graphs and (ii) examples of intensity profiles for the features that define epi- and endocardial surfaces, which lead to costs at each node in the PO graph.

We begin by clustering the examples (roughly) based on shape. For this, we compute distance transforms, represented as volumes, of each endocardial surface. Training images are aligned via translation so that they all have the same center of mass for the blood pool (region bounded by the endocardium). We then compute clusters using k-means with a metric of mean-squared-distance between these volumes. We choose the number of clusters, based on the cluster residual curve, to be 5, and we removed one of these clusters from the test, because it contained only two (high distorted) examples. Surface meshes associated with the distance-transform means of these 4 clusters are shown in Figure 1(b).

The cost assigned to each vertex is designed to reflect the degree to which that vertex is a good candidate for the desired boundary or surface, which will be found via a graph cut. Here we use the training data to derive an intensity profile along a line segment, or stick, perpendicular to the surface associated with each vertex. We sample the stick at a spacing of one voxel. The intensity along each stick on each vertex of each template is computed by a weighted average of intensities of sticks for each feature point in each training image. Thus, for a particular vertex in a particular cluster, the intensities on a stick would be a Gaussian weighted average, with standard deviation of 2 voxels, of several nearby sticks from different images (that share the same blood-pool center). The costs are computed via a normalized cross correlation. Figure 1(d) shows a diagram of the stick configuration and several stick intensity profiles for parts of a particular template.

2.3. Segmentation by Graph Cuts

To segment a particular test image, we rely on user input to position the template, by specifying the center of the atrium. The algorithm is robust to this position, as long as the layers of the template do not lie outside or inside the desired surface. We sample the input image along all of the sticks at all nodes and compute the correlation with the template. This results in costs, weights, edge capacities, and then an optimal cut. The geometric parameters used for constructing our graph include Δs = 4, Δl = 3 and Δu = 10 which reflect the complexity of surfaces and the inter-surface separation between them. These values have been employed on all datasets including synthetic and LA images that proves algorithm’s robustness. We employ all of the learned templates to the input image, choosing the segmentation that produces the best average correlation with the local intensity models for the optimal cut. Once the segmented mesh is retrieved from the cut, it is scan converted to reproduce the segmented volume(s). The processing time to find an optimal cut is few seconds.

3. EXPERIMENTS AND RESULTS

The experiments were evaluated on 100 simulated images of size 64 × 64 × 96 voxels each and 32 DE-MRI images of the LA of size 400 × 400 × 107 voxels. The simulated images include two oblong non-crossing surfaces with the inner surface translated randomly (Gaussian distribution) in 3D to mimic variations in heart-wall thickness; each image was corrupted with Rician noise (σ = 20 for the underlying Gaussian model) and a smoothly-varying bias field.

In all of our experiments, 30 mesh layers were generated, spaced at 0.5 voxels each, which gives each template a capture range of approximately 15 voxels. In case of simulated data, 50 training data sets and 50 test sets were considered for analysis. We evaluate the segmentation accuracy for LA based on leave-one out strategy for a test dataset, against templates from the training data.

Figures 2(a, c, e, f, g, h) illustrate our segmented boundaries for epicardial (outer) and endocardial (inner) heart-wall surfaces. These boundaries are overlaid on the original data (a, c) and their corresponding cost functions (e–h). Figure 2(b, d) shows the intensity profiles for outer and inner models.

Fig. 2.

(a),(c) Results of our algorithm on simulated and LA images (red and green curves represent outer boundaries extracted by our algorithm and ground truth, blue and purple curves represent inner boundaries extracted by our algorithm and ground truth) (b),(d) intensity profiles for outer/epicardium and inner/endocardium surfaces. (e),(g) our algorithm results and ground truth boundaries overlaid on outer and epicardial cost function images. (f),(h) our algorithm results and ground truth boundaries overlaid on inner and endocardial cost function images. (i),(k) distance histogram plot (in mm) between the surfaces extracted by our algorithm and ground truth over all images for both surfaces. (j),(l) histogram of dice co-efficients for the middle region/myocardium to represent the number of images against the percentage overlap.

We quantify the segmentation accuracy using distance metric. The distance metric is based on the aggregate of pairwise distances between corresponding points on the ground truth and our segmentation. For each point on our segmented surface, we measure the distance to the nearest point on the ground truth; and vice versa. The histograms of these measured distances (Figure 2(i, k)), indicate the percentage of voxels, on either surface, which were a specific distance away from the other surface. For a perfect delineation of the boundary, all these distances would be zero. The curves indicate the power of our algorithm in extracting boundaries very close to the real surfaces even in such challenging conditions.

To evaluate the overlap quantitatively for myocardium (heart wall), we used Dice measures between the ground truth and our segmented regions. Figure 2(j, l) shows the histograms of Dice measures. For synthetic data, the Dice values indicate excellent matches. However, in the case of the myocardium, the Dice values are little lower due to its varying thinness (2–6mm) and undefined ground truth. The ground truth is a single hand segmentation from an expert. Therefore, much of the observed error is near the veins which is subjected to the indefinite cutoff between atrium and vessel. Otherwise, the results are always close. While more overlap with the wall is desirable, these results also reflect the difficulty of quantifying efficacy using overlap. For instance, the ground truth results for the wall do not always form a complete boundary around the blood pool (even ignoring the vessels), and experiments show that when using overlap, human raters disagree significantly, as much as 50% from the average, demonstrating very high overlaps in pairwise comparisons between raters. Thus, these results appear to be clinically usable for many cases, but will still require human experts to do quality control, making slight corrections with manual tools. Furthermore, we expect results will be improved if we can increase the set of training images and form more templates in order to better match a given input image.