Abstract
Magnetic resonance (MR) imaging (MRI) is widely used to study the structure of human brains. Unlike computed tomography (CT), MR image intensities do not have a tissue specific interpretation. Thus images of the same subject obtained with either the same imaging sequence on different scanners or with differing parameters have widely varying intensity scales. This inconsistency introduces errors in segmentation, and other image processing tasks, thus necessitating image intensity standardization. Compared to previous intensity normalization methods using histogram transformations–which try to find a global one-to-one intensity mapping based on histograms–we propose a patch based generative model for intensity normalization between images acquired under different scanners or different pulse sequence parameters. Our method outperforms histogram based methods when normalizing phantoms simulated with various parameters. Additionally, experiments on real data, acquired under a variety of scanners and acquisition parameters, have more consistent segmentations after our normalization.
Index Terms: MRI, intensity normalization, intensity standardization, brain, segmentation
1. INTRODUCTION
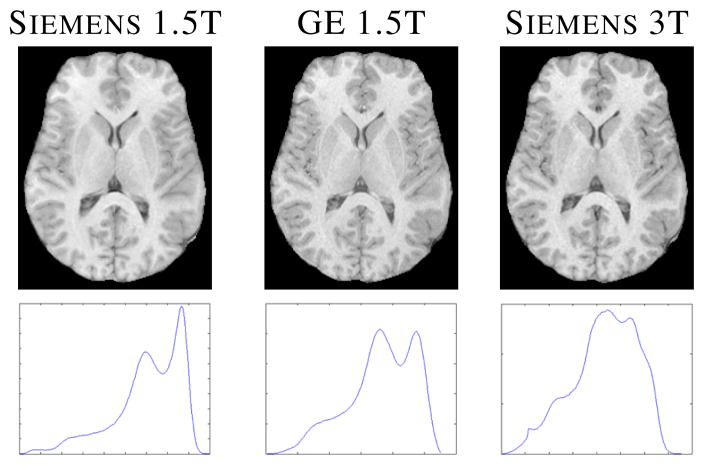
MRI is a non-invasive modality that has been widely used to gain understanding of the human brain. MR image processing techniques, such as segmentation, are needed to understand normal aging as well as the progression of diseases. For almost all MR image processing algorithms, image intensities are used as a primary feature. Unlike CT, MR intensities do not possess any tissue specific meaning. Thus a subject scanned in different scanners or with different pulse sequence parameters, will have variable image contrast between tissues (see Fig. 1 for example). It has been shown that the variability in tissue contrast gives rise to inconsistencies in segmentation [1].
Fig. 1.
Top row shows a subject’s SPGR (spoiled gradient recalled) from three different scanners [2], while the bottom row shows their histograms–scale is arbitrary.
Several intensity standardization algorithms have been proposed to bring MR intensities to a common scale. To normalize a subject T1-weighted scan to another reference T1-w scan, histogram matching algorithms try to match the subject histogram to the reference histogram by matching the intensities of manually or automatically chosen landmarks [3] or by minimizing some information-theoretic criteria [4] between the histograms. Another method uses intrinsic MR properties, such as longitudinal and transverse relaxation times (T1 and T2) or proton density (PD), to normalize the subject intensities to a reference volume, acquired with a different pulse sequence [5]. A segmentation based technique has also been proposed to account for the scanner variations, by matching intensity distributions of similar tissues between two images [6]. Landmark based methods usually suffer from the fact that reliable landmarks are sometimes difficult to find as they are either manually chosen or based on a segmentation itself. While, using tissue properties can be difficult as one needs precise knowledge of the imaging equations and pulse sequence parameters, which are often not known or difficult to estimate accurately.
We have previously reported a patch-based intensity normalization method called MIMECS [7] to overcome these problems. In this paper, a generative model based intensity normalization technique is developed independent of but having strong parallels with the idea of coherent point drift [8]. We still use patches instead of intensities of a single voxel as features, because a patch around a voxel contains neighborhood information of that center voxel. We propose a patch matching technique that takes patches from the subject image and finds its best matching patches in a target image. We benefit from not having to choose landmarks and no pulse sequence parameters are required.
2. METHOD
We want to normalize the intensities of a normal subject
 to a normal atlas
to a normal atlas
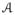 . We assume that
. We assume that
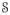 and
and
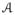 are acquired with similar imaging sequences, e.g. either T1-w SPGR or MPRAGE (magnetization prepared rapid gradient echo), but differ in either or both the scanner or the imaging parameters (e.g., repetition time, echo time, or flip angle). At each voxel of an image, 3D patches are considered and stacked into 1D vectors of size d × 1. There are N subject patches xi and M atlas patches yk, where N and M are the number of non-zero image voxels in
are acquired with similar imaging sequences, e.g. either T1-w SPGR or MPRAGE (magnetization prepared rapid gradient echo), but differ in either or both the scanner or the imaging parameters (e.g., repetition time, echo time, or flip angle). At each voxel of an image, 3D patches are considered and stacked into 1D vectors of size d × 1. There are N subject patches xi and M atlas patches yk, where N and M are the number of non-zero image voxels in
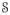 and
and
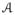 , respectively. Define X = {xi} and Y = {yj } to be the collection of subject and atlas patches. To match the subject intensities to the atlas, we match X to Y. First, we make sure that the peak white matter (WM) intensities of both
, respectively. Define X = {xi} and Y = {yj } to be the collection of subject and atlas patches. To match the subject intensities to the atlas, we match X to Y. First, we make sure that the peak white matter (WM) intensities of both
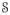 and
and
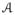 are the same (which provides a rough normalization of the two data sets). We assume that each subject patch xi is a realization of a Gaussian random vector whose mean is one of the atlas patches—i.e., xi ~
are the same (which provides a rough normalization of the two data sets). We assume that each subject patch xi is a realization of a Gaussian random vector whose mean is one of the atlas patches—i.e., xi ~
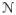 (yj, Σj) for some j. Then both the best matching atlas patch for each subject patch and the covariances of all atlas patches are defined by maximum likelihood and found using the expectation maximization algorithm (EM) [9], as described in detail below. The normalized image is produced by replacing the center pixel of each observed patch by the corresponding value of the matching atlas patch.
(yj, Σj) for some j. Then both the best matching atlas patch for each subject patch and the covariances of all atlas patches are defined by maximum likelihood and found using the expectation maximization algorithm (EM) [9], as described in detail below. The normalized image is produced by replacing the center pixel of each observed patch by the corresponding value of the matching atlas patch.
To motivate the key assumption of the Gaussian perturbation, we first observe that the image intensities are related to the intrinsic MR tissue properties, T1, T2,
, and PD, by nonlinear imaging equations. However, we can use a linear approximation to write the intensities of a patch as xi = H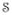 Θ
Θ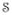 (i) and yj = H
(i) and yj = H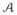 Θ
Θ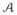 (j), where H
(j), where H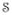 and H
and H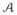 are linear approximations of the imaging equations and Θ
are linear approximations of the imaging equations and Θ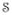 (i) and Θ
(i) and Θ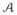 (j) are the underlying MR tissue properties of the patches. If patches xi and yj are from the same tissue, we can assume that their MR tissue properties follow a Gaussian distribution, Θ
(j) are the underlying MR tissue properties of the patches. If patches xi and yj are from the same tissue, we can assume that their MR tissue properties follow a Gaussian distribution, Θ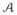 (j),
Θ
(j),
Θ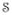 (i) ~
(i) ~
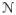 (μ, Ω). Then,
and
. Similarly, xi − yj ~
(μ, Ω). Then,
and
. Similarly, xi − yj ~
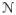 ((H
((H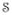 − H
− H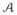 )μ, (H
)μ, (H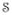 + H
+ H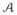 )Ω(H
)Ω(H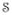 + H
+ H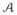 )T). We note that it is not feasible to estimate H
)T). We note that it is not feasible to estimate H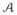 or H
or H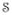 because neither the imaging equations nor the pulse sequence parameters are always exactly known. But we assume
because neither the imaging equations nor the pulse sequence parameters are always exactly known. But we assume
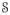 and
and
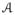 are acquired with “similar” pulse sequences, so we can thus make the assumption that H
are acquired with “similar” pulse sequences, so we can thus make the assumption that H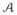 ≈ H
≈ H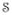 , implying xi − yj ~
, implying xi − yj ~
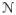 (0, Ω′). Here, Ω′ is a tissue-specific constant dependent on the nature of Θ
(0, Ω′). Here, Ω′ is a tissue-specific constant dependent on the nature of Θ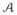 (j) and Θ
(j) and Θ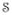 (i), or in essence, the classification of xi and yj. However, it is very difficult to estimate intrinsic tissue MR properties (μ and Ω′) since the exact nature of the imaging equations (H
(i), or in essence, the classification of xi and yj. However, it is very difficult to estimate intrinsic tissue MR properties (μ and Ω′) since the exact nature of the imaging equations (H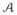 or H
or H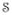 ) is usually not known. We avoid the classification and estimation problem of tissue MR properties by assuming that Ω′ is a characteristic of yj, thereby creating an M-class Gaussian mixture model with means as the M atlas patches. We note that the same analysis can be extended even if a patch contains more than one tissue class. This idea of an M -class problem was explored previously for a registration algorithm [8].
) is usually not known. We avoid the classification and estimation problem of tissue MR properties by assuming that Ω′ is a characteristic of yj, thereby creating an M-class Gaussian mixture model with means as the M atlas patches. We note that the same analysis can be extended even if a patch contains more than one tissue class. This idea of an M -class problem was explored previously for a registration algorithm [8].
To find the correspondence between patches, let zij be an indicator function having the value one when the ith subject patch xi originates from a Gaussian distribution having its mean as the jth atlas patch yj with co-variance matrix Σj, and is zero otherwise. The probability of observing xi is written as
| (1) |
For computational simplicity, we make the assumption that Σj is a diagonal matrix–i.e. , where I is a d × d identity matrix. Assuming the i.i.d. nature of the patches and a uniform prior probability and, the joint probability distribution of all the subject patches is given by
| (2) |
where Z = {zij}, Θ = {σj: j = 1, …, M}, and C is a normalizing constant. An estimate of σj’s and posterior probabilities P (zij = 1|X, Y, Θ) can be obtained by maximizing the joint probability using EM.
EM is a two-step iterative process, that estimates the true zij’s based on the current estimates of the parameters Θ, and then updates Θ based on the estimates of zij. This is described as:
E-step: to find new update Θ(m+1) at the mth iteration, compute the expectation Q(Θ(m+1)|Θ(m)) = E[log P (Z|X, Y, Θ(m+1))|X, Y, Θ(m)].
- M-step: find new estimates Θ(m+1) based on the previous estimates by solving,
Assuming wij = E(zij |xi, yj, sj ), the E-step gives
| (3) |
The M-step gives the update equations for σj s as
| (4) |
The algorithm is deemed to have converged when the maximum difference between the posteriors in successive iterations is below a threshold. Then the central voxel of the subject patch xi is replaced with the central voxel of yt, where t = arg maxj (wij ).
For all of the experiments, we use 3 × 3 × 3 patches, thus d = 27. For a 256 × 256 × 199 MR brain image of resolution 1 mm3, M and N are typically ≈ 107. It is therefore memory and time intensive to compute wij’s for every xi’s. We observed experimentally that wij is very close to zero if ||xi − yj|| is large. Following the assumption that Θ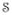 (i) and Θ
(i) and Θ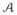 (j) should be the same tissue, we assume wij = 0 if ||xi − yj|| > δ, which is similar to a non-local criteria [10]. However, in our computation, for each i, we choose its closest D atlas patches to have non-zero wij, their indices denoted by Ψi, a set of cardinality D. Thus if any atlas index j is not in Ψi, we fix wij = 0. Eqn. 4 is modified as follows
(j) should be the same tissue, we assume wij = 0 if ||xi − yj|| > δ, which is similar to a non-local criteria [10]. However, in our computation, for each i, we choose its closest D atlas patches to have non-zero wij, their indices denoted by Ψi, a set of cardinality D. Thus if any atlas index j is not in Ψi, we fix wij = 0. Eqn. 4 is modified as follows
| (5) |
3. RESULTS
3.1. Phantom validation
We first validate the algorithm on the Brainweb phantom data [11]. We use flip angle α as the varying imaging parameter of SPGR scans of a normal phantom. Phantoms with α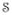 = 30°, 45°, 60°, 75° with noise levels n = 0, 1, 3, 5% are used to normalize to a phantom with α
= 30°, 45°, 60°, 75° with noise levels n = 0, 1, 3, 5% are used to normalize to a phantom with α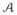 = 90° and 0% noise. Our method is compared with histogram matching and a landmark based method [3] where the landmarks are found using a Gaussian mixture model algorithm. Fig. 2 shows the mean squared errors (MSE) between the atlas and the subjects before and after normalization with these three methods. Clearly the patch based method outperforms the other two for all values of α
= 90° and 0% noise. Our method is compared with histogram matching and a landmark based method [3] where the landmarks are found using a Gaussian mixture model algorithm. Fig. 2 shows the mean squared errors (MSE) between the atlas and the subjects before and after normalization with these three methods. Clearly the patch based method outperforms the other two for all values of α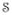 , and n = 1, 3, 5. For 0% noise, all three methods perform similarly, because the lack of any partial volume or noise makes the choice of landmarks accurate and histogram matching perfect. At higher noise levels, histogram matching becomes dependent on the number of bins and the estimation of landmarks becomes less robust. The atlas and a subject with α
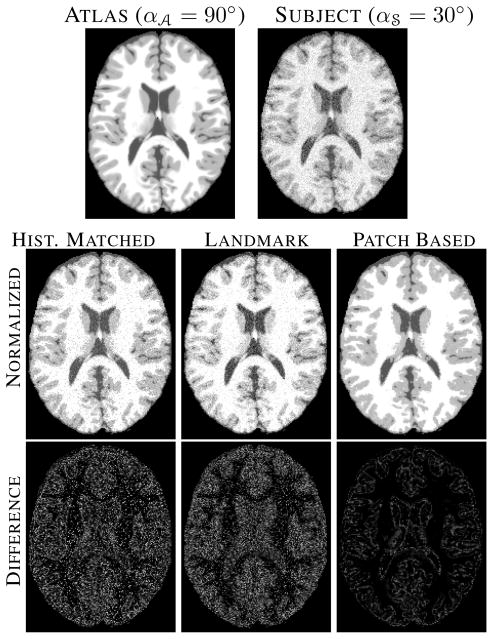
, and n = 1, 3, 5. For 0% noise, all three methods perform similarly, because the lack of any partial volume or noise makes the choice of landmarks accurate and histogram matching perfect. At higher noise levels, histogram matching becomes dependent on the number of bins and the estimation of landmarks becomes less robust. The atlas and a subject with α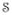 = 30° at 5% noise are shown in Fig. 3 the top row, the normalized images and their differences from the atlas are shown in the middle and bottom row, respectively. Clearly, both histogram matching and landmark based normalization leaves a bias in intensities in large regions, e.g., gray matter (GM), while our patch-based method fails only in recovering sharp edges such as at GM to WM transitions.
= 30° at 5% noise are shown in Fig. 3 the top row, the normalized images and their differences from the atlas are shown in the middle and bottom row, respectively. Clearly, both histogram matching and landmark based normalization leaves a bias in intensities in large regions, e.g., gray matter (GM), while our patch-based method fails only in recovering sharp edges such as at GM to WM transitions.
Fig. 2.
Mean squared errors (MSE) between atlas (α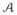 = 90°) and subject images (α
= 90°) and subject images (α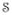 = 30°, 45°, 60°, 75°) are shown for various noise levels.
= 30°, 45°, 60°, 75°) are shown for various noise levels.
Fig. 3.
Top row shows the atlas (α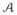 = 90°) and the subject (α
= 90°) and the subject (α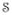 = 30°). Middle row shows the histogram matched, landmark based normalized and patch based normalized images. Bottom row shows their differences with the atlas.
= 30°). Middle row shows the histogram matched, landmark based normalized and patch based normalized images. Bottom row shows their differences with the atlas.
3.2. Experiments on real data
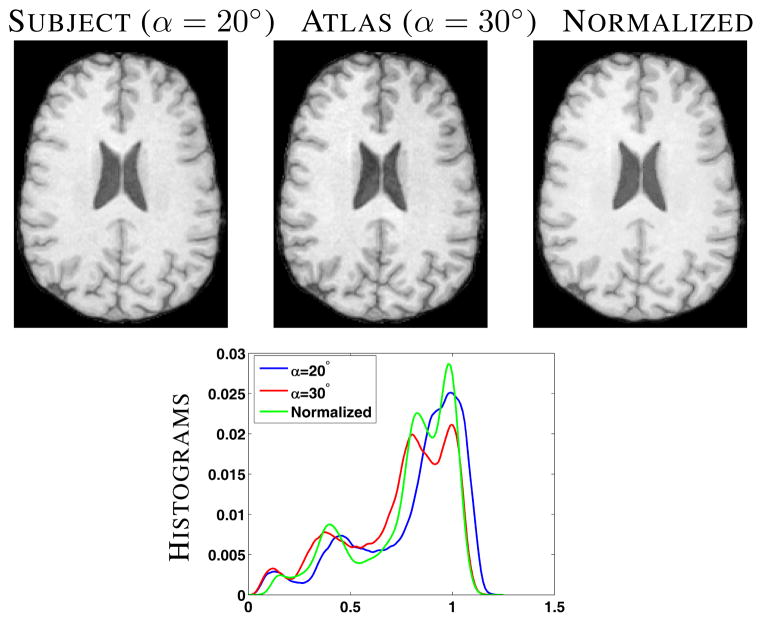
We next used five healthy subjects from the morphometry BIRN [2] calibration study to show the effects of normalization. Each subject has 14 SPGR scans, 7 each with α = 20° and 30° from 4 different scanners. Each scan of a subject was first rigidly registered to its GE 1.5T α = 30° scan and then skull-stripped [12] using the same mask generated from the GE 1.5T α = 30° scan. Then each image is corrected for any intensity inhomogeneity using N3 [13]. For every subject, we normalize every α = 20° scan to the corresponding α = 30° scan. Fig. 4 shows one set of α = 20° and α = 30° scans of a subject along with the normalized image in the top row.
Fig. 4.
Top row shows the subject (α = 20°), atlas (α = 30°) and the corresponding normalized image. Bottom row shows a plot of the histograms of the above three images.
Our method does not seek to match histograms, however it is useful to compare them after normalization. Fig. 4 bottom row, shows that the histogram of the normalized image more strongly resembles the atlas than the original subject image.
As described earlier, segmentations can become inconsistent with the variation of scanners and imaging parameters [1, 5, 6]. We demonstrate that the patch based normalization achieves more consistent segmentation between images acquired with different scanners and pulse sequence parameters. We compare our method with histogram matching and a landmark based intensity transformation [3] where three landmarks on the subject and the atlas are automatically chosen based on a 3-class Gaussian mixture model segmentation. After normalization, we use fuzzy C-means [14] to generate segmentations. We report Dice similarity coefficients in Table 1 between segmentations of the three primary tissues, cerebrospinal fluid (CSF), GM, and WM, and their weighted average. The values are averaged over five subjects, each with seven scans. Patch based normalization produces significantly higher Dice coefficients for GM and WM compared to the other two, while the CSF Dice segmentations are comparable. Histogram matching often decreases the similarity with the original, as it is heavily dependent on the number of bins. Landmark based matching can also deteriorate the segmentation consistency, when a suitable landmark is not found. This is often the case if the image histogram is not multi-modal (e.g., the blue line in Fig. 4). Both Figs. 3 and 4 reveal a smoothing effect on the reconstructed images. Though not unexpected in patch-based methods, this effect needs further investigation.
Table 1.
Average Dice coefficients of hard segmentations are obtained from 35 scans, before and after normalization, comparing our method with histogram matching and a landmark based matching [3].
| CSF | GM | WM | Mean | |
|---|---|---|---|---|
|
|
||||
| Original | 0.882 | 0.788 | 0.927 | 0.884 |
| Hist. Match | 0.881 | 0.828 | 0.917 | 0.891 |
| Landmark based | 0.876 | 0.776 | 0.926 | 0.882 |
| Patch based | 0.874 | 0.845* | 0.943* | 0.902 |
Statistically significantly larger than the other three (p-value < 0.05).
4. DISCUSSION AND CONCLUSION
We have described a patch based MR intensity normalization framework that can normalize scans having similar acquisition protocol but acquired on different scanners or with different acquisition parameters. We validated our algorithm on phantoms and real scans and shown it gives rise to more consistent segmentations after normalization.
Acknowledgments
This work was supported by the NIH/NIBIB under grant 1R21EB012765. We would like to thank Dr. Sarah Ying for providing the MR data. Some data used for this study were downloaded from the Biomedical Informatics Research Network (BIRN) Data Repository, supported by grants to the BIRN Coordinating Center (U24-RR019701), Function BIRN (U24-RR021992), Morphometry BIRN (U24-RR021382), and Mouse BIRN (U24-RR021760) Testbeds, funded by the National Center for Research Resources at the National Institutes of Health, U.S.A.
Contributor Information
Snehashis Roy, Email: snehashisr@jhu.edu.
Aaron Carass, Email: aaron_carass@jhu.edu.
Jerry L. Prince, Email: prince@jhu.edu.
References
- 1.Clark KA, Woods RP, Rottenber DA, Toga AW, Mazziotta JC. Impact of acquisition protocols and processing streams on tissue segmentation of T1 weighted MR images. NeuroImage. 2006;29:185–202. doi: 10.1016/j.neuroimage.2005.07.035. [DOI] [PubMed] [Google Scholar]
- 2.Friedman L, et al. Test-Retest and Between-Site Reliability in a Multicenter fMRI Study. Human Brain Mapping. 2008 Aug;29(8):958–972. doi: 10.1002/hbm.20440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nyul LG, Udupa JK. On Standardizing the MR Image Intensity Scale. Mag Res in Medicine. 1999;42(6):1072–1081. doi: 10.1002/(sici)1522-2594(199912)42:6<1072::aid-mrm11>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 4.Jager F, Hornegger J. Nonrigid Registration of Joint Histograms for Intensity Standardization in Magnetic Resonance Imaging. IEEE Trans Med Imag. 2009;28(1):137–150. doi: 10.1109/TMI.2008.2004429. [DOI] [PubMed] [Google Scholar]
- 5.Fischl B, et al. Sequence-independent segmentation of magnetic resonance images. NeuroImage. 2004;23:69–84. doi: 10.1016/j.neuroimage.2004.07.016. [DOI] [PubMed] [Google Scholar]
- 6.Han X, Fischl B. Atlas Renormalization for Improved Brain MR Image Segmentation Across Scanner Platforms. IEEE Trans Med Imag. 2007;26(4):479–486. doi: 10.1109/TMI.2007.893282. [DOI] [PubMed] [Google Scholar]
- 7.Roy S, Carass A, Prince JL. A Compressed Sensing Approach For MR Tissue Contrast Synthesis. 22nd Conf. on Info. Proc. in Medical Imag. (IPMI 2011); 2011. pp. 371–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Myronenko A, Song X. Point-Set Registration: Coherent Point Drift. IEEE Trans Patt Anal and Machine Intell. 2010;32(12):2262–2275. doi: 10.1109/TPAMI.2010.46. [DOI] [PubMed] [Google Scholar]
- 9.Dempster AP, Laird NM, Rubin DB. Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of the Royal Stat Soc Series B (Method) 1977;39(1):1–38. [Google Scholar]
- 10.Mairal J, Bach F, Ponce J, Sapiro G, Zisserman A. Non-local sparse models for image restoration. IEEE Intl Conf on Comp Vision. 2009:2272–2279. [Google Scholar]
- 11.Cocosco CA, Kollokian V, Kwan RKS, Evans AC. BrainWeb: Online Interface to a 3D MRI Simulated Brain Database. NeuroImage. 1997;5(4):S425. [Google Scholar]
- 12.Carass A, Cuzzocreo J, Wheeler MB, Bazin PL, Resnick SM, Prince JL. Simple paradigm for extra-cerebral tissue removal: Algorithm and analysis. NeuroImage. 2011;56(4):1982–1992. doi: 10.1016/j.neuroimage.2011.03.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sled JG, Zijdenbos AP, Evans AC. A non-parametric method for automatic correction of intensity non-uniformity in mri data. IEEE Trans Med Imag. 1998;17(17):87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- 14.Bezdek JC. A Convergence Theorem for the Fuzzy ISO-DATA Clustering Algorithms. IEEE Trans Patt Anal Machine Intell. 1980;20(1):1–8. doi: 10.1109/tpami.1980.4766964. [DOI] [PubMed] [Google Scholar]