Abstract
Dislocations represent an important and ubiquitous class of topological defect found at the surfaces of metal oxide materials. They are thought to influence processes as diverse as crystal growth, corrosion, charge trapping, luminescence, molecular adsorption, and catalytic activity; however, their electronic and chemical properties remain poorly understood. Here, through a detailed first-principles investigation into the properties of a surface-terminated screw dislocation in MgO we provide atomistic insight into these issues. We show that surface dislocations can exhibit intriguing electron trapping properties which are important for understanding the chemical and electronic characteristics of oxide surfaces. The results presented in this article taken together with recent experimental reports show that surface dislocations can be equally as important as more commonly considered surface defects, such as steps, kinks, and vacancies, but are now just beginning to be understood.
Introduction
The inextricable relationship between the structure and properties of surfaces is one of the most universal concepts in materials chemistry.1 Nowhere is this more true than in metal oxide materials, where the defect structure of surfaces determines many of their unique chemical, optical, and electronic properties.2 In particular, topological defects such as steps, kinks, and vacancies have been found to play a key role in processes as diverse as crystal growth, charge trapping, luminescence, molecular adsorption, and catalytic activity.3−9 Dislocations represent another class of topological defect that has recently become the subject of increasing attention. The structure and mechanical properties of dislocations in oxide materials, particularly in ceramics, have been well studied for many years.10 However, their electronic and chemical properties are far less well understood and it remains unclear how their properties may differ from those of other topological sites at surfaces. In this paper, we use theoretical modeling to investigate a dislocation in a metal oxide material in order to develop a more detailed picture of its electronic and chemical properties.
Understanding the electronic and chemical properties of surface dislocations is a fundamental problem of relevance to a wide range of applications. For example, dislocations in oxides play key roles in corrosion processes in biomedical implants,11 the growth of catalytically active oxide-supported metal nanoparticles,12,13 contrast formation in scanning probe microscopies,14 the electrical reliability of oxide dielectrics in transistors and memories, magnetism,15,16 and superconductivity. Dislocations can be formed in oxides as a result of nonequilibrium growth processes, as a means to relieve stress in lattice mismatched thin film heterostructures, or as induced by mechanical deformation.17 Dislocations in oxides often act as favorable sites for the segregation of point defects and impurities18 as well as paths for their enhanced diffusion.19 The reduced ion coordination and local strain in the dislocation core is also known to affect their electronic properties. For example, there are experimental indications that dislocations in oxides can present favorable electrical conduction paths17 or may trap electrons;20,21 however, a detailed understanding of these effects is still missing.
Theoretical modeling has been instrumental in the development of our current understanding of surface defects in oxides.22 Perhaps the most studied oxide in this respect is MgO, a material important for applications in electronics23 and catalysis24−26 as well as a useful model oxide owing to its high ionicity and simple rock salt structure. MgO is also one of the most abundant materials in the Earth’s lower mantle, and dislocations are important for understanding its rehology.27 The properties of a plethora of defects in MgO, including steps, kinks, vacancies, and impurities, have been investigated using a range of first-principles methods.28−32 Together with experimental probes such as electron paramagnetic resonance (EPR) spectroscopy, scanning probe microscopy, optical absorption, and luminescence spectroscopy, these models have been invaluable in elucidating their intriguing electronic, optical, and chemical properties.7,8,33−36 In contrast, there have been far fewer theoretical studies of surface dislocation defects in MgO. In one of the few examples Watson et al. considered their role in crystal growth processes using classical interatomic potentials.37 To date there have been no theoretical studies of their electronic or chemical properties; however, experimental evidence concerning the properties of dislocations in MgO is mounting.
Recent scanning tunneling microscopy studies of misfit dislocations in thin MgO/Mo(001) films by Benia et al. have provided evidence that dislocations may be able to trap electrons.20 They showed that dislocations could be reversibly filled with electrons via electrical injection or adsorption of atomic hydrogen. The latter gave rise to a free-electron-like EPR signal and small hyperfine interaction, suggesting dissociation of the proton and electron. A separate study on the nucleation of gold clusters on MgO using infrared (IR) and X-ray photoelectron spectroscopy suggested that Au atoms become positively charged on adsorption.21 It was proposed that this was a result of electron transfer to extended defects, such as grain boundaries or dislocations, or to associated OH groups. Similar results have also been observed for Mg adsorption on MgO.38 Electron transfer processes involving other types of surface defects have been well studied for MgO and are thought to be important for understanding reactivity.39,40 For example, low-coordinated cations exposed at steps, kinks, and corners are known to be Lewis acid sites with predicted electron affinities of up to 1 eV.8,30,41 The experimental evidence suggests that dislocations may also act as Lewis acid sites; however, it is unclear whether this is an inherent property of dislocations or is related to associated defects such as hydroxyls and vacancies. For this reason, theoretical modeling of surface dislocations, which can help facilitate a deeper understanding of their properties, is long overdue.
In this paper, we address these issues by characterizing the electronic and chemical properties of a surface-terminated screw dislocation in MgO using first principles methods. We show that the dislocation is able to trap electrons and that the nature of the electron trapping is unusual in that the electron is not localized on a low-coordinated cation, as is usually the case at surfaces, but is instead localized in a electrostatic potential well near the dislocation core. We show how protons and hydrogen atoms interact with the dislocation, which helps to explain previous experimental observations. In order to guide quantitative experimental characterization of dislocations, we compute spectroscopic signatures (in particular, EPR and IR) for various defect configurations. More generally, these results provide a more detailed picture of the electronic and chemical properties of surface dislocations that should be relevant for similar materials such as NiO and CoO, which have the same crystal structure, as well as for other technologically important oxides, such as TiO2 and ZrO2.
The paper is organized in the following way. First we present the theoretical approach for modeling the structure and electronic and chemical properties of surface-terminated dislocations in oxides. We then present the results of a detailed investigation into the properties of a particular screw dislocation in MgO, including elucidation of its structure and stability, electron-trapping properties, optical spectra, and interaction with H-related defects and Au atoms. Finally we summarize the results and discuss their implications.
Modeling MgO Dislocations
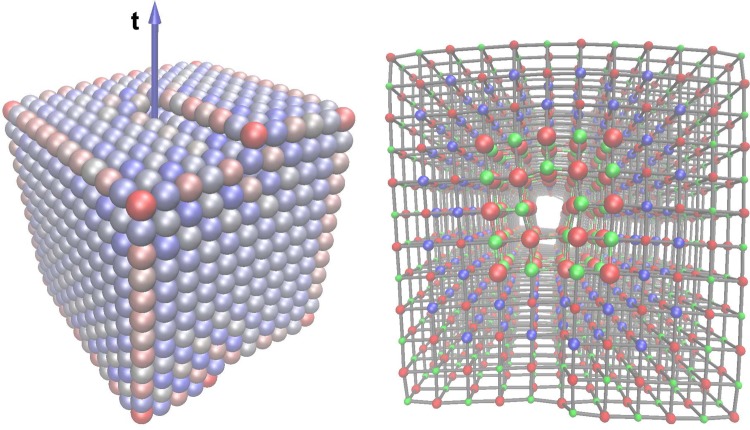
One-dimensional dislocation defects are characterized geometrically by a Burgers vector b and dislocation line vector t.42 They are challenging to model atomistically, owing to their inherently nonperiodic structure and associated long-range strain field. One common approach to modeling dislocations at a quantum-mechanical level is to consider pairs of well-separated dislocations within a periodic supercell.43 However, the large supercells required for a surface-terminated dislocation make such calculations at the quantum mechanical level computationally prohibitive. Here we tackle this problem in a different way. We consider a single dislocation in the center of a finite nanocrystal rather than a periodic array of dislocations in an extended infinite crystal (e.g., see Figure 1). In this case the long-range strain field around the dislocation is clearly different from that of an isolated dislocation in a infinite crystal; however, we find the structure of the dislocation core is relatively insensitive to the shape and size of the nanocrystal, at least above a certain size. We also considered a range of nanocrystal sizes, the largest containing 14300 atoms with approximate dimensions 5 × 5 × 4 nm. In all cases the bond lengths characterizing the structural arrangement of atoms near the dislocation core were equivalent to within 0.05 Å. A dislocation within a finite nanocrystal is also in some ways more representative of real polycrystalline materials which consist of finite-size grains.
Figure 1.
(left) Predicted structure of a MgO nanocrystal containing a b = a/2[110] screw dislocation. Ions are colored according to the absolute value of the onsite electrostatic potential (red is low, blue is high). The arrow depicts the dislocation line vector t. (right) The embedded cluster approach used to model the nanocrystal (viewed along the dislocation line vector from above). Large red and green spheres represent atoms in the quantum cluster, blue spheres represent the interfacial Mg ions, and the remaining spheres represent classical ions. Please refer to the online version of this article for references to color.
We model ion interactions using classical interatomic potentials in order to predict the structure of the nanocrystal. For MgO we employ the polarizable shell model potential of Lewis and Catlow, which has proven to be robust and accurate in many previous studies.44−46 The dislocation is introduced into an ideal cubic nanocrystal by removing half a plane of atoms and displacing the remaining atoms in order to rebond the two exposed surfaces. The dislocation line vector and Burgers vector is defined by which atoms are removed and how the exposed surfaces are displaced. Using this initial structure, the total energy of the nanocrystal is minimized using a conjugate gradients algorithm to a tolerance of 10–5 eV. We note that dislocations represent a metastable configuration and in the absence of external stress it will always be energetically profitable for the dislocation to annihilate at the surface producing step defects (this is discussed in more detail below).
To calculate the electronic properties of nanocrystals such as that depicted in Figure 1 (which contains 1644 ions), we employ an embedded cluster approach. Briefly, the idea is to divide a large complex system into two subregions: a region near a point of interest that is treated at a quantum mechanical level (known as the quantum cluster) and the rest of the system, which is treated using a simpler approach (known as the classical region). In this case we describe the quantum cluster at the all-electron level with density functional theory (DFT) and the nonlocal B3LYP hybrid density functional.47,48 The 6-31G* basis set is used for Mg and O ions and 6-311+G* for H (referred to as the standard basis set). For some of the calculations the basis set on undercoordinated oxygen ions was increased to 6-311+G* (referred to as the extended basis set). Au atoms are described using the LANL pseudopotential, and the valence electrons are treated using the triple-ζ LANL08 basis set.49 The remaining atoms are described using the polarizable shell model potential of Lewis and Catlow as described above. Mg ions within 5 Å of the quantum cluster are described using effective core pseudopotentials with no associated basis, to prevent artificial spilling of the wave function into the classical region (Figure 1). The Kohn–Sham equations are solved in the quantum cluster, including the electrostatic environment provided by the remaining ions. The total energy of the entire system (quantum and classical) is then minimized with respect to the positions of all ions using the BFGS algorithm. This method is implemented in the GUESS code29 interfaced to the NWChem code for the quantum mechanical part of the calculation.50,51 Similar approaches have been employed in many previous investigations of defects in MgO, and in the cases where there are experimental data to compare to, the accuracy of the predictions is generally very good.7,29,52−56
Optical excitation spectra are calculated using time-dependent DFT using the optimized geometry obtained above. We also obtain vibrational frequencies for OH– by calculating the dynamical matrix numerically using finite ion displacements and diagonalizing to obtain eigenenergies and eigenvectors. We tested the effect of the size of displacement used (Δ) and find that decreasing Δ from 10 to 5 pm leads to only a 3 cm–1 decrease in the vibrational frequency. All frequencies reported in this article were determined using Δ = 5 pm.
Results and Discussion
1. Structure and Stability of the a/2[110] Screw Dislocation
In the following we investigate the electronic, chemical and optical properties of a surface-terminated screw dislocation characterized by b = a/2[110] and t = [100]. In general, the types of dislocation that are formed in MgO will depend upon the growth conditions and mechanical treatment; therefore, we consider this one as a particular example. It is an interesting case from the point of view of crystal growth, since it represents a source or sink of steps on the MgO(001) surface. Following minimization of atomic forces using the shell model potential, we obtain the metastable structure shown in Figure 1. It is instructive to examine the on-site electrostatic potential throughout the nanocrystal, since this has been shown to correlate strongly with electronic and optical properties. For example, low-coordinated anions and cations can act as hole- and electron-trapping sites owing to their significantly perturbed electrostatic environment. The ions in Figure 1 are colored according to the magnitude of the on-site electrostatic potential (red is low, blue is high). The strong variation in potential at the low-coordinated edge and step ions is clearly evident; however, ions forming the dislocation core are not significantly perturbed with respect to the rest of the surface. This suggests ions near the dislocation core are not likely to present particularly favorable sites for electron or hole trapping. However, as we shall show below, while this is indeed the case, it does not mean that dislocations are unable to trap charge.
As discussed in the previous section, the nanocrystal containing a dislocation is a metastable configuration, since it is energetically profitable for the dislocation to annihilate at the surface-producing steps. In fact, the dislocated nanocrystal is 47 meV per atom less stable than a dislocation-free nanocrystal containing the same number of atoms. To assess the local stability of the dislocation, we perform molecular dynamics simulations of 1 ns duration for a series of temperatures. We find the dislocation is immobile and stable up to 800 K, at which point it is observed to annihilate at the surface. However, at extended surfaces such dislocations, which may be introduced by strain or through nonequilibrium growth processes, will be much more immobile.
2. Electron Trapping
The analysis of on-site electrostatic potential in the previous section suggests that ions forming the core of a screw dislocation core at the MgO(001) surface are unlikely to act as electron or hole traps. However, the electron affinity calculated using the embedded cluster method is found to be 0.50 eV (increased slightly to 0.56 eV using the extended basis set). To rationalize this discrepancy, we analyze the electron spin density associated with the trapped electron (Figure 2). Unusually, the electron is not localized at a low-coordinated cation as is found for corner and kink sites but is instead trapped in the space just above the dislocation core. The origin of this trapping effect is purely electrostatic. The three ions closest to the center of the trapped electron charge distribution are Mg ions (at a distance of 1.7, 1.9, and 2.3 Å). The positive charge of these ions creates an electrostatic potential well in which the electron can localize. Trapping is further stabilized by polarization of the surrounding material.
Figure 2.
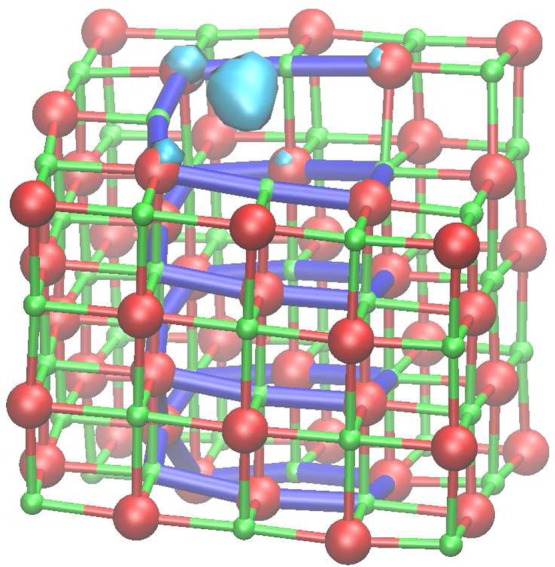
Spin density associated with a trapped electron at the surface-terminated b = a/2[110] screw dislocation (only ions in the quantum cluster are shown). Large red spheres represent O ions, and smaller green spheres represent Mg ions. The bonds highlighted in blue are to guide the eye through the dislocation core. Please refer to the online version of this article for references to color.
In many ways the nature of this electron trap is very similar to the classic F-center defect.57 The F-center defect is produced by removing an oxygen ion from the ideal crystal. The electrostatic potential well in the void created is sufficiently deep to enable up to two electrons to be trapped. The surface-terminated screw dislocation exhibits a similar effect, except that in this case the surface is fully stoichiometric and it is the topological perturbation of the dislocation alone which creates the electrostatic potential well. Just as for the F-center the dislocation is able to trap a second electron which is localized in the same well. This particular dislocation is found to have no affinity for further electrons. However, previous studies have shown that electrons can be trapped deep inside the cores of other types of dislocation.54
To aid experimental detection of this unusual electron trap by EPR spectroscopy, we compute the corresponding g tensor for the case where a single electron is trapped at the surface. The principal components of the diagonalized g tensor are g = (1.99959, 1.99988, 2.00057). The third component is aligned close to the surface normal, while the other two components are primarily within the (001) surface plane. We note that the symmetry and anisotropic part of the g tensor are very similar to those calculated for a surface F+ defect in MgO.56
3. Optical Excitation of the Screw Dislocation
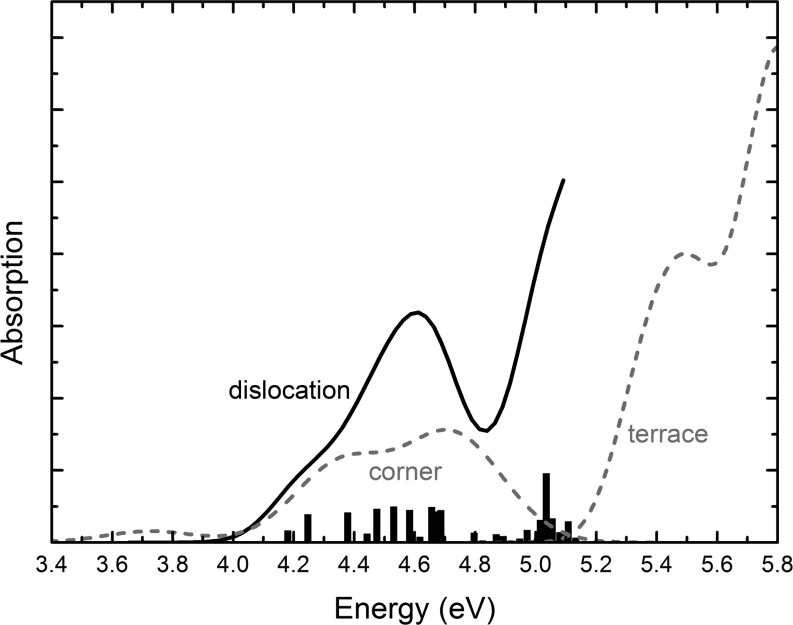
Previous theoretical and experimental studies have shown that undercoordinated topological features at the surface of MgO exhibit distinct optical absorption which is red-shifted with respect to the bulk and ideal (001) surface.6,30 The features which introduce the lowest energy excitations (close to 4.6 eV) are three-coordinated defects such as steps, kinks, and corners. It is interesting to investigate whether the surface-terminated screw dislocation considered here can also introduce red-shifted absorption energies in light of the electron trapping state elucidated in the previous section. Figure 3 shows the optical absorption spectra calculated using time-dependent DFT within the embedded cluster approach and the extended basis set. The bars indicate the oscillator strength, while the curve is a simulated absorption spectrum obtained by summing discrete excitations broadened by a Gaussian of width 0.1 eV. There are low-energy excitations in the range 4.4–4.7 eV which involve electron excitations from delocalized hole states in the bulk to the surface-localized electron state. These excitation energies are similar to those associated low-coordinated features in MgO nanocrystals, such as corners; however, the nature of the electronic transitions is very different. For example, at corner features low-energy excitations involve electronic transitions between occupied and unoccupied molecular orbitals which are localized on one or a small number of ions near the corner. At the dislocation excitation involves electronic transitions to molecular orbitals which are not localized on undercoordinated ions but are associated with an electrostatic potential well near the dislocation core. In many ways the nature of these excitations is similar to those of F-center defects in MgO.58,59 Importantly, these calculations predict that surface-terminated dislocations may introduce absorption features similar to those of low-coordinated surface sites, as highlighted in Figure 3.
Figure 3.
Calculated optical absorption spectra of the surface-terminated b = a/2[110] screw dislocation (solid line). The height of the bars indicates the oscillator strength, while the curve is a simulated absorption spectrum using a Gaussian width of 0.1 eV. The simulated absorption spectra associated with low-coordinated corners features and the extended (001) terrace are also shown for comparison60 (dashed lines).
4. Hydrogen-Related Defects
Hydrogen-related defects are common in many oxide materials. They can be introduced during the growth or postprocessing of materials or be incorporated through the adsorption and dissociation of water, hydrogen, or other molecules on exposed surfaces.61 For example, heterolytic dissociation of water on MgO leads to the formation of a proton adsorbed on a surface oxygen ion and a OH– adsorbed on a surface magnesium ion. One of the main indicators of the presence of H in oxides is the presence of absorption features in their IR spectra. Numerous IR bands have been observed on MgO surfaces which have been attributed to H-related defects at topological sites of reduced coordination. However, there is still considerable debate concerning the precise nature of many of the observed absorption features.62 In the following we investigate how protons and H atoms interact with the surface-terminated screw dislocation and how their vibrational IR signature is affected.
To find stable adsorption sites for protons in the vicinity of the screw dislocation, we performed a series of geometry optimizations with protons starting in many different positions in the quantum cluster. We found that the adsorption energies were changed by less than 0.01 eV on switching to the extended basis set; therefore, all subsequent calculations were performed using the standard basis set. Of these, the four most stable configurations that were obtained are shown in Figure 4 (the O ions to which the protons are attached are denoted a–d). In all cases protons are bound more strongly at the MgO(001) surface than near the dislocation (see Table 1), although for protons deep inside the dislocation (site d) this difference is less than 0.2 eV. As has been shown previously, protons are 1.65 eV more stable at the MgO(001) surface than in the bulk;56 therefore, segregation of protons from the bulk to dislocations is always energetically preferable. The frequency of the OH– stretching mode is also calculated for each adsorption site, as shown in Table 1. The vibrational frequency is given relative to that for a proton adsorbed at the MgO(001) surface (which is calculated to be 3787 cm–1 in this study). For protons deep inside the dislocation the OH– stretching mode the frequency is predicted to be red-shifted by about 700 cm–1 with respect to the ideal surface.
Figure 4.
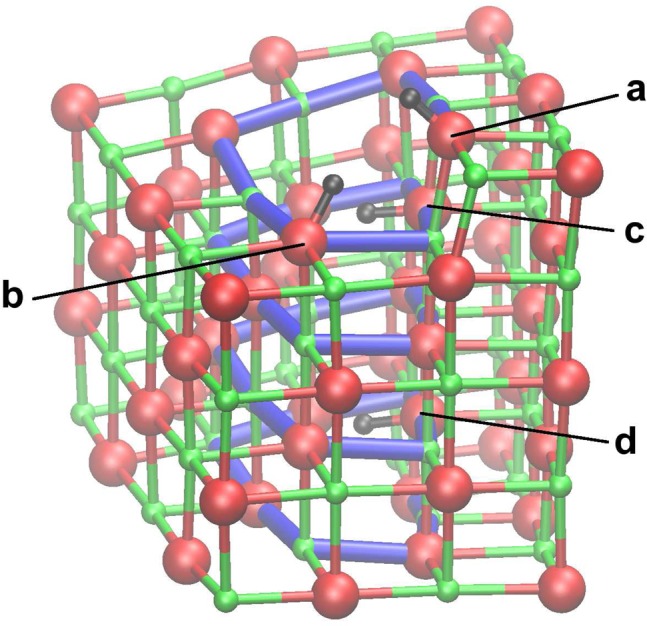
Stable proton adsorption sites within the surface-terminated b = a/2[110] screw dislocation (labeled a–d). Large red spheres represent O ions, smaller green spheres represent Mg ions, and small black spheres represent protons. Please refer to the online version of this article for references to color.
Table 1. Adsorption Energies for Proton and H Defects at Sites a–d (Figure 4) Relative to the Adsorption Energy for the Corresponding Defect Adsorbed at the MgO(001) Surface (ΔEads)a.
| proton |
hydrogen |
|||
|---|---|---|---|---|
| site | ΔEads (eV) | Δf (cm–1) | ΔEads (eV) | Δf (cm–1) |
| a | +0.84 | –510 | –0.43 | –356 |
| b | +0.37 | –424 | –0.41 | –385 |
| c | +0.53 | –624 | –0.35 | –596 |
| d | +0.18 | –685 | –0.18 | –702 |
Δf is the OH– stretching vibrational frequency relative to that of a proton adsorbed at the (001) surface.
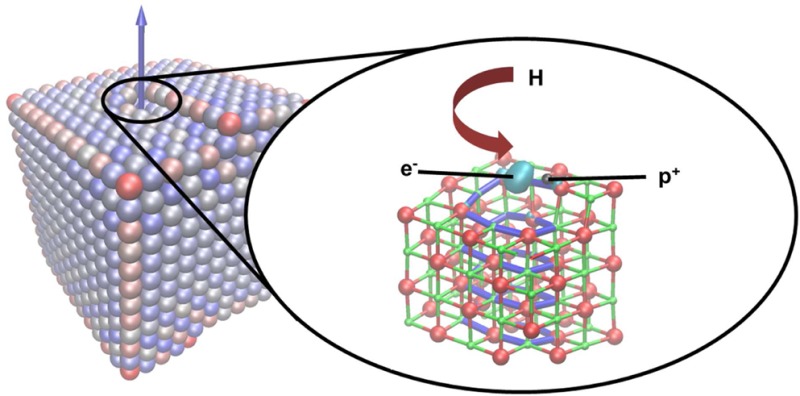
We next consider the interaction of atomic hydrogen with the screw dislocation in order to explore the possibility that H atoms could donate an electron which is then trapped inside the dislocation, as proposed by Benia et al. to explain their experimental observations.20 The most stable adsorption positions for H atoms are found to be the same as those shown in Figure 4 for protons. Table 1 shows the corresponding adsorption energies relative to a H atom adsorbed at the MgO(100) surface. In contrast to the case of protons, adsorption of H inside the dislocation is energetically favorable with respect to surface adsorption. The most stable adsorption site (a) is at the terminus of the dislocation, and Figure 5 shows the corresponding structure and electron spin density. The H atom adsorbs as a separated electron–proton pair, with the electron trapped inside the F-center-like potential well inside the dislocation core and the proton adsorbed on a nearby oxygen ion. For adsorption at the other sites (b–d) the electron stays in the same place but the proton is adsorbed on different O ions. The electrostatic attraction between the proton and electron makes site a the most favorable, but it only costs 0.25 eV to separate them by nearly 8 Å (i.e., site a → site d).
Figure 5.
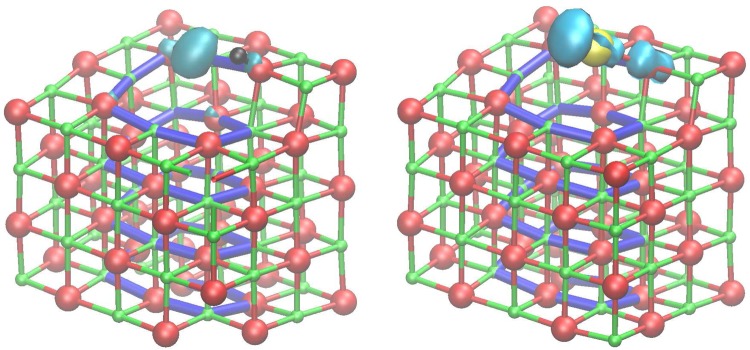
(left) Structure and spin density for a H atom adsorbed at site a in the surface-terminated screw dislocation. Large red spheres represent O ions, smaller green spheres represent Mg ions, the yellow sphere represents an Au atom, and small black spheres represent protons. (right) Structure and spin density for a Au atom adsorbed at the most stable position near the screw dislocation. Please refer to the online version of this article for references to color.
Another indication that the proton and electron dissociate inside the dislocation core is that the proton–oxygen vibrational frequencies are very similar to that for OH–, particularly for site d, where the electrostatic influence of the trapped electron is the weakest. We also calculated the isotropic hyperfine interaction for the most stable adsorption site, which is found to be very small (−11.52 MHz in comparison to 1327.76 MHz for a free H atom), further indicating the detachment of the electron. The disappearance of the hyperfine interaction for H adsorbed near dislocations was also observed in thin MgO films by Benia et al., suggesting a likely explanation for the effect. The calculated principal components of the g tensor for this defect are g = (1.99982, 2.00019, 2.00085), which has a much lower symmetry than that of the isolated trapped electron, owing to the presence of the nearby proton.
While the adsorption of the dissociated electron–proton pair inside the dislocation is stable with respect to atomic hydrogen, it is unstable with respect to the hydrogen molecule. For example, the most stable configuration for two dissociated H atoms consists of two protons (adsorbed at sites a and b) and two electrons (trapped in the dislocation core). This configuration is 1.4 eV less stable than a free hydrogen molecule, indicating that molecular hydrogen will not dissociate at this dislocation. We confirmed this result with the extended basis, finding only a 0.01 eV change in adsorption energy and no qualitative change in electron localization.
5. Interaction with Au Atoms
Surface defects such as dislocations are suspected to play an important role in the growth of supported metallic clusters by acting as stable nucleation sites. On the other hand, there have been suggestions that Au atoms may become charged by electron transfer to or from dislocations in MgO films which would hinder the nucleation and growth of clusters.21 To explore this effect, we investigate the stability and electronic properties of a Au atom near the surface-terminated screw dislocation. Figure 5 shows the most stable adsorption configuration for an Au atom near the surface, which is 0.48 eV more stable than adsorption on a O site on the regular MgO(001) surface. While we find the absolute adsorption energy of Au is affected slightly by the basis set (decreasing by 0.12 eV on switching to the extended basis set), the relative adsorption energies are unaffected. The Au atom is adsorbed bonding to O site a at a distance of 2.25 Å. Figure 5 also shows the corresponding spin density which is localized mainly on the Au atom with a small contribution on the adjacent O atom indicating partial charge transfer. This result suggests that there is no tendency for positive charging of Au by electron transfer to the screw dislocation. This is expected, since the ionization energy of Au at the MgO(001) surface is much higher than the electron affinity of the dislocation. On examination of the electronic structure of the system, we could find no evidence of a low-lying (i.e., less than 3 eV) charge transfer state that could produce positively charged Au.
On the other hand, it has also been suggested that H-related defects segregated near dislocations could be the electron-trapping centers responsible for the formation of cationic Au on MgO. Our calculations predict the electron affinity of protons in the dislocation range from 2.1 to 2.6 eV for sites a–d (Figure 4). Since the ionization energy of Au at the surface is much higher (calculated to be about 5.5 eV near the dislocation), these results predict that there is no tendency for positive charging of Au by electron transfer to the MgO dislocation or associated H defects. However, the high electron affinity of the Au atom means that negative charging of Au in the presence of electron-rich dislocations is much more favorable.63
Summary
In summary, this article provide atomistic insight into the electronic, optical, and chemical properties of surface dislocations, an important class of defect that has so far been overlooked in terms of first-principles theoretical modeling. This is extremely timely, given the increasing number of reports which implicate dislocations in processes such as electron trapping, cluster growth, and reactivity and which have particular relevance to applications in electronics and catalysis.3−9 Here we have focused on the well-studied ionic oxide MgO and modeled an extended dislocation within a finite nanocrystal. Modeling dislocations within finite nanocrystals as opposed to considering arrays of dislocations in periodic models has the advantage that artificial dislocation interactions are eliminated. It is also more representative of real materials, which are often polycrystalline. We employed this approach in conjunction with the embedded cluster method, which is well suited to highly ionic oxides such as MgO. However, for more covalent materials such an embedded cluster approach may not be suitable. With advances in linear-scaling DFT methods an alternative would be to model the entire nanocrystal at the DFT level. Therefore, the methods we have described have potential for characterizing a far wider range of dislocation types in different oxide materials.
One of the intriguing predictions of this study is that a screw dislocation at the MgO surface can act as an electron trap. However, the nature of the trapping is rather different from other common electron traps at oxide surfaces in that the electron is not trapped by an ion but is trapped in an electrostatic potential well associated with the dislocation. In many ways this trap is more closely related to the classic F-center defect; however, in this case no substoichiometry is required. Electron trapping centers, such as corners and kinks at the oxide surface, are known to play an important role in chemical reactivity (Lewis acid sites), and these predictions suggest that surface dislocations should be included in this category. The red-shifted optical absorption and preferential adsorption of Au atoms are also characteristics shared by other topological defects at oxide surfaces. The prediction that atomic hydrogen dissociates into a proton and a trapped electron at the surface dislocation provides a theoretical model for experimental observations on thin MgO films containing misfit dislocations.20 On the other hand, the results suggest that dislocations are unlikely candidates for the experimentally observed cationic charging Au atoms on MgO.21
Theoretical modeling has played a vital role in the development of our current understanding of the structure and electronic, optical, and chemical properties of surface defects in oxides. In many cases it is only by the application of different experimental probes and complementary theoretical modeling that the roles of defects in the chemistry of oxide surfaces, optical excitation, and electron transfer processes have been unraveled. The established picture recognizes the important role of point defects such as impurities and vacancies as well as topological defects such as steps, kinks, and corners in diverse processes such as crystal growth, charge trapping, luminescence, molecular adsorption, and catalytic activity. The results presented in this article, taken together with recent experimental reports, show that surface dislocations are equally important but their complex properties are now just beginning to be understood.
Acknowledgments
I gratefully acknowledge support from the EPSRC (grant EP/K003151) and COST Action CM1104. Computer resources on the Hector service were provided via membership of the UK’s HPC Materials Chemistry Consortium and funded by the EPSRC (portfolio grant EP/F067496). Some of the calculations were performed on the Chinook supercomputer at EMSL, a national scientific user facility sponsored by the US Department of Energy’s Office of Biological and Environmental Research and located at Pacific Northwest National Laboratory.
The authors declare no competing financial interest.
References
- Barteau M. A. J. Vac. Sci. Technol., A 1993, 11, 2162–2168. [Google Scholar]
- Gai-Boyes P. L. Catal. Rev. 1992, 34, 1–54. [Google Scholar]
- Morin S. A.; Bierman M. J.; Tong J.; Jin S. Science 2010, 328, 476–480. [DOI] [PubMed] [Google Scholar]
- Henrich V. E. Rep. Prog. Phys. 1985, 48, 1481. [Google Scholar]
- Zecchina A.; Scarano D.; Bordiga S.; Spoto G.; Lamberti C. Adv. Catal. 2001, 46, 265. [Google Scholar]
- Stankic S.; Müller M.; Diwald O.; Sterrer M.; Knözinger E.; Bernardi J. Angew. Chem., Int. Ed 2005, 44, 4917. [DOI] [PubMed] [Google Scholar]
- Sterrer M.; Fischbach E.; Risse T.; Freund H.-J. Phys. Rev. Lett. 2005, 94, 186101. [DOI] [PubMed] [Google Scholar]
- Chiesa M.; Paganini M. C.; Giamello E.; Murphy D. M.; Valentin C. D.; Pacchioni G. Acc. Chem. Res. 2006, 39, 861–867. [DOI] [PubMed] [Google Scholar]
- Sousa C.; Tosoni S.; Illas F. Chem. Rev. 2013, 113, 4456–4495. [DOI] [PubMed] [Google Scholar]
- Shibata N.; Chisholm M. F.; Nakamura A.; Pennycook S. J.; Yamamoto T.; Ikuhara Y. Science 2007, 316, 82–85. [DOI] [PubMed] [Google Scholar]
- Shih C.-C.; Lin S.-J.; Chung K.-H.; Chen Y.-L.; Su Y.-Y. J. Biomed. Mater. Res. 2000, 52, 323–332. [DOI] [PubMed] [Google Scholar]
- Venables J. A. Surf. Sci. 1994, 299–300, 798–817. [Google Scholar]
- Campbell C. T. Surf. Sci. Rep. 1997, 27, 1–111. [Google Scholar]
- Heyde M.; Simon G. H.; Lichtenstein L. Phys. Status Solidi B 2013, 250, 895–921. [Google Scholar]
- Stoneham M. J. Phys.: Condens. Matter 2010, 22, 074211. [DOI] [PubMed] [Google Scholar]
- Maoz B. M.; Tirosh E.; Bar Sadan M.; Markovich G. Phys. Rev. B 2011, 83, 161201. [Google Scholar]
- Nakamura A.; Matsunaga K.; Tohma J.; Yamamoto T.; Ikuhara Y. Nat. Mater. 2003, 2, 453–456. [DOI] [PubMed] [Google Scholar]
- Blavette D.; Cadel E.; Fraczkiewicz A.; Menand A. Science 1999, 286, 2317–2319. [DOI] [PubMed] [Google Scholar]
- Atkinson A.; Taylor R. I. Philos. Mag. A 1979, 39, 581–595. [Google Scholar]
- Benia H.-M.; Myrach P.; Gonchar A.; Risse T.; Nilius N.; Freund H.-J. Phys. Rev. B 2010, 81, 241415. [Google Scholar]
- Brown M. A.; Ringleb F.; Fujimori Y.; Sterrer M.; Freund H.-J.; Preda G.; Pacchioni G. J. Phys. Chem. C 2011, 115, 10114–10124. [Google Scholar]
- Henrich V. E.; Cox P. A.. The surface science of metal oxides; Cambridge University Press: Cambridge, U.K., 1994. [Google Scholar]
- Parkin S. S. P.; Kaiser C.; Panchula A.; Rice P. M.; Hughes B.; Samant M.; Yang S.-H. Nat. Mater. 2004, 3, 862. [DOI] [PubMed] [Google Scholar]
- Itoh H.; Utampanya S.; Stark J. V.; Klabunde K. J.; Schulp J. R. Chem. Mater. 1993, 5, 71. [Google Scholar]
- Nieves I.; Klabunde K. J. Mater. Chem. Phys. 1988, 18, 485. [Google Scholar]
- Arndt S.; Laugel G.; Levchenko S.; Horn R.; Baerns M.; Scheffler M.; Schlögl R.; Schomäcker R. Catal. Rev. 2011, 53, 424–514. [Google Scholar]
- Cordier P.; Amodeo J.; Carrez P. Nature 2012, 481, 177–180. [DOI] [PubMed] [Google Scholar]
- Shluger A. L.; Sushko P. V.; Kantorovich L. N. Phys. Rev. B 1999, 59, 2417–2430. [Google Scholar]
- Sushko P. V.; Shluger A. L.; Catlow C. R. A. Surf. Sci. 2000, 450, 153–170. [Google Scholar]
- Sushko P. V.; Gavartin J. L.; Shluger A. L. J. Phys. Chem. B 2002, 106, 2269–2276. [Google Scholar]
- Ricci D.; Pacchioni G.; Sushko P. V.; Shluger A. L. J. Chem. Phys. 2002, 117, 2844. [Google Scholar]
- Richter N. A.; Sicolo S.; Levchenko S. V.; Sauer J.; Scheffler M. Phys. Rev. Lett. 2013, 111, 045502. [DOI] [PubMed] [Google Scholar]
- Coluccia S.; Tench A.; Segall R. J. Chem. Soc., Faraday Trans. 1 1978, 74, 2913. [Google Scholar]
- Cox P. A.; Williams A. A. Surf. Sci. Lett. 1986, 175, L782. [Google Scholar]
- Giamello E.; Paganini M. C.; Murphy D. M.; Ferrari A. M.; Pacchioni G. J. Phys. Chem. B 1997, 101, 971–982. [Google Scholar]
- Spoto G.; Gribov E.; Ricchiardi G.; Damin A.; Scarano D.; Bordiga S.; Lamberti C.; Zecchina A. Prog. Surf. Sci. 2004, 76, 71–146. [Google Scholar]
- Watson G. W.; Oliver P. M.; Parker S. C. Surf. Sci. 2001, 474, L185–L190. [Google Scholar]
- Benedetti S.; Nilius N.; Myrach P.; Valenti I.; Freund H.-J.; Valeri S. J. Phys. Chem. C 2011, 115, 3684–3687. [Google Scholar]
- Pacchioni G.; Freund H. Chem. Rev. 2013, 113, 4035–4072. [DOI] [PubMed] [Google Scholar]
- Sicolo S.; Sauer J. J. Phys. Chem. C 2013, 117, 8365–8373. [Google Scholar]
- Chiesa M.; Paganini M. C.; Giamello E.; Valentin C. D.; Pacchioni G. Angew. Chem., Int. Ed. 2003, 42, 1759–1761. [DOI] [PubMed] [Google Scholar]
- Hirth J. P.; Lothe J.. Theory of Dislocations; Krieger: Malabar, FL, 1991. [Google Scholar]
- Pizzagalli L.; Beauchamp P. Phil. Mag. Lett. 2004, 84, 729–736. [Google Scholar]
- Lewis G. V.; Catlow C. R. A. J. Phys. C: Solid State Phys. 2004, 18, 1149. [Google Scholar]
- Watson G. W.; Kelsey E. T.; de Leeuw N. H.; Harris D. J.; Parker S. C. J. Chem. Soc., Faraday Trans. 1996, 92, 433. [Google Scholar]
- Harding J. H.; Harris D. J.; Parker S. C. Phys. Rev. B 1999, 60, 2740. [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Phys. Rev. B 1988, 37, 785. [DOI] [PubMed] [Google Scholar]
- Becke A. D. J. Chem. Phys. 1993, 98, 5648. [Google Scholar]
- Roy L. E.; Hay P. J.; Martin R. L. J. Chem. Theory Comput. 2008, 4, 1029–1031. [DOI] [PubMed] [Google Scholar]
- Valiev M.; Bylaska E.; Govind N.; Kowalski K.; Straatsma T.; Dam H. V.; Wang D.; Nieplocha J.; Apra E.; Windus T.; de Jong W. Comput. Phys. Commun. 2010, 181, 1477–1489. [Google Scholar]
- Govind N.; Sushko P.; Hess W.; Valiev M.; Kowalski K. Chem. Phys. Lett. 2009, 470, 353–357. [Google Scholar]
- Ferrari A. M.; Pacchioni G. J. Phys. Chem. 1996, 100, 9032. [Google Scholar]
- Ricci D.; Di Valentin C.; Pacchioni G.; Sushko P. V.; Shluger A. L.; Giamello E. J. Am. Chem. Soc. 2003, 125, 738. [DOI] [PubMed] [Google Scholar]
- McKenna K. P.; Sushko P. V.; Shluger A. L. J. Am. Chem. Soc. 2007, 129, 8600–8608. [DOI] [PubMed] [Google Scholar]
- Shluger A. L.; McKenna K. P.; Sushko P. V.; Muñoz Ramo D.; Kimmel A. V. Model. Simul. Mater. Sci. Eng. 2009, 17, 084004. [Google Scholar]
- McKenna K. P.; Shluger A. L. Phys. Rev. B 2009, 79, 224116. [Google Scholar]
- Stoneham A. M.Theory of Defects in Solids: Electronic structure of defects in insulators and semiconductors; Oxford University Press: Oxford, U.K., 1975. [Google Scholar]
- Sousa C.; Pacchioni G.; Illas F. Surf. Sci. 1999, 429, 217–228. [Google Scholar]
- Rinke P.; Schleife A.; Kioupakis E.; Janotti A.; Rödl C.; Bechstedt F.; Scheffler M.; Van de Walle C. G. Phys. Rev. Lett. 2012, 108, 126404. [DOI] [PubMed] [Google Scholar]
- McKenna K. P.; Koller D.; Sternig A.; Siedl N.; Govind N.; Sushko P. V.; Diwald O. ACS Nano 2011, 5, 3003–3009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Włodarczyk R.; Sierka M.; Kwapień K.; Sauer J.; Carrasco E.; Aumer A.; Gomes J. F.; Sterrer M.; Freund H.-J. J. Phys. Chem. C 2011, 115, 6764–6774. [Google Scholar]
- Chizallet C.; Costentin G.; Che M.; Delbecq F.; Sautet P. J. Am. Chem. Soc. 2007, 129, 6442–6452. [DOI] [PubMed] [Google Scholar]
- McKenna K.; Trevethan T.; Shluger A. Phys. Rev. B 2010, 82, 085427. [Google Scholar]