AUTOMATIC MULTI-ATLAS-BASED CARTILAGE SEGMENTATION FROM KNEE MR IMAGES

Abstract

In this paper, we propose a multi-atlas-based method to automatically segment the femoral and tibial cartilage from T1 weighted magnetic resonance (MR) knee images. The segmentation result is a joint decision of the spatial priors from a multi-atlas registration and the local likelihoods within a Bayesian framework. The cartilage likelihoods are obtained from a probabilistic k nearest neighbor classification. Validation results on 18 knee MR images against the manual expert segmentations from a dataset acquired for osteoarthritis research show good performance for the segmentation of femoral and tibial cartilage (mean Dice similarity coefficient of 75.2% and 81.7% respectively).

1. INTRODUCTION

Osteoarthritis (OA) is the most common form of joint disease and is characterized by cartilage loss. Magnetic resonance imaging is increasingly accepted as a primary method to evaluate progression of OA. An accurate cartilage segmentation from magnetic resonance (MR) knee images is crucial to study OA. Due to the size of image databases acquired for OA studies, a fully automatic segmentation is needed. In this paper, we therefore propose a new cartilage segmentation method from knee magnetic resonance (MR) images, which requires no user interaction (besides quality control). The method is a step towards automatic analysis of large OA image databases.

Recently, several automatic methods have been proposed for cartilage segmentation. Folkesson et al. [1] proposed a hierarchical classification scheme for cartilage segmentation. Fripp et al. [2] used active shape models for bone segmentation in order to extract the bone-cartilage interface followed by tissue classification. A simultaneous segmentation of interacting bone and cartilage was developed by Yin et al. [3].

To allow for localized analysis and the suppression of unlikely voxels in a segmentation, introducing a spatial prior is desirable. This can be achieved through an atlas-based analysis method. While such methods have been successfully used in brain imaging, they are typically not used for cartilage segmentation in the knee. The work by Glocker et al. [4], which used a statistical shape atlas from a set of pre-aligned knee images, is an exception.

Atlas-based segmentation methods can be categorized into three groups [5], namely single-atlas-based, average-shape atlas-based and multi-atlas-based methods. The work by Glocker et al. [4] falls into the second group. Rohlfing et al. [6] demonstrated that the multi-atlas-based segmentation is more accurate than the other two types of atlas-based segmentation methods. However, little work has been done to apply multi-atlas-based segmentation methods to knee images.

In this work we discuss a fully automatic multi-atlas-based cartilage segmentation method. To the best of our knowledge, this is the first work to apply multi-atlas-based methods to cartilage segmentation. We first perform bone segmentation with spatial priors obtained from multi-atlas registration and local likelihoods from image intensities. Then we compute spatial priors for femoral and tibial cartilage through multi-atlas registration based on bone segmentations. The spatial priors are then integrated into a Bayesian framework where the likelihoods are provided by a probabilistic k nearest neighbor (kNN) classification.

Section 2 discusses the multi-atlas-based bone segmentation method. Section 3 discusses the probabilistic kNN classification and the multi-atlas-based cartilage segmentation. Experimental results are given in section 4. The paper closes with conclusions and future work.

2. MULTI-ATLAS BONE SEGMENTATION

Given a knee MR image I, a segmentation S can be obtained by assigning the label with the maximum posterior probability to each voxel x ∈ I. The bone segmentation can be modeled as

$$S\left(x\right)=\underset{l\in \left\{\mathrm{FB},\mathrm{TB},\mathrm{BG}\right\}}{\text{argmax}}p(l\mid x),$$ (1)

in which “FB”, “TB” and “BG” denote the femur, the tibia and the background respectively. According to the Bayes' theorem, we have

$$\begin{array}{cc}\hfill & p(\text{FB}\mid x)=p(x\mid \text{FB})\cdot p\left(\text{FB}\right)∕p\left(x\right),\hfill \\ \hfill & p(\text{TB}\mid x)=p(x\mid \text{TB})\cdot p\left(\text{TB}\right)∕p\left(x\right),\hfill \\ \hfill & p(\text{BG}\mid x)=1-p(\text{FB}\mid x)-p(\text{TB}\mid x).\hfill \end{array}$$ (2)

The likelihood terms p(x|FB) and p(x|TB) are computed from image intensities. Since bones appear dark in T1 weighted MR images, we assume a simple model (3) to estimate bone likelihoods,

$$p(x\mid \text{FB})=p(x\mid \text{TB})=exp(-\beta I\left(x\right)),$$ (3)

where β is set to 0.02 in our implementation.

To compute the prior terms p(FB) and p(TB) in (2), we employ a multi-atlas registration approach followed by label fusion. Suppose we have N atlases A_i and their bone segmentations $S_i^{\text{FB}}$ and $S_i^{\text{TB}}$ (i = 1,2, …, N). Registration from an atlas A_i to a query image I is an affine registration $T_i^{\mathit{affine}}$ followed by a B-Spline registration $T_i^{\mathit{bspline}}$ based on mutual information. Averaging all N propagated atlas labels yields a spatial prior of femur and tibia for the query image:

$$\begin{array}{cc}\hfill & p\left(\text{FB}\right)=\frac{1}{N}\sum _{i=1}^N\left(T_i^{\text{bspline}}\circ T_i^{\text{affine}}\circ S_i^{\text{FB}}\right),\hfill \\ \hfill & p\left(\text{TB}\right)=\frac{1}{N}\sum _{i=1}^N\left(T_i^{\text{bspline}}\circ T_i^{\text{affine}}\circ S_i^{\text{FB}}\right).\hfill \end{array}$$ (4)

So far we have computed the likelihood and the prior for femur and tibia. Choosing the label with the maximum posterior probability gives us a bone segmentation S^FB and S^TB for the query image I.

As we are primarily interested in the femoral and tibial cartilage, we make use of the bone segmentation to extract a fixed-sized joint region (centered at the geometric center between femur and tibia) out of the original image. From now on, we work in a smaller cartilage ambient space.

3. MULTI-ATLAS CARTILAGE SEGMENTATION

We use the same segmentation framework (1) to segment cartilages as we use for the bone segmentation in section 2. A probabilistic kNN classification [7] is employed to generate the cartilage likelihoods because image intensity alone is not sufficient for cartilage segmentation. The spatial prior for the cartilage is obtained through a multi-atlas registration of the bone segmentation in the joint region.

3.1. Probabilistic kNN

Folkesson et al. [1] proposed a hierarchical kNN classification scheme for cartilage segmentation. Compared to [1], we use a probabilistic version of kNN classification to integrate the classification results into a Bayesian framework. We choose a reduced set of 15 features compared to [1]: intensities on three scales, first-order derivatives in three directions on three scales and second-order derivatives in axial direction on three scales. The three different scales are obtained by convolving with Gaussian kernels of σ = 0.3 mm, 0.6 mm and 1.0 mm. All features are normalized to be centered at 0 and to have unit standard deviation. We use a one-versus-other classification strategy and expert segmentations of femoral and tibial cartilage to build the kNN classifier. Specifically, let “FC” denote the femoral cartilage, “TC” the tibial cartilage and “BG” the background class. The training samples of the femoral cartilage class and the tibial cartilage class are the voxels labeled as femoral cartilage and tibial cartilage respectively. The training samples of the background class are the voxels surrounding the femoral and tibial cartilage within a specified distance. The outputs of the probabilistic kNN classifier given a query voxel x with its feature vector f(x) are:

$$\begin{array}{cc}\hfill & p(x\mid \text{FC})=n_{\text{FC}}\left(\text{f}\left(x\right)\right)∕k,\hfill \\ \hfill & p(x\mid \text{TC})=n_{\text{TC}}\left(\text{f}\left(x\right)\right)∕k,\hfill \\ \hfill & p(x\mid \text{BG})=n_{\text{BG}}\left(\text{f}\left(x\right)\right)∕k.\hfill \end{array}$$ (5)

Here n_FC, n_TC, n_BG denote the number of votes for the femoral cartilage, the tibial cartilage, and the background respectively; k is the number of nearest neighbors of concern and chosen to be 30 in our implementation. Since kNN is sensitive to the number of training samples, we scale the outputs according to the training class sizes to balance the three classes.

3.2. Multi-atlas cartilage registration

We have N joint atlases A_i, together with their femur segmentations $S_i^{\text{FB}}$, tibia segmentations $S_i^{\text{TB}}$, femoral cartilage segmentations $S_i^{\text{FC}}$ and tibial cartilage segmentations $S_i^{\text{TC}}$ (i = 1,2, …, N). For a query image I, we have the bone segmentation S^FB and S^TB from section 2.

Joint atlas bone segmentations $S_i^{\text{FB}}$ and $S_i^{\text{TB}}$ are registered to the bone segmentation S^FB and S^TB of the joint region in the query image separately by B-Spline transforms $T_i^{\text{FB}}$ and $T_i^{\text{TB}}$. Rather than averaging over all propagated atlas cartilage segmentations, we apply a locally weighted label fusion strategy [5], which was shown to yield a better segmentation accuracy. We choose to favor the atlases which locally agree better with the cartilage likelihoods p(x|FC) and p(x|TC) from the probabilistic kNN classification in section 3.1. The spatially varying weighting functions ${\lambda }_i^{\text{FC}}$ for the femoral cartilage and ${\lambda }_i^{\text{TC}}$ for the tibial cartilage are calculated as

$$\begin{array}{cc}\hfill & {\lambda }_i^{\text{FC}}\left(x\right)=\frac{1}{\alpha \mid T_i^{\text{FB}}\circ S_i^{\text{FC}}-p(x\mid \text{FC})\mid +∊},\hfill \\ \hfill & {\lambda }_i^{\text{TC}}\left(x\right)=\frac{1}{\alpha \mid T_i^{\text{TB}}\circ S_i^{\text{TC}}-p(x\mid \text{TC})\mid +∊},\hfill \end{array}$$ (6)

followed by a small amount of diffusion smoothing. We choose α = 0.2 and ∈ = 0.001 in our implementation. The spatial prior for each cartilage is then the weighted average of the propagated atlas cartilage segmentations

$$\begin{array}{cc}\hfill & p\left(\text{FC}\right)=\sum _{i=1}^N\frac{{\lambda }_i^{\text{FC}}}{{\sum }_{i=1}^N{\lambda }_i^{\text{FC}}}(T_i^{\text{FC}}\circ S_i^{\text{FB}}),\hfill \\ \hfill & p\left(\text{TC}\right)=\sum _{i=1}^N\frac{{\lambda }_i^{\text{TC}}}{{\sum }_{i=1}^N{\lambda }_i^{\text{TC}}}(T_i^{\text{TC}}\circ S_i^{\text{TB}}).\hfill \end{array}$$ (7)

Once we have computed the spatial priors and the local likelihoods, the cartilage segmentation can be easily constructed by picking the label with the maximum posterior probability. Segmentation holes and islands are eliminated as a refinement step to improve the final result.

4. RESULTS AND VALIDATION

We test the proposed approach on a set of 18 MR images (T1 weighted SPGR images acquired coronally at a resolution of 1.00×0.31×0.31 mm³) from different subjects. Expert bone and cartilage segmentations are available for all images. Each of the 18 images is segmented using the remaining 17 images as atlases and kNN training samples. The original size of the images is 116 × 512 × 512. The extracted joint region has a size of 60 × 128 × 256.

The primary goal of this work is to segment cartilage from knee images. An accurate bone segmentation is of great importance to achieve a satisfactory cartilage segmentation since the multi-atlas registration of cartilage is based on bone segmentations in the joint region. We can see from Fig. 1 that the multi-atlas prior captures the bone very well and our segmentation result is very close to the expert segmentation especially in the joint region. Figure. 2 shows the good quality of the cartilage segmentation result achieved by the multi-atlas prior.

Fig. 1.

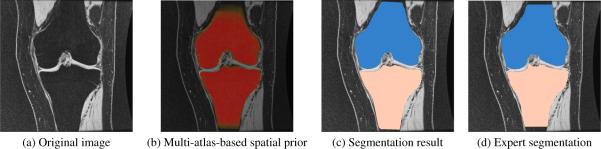
Bone segmentation of one example slice in coronal view.

Fig. 2.

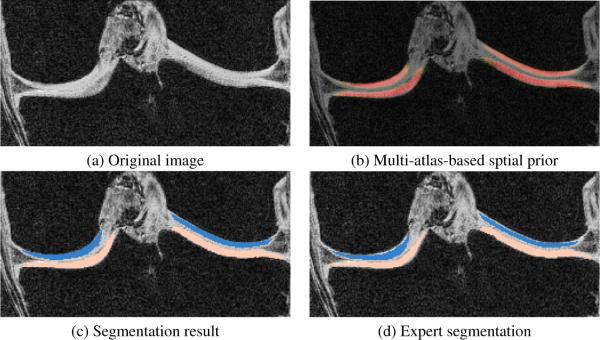
Cartilage segmentation of one example slice in coronal view. Only joint region is shown.

Table 1 shows the accuracy of the bone and cartilage segmentation, which is comparable to those reported in the existing literature (e.g., [1, 2, 3])¹. Our method is easy to implement (the major components are affine registration, B-Spline registration and kNN). Note that the femoral cartilage segmentation is drawn only on the weight-bearing part while the tibial cartilage segmentation covers the entire region. Therefore, we expect partial femoral cartilage segmentations and full tibial cartilage segmentations.The Dice similarity coefficient (DSC) for the femoral cartilage is lower than tibial cartilage because of the smaller volume.

Table 1.

Statistics (mean and standard deviation (STD)) of cartilage segmentation validation results. DSC is Dice similarity coefficient. SENS is sensitivity and SPEC is specificity. Note that we only segment the weight-bearing region of the femoral cartilage which makes the segmentation harder because of the smaller volume.

		DSC	SENS	SPEC
Femur	Mean STD	97.3% 0.8%	97.1% 1.2%	99.2% 0.3%
Tibia	Mean STD	96.5% 1.1%	97.3% 1.1%	98.8% 0.6%
Femoral cartilage	Mean STD	75.2% 4.9%	80.7% 7.8%	99.8% 0.06%
Tibial cartilage	Mean STD	81.7% 2.6%	83.3% 6.2%	99.8% 0.06%

5. CONCLUSION AND FUTURE WORK

We propose an automatic multi-atlas-based cartilage segmentation approach. Bones are first segmented from the knee images based on the multi-atlas registration and the local bone likelihoods which are computed from image intensities. The spatial prior for the cartilage is obtained by locally weighted fusion of propagated cartilage segmentations based on bone segmentations in the joint region. Cartilage likelihoods are obtained through a probabilistic kNN classifier. Validation of the proposed method on 18 cases in a leave-one-out manner shows good performance (a mean DSC of 75.2% for the femoral cartilage and 81.7% for the tibial cartilage).

A number of improvements over the current approach are conceivable. While kNN is a sensible classification choice, a more advanced classifier could potentially improve the classification accuracy. Integrating the probabilities into a segmentation framework with spatial regularization, e.g., a three-label segmentation [8] could conceivably lead to a performance improvement. An atlas selection method and a better label fusion strategy for the cartilage will be explored in the future. We will also test our method on the SKI10 [9] dataset to compare with other methods. Most crucially, our current test is performed on a limited number of images. We will test our method on a large set of images and evaluate it for different stages of OA separately.