Abstract
Multi-atlas label fusion has been widely applied in medical image analysis. To reduce the bias in label fusion, we proposed a joint label fusion technique to reduce correlated errors produced by different atlases via considering the pairwise dependencies between them. Using image similarities from image patches to estimate the pairwise dependencies, we showed promising performance. To address the unreliability in purely using local image similarity for dependency estimation, we propose to improve the accuracy of the estimated dependencies by including empirical knowledge, which is learned from the atlases in a leave-one-out strategy. We apply the new technique to segment the hippocampus from MRI and show significant improvement over our initial results.
1. INTRODUCTION
Enabled by availability and low cost of multi-core processors, multi-atlas label fusion (MALF) warps multiple labeled images, called atlases, to a target image, and uses a label fusion strategy to derive a consensus segmentation. Some of the best published automatic segmentation results have been produced by MALF, e.g. [1].
After warping multiple atlases to a target image through deformable registration, most label fusion techniques apply weighted voting to combine the segmentations produced by referring to different atlases, where each warped atlas contributes to the final solution according to a non-negative weight. The weights are usually computed independently for each atlas based on the estimated registration quality, such that atlases more accurately registered to the target image are counted more heavily in voting. The limitation of these methods is that they are less effective when the errors produced by multiple atlases are correlated 1.
To address this problem, we proposed joint label fusion that explicitly accounts for the dependencies between the atlases in estimating the voting weights [2]. This method captures the pairwise dependencies between atlases in terms of producing common segmentation errors for a target image. Using image similarity between the warped atlas image and the target image as an indicator of segmentation accuracy, we estimated the pairwise dependencies from image similarities computed using image patches and produced promising results. Since image similarity may be unreliable in predicting segmentation errors, to further improve the performance, we propose to incorporate empirical dependency information that is empirically learned from the atlases to compliment the similarity-based estimation.
We apply our method to segment the hippocampus from MRI and show significant improvement over our initial study. Using significantly fewer atlases, we produce significantly better results than the published state of the art hippocampus segmentation produced by MALF.
2. JOINT LABEL FUSION BY INCORPORATING DEPENDENCIES BETWEEN ATLASES
We briefly describe the joint label fusion approach[2]. We model segmentation errors produced in atlas based segmentation as , where l is a label in the target image. and are the observed votes for label l produced by the target image and the ith warped atlas, respectively. Here, we only consider discrete votes, i.e. . Hence, δi(x) ∈ {−1, 0, 1} is the observed label difference produced by the ith atlas at location x. The probability that different atlases produce the same label error at location x are captured by a dependency matrix Mx, with measuring the error correlation between ith and jth atlases. FT is the target image, Fi is the ith warped atlas image. Large dependencies indicate candidate segmentations produced by the corresponding atlases contain significant similar errors. The expected label difference between the weighted combined solution and the target segmentation can be computed from the dependency matrix by:
| (1) |
where n is the number of atlases and wx(i) is the weight for ith atlas with the constraint . t stands for matrix transpose. To minimize the expected label difference, the optimal weights can be solved by applying Lagrange multipliers and the solution is , where 1n = [1; 1; … 1] is a vector of size n.
3. ESTIMATING THE DEPENDENCY MATRIX
Our approach relies on knowing Mx, the matrix of expected pairwise joint label differences between the atlases and the target image. In [2], we used image similarity to approximate registration accuracy and estimate expected pairwise joint label differences from the image intensities as follows:
| (2) |
where is a neighborhood centered around x. In our experiment, periment, we use a cubic neighborhood definition, specified by a radius r. For robustness, we normalize the intensity vector obtained from a neighborhood, i.e. , such that it has zero mean and a constant norm. Although we report superior performance than the published state of the art label fusion methods using this estimation, it is well known that image similarities over small image patches are not always a reliable estimator for registration accuracy, therefore may not always give reliable estimations for the error correlations. For more reliable estimation, we propose to enhance the image similarity based estimation with empirical knowledge learned from the atlases, as described below.
Empirical dependency matrix learned from training data
Given a training image FT whose manual segmentation ST is given, the joint label error between any two atlases can be straightforwardly estimated by independently registering and warping2 the two atlases to the target training image.
| (3) |
is the estimated joint label error obtained from the training image FT. I(·) is an indicator function that outputs 1 if the input is true and 0 otherwise. Note that the empirical dependencies are spatially varying at different location x.
Incorporating multiple training data by normalization-based averaging
A more reliable empirical pairwise dependency estimation may be obtained by averaging over the estimations independently produced from using multiple training images. However, the estimations are obtained within the native space of each training image, which may not be comparable with each other. To address this problem, we register each training image to a template space, which allows us to warp the joint label error estimated from each training image into the template space. Let be the warped joint label error in the template space obtained from using training image FT. A more reliable estimation is obtained by averaging the estimations from all training images:
| (4) |
where is the set containing all training images and is the number of training images. To apply the empirical dependencies to segment a target image, Nx is warped into the native space of the target image through registering the template to the target image.
Empirical estimation using the atlases
Without requiring additional training images, empirical dependencies can be estimated using the atlases through a leave-one-out cross-validation strategy. First, pointwise correspondences between every pair of atlases is established through deformable registrations. This allows every atlas to be segmented by each of the remaining atlases, from which the pairwise joint label error between each pair of the remaining atlases can be estimated. The final estimation is obtained by averaging over the estimations from all the leave-one-out experiments.
Integration of the estimated dependencies
The empirical estimation approximates the expectation that any two atlases produce common errors, but it completely ignores the actual registration performance. On the other hand, the image similarity based estimation aims to capture the dependencies in the actual registration. Hence, integrating these two complementary estimations may improve the reliability. We use a linear integration as follows:
| (5) |
λ is a non-negative parameter balancing the contributions of the two estimations. Again, without requiring additional training data, the optimal λ can be determined by the same leave-one-out scheme on the atlases.
Refining label fusion by local patch search
As recently shown in [3], the performance of atlas-based segmentation can be moderately improved by applying a local search technique. This method also uses image similarities over local patches as indicators of registration accuracy and remedies registration errors by searching for the correspondence that gives the most similar appearance matching, within a small neighborhood around the registered correspondence in each warped atlas. The searched optimal correspondence is:
| (6) |
ξi(x) is the location in ith atlas with the best image matching for location x in the target image within the local neighborhood . Again, we use a cubic neighborhood definition, specified by a radius rs. Note that and may represent different neighborhoods and they are free parameters. Given the set of local search correspondence maps {ξi}, we estimate the empirical error dependency estimation (3) by:
| (7) |
4. EXPERIMENTS
We validate our method in a hippocampus segmentation task.
Data and experiment setup
We use the data in the Alzheimer's Disease Neuroimaging Initiative (ADNI). Our study is conducted using 3 T MRI and only includes data from mild cognitive impairment (MCI) patients and controls. Overall, the data set contains 57 controls and 82 MCI patients. The images are acquired sagitally, with 1 × 1 mm in-plane resolution and 1.2 mm slice thickness. To obtain reference segmentation, we first apply a landmark-guided atlas-based segmentation method [4] to produce an initial segmentation for each image. Each fully-labeled hippocampus is manually edited by one trained rater following a previously validated protocol [5]. Our intra-rater segmentation performance is 0.923 Dice overlap (See [6] Appendix for more details about our manual segmentation).
For cross-validation evaluation, we randomly select 20 images to be the atlases and another 20 images for test. Image guided registration is performed by the Symmetric Normalization (SyN) algorithm implemented by ANTS [7] between each pair of the atlas image and the test image. The cross-validation experiment is repeated 10 times. In each cross-validation experiment, a different set of atlases and testing images are randomly selected from the ADNI dataset.
Implementation details
For hippocampus segmentation, we apply shape-based normalization using the continuous medial representation (cm-rep) [8] to establish the pointwise correspondence between each training/test image and a template. When reliable segmentation of the hippocampus is available, shape-based normalization can be conducted more reliably than deformable image registration for registering regions with homogenous intensity patterns, such as the hippocampus in MRI. This technique has been successfully applied for hippocampal subfield segmentation in our previous study [9].
We first apply joint label fusion to segment each atlas and each test image. For this task, we use the appearance window with r = 2 without local search, i.e. rs = 0, to compute the image based dependency matrix (2). The resulting segmentation has accuracy comparable to inter-rater performance, which is reliable for shape-based normalization. Then, a deformable cm-rep model is separately fitted to each automatic hippocampus segmentation and the manual hippocampus segmentation of a template. Based on geometrical properties derived from the medial axes of the hippocampi, the model imposes a 3D coordinate system on the interior and exterior of the hippocampus, establishing a one to one correspondence between each atlas/test image and the template.
Our method has three parameters, r for the local appearance window used in similarity-based dependency estimation, rs for the local search window used in remedying registration errors and λ for combining the dependency estimations. For each cross-validation, the parameters are optimized by evaluating a range of values (r ∊ {1,2,3}; rs ∊ {0,1,2,3}; λ ∊ {0, 0.5, 1, 1.5, 2}) using the atlases. We measure the average overlap between the automatic segmentation of each atlas segmented by the remaining atlases and the reference segmentation of that atlas, and find the parameters that maximize this average overlap. The selected parameters are applied to segment test images in this cross-validation.
To compare with the state of the art in label fusion, we implemented two similarity-based local weighting methods: Gaussian weighting (8) (LWGaussian) and inverse distance weighting (9) (LWInverse), which as shown in recent experimental studies, e.g. [10, 11], are the most effective techniques. These two methods assign weights to atlases according to image similarity between the warped atlas image and the target image using the following functions, respectively:
| (8) |
| (9) |
where Z(x) is a normalization constant. σ and β are model parameters for these two methods, respectively. As for our method, we apply the leave-one-out strategy on the atlases to select the optimal model parameters (σ ∊ [0, 0.05, 0.1, …, 1] and β ∊ [0, 0.5, 1, …, 10]). The optimal local search window and local appearance window are determined using the atlases as well. In addition, we use majority voting (MV) and the STAPLE algorithm [12] to define the baseline performance.
To reduce the noise effect, we apply mean filter smoothing with the smoothing window , the same neighborhood used for local appearance window, to spatially smooth the weights computed by each method for each atlas.
Results
Fig. 1 shows that including the empirical dependencies consistently improves segmentation performance. The most improvement is achieved when the image similarity based dependency estimation can not be reliably conducted using small appearance windows with r = 1. When the similarity-based estimation is more reliable using larger appearance windows, including the empirical dependencies still makes a prominent improvement. Table 1 shows the results in terms of Dice overlap produced by each method. In terms of average number of mislabeled voxels, LWGaussian and LWInverse produce 371 and 373 mislabeled voxels for each hippocampus, respectively. Joint label fusion produces 352 and 341 mislabeld voxels using similarity-based dependency estimation and the proposed approach, respectively. The improvement brought by including empirical dependencies is statistically significant, with p < 0:001 on the paired Student's t-test for each cross-validation experiment. Note that our results are also better than other recent hippocampus segmentation results produced by MALF, such as [1, 13].
Fig. 1.
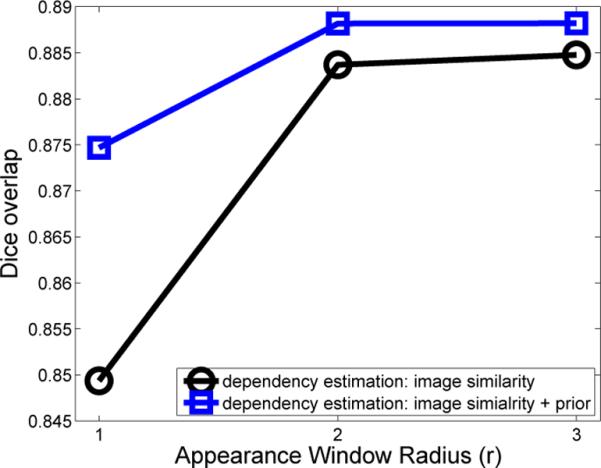
Performance (in Dice) with/without including empirical dependencies when different local appearance windows are used for similarity based dependency estimation. In this test, local search is not applied.
Table 1.
Performance (Dice) produced by each method.
| method | left | right |
|---|---|---|
| MV | 0.836±0.084 | 0.829±0.069 |
| STAPLE | 0.846±0.086 | 0.841±0.086 |
| LWGaussian | 0.887±0.026 | 0.876±0.029 |
| LWInverse | 0.887±0.026 | 0.875±0.030 |
| similarity | 0.894±0.024 | 0.885±0.027 |
| similarity+empirical | 0.897±0.024 | 0.890±0.027 |
5. CONCLUSIONS
We proposed to incorporate empirical dependencies between atlases, which is learned via a normalization-based technique using the atlases in a leave-one-out strategy, to improve the performance of MALF. The empirical dependencies are complementary to the previously applied image similarity-based dependency estimation. Combining them results in significant improvement over only using the similarity-based estimation. On a hippocampus segmentation task, our results outperformed the published state of the art MALF.
Acknowledgments
This work was supported by the Penn-Pfizer Alliance grant 10295 (PY) and the NIH grants K25 AG027785 (PY) and R01 AG037376 (PY)
Footnotes
As a simple example, suppose that a single atlas is duplicated multiple times in the atlas set. If weights are derived only from atlas-target similarity, the total contribution of the repeated atlas to the consensus segmentation will increase in proportion to the number of times the atlas is repeated.
In this empirical estimation, the same image-based deformable registration technique that is used by the MALF implementation should be applied.
6. REFERENCES
- [1].Heckemann R, Hajnal J, Aljabar P, Rueckert D, Hammers A. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. NeuroImage. 2006;33:115–126. doi: 10.1016/j.neuroimage.2006.05.061. [DOI] [PubMed] [Google Scholar]
- [2].Wang H, Suh JW, Pluta J, Altinay M, Yushkevich P. IPMI. 2011. Optimal weights for multi-atlas label fusion. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Wang H, Suh JW, Das S, Pluta J, Altinay M, Yushkevich P. CVPR. 2011. Regression-based label fusion for multi-atlas segmentation. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Pluta J, Avants B, Glynn S, Awate S, Gee J, Detre J. Appearance and incomplete label matching for diffeomorphic template based hippocampus segmentation. Hippocampus. 2009;19:565–571. doi: 10.1002/hipo.20619. [DOI] [PubMed] [Google Scholar]
- [5].Hasboun D, Chantome M, Zouaoui A, Sahel M, Deladoeuille M, Sourour N, Duymes M, Baulac M, Marsault C, Dormont D. MR determination of hippocampal volume: Comparison of three methods. Am J Neuroradiol. 1996;17:1091–1098. [PMC free article] [PubMed] [Google Scholar]
- [6].Wang H, Das SR, Suh JW, Altinay M, Pluta J, Craige C, Avants B, Yushkevich PA. A learning-based wrapper method to correct systematic errors in automatic image segmentation: Consistently improved performance in hippocampus, cortex and brain segmentation. NeuroImage. 2011;55(3):968–985. doi: 10.1016/j.neuroimage.2011.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Avants B, Epstein C, Grossman M, Gee J. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Medical Image Analysis. 2008;12:26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Yushkevich P, Zhang H, Gee J. Continuous medial representation for anatomical structures. IEEE TMI. 2006;25(2):1547–1564. doi: 10.1109/tmi.2006.884634. [DOI] [PubMed] [Google Scholar]
- [9].Wang H, Das S, Pluta J, Craige C, Altinay M, Weiner M, Mueller S, Yushkevich P. ISBI. 2010. Shape-based semi-automatic hippocampal subfield segmentation with learning-based bias removal. [Google Scholar]
- [10].Artaechevarria X, Munoz-Barrutia A, Ortiz de Solorzano C. Combination strategies in multi-atlas image segmentation: Application to brain MR data. IEEE TMI. 2009;28(8):1266–1277. doi: 10.1109/TMI.2009.2014372. [DOI] [PubMed] [Google Scholar]
- [11].Sabuncu M, Yeo BTT, Van Leemput K, Fischl B, Golland P. A generative model for image segmentation based on label fusion. IEEE TMI. 2010;29(10):1714–1720. doi: 10.1109/TMI.2010.2050897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Warfield S, Zou K, Wells W. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE TMI. 2004;23(7):903–921. doi: 10.1109/TMI.2004.828354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Collins D, Pruessner J. Towards accurate, automatic segmentation of the hippocampus and amygdala from MRI by augmenting ANIMAL with a template library and label fusion. NeuroImage. 2010;52(4):1355–1366. doi: 10.1016/j.neuroimage.2010.04.193. [DOI] [PubMed] [Google Scholar]


