Quantifying Digit Force Vector Coordination during Precision Pinch

Abstract

A methodology was established to investigate the contact mechanics of the thumb and the index finger at the digit-object interface during precision pinch. Two force/torque transducers were incorporated into an apparatus designed to overcome the thickness of each transducer and provide a flexible pinch span for digit placement and force application. To demonstrate the utility of the device, five subjects completed a pinch task with the pulps of their thumb and index finger. Inter-digit force vector coordination was quantified by examining the 1) force vector component magnitudes, 2) resultant force vector magnitudes, 3) coordination angle – the angle formed by the resultant vectors of each digit, 4) direction angles – the angle formed by each vector and the coordinate axes, and 5) center of pressure locations. It was shown that the resultant force magnitude of the index finger exceeded that of the thumb by 0.8 ± 0.3 N and that the coordination angle between the digit resultant force vectors was 160.2 ± 4.6°. The experimental apparatus and analysis methods provide a valuable tool for the quantitative examination of biomechanics and motor control during dexterous manipulation.

1. Introduction

The thumb and index finger work together to perform countless precision pinch tasks such as holding a pen, picking up small objects, and buttoning clothing. These manipulations require intricate coordination of the two digits, applying the proper amount of force in the desired direction at the needed location. The force coordination associated with precision pinch is complicated by the anatomical arrangement of the thumb, which abducts and internally rotates to establish a posture to oppose the index finger in a dexterous manner.¹ Disruption of coordinated pinch mechanics may impair object manipulation and interfere with performing activities of daily living.

The biomechanics and motor control of precision pinch have been extensively investigated for the past few decades. Previous studies have shown that the thumb and index finger apply an optimal normal force adjusted to the digit-object friction condition,^2–4 the object weight,^5,6 the motion-induced inertia,⁷ and perturbations.^5,8 Additionally, these digit forces can independently adjust to compensate for different surface friction conditions³ and can exert varying force magnitudes dependent on the task instructions.⁹ Many of these early studies utilized unidirectional force transducers to address the control of grip force magnitude. However, object manipulation involves complex mechanical interactions at each digit-object interface, requiring the use of transducers with multiple degrees of freedom for each digit.

Recently attempts have been made to use six-component force/torque transducers to study handwriting^10,11, whole hand grasping^12–15, and two- or three-digit gripping^16–19. Biomechanics studies of precision pinch with the thumb and index finger have shown that the force vector magnitude^17,18, force vector direction^19,18 and the alignment of opposing digit contact points¹⁸ impact precision pinch performance and may be distinguishing characteristics between different subject populations. Although insight was provided regarding the mechanical differences between the thumb and index finger in these preceding studies the digit force vectors were analyzed in independent coordinate systems which limited the examination of digit force vector coordination and force vector visualization at the digit-object interface.

The purpose of this study was to develop methodology to examine the force vector coordination of two digits at the digit-object interface during precision pinch. An apparatus with two six-component force/torque transducers, one at each digit-object interface, was used to record the contact mechanics. A series of coordinate transformations were established to permit examination of digit force vector magnitude, direction, and point of force application for the two digits in a single, common coordinate system.

2. Methods

2.1. Pinch apparatus

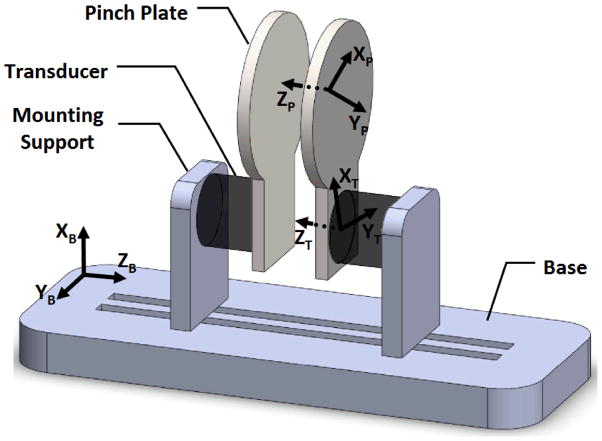
A pinch apparatus (Figure 1) was designed using two six-component force/torque transducers (Nano17, ATI Industrial Automation, Inc., Apex, NC). The mounting side of each transducer was attached to an aluminum mounting support and the tool side of the transducer was rigidly fixed to a stainless steel pinch plate. Each mounting support was secured to an aluminum base with an adjustable track. The pinch plates not only provided a 40 mm diameter surface for digit placement and force application, but also overcame the thickness of each transducer to provide a flexible pinch span of 10–120 mm along the adjustable track of the base. Force/torque signals were amplified and multiplexed using a custom ATI interface box (ATI Industrial Automation, Inc., Apex, NC) and converged to a 16-bit analog-digital converter (PXI-6289, National Instrument, Austin, TX).

Figure 1.

A schematic of the pinch apparatus.

2.2. Coordinate system transformations

To quantify digit force vector coordination, a common coordinate system on the pinch apparatus base was established to convert data from each local transducer coordinate system. Three non-collinear points, B₀, B₁, and B₂, on the apparatus base were digitized using a MicroScribe device (MicroScribe G2X, Immersion Corporation, San Jose, CA) to form an orthogonal coordinate system, [B], with its origin at B₀. The digitizer coordinate system served as a global coordinate system, [D]. Therefore, the transformation matrix [T_DB] from the base coordinate system, [B], to the digitizer coordinate system, [D], was determined according to a standard matrix transformation.^13,14

The relationship of each transducer coordinate system to the digitizer coordinate system was established using a unique procedure of simultaneous digitization and center of pressure (COP) measurement. This concurrent data collection permitted the expression of a single point in the digitizer coordinate system and the transducer coordinate system. The following procedure was implemented for each transducer. Three random, non-collinear points, P₀, P₁, and P₂, on the pinch plate were digitized while also applying force to each point with the digitizer tip. A local coordinate system was defined on the pinch plate surface, [P], with its origin at P₀, from the three digitized points. The transformation matrix [T_DP] from the plate coordinate system, [P], to the digitizer coordinate system, [D], was then determined.^13,14 Additionally, the force applied at each digitized point permitted the expression of each point in the transducer coordinate system as COP data. The components of each COP position measured in the transducer coordinate system were computed using the following equations:

$$x^{\mathit{COP}}=\frac{-(M_y+F_x\ast c)}{F_z}$$ (1)

$$y^{\mathit{COP}}=\frac{M_x-F_y\ast c}{F_z}$$ (2)

$$z^{\mathit{COP}}=c.$$ (3)

Where F_x, F_y, and F_z were the forces acting in the x-, y-, and z-directions of the transducer coordinate system, respectively. M_x and M_y were the torques about the x- and y-axes, respectively, and c was the thickness of a material covering the pinch plate surface. Notice that the thickness of the pinch plate did not affect the calculation because the digit interfaced at the transducer side of the plate.

From the apparatus configuration, the x–y planes of the plate coordinate system and the transducer coordinate system were parallel to each other, separated by a distance of c, and therefore their z-axes were oriented in the same direction. Thus, the transformation matrix [T_TP] from the plate coordinate system, [P], to the transducer coordinate system, [T], was defined by a rotation of θ_TP about the z-axis of the plate coordinate system and a translation (a_TP,b_TP,c_TP)^T which located the origin of the plate coordinate system relative to the transducer coordinate system (Figure 2; (4)). A vector in both the plate and transducer coordinate systems was created from points P₀ to P₁. The angle θ_TP between these vectors was found using trigonometry and the translation (a_TP,b_TP,c_TP)^T was equal to the coordinates of P₀ in the transducer coordinate system.

Figure 2.

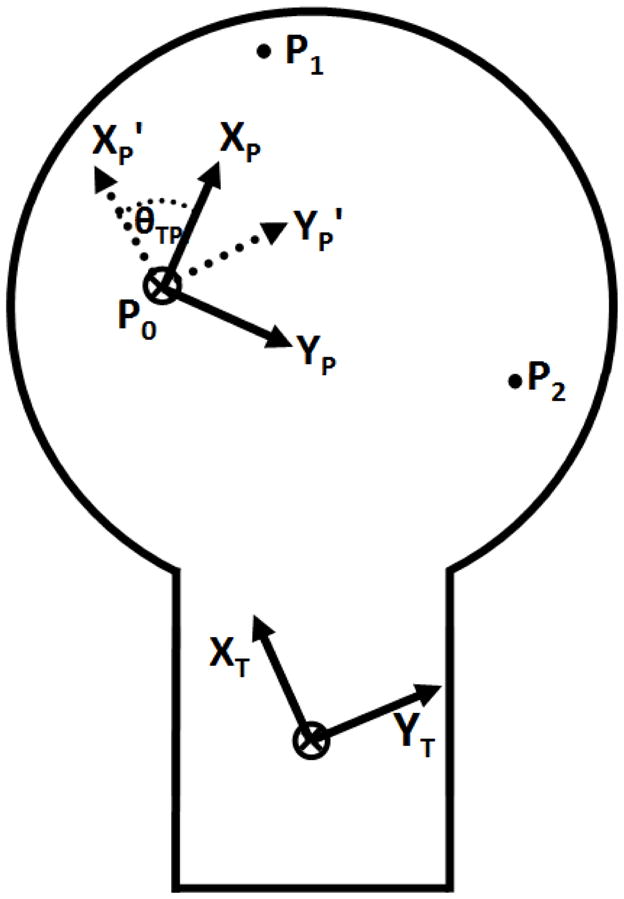
An illustration of the method used to determine the rotation θ_TP and the translation (a_TP,b_TP,c_TP)^T between the transducer and the plate coordinate systems.

$$[T_{TP}]=\left[\begin{array}{cccc}cos({\theta }_{TP})& -sin({\theta }_{TP})& 0& a_{TP}\\ sin({\theta }_{TP})& cos({\theta }_{TP})& 0& b_{TP}\\ 0& 0& 1& c_{TP}\\ 0& 0& 0& 1\end{array}\right].$$ (4)

The transformations among the base, digitizer, and transducer coordinate systems were inter-related by chain multiplication of the determined transformation matrices (5).

$$[T_{DP}]=[T_{DB}]·[T_{BT}]·[T_{TP}].$$ (5)

Therefore, the transformation matrix [T_BT] between a transducer coordinate system, [T], and the base coordinate system, [B], was defined as follows:

$$[T_{BT}]={[T_{DB}]}^{-1}·[T_{DP}]·{[T_{TP}]}^{-1}.$$ (6)

A position vector expressed in a transducer coordinate system was converted to the base coordinate system by

$$\left(\begin{array}{c}{x}_B\\ y_B\\ z_B\\ 1\end{array}\right)=[T_{BT}]·\left(\begin{array}{c}{x}_T\\ y_T\\ z_T\\ 1\end{array}\right).$$ (7)

The COP point in the transducer coordinate system was given by its position vector components ( $x_T^{\mathit{COP}},y_T^{\mathit{COP}},z_T^{\mathit{COP}}$) and this position vector was transformed to the base coordinate system, with position vector components ( $x_B^{\mathit{COP}},y_B^{\mathit{COP}},z_B^{\mathit{COP}}$), according to (8).

$$\left(\begin{array}{c}{x}_B^{\mathit{COP}}\\ y_B^{\mathit{COP}}\\ z_B^{\mathit{COP}}\\ 1\end{array}\right)=[T_{BT}]·\left(\begin{array}{c}{x}_T^{\mathit{COP}}\\ y_T^{\mathit{COP}}\\ z_T^{\mathit{COP}}\\ 1\end{array}\right).$$ (8)

Similarly, a force vector in the transducer coordinate system, ( $F_T^x,F_T^y,F_T^z$), was transformed to a force vector in the base coordinate system, ( $F_B^x,F_B^y,F_B^z$), as follows:

$$\left(\begin{array}{c}{F}_B^x\\ F_B^y\\ F_B^z\\ 1\end{array}\right)=[T_{BT}]·\left(\begin{array}{c}{F}_T^x\\ F_T^y\\ F_T^z\\ 1\end{array}\right).$$ (9)

2.3. Experimental procedures

To demonstrate the utility of the apparatus, five healthy subjects (three males and two females; 30.2 ± 3.6 years) participated in this study after signing a consent form approved by the Institutional Review Board. Subjects sat in a height adjustable chair with their right arm positioned at approximately 30° abduction in the frontal plane and 0° flexion in the sagittal plane; their forearm was supported by a table. The pinch apparatus was rigidly fixed to the table 35 cm in front of the subject and aligned with their right shoulder. The pinch plate surface planes were obliquely oriented 45° with respect to the subject’s sagittal plane. The grip span of the apparatus was 20mm and the pinch plate contact surfaces were covered with 100 grit sandpaper (thickness = 0.6mm).

Subjects applied force to the pinch apparatus with the pulps of their right thumb and index finger and traced a target force ramp with the mean normal force of their digits as displayed on a computer monitor. The force ramp linearly increased from 0 to 15 N in 5 seconds, a rate of 3 N · s⁻¹. The mean normal force of the digits and the target force ramp were plotted vs. time on the computer monitor in a single display permitting real-time force tracking by the subject. Visual feedback and data acquisition were performed using a custom LabVIEW (National Instrument, Austin, TX) program. Each subject completed three trials with two minutes of rest between trials to prevent muscle fatigue. The twelve force/torque signals were simultaneously recorded at a sampling frequency of 100 Hz.

2.4. Digit force vector quantification

Analysis was completed after all data was transformed to the base coordinate system. To quantify force vector coordination between the thumb and the index finger, the following parameters were analyzed: 1) the magnitude differences between the digits resultant force vectors, 2) the magnitude differences between the digits component force vectors, 3) the coordination angle between the digit resultant force vectors, 4) the direction angles of each force vector with respect to the base coordianate system axes, and 5) the distance between the digit COPs in the x–y plane.

The coordination angle, θ, between the thumb and index finger resultant vectors was calculated according to (10)

$$\theta ={cos}^{-1}\frac{FT·FI}{\left|\right|FT\left|\right|\left|\right|FI\left|\right|}.$$ (10)

Where FT and FI were the force vectors of the thumb and the index finger, respectively. Additionally, the direction angles, (α, β, γ), of each digit’s force vector were calculated relative to the base coordinate system axes. The COP coordinates were computed as described previously (1)–(3). COP data were only considered in the x–y plane without inclusion of the z-component. The distance between the thumb and index finger COP at each time point was calculated in the x–y plane.

Unless otherwise noted, data analysis was performed after the mean normal force for the digits exceeded 1.0 N. The mean and standard deviation (mean ± SD) for all subjects and trials were calculated for each parameter.

3. Results

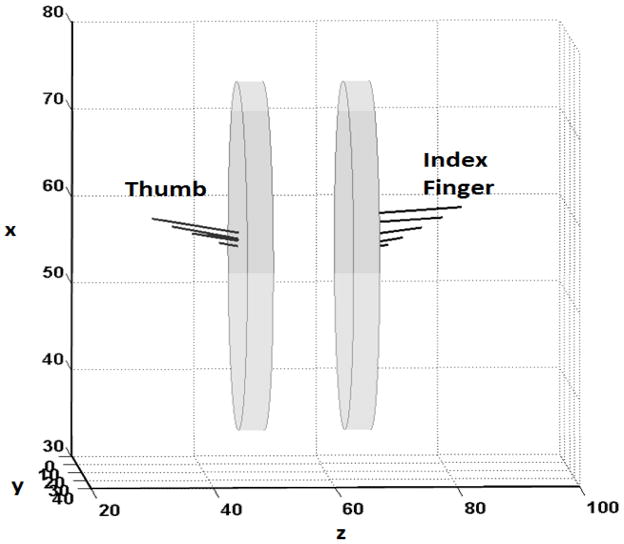
Thumb and index finger force vector coordination was examined as subjects increased their mean normal force magnitude from 0 to 15 N following a target force ramp. A three-dimensional (3D) representation of the force vectors applied at the digit-object interface for a representative subject at selected time points is provided for visualization (Figure 3).

Figure 3.

A 3D reconstruction of the force vectors applied by each digit at the digit-object interface for a representative subject. As time increased, t= 1, 2, 3, 4, and 5 s, the normal force magnitude at each digit increased to approximately 3, 6, 9, 12 and 15 N, respectively.

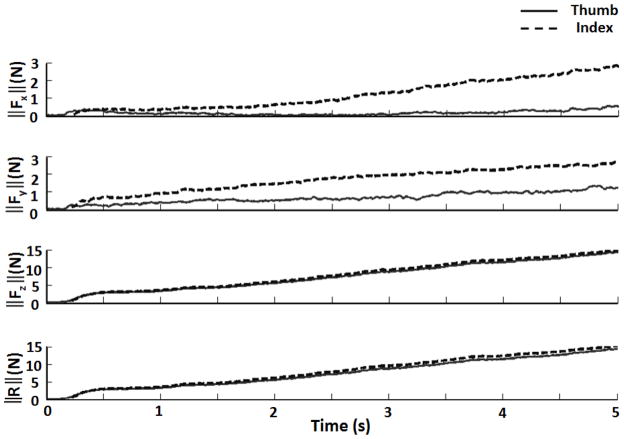
Examination of the thumb and index finger digit force vector magnitudes revealed differences among the resultant vectors, as well as the individual vector components (Figure 4). The mean index finger resultant force vector magnitude exceeded that of the thumb by 0.8 ± 0.3 N across all subjects. Similarly, the magnitude of the index finger vector components were greater than the thumb vector components magnitude throughout the task, with average differences of 0.5 ± 0.3 N, 0.8 ± 0.4 N, and 0.7 ± 0.3 N for F_x, F_y, and F_z, respectively.

Figure 4.

Thumb and index finger vector magnitudes for a representative subject. Note that the values shown are the absolute value of each component and the F_x components for the thumb and index finger force vectors were negative.

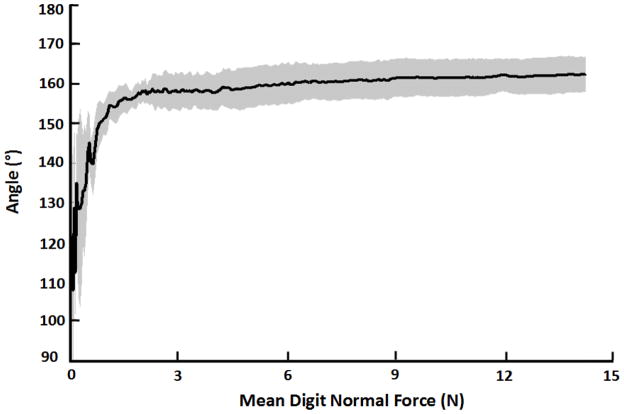
The mean coordination angle throughout the ramp task was 160.2 ± 4.6°, changing from 154.0 ± 8.8° at 1 N mean normal force to 161.7 ± 4.7° at 1 0N mean normal force (Figure 5). The direction angles, (α, β, γ), for the thumb were 91.6 ± 0.7°, 85.2 ± 1.2°, and 8.5 ± 0.7° and for the index finger were 97.7 ± 0.5°, 78.4 ± 1.0°, 165.4 ± 0.7°, respectively.

Figure 5.

The mean coordination angle (solid black line) with standard deviation (gray shading) between the thumb and index finger resultant force vectors as the mean normal force of the digits increased.

The COP locations for the thumb and index finger resultant force vectors for a representative subject are shown in Figure 6. The mean distance between the thumb and index finger COP was 5.0 ± 0.2 mm throughout the ramp task. As each digit’s normal force increased from approximately 1 to 15 N, COP migration for the thumb was 3.9 ± 2.2 mm and 2.1 ± 0.5 mm and for the index finger was 4.3 ± 2.5 mm and 2.2 ± 0.7 mm in the x- and y-directions, respectively.

Figure 6.

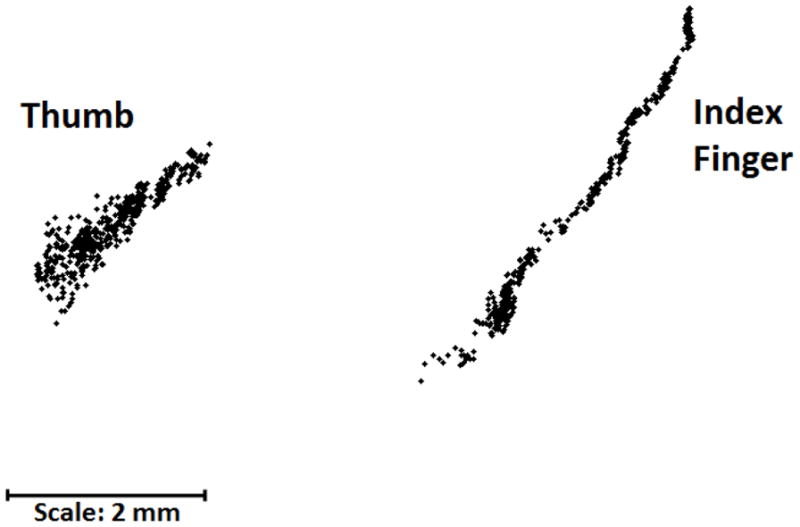
The center of pressure (COP) migration of the thumb and the index finger for a representative subject as the mean normal force applied by each digit increased from 1 to 15 N.

4. Discussion

In this study, methodology was developed to examine inter-digit force vector coordination from data collected by independent transducers at the digit-object interface of the thumb and the index finger. Without loss of generality, a robust procedure was used to transform the biomechanical data collected in each independent transducer coordinate system to a common coordinate system. This methodology facilitated analysis of the inter-digit force vector coordination between the thumb and the index finger during a precision pinch task in 3D. The apparatus developed included a key feature which overcame the thickness of the transducers, permitting examination at a small grip span and also providing each digit with a large contact surface for digit placement and force application.

The coordinate system transformations were determined using techniques of direct digitization and COP measurements. Previously, studies have directly digitized points on the surface of a transducer to define the relationship between the transducer coordinate system and a common coordinate system.¹⁴ In this study, three points were digitized on the pinch plate surface while simultaneously recording the force/torque measurements, and therefore COP, in the transducer coordinate system. This permitted the establishment of the relationship between the coordinate system of the transducer and the digitizer in a novel manner.

The robust methodology established revealed subtle differences between the thumb and index finger force vectors. It was found that the index finger exerted slightly greater resultant and component forces than the thumb throughout the ramp task. Previously, unbalanced normal force exertions by the thumb and the index finger have been reported¹⁹, however, direct comparison could not be made because of varying experimental protocol conditions. Analysis of force vector direction revealed that the coordination angle between the resultant vectors of the thumb and the index finger was approximately 160° throughout the ramp task. This indicates that the resultant force vectors did not linearly oppose each other. Additionally, at the onset of force application, there appeared to be increased variability in the coordination angle, in particular below 2 N of normal force (Figure 5). This observation warrants further investigation because the force typically used in dexterous manipulation is between 1 and 4 N^3,20 and angle variability at low levels of force exertion may impair grip configurations. Finally, the COP locations for the digits migrated throughout the experiment. Similar COP migration has been reported during five-digit manipulation tasks.^14,15

The authors acknowledge limitations in this study. The experimental protocol required all subjects exert the same ramp force pattern on a standardized grip span, despite the ability to normalize force and grip span for each subject. This protocol simplified the experimental procedures without interfering with the purpose of this study to establish a methodology to investigate inter-digit force vector coordination. Additionally, the pinch apparatus was rigidly fixed to the testing table during the experimental task. This set-up was chosen to explore gross inter-digit force vector coordination without imposing that the laws of static equilibrium must be satisfied. It is unknown how the analyzed parameters may change during an unstable testing condition.

In conclusion, methodology was developed to collect 3D force/torque measurements at the digit-object interface for two digits to investigate inter-digit force vector coordination. A series of systematic coordinate system transformations were established to permit analysis of the digit force vectors in a common coordinate system and allowed for 3D force vector representation. Analyses revealed differences in force vector magnitude, direction, and point of force application between the thumb and the index finger during a precision pinch task. Future work may include the integration of kinetic and kinematic data collection and analyses to permit advanced biomechanical studies of the human hand.