Abstract
This article addresses the boundary layer flow and heat transfer in third grade fluid over an unsteady permeable stretching sheet. The transverse magnetic and electric fields in the momentum equations are considered. Thermal boundary layer equation includes both viscous and Ohmic dissipations. The related nonlinear partial differential system is reduced first into ordinary differential system and then solved for the series solutions. The dependence of velocity and temperature profiles on the various parameters are shown and discussed by sketching graphs. Expressions of skin friction coefficient and local Nusselt number are calculated and analyzed. Numerical values of skin friction coefficient and Nusselt number are tabulated and examined. It is observed that both velocity and temperature increases in presence of electric field. Further the temperature is increased due to the radiation parameter. Thermal boundary layer thickness increases by increasing Eckert number.
Introduction
There is a substantial interest of the recent researchers in the flows of non-Newtonian fluids. Such motivation in these fluids is mainly because of their use in the industrial and technological applications. Many materials like mud, pasta, personal care products, ice cream, paints, oils, cheese, asphalt etc. are non-Newtonian fluids. Most biological fluids with higher molecular weight components are also non-Newtonian in nature. The usual properties of polymer melts and solutions together with the desirable attributes of many polymeric solids, have given rise to the world-wide industry of polymer processing. The non-Newtonian fluids in particular have key importance in geophysics, chemical and nuclear industries, material processing, oil reservoir engineering, bioengineering and many others. Rheological properties of all the non-Newtonian fluids cannot be predicted using single constitutive equation (unlike the case of viscous fluids). Therefore many models of non-Newtonian fluids are based either on “natural” modifications of established macroscopic theories or molecular considerations. The additional rheological parameter in the constitutive equations of non-Newtonian fluids are the main culprit for the lack of analytical solutions. The resulting equations are more complex and higher order than the Navier-Stokes equations. Hence these equations have been attracted from modelling as well as solutions point of view. The advancement in the study of non-Newtonian fluids has been made even by the recent investigators (See [1]–[10] and many studies therein).
The flow induced over a stretching surface is very well documented problem in fluid mechanics. It is encountered in extrusion of polymer sheet from a die, glass fiber and paper production, continuous casting, cooling of metallic plate in a bath etc. Such flow problem in presence of heat transfer has been attracted by the researchers due to its applications in polymer processing technology. The quality of end product in industry depends upon both the stretching and cooling rates. Further, the thermal radiation effect has pivotal role in nuclear plants, gas turbines and devices for satellites, space vehicles, aircraft etc. The literature on this topic is quite sizeable. Rana and Bhargava [11] presented the numerical analysis for heat transfer of nanofluid over a nonlinearly stretching sheet. Bhattacharyya et al. [12] analyzed the solutions of boundary layer flow of viscoelastic fluid and heat transfer over a stretching sheet with internal heat generation or absorption. Makinde and Aziz [13] numerically studied the boundary layer flow of viscous nanofluid bounded by a stretching sheet. They considered the transport equation which includes the effects of Brownian motion and thermophoresis. Mandal and Mukhopadhyay [14] considered the boundary layer flow and heat transfer towards an exponentially stretching porous sheet embedded in a porous medium with variable surface heat flux. They found that the momentum and thermal boundary layer thickness decrease with increasing exponential parameter. Hayat et al. [15] examined the heat transfer in flow of second grade fluid over a stretching sheet. Thermal radiation effect in the boundary layer flow by stretching surface has been explored by Sajid and Hayat [16]. Bhattacharyya [17] discussed the unsteady stagnation point flow towards a stretching surface. Effect of heat transfer in flow over an exponentially stretching surface has been explored by Mukhopadhyay [18]. The radiation effect in flow of micropolar fluid towards a stretching surface is addressed by Hussain et al. [19]. Rashidi et al. [20] developed approximate solutions for heat transfer analysis in flow of micropolar fluid. Moreover, the interest in the study of magnetohydrodynamic flow for an electrically conducting fluid over heated surface is motivated by its great value in a wide range of engineering problems such as plasma studies, petroleum industries, MHD power generators, cooling of nuclear reactors, the boundary layer control in aerodynamics and crystal growth. Hence Turkyilmazoglu [21] found exact solution for magnetohydrodynamic flow of viscous fluid due to a rotating disk. Hayat and Nawaz [22] has investigated the Soret and Dufour effects in mixed convection three dimensional boundary flow of an electrically conducting second grade fluid over a vertical stretching sheet. Ahmad and Nazar [23] considered the problem of unsteady magnetohydrodynamic viscoelastic fluid flowing towards a stagnation point on a vertical surface. Pal and Mondal [24] discussed the hydromagnetic flow of viscous fluid over a stretching surface in presence of both electric and magnetic fields. Abel et al. [25] presented MHD flow analysis for viscoelastic fluid. Both viscous and Ohmic dissipations are presented in this attempt. More, the analysis here is made when magnetic and electric fields are present. Hayat and Qasim [26] considered radiation effect in MHD flow of second grade fluid over unsteady porous stretching surface. The effect of internal heat generation in hydromagnetic non-Darcy flow and heat transfer over a stretching surface with thermal radiation and Ohmic dissipation is examined by Olanrewaju [27]. Elbashbeshy et al. [28] numerically analyzed the problem of unsteady laminar two-dimensional MHD boundary layer flow and heat transfer of an incompressible viscous fluid over a porous surface in the presence of thermal radiation and internal heat generation or absorption. MHD flow caused by a rotating disk is presented by Rashidi et al. [29]. The well-known Jeffery-Hamel problem in presence of magnetic field is examined by Motsa et al. [30]. Most of the studies on MHD flow over a stretching surface with heat transfer do not take into account the effect of electric field and Ohmic dissipation. Very little exists yet about such aspects in the stretched flows of viscous fluids. Such consideration further narrowed down when non-Newtonian fluids have been considered. To our knowledge there is only one such attempt for viscoelastic fluid [25]. The fluid employed although exhibits the normal stress effects but it cannot describe the features of shear thinning or shear thickening. Having such in view, the flow of third grade fluid is considered. This fluid even can capture shear thinning/shear thickening effects for one-dimensional flow over a rigid surface. The main objective here is to analyze the two-dimensional flow of third grade fluid over an unsteady stretching sheet. The effects of both electric and magnetic fields are retained in the momentum and energy equations. Thermal radiation and Ohmic dissipation are taken into account. The solutions for velocity component and temperature are developed by homotopy analysis method (HAM) [31]–[40]. The plots of physical quantities of interest reflecting the novel features of embedded parameters in the problems are given and analyzed. Tables for skin friction coefficient and local Nusselt number are made and explained carefully.
Mathematical Formulation
We examine the two-dimensional boundary layer flow of magnetohydrodynamic (MHD) third grade fluid over a porous stretching surface. Here the fluid is electrically conducting in the presence of applied magnetic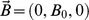 
and electric 
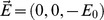fields. The flow is because of stretching of sheet from a slit through two equal and opposite forces. The sheet velocity is taken linear parallel to the flow direction. The electric and magnetic fields obey the Ohm's law 
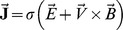. Here 
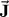is the Joule current, 
is the electrical conductivity and 
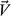is the fluid velocity. The induced magnetic field and Hall current effects are ignored subject to small magnetic Reynolds number. Both the electric and magnetic fields contribute into the momentum and thermal boundary layer equations. The relevant equations in the aforestated conditions can be expressed as follows:
 |
(1) |
 |
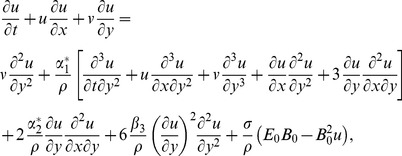(2) |
 |
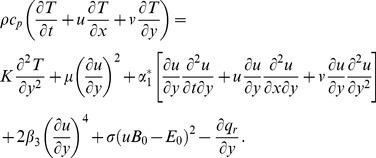(3) |
In above equations 
and 
denote the velocity components in the 
and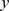 
directions, 
, 
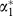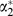and 
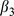are the fluid parameters, 
is the kinematic viscosity,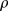 
is the density of fluid, 
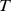is the fluid temperature, 
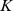is the thermal conductivity of fluid, 
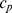is the specific heat at constant pressure and the radiative heat flux 
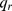is first given by Sparrow and Cess [41] and Raptis [42]
 |
(4) |
where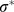 
is the Stefan-Boltzmann constant and 
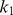is the mean absorption coefficient. Through expansion of 
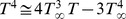, Eq. (3) becomes
 |
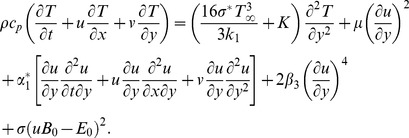(5) |
The subjected conditions can be mentioned as follows:
 |
 |
(6) |
with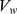 
defined by
 |
(7) |
Here the mass transfer at surface with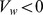 
is for injection and 
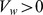for suction. Also the stretching velocity 
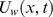and the surface temperature 
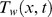are taken in the forms:
 |
(8) |
where 
and 
are the constants with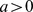 
and 
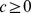(i.e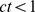 
).
If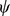 
is the stream function then defining
 |
(9) |
 |
(10) |
The incompressibility condition is identically satisfied and the resulting problems for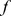 
and 
are reduced into the following forms
 |
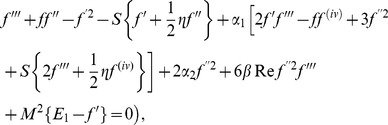(11) |
 |
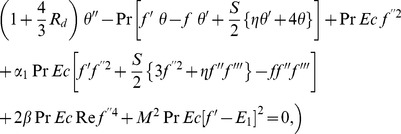(12) |
 |
(13) |
with
 |
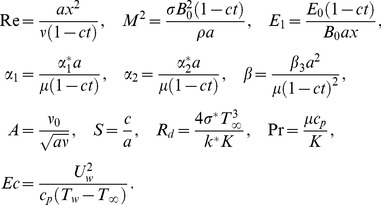(14) |
Here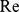 
denotes the Reynolds number, 
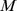the magnetic parameter, 
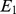is the electric parameter, 
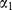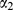and 
and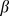 
are the fluid parameters, 
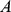is the suction parameter, 
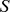is the unsteadiness parameter, 
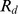is the radiation parameter, 
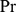is the Prandtl number and 
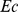is the Eckert number.
The local skin friction coefficient is defined as
 |
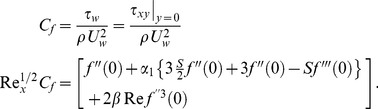(15) |
The Nusselt number is given by
 |
 |
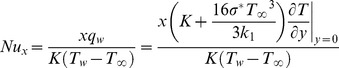(16) |
in which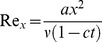 
is the local Reynolds number.
Solutions
The velocity and temperature can be expressed in the set of base functions
 |
(17) |
can be expressed as follows
 |
(18) |
 |
(19) |
where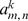 
and 
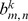are the coefficients.
The initial guesses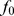 
and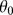 
in homotopy solutions are taken through the expressions
 |
(20) |
The auxiliary linear operators and their associated properties are
 |
(21) |
satisfy the following properties
 |
(22) |
 |
(23) |
Where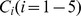 
depict the arbitrary constants.
The zeroth order problems are
 |
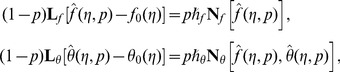(24) |
 |
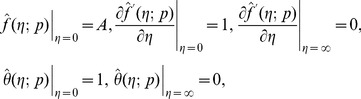(25) |
with non-linear operators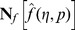 
and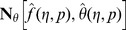 
defined by
 |
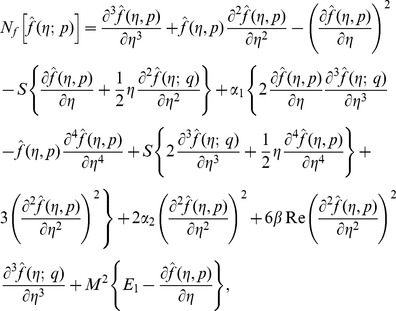(26) |
 |
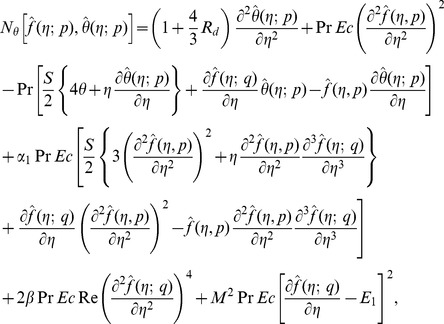(27) |
in which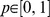 
indicates the embedding parameter 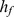and 
and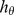 
the nonzero auxiliary parameters.
Setting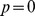 
and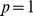 
we have
 |
(28) |
When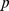 
increases from 0 to 1, 
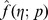and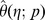 
deforms from the initial solutions 
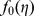and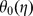 
to the final solutions 
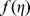and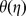 
, respectively. Taylor series, of 
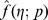and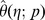 
gives
 |
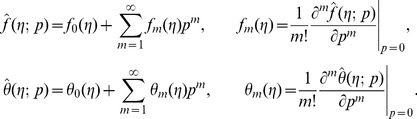(29) |
The auxiliary parameters are properly chosen such that the series solutions converge at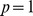 
. Therefore
 |
(30) |
The 
th-order deformation problems are
 |
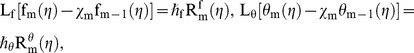(31) |
 |
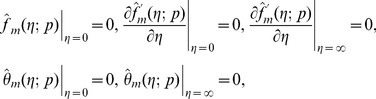(32) |
 |
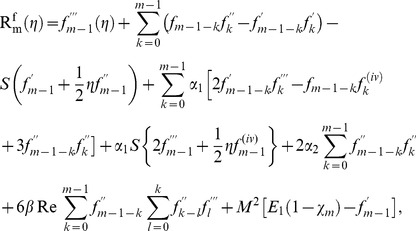(33) |
 |
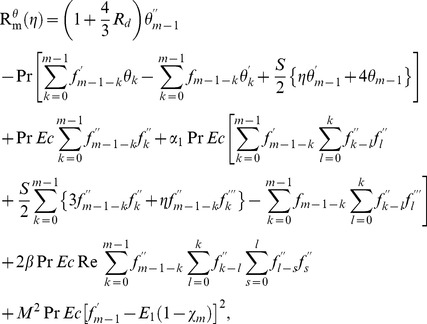(34) |
 |
(35) |
The general solutions of the Eqs. (31)–(32) are
 |
in which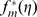 
and 
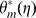denote the special solutions.
Convergence of the Derived Solutions
We note that the series solutions (33) and (34) contain the non-zero auxiliary parameters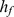 
and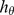 
. These parameters are useful in adjusting and controlling the convergence. The 
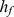and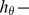 
curves are plotted for 10th order of approximation in Fig. 1 for the suitable ranges of the auxiliary parameters. Here the suitable values for 
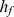and 
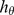are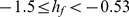 
, 
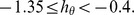Furthermore, convergence of series solution is checked and shown in Table 1. Note that the series solutions converge at 26th order of approximation up to 6 decimal places.
Figure 1. ħ-curves of the functions f″(0) and θ′(0) at 10th order of approximation.
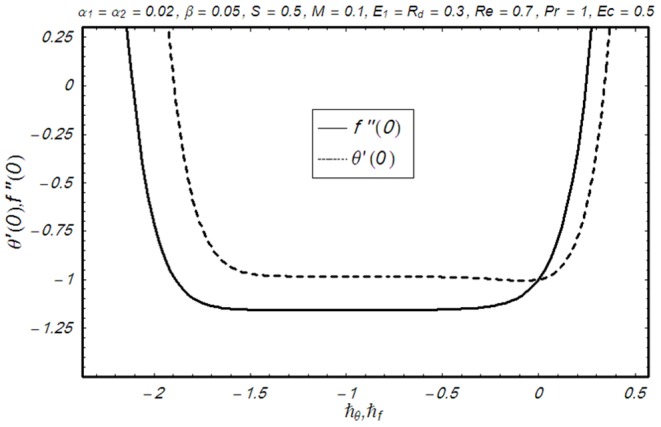
Table 1. Convergence of homotopy solutions when 
.
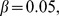
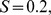
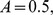
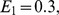
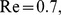
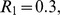
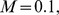
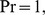
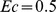| Order of approximation |
|
|
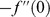
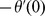
| 1 | 1.0419 | 1.0059 |
| 2 | 1.0720 | 1.0079 |
| 5 | 1.1210 | 1.0041 |
| 10 | 1.1442 | 0.99450 |
| 12 | 1.1458 | 0.99211 |
| 14 | 1.1458 | 0.99051 |
| 40 | 1.1458 | 0.99051 |
Results and Discussion
This section illustrates the impact of physical parameters. The results are displayed graphically in the Figs. 2–20. The conclusions for flow field and other physical quantities of interest are drawn. The numerical values of the skin friction coefficient and local Nusselt number are presented in the Tables 2 and 3 for various values of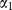 
, 
, 
, 
, 
, 
, 
, 
, 
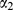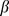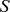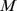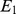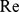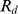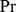and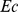 
. Fig. 2 displays the effect of Hartman number 
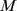on velocity profile by keeping other physical parameter fixed. It is of interest to note that the velocity profile decreases with an increase in 
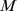whereas the boundary layer thickness reduces. Clearly by increasing magnetic force, the Lorentz force increases which cause resistance in the fluid flow and consequently the velocity profile decreases. Fig. 3 shows the influence of third grade parameter 
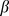on the velocity profile 
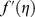. Here we noticed that the velocity increases near the wall with an increased 
whereas it vanishes away from the wall. Figs. 4 and 5 illustrate the variation of second grade parameters 
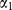and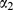 
on the velocity profile 
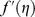respectively. It is observed that the velocity profile 
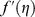is an increasing function of 
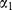. The velocity profile also increases when 
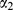is increased. Fig. 6 is plotted for the effects of the suction parameter 
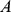on the velocity profile 
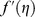. The velocity profile decreases by increasing parameter 
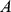and further the boundary layer is also decreasing function of 
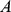. Fig. 7 is sketched for the influence of unsteadiness parameter 
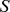on the velocity profile. The velocity profile and the thermal boundary layer decreases for larger values of 
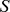. The behavior of Reynolds number 
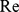on velocity profile is shown in Fig. 8. It is observed that the velocity profile decreases with an increase in Reynold number 
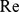. The influence of electric parameter 
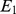is shown in Fig. 9. This Fig explains that as the electric parameter 
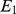increases, the velocity boundary layer increases near the plate with small rate but increases away from the stretching plate more rapidly. In fact the Lorentz force (arising due to the electric field acts like an accelerating force) reduces the frictional resistance which causes to shift the stream line away from the stretching sheet. Fig. 10 portrays the effects of magnetic parameter 
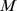on the temperature profile 
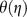. It is depicted that temperature profile and thermal boundary layer thickness increase with an increase in magnetic parameter. Fig. 11 is the plot of temperature profile 
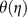for various values of third grade parameter 
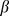. The effect of third grade parameter 
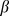on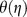 
shows a decrease near the wall. The boundary layer thickness also decreases. Figs. 12 and 13 describe the effects of second grade parameters 
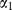and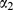 
on temperature profile 
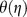. Fig. 12. depicts that the effect of second grade parameter 
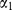is to reduce the temperature distribution in the boundary layer which results in thinning of the boundary layer thickness. Same behavior is shown in Fig. 13 for various values of 
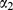. The influence of suction parameter 
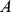and unsteadiness parameter 
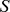are analyzed in the Figs. 14 and 15. Here the temperature profile decreases with the increase of unsteadiness parameter 
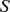and the suction parameter 
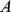. Further the thermal boundary layer also decreases by increasing both the unsteadiness parameter 
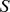and the suction parameter 
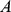. Fig. 16 shows that the temperature profile and thermal boundary layer is decreasing function of Reynold number 
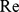. The effects of thermal radiation parameter 
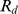on temperature is shown in Fig. 17. It is revealed that the radiation parameter 
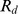causes increase in the fluid temperature 
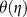. On the other hand the thermal boundary layer thickness also increases. In Fig. 18 the influence of electric parameter 
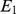on temperature profile is given. This Fig. depicts that the temperature profile and the boundary layer thickness increase with an increase of electric parameter 
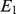. Fig. 19. illustrates the effects of Prandtl number 
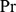on the temperature profile 
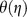. Both the temperature and thermal boundary layer thickness are decreased by increasing 
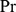. We displayed the temperature field for various values of Eckert number 
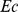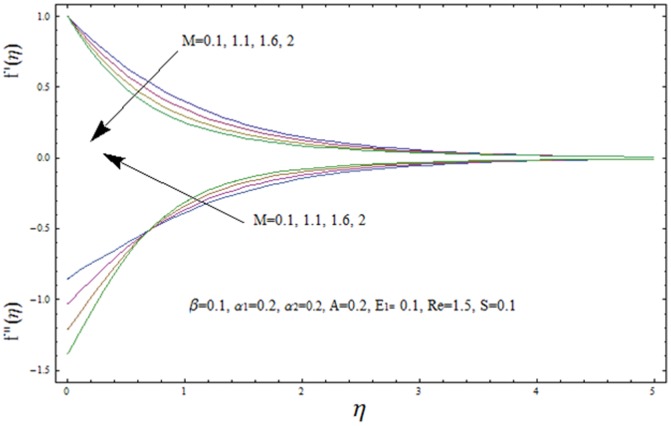
in Fig. 20. The effect of Eckert number is to increase the temperature boundary layer thickness due to the frictional heating. Fig. 21 shows the effects of Hartman number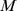 
on velocity 
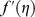and shear stress 
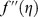. With the increase in 
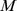, the velocity field 
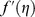decreases near the wall and vanishes far away from the wall while shear stress 
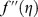has same behavior for larger values of Hartman number 
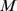. An opposite behavior is noted when 
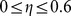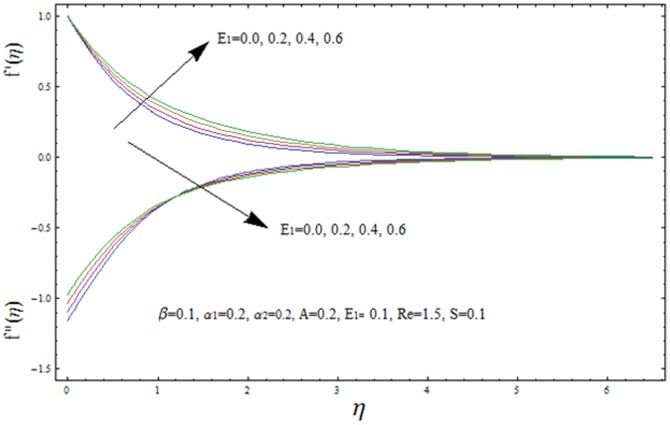
. Fig. 22 demonstrates the effects of electric parameter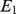 
on velocity 
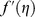and shear stress 
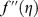. It is worthmentioning to point out that velocity is increasing function of electric parameter 
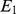near the wall whereas opposite behavior for shear stress is observed for 
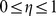. The numerical values of skin friction coefficient for various physical parameters are shown in Table 2. Here the magnitude of skin friction coefficient increases with the increase of second grade parameters (
, 
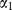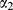), third grade parameter 
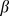, unsteadiness parameter 
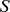, Hartman number 
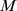and Reynold number 
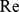whereas it decreases with an increase in electric parameter 
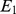. Table 3 shows the effect of physical parameters on heat transfer characteristics at the wall 
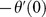. From this table, we observe that for large values of second grade parameters (
, 
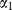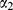), third grade parameter 
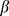, unsteadiness parameter 
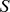, radiation parameter 
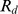and Prandtl number 
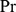the heat transfer coefficient at the wall 
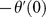increases while it decreases for Hartman number 
, Reynold number 
, electric parameter E1 and Eckert number 
.
Figure 2. Influence of M on f′(η).
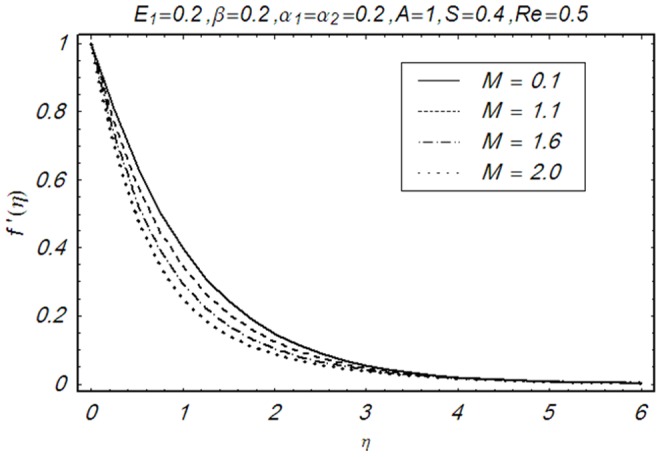
Figure 20. Influence of Ec on θ(η).
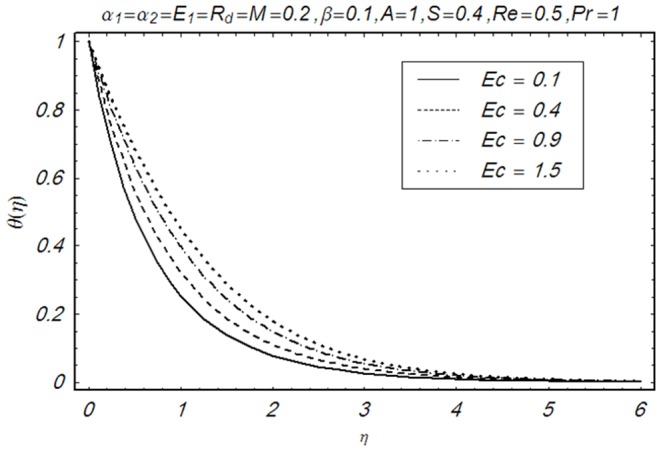
Table 2. Numerical values of skin friction coefficients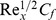 
for different values of physical parameters.
|
|
|
|
|
|
|
|
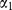
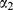
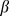
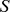
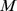
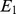
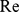
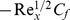
| 0.00 | 0.1 | 0.2 | 0.5 | 0.1 | 0.3 | 0.7 | 1.453 |
| 0.10 | 1.532 | ||||||
| 0.14 | 1.567 | ||||||
| 0.1 | 0.0 | 0.2 | 0.5 | 0.1 | 0.3 | 0.7 | 1.600 |
| 0.1 | 1.632 | ||||||
| 0.2 | 1.668 | ||||||
| 0.1 | 0.1 | 0.0 | 0.5 | 0.1 | 0.3 | 0.7 | 1.433 |
| 0.1 | 1.489 | ||||||
| 0.2 | 1.532 | ||||||
| 0.1 | 0.1 | 0.2 | 0.5 | 0.1 | 0.3 | 0.7 | 1.532 |
| 0.6 | 1.592 | ||||||
| 0.7 | 1.670 | ||||||
| 0.1 | 0.1 | 0.2 | 0.5 | 0.1 | 0.3 | 0.7 | 1.532 |
| 0.2 | 1.536 | ||||||
| 0.3 | 1.545 | ||||||
| 0.01 | 0.01 | 0.2 | 0.5 | 0.1 | 0.5 | 0.7 | 1.492 |
| 0.6 | 1.487 | ||||||
| 0.7 | 1.482 | ||||||
| 0.1 | 0.1 | 0.2 | 0.5 | 0.1 | 0.3 | 0.7 | 1.532 |
| 0.8 | 1.542 | ||||||
| 0.9 | 1.551 |
Table 3. Numerical values of Nusselt number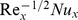 
for different values of physical parameters.
|
|
|
|
|
|
|
|
|
|
|
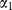
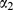
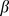
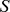
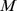
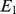
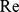
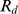
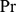
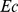
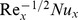
| 0.0 | 0.2 | 0.2 | 0.5 | 0.1 | 0.3 | 0.7 | 0.3 | 1.0 | 0.5 | 1.668 |
| 0.1 | 1.689 | |||||||||
| 0.2 | 1.706 | |||||||||
| 0.1 | 0.0 | 0.2 | 0.5 | 0.1 | 0.3 | 0.7 | 0.3 | 1.0 | 0.5 | 1.660 |
| 0.1 | 1.674 | |||||||||
| 0.2 | 1.689 | |||||||||
| 0.1 | 0.2 | 0.0 | 0.5 | 0.1 | 0.3 | 0.7 | 0.3 | 1.0 | 0.5 | 1.683 |
| 0.3 | 1.691 | |||||||||
| 0.4 | 1.731 | |||||||||
| 0.1 | 0.2 | 0.2 | 0.5 | 0.1 | 0.3 | 0.7 | 0.3 | 1.0 | 0.5 | 1.689 |
| 0.6 | 1.805 | |||||||||
| 0.7 | 1.920 | |||||||||
| 0.1 | 0.2 | 0.2 | 0.5 | 0.1 | 0.3 | 0.7 | 0.3 | 1.0 | 0.5 | 1.689 |
| 0.5 | 1.669 | |||||||||
| 0.8 | 1.638 | |||||||||
| 0.1 | 0.2 | 0.2 | 0.5 | 0.5 | 1.0 | 0.7 | 0.3 | 1.0 | 0.5 | 1.938 |
| 1.5 | 1.889 | |||||||||
| 2.0 | 1.780 | |||||||||
| 0.1 | 0.2 | 0.2 | 0.5 | 0.1 | 0.3 | 0.7 | 0.3 | 1.0 | 0.5 | 1.689 |
| 1.0 | 1.668 | |||||||||
| 1.5 | 1.652 | |||||||||
| 0.1 | 0.2 | 0.2 | 0.7 | 0.1 | 0.5 | 0.5 | 0.3 | 1.0 | 0.5 | 1.920 |
| 0.4 | 1.991 | |||||||||
| 0.5 | 2.060 | |||||||||
| 0.1 | 0.2 | 0.2 | 0.7 | 0.1 | 0.5 | 0.5 | 0.4 | 1.0 | 0.5 | 1.991 |
| 1.1 | 2.109 | |||||||||
| 1.2 | 2.223 | |||||||||
| 0.1 | 0.2 | 0.2 | 0.7 | 0.1 | 0.5 | 0.5 | 0.4 | 1.0 | 0.5 | 1.991 |
| 0.6 | 1.938 | |||||||||
| 0.7 | 1.886 |
Figure 3. Influence of β on f′(η).
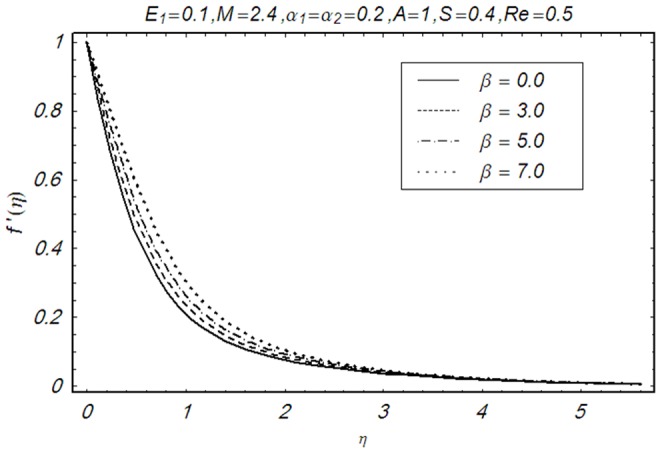
Figure 4. Influence of α1 on f′(η).
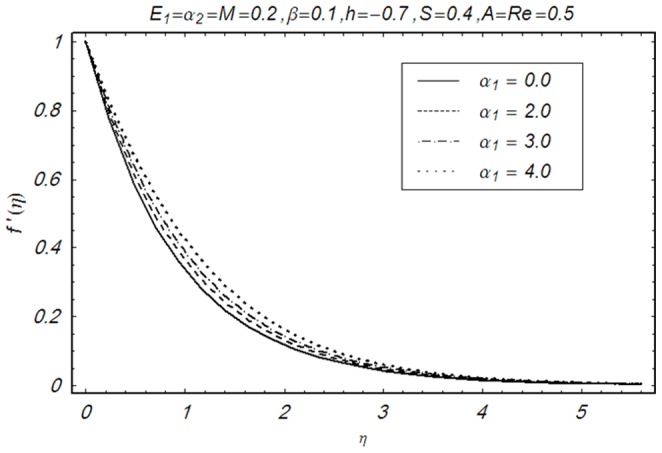
Figure 5. Influence of α2 on f′(η).
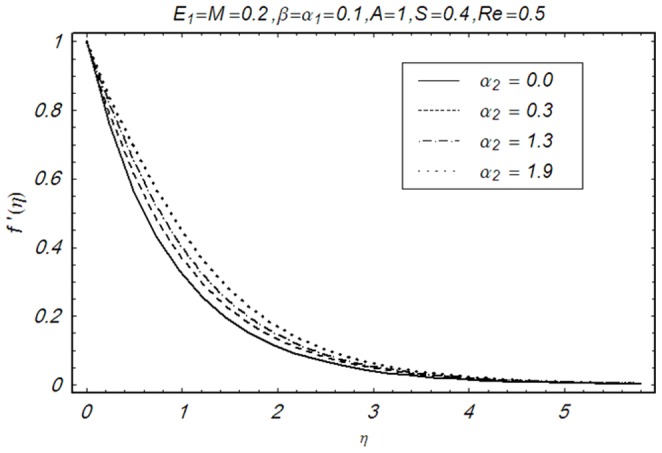
Figure 6. Influence of A on f′(η).
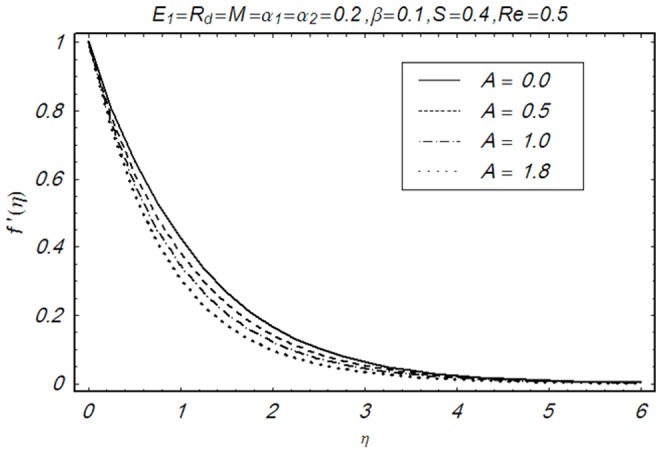
Figure 7. Influence of S on f′(η).
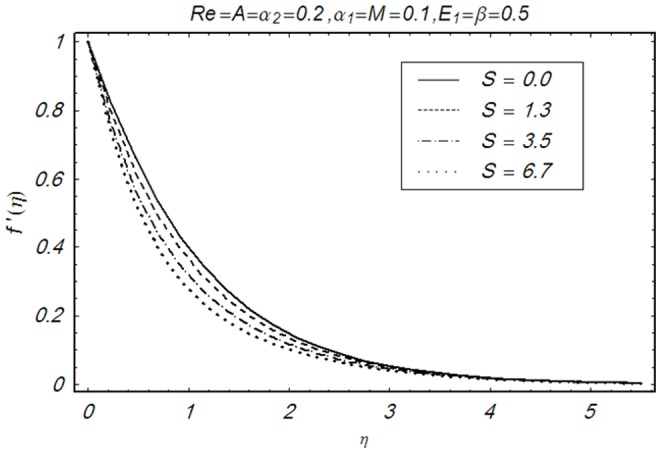
Figure 8. Influence of Re on f′(η).
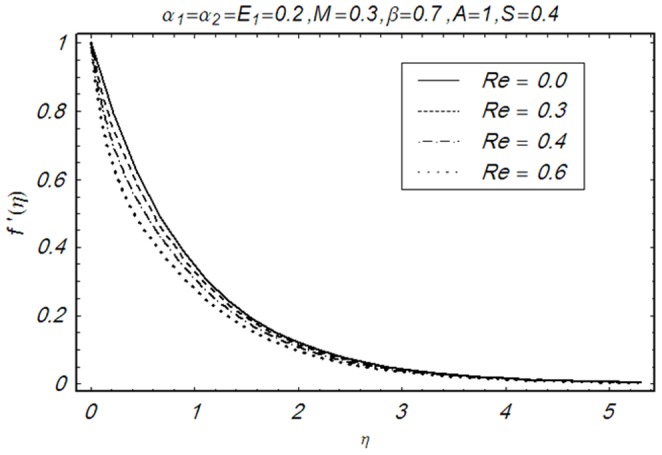
Figure 9. Influence of E1 on f′(η).
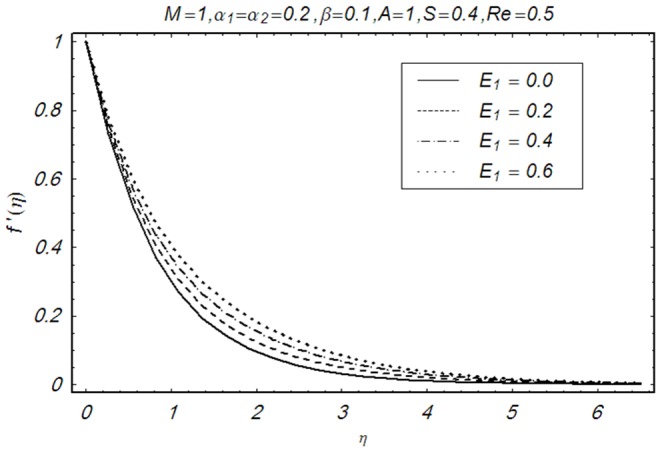
Figure 10. Influence of M on θ(η).
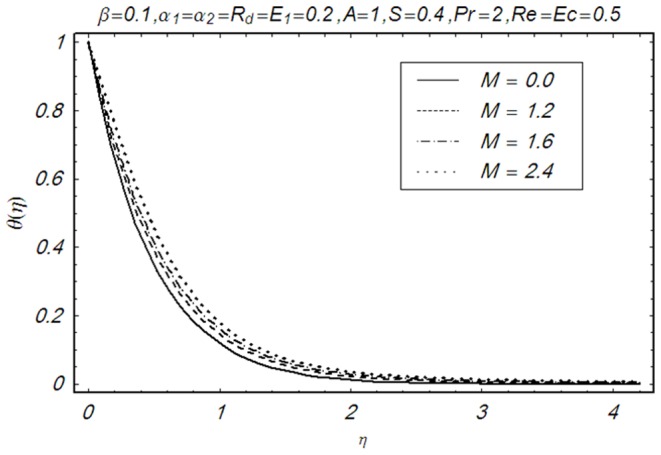
Figure 11. Influence of β on θ(η).
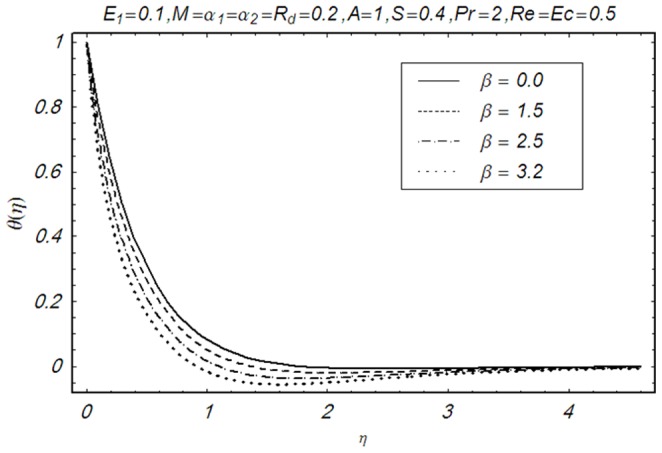
Figure 12. Influence of α1 on θ(η).
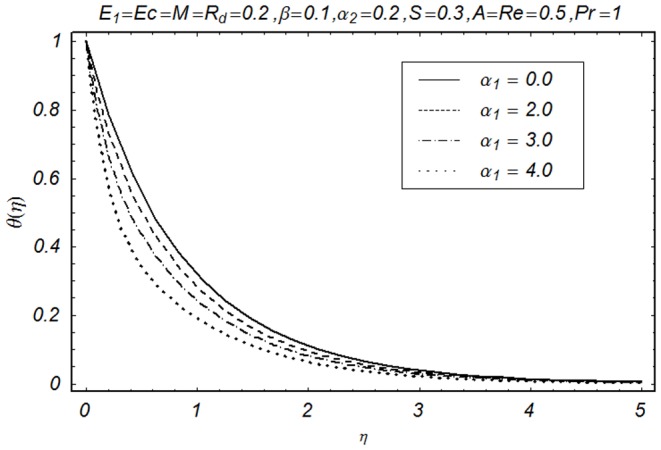
Figure 13. Influence of α2 on θ(η).
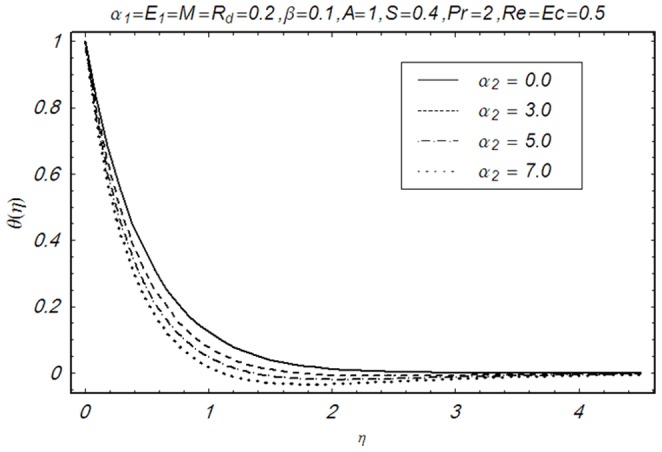
Figure 14. Influence of A on θ(η).
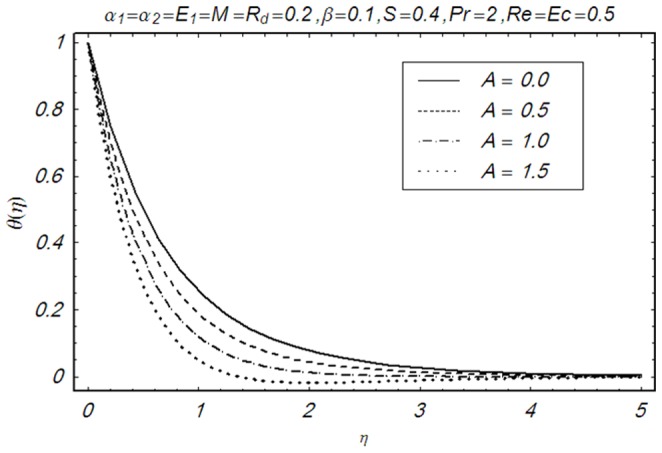
Figure 15. Influence of S on θ(η).
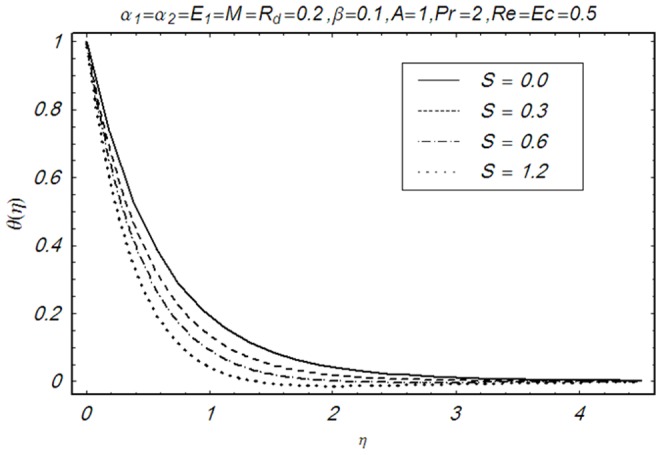
Figure 16. Influence of Re on θ(η).
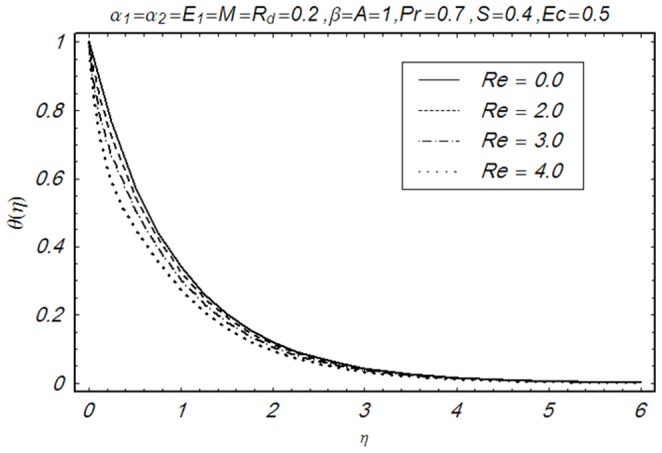
Figure 17. Influence of Rd on θ(η).
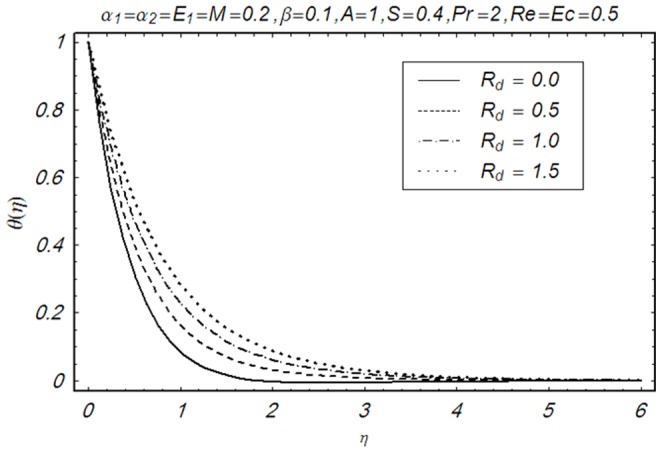
Figure 18. Influence of E1 on θ(η).
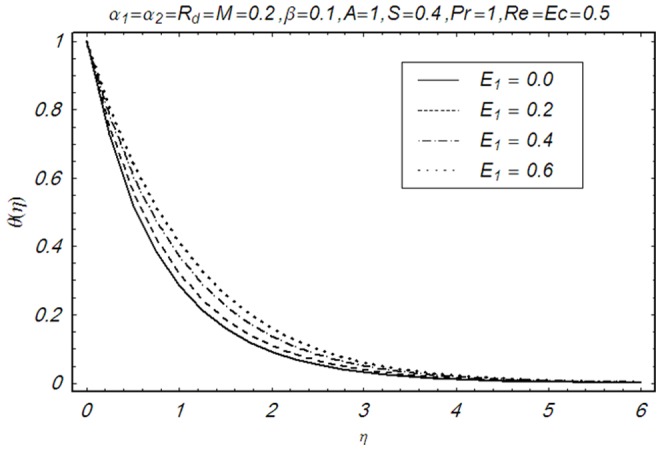
Figure 19. Influence of Pr on θ(η).
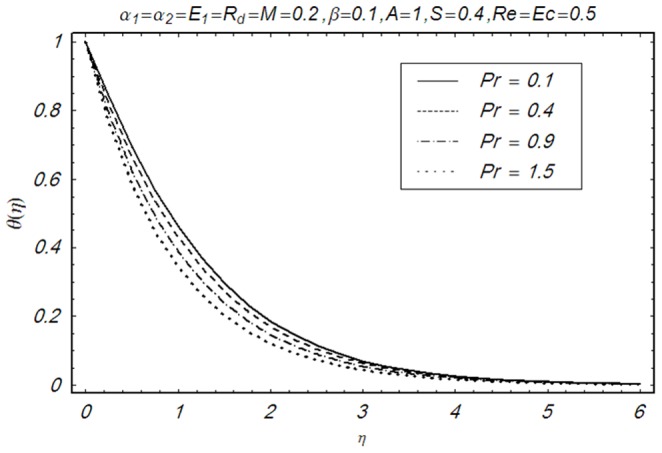
Figure 21. Variation of velocity f′(η) and shear stress f″(η) with η for several values of Hartman number M.
Figure 22. Variation of velocity f′(η) and shear stress f″(η) with η for several values of electric parameter E1.
Concluding remarks
The flow of third grade fluid and heat transfer in the presence of thermal radiation and Ohmic dissipation are examined. The graphs are prepared to study the influence of the pertinent flow parameters including the second grade parameter (
, 
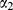), third grade parameter 
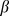, unsteadiness parameter 
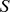, magnetic parameter 
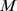, electric field parameter 
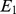, Reynolds number 
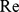, radiation parameter 
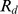, Prandtl number 
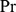and Eckert number 
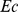. The following observations hold:
The effect of third grade parameter
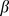is to increase the boundary layer thickness.The maximum velocity is attained for higher values of electric parameter
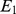.Effect of suction parameter, unsteadiness parameter and Reynolds number on boundary layer thickness is similar in a qualitative sense.
Effects of
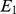and 
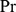on temperature profile are quite opposite.The velocity field
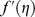is decreasing function of Hartman number 
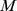.Magnitude of skin friction coefficient
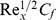is increasing function of 
, 
, 
, 
, 
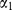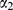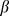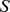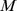and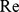 
.Electric parameter
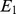decreases the magnitude of skin friction coefficient.
Funding Statement
This paper was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah under grant no. (10-130/1433 HiCi). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Loureiroa JBR, Silva Freirea AP (2013) Asymptotic analysis of turbulent boundary-layer flow of purely viscous non-Newtonian fluids,. Journal of Non-Newtonian Fluid Mechanics 199: 20–28. [Google Scholar]
- 2. Keimanesha M, Rashidi MM, Chamkha AJ, Jafari R (2011) Study of a third grade non-Newtonian fluid flow between two parallel plates using the multi-step differential transform method,. Computers and Mathematics with Applications 62: 2871–2891. [Google Scholar]
- 3. Mustafa M, Hayat T, Obaidat S (2012) Stagnation-point flow and heat transfer of a Casson fluid towards a stretching sheet,. Z Naturforsch 67: 70–76. [Google Scholar]
- 4. Abbasbanday S, Hayat T (2011) On series solution for unsteady boundary layer equations in a special third grade fluid,. Commun Nonlinear Sci Numer Simulat 16: 3140–3146. [Google Scholar]
- 5. Mahmoud AAM (2011) Slip velocity effect on a non-Newtonian power-law fluid over a moving permeable surface with heat generation,. Mathematical and Computer Modelling 54: 1228–1237. [Google Scholar]
- 6. Hayat T, Asad S, Qasim M, Hendi AA (2012) Boundary layer flow of a Jeffrey fluid with convective boundary conditions,. Int J Numer Meth Fluids 69: 1350–1362. [Google Scholar]
- 7. Renardy M, Wang X (2012) Boundary layer for the upper convected Maxwell fluid,. J Non-Newtonian Fluid Mech 189–190: 14–18. [Google Scholar]
- 8. Ramzan M, Farooq M, Alsaedi A, Hayat T (2013) MHD three dimensional flow of couple stress fluid with Newtonian heating,. Eur Phys J Plus 128: 49. [Google Scholar]
- 9. Shafiq A, Nawaz M, Hayat T, Alsaedi A (2013) Magnetohydrodynamic axisymmetric flow of a third grade fluid between two porous disks,. Brazilian J Chem Engineer 30 3. [Google Scholar]
- 10. Sahoo B, Labropulu F (2012) Steady Homann flow and heat transfer of an electrically conducting fluid,. Computers Math Appli 63: 1244–1255. [Google Scholar]
- 11. Rana P, Bhargava R (2012) Flow and heat transfer of a nanofluid over a nonlinearly stretching sheet: A numerical study,. Commun Nonlinear Sci Num Simu 17: 212–226. [Google Scholar]
- 12. Bhattacharyya K, Uddin MS, Layeka GC, Ali Pk W (2011) Unsteady helical flows of Oldroyd-B fluids,. Comm Nonlinear Sci Num Simu 16: 1378–1386. [Google Scholar]
- 13. Makinde OD, Aziz A (2011) Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition,. Int J Thermal Sciences 50: 1326–1332. [Google Scholar]
- 14. Mandal IC, Mukhopadhyay S (2013) Heat transfer analysis for fluid flow over an exponentially stretching porous sheet with surface heat flux in porous medium,. Ain Shams Engineering Journal 4: 103–110. [Google Scholar]
- 15. Hayat T, Iqbal Z, Mustafa M (2012) Flow of a second grade fluid over a stretching surface with Newtonian heating,. Journal of Mechanics 28 1: 209–216. [Google Scholar]
- 16. Sajid M, Hayat T (2008) Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheet,. Int Commun Heat Mass Transfer 35: 347–356. [Google Scholar]
- 17. Bhattacharyya K (2013) Heat transfer analysis in unsteady boundary layer stagnation point flow towards a shrinking/stretching sheet,. Ain Shams Eng Journal 4: 259–264. [Google Scholar]
- 18. Mukhopadhyay S (2013) MHD boundary layer flow and heat transfer over an exponentially stretching sheet embedded in a thermally stratified medium,. Alexandria Eng Journal 52: 259–265. [Google Scholar]
- 19. Hussain M, Ashraf M, Nadeem S, Khan M (2013) Radiation effects on the thermal boundary layer flow of a micropolar fluid towards a permeable stretching sheet,. J Fran Institute 350: 194–210. [Google Scholar]
- 20. Rashidi MM, Mohimanian Pour SA, Abbasbandy S (2011) Analytic approximate solutions for heat transfer of a micropolar fluid through a porous medium with radiation,. Comm Nonlinear Sci Numer Simulation 16: 1874–1889. [Google Scholar]
- 21. Turkyilmazoglu M (2011) Exact solutions for the incompressible viscous magnetohydrodynamic fluid of a rotating disk flow. Int J Nonlinear Mech 46: 306–311. [Google Scholar]
- 22. Hayat T, Nawaz M (2011) Soret and Dufour effects on the mixed convection flow of a second grade fluid subject to Hall and ion-slip currents,. Int J Numer Meth Fluids 67: 1073–1099. [Google Scholar]
- 23. Ahmad K, Nazar R (2010) Unsteady magnetohydrodynamic mixed convection stagnation point flow of a viscoelastic fluid on a vertical surface,. JQMA 6 2: 105–117. [Google Scholar]
- 24. Pal D, Mondal H (2010) Hydromagnetic non-Darcy flow and heat transfer over a stretching sheet in the presence of thermal radiation and ohmic dissipation,. Commun Nonlinear Sci Numer Simulat 15: 1197–1209. [Google Scholar]
- 25. Abel MS, Sanjayanand E, Nandeppanavar MM (2008) Viscoelastic MHD flow and heat transfer over a stretching sheet with viscous and Ohmic dissipations. Commun Nonlinear Sci Numer Simulat 13: 1808–1821. [Google Scholar]
- 26. Hayat T, Qasim M (2011) Radiation and Magnetic field effects on the unsteady mixed convection flow of a second grade fluid over a vertical stretching sheet,. Int J Numer Meth Fluids 66: 820–832. [Google Scholar]
- 27. Olanrewaju PO (2012) Effects of internal heat generation on hydromagnetic non-Darcy flow and heat transfer over a stretching sheet in the presence of thermal radiation and ohmic dissipation,. World Applied Sciences Journal 16: 37–45. [Google Scholar]
- 28. Elbashbeshy EMA, Emam TG, Abdelgaber KM (2012) Effects of thermal radiation and magnetic field on unsteady mixed convection flow and heat transfer over an exponentially stretching surface with suction in the presence of internal heat generation/absorption,. Journal of the Egyptian Mathematical Society 20: 215–222. [Google Scholar]
- 29. Rashidi MM, Abelman S, Mehr NF (2013) Entropy generation in steady MHD flow due to a rotating disk in a nanofluid,. Int J Heat Mass Transfer 62: 515–525. [Google Scholar]
- 30. Motsa SS, Sibanda P, Awad FG, Shateyi S (2010) A new spectral homotopy analysis method for the MHD Jeffery Hamel problem,. Computers and Fluids 39: 1219–1225. [Google Scholar]
- 31. Liao SJ (2009) Notes on the homotopy analysis method: Some definitions and theorems,. Comm Nonlinear Sci Num Simu 14: 983–997. [Google Scholar]
- 32.Liao SJ (2012) Homotopy analysis method in nonlinear differential equations, Springer & Higher Education Press. [Google Scholar]
- 33. Hassan HN, El-Tawil MA (2012) A new technique of using homotopy analysis method for second order nonlinear differential equations,. Appl Math Comput 219: 708–728. [Google Scholar]
- 34. Bataineh AS, Noorani MSM, Hashim I (2009) On a new reliable modification of homotopy analysis method,. Commn Nonlinear Sci Numer Simulation 14: 409–423. [Google Scholar]
- 35. Rashidi MM, Ali M, Freidoonimehr N, Nazari F (2013) Parametric analysis and optimization of entropy generation in unsteady MHD flow over a stretching rotating disk using artificial neural network and particle swarm optimization algorithm,. Energy 497–510. [Google Scholar]
- 36. Ellahi R, Shivanian E, Abbasbandy S, Rahmanb SU, Hayat T (2012) Analysis of steady flows in viscous fluid with heat/mass transfer and slip effects,. Int J Heat Mass Transfer 55: 6384–6390. [Google Scholar]
- 37. Hayat T, Shafiq A, Nawaz M, Alsaedi A (2012) MHD axisymmetric flow of third grade fluid between porous disks with heat transfer,. Appl Math Mech 33 6: 749–764. [Google Scholar]
- 38. Hayat T, Farooq M, Alsaedi A, Iqbal Z (2013) Melting heat transfer in the stagnation point flow of Power-Eyring fluid. J Thermophys Heat Trans 27: 761–766. [Google Scholar]
- 39. Ramzan R, Farooq M, Alsaedi A, Hayat T (2013) MHD three dimensional flow of couple stress fluid with Newtonian heating. Eur Phys J Plus 128: 49. [Google Scholar]
- 40. Turkyilmazoglu M (2012) Solution of the Thomas–Fermi equation with a convergent approach,. Commun Nonlinear Sci Numer Simulat 17: 4097–4103. [Google Scholar]
- 41.Sparrow EM, Cess RD (1978) Radiation Heat Transfer. Washington: Hemisphere. [Google Scholar]
- 42. Raptis A (1998) Radiation and free convection flow through a porous medium. Int Commun Heat Mass Transf 25: 289–295. [Google Scholar]