Social Discounting and the Prisoner’s Dilemma Game

Abstract

Altruistic behavior has been defined in economic terms as “…costly acts that confer economic benefits on other individuals” (Fehr & Fischbacher, 2003). In a prisoner’s dilemma game, cooperation benefits the group but is costly to the individual (relative to defection), yet a significant number of players choose to cooperate. We propose that people do value rewards to others, albeit at a discounted rate (social discounting), in a manner similar to discounting of delayed rewards (delay discounting). Two experiments opposed the personal benefit from defection to the socially discounted benefit to others from cooperation. The benefit to others was determined from a social discount function relating the individual’s subjective value of a reward to another person and the social distance between that individual and the other person. In Experiment 1, the cost of cooperating was held constant while its social benefit was varied in terms of the number of other players, each gaining a fixed, hypothetical amount of money. In Experiment 2, the cost of cooperating was again held constant while the social benefit of cooperating was varied by the hypothetical amount of money earned by a single other player. In both experiments, significantly more participants cooperated when the social benefit was higher.

Explaining behavior

In the Cartesian model of human behavior, the mind has a definite location—in the center of the brain—and is the ultimate cause (after God) of all voluntary behavior. Given this model, it is natural to try to explain overt behavior in terms of more central causes, causes closer to the ultimate one. Although most modern philosophers and psychologists claim to have broken with that tradition (e.g., Searle, 1997) they persist in seeking central explanations—spiritual, neural or cognitive—for overt behavioral events. Skinner’s (1938) profound break with that tradition placed the cause of voluntary behavior, not in the center of the brain but in the environment: in the contingencies of reinforcement.

The influence of the Cartesian model has been so strong in Western society that, even when the importance of the environment in causing behavior is recognized, the mind and all mental acts (including sensing, perceiving, imagining, thinking, feeling, etc.) are still assumed to be located somewhere in the brain. Skinner himself assumed (1945) that, although mental events did not directly cause behavior, mental terms (“psychological terms”) referred to covert behavior —to acts more central than the behavior he observed. No one can doubt that the mechanisms underlying behavior—its efficient causes—are in the brain. Studies of such mechanisms are highly important and valuable. However, there is no evidence that mental events themselves are in the brain or elsewhere within the body.¹ To confound behavior with the mechanism underlying it is like confounding the time with the mechanism inside of a clock. The only evidence ever put forth for the supposition that our minds are inside our brains is introspective, the same sort of evidence that tells us the sun goes around the earth. But, as Skinner also pointed out (1957), different reinforcement histories will lead to different introspections.² Rachlin (1992, 1994) has argued that the location of the mind, and the proper locus of our mental vocabulary, is in the opposite direction from that supposed by Descartes—outward not inward—in the reinforcement contingencies themselves that Skinner showed are the true causes of voluntary behavior.

What does such an attitude mean for the study of behavior? It means that when a behavioral phenomenon is discovered at the level of overt behavior, the investigation of its broader reinforcement contingencies is at least as valid and at least as useful as the investigation of its underlying mechanisms within the body. A theoretical framework for such investigation is provided ready-made in economics (Becker, 1976). In economic utility theory, an individual is conceived as maximizing utility within the bounds of behavioral constraints (i.e., contingencies). On the basis of observations under several different sets of constraints, the behaviorist may derive a utility function and use it to predict behavior under other sets of constraints (Rachlin, Battalio, Kagel, & Green, 1981). Where do these utility functions exist? Not in our brains but in the environmental contingencies themselves and in our overt behavior.

A large area in cognitive decision theory consists of the study of apparent psychological exceptions to utility theory (Tversky & Kahneman, 1974). The relation of this area to standard economic theory is analogous to the relation of biological exceptions to the behavior of organisms—the “misbehavior of organisms” (Breland & Breland, 1961). As time has gone on, the apparent exceptions have led to modifications in the main theory and been incorporated into it. One apparent psychological exception to standard economic theory is the preference reversal often found in self-control situations. Such reversals have been shown to be due to hyperbolic delay discounting (Ainslie, 1992) and, as time has gone on, hyperbolic discounting has come to be seen as a normal part of the theory rather than as an exception to it (Rachlin, 2006).

One important component of a utility function is a delay discount function. In economic theory, a choice alternative consists not only of its immediate consequences but also of its delayed consequences. However, the delayed consequences are discounted as a function of delay —the more delayed, the less the value (positive or negative). The study of delay discounting (its internal mechanism and its external context) has become a major part of behavioral research today (Madden & Bickel, 2010). Another utility-function component—social discounting—has been much less studied. A choice alternative may have consequences not only for the chooser but also for other individuals, socially close to or socially distant from the chooser. Such consequences influence choice but, like delay, are discounted; the greater the social distance from the chooser to the receiver, the less the value to the chooser (Jones & Rachlin, 2006). Although social discounting has been much less studied than delay discounting it may be equally important, at least in explaining human behavior. The present article uses social discounting to explain behavior in various versions of a prisoner’s dilemma game, a choice situation that pits individual versus group benefit, which does not seem amenable to explanation by standard economic theory (that is, without social discounting).

The Prisoner’s Dilemma Game

Whenever he speaks at colloquia or meetings, Rachlin begins by playing a 10-person prisoner’s dilemma (PD) game with the audience. Ten randomly selected audience members are given cards and asked to write X or Y on their card according to the following rules:

1. If you choose Y, you will receive $100 times Z.

2. If you choose X, you will receive $100 times Z plus $300.

3. Z is equal to the number of players who choose Y.

Before choosing, the audience is told that the money is hypothetical but asked to try their best to choose as they would if it were real. It is then pointed out that, regardless of what any of the other players choose, an audience member will earn $200 more by choosing X than by choosing Y (the audience member would lose $100 by reducing Z by one but would also gain the $300 bonus). Thus, a Y-choice may be said to cost $200. However, if all the players chose X, Z would equal zero and each player would earn $300 whereas, if they all chose Y, Z would equal 10 and each would earn $1,000. Each player’s own interests are thus opposed to those of the group; it is in each player’s own interest to choose X but in the group’s interest for all to choose Y. Players are then assured that their choice will be completely anonymous and asked to write X or Y on their cards.

Audiences playing this one-shot PD game have varied considerably in sophistication, ranging from undergraduates to graduate students to Japanese, American, Italian, or Polish psychologists, to economists, to a seminar of philosophers, mathematicians and computer scientists specializing in game theory. The results, however, have been remarkably uniform: about half X’s (defection) and half Y’s (cooperation). Informal observation reveals no correlation between audience sophistication and degree of cooperation. As has been long understood, there is no correct or incorrect choice in this game (Axelrod, 1980; Rapoport, 1974). Yet, although the benefits of defecting are clear, there is no clear reason to cooperate. The cost to an individual of a Y-choice in the lecture game is $200. What is the gain?

Sometimes, depending on circumstances, the lecture game is followed by a discussion (without revealing what anyone actually chose) of why a person should choose Y in this anonymous game. One reason people often give for choosing Y is that they believe that many or most of the other players will choose Y. This rationale is common but not strictly rational. Since the cost of a Y-choice is constant at $200, regardless of what anyone else chooses, other players’ choices should, in theory, not influence any person’s individual choice. What others choose in this game will indeed have a strong effect on a player’s earnings. But, within this one-shot, anonymous game, no player can have any direct influence on another player’s choice. It is true that if a person chooses Y she will be better off if all other players chose Y (and she earns $1,000) than if any other player or players had chosen X. But, given that all other players chose Y, she would be still better off if she alone had chosen X (and earned $1,200).

The philosopher, Derek Parfit (1984, pp. 61–62) listed a sample of situations from everyday life modeled by multiperson prisoner’s dilemma games such as the lecture game:

• Commuters: Each goes faster if he drives, but if all drive each goes slower than if all take buses;

• Soldiers: Each will be safer if he turns and runs, but if all do more will be killed than if none do;

• Fishermen: When the sea is overfished, it can be better for each if he tries to catch more, worse for each if all do;

• Peasants: When the land is overcrowded, it can be better for each if he or she has more children, worse for each if all do.

  There are countless other cases. It can be better for each if he adds to pollution, uses more energy, jumps queues, and breaks agreements; but if all do these things, that can be worse for each than if none do…. In most of these cases the following is true. If each rather than none does what will be better for himself, or his family, or those he loves, this will be worse for everyone.³

Parfit (1984, pp. 100–101) considers choosing Y because you believe that others will choose Y as a rationale for cooperating and makes an appealing suggestion for quantifying this rationale. First, he suggests, determine how much you would earn if all players, including you, defected (chose X); in the lecture game, that would be $300. Then make your best guess of how many other players will probably cooperate (how many would choose Y). Then determine how much you would earn if you also cooperated. If the amount you earned by cooperating is at least as great as the amount you would earn if all players including you defected then, according to Parfit, you should cooperate. In order to earn $300 or more by cooperating in the lecture game, at least two other players would also have to cooperate. If you were a player in the lecture game, knowing that about half of the 10 players usually cooperate, and you wanted to follow Parfit’s suggestion, you would cooperate. However, as Parfit admits, his suggestion does not resolve the dilemma. If two other lecture-game players chose Y and you also chose Y, you would earn $300 whereas, if you had chosen X, you would have earned $500. Thus a rational person, acting in her own self-interest, would choose X. Parfit’s suggestion does not by itself explain why such a person should choose Y. Although Parfit’s suggestion has intuitive appeal, and corresponds to people’s verbal rationalizations, it is not a good explanation, in itself, of why people cooperate.

One approach to determining what an individual gains by cooperating in a PD game is to note that, in the lecture game, by choosing Y, each player increases the earnings of each of the nine other players by $100 (regardless of whether they themselves chose X or Y). We can therefore ask: What is the benefit for an individual player of giving $100 to each of the nine other players? And, is that benefit worth the $200 cost? Within traditional economic theory, a benefit to another person does not normally enter into the calculation of an individual’s well-being. But, according to the economist Julian Simon (1995), it should be no more surprising that people value rewards to other people, but discount those rewards more as those people are more socially distant, than it is that people value their own future rewards but discount those rewards more as the time to their receipt grows more temporally distant. According to Simon, people allocate available resources on three dimensions:

1. Current consumption by the person;

2. Consumption by the same person at later times (delay discounting);

3. Consumption by other people (social discounting).

Simon says, “Instead of a one-dimensional maximizing entity, or even the two-dimensional individual who allocates intertemporally, this model envisages a three-dimensional surface with an interpersonal ‘distance’ dimension replacing the concept of altruism” (p. 367, italics ours).

Delay discounting enters normally into economic utility functions and is not considered to be irrational in itself. But the third of Simon’s (1995) dimensions, consumption by other people, may seem fundamentally different from delay. The sacrifice of your own well-being for that of someone else may seem irrational; altruism may seem to be an exception to utility maximization. But from Parfit’s (1984) and Simon’s and our own viewpoints, a person who values a benefit to another person at some fraction of a benefit to himself is not acting any less rationally (or more altruistically for that matter) than a person who values a delayed reward at some fraction of a current reward. The purpose of the experiments described in this article is to see how far we can go in predicting PD game behavior in terms of economic costs and benefits where benefits include socially discounted rewards to another person or other people. We will now describe previously published research showing how social discount functions are obtained, and then in two new experiments we will use those functions to calculate benefits and predict behavior in PD games.

Social Discount Functions

Experiments in our laboratory at Stony Brook (e.g., Jones & Rachlin, 2006; Rachlin & Jones, 2008) have shown that, as Simon (1995) speculated, rewards to others are discounted by social distance to the recipient. Figure 1 shows a social discount function obtained by Rachlin & Jones (2008) using a method similar to that used to obtain delay discount functions. Participants (Stony Brook undergraduates) read these instructions:

The following experiment asks you to imagine that you have made a list of the 100 people closest to you in the world ranging from your dearest friend or relative at position #1 to a mere acquaintance at #100. The person at number one would be someone you know well and is your closest friend or relative. The person at #100 might be someone you recognize and encounter but perhaps you may not even know their name.

You do not have to physically create the list – just imagine that you have done so.⁴

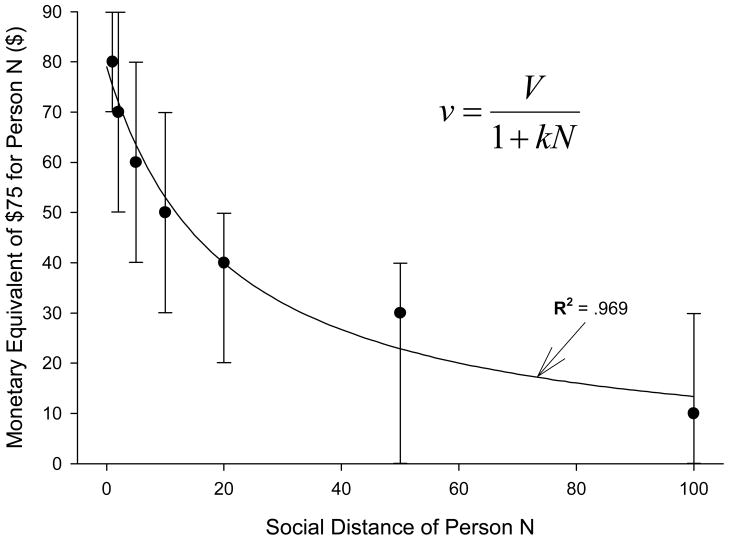
Figure 1.

A social discount function adapted from Rachlin & Jones (2008). The median amount of money (for oneself) that was equally preferred to $75 for the person at social distance N. The error bars indicate interquartile ranges. The curve shows the best fit of Equation 1.

Then participants chose between a hypothetical fixed $75 reward for a recipient at a given social distance from them (social distance, N, was defined as the recipient’s ordinal position on their list) and an equal or lesser reward for themselves. By varying the participant’s reward up and down, a point of equality was found where the value to the participant of a lesser reward for herself was equal to that of $75 for the recipient. Figure 1 plots these median values as a function of position on the list.⁵

As with delay discounting, the medians of 219 participants were well described by a hyperbolic discount function (R² = .969):

$$v=\frac{V}{1+kN}$$ (1)

where V is the undiscounted value of the reward ($75) given to the recipient, v is the value of the reward to the participant, N is the social distance between participant and recipient, and k is a constant that varies among individuals. The median k of individual social discount functions for the data of Figure 1 is 0.055. This is the value of k we used to predict results of Experiments 1 and 2.

Let us assume now that the players in the lecture game are Stony Brook undergraduates in an introductory psychology class. If we knew the social distance between a member of the class and a random other member (one of the nine other players) we could rescale the discount function of Figure 1 from $75 to $100 on the y-axis and determine how much it is worth for a player to give $100 to another player at that social distance. A separate experiment with a group of 44 undergraduates from the same population was performed to make that determination.

After reading instructions (as in social discounting experiments) to imagine a list of 100 of their closest friends or relatives, each participant read the following:

Now try to imagine yourself standing on a vast field with those 100 people. The actual closeness between you and each other person is proportional to how close you feel to that person. For example, if a given person were 10 feet away from you then another person to whom you felt twice as close would be 5 feet away from you and one to whom you felt half as close would be 20 feet away. We are going to ask you for distances corresponding to some selected individuals of the 100 on your hypothetical list.

Remember that there are no limits to distance – either close or far; even a billionth of an inch is infinitely divisible and even a million miles can be infinitely exceeded. Therefore, do not say that a person is zero distance away (no matter how close) but instead put that person at a very small fraction of the distance of one who is further away; and do not say that a person is infinitely far away (no matter how far) but instead put that person at a very great distance compared to one who is closer.

Of course there are no right or wrong answers. We just want you to express your closeness to and distance from these other people in terms of actual distance; the closer you feel to a person, the closer you should put them on the field; the further you feel from a person, the further they should be from you on the field. Just judge your own feelings of closeness and distance.

Each of the following seven pages differed in N-value, randomly ordered, and stated the following question:

How far away from you on the field is the [Nth] person on your list?

Feel free to use any units you wish (inches, feet, miles, football fields, etc. Just indicate what the unit is).

Please write a number and units of measurement for the [Nth] person on your list:

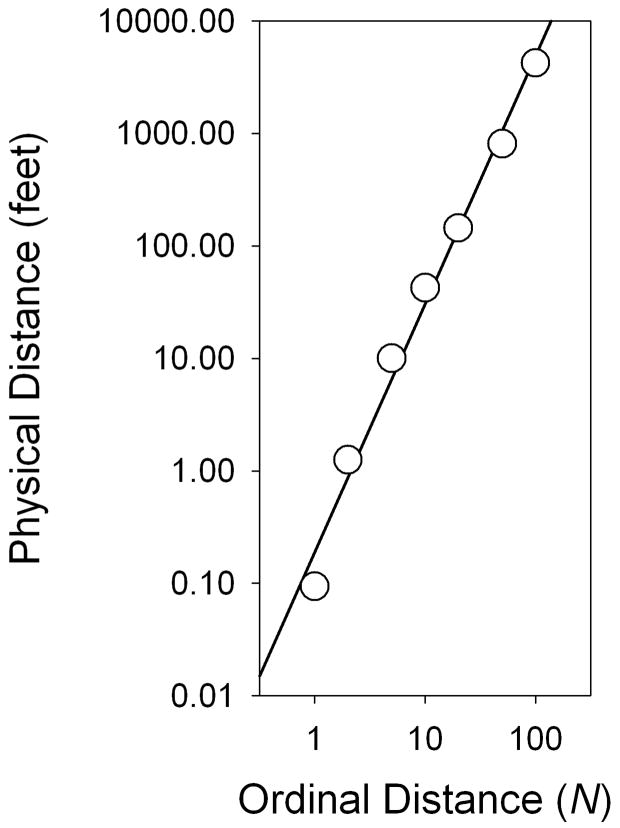
Participants found no difficulty in responding consistently to the rather odd instructions of this experiment. The distance judgments were converted to feet from whatever units the participants used and then averaged. Medians across participants are plotted in Figure 2 on a log-log scale. The best-fitting straight line (r² = .988) is:

$$\begin{array}{l}logd=2.2(logN)-0.72\\ d=0.19N^{2.2}\\ N=2.1d^{0.45}\end{array}$$ (2)

where d = distance in feet. As in psychophysical magnitude estimation experiments, a power function describes the median data well.

Figure 2.

Median judged physical distance to another person as a function of that person’s social distance (rank in a list of 100 socially closest people).

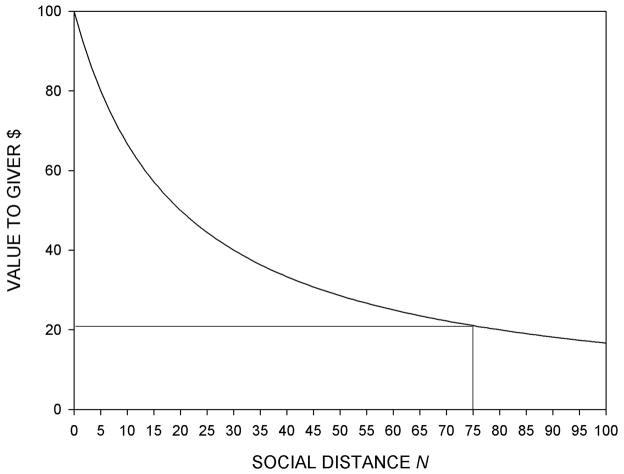
Still a third group of 50 Stony Brook introductory psychology students was given the instructions above, but instead of placing a series of people at various social distances (N’s) on the field, they were asked to place on the field only a single random member of the class. The median distance from a participant of a random classmate was 2,300 feet! From the above equation, at d = 2300, N ≈ 75. Figure 3 normalizes the y-axis of Figure 2 at $100. At N = 75, the crossover point is about $21. That is, a typical Stony Brook introductory psychology student would be indifferent between $21 for herself and $100 for a random member of the class.⁶

Figure 3.

The social discount function of Figure 1. Value rescaled from $75 to $100. Receipt of $100 by the 75^th person on a list of 100 closest people is worth about $21 to the participant.

In the lecture game, a player’s Y-choice gives $100 to nine other players. Assuming (provisionally) that the value of giving nine other players $100 each is 9 times the value of giving one other player $100, the total benefit obtained by a Y-choice is $180 (9 × $20). This gain is a ballpark approximation to the cost of a Y-choice ($200) and would account for the close to 50:50 ratio of X and Y choices typically found with this game.

Perhaps the most obvious prediction of the social discounting account of PD behavior is that, in a PD game, individuals with steep social discount functions will act selfishly and individuals with shallow social discount functions will act altruistically. Jones and Rachlin (2009) tested this prediction with a form of PD called a “public goods” game. Participants read the following instructions:

Imagine the following situation (purely hypothetical we regret to say):

1. The experimenter gives you $100.

2. A box is passed around to each person in this room.

3. Each person may put all or any part or none of the $100 into the box. No one else will know how much money anyone puts into the box.

4. After the box goes around the room, the experimenter doubles whatever is in the box and distributes it equally to each person in the room regardless of how much money they put into the box.

   Each person will then go home with whatever they kept plus what they received from the box.

   Note that you will maximize the money you receive by not putting any money in the box. Then you will take home the original $100 you kept plus what the experimenter distributes after doubling whatever money was in the box.

   HOWEVER: If everybody kept all $100, nothing would be in the box and each person would take home $100. Whereas, if everybody put all $100 in the box, each person would take home $200 after the money in the box was doubled and distributed.

   Please indicate below how much of the $100, if any, you would put into the box. Please try to answer the question as if the money were real:

   I would put the following amount into the box:	$______
   I would keep the following amount:	$_____
   Sum must equal $100.

After answering this question, individual social discount functions were obtained by the method described above. Individual delay discount functions were also obtained. In two separate replications, amount donated in the public goods game was significantly (negatively) correlated with steepness of the social discount function (but not correlated with the steepness of the delay discount function). That is, the steeper a person’s social discount function, the less money they donated to the common good in this public goods game.

The two experiments presented below test two further predictions of the social discounting account. The first tests the assumption that, all else held equal, the more lecture-game players, the greater should be the percentage of Y-choices (cooperations). The second experiment, with a 2-player PD game, tests whether increasing the social benefit of cooperation (the reward to the other player), while keeping the cost of cooperation constant, increases cooperation.

EXPERIMENT 1

Group-Size Effects in Multiplayer PD Games

Equation 1 may be used to calculate the value to a player of a reward given to a single other player at a given social distance. If, as a consequence of the player’s choice, more than one other player all received the same reward, at about the same social distance from the chooser, then the value to the chooser would be expected to increase proportionally to the number of other players. It is therefore an essential part of the above cost-benefit account of the lecture game that, all else equal, the larger the group the greater the percent of its members who should cooperate. We tested this prediction with some doubt as to the outcome since social psychological studies have typically found less altruism by individuals in larger groups (Latane & Darley, 1970). But in those studies group size affected individual anonymity – greater numbers affording greater anonymity. In the lecture game, as in Experiment 1, anonymity was not an issue; all choices were equally anonymous.

Method

Participants

Sixty undergraduate students were recruited through the psychology subject pool at Stony Brook University. Each participant was randomly assigned to one of three groups: the 5-player group (n = 20), the 10-player group (n = 20), or the 20-player group (n = 20).

Apparatus & Instructions

Participants were seated individually on a couch in a small room (approximately 3 m wide by 3 m deep). A white box and a black box, each an approximately 20-cm cube, rested atop a table in front of the couch, within arm’s reach. Each box had a slit, about 5 cm wide, across the top.

Participants were handed a single sheet of paper with instructions. For the 10-player group, the instructions were as follows:

Please imagine the following situation:

You are playing a 10-player game with 9 other players randomly selected from various psychology classes. Each of the 10 players (including you) is asked to choose X or Y. You will then receive an amount of money depending on your choice and the choices of the 9 other players.

This table [Table 1] indicates the possible money awards:

Table 1.

Money earned for choosing X or Y as a function of the number of players who choose Y

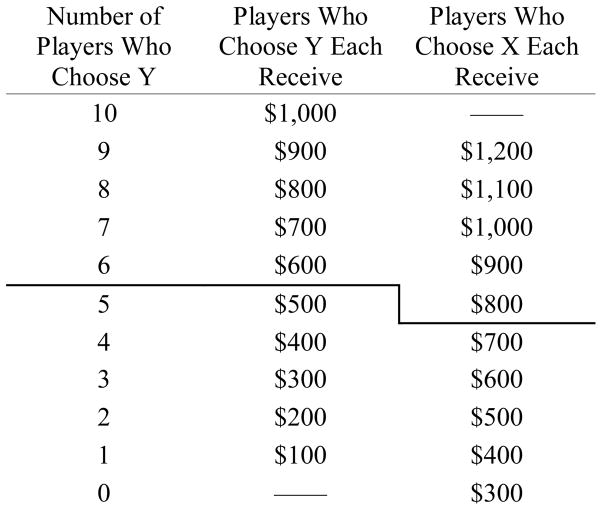
By individually choosing Y:

• you increase the number of players who choose Y by 1, moving 1 row up the table and gaining $100

• but you also move to the left, losing $300

• thus, you will always have a net loss of $200 by choosing Y.

  Just to be clear: You will ALWAYS lose $200 by choosing Y rather than X. That is, it costs you $200 to choose Y. This is true regardless of what the other players choose.

  Thus, any lawyer would advise you to choose X. However, if every one of the players (including you) followed their lawyer’s advice and chose X, each would earn $300 as shown in the bottom row of the table.

  Choosing Y moves up the table, not only for you, but for each of the other 9 players. By choosing Y you essentially give $100 to each of the 9 other players. Thus, if all of the 10 players disobeyed their lawyers and chose Y, each of you would earn $1,000 as shown in the top row of the table.

  This is the dilemma: If you choose X, you personally benefit (by $200) regardless of what others choose. But if you choose Y, you move up the table and each of the 9 other players earns $100 more.

  Remember, your choice is completely anonymous.

  There is no right or wrong choice in this game. We just want to know what you would choose if the money were real.

The table shown to the 5-player group was cut off at the bold line in Table 1 at $500 (participants in the 10-player and 20-player groups did not see a bold line). The table shown to the 20-player group was extended upwards to $2,000 in the top row. After the participant had read the instructions and the experimenter verified comprehension, the participant was handed a small slip of paper with the following question:

• 1Given all these considerations, and imagining as best as you can that the money is real, which would you choose? (Circle ONE only) X or Y

The experimenter turned so as to not be facing the participant while the question was answered. The participant was instructed to fold up the slip of paper and place it in the white box after answering the question. After this was accomplished, the experimenter handed the participant another slip of paper which read:

• 2Out of the other 9 players, how many do you think would have chosen Y? (Circle ONE only) 0 1 2 3 4 5 6 7 8 9

Once again, the experimenter demonstratively avoided observation of the participant as this second question was answered. The participant was then instructed to fold up the slip of paper and place it in the black box after answering the question.

This completed the 10-player game. Each of the other two games were identical to the 10-player game except that the instructions and questions were altered as necessary to reflect either 5 or 20 players instead of 10. For example, in the 20-player game, participants were instructed: “If all of the 20 players disobeyed their lawyers and chose Y, each of you would earn $2,000 as shown in the top row of the table.”

Results

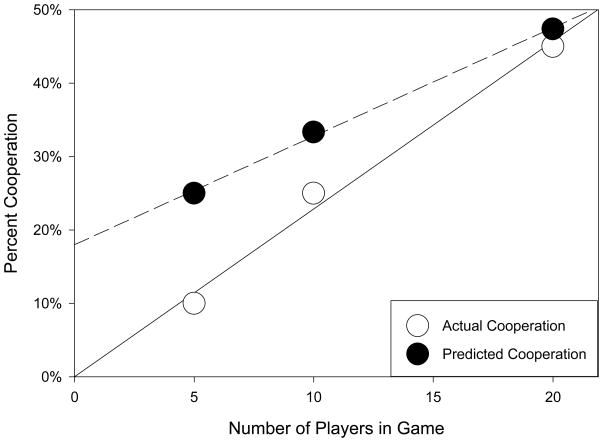
Percent cooperation (percent Y-choices) increased with the number of players in the game. The open circles in Figure 4 show percent cooperation for each of the three groups. A Chi-Squared Test for Trend indicated a significant increase in cooperation as a function of the number of players in the game (X² (1, N = 60) = 6.264, p = .0123).

Figure 4.

Percent of participants who cooperated (open circles) and median predicted cooperation of others (closed circles) as a function of the number of players in the game.

The second question asked participants to predict how many other players would have cooperated (chosen Y). The solid circles in Figure 4 show median predicted percentage of cooperation for each of the three groups. The median predictions were 1 out of 4 for the 5-player group, 3 out of 9 for the 10-player group, and 9 out of 19 for the 20-player group. There was no statistically significant effect of group on predicted percentages of others’ cooperation (ANOVA, F (2, 57) = 0.586, p = .560). However, cooperation and predicted cooperation, across groups, were highly correlated. In the 5-player game, 100% of participants who chose Y and 0% of participants who chose X predicted 75% or more cooperation from others. In the 10-player game, 80% of participants who chose Y and 7% of participants who chose X predicted 65% or more cooperation from others. In the 20-player game, 67% of participants who chose Y and 18% of participants who chose X predicted 50% or more cooperation from others.

Discussion

The results of Experiment 1 were consistent with the social discounting model. With a fixed cost, the greater the social benefit (in terms of the greater number of other players each receiving a fixed amount of money) the more likely a player was to cooperate. But there are other conceivable explanations of these results. Although the instructions emphasized that the $200 cost of choosing Y was independent of the number of other players who cooperated, participants may nevertheless have based their decision on their prior estimation of that number. XXXThe strong correlation between participants’ own cooperation and their predicted cooperation of other players suggests that this may have been a factor. However, an explanation based on estimations of others’ cooperation does not explain why participants in smaller groups should estimate that a smaller percentage of other participants would have cooperated. Any explanation of PD results based on estimates of the cooperation of others, merely substitutes one puzzle (why different-sized groups should estimate others’ cooperation differently) for another (why different-sized groups should themselves cooperate at different rates). Although the decision to cooperate is highly correlated with estimates that others will cooperate, it is not clear which factor causes the other or whether a third factor (such as an estimate of the costs and benefits of cooperation) causes both.

Experiment 1 varied the benefit of cooperation, with a fixed cost, by varying the number of other players receiving a fixed amount. Experiment 2 varied the benefit of cooperation, also with a fixed cost, by varying the amount received by a single other player.

EXPERIMENT 2

Social Costs And Benefits In Two-Player PD Games

Although multi-player PD games are common in everyday life, as Parfit (1984) states, the PD game most studied in the laboratory is the two-player game (Rapoport, 1974; Silverstein, Cross, Brown, & Rachlin, 1998). Figure 5a shows a two-player PD 1-2-3-4 reward matrix. If both Player-A and Player-B choose Y (cooperate), each receives 3 reward units. If both choose X (defect) each receives 2 reward units. Clearly it is better for both if both cooperate. However, if one cooperates and one defects, the cooperator receives 1 unit and the defector receives 4 units.

Figure 5.

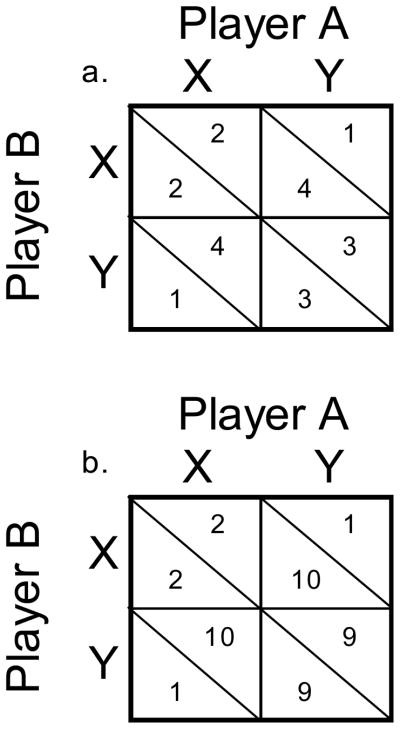
The (a) 1-2-3-4 and (b) 1-2-9-10 prisoner’s dilemma reward matrices. Player A’s choice determines the active column and Player B’s choice determines the active row. The reward above each “\” is for Player A and the reward below is for Player B.

As in the multi-player game, cooperation is costly for the individual player. Cooperation costs a player one unit regardless of what the other player chooses. On the other hand, a player’s cooperation gives 2 units to the other player. If Player-A cooperates, Player-B will earn 3 units (by cooperating) or 4 units (by defecting); if Player-A defects, Player-B will earn only 1 unit (by cooperating) or 2 units (by defecting). The question addressed here is whether a 1-unit undiscounted cost of cooperating is counterbalanced by a 2-unit socially-discounted gain of cooperating. Equation 1 can be used to answer this question. An average Stony Brook introductory psychology student ranks a random classmate at a social distance of about 75^th on a list of 100 people closest to her (Rachlin & Locey, 2011). Substituting in Equation 1: V = 2 units, k = 0.055, N = 75; v is calculated to be 0.39 units. Since the 0.39-unit discounted gain is less than the 1-unit undiscounted cost, the average Stony Brook undergraduate should defect in the PD game of Figure 5a.

Figure 5b shows a 2-player 1-2-9-10 PD matrix. As with the 1-2-3-4 PD matrix, the individual player gains 1 unit of reward by choosing X (defecting) regardless of the other player’s choice (2 versus 1 or 10 versus 9 units). However, if both players choose Y (cooperate), each gains 9 units whereas, if both choose X (defect), each gains only 2 units. In this game the 1-unit cost of cooperating is opposed to an 8-unit gain by the other player: 4 times that of the 1-2-3-4 matrix. Therefore, according to Equation 1, the socially discounted reward for cooperating with the 1-2-9-10 matrix is 4 times that with the 1-2-3-4 matrix, or 1.56 reward units. Since the socially discounted 1.56 unit gain is greater than the 1-unit undiscounted cost, Equation 1 predicts that the average Stony Brook undergraduate should cooperate in the PD game of Figure 5b. Given the variability of individual k-values, subjective values of undiscounted costs and benefits, and social distances to random other players, it is not possible to predict absolute levels of cooperation. But a clear prediction of the present cost-benefit analysis is that a greater percentage of players will cooperate with the 1-2-9-10 reward matrix of Figure 5b than with the 1-2-3-4 reward matrix of Figure 5a. Experiment 2 tested this expectation.

Method

Participants

426 undergraduates were recruited through the Stony Brook psychology subject pool. Participants completed a number of unrelated online surveys as part of the psychology department’s Mass Testing. Participants were randomly assigned to the 1-2-3-4 reward unit matrix (n = 225) or the 1-2-9-10 reward unit matrix (n = 201).

Instructions

Participants in the 1-2-3-4 reward-unit matrix group were given the following instructions:

Each participant in this experiment has a randomly assigned partner, one of the other participants in this experiment. We ask you to make a single choice between hypothetical monetary rewards for you and your partner. No other participant will know what you chose unless you reveal it yourself.

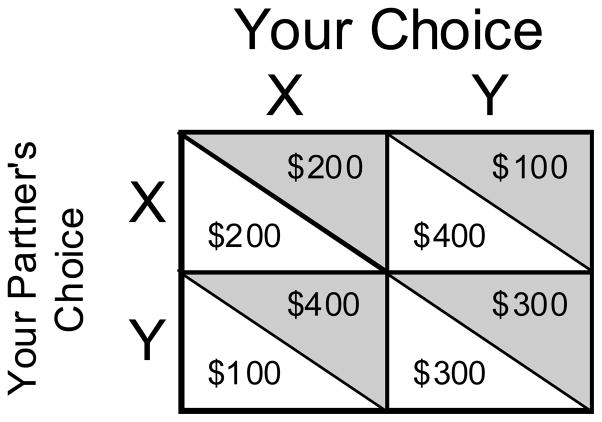
The amount of your reward depends on both your own choice and your partner’s choice. The amount of your partner’s reward also depends on both your own choice and your partner’s choice. Rewards are determined by the following table [shown in Figure 6]:

The blue triangle of each box indicates what you get for each combination of choices by you and your partner. The white triangle indicates what your partner gets.

In other words, if you and your partner both choose X, you each earn $200. If you both choose Y, you each earn $300. But, if one of you chooses X and the other chooses Y, the one who chooses X earns $400 while the one who chooses Y earns $100.

There is no right or wrong choice. We just want to know what you would choose if the money were real. Remember, you have to make one and only one choice. Please take your time and carefully consider the alternatives.

Given all of the above, which do you choose? (X or Y)

Figure 6.

The Prisoner’s Dilemma reward matrix shown to the 1-2-3-4 reward matrix group. Triangles in gray indicate areas shaded blue for participants.

The instructions included a picture of Figure 6 in which the top-right triangle in each box was colored blue. For the 1-2-9-10 reward matrix group, references to $300 and $400 (in the figure and instructions) were replaced by $900 and $1000. Participants in each group were asked only the one question: whether they would choose X or Y in the situation described in the instructions.

Results

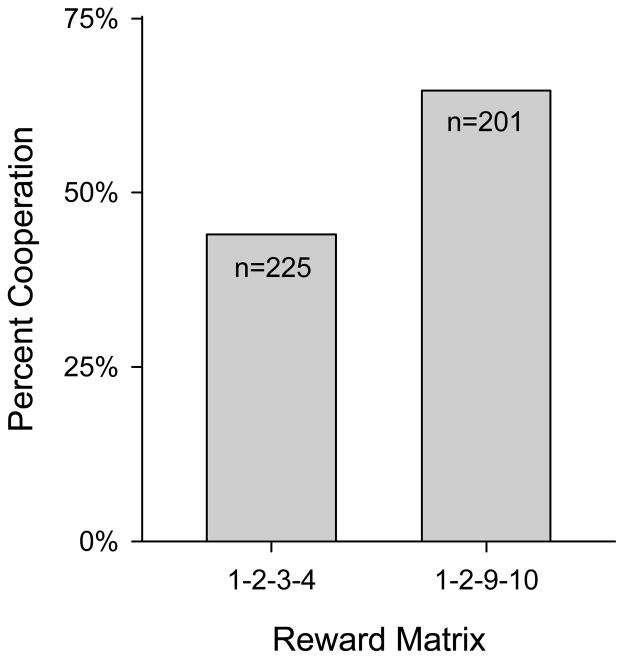
Figure 7 shows the percentage of cooperation – choices of Y – for both reward matrices. Fisher’s Exact Test (FET) indicated significantly fewer participants (44.0%) in the 1-2-3-4 reward matrix group cooperated than in the 1-2-9-10 reward matrix group (p < .0001). The 1-2-9-10 reward matrix group also cooperated significantly more than chance (FET, p = .003).

Figure 7.

Percent of participants who cooperated (chose Y) for each of the two reward matrices.

Discussion

As predicted, the 1-2-9-10 PD matrix generated more cooperation in a one-shot game than did the 1-2-3-4 PD matrix. We believe that this was due to the higher social benefit that the 1-2-9-10 participants received. Participants were told that their choice was anonymous and that this was a one-shot game. Cooperation could bring them no enhancement of reputation or direct reciprocation from their partner. In our calculations, we subtracted absolute costs from absolute benefits. However, it is possible that what counts for decision making are ratios of costs and benefits to reward amounts. Nevertheless, regardless of the metric, the socially discounted benefits of the 1-2-9-10 matrix must be greater, relative to costs, than those of the 1-2-3-4 matrix, and this difference was the basis of our prediction.

It is conceivable that those participants who cooperated were (perhaps unconsciously) following a general rule: cooperate in social situations, and don’t make decisions on a case-by-case basis. Such a rule would be similar to the one many of us follow: stop at red lights even if there are no cars or pedestrians on the crossroad and no police in sight. This explanation assumes that people learn to extend the boundaries of their selves socially (beyond their own skin) as well as temporally (beyond the present moment). We proposed a learning mechanism for such rules analogous to the biological, evolutionary mechanism of group selection (Rachlin & Jones, 2009; Rachlin & Locey, 2011). But such rules, even the stop-at-red-lights rule, may be modified when the benefits of violation are high (rushing someone to the hospital) or the costs are low (when we’re pedestrians ourselves and jaywalking is not punished). Sensitivity to costs and benefits, such as these experiments show, is thus compatible with a more molar explanation of altruistic behavior.

Conclusions

A reasonable question to ask is: Why do we have social discount functions? Why do they not simply drop off to zero beyond your closest friends and family? But you could just as reasonably ask: Why do we have delay discount functions? Why do they not drop off after a day or even a minute? Ainslie (1992) has argued that delay discounting arises from an economic interaction between present and future selves. We would put it differently: Delay discounting arises from an economic interaction, not between individual present and individual future selves, but between a temporally narrow self and a temporally wider self (Rachlin & Jones, 2010). The prisoner’s dilemma game is the social equivalent of that interaction.

The interests of our temporally narrower selves overlap with those of our temporally wider selves. Delay discount functions are measures of those overlapping interests. Similarly, the interests of our socially narrower selves overlap with those of our socially wider selves and social discount functions are measures of those overlapping interests. What we mean by “self-control” is dominance of a temporally wider over a temporally narrower self; what we mean by “social cooperation” is dominance of a socially wider over a socially narrower self.

It may be that delay discounting arises in development and learning before social discounting and that the well-being of others is merely an extension of the well-being of our future selves. But the reverse may actually be the case. We may care for our future selves only because we first care for others. Or, more likely, both of these extensions of our present selves develop and are learned together. There is a significant (although low) correlation between the steepness of social and delay discount functions across individuals (Rachlin & Jones, 2008). As Simon (1995) implies, depriving yourself of something for the benefit of someone else is no more mysterious than depriving yourself of something now for the benefit of yourself in the future.

APPENDIX

One apparent weakness of the procedures of these experiments is their use of hypothetical rewards. Participants might honestly imagine that they would be generous in a certain situation with hypothetical rewards yet choose selfishly when real rewards are offered. But results with real rewards may not be any more indicative of what people will do in real-life situations, where motives and incentives are strong, than are results with larger, hypothetical rewards. Experiments in our laboratory (Locey, Jones & Rachlin, 2011) have failed to find significant differences with real versus hypothetical money in PD-type games or in social discounting. Moreover, where they have been compared, delay discount functions for real and hypothetical rewards have been similar (Madden, Begotka, Raiff, & Kastern, 2003) whereas varying the amount of hypothetical rewards produces strong and significant effects on behavior.

A related issue is the detailed scenarios contained in some of the instructions (e.g., “…any lawyer would advise you to choose X.”). The reason for these scenarios is the fact that no experimental situation, especially one with human participants, is conducted in a vacuum. There is always a context – a “meta- discriminative stimulus” that governs behavior overall (Frankel & Rachlin, 2010). With real monetary rewards, the context may be real-life games played for money. That may not be the most appropriate context, especially in studies of altruistic behavior. With hypothetical monetary rewards, the context is left up in the air so to speak. We ask participants to behave as they would if the rewards were real. If the real-world context is not specified, each participant may provide his or her own. We therefore believe that better experimental control may be obtained when the hypothetical context is filled in to some extent. However, this is a testable speculation and an area for future research.