Advances in Doppler OCT

Abstract

We review the principle and some recent applications of Doppler optical coherence tomography (OCT). The advances of the phase-resolved Doppler OCT method are described. Functional OCT algorithms which are based on an extension of the phase-resolved scheme are also introduced. Recent applications of Doppler OCT for quantification of flow, imaging of microvasculature and vocal fold vibration, and optical coherence elastography are briefly discussed.

1. Introduction

Optical coherence tomography (OCT) is a non-invasive, high resolution imaging modality capable of capturing 3D images from highly scattering biological tissue^[1]. In the past few years, due to the development of fast swept laser sources and high speed detector arrays, Fourier domain OCT (FD-OCT) systems have experienced dramatic improvement compared with the time domain OCT (TD-OCT) systems in terms of imaging speed and sensitivity^[2,3]. OCT was first used clinically in ophthalmology for imaging and diagnosis of retinal disease. Recently, the application of OCT has been extended to image subsurface structures in vessels, oral cavities, and skin, as well as respiratory, urogenital, and gastrointestinal tracts^[4].

OCT contrast originates from variations in tissue scattering, which are caused by the inhomogeneity of the optical index of refraction in the tissue. However, in many instances, especially during early stages of disease, the change in tissue scattering properties between normal and diseased tissue is small and difficult to measure. The functional extension of OCT has further expanded its applications to provide physiological information in addition to morphological structure. Doppler OCT (D-OCT) is one of the most important functional extensions of OCT. D-OCT combines the Doppler principle with OCT to obtain high-resolution tomographic images of static and moving constituents, simultaneously, in highly scattering biological tissue. D-OCT can image blood vessels in vivo with high resolution and sensitivity and offer valuable information regarding the blood flow direction and velocity. One important application of D-OCT is to map tissue microvasculature, which is essential for diagnosis and management of many diseases that have a vascular etiology^[5,6]. In ophthalmology, many ophthalmic diseases such as diabetic retinopathy, low tension glaucoma, anterior ischemic optic neuritis, and macular degeneration may involve disturbances in ocular blood flow^[4]. 3D mapping of microcirculation may also provide important information for the diagnosis and management of cancer and cardiovascular diseases^[4].

The first 2D in vivo D-OCT imaging was demonstrated in 1997^[5–7]. In early D-OCT systems, the Doppler frequency shift was obtained by a spectrogram method, which used short time fast Fourier transformation (STFFT) or wavelet transformation^[5,6]. However, the spectrogram method suffers from low sensitivity and limited imaging speed, resulting in limited clinical applications. It was not until 2000, when the phase-resolved D-OCT (PR-D-OCT) was developed, that D-OCT was applied to imaging vasculature in clinical studies^[8–10]. PR-D-OCT uses the phase change between sequential A-line scans for velocity image reconstruction^[8,9]. PR-D-OCT decouples spatial resolution and velocity sensitivity in flow images and increases imaging speed by more than two orders of magnitude without compromising spatial resolution and velocity sensitivity^[8]. PR-D-OCT was first demonstrated with TD-OCT systems. Recent developments of FD-OCT systems have greatly improved the imaging speed and sensitivity, and FD-OCT systems have become the preferred system for OCT imaging^[3,11,12]. Fourier domain D-OCT systems have been demonstrated with both a spectrometer-based OCT system and a swept source laser based OCT system by several groups^[13–17]. In many clinical applications, the mapping of microvasculature is more important than the measurement of the flow velocity. Doppler variance (DV, or standard deviation) tomography developed by our group provides an excellent method for mapping microvasculature^{[9,10,18–22]}. It was demonstrated that DV imaging had the advantages of being less sensitive to the pulsatile nature of the blood flow and complex variation of incident angle. Recently, several groups have successfully extended a number of similar methods for mapping blood vessel networks. Ren et al. demonstrated a power Doppler angiography method by using band-pass filtered intensity image for mapping the moving scatterer in tissue^[23]. Barton et al. proposed a method based on the speckle of conventional amplitude OCT images^[24]. Mariampillai et al. used the speckle variance in a small 3D volume to image blood vessels^[25]. The logarithmic intensity variance and differential logarithmic intensity variance for mapping vasculatures was also demonstrated^[26]. Yasuno et al. used the intensity threshold binarization-based method for retinal and choroidal blood vessel imaging^[27–29]. Jonathan et al. used a 2D correlation map based on OCT intensity images for blood vessel extraction^[30]. Jia et al. developed a split-spectrum amplitude-decorrelation angiography method^[31]. Wang et al. proposed a method called optical microangiography (OMAG) to separate static and moving signals with a modified Hilbert transform that removed low frequency static signals^[32–34].

There have been great review articles and book chapters about D-OCT in the past few years^[35–38]. This paper will review the principle and technology of D-OCT with a special focus on phase-resolved methods implemented with FD-OCT systems. Functional OCT methods which are based on an extension of the phase-resolved scheme will also be introduced. The recent applications of D-OCT for quantification of flow, imaging of microvasculature and vocal fold vibration, and optical coherence elastography (OCE) will be briefly discussed.

2. Principle of D-OCT

D-OCT, also named optical Doppler tomography (ODT), combines the Doppler principle with OCT. Due to the Doppler effect, the frequency of light scattered from a moving particle is shifted. The amount of the shift can be described as^[5]

$$f_{\mathrm{d}}=\frac{1}{2\pi }(\overrightarrow{k_{\mathrm{s}}}-\overrightarrow{k_{\mathrm{t}}})\cdot \overrightarrow{V},$$ (1)

where $\overrightarrow{k_{\mathrm{t}}}$ and $\overrightarrow{k_{\mathrm{s}}}$ are wave vectors of incoming and scattered light, respectively, and $\overrightarrow{V}$ is the velocity vector of the moving particles. If the angle between the incident beam and the flow direction is θ, the Doppler shift (Eq. (1)) is simplified to^[5]

$$f_{\mathrm{d}}=\frac{2V\cos \left(\theta \right)}{{\lambda }_0},$$ (2)

where λ₀ is the vacuum center wavelength of the target beam. The velocity of the moving particles (V) can be determined from the Doppler shift (f_d), the Doppler angle (θ) and the center wavelength (λ₀). Since the center wavelength is usually known, the research and development in D-OCT is focusing on the development of algorithms and methods to obtain the Doppler shift and the Doppler angle.

The first 2D in vivo D-OCT imaging was reported using the spectrogram method^[5]. Researchers used the spectrogram method based on either STFFT or wavelet transformation to determine the power spectrum of the measured fringe signal^[5–7,39]. However, in the spectrogram method, the spatial resolution and the velocity sensitivity are coupled because both of the parameters are related to the STFFT window size^[8]. A large pixel time-window size increases velocity sensitivity while decreasing spatial resolution. To overcome these limitations, we developed a method that used the phase change between sequential line scans for velocity image reconstruction^[8]. This PR-D-OCT method measured the Doppler shift using the phase change between sequential A-line scans:

$$f_{\mathrm{d}}=\frac{\Delta \varphi }{2\pi \Delta T},$$ (3)

where ΔT is the time difference between sequential A-line scans and Δϕ is the phase change between sequential A-line scans. PR-D-OCT also reduces speckle noise in the velocity image because two sequential A-line scans are compared at the same location; speckle modulations in the fringe signal cancel each other. In addition, the velocity sensitivity can be increased further when the phase difference between sequential frames is used^[8]. The PRD-OCT was first demonstrated with a TD-OCT system and a minimum flow velocity as low as 10 μm/s was shown with the system. In the TD-OCT system, the phase information of the fringe signal can be determined from the complex analytical signal, which can be determined through analytic continuation of the measured interference fringes function by the use of a Hilbert transformation. However, recent advance in the FD-OCT system has made this process simpler. The complex signal in a FD-OCT system is obtained from the Fourier transformation of the acquired fringe and is compatible with the data process procedure of a FD-OCT system.

In this paper, we will focus on phase-resolved D-OCT systems based on high sensitivity and high speed FD-OCT systems. There are two kinds of FD-OCT systems: the spectrometer-based FD-OCT and the swept source based FD-OCT (SS-FD-OCT). In both types of FD-OCT systems (Fig. 1), light from a broadband partial coherence source is coupled into a fiber interferometer by a 2×2 fiber coupler and then split into reference and sample arms of the interferometer. Light backscattered from the sample is coupled back into the fiber and forms interference fringes with the light reflected from the reference arm. In a spectrometer-based FD-OCT system (Fig. 1(a)), interference fringes are spatially dispersed by a dispersive element, such as grating, into the detector array in the spectrometer^[40,41]. In a SS-FD-OCT system (Fig. 1(b)), the broadband wavelength sweeping laser source temporally disperses the wavelength and outputs different wavelengths at different times^[2,42]. A single element detector is used to acquire the temporally dispersed interference fringe.

Fig. 1.

Schematic diagram of (a) spectrometer-based FD-OCT system setup and (b) SS-FD-OCT system.

From Eqs. (2) and (3), the following equation can be obtained:

$$V\cos \left(\theta \right)=\frac{\Delta \varphi {\lambda }_0}{4\pi \Delta T}.$$ (4)

For an OCT system, minimum detectable Doppler frequency is decided by the minimum resolvable phase difference and the A-line rate of the system. The minimum resolvable phase difference is related to the phase stability of the system, and is affected by factors such as mechanical stability of the system and image signal to noise ratio (SNR). The phase stability of the system can be determined by statistically analyzing the adjacent A-line phase difference of a static mirror. The minimum resolvable phase difference of typical FD-OCT systems is several milliradians to tens of milliradians. The phase stability of an OCT system is important for high sensitive velocity imaging. The spectrometer-based FD-OCT systems usually show better phase stability than SS-FD-OCT systems. A phase correction scheme with either hardware or software methods can be used to improve the phase stability of SS-FD-OCT systems^{[14,21,43–45]}. Since PR-D-OCT uses the phase difference to detect the Doppler frequency and the phase values obtained are always limited between –π and π, this limitation sets the maximum resolvable velocity of PR-D-OCT. However, so long as the exact phase values can be unwrapped, the maximum detectable Doppler velocity of PR-D-OCT can be greater than the limit set by phase wrapping. A recent study has suggested that maximum detectable Doppler velocity is determined by the fringe washout limit^[46]. Assuming that the A-line rate and A-line duty cycle are the same, the detector integration time in each A-line for a spectrometer-based FD-OCT system is much longer than that for a SS-FD-OCT system. Therefore, SS-FD-OCT systems are more robust against fringe washout than spectrometer-based FD-OCT systems; in addition, SS-FD-OCT systems show a larger dynamic velocity range^[46].

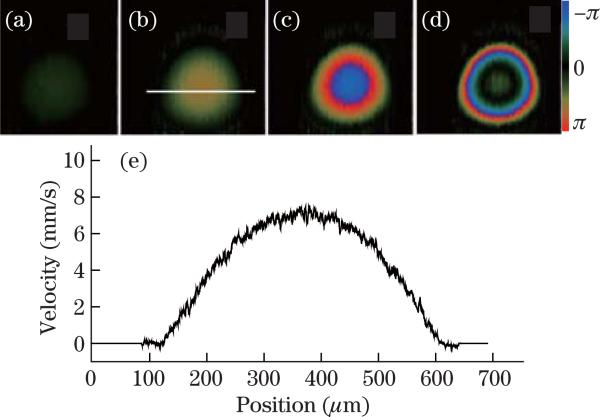
Figure 2 shows PR-D-OCT images of a flow phantom pumped by a syringe pump at different speeds. Figures 2(a)–(d) are PR-D-OCT images of the flow phantom pumped at, respectively, 0.1, 0.3, 0.6, and 1.1 μl/min. The system is a SS-FD-OCT system with an A-line rate of 50 kHz. It should be noted that the phase is wrapped in Figs. 2(c) and (d). The increase of Doppler frequency shift with the increase of syringe pumping speed can be clearly seen from the PR-D-OCT images. Figure 2(e) shows the velocity profile along a horizontal cross section passing through the center of the tube in Fig. 2(b). PR-D-OCT will enable quantitative analysis of the axial velocity profile.

Fig. 2.

PR-D-OCT images of a flow phantom which is pumped at, respectively, (a) 0.1, (b) 0.3, (c) 0.6, and (d) 1.1 μl/min. (e) Velocity profile along a horizontal cross section passing through the center of the tube in (b).

For PR-D-OCT, only the component of the velocity parallel to the incident optical beam direction can be measured. The Doppler frequency shift is related to the Doppler angle and the velocity of the sample (or moving particle in the sample). For Figs. 3(a)–(d), the Doppler angle was set at 90°, 87°, 84°, and 81°, respectively, and the syringe pump speed was kept constant. From Fig. 3, we can verify that the Doppler frequency shift (which is proportional to the phase changes) is related to the Doppler angle. As shown in Fig. 3(a), the Doppler frequency shift is close to zero when the Doppler angle is close to 90°. The Doppler frequency shift increases with the decrease of the Doppler angle (assuming that the Doppler angle is between 0° and 90°). When imaging the tissue in vivo, the Doppler angle is unknown in most cases and the actual absolute flow velocity cannot be measured directly with PR-D-OCT method. Several methods have been proposed to solve this problem. Davé et al. described a dual-channel method in which two probe beams were oriented at a precisely known relative angle that allows for Doppler-angle measurement^[47]. By introducing a glass plate midway into the OCT beam path, Ahn et al. divided the sample beam into several components, each with a different group delay and each providing a separate interferogram with its own effective Doppler angle^[48]. By combining the Doppler shift measured in each of these component interferograms, the flow velocity vector is fully determined. Meng et al. proposed a transit-time based method to ascertain the azimuth angle of a velocity vector, so that the 3D velocity vector can be quantified^[49]. The DV (or bandwidth) method has also been used to determine the Doppler angle and flow vector^[50,51]. For in vivo biomedical application, determining the Doppler angle from 3D orientation of a blood vessel has been demonstrated by several groups^[52–54].

Fig. 3.

PR-D-OCT images of the flow phantom at Doppler angle of (a) 90°, (b) 87°, (c) 84°, and (d) 81°.

3. Implementation and extension of D-OCT method

3.1 Phase-resolved Doppler method

To calculate the phase difference Δϕ in Eqs. (3) and (4), the algorithm derived from a cross-correlation algorithm have been shown to offer better performance and is usually preferred^[8,50,55]. In addition, averaging can be used to improve the SNR^[55]. The auto-correlation algorithm together with averaging can be described as

$$\Delta \varphi =\arctan \left\{\frac{\sum _{j=1}^J\sum _{z=1}^N[\mathrm{Im}\left(A_{j+1,z}\right)\mathrm{Re}\left(A_{j,z}\right)-\mathrm{Im}\left(A_{j,z}\right)\mathrm{Re}\left(A_{j+1,z}\right)]}{\sum _{j=1}^N\sum _{z=1}^N[\mathrm{Re}\left(A_{j+1,z}\right)\mathrm{Re}\left(A_{j,z}\right)-\mathrm{Im}\left(A_{j,z}\right)\mathrm{Im}\left(A_{j+1,z}\right)]}\right\},$$ (5)

where J is the number of A-lines that are averaged, N is the number of depth points that are averaged, and A_j,z is the complex data at the jth A scan and depth of z. The choice of J and N are dependent on application. Generally, a larger J and N will increase SNR, increase computing time, and decrease resolution.

In practice, the Doppler frequency produced by a moving target will produce a spectrum of Doppler frequencies or a series of frequency shifts instead of a single frequency. This spectrum broadening is attributed to several sources, such as the cone-geometrical focusing beam, Brownian motion, and speckle^[50]. The PR-D-OCT method gives the averaged Doppler frequency shift, which is usually displayed as color images. Positive and negative averaged frequency shifts are displayed in different colors, which provide quantitative information on the flow speed and flow direction.

Several other implementations of PR-D-OCT have been reported. A joint spectral and TD-OCT method was proposed that uses a set of time-dependent spectral fringe signals acquired^[56]. The fringes were analyzed by two independent Fourier transformations performed in time and optical frequency domains to map Doppler frequency shift with high sensitivity. However, this method requires high sampling density which limits the acquisition frame rate for real-time imaging.

3.2 Doppler variance (DV) method

The broadening of the Doppler spectrum can also be quantified with numerical methods and this method is named DV or Doppler standard deviation method^[18]. Brownian motion dominates the broadening of the Doppler spectrum at low flow speed, and probe-beam geometry dominates at high flow speed. In a DV image, the variance or the standard deviation of the Doppler frequency shift is displayed,which can be used to quantify Brownian motion or measure transverse flow^[18,50]. The DV has the benefit of being less sensitive to the pulsatile nature of the blood flow, less sensitive to the incident angle, and may provide better mapping of microvasculature. DV method may also be used to obtain the transverse flow velocity and determine the flow vector^[50]. Similar to the PR-D-OCT method, an autocorrelation algorithm with averaging is usually used to quantify the variance:

$${\sigma }^2=1-\frac{\mid \sum _{J=1}^J\sum _{z=1}^N\left(A_{j+1,z}{A}_{j,z}^{\ast }\right)\mid }{\frac{1}{2}\sum _{j=1}^J\sum _{z=1}^N({\mid A_{j+1,z}\mid }^2+{\mid A_{j,z}\mid }^2)},$$ (6)

where J is the number of A-lines that are averaged and N is the number of depth points that are averaged. Equation (6) involves the phase terms and we also call these algorithms the phase-resolved DV (PRDV).

There are several variations of the DV method for mapping vascular network, including methods using the power of the Doppler shift (|Δϕ|²) image^[27,57] and the variance of phase difference $(\mathrm{Var}\left(\Delta \varphi \right)=\overline{{(\Delta \varphi -\overline{\Delta \varphi })}^2})$^[58]. Although the quantitative flow and directions cannot be determined with such methods, these methods may be better for the mapping and visualization of blood vessel locations.

3.3 Intensity-based DV method

Methods that are dependent on the intensity or amplitude fluctuation can also be used for mapping vascular network. Barton et al. proposed a method based on the speckle of conventional amplitude OCT images^[24]. Mariampillai et al. used the intensity variance along the B-scan frames to image blood vessels^[25]. The inter-frame variance is calculated from the structural OCT signal by^[25]

$$S{V}_{ijk}=\frac{1}{N}\sum _{i=1}^N{\left(I_{i,j,z}-\frac{1}{N}\sum _{i=1}^N{I}_{i,j,z}\right)}^2,$$ (7)

where N is the number of frames used in the variance calculation and i, j, and z are indices for the frame, transverse, and axial pixels, respectively. The algorithm of the speckle variance method is intuitive and simple to implement. However, it suffers strongly from blood vessel shadowing effect^[59]. Srinivasan et al. have shown that with a scan protocol that samples the same transverse location twice per volume, it is possible to map the blood vessels with the signal magnitude difference between two frames acquired at the same transverse location^[60]. Instead of using the intensity variance as shown in Eq.(7), a logarithmic intensity variance and differential logarithmic intensity variance are proposed by Motaghiannezam et al.^[26]. Jonathan et al. used a 2D correlation map based on the OCT intensity images for blood vessel extraction^[30]. Generally, these methods use different algorithms to calculate the intensity difference between adjacent B-scan frames and detect the vessel flow in biological tissue.

Jia et al. developed a split-spectrum amplitude-decorrelation angiography method^[31]. The full OCT spectrum is split into several narrower bands and these bands are used to generate OCT images of reduced axial resolution and reduced susceptibility to axial motion noise. Decorrelation between consecutive B-scans was computed using the spectral bands separately and then averaged. This decorrelation is used to detect flow. This method splits the spectrum to generate several images in a single B-scan and eventually increase the computation time.

Recently, we proposed an intensity-based method that uses an algorithm derived from a modified PRDV algorithm^[22]. PRDV is not sensitive to gradient phase changes and can be used without bulk-motion-correction for in vivo imaging^[22]. In the phase instable situation where there is phase jumping or jittering between adjacent A-lines, the variance value will be affected greatly by the abrupt change in phase terms. The phase instability may produce artifacts, and the performance of the PRDV method will be degraded. An intensity based DV (IBDV) method can minimize the artifact from the phase instability^{[24,25,30,31,59,61]}. The IBDV can be calculated by^[61]

$${\sigma }^2=\left[1-\frac{\sum _{j=1}^J\sum _{z=1}^J\mid A_{j+1,z}{A}_{j,z}^{\ast }\mid }{\frac{1}{2}\sum _{j=1}^J\sum _{z=1}^N{({\mid A_{j+1,z}\mid }^2+\mid A_{j,z})\mid }^2}\right].$$ (8)

Similar to the speckle variance method, the IBDV method also suffers from the blood vessel shadowing effect.

In addition to the above methods, there is a power Doppler mode that displays the flow power signal by filtering out the signal from stationary tissue^[23]. In FD-OCT systems, the filtering process may be realized with either hardware-based or software-based schemes. Wang et al. developed a method called OMAG^[62]. In OMAG, a Doppler frequency is introduced in the lateral beam scanning direction (B-scan) so that the moving and static scattering components within the sample are separated. The Doppler frequency may be introduced by either the reference mirror mounted on a linear piezo translation stage or by offsetting the sample arm beam from the scanning galvomirror pivot. Yuan et al. proposed a digital frequency ramping method by numerically introducing a phase shift into the original spectral interferometric signal using a Hilbert transform^[63]. Tao et al. proposed single-pass flow imaging spectral domain OCT (SP-FI-OCT) with a modified Hilbert transform algorithm to separate moving and non-moving scatters and enable volumetric bidirectional flow mapping^[64]. Figure 4 shows the flow chart for the SP-FI-OCT signal processing. Generally, the processing procedures of these methods require lateral Fourier transform of the raw fringe for each wavelength (row by row). A bandpass filter is then applied and the data set is transformed back using inverse Fourier transform. The filtered data set is then Fourier transformed for each location (column by column) to get the structure and/or flow information. The processing procedures are more complex and the overall processing time increases. In addition, the sample movement induced artifacts have to be corrected using the phase-resolved method in order to get high quality images.

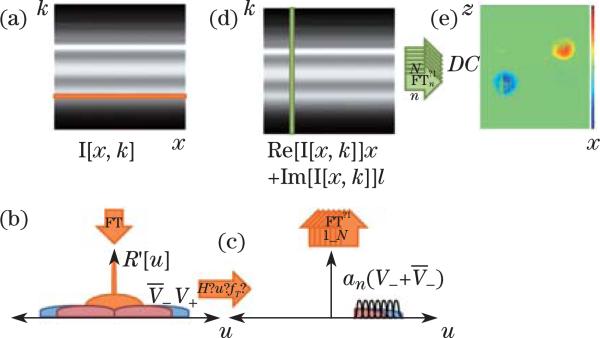
Fig. 4.

Flow chart of velocity-resolved SP-FI-OCT signal processing. (a) Lateral Fourier transform (FT) of raw fringes yields (b) spatial frequency of stationary scatterers centered around DC, and spatial frequency of moving scatterers shifted by their respective Doppler frequencies. (c) Applying a frequency-shifted Heaviside step function, spatial frequency windowing, and inverse Fourier transforming each frequency range recreates (d) the analytic interferometric signal. (e) Spectral inverse FT of the analytic interferometric signal maps depth-solved reflectivities of moving scatterers for each corresponding velocity range into a data cube. Bidirectional flow is mapped onto opposite image half-planes^[64].

3.4 Time interval ΔT and sensitivity

From Eqs. (3) and (4), it should be noted that the time interval plays an important role in deciding the velocity sensitivity of the D-OCT system. Assuming the minimum resolvable phase difference of a D-OCT system is 5 mrad, a ΔT of 1 ms (corresponding to an A-line rate of 1 kHz) will allow a velocity sensitivity of 0.5 μm/s. However, if ΔT is 10 μs (corresponding to an A-line rate of 100 kHz), the velocity sensitivity of the system is dropped to 50 μm/s. With advances in technology, the A-line rate of OCT systems has increased by several orders of magnitude. The increase of the A-line rate means a decrease of D-OCT velocity sensitivity if the algorithm is used among the adjacent A-lines. Therefore, increasing the time interval ΔT will increase the D-OCT velocity sensitivity. Our recent works have shown that increasing the time interval can also improve the velocity sensitivity of IBDV and PRDV methods^[65,66]. With a flow phantom, the effects of the time difference on the PR-D-OCT, PRDV, and IBDV were investigated with a SS-FD-OCT at A-line rate of 50 kHz. One frame of data with a very high sampling density level (ratio of beam spot size over A-line separations is about 134) was acquired and part of the acquired data was processed to obtain results at different time intervals. For example, for a system with adjacent A-line time difference ΔT , to test the time interval of 2ΔT , we took data points from all the even (or odd) number A-lines in the original data set to form a new data set. The algorithm was then applied to this new data set to obtain an IBDV image with a neighboring A-line time interval of 2ΔT. Accordingly, to test the algorithm with a neighboring A-line time interval of 3ΔT, every third A-line was extracted from the original data set to form a new data set and the IBDV algorithm was applied to the new data set. Figure 5 shows the OCT images of a flow phantom processed with the scheme from one single frame dataset of 9216 A-lines. Figures 5(a)–(d) are the PR-D-OCT images processed with time intervals of 20, 60, 120, and 200 μs, respectively. Figures 5(e)–(h) are the PRDV images processed with time intervals of 20, 60, 120, and 200 μs, respectively. Figures 5(i)–(l) are the IBDV images processed with time intervals of 20, 60, 120, and 200 μs, respectively. Clearly, the three methods are all sensitive to the time interval. A longer time interval increases the velocity sensitivity of all three methods.

Fig. 5.

PR-D-OCT images processed with time intervals of, respectively, (a) 20, (b) 60, (c) 120, and (d) 200 μs. PRDV images processed with time intervals of, respectively, (e) 20, (f) 60, (g) 120, and (h) 200 μs. IBDV images processed with time intervals of, respectively, (i) 20, (j) 60, (k) 120, and (l) 200 μs.

Although reducing the A-line rate is an effective way to increase the velocity sensitivity of D-OCT, a faster A-line rate is always preferred, especially for in vivo applications. One scheme to increase the ΔT while still maintaining the A-line rate is to apply the algorithm along the slowing scanning (B-scan) direction or by using a dual beam setup^[26,66–68]. Although increasing velocity sensitivity by using phase-resolved algorithms between adjacent frames or along the slow scanning direction without sacrificing system speed was proposed in 2000^[8], recent development of high speed FD-OCT makes it viable to be implemented in D-OCT systems. Several different methods using this inter-frame scheme have shown the capability to image the Brownian motion^[66,69]. We have used the inter-frame scheme to image the microvasculature of mouse brain with high sensitivity. Figure 6 shows the in vivo OCT imaging of a mouse brain with intact skull using this inter-frame processing scheme^[65]. Figure 6(a) is the OCT structure image. Figures 6(b) and (c) are the inter-frame PRDV (IF-PRDV) and inter-frame PR-D-OCT (IF-PR-D-OCT) images. The bulk phases induced by the sample miniature movement (the vertical lines in Figs. 6(b) and (c)) overwhelm the images, and it is hard to identify the vessels from the images. For phase-resolved methods, advanced algorithms to remove the bulk phase are necessary for high quality images^[22,55]. Figures 6(e) and (f) show the images with bulk phase removed. Figure 6(d) shows the inter-frame IBDV (IF-IBDV) image without applying any bulk motion correction method. All the methods are able to image the vessels with high sensitivity.

Fig. 6.

In vivo OCT imaging of mouse brain with intact skull: (a) OCT image; (b) IF-PRDV image without bulk phase removal; (c) IF-PR-D-OCT image without bulk phase removal; (d) IF-IBDV image; (e) IF-PRDV image with bulk phase removal; (f) IF-PR-D-OCT image with bulk phase removal^[65]. Scale bar: 1 mm.

4. Application

Due to its high spatial resolution and velocity sensitivity, D-OCT has a number of applications in biomedical research and clinical medicine. D-OCT was initially developed for the imaging of blood vessels and characterization of flow parameters. D-OCT has been demonstrated for imaging ocular blood flow, mapping cortical hemo-dynamics for brain research, drug screening, monitoring changes in image tissue morphology and hemodynamics following pharmacological intervention and photodynamic therapy, evaluating the efficacy of laser treatment in port wine stain (PWS) patients, assessing the depth of burn wounds, imaging tumor microenvironment, and quantifying cerebral blood flow^{[8,9,19,70–75]}. Furthermore, the applications of D-OCT have been extended to other fields beyond vasculature imaging and flow characterization. We have demonstrated the application of D-OCT for quantifying vocal folds vibration^[21]. D-OCT can also be used to analyze a tissue's local or global micromovement^[76]. In OCE, the D-OCT method is used to measure the tissue micromovement induced by external load or force to extract the elastic properties of the tissue. We will discuss several recent applications of D-OCT from our group.

4.1 Quantifying the flow characteristics in micro-channel

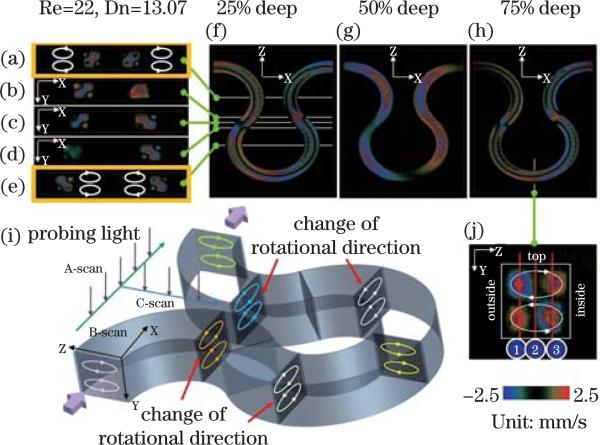
D-OCT can provide cross-sectional imaging of channel geometry and flow velocity within a microfluidic channel with a spatial resolution on the order of a micrometer and a velocity sensitivity of 1 μm/s. D-OCT has been used to quantify the secondary flow, which plays a critical role in mixing in micro-channels^[77]. A Y-branch device of a meandering micro-channel with a square cross section is shown in Fig. 7. An aqueous suspension of polystyrene beads with a diameter of 0.2 μm and concentration of 20.5 mg/cc was injected into both inlets of the device. The device was imaged with a spectrometer-based D-OCT system. The probe beam of the D-OCT was adjusted to be approximately perpendicular to the plane of the micro-channel (x – z plane) so that only the secondary flow along the y-direction will contribute to the Doppler signal^[77]. The y-component of the secondary flow velocity V_y(x, y, z) was imaged and quantified with D-OCT. Counter rotating vortices and alternating flow direction of the secondary flow at different depths in the x – z plane can be clearly visualized. This result clearly demonstrates that D-OCT can be used to image and quantify secondary flow.

Fig. 7.

3D images of secondary flow along the out-of-plane velocity (y direction). The out-of-plane velocity fields are sectioned by (a)–(e) x-y planes,(f)–(h) x-z planes, and (j) y-z plane. The velocity field shows a pair of counter rotating vortices ((a)–(e)). Since the curvature is alternating, the rotational direction of the vortices is also alternating ((a)–(e)). Alternating flow direction of the secondary flow at different depths in the X-Z plane can be clearly visualized ((f)–(h))^[77].

4.2 In vivo imaging of human retinal blood vessel and vascular network

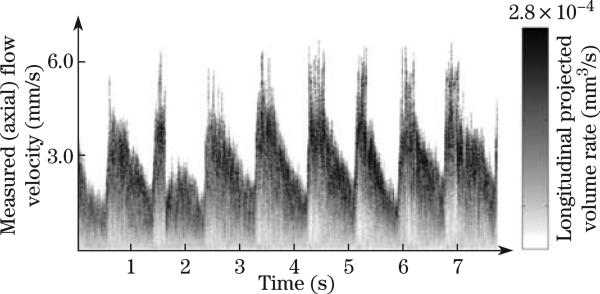
D-OCT has been used to quantify blood velocity profiles in human retina blood vessels, determine vessel boundaries, and analyze time-dependent bi-directional flow dynamics in retinal artery-vein pairs^{[17,19,22,33,53,58,78–82]}. However, the blood flow is pulsatile, and the flow changes within the cardiac cycle. The development of high speed Fourier domain D-OCT allows fast scanning of a single blood vessel multiple times over a cardiac cycle. Spectral Doppler waveforms can be obtained by performing spectral analysis of the time sequences of Doppler images^[81]. In this method, repeated D-OCT scans across a few selected vessels were performed to get Doppler flow maps of a certain time period, which provides an accurate estimation of 2D flow dynamics across the vessels. Spectral Doppler analysis of continuous Doppler images demonstrates how velocity components and longitudinally projected flow-volume-rate change over time for scatters within the imaging volume using spectral Doppler waveforms. Various velocity envelope curves can be derived from spectral Doppler waveforms and used to extract the corresponding pulsatility index, resistance index (RI), and several other indices that can provide interpretable Doppler-angle-independent information needed to quantify the pulsatile nature of blood flow. Figure 8 shows spectral Doppler waveforms for a retinal blood vessel^[81]. The D-OCT imaging and quantification of human retina and choroid microvascular network provide important information for the diagnosis and management of ocular diseases, such as glaucoma, diabetic retinopathy, and age-related macular degeneration^{[17,19,22,33,53,58,78–82]}.

Fig. 8.

Spectral Doppler waveforms that show the change of axial velocity and flow-volume-rate within a time span of 7.9 s (the right grayscale bar is used to represent the volume-rate contribution for a given velocity bin)^[81].

4.3 D-OCT images of brain hemodynamics

D-OCT has also been used to image brain hemodynamics in the cerebral cortex of the brain. The cerebral cortex is generally believed to be composed of functional units, called “columns,” which are arranged in clusters perpendicular to the surface of the cortex^[83]. Alterations in the brain's blood flow are known to be coupled to regions of neuronal activity^[83]. Recent development of D-OCT with inter-frame scheme has greatly improved the velocity sensitivity, which makes it possible to map microvasculature of brain cortex. These D-OCT results have been verified with fluorescence imaging, multiphoton microscopic imaging, laser speckle imaging, and photographic imaging^{[27,59,66,75,84]}. The benefits of using D-OCT from microvaculature imaging include depth-resolved, labeling free, and high sensitivity. Figure 9(a) shows the en-face maximum intensity projection (MIP) microvasculature of mouse cerebral cortex with intact skull. Figure 9(b) shows the en-face MIP microvasculature of rat cerebral cortex with thinned skull. These images are obtained with a SS-FD-OCT system with an A-line rate of 50 kHz and are processed with the IF-IBDV method. D-OCT shows great promise in brain research for imaging the entire depth of the cortex. D-OCT can be used to measure stimulus-induced changes in blood flow^[73], and to evaluate and monitor brain ischemia and trauma^[20,85].

Fig. 9.

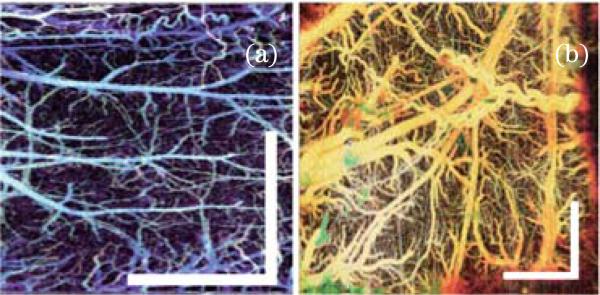
D-OCT images of microvasculatures of (a) mouse cerebral cortex and (b) rat cerebral cortex. Scale bar: 1 mm.

4.4 D-OCT images of skin microcirculation

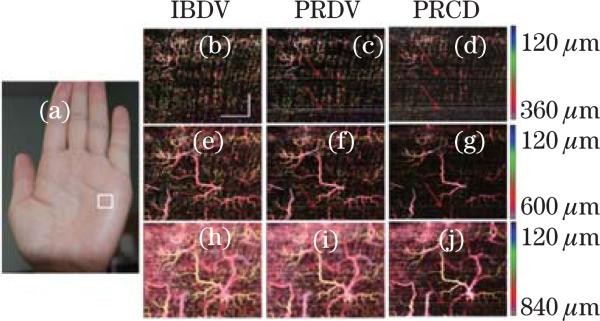
Many skin diseases have a vascular etiology or component. For example, the superficial dermal plexus alone is particularly affected by the presence of disease (e.g., psoriasis, eczema, scleroderma), malformation (e.g., port-wine stain, hemangioma, telangiectasia), or trauma (e.g., irritation, wound, burn). In these situations, it would be most advantageous to the clinician if blood flow and structural features could be isolated and probed at user-specified discrete spatial locations in either the superficial or deep dermis. Figure 10 shows the results of depth-resolved microvasculature for human palm skin^[65]. Figure 10(a) shows a photograph of the imaged region. Figures 10(b)–(j) show the depth-resolved en-face MIP microvasculature images. These images are processed using IF-PR-D-OCT, IF-PRDV, and IF-IBDV and are from the same acquired dataset. All methods are able to image high resolution vascular images with high sensitivity. In the superficial regions (120–360 μm), the capillary loops, which show up as bright dots in the en-face MIP images, are clearly visible (Figs. 10(b)–(d)). With an increase in depth, several miniature vessel branches are also clear in the images (Figs. 10(e)–(g)). The vessel diameter increases in deeper regions (Figs. 10(h)–(j)). The results match well with the skin vascular anatomy, which shows small capillary loops coming up from the deeper layer of arterioles and venules. However, there are minor differences among these images processed with different methods. There are a few horizontal lines in both the IF-PRDV and IF-PR-D-OCT images as indicated by the arrows (Figs. 10(c), (d), (f), (g), and (j)). However, these horizontal lines are not shown in the IF-IBDV images. The high spatial resolution and high velocity sensitivity of D-OCT has been used clinically for in vivo imaging and monitoring the efficacy of laser treatment of port-wine stain^[8,10,18].

Fig. 10.

(Color online) En-face MIP view image of human palm skin. (a) Photograph of the imaging area (in the white rectangle). En-face MIP view of IF-IBDV images for depths of (b) 120–360, (e) 120–600, and (h) 120–840 μm; En-face MIP view of IF-PRDV images for depths of (c) 120–360, (f) 120–600, and (i) 120–840 μm; En-face MIP view of IF-PR-D-OCT images for depths of (d) 120–360, (g) 120–600, and (j) 120–840 μm^[45]. Scale bar: 1 mm.

4.5 Imaging the vocal fold vibration

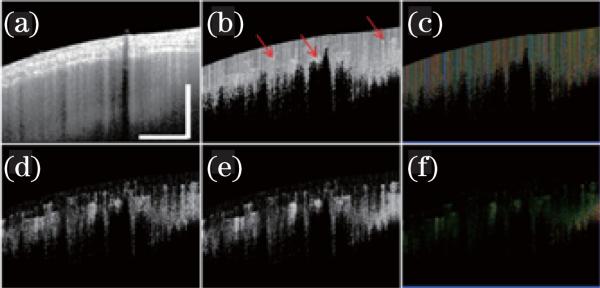
Vocal fold vibration is vital in phonation and the correct pitch of speech. We have recently utilized D-OCT for functional imaging of vibrating vocal folds^[86]. Figure 11 shows the OCT images of an ex-vivo vibration swine vocal fold^[21]. The system was a SS-FD-OCT system with an A-line rate of 100 kHz. Functional information, such as vibration frequency and vibration amplitude, can be obtained by analyzing the tissue surface during vibration^[21]. The axial direction velocity distribution in the cross-sectional images of the vibrating vocal folds was obtained with the D-OCT image (Fig. 11(b)). The quantitative transverse direction velocity distribution in the cross-sectional image was obtained with the DV image (Fig. 11(c)) In Fig. 11(b), a quasi-periodic pattern was caused by phase wrapping, and the phase difference is wrapped between –π and π. However, phase wrapped images also give qualitative information regarding acceleration. Quantitative analysis of the D-OCT image will provide more valuable information. The velocity distribution in the up slope and that of the down slope are different. In the down slope, the velocity distribution is more like a sinusoidal function. In addition, the velocity changes faster at the peak and valley regions and slower at the waist regions. Consequently, the acceleration is larger at the peak and valley regions and smaller at the waist regions. However, the acceleration in the up slope is more uniform than that in the down slope, and the acceleration at the peak region is larger than that at the valley region.

Fig. 11.

OCT images of a vibrating vocal fold with a frequency of 94.3 Hz. (a) B-mode OCT structure image; (b) B-mode PRCD OCT image; (c) B-mode PRDV image^[21]. Scale bar: 500 μm.

4.6 PR-D-OCT for high speed OCE

Many diseases involve changes in the biomechanical properties of tissue. Cancerous tumors, for example, usually appear as hard nodules, and their stiffness differs from the surrounding tissue. A calcified plaque is markedly stiffer than the micro environment around it. Therefore, tissue mechanical properties provide critical information for diagnosis of cancers and assessment of the vulnerability of plaques^[87–91].

OCE uses OCT to map the mechanical property of the tissue. In OCE, an external force (or load) is usually applied to the sample to excite tissues for a certain deformation. The tissue deformation is then quantified with algorithms. The first demonstration of OCE utilized a tissue compressor consisting of a piezoelectric actuator with a circular glass cover slip glued to its ring-shaped head^[92]. To quantify the deformation, the author used the normalized cross correlation of the OCT images of the pre-deformed and deformed sample within a pre-defined window and then estimated the displacement from the maximum of the resultant cross-correlation function. Recently, a cross correlation OCT using a similar algorithm was also developed for the imaging of blood vessels^[30]. Doppler OCE, which used a phase-resolved Doppler algorithm, was developed to image tissue movements, strain rates, and strains of soft tissue in real time^[76,93]. The applications of OCE have been demonstrated in ophthalmology, dermatology, cardiology, and oncology^[94]. However, adoption of these methods to in vivo real-time imaging is limited by low cycling frequency of external forces.

Recently, our group has developed a phase-resolved acoustic radiation force OCE (PR-ARF-OCE) method to evaluate the elastic properties of tissue^[95]. This method utilizes chirped ARF to produce excitation along the sample's axial direction and PR-D-OCT to measure the vibration of the sample. ARF-OCE has the advantage of combining high speed excitation force with high sensitivity displacement detection of PR-D-OCT. PR-ARF-OCE has been demonstrated to be able to determine the relative Young's modulus in various phantoms and human coronary artery tissues^[95]. Figure 12 shows ex vivo 3D images of atherosclerotic human coronary artery obtained with PR-ARF-OCE. An OCT intensity image, shown in Fig. 12(a), provides a general morphological view of the tissue, but no obvious evidence of atherosclerosis was found. However, an ARF-OCE image (Fig. 12(b)) shows a strong vibration phase contrast between normal and plaque regions. The red-colored region indicated by the blue arrow in the ARF-OCE image is characterized by smaller phase change and less vibration, and therefore represents stiffer tissue such as plaques. The stronger vibration representing softer tissue (dark area) is indicated by yellow arrows. In this ARF-OCE image, the stiffer tissue, corresponding to the atherosclerotic lesion in the blue box in the histological image (Fig. 12(c)), is clearly distinguishable from the softer (normal) tissue area. The transition between plaque and normal regions appears orange in color (indicated by the red arrow) and is characterized by intermediate elasticity. This preliminary result clearly shows that the ARF-OCE method has great potential for characterizing tissue mechanical properties quantitatively and thereby delineating diseased tissue from normal tissue. The high-speed and high-spatial-resolution PR-ARF-OCE has the potential to measure and quantify in vivo tissue elasticity in real-time.

Fig. 12.

(Color online) (a) OCT structural, (b) ARF-OCE phase images of a human cadaver coronary artery under 500-Hz, 350-mV AM modulated excitation; an atherosclerotic lesion was identified as the red region corresponding to the blue box in (c). (c) Histological image. (d) Close-up view of the atherosclerotic lesion^[95]. Scale bars: 1 mm.

5. Limitations, challenges, and future direction

Since our first demonstration of D-OCT in 1997, significant advances have been made to improve velocity sensitivity and imaging speed. The development of Fourier domain PR-D-OCT has enabled imaging and mapping of microvasculature down to the capillary level. However, improving the velocity sensitivity by increasing the time interval usually requires a decrease of system speed or use of special scanning protocols. In addition, due to phase wrapping and phase washout, quantitative flow information can only be obtained for flow in a certain velocity range. To extend the quantifiable flow velocity range, repeated multiple scanning protocols with different adjacent A-line time intervals or a dual-beam setup have been demonstrated. Although effective, these schemes either increase the total imaging time or increase the system complexity. The further development of new system/algorithm that enables us to quantify flow with full velocity dynamic range and fast imaging speed is needed.

D-OCT is a rapidly developing imaging technology. New developments in all components of an OCT system can be integrated into a D-OCT system, including new light sources for high resolution and high speed, new scanning probes for endoscopic imaging, and new processing algorithms. Although currently it is possible to have D-OCT imaging processing and display in real-time, further increases in imaging speed of D-OCT will likely require the development of a more efficient computational algorithm and faster processor. Parallel processing based on multiple CPUs and GPUs will enable real-time imaging processing and display of D-OCT in the megahertz A-line speed.

Furthermore, we anticipate that D-OCT will be extended to elastography and other applications where nanometer resolution of the phase-resolved method is required. For example, PR-D-OCT can be used for imaging nano-particles based on thermal expansion^[86,96]. Finally, multimodal imaging systems which combine D-OCT with other imaging modalities is one of the most important future research directions. Integration of D-OCT with other functional OCT, such as polarization sensitive OCT, spectroscopic OCT, and second harmonic OCT, can greatly enhance the potential applications of this technology. Given the noninvasive nature and exceptionally high spatial resolution and velocity sensitivity, functional OCT that can simultaneously provide tissue structure, blood perfusion, birefringence, and other physiological information has great potential for basic biomedical research and clinical medicine^[72,97].