Abstract
With the development of next-generation sequencing technology, there is a great demand for powerful statistical methods to detect rare variants (minor allele frequencies (MAFs)<1%) associated with diseases. Testing for each variant site individually is known to be underpowered, and therefore many methods have been proposed to test for the association of a group of variants with phenotypes, by pooling signals of the variants in a chromosomal region. However, this pooling strategy inevitably leads to the inclusion of a large proportion of neutral variants, which may compromise the power of association tests. To address this issue, we extend the 
-MidP method (Cheung et al., 2012, Genet Epidemiol 36: 675–685) and propose an approach (named ‘adaptive combination of P-values for rare variant association testing’, abbreviated as ‘ADA’) that adaptively combines per-site P-values with the weights based on MAFs. Before combining P-values, we first imposed a truncation threshold upon the per-site P-values, to guard against the noise caused by the inclusion of neutral variants. This ADA method is shown to outperform popular burden tests and non-burden tests under many scenarios. ADA is recommended for next-generation sequencing data analysis where many neutral variants may be included in a functional region.
Introduction
Next-generation sequencing acts as a new approach to explore the genetic basis of complex human diseases [1]. With this new technology, we are able to identify rare causal variants (minor allele frequency (MAF)<1%) that are not genotyped in genome-wide association studies (GWAS) but are actually responsible for part of the heritability of complex diseases. However, the power of an association test is largely compromised by the low frequencies of rare causal variants. To increase the power of an association test, many methods have been proposed to test for the collective effect of a group of variants in a chromosomal region [2]–[11]. These methods can be categorized as burden tests and non-burden tests.
Burden tests pool signals of multiple rare variants within a functional unit, such as a candidate gene, and then test for the association between the pooled signal (usually called “genetic score”) and the phenotype [2]–[5], [12]. In the Combined Multivariate and Collapsing (referred to as “CMC”) method, a subject's genetic score is defined as 1 if he/she has at least one rare variant in the gene and 0 otherwise [2]. The weighted-sum approach (referred to as “WS”) sums up the variant counts that are inversely weighted by the standard deviations of the variant frequencies [3]. Morris and Zeggini proposed to construct a genetic score by accumulating the variant counts in a functional unit (say, a gene or a pathway) [4], which was a variant of the CMC method. If only the counts of variants with frequencies smaller than 5% (or 1%) are aggregated as the genetic score, the test is referred to as “T5” (or “T1”). The threshold to discriminate rare variants from common variants is crucial, but the optimal threshold varies with the underlying genetic architecture and changes across studies [12]. The variable threshold (referred to as “VT”) approach was therefore proposed without a preset threshold. Instead, it searches for the optimal threshold that maximizes the difference between trait distributions for subjects with and without rare variants [5]. The above methods (including CMC, T1, T5, WS, and VT) are categorized as “burden tests”. These burden tests are more powerful when rare causal variants in a region have effects on the phenotype in the same direction, i.e., all are deleterious or all are protective [13].
On the other hand, non-burden tests, such as the so-called C-alpha test [9] or the sequence kernel association test (SKAT) [7] based on a kernel machine regression framework, are more robust to the inclusion of causal variants with disparate or even opposite effects on phenotype (we consider SKAT as a representative method of the non-burden tests, because it is a generalization of the C-alpha test). However, the non-burden tests such as SKAT can be less powerful than the burden tests if a large proportion of rare variants are associated with the phenotype in the same direction [13]. Because the underlying genetic function of a region is usually unknown, choosing an ideal statistical test (burden tests or SKAT) in advance is impossible. To develop a powerful test that is also robust to the directions of effects of rare variants, Lee et al. [8] have proposed an optimal test to combine SKAT [7] and the burden tests [2]–[5], [12]. This optimal test (referred to as “SKAT-O”) has been shown to outperform the burden tests and SKAT in a wide range of scenarios [8].
Both the burden tests and the non-burden tests suffer from power loss with the inclusion of neutral variants. A preferable method to analyze next-generation sequencing data should have the robustness to this type of noise. To this end, Cheung et al. [14] proposed a 
-MidP method that combines P-values of individual variants with the weighting scheme proposed by Madsen and Browning [3]. To guard against the noise caused by neutral variants, the 
-MidP method excludes the variants with equal rare-variant counts in cases and in controls. Furthermore, 
-MidP uses the Fisher's combination of P-values [15] on individual variants with the Madsen and Browning's [3] weighting scheme. This method has been shown to be more powerful than many existing methods [3]–[7], [9], [16], [17], when both deleterious and protective variants, or a large proportion of neutral variants, are present in a region [14].
Instead of testing for the association of a genetic score (some linear combination of variant counts) with the phenotype, 
-MidP, inspired by the Fisher's combination of P-values, can take the significance of each variant site into account. To simplify, in the following small example we discuss the Fisher's combination method (
-MidP further uses the Madsen and Browning's [3] weighting scheme to facilitate the discovery of rare causal variants). Suppose there are K variants in a region of interest, the P-values of the K single-variant tests are combined with the Fisher's statistic: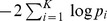 
[15]. If there is a causal variant with a P-value of 0.05, it contributes 
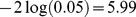to the Fisher's statistic. However, the contribution to the Fisher's statistic will be only 
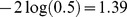for a neutral variant with a P-value of 0.5. Because the P-values of causal variants are usually smaller than those of neutral variants, the contribution from causal variants to the Fisher's statistic is usually more prominent than that of neutral variants. Thus, different from testing the genetic score after summing variant counts (including causal variants and neutral variants), combining P-values after association testing can strengthen the association signal and guard against the noise caused by neutral variants.
To more effectively guard against the noise caused by neutral variants, variants with P-values larger than a threshold (they are more likely to be neutral) may be truncated (see [18] for the methodology and [19] for its application). However, the P-value truncation threshold of 0.05 (used in [19]) may be too stringent, because testing for each rare variant is usually underpowered [2], [20]–[22]. For rare variants detection, there is no general rule to choose a more “suitable” P-value truncation threshold. To address this issue, we here propose to determine the truncation threshold adaptively. Therefore, this method is termed ADA (full name: adaptive combination of P-values for rare variant association testing), which is inspired by the adaptive combination of P-values for pathway analysis in GWAS [23]. Instead of fixing a P-value truncation threshold, the proposed method allows multiple candidate truncation thresholds (say, 0.10, 0.11, 0.12, …, 0.20) and works out the optimal threshold for a given data set. The significance of our test is quantified with permutations. Comprehensive simulation studies indicate that the ADA method has a higher power than 
-MidP
[14]. It also outperforms some popular approaches, including the burden tests such as T1, T5, WS, VT mentioned above, SKAT
[7], and SKAT-O
[8]. As an application, the data set from Dallas Heart Study [24], [25] is analyzed with the proposed method.
Materials and Methods
Suppose there are K variants in a region of interest, and the P-values of testing for the associations of individual variants with the disease status are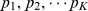 
, respectively. Without loss of generality, although we here focus on binary traits, the proposed method can be applied to continuous traits as well. In rare variants detection for binary traits, 
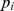's are commonly obtained by the Fisher's exact test [14], [26]. Suppose we consider J candidate truncation thresholds on per-site P-values, 
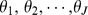. We term the sites with larger variant frequencies in cases than in controls “deleterious-inclined variant sites”. Among the K sites, the significance score of the deleterious-inclined variant sites is
 |
(1) |
where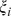 
is an indicator variable coded as 1 if the ith site is deleterious-inclined and 0 otherwise, 
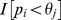is an indicator variable coded as 1 if the ith site has a P-value smaller than 
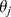(the jth truncation threshold) and 0 otherwise, and 
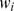is a weight given to the ith site. Following Madsen and Browning [3], we specify 
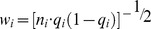, where 
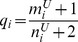is the frequency for variant i in the unaffected individuals, 
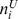is the number of unaffected individuals genotyped for variant i, and 
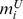is the number of mutant alleles observed for variant i in the unaffected individuals [3]. We recommend using J = 11 candidate truncation thresholds, and we specify 
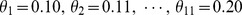throughout this study (we will discuss the selection of candidate truncation thresholds in the Discussion section).
On the other hand, we term the sites with larger variant frequencies in controls than in cases “protective-inclined variant sites”. Among the K sites, the significance score of the protective-inclined variant sites is
 |
(2) |
where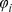 
is an indicator variable coded as 1 if the ith site is protective-inclined and 0 otherwise. From Equations (1) and (2), we obtain the significance score accumulated by deleterious-inclined variants (
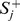) and that accumulated by protective-inclined variants (
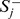), respectively. A test statistic regardless of the effect directions (deleterious or protective) is 
.
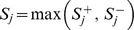Because variant sites within a functional region are usually not independent, we need permutations to obtain the P-value of the observed statistic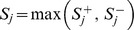 
, for j = 1, …, J. For the bth permutation (
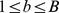), we randomly shuffle the case/control status and obtain 
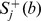and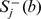 
according to Equations (1) and (2). Then, we obtain the statistic 
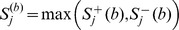, for j = 1, …, J.
With a total of B permutations, we can estimate the P-value of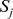 
for the observed sample as 
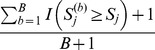, for each truncation threshold (j = 1, …, J). The P-value of 
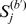for the 
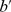th permutation is estimated by 
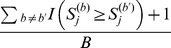, for j = 1, …, J and 
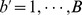. We can then find the minimum P-value 
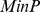across the J candidate truncation thresholds for the observed sample, and the minimum P-value 
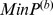for the bth permuted samples (b = 1,…, B). For the observed and permuted samples, 
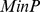and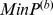 
(b = 1,…, B) are P-values obtained from the “optimal” truncation thresholds that yield the most significant results (or, the minimum P-values) across candidate truncation thresholds. These “optimal” thresholds may vary across permuted samples, in order to preserve the validity of the proposed method. We then compare 
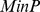with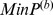 
(b = 1,…, B) to assess the significance of the observed sample. The “adjusted P-value” is calculated by 
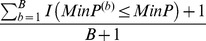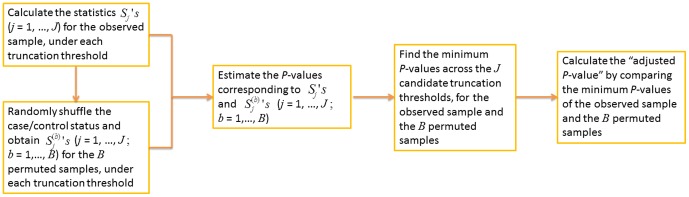
. This method is referred to as “ADA”, because the per-site P-values of variant sites are combined adaptively. Figure 1 is a workflow diagram of the ADA method.
Figure 1. The workflow diagram of the ADA method.
Simulation Study
With the Cosi program [27], we first generated 200 data sets, each containing 10,000 chromosomes of 1 Mb regions. The Cosi program is based on the coalescent population genetic model [28] and is widely used to simulate human genome sequences. The chromosomes were generated according to the linkage disequilibrium patterns of the HapMap CEU (Utah residents with ancestry from northern and western Europe) samples. We randomly specified 25% of the variants with population MAF<1% to be causal variants. A region containing d causal variants was randomly selected as the causal region, where d = 3, 5, 10, 15, or 20. On average, a causal region spanned ∼3.6, ∼6.4, ∼12.8, ∼19.2, and ∼25.6 kb, for d = 3, 5, 10, 15, and 20, respectively. The numbers of neutral variants were ∼60, ∼100, ∼200, ∼300, ∼400, for the regions spanning ∼3.6, ∼6.4, ∼12.8, ∼19.2, and ∼25.6 kb, respectively. Across the 200 simulated data sets, the proportions of causal variants among all non-synonymous variants ranged from ∼4% to ∼8%. We randomly assigned risk % of the d causal variants as deleterious variants, and let the remaining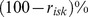 
causal variants be protective variants. The value of risk was set at 5, 20, 50, 80, and 100, respectively. In this way, we considered the simulation settings with mixtures of deleterious and protective variants. The population attributable risk (PAR) of each causal variant was specified at 0%, 0.1%, …, 0.5%, respectively.
Following the simulation setting of previous studies [3], [29]–[31], the genotype relative risk (GRR) of the jth causal variant is:
 |
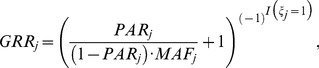(3) |
where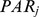 
and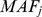 
are the PAR and the population MAF of that variant, respectively. The indicator function 
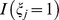is 1 if the jth causal variant is protective, and is 0 if deleterious. Figure S1 shows the distributions of population MAFs and GRRs of the causal variants in our 200 simulated data sets. Because we focused on the detection of rare causal variants, the population MAFs of the causal variants were all smaller than 1% in our simulation. To generate the genotypes of a subject, we randomly selected two chromosomes from the pool of 10,000 chromosomes. The disease status of a subject with chromosomes 
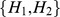was determined by
 |
(4) |
[29]–[31], where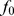 
was the baseline penetrance, and 
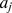was the minor allele at the jth causal variant site. Following Cheung et al. [14], 
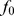was specified at 1%, and the sample size was set at 1000. Pairs of chromosomes were drawn from the chromosome pool with replacement until 500 cases and 500 controls were sampled.
Tests under Comparison
We compared ADA with 
-MidP
[14], burden tests, and non-burden tests. Cheung et al.'s [14] R script was used to implement their 
-MidP method (http://www.columbia.edu/~sw2206/softwares.htm). We followed the default of the 
-MidP R script, single-nucleotide polymorphisms with MAF>5% in the combined sample of cases and controls were excluded from the analyses of 
-MidP and ADA. To have a fair comparison between these two methods, the P-values used in Equations (1) and (2) (i.e.,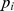 
's) are obtained by the mid P-values according to the Fisher's exact test [14], [26].
Four burden tests including the fixed-threshold approach with MAF thresholds of 1% and 5% (i.e., “T1” and “T5”, respectively) [4], the weighted-sum approach (i.e., “WS”) [3], and the variable-threshold approach (i.e., “VT”) were implemented with the R script by Price et al. [5] (http://genetics.bwh.harvard.edu/rare_variants/). Because VT needs permutations to get P-values, Price et al. [5] performed permutations for all the four tests (VT, WS, T1, and T5) in their R script, at almost no extra computational cost. Note that the original VT script performs right-tailed tests for all the four methods, and therefore they are underpowered when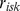 
is low. We modified the original VT script to perform two-tailed tests and used the revised R script to implement the four burden tests.
Two non-burden tests including the sequence kernel association test (i.e., “SKAT”) [7] and the optimal test (i.e., “SKAT-O”) [8] that optimally combines the burden tests and SKAT were implemented with the R package “SKAT” [32]. We used the default weight function in the package “SKAT”,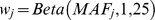 
, as the weight given to the jth variant site with MAF of 
.
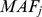The P-values of ADA, 
-MidP, VT, WS, T1, and T5 were obtained with 10,000 permutations when evaluating the type-I error rates and 1,000 permutations when evaluating power, respectively. For SKAT and SKAT-O, we used the default method in the package “SKAT” to compute P-values, which was an exact method that computed P-values by inverting the characteristic function of the mixture chi-square distribution [33].
Results
Type-I Error Rates
By setting the PAR at exactly 0% and using ∼25.6 kb regions, we evaluated type-I error rates by performing 1,000 replications for each of the 200 simulated data sets. Based on the 200,000 ( =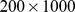 
) replications across the 200 simulated data sets, Table 1 shows that all of the eight tests are valid in the sense that their type-I error rates match the nominal significance levels.
Table 1. Type-I error rates.
| nominal significance level | 0.0001 | 0.005 | 0.010 | 0.015 | 0.020 | 0.025 | 0.030 | 0.035 | 0.040 | 0.045 | 0.050 |
| SKAT-O | 0.0001 | 0.0054 | 0.0102 | 0.0151 | 0.0196 | 0.0246 | 0.0295 | 0.0347 | 0.0396 | 0.0444 | 0.0492 |
| SKAT | 0.0001 | 0.0048 | 0.0096 | 0.0142 | 0.0191 | 0.0237 | 0.0288 | 0.0337 | 0.0384 | 0.0434 | 0.0482 |
| σ-MidP | 0.0001 | 0.0050 | 0.0101 | 0.0149 | 0.0199 | 0.0248 | 0.0298 | 0.0348 | 0.0398 | 0.0448 | 0.0498 |
| ADA | 0.0001 | 0.0050 | 0.0100 | 0.0148 | 0.0199 | 0.0247 | 0.0297 | 0.0351 | 0.0400 | 0.0451 | 0.0500 |
| T1 | 0.0001 | 0.0046 | 0.0096 | 0.0146 | 0.0196 | 0.0245 | 0.0294 | 0.0346 | 0.0399 | 0.0449 | 0.0501 |
| T5 | 0.0001 | 0.0046 | 0.0098 | 0.0149 | 0.0198 | 0.0247 | 0.0296 | 0.0346 | 0.0398 | 0.0449 | 0.0498 |
| WS | 0.0001 | 0.0052 | 0.0103 | 0.0153 | 0.0204 | 0.0254 | 0.0304 | 0.0356 | 0.0402 | 0.0452 | 0.0502 |
| VT | 0.0001 | 0.0050 | 0.0100 | 0.0150 | 0.0201 | 0.0250 | 0.0302 | 0.0352 | 0.0404 | 0.0453 | 0.0503 |
Power Comparisons
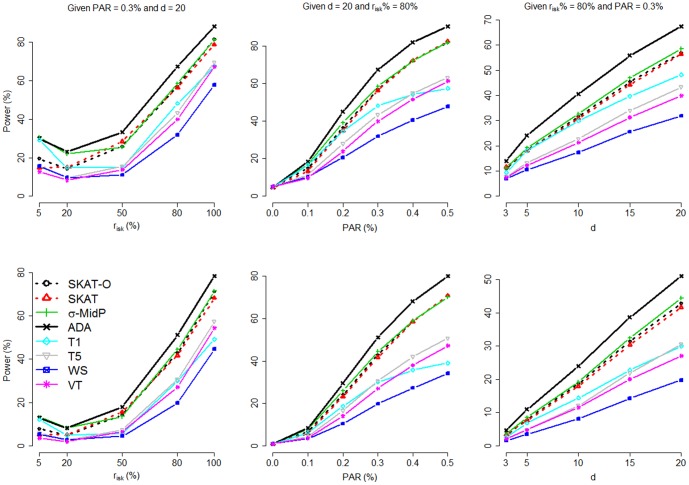
When we evaluated power, a total of 100 replications were performed under each scenario (each combination of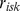 
, PAR, and d) for each of the 200 simulated data sets. Figure 2 presents the power averaged over the 200 data sets, where 100 replications were performed for each data set. Each point represents the result averaged from 
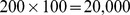replications performed for some combination of 
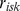, PAR, and d. The nominal significance level was set at 0.05 (top row) and 0.01 (bottom row), respectively. In the first column of Figure 2, power was assessed with a varying 
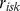, a fixed PAR (0.3%), and a fixed d (20).
Figure 2. Comparison of power by risk (the percentage of deleterious variants among the d causal variants), PAR, and d (the number of causal variants).
The figure shows the power comparison by risk (left column, given PAR = 0.3% and d = 20), PAR (middle column, given d = 20 and risk = 80%), and d (right column, given risk = 80% and PAR = 0.3%). The nominal significance level was set at 0.05 (top row) and 0.01 (bottom row), respectively.
Note that the lowest power occurs around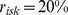 
(among the five values of 
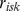), rather than 
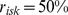(the first column of Figure 2). This is because, in our simulation setting (following [29]), a deleterious variant has a larger effect size than a protective variant, given that they have the same MAF. For simplicity of illustration, we consider only one causal variant site. The probability that a subject has two rare variants at this site is extremely small and thus can be ignored. Equation (4) can be simplified as
 |
where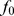 
is the baseline penetrance and GRR is the genotype relative risk of the causal variant. Based on Equation (3),
 |
where the subscripts have been removed for simplification. Let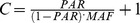 
. For case-control studies, the odds ratio (OR) of being affected among subjects who have a causal variant versus those who do not is an appropriate measure for effect size. Let 
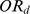be the OR of being affected among subjects who have a deleterious variant versus those who do not. We have
 |
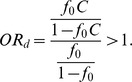Let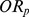 
be the OR of being affected among subjects who have a protective variant versus those who do not. We have
 |
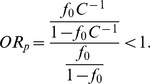Because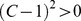 
,
 |
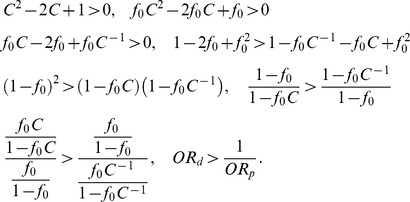Thus, in our simulation setting (following [29]), a deleterious variant has a larger effect size than a protective variant, given that they have the same MAF. This is why the lowest power occurs at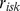 
smaller than 
.
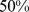In the second column, PAR varied, while d was fixed at 20 and risk % was fixed at 80%. The setting of risk % (80%) was chosen because regulatory sequences are likely to contain many more deleterious variants than protective variants [34], [35]. As for the third column, power was compared while d was varying, but risk % was fixed at 80%, and PAR was fixed at 0.3%. ADA test showed the best performance under the majority of simulation scenarios.
Application to Data from Dallas Heart Study
We applied the eight tests to a population-based resequencing study for the ANGIOPOIETIN–LIKE 4 (ANGPTL4) gene [24], [25]. To learn the role of ANGPTL4 in plasma triglyceride levels, Romeo et al. [24], [25] sequenced seven exons and the intron-exon boundaries of ANGPTL4. The important confounders when investigating plasma triglyceride levels include ethnicity, age, sex, and body-mass index (BMI) [24]. To remove the potential influence of ethnicity on triglyceride, we only analyzed the 1,045 European Americans from the total 3,551 subjects sampled from Dallas County residents [36]. The log-transformed triglyceride levels were adjusted for age, sex, and BMI, with a linear regression. The regression residuals were treated as new phenotypes that have been adjusted for important confounders. Subjects with residuals larger than the 70th percentile and smaller than the 30th percentile were treated as cases and controls, respectively. Then the subjects with missing genotypes were removed from our analysis. Finally, we had 179 cases and 213 controls (the numbers of cases and controls were not necessarily equal, because we removed the subjects with missing genotypes after marking the 30th and 70th percentiles of the phenotype).
We then applied the eight tests to this data set. The variants with MAF<5% in the ANGPTL4 gene were analyzed to test for their associations with triglyceride. The significant association of ANGPTL4 with triglyceride was previously reported by other investigators [14], [37]. With a significance level of 0.05, the four burden tests (VT, WS, T1, and T5) did not show significant association of ANGPTL4 with triglyceride, whereas the other four tests including ADA, SKAT, SKAT-O, and 
-MidP confirmed this association (see Table 2).
Table 2. Analysis of the Dallas Heart Study data.
| SKAT-O | SKAT | σ-MidP a | ADA a | T1 a | T5 a | WS a | VT a | |
| P-value | 0.024 | 0.012 | 0.028 | 0.011 | 0.584 | 0.070 | 0.184 | 0.486 |
a P-values were estimated based on 104 permutations.
Discussion
In this work, we have proposed a powerful ADA method for rare causal variants detection. Instead of fixing a threshold to truncate P-values, we recommend searching for the “optimal” threshold from among multiple candidate truncation thresholds. The validity of ADA is preserved because we allow the permuted and observed data to have different “optimal” truncation thresholds. Here, we use 11 candidate P-value truncation thresholds, 0.10, 0.11, 0.12, …, 0.20. We do not consider a more stringent threshold (<0.10), because testing for a single rare variant is usually underpowered [2], [20]–[22] and a stringent threshold may exclude the information of causal variants. We neither consider a more liberal threshold (>0.20), because that may include more noise from neutral variants. To show this, we also evaluated the ADA method with 21 candidate P-value truncation thresholds (0.05, 0.06, 0.07, …, 0.25). Table 3 lists the power of the ADA method with two sets of candidate P-value truncation thresholds. Using 21 candidate P-value truncation thresholds (0.05, 0.06, 0.07, …, 0.25) does not contribute a noticeable power gain to ADA.
Table 3. Power (%) of the ADA method with two sets of candidate P-value truncation thresholds.
| candidate P-value truncation thresholds | Given PAR = 0.3% and d = 20 | Given d = 20 and risk = 80% | Given risk = 80% and PAR = 0.3% | |||||||||||||
| risk (%) | PAR (%) | d | ||||||||||||||
| 5 | 20 | 50 | 80 | 100 | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 3 | 5 | 10 | 15 | 20 | |
| Nominal significance level = 5% | ||||||||||||||||
| 0.10, 0.11,… 0.20 | 29.97 | 23.17 | 33.28 | 67.41 | 88.24 | 4.84 | 18.45 | 45.06 | 67.41 | 82.03 | 90.47 | 14.00 | 24.16 | 40.58 | 55.80 | 67.41 |
| 0.05, 0.06,…, 0.25 | 29.38 | 23.50 | 35.04 | 68.73 | 89.31 | 5.04 | 18.56 | 46.09 | 68.73 | 83.60 | 91.91 | 14.64 | 25.50 | 42.24 | 57.30 | 68.73 |
| Nominal significance level = 1% | ||||||||||||||||
| 0.10, 0.11,…, 0.20 | 13.00 | 8.17 | 17.99 | 51.10 | 78.32 | 1.00 | 8.39 | 29.50 | 51.10 | 68.09 | 80.03 | 4.68 | 10.99 | 24.01 | 38.65 | 51.10 |
| 0.05, 0.06,…, 0.25 | 12.25 | 8.22 | 18.74 | 51.98 | 79.17 | 0.93 | 8.46 | 30.03 | 51.98 | 69.45 | 81.22 | 4.88 | 11.50 | 24.93 | 39.59 | 51.98 |
Note that the statistic,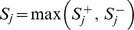 
, is the maximization of the score accumulated by deleterious-inclined variants and that accumulated by protective-inclined variants. Another justifiable statistic is 
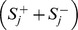, which is more powerful than ADA when the numbers of deleterious and protective variants are comparable, but it is less powerful when the region contains more deleterious variants than protective variants (or, more protective variants than deleterious variants). Because both evolutionary mechanisms and empirical studies support the hypothesis that regulatory sequences contain substantial amounts of weakly deleterious variation [34], [35], [38], [39], the number of deleterious variants may surpass that of protective variants in most situations. Therefore, we still advocate using 
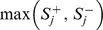, rather than 
.
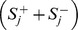The computation time of ADA is slightly longer than that of 
-MidP. For simulated data sets each containing 500 cases and 500 controls in ∼3.6 kb regions (include ∼60 nonsynonymous variant sites), 
-MidP (http://www.columbia.edu/~sw2206/softwares.htm) with 1000 permutations on average needs ∼27.8 sec, ADA with 1000 permutations needs ∼28.6 sec, SKAT-O needs ∼6.7 sec, while VT with 1000 permutations takes only ∼0.9 sec. When the region was enlarged to ∼6.4 kb (include ∼110 nonsynonymous variant sites), 
-MidP with 1000 permutations on average needs ∼45.3 sec, ADA with 1000 permutations needs ∼45.9 sec, SKAT-O needs ∼9.2 sec, while VT with 1000 permutations takes 1.2 sec. These were measured on a Linux platform with an Intel Xeon E5-2690 2.9 GHz processor and 2 GB memory. Although the computation time of VT or SKAT-O is much shorter than that of ADA (or 
-MidP), the power of VT or SKAT-O is not comparable to ADA.
Rare causal variants are likely to play an important role in the etiology of some complex diseases [40]–[45], but they are difficult to detect by single-locus tests [2], [20]–[22]. Grouping variant sites in a functional region and testing for association with an omnibus statistic is a promising strategy. Compared with the burden tests (VT, WS, T1, and T5) and the non-burden tests (SKAT and SKAT-O) evaluated here, ADA is more robust to the inclusion of neutral variants. With the advancement in next-generation sequencing technology, all single-nucleotide variants (causal or neutral) can be sequenced. ADA is recommended for its ability to guard against the noise of neutral variants.
Supporting Information
The distributions of the population minor allele frequencies (MAFs) and genotype relative risks (GRRs) of the causal variants in our 200 simulated data sets.
(TIFF)
Acknowledgments
We thank the Academic Editor and the anonymous reviewers for their constructive comments. We also thank Drs. Jonathan C. Cohen and Helen H. Hobbs for kindly providing the Dallas Heart Study data.
Funding Statement
This work was supported by grants NSC 102-2628-B-002-039-MY3 and NSC 102-2314-B-002-001-MY2 from the National Science Council of Taiwan, and NTU-CESRP-101R7622-8, NTU-CESRP-102R7622-8, and NTU-CDP-102R7769 from National Taiwan University (W-Y.L.), and NIH grants R01GM081488, R01HL092173, P01AR049084, P60AR048095 (N.L.), R01DA095025 (X.L.), and R01GM073766 (G.G.) from the National Institutes of Health. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Kiezun A, Garimella K, Do R, Stitziel NO, Neale BM, et al. (2012) Exome sequencing and the genetic basis of complex traits. Nat Genet 44: 623–630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Li B, Leal SM (2008) Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am J Hum Genet 83: 311–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Madsen BE, Browning SR (2009) A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet 5: e1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Morris AP, Zeggini E (2010) An evaluation of statistical approaches to rare variant analysis in genetic association studies. Genet Epidemiol 34: 188–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Price AL, Kryukov GV, de Bakker PI, Purcell SM, Staples J, et al. (2010) Pooled association tests for rare variants in exon-resequencing studies. Am J Hum Genet 86: 832–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Han F, Pan W (2010) A data-adaptive sum test for disease association with multiple common or rare variants. Hum Hered 70: 42–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Wu MC, Lee S, Cai T, Li Y, Boehnke M, et al. (2011) Rare-variant association testing for sequencing data with the sequence kernel association test. Am J Hum Genet 89: 82–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Lee S, Wu MC, Lin X (2012) Optimal tests for rare variant effects in sequencing association studies. Biostatistics 13: 762–775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Neale BM, Rivas MA, Voight BF, Altshuler D, Devlin B, et al. (2011) Testing for an unusual distribution of rare variants. PLoS Genet 7: e1001322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Yi N, Liu N, Zhi D, Li J (2011) Hierarchical generalized linear models for multiple groups of rare and common variants: jointly estimating group and individual-variant effects. PLoS Genet 7: e1002382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Yi N, Zhi D (2011) Bayesian analysis of rare variants in genetic association studies. Genet Epidemiol 35: 57–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Lin WY, Zhang B, Yi N, Gao G, Liu N (2011) Evaluation of pooled association tests for rare variant identification. BMC Proc 5 Suppl 9: S118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Basu S, Pan W (2011) Comparison of statistical tests for disease association with rare variants. Genet Epidemiol 35: 606–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Cheung YH, Wang G, Leal SM, Wang S (2012) A fast and noise-resilient approach to detect rare-variant associations with deep sequencing data for complex disorders. Genet Epidemiol 36: 675–685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fisher RA (1932) Statistical methods for research workers. London: Oliver and Boyd. [Google Scholar]
- 16. Ionita-Laza I, Buxbaum JD, Laird NM, Lange C (2011) A new testing strategy to identify rare variants with either risk or protective effect on disease. PLoS Genet 7: e1001289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Lin DY, Tang ZZ (2011) A general framework for detecting disease associations with rare variants in sequencing studies. Am J Hum Genet 89: 354–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Zaykin DV, Zhivotovsky LA, Westfall PH, Weir BS (2002) Truncated product method for combining P-values. Genet Epidemiol 22: 170–185. [DOI] [PubMed] [Google Scholar]
- 19. Yang HC, Chen CW (2011) Region-based and pathway-based QTL mapping using a p-value combination method. BMC Proc 5 Suppl 9: S43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Gorlov IP, Gorlova OY, Sunyaev SR, Spitz MR, Amos CI (2008) Shifting paradigm of association studies: value of rare single-nucleotide polymorphisms. Am J Hum Genet 82: 100–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Altshuler D, Daly MJ, Lander ES (2008) Genetic mapping in human disease. Science 322: 881–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Bansal V, Libiger O, Torkamani A, Schork NJ (2010) Statistical analysis strategies for association studies involving rare variants. Nat Rev Genet 11: 773–785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Yu K, Li Q, Bergen AW, Pfeiffer RM, Rosenberg PS, et al. (2009) Pathway analysis by adaptive combination of P-values. Genet Epidemiol 33: 700–709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Romeo S, Pennacchio LA, Fu Y, Boerwinkle E, Tybjaerg-Hansen A, et al. (2007) Population-based resequencing of ANGPTL4 uncovers variations that reduce triglycerides and increase HDL. Nat Genet 39: 513–516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Romeo S, Yin W, Kozlitina J, Pennacchio LA, Boerwinkle E, et al. (2009) Rare loss-of-function mutations in ANGPTL family members contribute to plasma triglyceride levels in humans. J Clin Invest 119: 70–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Fisher RA (1922) On the interpretation of χ2 from contingency tables, and the calculation of P. Journal of the Royal Statistical Society 85: 87–94. [Google Scholar]
- 27. Schaffner SF, Foo C, Gabriel S, Reich D, Daly MJ, et al. (2005) Calibrating a coalescent simulation of human genome sequence variation. Genome Res 15: 1576–1583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Hudson RR (2002) Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18: 337–338. [DOI] [PubMed] [Google Scholar]
- 29. Li Y, Byrnes AE, Li M (2010) To identify associations with rare variants, just WHaIT: Weighted haplotype and imputation-based tests. Am J Hum Genet 87: 728–735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Lin WY, Yi N, Lou XY, Zhi D, Zhang K, et al. (2013) Haplotype kernel association test as a powerful method to identify chromosomal regions harboring uncommon causal variants. Genet Epidemiol 37: 560–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Lin WY, Yi N, Zhi D, Zhang K, Gao G, et al. (2012) Haplotype-based methods for detecting uncommon causal variants with common SNPs. Genet Epidemiol 36: 572–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lee S, Miropolsky L, Wu M (2013) Package ‘SKAT’, http://cran.r-project.org/web/packages/SKAT/index.html. Accessed Jan 2, 2013.
- 33. Davies RB (1980) Algorithm AS 155: the distribution of a linear combination of χ2 random variables. Journal of the Royal Statistical Society Series C (Applied Statistics) 29: 323–333. [Google Scholar]
- 34. Abecasis GR, Auton A, Brooks LD, DePristo MA, Durbin RM, et al. (2012) An integrated map of genetic variation from 1,092 human genomes. Nature 491: 56–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Kryukov GV, Pennacchio LA, Sunyaev SR (2007) Most rare missense alleles are deleterious in humans: implications for complex disease and association studies. Am J Hum Genet 80: 727–739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Victor RG, Haley RW, Willett DL, Peshock RM, Vaeth PC, et al. (2004) The Dallas Heart Study: a population-based probability sample for the multidisciplinary study of ethnic differences in cardiovascular health. Am J Cardiol 93: 1473–1480. [DOI] [PubMed] [Google Scholar]
- 37. Liu DJ, Leal SM (2010) A novel adaptive method for the analysis of next-generation sequencing data to detect complex trait associations with rare variants due to gene main effects and interactions. PLoS Genet 6: e1001156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Cirulli ET, Goldstein DB (2010) Uncovering the roles of rare variants in common disease through whole-genome sequencing. Nat Rev Genet 11: 415–425. [DOI] [PubMed] [Google Scholar]
- 39. Gibson G (2012) Rare and common variants: twenty arguments. Nat Rev Genet 13: 135–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Azzopardi D, Dallosso AR, Eliason K, Hendrickson BC, Jones N, et al. (2008) Multiple rare nonsynonymous variants in the adenomatous polyposis coli gene predispose to colorectal adenomas. Cancer Res 68: 358–363. [DOI] [PubMed] [Google Scholar]
- 41. Cohen JC, Kiss RS, Pertsemlidis A, Marcel YL, McPherson R, et al. (2004) Multiple rare alleles contribute to low plasma levels of HDL cholesterol. Science 305: 869–872. [DOI] [PubMed] [Google Scholar]
- 42. Hershberger RE, Norton N, Morales A, Li D, Siegfried JD, et al. (2010) Coding sequence rare variants identified in MYBPC3, MYH6, TPM1, TNNC1, and TNNI3 from 312 patients with familial or idiopathic dilated cardiomyopathy. Circ Cardiovasc Genet 3: 155–161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Bodmer W, Bonilla C (2008) Common and rare variants in multifactorial susceptibility to common diseases. Nat Genet 40: 695–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Dickson SP, Wang K, Krantz I, Hakonarson H, Goldstein DB (2010) Rare variants create synthetic genome-wide associations. PLoS Biol 8: e1000294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Pritchard JK (2001) Are rare variants responsible for susceptibility to complex diseases? Am J Hum Genet 69: 124–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The distributions of the population minor allele frequencies (MAFs) and genotype relative risks (GRRs) of the causal variants in our 200 simulated data sets.
(TIFF)