COMPETITIVE BIDDING IN MEDICARE ADVANTAGE: EFFECT OF BENCHMARK CHANGES ON PLAN BIDS

Abstract

Bidding has been proposed to replace or complement the administered prices in Medicare pays to hospitals and health plans. In 2006, the Medicare Advantage program implemented a competitive bidding system to determine plan payments. In perfectly competitive models, plans bid their costs and thus bids are insensitive to the benchmark. Under many other models of competition, bids respond to changes in the benchmark. We conceptualize the bidding system and use an instrumental variable approach to study the effect of benchmark changes on bids. We use 2006–2010 plan payment data from the Centers for Medicare and Medicaid Services, published county benchmarks, actual realized fee-for-service costs, and Medicare Advantage enrollment. We find that a $1 increase in the benchmark leads to about a $0.53 increase in bids, suggesting that plans in the Medicare Advantage market have meaningful market power.

1. Introduction

Bidding is one of the most important price-setting mechanisms in economics. It is central to auctions, which are commonly used to set prices in the absence of a preexisting market (Hansen, 1988; Vickrey, 1961). The outcome of bidding markets depends, in part, on the nature of competition in the market (McAfee and McMillan, 1987; Klemperer, 1999). Early theoretical work on auctions has been followed by a growing empirical literature (Athey and Haile, 2006; Hendricks and Porter, 2007). Bidding has long been at the center of government procurement contracts. For example, the U.S. government leases offshore drilling rights to private companies through a bidding process (Hendricks, Pinske, and Porter, 2003). Bidding is also increasing used in government procurement contracts for the delivery of public services through the private sector (Laffont and Tirole, 1993; Bajari and Tadelis, 2001). In recent years, bidding has assumed an increasingly important role in medical care and related discussions about the financing of health care in an era of unsustainable spending growth (Antos, Pauly, and Wilensky, 2012; Emanuel, Tanden, and Altman 2012; Feldman, Coulam, and Dowd, 2012). In particular, the Medicare Part D prescription drug market (Duggan, Healy, and Scott Morton, 2008), the market for durable medical equipment (Center for Medicare and Medicaid Services, 2012), and the Medicare Advantage program (McGuire, Newhouse, and Sinaiko, 2011), in which commercial insurers contract with Medicare to provide alternative insurance options to standard Medicare Part A and Part B coverage for Medicare beneficiaries, all use bidding as a way to set price.

Proposals to control Medicare spending rely on bidding as a market-based alternative to administratively imposed payment reduction (Antos, 2012; Wilensky, 2012). Bidding is the foundation of the 2012 Republican House budget, based on a proposal by Congressman Paul Ryan (R-WI) and Senator Ron Wyden (D-OR) to replace the traditional Medicare financing system with a wholesale competitive bidding system (Wyden and Ryan, 2011). Specifically, the Ryan-Wyden plan would treat traditional Medicare as one plan choice among many, setting the plan payment rate in each county according to the second-lowest private plan bid or traditional Medicare cost (whichever is lower). Some analysts predict that expanding the role of bidding in Medicare could save $339 billion or 9.5 percent of Medicare spending through 2020, 5.6 percentage points more than projected savings under the Patient Protection and Affordable Care Act (Feldman, Coulam, and Dowd, 2012).

Bidding has been central to the procurement process in Medicare Advantage (MA) since 2006. Despite this relevant experience and the likely importance of bidding going forward, little empirical work studies the economics of plan bidding behavior in MA.

In the existing MA bidding system, any commercial insurer that would like to offer an MA plan submits a plan-specific bid (an amount covering the expected costs of a standard benefit package for an average risk beneficiary) to the Centers for Medicare and Medicaid Services (CMS). This bid, which must also be accompanied by projected enrollment in the counties covered by the plan, is measured against county-level benchmark rates set by CMS. From the bid and projected enrollment, CMS determines a plan-specific payment and an associated premium (or rebate) charged (or given) to beneficiaries. Competition gives plans an incentive to bid low in order to attract consumers. Low bids attract beneficiaries through higher “rebates” (additional coverage benefits or reduced cost sharing for Medicare Part B or Part D). The success of this system, and likely success of alternative bid based systems, depends on the extent of competition in the MA market. By examining how plans change their bids in response to the benchmark, we can shed light on the functioning of markets for health plans. Specifically, variation in benchmark updates can be used to assess the nature of competition in this market.

Moreover, understanding the relationship between county-level benchmark rates and plan bids is also important for forecasting the likely impact of impending changes to MA payments. In 2012, the Patient Protection and Affordable Care Act will begin phasing in a modification of the benchmark rate formula that will likely have substantial effects on plan behavior and MA enrollment. Designed to reduce excessive payments to MA plans, benchmarks will be set as a percentage of average fee-for-service Medicare spending in a county, with the percentage determined by how a county’s fee-for-service spending compares with that of other counties (MedPAC, 2011). Counties in the highest quartile of FFS spending will face benchmarks equal to 95 percent of average risk-adjusted fee-for-service spending in their region; those in the lowest quartile will face benchmarks equal to 115 percent. Since MA plans are concentrated in the highest spending counties, resulting benchmarks may have large impacts on plan rebates and subsequent MA enrollment.

We study the relationship between benchmark rates and plan bids using plan payment, enrollment, and county-level fee-for-service Medicare spending data from CMS. Our central question, how plan bids respond to changes in the benchmark, is similar to a preliminary analysis (Song, Landrum, and Chernew, 2012). In the earlier work, we used an OLS approach with 2006–2009 data and found that a $1 increase in the benchmark was associated with a $0.49 increase in bids among HMO plans. While this result was robust to our sensitivity analyses, our approach did not address the potential endogeneity of the benchmark or the influence of provider competition. This paper improves upon the prior analysis by presenting a theoretical context, adding 2010 data to the model, examining the role of provider competition, and addressing the issue of endogeneity.

We address endogeneity in two ways. First, we use an instrumental variables approach to isolate the effect of exogenous changes in benchmark rates on plan bids. Our instrument is a simulated benchmark that captures the plausibly exogenous components of the benchmark updates. Second, we separately analyzed the years in which benchmark updates underwent “rebasing” by CMS, in which benchmarks in all counties were updated using a national or regional floor update rate that was plausibly unrelated to changes in unmeasured time-varying factors in a given county. Similar to our prior work, we find that on average bids for HMO plans increase by $0.53 in response to a $1 increase in the benchmark rate, suggesting that insurers have some degree of market power and that plan rebates also move with benchmark rates, but to a lesser degree than bids. We also find that the number of insurers in a market is negatively related to bids, consistent with competition among insurers. Meanwhile, contrary to theory, greater provider concentration, as measured by the Herfindahl–Hirschman Index using the number of beds, was related to lower bids.

The paper proceeds as follows. Section 2 provides background on the MA program and its competitive bidding system. Section 3 reviews the theory of price-setting in the MA context under perfect and imperfect competition. Section 4 describes the data and section 5 presents the empirical strategy. Results are shown in section 6, and section 7 concludes.

2. Background

The MA program, formerly known as Medicare Part C and Medicare+Choice, provides Medicare beneficiaries the choice of health insurance plans that provide Medicare coverage offered by commercial insurers in lieu of traditional FFS Medicare. More than 25 percent of Medicare beneficiaries today are enrolled in MA. In the last decade, MA enrollment has more than doubled from 4.5 million in 2003 to 11.4 million in 2010 (MedPAC 2011), its highest level since the inception of the program (Figure 1). During this time, MA has commanded increasing policy interest, with growing implications for the trajectory of Medicare spending as well as beneficiary access and quality of care (Gold, 2012; Guram and Moffit, 2012).

Figure 1.

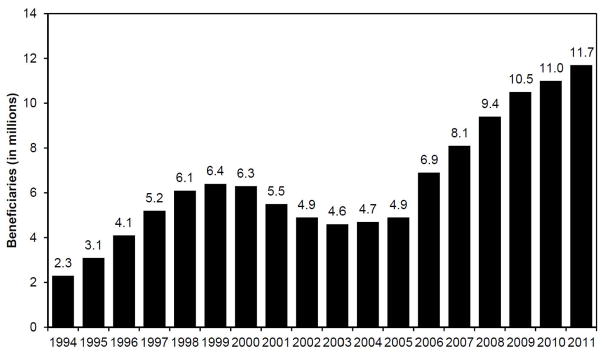
Total Medicare Advantage enrollment, 1994–2011.

Source: Medicare Payment Advisory Commission. A Data Book: Health care spending and the Medicare Program, June 2011. Section 9, Chart 9-3, p. 147.

Private insurers in MA accept prospective payments that vary at the county level and agree to provide coverage for Medicare Part A and Part B services. Plans may also supply prescription drug, or Medicare Part D, coverage. Commercial plans that enter MA compete in a regulated market. The 1982 Tax Equity and Fiscal Responsibility Act (TEFRA), which ushered in managed care plans in Medicare, was designed to encourage private plans to improve efficiency and lower Medicare spending. Another important objective was giving beneficiaries the opportunity to choose among plans. Plans have flexibility to contract with providers, use managed care techniques, and design beneficiary incentives. Under TEFRA, plan payments were based on average fee-for-service Medicare spending in a county with minimal risk adjustment. The 1997 Balanced Budget Act (BBA) introduced a new method of determining plan payments, in which annual updates were based on the maximum of several paths: a 2 percent increase, a legislated “floor” update of a certain amount, and a weighted average of national fee-for-service Medicare spending and the county’s own fee-for-service Medicare spending, the “blended” rate. The BBA also introduced patient diagnoses into the risk adjustment formula.

The 2003 Medicare Modernization Act (MMA) further altered the way benchmark payments were set and dramatically increased Medicare payments to MA plans. Beginning in 2006, MA plan payments were determined via a competitive bidding system, which sought to leverage market forces to encourage more efficient and higher quality plan options (McGuire, Newhouse, and Sinaiko, 2011). CMS began to calculate plan payments by comparing their bids against pre-determined county-level “benchmark” rates in the counties a plan proposed to serve. Benchmark updates were determined by the maximum of: a 2 percent increase, an urban or rural “floor” update, the prior year national average growth in fee-for-service Medicare spending, and an own-county fee-for-service update. This final update path was calculated by trending forward a county’s own fee-for-service spending in a five-year period spanning eight years prior to three years prior. The MMA also updated the risk adjustment system used in setting the benchmark, adopting the CMS Hierarchical Condition Category (CMS-HCC) system.

A number of studies have examined the relationship between plan payments and MA enrollment (see, for example, Atherly et al., 2004; Cawley et al., 2005; Dowd et al., 2003; Gowrisankaran and Town, 2006; Maruyama, 2011; Town and Liu, 2003). They use different datasets across varying time horizons and different estimation techniques, and find largely heterogeneous elasticities of MA enrollment with respect to plan payments. In addition, several studies find that payment rates affect the number of HMO plans that enter the market (Afendulis, Landrum, and Chernew, 2012; Cawley et al., 2002; Town and Liu, 2003; Pizer and Frakt, 2002). However, most of this literature predates the introduction of competitive bidding in 2006. Since then, there is little work on the relationship between benchmarks and enrollment (Chernew et al., 2008), and virtually no work on the effect of benchmarks on plan bidding.

Competitive bidding and a response to a benchmark change

The Medicare bidding system can be summarized in the following four steps. Let j denote plans and k denote counties.

• (1)CMS sets a benchmark payment rate for each county, bench_k. The benchmark is a function of lagged fee-for-service spending and a series of update rules, such as a minimal update factor and county floor payment rates.
• (2)Each plan j submits a single sealed bid, bid_j, for the price it is willing to accept to insure a beneficiary (the bid is standardized to a beneficiary of 1.0 risk to make bids from different plans comparable), along with projected enrollment in counties the plan will serve.
• (3)After reviewing a plan’s bid and projected enrollment, CMS assigns plans a plan-specific payment benchmark, pay_j. This payment benchmark is an average of benchmark rates in the counties served by the plan weighted by projected plan enrollment across counties. This payment does not vary by county as plans receive a single price (and will be adjusted for actual enrollment patterns after they become apparent).

  Together, the plan payment benchmark (pay_j) and plan bid (bid_j) determine the rebate and premium that a plan will offer enrollees. If the plan’s bid exceeds its benchmark, its actual realized payment (P_j) from CMS equals its payment benchmark. In this case, the plan must collect the difference through a supplemental (extra) enrollee premium (prem_j). This extra premium is charged above the base Medicare Part B (and Part D) premiums.

Case 1: bid exceeds benchmark

$$P_j={\mathit{pay}}_j$$ (1)

$${\mathit{prem}}_j={\mathit{bid}}_j-{\mathit{pay}}_j$$ (2)

On the other hand, if the plan’s bid is less than its payment benchmark, the plan receives its bid. In addition, however, during our study period, the plan would also receive 75 percent of the difference between its payment benchmark and bid—a rebate (reb_j)— which it must return to beneficiaries in the form of additional benefits or lower premiums. The rebate itself may be given as a reduction in the base Part B or Part D premiums, or it may comprise of extra benefits such as dental or vision care. As many as over 90 percent of MA plans offer a rebate, as opposed to charging a supplemental premium, making this the dominant case. The rebate is effectively a negative premium; in the presence of a rebate, the additional supplemental premium is zero. The remaining 25 percent of the difference is retained by Medicare as an effective tax (Figure 2).

Figure 2.

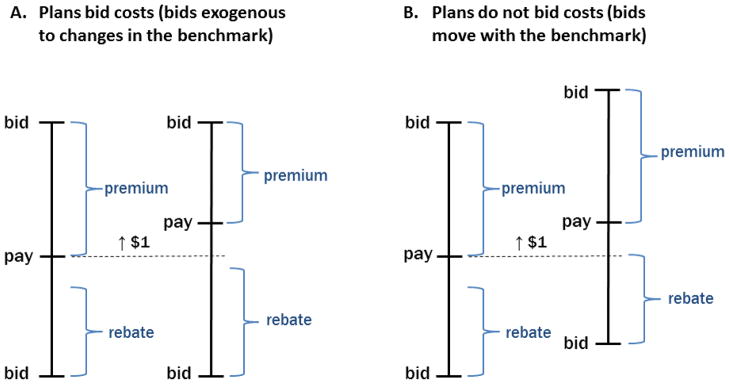
Two simple models of plan bidding.

This figure illustrates the different predictions of the perfect competition model and models of imperfect competition. In panel A, a $1 change in the benchmark payment rate (pay) does not affect the bid, consistent with plans bidding their costs (zero-profit condition) in a perfectly competitive market. Given the design of the bidding system, we would expect Δrebate/Δpay >0 and Δpremium/Δpay < 0. In contrast, panel B illustrates a situation in which a $1 change in the benchmark is reflected in a $1 change in the bid, consistent with a monopoly plan extracting the surplus. In this case, we would expect Δrebate/Δpay =0 and Δpremium/Δpay =0.

Case 2: benchmark exceeds bid

$$P_j={\mathit{bid}}_j+{\mathit{reb}}_j={\mathit{bid}}_j+0.75({\mathit{pay}}_j-{\mathit{bid}}_j)$$ (3)

$${\mathit{prem}}_j=0$$ (4)

• (4)Given a set of plan options, which differ in premiums and rebates, Medicare beneficiaries choose to enroll in a plan (or in traditional Medicare). The beneficiary’s enrollment can be modeled as a discrete choice function and is outside the scope of the current paper.

In this structure, the benchmark can be thought of as a subsidy that effectively shifts demand. If the benchmark rises by $1, the bid needed to generate any given premium rises by $1 in the case when the target premium exceeds zero and by less than $1 in the case when the target premium is negative (when there is a rebate).

3. Theory

In a perfectly competitive market, price equals marginal cost and firms earn zero profits (in the long run). The impact of an exogenous demand shift depends on the shape of the supply curve. Evidence that suggests the supply curve in the health insurance industry is flat (Newhouse, 1992; Cutler and Zeckhauser, 2000). This is because the insurance industry likely exhibits few diseconomies of scope in the relevant range. Of course, even if there are no diseconomies of scale in insurance, the supply curve may be upwards sloping if incremental enrollees are systematically sicker. Yet because CMS risk adjusts payments, this effect is likely small. Moreover, evidence suggests that the CMS risk adjustment system overcompensates for certain enrollees with chronic conditions because Medicare advantage plans can care for these beneficiaries more efficiently that the traditional Medicare system upon which risk adjustment is based (Newhouse et al., 2012). This implies that any increase might be associated with an effectively downward sloping demand curve net of risk adjustment. In the model with a flat supply curve, shifts in demand (benchmark) would change quantity (enrollment) but not bids in equilibrium. Differences in the predictions between the case of perfect competition and models of imperfect competition are illustrated in Figure 2.

Imperfect competition

Many models of imperfect competition may yield a different conclusion. In a monopoly model, the supplier’s price (bid) will respond to shifts in demand even if the marginal cost curve is flat. In the MA context, one can consider what the optimal markups should be in a standard imperfect competition framework. Assume MA plans maximize a simple profit function characterized by markups (price above cost) and enrollment (quantity demanded), π_jk = (p_jk−c_jk)N_jk = (p_jk−c_jk)s_jkM_k, where p_jk represents the price which equals the bid if the bid is less than the benchmark, c_jk denotes plan cost_j (which may be endogenous), s_jk is the plan’s market share in a county, and M_k is the number of Medicare eligible in a county.

In a world with differentiated products, plans would maximize their profits taking other insurers’ prices (bids) as given. Benchmark rates affect bids because they affect the relationship between bids and premiums or rebates (i.e. between the bids and net benefit of the plan). The solution depends on the elasticity of demand, nature of competition, and the share of the difference between the bid and the benchmark rate returned to Medicare (25% under current law). The solution has a positive relationship between benchmark rates and bids.

$$\frac{\partial {\pi }_{jk}}{\partial p_{jk}}=\left(1-\frac{\partial c_{jk}}{\partial p_{jk}}\right)s_{jk}+\left(p_{jk}-c_{jk}\right)\frac{\partial s_{jk}}{\partial p_{jk}}=0$$ (5)

Benchmark rates affect bids because they shift the demand curve. For example, if a plan’s equilibrium net benefit package to enrollees is x*, and the benchmark increases, the optimal plan bid to achieve x* may also rise. This exemplifies the standard result from models of imperfect competition. In the short run, a shift in demand will increase prices even if the marginal cost curve is perfectly elastic. Other models could also produce a positive relationship between benchmarks and bids. For example, in a bilateral bargaining model, a shift in benchmarks (which are known) could affect reservation prices of each side, which could affect plan costs and hence bids. If providers anticipate that plans will receive higher benchmarks, they may negotiate for higher fees to extract a part of that rent.

Our goal in this paper is to highlight the differences between the predictions of perfect competition ) and the predictions of imperfect competition (Figure 2). We are agnostic to the structural underpinnings of the various imperfect competition models that one could think of to explain the correlation between changes in bids and changes in the benchmark. This is because we cannot identify the exact model of competition in the MA market, and we are not able to test specific models of imperfect competition with our estimates. However, we are able to interpret our results against the norm of perfect competition with a flat supply curve.

4. Data

We used public CMS databases containing MA plan payment data at both the county and plan level from 2006–2010. We also used county-level published benchmark rates, actual FFS costs per beneficiary, and CMS data on plan location and enrollment by county in each year. We merged these public datasets to create market-level data, as described below.

The county-level data contains payments, rebates, and risk scores averaged across plans that serve the county. Risk scores are the CMS-HCC risk scores. The plan-level data contains plan payments, rebates, and plan risk scores. The plan’s payment rate is the plan’s bid standardized to a beneficiary of 1.0 risk. When plans submit a bid to CMS, they submit a bid based on the expected risk profile of their enrollees as expected enrollment in the counties they serve. CMS subsequently converts this bid to a standardized bid, which is what we use in our analyses. Published county benchmark payment rates are drawn from the MA Ratebook. Specifically, they are the overall “risk” rates for each county, standardized to a beneficiary of 1.0 risk. County level realized FFS costs up to 2009 are also available online through CMS. Like the prior variables, these costs are standardized to the 1.0 risk enrollee. Enrollment is the total number of beneficiaries enrolled in a MA plan.

We conduct our analyses at three levels of plan aggregation. In our base models, we restrict analysis to health maintenance organization (HMO) plans only. In sensitivity analyses, we expand our sample to local preferred provider organization (LPPO) plans, and private fee-for-service (PFFS) plans. Employer plans and special needs plans are excluded, as are regional PPO plans that use a different regional benchmark system.

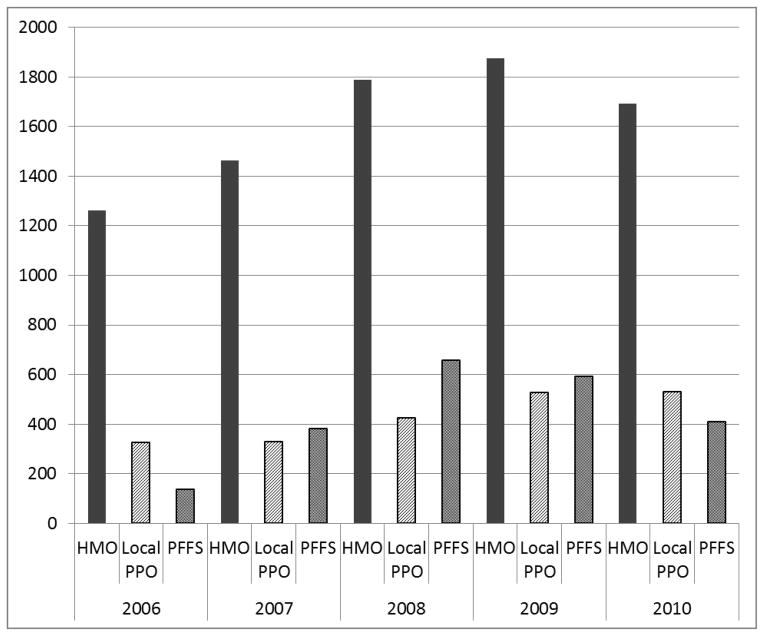
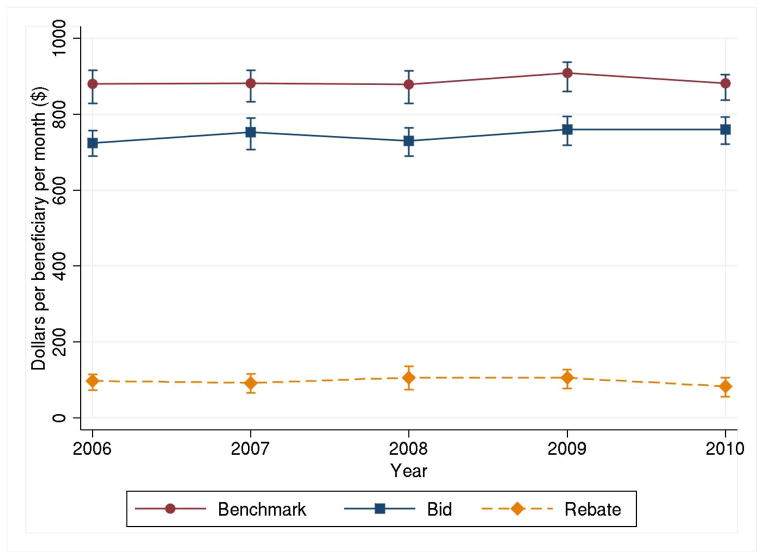
From 2006–2010, there were over 12,000 unique Medicare Advantage plans. After excluding regional PPOs, special needs plans, and employer-sponsored plans, Figure 3 shows the number of HMO, LPPO, and PFFS plans in each year. While less managed plans have grown in recent years, HMO plans remain the dominant plan type, especially in larger and more urban counties. We focus on HMO plans in our main analyses. Figure 4 shows the population-weighted average market benchmark rates, HMO plan bids, and HMO rebates. In econometric analysis, we use plausibly exogenous changes in benchmarks. Our basic identification comes from comparing how bids change in markets with large exogenous changes in benchmarks to how bids change in markets with small exogenous changes in benchmark.

Figure 3.

Number of Medicare Advantage plans, 2006–2010

Figure 4.

Average market benchmarks, bids, and rebates, 2006–2010.

Population-weighted average published benchmark rates, plan bids, and rebates per beneficiary per month at the market level standardized to a beneficiary of 1.0 risk, with interquartile range (2012 U.S. dollars).

5. Empirical strategy

Level of analysis

Both county-level and plan-level analyses of the relationship between benchmark rates and bids are inherently limited. Because MA plans are required to submit a single bid covering all counties they serve, relating the county benchmark to average bid in any given county ignores the effect of benchmarks in other (often adjacent) counties which may have affected the given county’s bid. Alternatively, a plan-level longitudinal model requires plans to be a stable unit of observation across time. Yet insurers frequently consolidate or split their plans from one year to the next. For example, a “silver” plan’s enrollees in one year may be subsumed under a “gold” plan in the next year, retaining the gold plan’s identification number. This would render the plan generosity on average higher in the second year, distorting the underlying relationship between its bid and benchmark. Alternatively, the silver plan’s identification number may be kept, thus producing a bias in the opposite direction. Other scenarios are also common. The two plans offered by the same insurer may merge and take on a new identification number altogether. Subsequently, this consolidated plan may split in the next year. Such plan dynamics complicate longitudinal fixed effects models with plans as the unit of the observation.

To address these limitations, we constructed, for each county, an effective “market” that takes into account the benchmarks in other counties that plans observe when making their bids in the given county. Each unique market is centered on a unique county, with market boundaries defined by the set of other counties served at any point in the study period by plans in the central county. Like counties, they are a stable unit of analysis over time, allowing for longitudinal models. Specifically, we constructed markets using the following methodology.

First, for each county, we identified all other counties served by plans in the target county over our study period. We then computed the share of enrollment across counties for all plans serving the target county over our study period. Second, we assigned the county benchmark payment rate in all non-target counties to the target county, weighted by the share of each of the target county plan’s enrollment in the non-target counties. We used each plan’s average share across the study period so that the weights were stable. This procedure was repeated for other variables. The resulting units of observation, which we call “markets,” are stable over time, allowing for longitudinal models. There is the same number of markets as counties, and markets may overlap geographically. Each observation in the final dataset is a unique market-year, and we will refer to them as markets in the rest of the paper.

Empirical framework

An initial approach for estimating effect of changes in benchmark rates on changes in plan bids may take the form of a reduced form market-level model:

$$\begin{array}{c}{\mathit{bid}}_{kt}={\beta }_1{\mathit{bench}}_{kt}+{\beta }_2\mathit{FFS}\_{TM}_{kt}+{\beta }_3\mathit{risk}\_{TM}_{kt}+{\beta }_4\mathit{risk}\_{MA}_{kt}+{\beta }_5{\mathit{insurers}}_{kt}\\ {\beta }_{6}po{p}_{kt}+{\lambda }_k+{\tau }_k+{\epsilon }_{kt}\end{array}$$ (6)

where bid_kt is the average bid in market k in year t, bench_kt is the market-level published benchmark rate in year t, and FFS_TM_kt is the actual realized (contemporaneous) FFS costs of the market’s traditional Medicare (TM) population, which we take as a marker for the underlying intensity of FFS spending in a county. We also control for health status through the CMS-HCC risk score: risk_TM_kt is the average risk score of the market’s TM population which may affect spending in MA through provider practice patterns, and risk_MA_kt is the average risk score of the market’s MA population which reflects the inherent sickness of MA enrollees. In addition, we include the number of insurers in a market and the total population of Medicare eligible persons in a market. Market fixed effects are represented by λ_k and year fixed effects by τ_t. Market fixed effects render our identification of the effect of benchmark rates on bids through within-market changes. This specification is preferable to cross-sectional or pooled OLS models to the extent that benchmark rates are correlated with unobservable market-level characteristics that also affect plan bids. Year fixed effects control for any underlying trends in bids across all counties. Observations are weighted by a fixed average of the total Medicare population in a market across 2006–2010. Given that markets overlap geographically, standard errors are clustered by state rather than by market.

In this framework, the error term ε_kt is assumed to be uncorrelated with the independent variables. However, the error term may be correlated with the benchmark due to unobservable time-varying market characteristics that are correlated with changes in the benchmark and bid. Despite controlling for the number of insurers, there are likely to be omitted aspects of insurer competition, such as overlap of competitors across counties and the entry and exit (or merging and splitting) of plans within an insurer. Similarly, controlling for provider concentration via HHI may leave relevant local variations in provider competition omitted, such as competition along specialty service lines or acquisitions and mergers among physician practices not reflected in a change in hospital beds, all of which could affect plan costs.

Additionally, the benchmark update formula in the study period has an own-county FFS spending update path, which introduces another potential source of endogeneity. Even though we control for contemporaneous FFS costs, the lagged design of the own-country FFS update, which calculates the benchmark based on a 5-year period of FFS costs ending 3 years prior, means that time-varying factors affecting prior FFS costs may be driving the current benchmark and bids. In reality, we believe this source of endogeneity is small because this update would only be binding if it renders a bigger benchmark change than the other update paths. During our study period, the administrative updates (2% update or national FFS growth update) was binding a majority of the time, with the own-county FFS update only binding in under 200 counties in 2007 and 2009.

Nevertheless, we address this potential endogeneity in several ways, including using instrumental variables and assessing the sensitivity to omitting FFS costs (which should increase the bias if omitted costs are a large concern). We also estimate models on 2006–2007 and 2008–2009 separately, because payment updates in those years (“rebasing years”) were dominated by legislative changes to payment floors that are plausibly more exogenous.

Instrumental variables

In order to address this potential bias, we use simulated benchmark rates to identify the effect of changes in benchmarks on bids. We construct simulated benchmarks by isolating the plausibly exogenous portion of benchmark updates in each year, and using that portion to update the (simulated) benchmark from the previous year. From 2006–2010, benchmarks were updated by the maximum value of 4 different paths: (1) a minimum update of 2 percent, (2) the national FFS Medicare growth rate, (3) the county FFS growth rate, or (4) an urban or rural floor update. Since the county’s own FFS growth rate is potentially endogenous as described above, we abolish this criterion and replace it with the FFS growth rate of the entire state that a given county belongs to, calculated using a weighted average of county growth rates in all counties in that state except the given county. One caveat, however, is that a state-level growth rate update contains, for any given target county, spending in non-target counties, which are often in the same state. Therefore, a simulated benchmark that undergoes this “state-not-self” update may be correlated with the error term in the second stage model. Empirically, the state-not-self path is rarely binding (133 of 3109 counties were updated via this path in 2007, and 159 counties in 2009), due to the aforementioned dominance of the administrative updates in the study period. Overall, to the extent that simulated benchmarks are correlated with observed benchmarks but uncorrelated with the error, the IV estimate would represent an improvement over our base OLS estimate. This is less of an issue when we focus on rebasing years.

While the effect of simulated benchmark changes on bids may be less related to the error term, simulated benchmarks may still be a weak instrument if simulated updates are uncorrelated with actual benchmark updates. We test the strength of the instrument using a standard F-test. On the other hand, because the simulated benchmark is used to instrument for the actual benchmark, which is inherently very similar in construction (differing only in the own-county FFS update), we are also concerned that the instrument may be limited in its ability to improve upon OLS. We conduct a Durbin-Wu-Hausman test for regressor endogeneity (Wooldridge, 2002).

We also conduct a number of basic sensitivity analyses, including using OLS. To assess the impact of selection effects, we repeat the model while omitting TM risk or plan risk. We also reproduce our estimate using a linear trend in place of year dummies. Additionally, we repeat the model omitting the fixed market weights, restricting attention to big counties, and including an interaction between the benchmark and the number of insurers. To control for provider market power, we include HHI based on the number of hospital beds in one specification, and present a separate set of results with the HHI and the interaction between HHI and benchmark.

Since we exploit variation in benchmark changes in absolute dollars, we also repeated the base model using a logarithmically transform bids and benchmarks. Variation in dollars may arise even when the percent change in the benchmarks are the same—for example when multiple counties with different base benchmarks receive the same minimum update of 2 percent or national traditional Medicare growth rate in a given year. The log-transformed model is a generalized linear model (GLM) that allows a more flexible functional form and removes the need to smear our estimates, which is required in the transformed OLS case. We transform the predictions of the GLM into dollars and find that they are very consistent with the base model.

6. Results

First stage

Results from our first-stage estimation are shown in Table 1. We present specifications for our main simulated benchmark, which replaces the own-county FFS update with the state-not-self FFS update, using our base model as well as with inclusion of HHI. We also show the first-stage results using an alternate simulated benchmark, which simply omits the own-county FFS update but does not replace it with our constructed state-not-self FFS update. Although we do not use this alternative simulated benchmark in our main estimates, its first stage shows that our constructed state-not-self FFS update does not meaningfully alter the benchmark changes.

Table 1.

First stage estimates^*

Variables	(1)	(2)	(3)	(4)
	Main Simulated Benchmark		Alternate Simulated Benchmark
Sim Benchmark	0.939*** (0.0486)	0.925*** (0.0482)	0.934*** (0.0650)	0.921*** (0.0627)
Risk (FFS)	−90.88** (41.82)	−84.13** (34.90)	−100.7*** (33.76)	−96.88*** (31.32)
Risk (Plan)	31.73*** (8.989)	29.98*** (9.471)	49.06*** (12.43)	48.05*** (12.41)
FFS cost	0.106** (0.0431)	0.100** (0.0378)	0.127*** (0.0370)	0.124*** (0.0355)
Pop (1000s)	−0.0119 (0.0202)	−0.0221 (0.0270)	−0.0327 (0.0367)	−0.0378 (0.0382)
Insurers	0.183 (0.331)	0.302 (0.377)	0.0886 (0.286)	0.160 (0.299)
HHI (beds)		−0.00550 (0.00375)		−0.00322* (0.00175)
Market FE	Y	Y	Y	Y
Year FE	Y	Y	Y	Y
Observations	7,669	7,669	7,669	7,669
Partial R-squared	0.628	0.622	0.571	0.558
F-statistic	258.92	250.57	302.44	263.82

Robust standard errors in parentheses clustered by state.

^***p<0.01,

^**p<0.05,

^*p<0.1

^*The dependent variable is actual (observed) changes in benchmarks. The main simulated benchmark strips out the “own-county” FFS update path and replaces it with the “state-not-self” FFS update path, as described in the text. The alternate simulated benchmark omits the “own-county” FFS update without replacing it with anything, allowing all benchmark updates to follow the 2%, national FFS growth rate, or floor updates. Both instruments are also discussed in Baicker, Chernew, and Robbins (2013, same issue). All covariates are at the market level. FFS costs are actual realized Medicare Part A and Part B costs among fee-for-service beneficiaries. Markets are determined using HMO plans in the Medicare Advantage program. All amounts are inflated to 2012 U.S. dollars.

The results show that the main simulated benchmark explains a significant amount of the variation in observed benchmark changes, controlling for covariates with market fixed effects and standard errors clustered by state (coefficient on the IV is 0.9.4, t-statistic of 22). Given that the potentially endogenous own-county FFS update path was binding only a small minority of the time, it is not surprising that the simulated benchmark generates similar updates for most counties. The very high F-statistic of around 250 strongly rejects the hypothesis that simulated benchmarks are uncorrelated with the actual benchmarks. However, such a close cousin of the observed benchmark raises the question of whether OLS estimation would be sufficient. We conduct a Durbin-Wu-Hausman test of the null hypothesis that the observed benchmark is exogenous, and find that we cannot reject the null hypothesis (p=0.45). When we include both instruments in the first stage, we similarly cannot reject the null hypothesis (p=0.35). Thus, we believe the theoretical advantage of the simulated benchmark is small in practice. We report OLS estimates as well and compare them with the IV estimates. The OLS model is similar to the base analysis in Song, Landrum, and Chernew (2012), but includes 2010 data and HHI. Overall, the OLS and IV estimates of interest differ by less than 10% in magnitude.

Main estimates

Table 2 presents the main IV estimates and sensitivity analyses for HMO plan markets. We find a positive and robust effect of benchmark changes on changes in plan bids. We find in our base specification that, on average, a $1 increase in the benchmark leads to a $0.53 increase in bids (S.E. = $0.06) (column 1). This result is largely robust to sensitivity analyses. Omitting plan enrollee risk or FFS beneficiary risk did not appreciably change the main estimate, which suggests that differential selection did not play a major role (columns 2–3). Models using a linear yearly trend, omitting the fixed population weights, and restricting attention to large markets also produced estimates near $0.50 (columns 4–6). These tight estimates support the rejection of the perfectly competitive model.

Table 2.

Main estimates and sensitivity analyses (market-level model).^*

Variables	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
	Base IV	No county risk	No plan risk	Linear year	Unweighted	Large markets	Interaction	HHI	HHI* bench
Benchmark	0.534*** (0.0556)	0.549*** (0.0566)	0.542*** (0.0547)	0.519*** (0.0535)	0.521*** (0.0707)	0.544*** (0.0555)	0.699*** (0.164)	0.515*** (0.0541)	0.571*** (0.0772)
Risk (FFS)	−79.79** (32.24)		−75.10** (31.94)	−97.62*** (32.23)	−89.27** (36.56)	−74.40*** (28.19)	−80.64** (32.70)	−72.93** (29.90)	−70.53** (28.20)
Risk (Plan)	26.13 (19.01)	19.55 (20.37)		20.25 (19.78)	21.46 (19.44)	28.54 (22.24)	22.78 (19.37)	24.52 (18.83)	26.19 (17.64)
FFS cost	0.0686* (0.0383)	−0.0149 (0.0155)	0.0659* (0.0378)	0.0654* (0.0372)	0.112** (0.0467)	0.0584 (0.0363)	0.0702* (0.0396)	0.0639* (0.0356)	0.0606* (0.0330)
Pop (1000s)	0.00743 (0.0121)	0.00587 (0.0130)	0.00703 (0.0120)	0.0272** (0.0120)	0.0441 (0.0298)	0.00403 (0.0127)	0.0119 (0.0118)	−0.00581 (0.0129)	−0.00937 (0.0134)
Insurers	−1.138*** (0.145)	−0.993*** (0.121)	−1.080*** (0.157)	−1.489*** (0.139)	−1.642*** (0.272)	−1.082*** (0.139)	4.370 (4.060)	−0.983*** (0.160)	−1.039*** (0.185)
Insurers* Bench							−0.00634 (0.00471)
HHI (beds)								−0.00699*** (0.00271)	0.0237 (0.0248)
HHI* Bench									−3.56e-05 (2.88e-05)
Market FE	Y	Y	Y	Y	Y	Y	Y	Y	Y
Year FE	Y	Y	Y		Y	Y	Y	Y	Y
Year (linear)				6.597*** (1.283)
Observations	7,299	7,299	7,299	7,299	7,299	5,135	7,299	7,299	7,299
R-squared	0.398	0.391	0.397	0.366	0.353	0.408	0.396	0.406	0.408
Markets	1,762	1,762	1,762	1,762	1,762	1,229	1,762	1,762	1,762

Robust standard errors in parentheses clustered by state.

^***p<0.01,

^**p<0.05,

^*p<0.1

^*The base IV model with market fixed effects has average market bids as the dependent variable using data from 2006–2010. All covariates are at the market level. FFS costs are actual realized Medicare Part A and Part B costs among fee-for-service beneficiaries. Markets are determined using HMO plans in the Medicare Advantage program. All amounts are inflated to 2012 U.S. dollars.

We find a fairly consistently negative effect of competition (number of insurers) on bids across different specifications. We would expect this finding given that plans have an incentive to bid low in order to offer a higher rebate (extra benefits) to attract enrollees. On average, each market had 12.1 insurers in 2009, up from 7.9 in 2006, suggesting overall competition increased over these years. Analogously, the average number of insurers in a county (disaggregated from our market-level analysis) grew from 5.7 to 10.2 over this period, capturing the overlap of counties within markets. Overall, the insurer effect is small in magnitude; an extra insurer on the margin is associated with about a $1 decrease in average bids. In column 7, the negative sign on the interaction term, while small in magnitude and marginally significant, suggests that bids are less responsive to benchmarks in areas with more insurers. This is consistent with our interpretation of the positive relationship between bids and benchmarks being a sign of imperfect competition.

We find that bids are inversely related to provider market HHI (column 8). The HHI is a standard measure of provider concentration in a market, with higher HHI representing greater concentration (or less competition). This finding is consistent with an extensive literature that finds health care costs are higher in markets with more hospitals. For example, providers may compete on expensive services, often referred to as the medical arms race (Bates, Mukherjee, and Santerre, 2006; Berenson, Bazzoli, and Au, 2006; Town and Vistnes, 2001). Additionally, a greater availability of services may lead providers to induce demand (McGuire and Pauly, 1991). However, the relationship between benchmarks and bids does not vary according the provider competition in the market (column 9). The effect of benchmark changes on bids is largely robust to the inclusion of provider market HHI and the HHI-benchmark interaction.

Additional sensitivity analyses

Our major concern is that the change in benchmark is related to unobserved changes in costs. This is unlikely because we condition on actual FFS costs and the benchmark is related to lagged costs. Nevertheless, the correlation between benchmark levels and FFS cost levels is 0.68. However, the correlation of changes in benchmarks and changes in FFS costs is 0.36. This is similar to the correlation of the residuals of benchmarks and FFS costs (0.37).

Table 3 shows several sensitivity tests related to endogeneity, with the base IV model replicated in column 1. First, we repeated the base model omitting actual FFS costs (column 2). If instrumented benchmark changes were strongly related to costs, we would expect that omission of FFS costs to create a stronger bias and affect the coefficient. Yet, when we omit FFS costs, the benchmark effect on bids is only slightly larger ($0.53).

Table 3.

Sensitivity analyses concerning endogeneity (market-level model).

Variables	(1)	(2)	(3)	(4)	(5)	(6)	(7)
	Base IV	No FFS	2006–07	2008–09	OLS	OLS No FFS	OLS with HHI
Benchmark	0.534*** (0.0556)	0.555*** (0.0531)	0.537*** (0.0831)	0.519*** (0.0878)	0.495*** (0.0467)	0.521*** (0.0438)	0.472*** (0.0483)
Risk (FFS)	−79.79** (32.24)	−27.69* (15.35)	−111.2** (54.26)	−161.8*** (62.07)	−85.74*** (30.51)	−26.39* (14.42)	−78.90*** (28.68)
Risk (Plan)	26.13 (19.01)	23.75 (19.99)	−40.96 (36.02)	15.12 (23.94)	29.47 (19.91)	26.60 (20.21)	28.03 (19.02)
FFS cost	0.0686* (0.0383)		0.161** (0.0710)	0.00431 (0.0415)	0.0782** (0.0373)		0.0740** (0.0359)
Pop (1000s)	0.00743 (0.0121)	0.00575 (0.0127)	−0.0630** (0.0279)	0.0619*** (0.0158)	0.0123 (0.0311)	0.0101 (0.0337)	−0.00148 (0.0323)
Insurers	−1.138*** (0.145)	−1.032*** (0.123)	−1.334*** (0.310)	−2.271*** (0.326)	−1.128*** (0.194)	−1.008*** (0.191)	−0.961*** (0.206)
HHI (beds)							−0.0075*** (0.00243)
Constant					306.4*** (37.62)	284.4*** (35.57)	338.9*** (39.65)
Market FE	Y	Y	Y	Y	Y	Y	Y
Year FE	Y	Y	Y	Y	Y	Y	Y
Observations	7,299	7,299	2,158	2,838	7,669	7,669	7,669
R-squared	0.398	0.394	0.397	0.524	0.399	0.395	0.407
Markets	1,762	1,762	1,079	1,419	2,132	2,132	2,132

Robust standard errors in parentheses clustered by state.

^***p<0.01,

^**p<0.05,

^*p<0.1

In 2007 and 2009, the updating of benchmarks underwent a “rebasing,” which is required by law to occur at least once every three years. The rebasing of benchmarks differentially increases lower benchmarks by more than higher ones, but is less likely tied to the annual change in costs. When we repeat our base model on just the 2006–2007 data, the effect of changes in benchmarks on bids is $0.54 (S.E. = $0.08) (column 3). Similarly, restricting our model to the 2008–09 data produces an effect of $0.52 (S.E. = $0.09) (column 4). The 2008–2009 period is particularly relevant because benchmark updates in 2060 of the approximately 3200 counties were determined by changes in floor payments, which are most likely exogenous to market level changes in cost.

Additionally, an OLS estimate of equation (6) is consistent with our base IV model, demonstrating that a dollar increase in benchmarks leads to about a $0.50 increase in bids (column 5). Similar to column 2, the last column repeats the OLS model omitting actual FFS costs. Again, the benchmark effect is marginally higher when FFS costs are omitted ($0.52).

The coefficient on benchmark in our logarithmically transformed GLM model indicated that a 1 percent increase in benchmark leads to a 0.62 percent (standard error 0.07) increase in bids (not shown). Transforming this estimate into dollars gives a prediction of $0.52, consistent with our base model and sensitivity analyses.

In the Appendix, we present analogous main estimates and sensitivity analyses when LPPO and PFFS plans are included in the market aggregation. In general, we find that the effect of benchmark changes on bids is slightly attenuated but largely consistent: $0.49 with LPPOs included (Appendix Table 1) and $0.43 with LPPOs and PFFS included (Appendix Table 2). Less managed MA plans, particularly PFFS plans, are largely located in small or rural counties. This suggests that PFFS plans may be more responsive to competition than HMO and LPPO plans, which is consistent with the larger negative coefficient on “number of insurers” in the sample with LPPO and PFFS plans included. HMO, LPPO, and PFFS plans all compete with each other simultaneously as they face the same benchmarks in all counties and enrollees are free to choose among them.

Appendix Table 1.

Effect of benchmark on bids, market-level longitudinal model (HMO and local PPO plans).^*

Variables	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
	Base IV	No county risk	No plan risk	Linear year	Unweighted	Large markets	Interaction	HHI	HHI* bench
Benchmark	0.491*** (0.0479)	0.516*** (0.0496)	0.493*** (0.0484)	0.434*** (0.0475)	0.482*** (0.0622)	0.504*** (0.0484)	0.598*** (0.132)	0.471*** (0.0463)	0.547*** (0.0636)
Risk (FFS)	−101.2** (41.06)		−100.7** (41.63)	−123.9*** (38.37)	−72.57 (46.46)	−105.3*** (30.17)	−103.3** (41.97)	−91.99** (38.95)	−87.52** (36.81)
Risk (Plan)	6.153 (21.61)	3.192 (22.85)		14.38 (22.97)	1.211 (22.49)	3.348 (22.16)	2.016 (22.41)	6.320 (21.24)	9.456 (20.52)
FFS cost	0.0994** (0.0491)	−0.00817 (0.0171)	0.0994** (0.0490)	0.103** (0.0461)	0.105* (0.0585)	0.0996** (0.0408)	0.103** (0.0505)	0.0922* (0.0472)	0.0858* (0.0445)
Pop (1000s)	0.00944 (0.0117)	0.00310 (0.0127)	0.00920 (0.0119)	0.0427*** (0.0129)	0.0578 (0.0354)	0.00418 (0.0122)	0.0134 (0.0123)	−0.00730 (0.0128)	−0.0131 (0.0127)
Insurers	−1.399*** (0.168)	−1.208*** (0.164)	−1.385*** (0.169)	−1.953*** (0.169)	−1.914*** (0.376)	−1.312*** (0.172)	2.175 (3.369)	−1.225*** (0.180)	−1.294*** (0.193)
Insurers* Bench							−0.00414 (0.00397)
HHI (beds)								−0.00779** (0.00304)	0.0312* (0.0182)
HHI* Bench									−4.55e-05** (1.98e-05)
Market FE	Y	Y	Y	Y	Y	Y	Y	Y	Y
Year FE	Y	Y	Y		Y	Y	Y	Y	Y
Year (linear)				8.057*** (1.084)
Observations	8,731	8,731	8,731	8,731	8,731	5,795	8,731	8,731	8,731
Partial R2	0.408	0.398	0.408	0.360	0.369	0.422	0.407	0.416	0.420
Markets	2,058	2,058	2,058	2,058	2,058	1,357	2,058	2,058	2,058

Robust standard errors in parentheses clustered by state.

^***p<0.01,

^**p<0.05,

^*p<0.1

^*Note that the number of markets increases as compared with the HMO sample. This is because in many (rural) counties, there can be a lack of HMO plans. Local PPOs and often PFFS plans are serving such counties.

Appendix Table 2.

Effect of benchmark on bids, market-level longitudinal model (HMO, local PPO, and PFFS plans).

Variables	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
	Base IV	No county risk	No plan risk	Linear year	Unweighted	Large markets	Interaction	HHI	HHI* bench
Benchmark	0.431*** (0.0945)	0.494*** (0.101)	0.468*** (0.0831)	0.447*** (0.0704)	0.386*** (0.0912)	0.459*** (0.0881)	0.467*** (0.145)	0.435*** (0.0995)	0.485*** (0.144)
Risk (FFS)	−233.0*** (59.62)		−224.9*** (58.89)	−243.2*** (59.14)	−206.0*** (55.59)	−231.7*** (62.73)	−229.0*** (61.12)	−221.6*** (62.95)	−223.5*** (63.43)
Risk (Plan)	89.00*** (27.41)	82.66*** (30.90)		80.94*** (29.29)	88.28*** (27.46)	74.09* (41.42)	86.20*** (28.60)	87.33*** (27.47)	89.66*** (27.23)
FFS cost	0.281*** (0.0785)	0.0386 (0.0299)	0.278*** (0.0770)	0.262*** (0.0740)	0.319*** (0.0729)	0.254*** (0.0808)	0.276*** (0.0801)	0.269*** (0.0827)	0.271*** (0.0832)
Pop (1000s)	−0.0449* (0.0251)	−0.0585** (0.0249)	−0.0465** (0.0235)	0.0283 (0.0199)	0.0240 (0.0396)	−0.0559* (0.0301)	−0.0311 (0.0196)	−0.0587** (0.0246)	−0.0673** (0.0297)
Insurers	−1.514*** (0.357)	−1.214*** (0.384)	−1.345*** (0.345)	−2.480*** (0.335)	−2.340*** (0.571)	−1.255*** (0.396)	1.377 (4.856)	−1.391*** (0.360)	−1.370*** (0.354)
Insurers* Bench							−0.00348 (0.00577)
HHI (beds)								−0.00783* (0.00427)	0.0116 (0.0234)
HHI* Bench									−2.41e-05 (2.76e-05)
Market FE	Y	Y	Y	Y	Y	Y	Y	Y	Y
Year FE	Y	Y	Y		Y	Y	Y	Y	Y
Year (linear)				13.74*** (0.765)
Observations	15,267	15,267	15,267	15,267	15,267	6,860	15,267	15,267	15,267
Partial R(2)	0.710	0.685	0.702	0.682	0.728	0.690	0.710	0.712	0.712
Markets	3,105	3,105	3,105	3,105	3,105	1,394	3,105	3,105	3,105

Robust standard errors in parentheses clustered by state.

^***p<0.01,

^**p<0.05,

^*p<0.1

7. Conclusion

This paper examines the competitive bidding system in MA, a relatively unstudied component of the MA program. Following upon prior work, we assessed the effect of benchmark changes on plan bids with an additional year of data and some refinements to our methodological approach. Consistent with our prior work, we found that a $1 increase in benchmark leads to approximately a $0.50 increase in bids among HMO plans in MA. Models of perfect competition predict that bids should be insensitive to changes in the benchmark. However, we demonstrate that bids move with benchmarks even after controlling for actual FFS costs, both plan (MA) and FFS beneficiary risk, as well as using plausibly exogenous variation in payment rates. Sensitivity analyses produced similar estimates.

Our results are consistent with several possible explanations. First, they are consistent with economic models of imperfect competition, in which insurers exercise their market power and use higher bids to boost profits at the expense of rebates to beneficiaries. Second, our findings are also consistent with providers exercising market power in their negotiations with insurers. Specifically, providers may observe (or anticipate) increases in the benchmark and capture some of the increase through negotiating for higher fees from the commercial plans. The extent to which providers, especially larger organizations, may be able to predict changes in the benchmark and changes their prices or negotiation is unknown. However, benchmark rates for each year tend to be published in early April of the prior year, presumably giving providers some time to respond. In this study, we cannot distinguish the relative contributions of insurer market power and provider market power to our resulting estimates.

This study has several limitations. Importantly, we do not observe actual plan costs. While we control for contemporaneous FFS costs in the model, unobserved plan costs could be different. For example, the risk profile of MA beneficiaries may be different from that of FFS Medicare beneficiaries, and MA plans may indirectly select for healthier beneficiaries through benefit design, advertising, or other means (Brown et al., 2011; Newhouse et al., 2012; Newhouse, 1996). We attempt to address this concern by controlling for FFS beneficiary and MA plan enrollee risk. We also acknowledge that the number of insurers may be a non-ideal proxy for insurer competition. Moreover, provider HHI as measured by hospital beds may not reflect provider competition accurately because provider consolidation may take place among physician practices without hospitals being involved. This is especially relevant in the current wave of provider consolidation in which primary care and specialty physician practices are merging or being acquired, often resulting in larger physician organizations that may affect prices but not the allocation of hospital beds across organizations.

Our findings have potential implications for proposals to expand the role of competitive bidding in Medicare, such as the Ryan-Wyden plan and Domenici-Rivlin proposal. These results suggest that competitive bidding markets in MA are not perfectly competitive and may not drive plan bids down to plan costs. Thus, they may temper the projected savings of replacing Medicare with a bidding system (Feldman, Coulam, and Dowd, 2012). Other models of bidding, including those in which the benchmark is not known in advance or is set for a larger geographic area, may yield different results. Still other settings in Medicare where bidding is used, such as the durable medical equipment market, may not necessarily reflect these implications.

As the debate over Medicare financing reform escalates, the design of market-based bidding mechanisms should be done with these cautions in mind. The bidding system in MA, in particular how administrative updates to the benchmark are determined, will likely benefit from knowledge of the nature of provider competition with respect to that of insurer competition within specific U.S. markets. That some major markets have one dominant insurer with several competing health systems, while other markets may concentrate market power on the provider side, likely has consequences for the plan’s cost structure and the degree to which insurers and provider organizations are able to extract surplus from updates to the benchmark. We encourage future research to further expand the understanding of bidding markets in Medicare.