Convergent Rhythm Generation from Divergent Cellular Mechanisms

Abstract

Different modulatory inputs commonly elicit distinct rhythmic motor patterns from a central pattern generator (CPG), but they can instead elicit the same pattern. We are determining the rhythm-generating mechanisms in this latter situation, using the gastric mill (chewing) CPG in the crab (Cancer borealis) stomatogastric ganglion, where stimulating the projection neuron MCN1 (modulatory commissural neuron 1) or bath applying CabPK (C. borealis pyrokinin) peptide elicits the same gastric mill motor pattern, despite configuring different gastric mill circuits. In both cases, the core rhythm generator includes the same reciprocally inhibitory neurons LG (lateral gastric) and Int1 (interneuron 1), but the pyloric (food-filtering) circuit pacemaker neuron AB (anterior burster) is additionally necessary only for CabPK rhythm generation. MCN1 drives this rhythm generator by activating in the LG neuron the modulator-activated inward current (I_MI), which waxes and wanes periodically due to phasic feedback inhibition of MCN1 transmitter release. Each buildup of I_MI enables the LG neuron to generate a self-terminating burst and thereby alternate with Int1 activity. Here we establish that CabPK drives gastric mill rhythm generation by activating in the LG neuron I_MI plus a slowly activating transient, low-threshold inward current (I_Trans-LTS) that is voltage, time, and Ca²⁺ dependent. Unlike MCN1, CabPK maintains a steady I_MI activation, causing a subthreshold depolarization in LG that facilitates a periodic postinhibitory rebound burst caused by the regular buildup and decay of the availability of I_Trans-LTS. Thus, different modulatory inputs can use different rhythm-generating mechanisms to drive the same neuronal rhythm. Additionally, the same ionic current (I_MI) can play different roles under these different conditions, while different currents (I_MI, I_Trans-LTS) can play the same role.

Introduction

Different modulatory inputs enable individual neuronal networks to generate different output patterns by changing the intrinsic and synaptic properties of network neurons (Dickinson, 2006; Briggman and Kristan, 2008; Doi and Ramirez, 2008; Rauscent et al., 2009; Harris-Warrick, 2011; Marder, 2012). However, different modulatory inputs can also elicit the same activity pattern from that network (Saideman et al., 2007b). Determining how different modulatory pathways influence network activity is challenging, because these different pathways can converge onto the same direct inputs to a network (Di Prisco et al., 2000; Korn and Faber, 2005; Derjean et al., 2010; White and Nusbaum, 2011), comparably modulate the same network (Doi and Ramirez, 2010), distinctly alter multiple cellular and synaptic properties in the same circuit neurons (MacLean et al., 2003; Prinz et al., 2004a; Goaillard et al., 2009; Calabrese et al., 2011; Marder, 2012), and/or configure different circuits (Saideman et al., 2007b). The cellular mechanisms underlying the last of these processes are not determined in any system.

We are determining the cellular mechanisms that enable two differently configured, network-driven central pattern generator (CPG) circuits to generate the same biphasic motor pattern, using the isolated crab stomatogastric ganglion (STG; Marder and Bucher, 2007; Stein, 2009). These two gastric mill (chewing) circuits are configured by the projection neuron MCN1 (modulatory commissural neuron 1) and bath-applied CabPK (Cancer borealis pyrokinin) peptide (Saideman et al., 2007a,b).

The core rhythm generator for both gastric mill circuits includes the reciprocally inhibitory neurons LG (lateral gastric) and Int1 (interneuron 1). Rhythmic MCN1 transmitter release is also necessary for the MCN1–gastric mill rhythm, while the pyloric pacemaker neuron AB (anterior burster) is necessary for the CabPK rhythm. The cellular and synaptic mechanisms underlying MCN1-gastric mill rhythm generation are established (Coleman et al., 1995; Bartos et al., 1999; DeLong et al., 2009a,b). A key MCN1 rhythm-generating mechanism is its activation of the modulator-activated, voltage-dependent inward current (I_MI) in the LG neuron, which waxes and wanes periodically due to rhythmic feedback inhibition of MCN1 transmitter release by LG. These events enable the LG neuron to periodically fire a self-terminating burst and alternate with Int1 activity.

Here we identify two CabPK-activated currents in the LG neuron that are necessary and sufficient for gastric mill rhythm generation. These currents include I_MI and a transient, low-threshold, slowly activating inward current (I_Trans-LTS). I_Trans-LTS exhibits voltage- and time-dependent properties. CabPK-gastric mill rhythm generation results from I_MI providing a constant depolarizing drive that enables periodic postinhibitory rebound (PIR) bursting, triggered by I_Trans-LTS. The rhythmic nature of the PIR burst generation results from the time- and voltage-dependent properties of I_Trans-LTS. Computational modeling and dynamic-clamp (DClamp) manipulations of these two currents support their necessity and sufficiency for CabPK–gastric mill rhythm generation, and reveal that the pyloric rhythm (AB)-timed influence on the LG neuron is necessary for triggering each PIR burst. Thus, distinct rhythm-generating mechanisms enable distinct circuits to generate the same rhythmic activity. Additionally, the same ionic current (I_MI) plays a different role under these two conditions, whereas different currents (I_MI, I_Trans-LTS) play a comparable role.

Materials and Methods

Animals.

Male Jonah crabs (C. borealis) were purchased from commercial suppliers (Fresh Lobster, Marine Biological Laboratory) and maintained in aerated, filtered artificial seawater at 10–12°C. Animals were cold anesthetized by packing them in ice for at least 30 min before dissection, after which the foregut was removed, in physiological saline at ∼4°C, and the stomatogastric nervous system (STNS) isolated.

Solutions.

C. borealis physiological saline contained the following (in mm): 440 NaCl, 26 MgCl₂, 13 CaCl₂, 11 KCl, 10 Trisma base, 5 maleic acid, and 5 glucose, pH 7.4–7.6. All preparations were superfused continuously with C. borealis saline (8–12°C). CabPK-I or CabPK-II (Saideman et al., 2007a; Biotechnology Center, University of Wisconsin, Madison, WI) was diluted from a stock solution (10⁻³ m) into physiological saline or voltage-clamp saline immediately before use. Bottles containing C. borealis saline and CabPK saline were connected to the same switching manifold for rapid solution changes. Oxotremorine (OXO; 10⁻⁵ m; Sigma), a muscarinic agonist, was applied in the same manner.

For voltage-clamp experiments, tetrodotoxin (TTX; 10⁻⁷ m; Sigma), picrotoxin (PTX; 10⁻⁵ m; Sigma), and tetraethylammonium chloride (TEACl; 10⁻² m; Sigma) were added to C. borealis saline (i.e., voltage-clamp saline). These substances were used to suppress voltage-dependent Na⁺ currents (TTX), glutamatergic inhibitory synaptic transmission (PTX), and a subset of K⁺ currents (TEACl; Marder and Eisen, 1984; Golowasch and Marder, 1992). In some experiments, the microelectrode was filled with a solution of CsCl (1 m; Sigma) and TEACl (1 m) to additionally suppress a subset of K⁺ currents. To test the sensitivity of CabPK-influenced currents to extracellular Na⁺, in some experiments Na⁺ in the saline was replaced by NMDG⁺ (n-methyl, d-glucamine; Fluka; Golowasch and Marder, 1992). The NMDG⁺ was added to the solution first and then neutralized with HCl before adding all other components. Additionally, in some experiments we used flufenamic acid (FFA; 10⁻⁵ m; Sigma), an inhibitor of Ca²⁺-activated, nonspecific cation current (I_CAN), dissolved in dimethylsulfoxide (DMSO) and added directly to C. borealis saline. The final DMSO concentration never exceeded 1%.

Electrophysiology.

Electrophysiology experiments were performed using standard techniques for this system (Beenhakker and Nusbaum, 2004). In brief, the isolated STNS (Fig. 1A) was pinned into a silicone elastomer (Sylgard 184, K.R. Anderson)-lined Petri dish. Extracellular nerve recordings were obtained using pairs of stainless steel wire electrodes (reference and recording) whose ends were pressed into the Sylgard-coated dish. A differential AC amplifier (Model 1700, AM Systems) amplified the voltage difference between the reference wire, in the main bath compartment, and the recording wire, isolated with a section of an individual nerve from the main bath compartment by petroleum jelly (Vaseline, Lab Safety Supply). This signal was then further amplified and filtered (Model 410 Amplifier; Brownlee Precision). For extracellular nerve stimulation, the pair of wires used to record nerve activity was placed into a stimulus isolation unit (Model SIU5; Astromed/Grass Instruments) connected to a stimulator (Model S88; Astro-Med/Grass Instruments).

Figure 1.

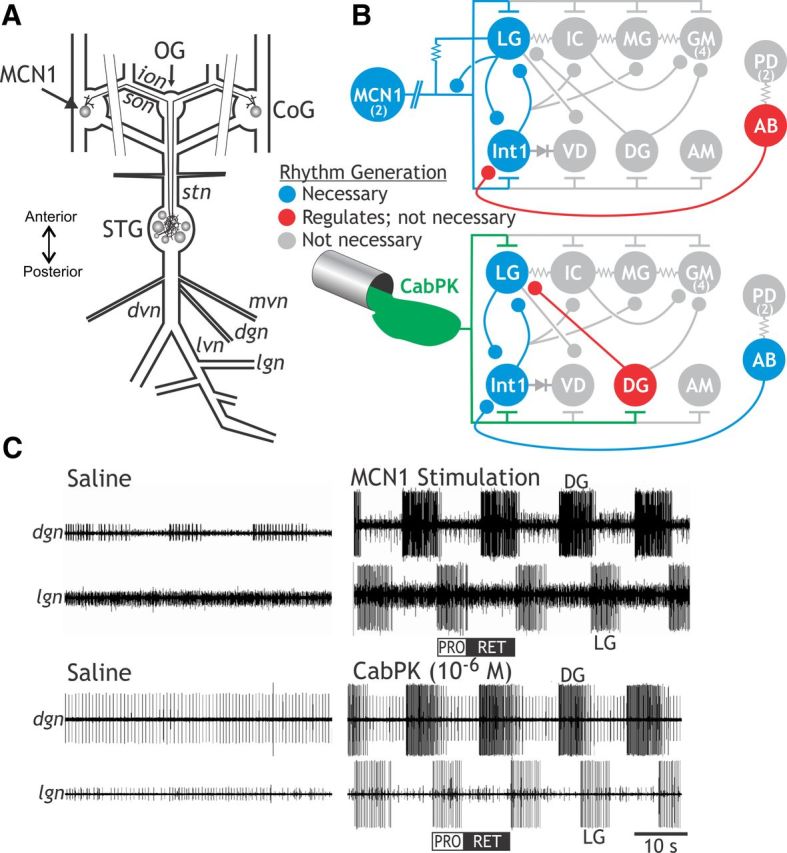
The projection neuron MCN1 and bath-applied CabPK peptide configure different gastric mill circuits but elicit the same gastric mill motor pattern. A, Schematic of the isolated STNS, including its four ganglia [paired CoGs, oesophageal ganglion (OG), STG] plus their connecting nerves and a subset of the peripheral nerves. Paired parallel lines crossing the superior oesophageal nerves (sons) and inferior oesophageal nerves (ions) represent their bisection, which occurred at the start of each experiment to separate the STG from the CoGs. dgn, dorsal gastric nerve; dvn, dorsal ventricular nerve; lgn, lateral gastric nerve; lvn, lateral ventricular nerve; mvn, medial ventricular nerve; stn, stomatogastric nerve. B, Schematic of the gastric mill circuit configured by MCN1 stimulation (top) and CabPK peptide superfusion (bottom). t bars, excitation; filled circles, inhibition; resistors, nonrectifying electrical coupling; diode, rectifying electrical coupling. Parallel lines crossing the MCN1 axon represent additional distance between the MCN1 soma in each CoG and its axon terminals in the STG. Numbers in parentheses indicate the copy number per STNS for each neuron type when it is present as more than one copy. C, MCN1 stimulation and CabPK bath application elicit the same gastric mill motor pattern. These two manipulations were performed in different preparations. From Saideman et al. (2007b). PRO, Protraction; RET, retraction.

For current-clamp experiments, intrasomatic recordings of STG neurons were made with sharp glass microelectrodes (15–30 MΩ) filled with either K₂SO₄ (0.6 m) plus KCl (10 mm) or KCl (1 m). For voltage-clamp experiments, neurons were impaled with separate recording and current injection electrodes. The recording electrode, in most experiments, contained CsCl (1 m) and TEACl (1 m) to suppress additional K⁺ currents. The current injection electrode was filled with KCl (2.5 m). All intracellular recordings were amplified using Axoclamp 900A amplifiers (Molecular Devices) in bridge mode or discontinuous current-clamp mode (2–5 kHz sampling rate) and digitized at 5 kHz using a Micro 1401 data acquisition interface and Spike2 software (Cambridge Electronic Design). To facilitate intracellular recording, the desheathed STG was viewed with light transmitted through a dark-field condenser (Nikon). In all experiments, the STG was isolated from the commissural ganglia (CoGs) by bisecting the inferior and superior oesophageal nerves (Fig. 1A). Individual STNS neurons were identified by their axonal pathways, activity patterns, and interactions with other neurons (Weimann et al., 1991; Blitz et al., 1999; Beenhakker and Nusbaum, 2004).

During the gastric mill rhythm, the LG neuron burst defines the protractor phase while its interburst duration, which is equivalent to the duration of Int1 activity, defines the retractor phase (Coleman et al., 1995; Bartos et al., 1999; Diehl et al., 2013). In experiments where Int1 activity was suppressed by hyperpolarizing current injection to trigger PIR in the LG neuron, the current was usually injected into the ventricular dilator (VD) neuron instead of directly into Int1. These two neurons are electrically coupled, VD has a larger soma and therefore is easier to impale and manipulate, and VD has no direct synapse onto LG (Fig. 1B). Suppressing Int1 activity via this approach was routinely confirmed by the absence of unitary IPSPs in LG, insofar as Int1 is the only source of unitary IPSPs in LG in the isolated STG. The hyperpolarizing current duration used to elicit PIR was standardized at 5 s, which approximates the retraction phase (Int1 active) duration of the gastric mill rhythm (Saideman et al., 2007b). The PIR burst was defined as having a minimum of three spikes with interspike intervals ≤2 s. In the TTX experiments, the PIR response was measured as the amount of depolarization following the hyperpolarizing step relative to the baseline voltage before the step.

Two-electrode voltage-clamp.

We used two-electrode voltage-clamp (TEVC) to record currents in the LG neuron. In these experiments, LG was impaled with designated recording and current-injecting electrodes. Recordings were used only if they exhibited a minimum input resistance (R_input) of 5 MΩ. The range of R_input was 5–15 MΩ. Protocols were developed and injected using pClamp software (Molecular Devices).

Modulator-activated currents were identified using two basic voltage-clamp protocols, including ramps and steps. I_MI was isolated by injecting voltage ramps into LG (−90 to 0 mV at 75 mV/s) in the presence of CabPK peptide (10⁻⁶ m) and saline, after which the currents recorded in control saline were subtracted from those recorded with peptide present (Swensen and Marder, 2000; DeLong et al., 2009a). In some experiments, voltage ramps were used instead to identify I_MI activated by OXO (10⁻⁵ m) application. I_MI was originally described by Golowasch and Marder (1992) as a proctolin-activated current and thus designated I_proct. However, many modulators are now known to activate this current in the STG (Swensen and Marder, 2000, 2001), so it is now designated as I_MI (DeLong et al., 2009a; Grashow et al., 2009).

Transient currents cannot be reliably identified with ramp protocols so, to determine whether any transient currents were influenced by CabPK, we also implemented a standard prestep voltage-clamp step protocol. To characterize CabPK-influenced transient currents, we obtained estimations of their activation (m) and inactivation (h) parameters by independently varying the holding voltage, prestep voltage, prestep duration, and step voltage, focusing primarily on the physiological range of LG membrane potentials (−65 to −30 mV). To measure the voltage dependence of activation, LG was hyperpolarized to a prestep voltage of −80 mV for 10 s followed by a step depolarization to a voltage between −65 and 0 mV, in 5 mV increments. To determine the voltage dependence of deinactivation of the CabPK-influenced transient currents, the LG neuron was held at −45 mV and given a hyperpolarizing prestep to −50, −60, −70, or −80 mV for 10 s, and then stepped back to −45 mV for 6 s. To measure the time dependence of deinactivation, LG was given a hyperpolarizing prestep to −80 mV for a range of durations (1–13 s) and then depolarized to −40 mV for 6 s. Currents measured in normal saline were subtracted from those measured during CabPK bath application (10⁻⁶ m). In all figures, unless otherwise indicated, the subtracted currents (CabPK saline − normal saline) are displayed. We assessed the sensitivity of the I_Trans-LTS to Ca²⁺ influx by replacing most of the Ca²⁺ in the saline with equimolar Mn²⁺ (0.1× Ca²⁺ saline). We also determined the sensitivity of I_Trans-LTS to Na⁺ influx by replacing Na⁺ with an equimolar concentration of NMDG⁺.

Dynamic clamp.

We used the dynamic-clamp to inject artificial versions of ionic [I_MI, transient, low-threshold fast inward current (I_Trans-LTF), I_Trans-LTS] and synaptic (Int1-mediated inhibition) currents into the LG neuron (Sharp et al., 1993; Bartos et al., 1999; Prinz et al., 2004b; Beenhakker et al., 2005; DeLong et al., 2009a,b; DeLong and Nusbaum, 2010; Blitz and Nusbaum, 2012). The dynamic-clamp software used the intracellularly recorded LG neuron membrane potential to calculate and continually update an artificial, dynamic-clamp current (I_dyn), using a predetermined reversal potential and a conductance [g_dyn(t)] that was numerically computed. The injected current was based on real-time computations, updated in each time step (0.2 ms) according to the new values of recorded membrane potential, and injected back into the LG neuron. The currents were computed according to the following equations:

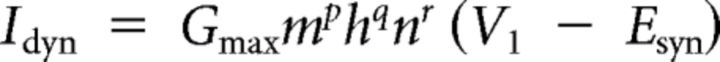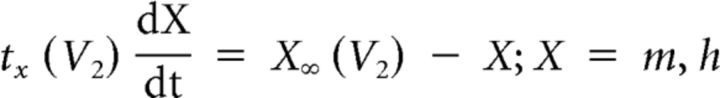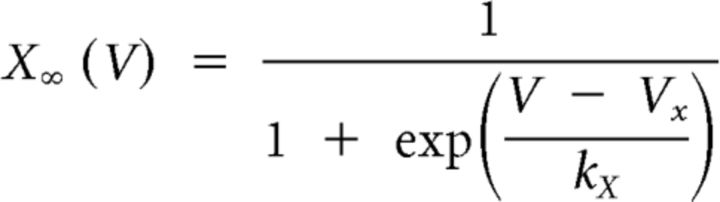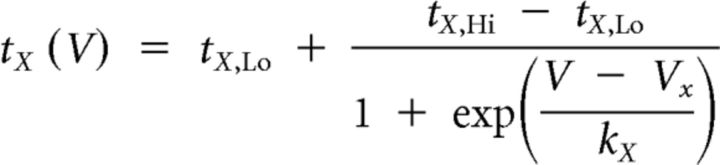where V₁ and V₂ both represent the membrane potential, and X represents either m or h for calculations involving activation or inactivation, respectively. The values are provided in Table 1.

Table 1.

Dynamic-clamp conductances

Neuron	Conductances	Parameters	V1/2 (mV)	k (mV)	tlo (ms)	thi (ms)	Exp (p, q, r)	Erev	Gmax
LG (biological)	ITrans-LTS	m	−50	−3	500	500	1	10	0.6
		h	−58	0.8	3500	1500	1
	IMI	m	−50	−5	5	5	1	10	0.1
Int1 (model)	Nav	m	−42	−5	1.5	0.45	3	45	7.5
		h	−52	9.2	10	2.4	1
	KV	m	−26	−9	27	3	4	−70	30
		h	−16	1.5	20	200	2
	Leak							−60	0.012
Int1 > LG	Synapse	m	−40	−1	200	200	1	−80	2
LG > Int1	Synapse	m	−30	−0.1	200	200	1	−80	15

V_1/2, half-activation voltage; E_rev, reversal potential.

We modeled our dynamic-clamp I_MI using previously determined parameters (Table 1; Golowasch and Marder, 1992; Swensen and Marder, 2000, 2001; DeLong et al., 2009a). Specifically, we set the half-maximum voltage of the activation curve at −42 mV, with the peak current occurring at −32 mV and the reversal potential (E_syn) at 0 mV. These values reflect the ones obtained from intraneurite LG neuron recordings within the STG neuropil (DeLong et al., 2009a). Hence, they occur at more hyperpolarized potentials than those obtained in the current study from intrasomatic recordings, which are electrotonically more distant from the site of these events within the neuropil. I_MI shows a voltage dependence to its activation (Golowasch and Marder, 1992; Swensen and Marder, 2000, 2001). Therefore, the integer power of the activation variable m(P) was set to a value of 1. The slope of the activation curve (K_m) was −5.0 mV, and the time constant of activation was 5.0 s⁻¹. I_MI does not inactivate, so the integer power of the inactivation variable h (abbreviated q above) was set to 0. The conductance value at maximum activation (G_max) varied between 50 and 200 nS. In all of our dynamic-clamp experiments, the maximum current injected into the LG neuron never exceeded 3 nA (see Results). Synaptic conductances were modeled in a manner similar to intrinsic conductances, except that activation depended on the presynaptic neuron voltage and was more depolarized than the presynaptic action potential threshold. These synapses have been well documented and incorporated into previous models of gastric mill rhythm generation (Nadim et al., 1998; Bartos et al., 1999; Kintos et al., 2008; DeLong and Nusbaum, 2010; Blitz and Nusbaum, 2012), and the G_max could be readily scaled to match the observed physiological synapses.

Our dynamic-clamp model for both of the low-threshold transient currents was based on the aforementioned voltage-clamp step protocol experiments. The results from activation protocols were manually fit to Hodgkin–Huxley equations using HHfit (version 3.2) software developed by the Nadim laboratory [New Jersey Institute of Technology (NJIT) and Rutgers University, Newark, NJ; available at http://stg.rutgers.edu/software/]. Occasionally, the resting V_m and action potential threshold coordinately varied between preparations, possibly due to impalement quality. Therefore, the dynamic-clamp parameters were linked to the resting V_m. Table 1 contains a full parameter set for a neuron resting at −60 mV.

We used two versions of the dynamic-clamp on a personal computer (PC) running Windows XP/7 and a NI PCI-6070-E data acquisition board (National Instruments). The first version was developed in the Nadim laboratory (NJIT and Rutgers University, Newark, NJ; available at http://stg.rutgers.edu/software/). The second version was developed by E. Brady Trexler (Fishberg Department of Neuroscience, Mt. Sinai School of Medicine; freely available through Gotham Scientific: http://gothamsci.com/NetClamp/). Dynamic-clamp current injections were performed while recording in single-electrode, DCC mode (sampling rates, 2–5 kHz) or with separate voltage recording and current-injecting electrodes.

Data analysis.

Data were collected onto a computer, with later playback onto a chart recorder (Everest; Astro-Med). Acquisition onto the computer (sampling rate, 5 kHz) used the Spike2 data acquisition and analysis system (Cambridge Electronic Design). Some analyses, including CabPK–gastric mill rhythm parameters, were conducted on the digitized data using a custom-written Spike2 program (The Crab Analyzer: freely available at http://www.neurobiologie.de/spike2).

Voltage-clamp data analysis was performed using PClamp (version 9; Molecular Devices), Spike2 (CED), and Igor Pro (Wavemetrics) software. For ramps, total neuron currents were determined by averaging 10 ramps in each condition and subtracting the control from the experimental condition. For prestep protocols, the protocols were run once in each condition and the control currents were subtracted before analysis.

For gastric mill rhythm analyses, unless otherwise stated, each data point in a dataset was derived by determining the mean for the analyzed parameter from 10 consecutive gastric mill cycles. One gastric mill cycle was defined as extending from the onset of consecutive LG neuron action potential bursts (Beenhakker and Nusbaum, 2004; Wood et al., 2004). Thus, the gastric mill cycle period was measured as the duration (in seconds) between the onset of two successive LG neuron bursts. The protractor phase was measured as the LG neuron burst duration, while the retractor phase was measured as the LG neuron interburst duration. The gastric mill rhythm-timed LG neuron burst duration was defined as the duration (in seconds) between the onset of the first and last action potential within an impulse burst, during which no interspike interval was >1.5 s (approximately one pyloric cycle period during the CabPK–gastric mill rhythm and briefer than the duration of each gastric mill phase; Saideman et al., 2007b). The intraburst firing rate of the LG neuron was defined as the number of action potentials − 1, divided by the burst duration.

Data were plotted with Igor Pro (version 6.10A). Figures were produced using CorelDraw (version 13.0 for Windows). Statistical analyses were performed with Microsoft Excel and SigmaStat 3.0 (SPSS). Comparisons were made to determine statistical significance using the paired Student's t test or ANOVA with repeated-measures followed by the Student–Newman–Keuls (SNK) post hoc test. In all experiments, the effect of each manipulation was reversible, and there was no significant difference between the premanipulation and postmanipulation groups. Data are expressed as the mean ± SE.

Gastric mill model.

We constructed a computational model of the CabPK-gastric mill rhythm generator modified from an existing conductance-based model of the MCN1–gastric mill rhythm generator (Nadim et al., 1998; Beenhakker et al., 2005; DeLong et al., 2009a,b). The previously published version modeled the LG, Int1, and MCN1 neurons as having multiple compartments separated by an axial resistance, with each compartment possessing intrinsic and/or synaptic conductances. The parameters of the CabPK–gastric mill rhythm generator model were based on both previously published voltage-clamp analyses in STG neurons (including LG) and on the LG neuron voltage-clamp results obtained in this study (Golowasch and Marder, 1992; Swensen and Marder, 2000, 2001; DeLong et al., 2009a). To mimic the effects of CabPK bath application to the biological system, we added I_MI to the LG neuron dendrite compartment as an intrinsic (nonsynaptically activated) current (Table 2). This approach was based on the fact that CabPK excites LG by activating I_MI (this study) and that CabPK was constantly present during its application. To more realistically mimic the biological system, in this version of the model we modified the CabPK-activated G_MI in the LG neuron dendrite compartment to include a voltage dependence (Table 2). Based on data collected in this study, we also added a CabPK-activated I_Trans-LTS to the LG neuron (Table 2). The time and voltage dependence of I_Trans-LTS were empirically determined in the present study with voltage-clamp analyses.

Table 2.

CabPK–gastric mill network model parameters

Neuron	Conductances	Parameters	V1/2 (mV)	k (mV)	tlo (ms)	thi (ms)	Exp (p, q, r)	Erev	Gmax
LG	ITrans-LTS	m	−55	−3	500	500	1
		h	−63	0.8	3500	1500	1
	IMI	m	−60	−5	5	5	1
Int1	Nav	m	−42	−5	1.5	0.45	3	45	7.5
		h	−52	9.2	10	2.4	1
	KV	m	−26	−9	27	3	4	−70	30
		h	−16	1.5	20	200	2
	Leak							−60	0.012
Int1 > LG	Synapse	m	−40	−1	200	200	1	−80	2
LG > Int1	Synapse	m	−30	−0.1	200	200	1	−80	15

V_1/2, half-activation voltage; E_rev, reversal potential.

Simulations were performed on a PC with the freely available Ubuntu Linux operating system (www.ubuntu.com). We used the Network simulation software developed in the Nadim laboratory (http://stg.rutgers.edu/software/network.htm). This included using a fourth-order Runge–Kutta numerical integration method with time steps of 0.05 and 0.01 ms. Results were visualized by plotting outputted data points using the freely available Gnuplot software package (www.gnuplot.info). In most figures showing the model output, we present conductance (g) instead of the associated current (I) to more clearly display the trajectory during the gastric mill retractor and protractor phases. The main difference between g and I is that the former lacks the fast transient changes that occur in the latter during each LG neuron action potential (DeLong et al., 2009a). In particular, the relatively slow kinetics of the CabPK-activated conductances make them insensitive to these fast transient changes in voltage.

The presentation of currents in the model and dynamic-clamp figures represent different conventions. Specifically, the model output uses the standard voltage-clamp convention, whereas the dynamic-clamp output uses the standard current-clamp convention. For example, depolarizing current has a downward trajectory in the model output figures but has an upward trajectory in the dynamic-clamp output figures.

Results

In the isolated crab STG, tonic MCN1 stimulation and bath-applied CabPK (≥10⁻⁷ m) elicit comparable gastric mill motor patterns, despite configuring different gastric mill circuits (Fig. 1B; Saideman et al., 2007b). MCN1 does not contain CabPK, and the CabPK–gastric mill rhythm can occur without MCN1 activity. CabPK is present in two or three pairs of CoG projection neurons that innervate the STG, although these neurons are not physiologically identified (Saideman et al., 2007a). However, bath-applied peptide can mimic the actions resulting from its neuronal release. For example, in the crab STG, bath application of the peptide proctolin (10⁻⁶ m) and direct stimulation of the modulatory proctolin neuron (MPN) elicit comparable responses from the pyloric CPG, despite the fact that MPN contains a small-molecule cotransmitter (Nusbaum and Marder, 1989a,b; Blitz et al., 1999).

There are also at least several additional gastric mill motor patterns in C. borealis, each distinct from the pattern elicited by MCN1 and CabPK, and driven by a different input pathway (Beenhakker and Nusbaum, 2004; Blitz et al., 2004; Christie et al., 2004; White and Nusbaum, 2011). These different rhythms all share the same basic structure, which includes a biphasic motor pattern exhibiting rhythmic alternating bursting of protraction- and retraction-related neurons across an overlapping range of cycle periods (∼5–20 s; Fig. 1C). They differ in the relative timing, intensity, duration, and pattern of activity in the component neurons. There are seven gastric mill motor neurons, including four protractor motor neurons and three retractor motor neurons, plus a single retraction-timed interneuron (Int1; Fig. 1B). As discussed below, the pyloric CPG pacemaker neuron AB also influences these gastric mill rhythms (Fig. 1B). Like the gastric mill rhythm, the pyloric (filtering of chewed food) rhythm is generated in the STG (Marder and Bucher, 2007).

A core component of the rhythm generator for the MCN1– and CabPK–gastric mill rhythms is the half-center formed by the reciprocally inhibitory protraction neuron LG and retraction neuron Int1 (Saideman et al., 2007b; Fig. 1B). The biphasic rhythm generated by these two neurons is then imposed on the other gastric mill neurons by synaptic actions from the rhythm generator plus the influences of MCN1 or CabPK. Under baseline conditions, the LG neuron is silent (Fig. 1C), and Int1 is spontaneously active, exhibiting a pyloric rhythm-timed activity pattern due to inhibitory input that it receives from the AB neuron (Fig. 1B; Bartos et al., 1999; Saideman et al., 2007b). The pivotal event for enabling gastric mill rhythm generation is the acquisition by the LG neuron of the ability to fire rhythmic bursts.

The cellular and synaptic mechanisms underlying MCN1 activation of the gastric mill rhythm generator are known (Coleman et al., 1995; Bartos et al., 1999; DeLong et al., 2009a). In brief, during the MCN1–gastric mill rhythm, there is a rhythmic release of the MCN1 cotransmitters, which include the peptides proctolin and CabTRP Ia (C. borealis tachykinin-related peptide Ia) plus GABA (Blitz et al., 1999). MCN1 uses only CabTRP Ia to influence LG (slow excitation) and only GABA to influence Int1 (fast excitation; Wood et al., 2000; Stein et al., 2007). MCN1 cotransmitter release is rhythmic, even when MCN1 is tonically active, because its STG terminals (MCN1_STG) receive ionotropic synaptic inhibition from LG (Fig. 1B; Coleman and Nusbaum, 1994). Thus, during retraction, continuous MCN1 release of CabTRP Ia drives a steady buildup of I_MI in LG that eventually is sufficient to enable LG to fire an action potential burst (DeLong et al., 2009a). During protraction, when MCN1_STG cotransmitter release is inhibited by LG, there is a steady decline in the amount of I_MI in LG until it can no longer sustain the LG neuron burst. This rhythmic activation of I_MI in LG appears to be sufficient to drive the gastric mill rhythm across the physiological range of MCN1 firing frequencies (DeLong et al., 2009a,b; DeLong and Nusbaum, 2010). MCN1-driven gastric mill rhythm generation is also facilitated by the pyloric rhythm (cycle period, ∼1 s), because every LG neuron burst initiates, after sufficient I_MI has accrued, during a pyloric-timed depolarization (i.e., disinhibition) that results from AB neuron inhibition of Int1 (Bartos et al., 1999; DeLong et al., 2009a). These disinhibitions reduce the MCN1–gastric mill cycle period by reducing the amount of I_MI-mediated depolarization needed to enable LG to fire a burst. However, this rhythm does persist, with a longer cycle period, when there is no pyloric rhythm (Bartos et al., 1999).

The cellular and synaptic mechanisms underlying the CabPK–gastric mill rhythm were not known, although it was determined previously that activity in LG, Int1, and AB was necessary to enable this rhythm (Saideman et al., 2007b). Additionally, as during the MCN1–gastric mill rhythm, it appeared that direct CabPK excitation of the LG neuron was a pivotal event for rhythm generation. Thus, we identified CabPK-influenced ionic currents in LG.

CabPK activates three voltage-dependent inward currents in the LG neuron

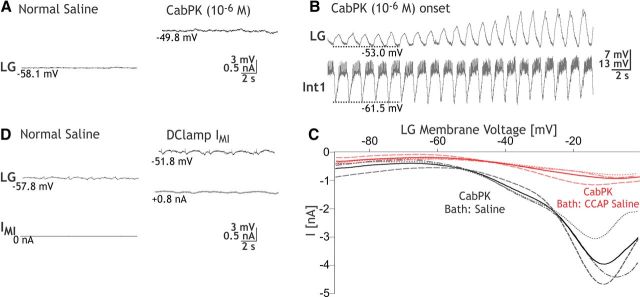
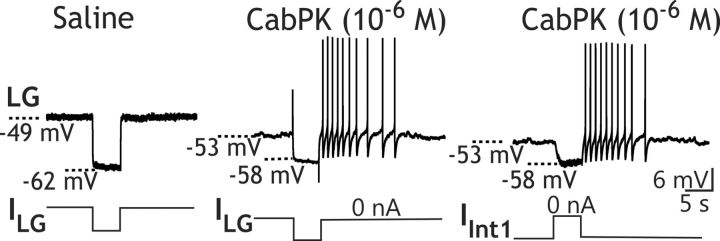
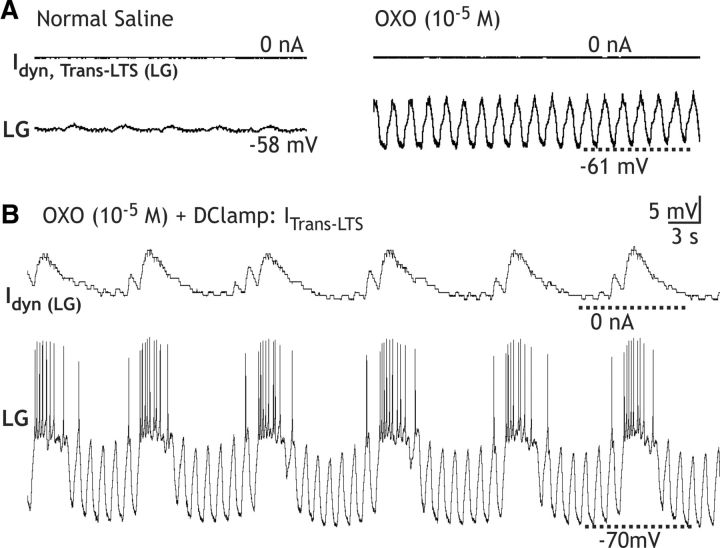
CabPK application (10⁻⁶ m) provides a depolarizing drive to LG from its resting potential (−57.5 ± 1.5 mV; n = 8). For example, under the most reduced conditions, with LG isolated from synaptic input, CabPK consistently elicited in LG a steady 5–10 mV depolarization. This depolarizing response occurred when LG was isolated by either hyperpolarizing Int1 (depolarizing response, 8.5 ± 1.1 mV; n = 8; Fig. 2A) or suppressing all glutamatergic inhibitory input to LG by bath-applying PTX (10⁻⁵ m; depolarizing response, 10.7 ± 0.54 mV; n = 11). The CabPK-mediated depolarization moved the LG neuron membrane potential closer to its spike threshold, which was not changed by CabPK (saline, −42.4 ± 1.3 mV; n = 9; CabPK, −44.5 ± 1.4 mV; n = 9, p = 0.15). When Int1 was active, the LG neuron membrane potential exhibited subthreshold, pyloric-timed oscillations that exhibited a more depolarized peak in the presence of CabPK (saline, −57.5 ± 1.4 mV; n = 10; CabPK, −48.7 ± 1.7 mV; n = 10, p < 0.01; Fig. 2B). These depolarized peaks remained subthreshold before the onset of the gastric mill rhythm, as well as during the ensuing gastric mill retraction phase. In contrast, CabPK did not alter the membrane potential at the trough of these LG neuron oscillations (saline, −59.8 ± 1.8 mV; n = 10; CabPK, −59.1 ± 1.7 mV; n = 10, p = 0.4; Fig. 2B; see below). Thus, the increased pyloric-timed oscillation amplitude was due to a more depolarized peak.

Figure 2.

Bath-applied CabPK peptide elicits a sustained, subthreshold depolarization in the isolated LG neuron by activating the voltage-dependent I_MI. A, With Int1 neuron activity suppressed by hyperpolarizing current injection, bath-applied CabPK elicited a sustained, subthreshold depolarization in the LG neuron. B, With Int1 neuron exhibiting its normal pyloric-timed burst pattern, thereby providing rhythmic inhibition to LG, bath-applied CabPK initially caused a gradual increase in the amplitude of the subthreshold, pyloric-timed oscillations in LG. Note that the oscillation peaks became more depolarized, while the membrane potential of the trough was not changed. CabPK superfusion was begun immediately before the start of this trace. Subsequently, the gastric mill rhythm commenced. C, I–V plots of CabPK-influenced current in LG, obtained using TEVC and a voltage ramp protocol, during focal pressure application (5 psi, 1 s) of CabPK (10⁻⁴ m) under control conditions (black) and during CCAP (10⁻⁶ m) bath application (red). Each curve represents the difference current (CabPK − control or CCAP condition) as indicated. Solid curves represent the mean values for each condition; broken lines represent three individual experiments. D, Injection of artificial I_MI (g_MI = 100 nS) into LG, via the dynamic-clamp, in a preparation where Int1 activity was weak (<5 Hz) caused a sustained depolarization comparable to that resulting from CabPK application.

Based on the assumption that the sustained depolarizing drive in the LG neuron during CabPK application resulted from CabPK influence on a persistent current, we isolated CabPK-sensitive currents using a voltage ramp protocol (see Materials and Methods) in TEVC. Difference currents between CabPK and control solutions revealed a voltage-dependent, inward net current at potentials more hyperpolarized than 0 mV (Fig. 2C). This inward current exhibited a small, relatively constant amplitude at membrane potentials more hyperpolarized than approximately −60 mV, whereas in the depolarizing direction from approximately −60 mV, the I–V plot for this current displayed a trajectory reminiscent of voltage-dependent inward currents. Specifically, it displayed a steadily increasing inward current that peaked at −8.1 ± 1.4 mV (peak amplitude: −4.4 ± 0.6 nA, n = 7), after which the amplitude steadily decreased (Fig. 2C). It was not possible to determine its reversal potential, likely due to an inability to completely clamp the residual, relatively large K⁺ currents at more depolarized potentials (DeLong et al., 2009a). This I–V relationship was comparable to that of the previously identified I_MI, which is activated by several different neuromodulators in crab STG neurons including the LG neuron (Golowasch and Marder, 1992; Swensen and Marder, 2000, 2001; DeLong et al., 2009a).

To further establish that the CabPK-activated, voltage-dependent inward current in the LG neuron that we identified in voltage ramp protocols was I_MI, we performed an occlusion experiment with a known I_MI activator in the LG neuron, crustacean cardioactive peptide (CCAP; DeLong et al., 2009a). CCAP application occludes the ability of the MCN1 peptide CabTRP Ia to activate I_MI in LG (DeLong et al., 2009a). In these experiments, CabPK (10⁻⁴ m) was first pressure applied onto the desheathed STG neuropil while recording LG in TEVC. CCAP (10⁻⁶ m) was then bath applied to activate I_MI, during which time CabPK (10⁻⁴ m) was again puffed onto the STG neuropil. As shown in Figure 2C, the maximal CabPK-activated current amplitude was decreased substantially during CCAP bath application (CabPK pre-CCAP: −4.2 ± 0.6 nA; CabPK during CCAP application: −0.9 ± 0.1 nA; CabPK post-CCAP: −3.5 ± 0.9; p = 0.01: CabPK pre-CCAP or CabPK post-CCAP vs CabPK during CCAP: p = 0.33, CabPK pre-CCAP vs CabPK post-CCAP; one-way repeated-measures ANOVA with SNK post hoc test; n = 3, F_(2,8) = 16.8). This occlusion effect of CCAP thus supported the hypothesis that the aforementioned CabPK-activated inward current in the LG neuron was I_MI. In contrast to the CabPK condition, in normal saline I_MI was either not expressed or was present at low levels, insofar as the LG neuron resting potential in normal saline was approximately −60 mV (see above), and even modest levels of modulator-activated I_MI elicit a more depolarized LG neuron membrane potential (Kirby and Nusbaum, 2007; DeLong et al., 2009a).

I_MI is also sensitive to changes in extracellular Ca²⁺ (Golowasch and Marder, 1992). Specifically, replacing most of the extracellular Ca²⁺ (0.1× normal Ca²⁺) in the saline with additional Mg²⁺, to maintain the total divalent cation concentration, linearizes the I–V curve for I_MI at hyperpolarized potentials. This linearization in reduced Ca²⁺/added Mg²⁺ saline also occurred for the CabPK-sensitive current (current measured at −90 mV: CabPK saline, −0.21 ± 0.3 nA; CabPK with reduced Ca²⁺ saline, −5.67 ± 1.3 nA; n = 3, p < 0.05), further supporting the hypothesis that CabPK activates I_MI in LG neuron.

To test the hypothesis that I_MI was responsible for the aforementioned, CabPK-mediated depolarization in LG, we used the DClamp to inject an artificial version of I_MI into LG in normal saline (Fig. 2D). Doing so using DClamp conductances comparable to those identified in voltage-clamp (50–300 nS), while Int1 was silent or only weakly active, consistently depolarized the LG neuron resting potential to the same extent as CabPK application (CabPK: 10.68 ± 0.5 mV; DClamp I_MI: 10.3 ± 2 mV; n = 6, p = 0.4; Fig. 2A,D).

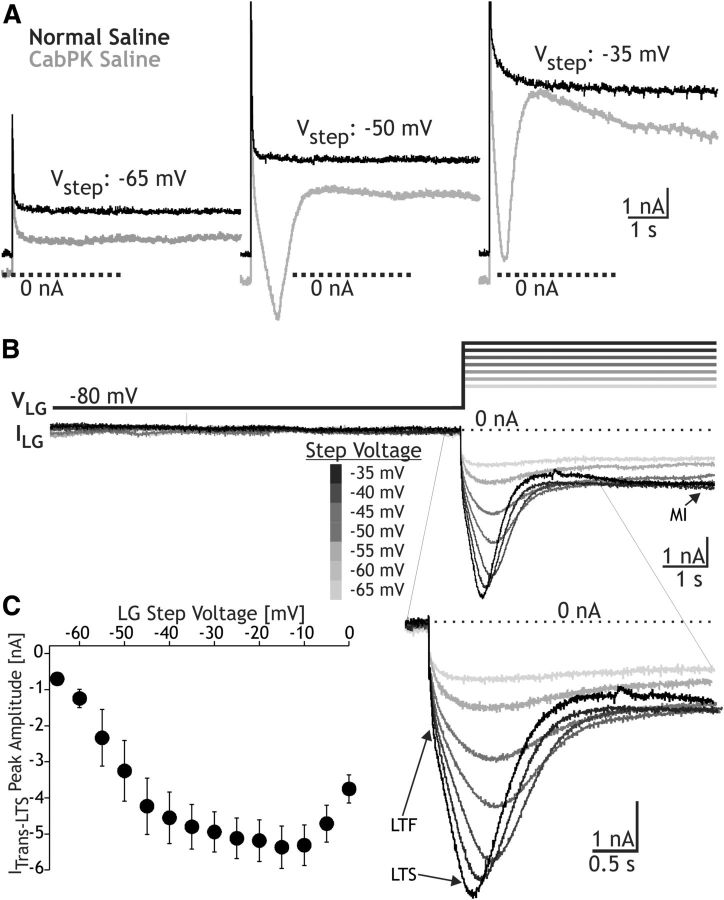
CabPK also activated other voltage-dependent inward currents in the LG neuron. These additional currents were not evident with our voltage ramp protocol, but they were present during a TEVC voltage step protocol. Their absence during our voltage ramp manipulations was likely due to their time-dependent inactivation (see below). We identified these other currents using a prestep hyperpolarization (−80 mV) whose duration was similar to the gastric mill retraction phase (see Materials and Methods). Using this approach, with relatively prolonged depolarizing steps (6 s) comparable to the gastric mill protraction phase during which LG is depolarized and spiking, we identified three inward currents (Figs. 3, 4, 5). These currents included (1) I_Trans-LTF, (2) I_Trans-LTS, and (3) sustained inward current. The I_Trans-LTF was not evident in the raw current recordings obtained during CabPK superfusion (Fig. 3A), due to overlap with the capacitative current, but was readily evident in the difference current traces (Figs. 3B, 4,5). In contrast, I_Trans-LTS was identifiable in both the raw CabPK and difference currents (Figs. 3, 4, 5), but was not evidently expressed under control conditions (Fig. 3A). Last, in the raw CabPK recordings the sustained inward current was evident as a smaller amplitude outward current relative to the control recordings (Fig. 3A).

Figure 3.

CabPK application influences both transient and sustained voltage-dependent inward currents in the LG neuron. A, Example raw current traces recorded during TEVC using a voltage step protocol (V_hold = −80 mV) to the indicated step potentials, during superfusion with voltage-clamp saline under control and CabPK conditions (see Materials and Methods). Note that, during the two more depolarized steps (−50 and −35 mV) in the presence of CabPK, there was a relatively large amplitude transient inward current, while during all three steps there was a reduction in the amplitude of the sustained outward current relative to the control condition. B, Top, CabPK-influenced currents (CabPK condition − control condition) resulting from a voltage step protocol during TEVC included a low threshold, fast transient current (I_Trans-LTF), I_Trans-LTS, and sustained current (I_MI). I_Trans-LTS was predominantly responsible for the transient current, while I_MI was predominantly responsible for the reduced outward current in A. I_Trans-LTF did not exhibit a distinct, separate peak in this experiment (Figs. 4A, 5A), but is evident as an initial steep inward slope before the shallower rising slope representing I_Trans-LTS. Entire voltage step protocol (hold at −80 mV, 10 s; step to test voltage, 6 s) is shown. Bottom, Expansion of the current traces to highlight the events occurring during each voltage step. C, I–V plot of the current (mean ± SE) at the peak of I_Trans-LTS for the step protocol used in experiments such as that in B (n = 9).

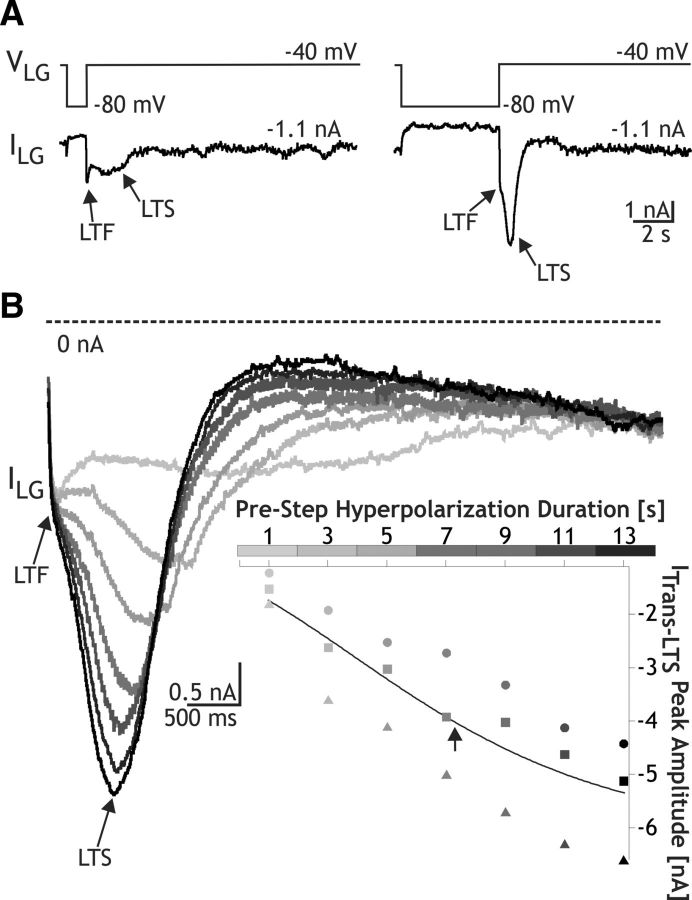
Figure 4.

CabPK-activated I_Trans-LTS in the LG neuron exhibits a time-dependent deinactivation. A, Using TEVC, hyperpolarizing voltage steps to −80 mV were injected into the LG neuron for relatively brief (left) and long (right) durations, and then returned to −40 mV. A larger peak I_Trans-LTS amplitude resulted upon the return to −40 mV after the longer duration hyperpolarization. In contrast, there was little change in the peak amplitude of I_Trans-LTF for both step durations. B, Superimposed series of current responses in the LG neuron, aligned to the return to −40 mV after hyperpolarizing steps of different durations to −80 mV (see the gray scale, representing the different step durations, aligned with the x-axis of the inset scatter plot). Inset, Plot of I_Trans-LTS peak amplitude as a function of hyperpolarizing step duration from three experiments. Each symbol represents a different experiment. The line represents the sigmoid fit to the data (Igor Pro), and the arrow represents the calculated midpoint.

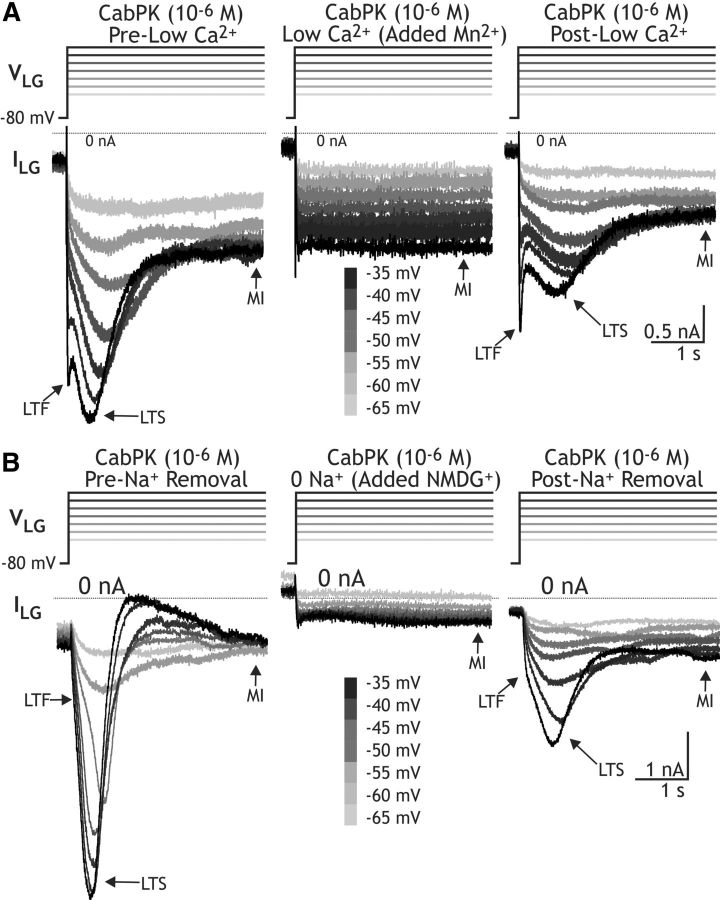
Figure 5.

CabPK-activated I_Trans-LTS is sensitive to changes in extracellular Ca²⁺ and extracellular Na⁺. A, Superimposed sweeps of current recordings from the LG neuron, recorded in TEVC with TEACl/CsCl-filled electrodes, during depolarizing steps to different membrane potentials (−65 to −35 mV) from a holding voltage of −80 mV, during CabPK application in control, reduced Ca²⁺ (0.1× normal), and post-reduced Ca²⁺ solutions. Note that in the reduced Ca²⁺ condition I_Trans-LTS is not evident, nor is I_Trans-LTF. B, Same protocol as in A, except that in the experimental condition (middle trace) extracellular Na⁺ was replaced with an equimolar concentration of NMDG⁺. Note the absence of I_Trans-LTS in the presence of NMDG⁺.

The CabPK-activated, sustained inward current was predominantly I_MI. During the last 3 s of the voltage step, we consistently observed a voltage-dependent, time-independent inward current, as anticipated from our voltage ramp experiments that identified CabPK activation of I_MI (Fig. 3B). There were three features of this sustained current in the voltage step protocols, however, that were distinct from I_MI measured from the voltage ramp protocol, as follows: (1) the peak amplitude was smaller (step: −1.6 ± 0.4 nA, n = 9; ramp: −4.6 ± 0.4 nA; n = 9, p < 0.01); (2) the current exhibited less voltage dependence at depolarized potentials (data not shown); and (3) in some recordings, particularly with steps more depolarized than −40 mV, a reduced inward current or small outward current was evident immediately following I_Trans-LTS, relative to the current amplitude at the end of the step (Figs. 3A,B, 4B, 5B). These features suggested that CabPK also activated a voltage- and time-dependent outward current. We did not, however, further isolate and characterize this additional component insofar as it did not appear to be necessary for the CabPK actions on gastric mill rhythm generation (see below).

The fast transient inward current exhibited a relatively rapid time to peak (32.9 ± 1.9 ms; n = 16) and small peak amplitude (∼0.5 nA), which occurred at approximately −10 mV. It exhibited an apparent voltage threshold of approximately −45 mV (range, −50 to −30 mV; n = 16). Only an approximate peak current amplitude is provided for I_Trans-LTF because we could not isolate this current from the other two CabPK-activated inward currents, and these other currents appeared to contribute substantially to the fast transient peak. In this context, it is noteworthy that I_MI reaches its peak current level relatively quickly in response to a depolarizing voltage step (Fig. 5A). We did not further characterize I_Trans-LTF, insofar as it was not necessary for the ability of CabPK to enable gastric mill rhythm generation (see below).

I_Trans-LTS exhibited a longer time to peak than I_Trans-LTF (time to peak at −45 mV: 633 ± 48 ms, n = 9, p < 0.01) as well as a larger peak amplitude (−5.3 ± 0.6 nA, measured at −15 ± 3.1 mV; n = 9; Fig. 3B,C). It exhibited a voltage threshold of approximately −55 mV (range, −60 to −50 mV; n = 9), and its amplitude increased with depolarization up to approximately −30 mV (n = 9; Fig. 3C). Note that this reported peak amplitude value includes the CabPK-activated I_MI amplitude and, at the more depolarized steps, likely also includes the aforementioned voltage- and time-dependent outward current. The unusually shallow slope of the I–V curve between −40 and −10 mV likely results, at least partly, from the contribution of this outward current (Fig. 3C). The I_Trans-LTS voltage threshold and time to peak suggested that this current was likely to be activated during the CabPK–gastric mill rhythm, during which time the LG neuron membrane potential exhibits rhythmic oscillations between approximately −70 and −40 mV (Saideman et al., 2007b). We could not measure the full time course of the I_Trans-LTS decay to the baseline because it merged into the sustained inward current, which persisted for the remainder of each step (Figs. 3B, 4A). I_Trans-LTS exhibited a reversal potential that was more depolarized than 0 mV (n = 16 each; Fig. 3C, I_Trans-LTS), suggesting that it is primarily carried by ions with positive equilibrium potentials (e.g., Ca²⁺ and/or Na⁺). Both of the CabPK-activated transient currents were clearly distinct from I_MI, because I_MI exhibits no time-dependent decrease in amplitude (Fig. 5; Golowasch and Marder, 1992).

I_Trans-LTS not only exhibited the property of inactivation, but it also exhibited deinactivation. This deinactivation was sensitive to the time and voltage range that occurs in the LG neuron during the CabPK–gastric mill rhythm. We therefore characterized this property by varying parameters of the voltage step protocol in voltage-clamp experiments. To determine the time dependence of this property, we maintained LG at a holding potential of −40 mV and systematically hyperpolarized it to −80 mV for a range of durations (1 to 13 s), stepping the voltage back to −40 mV after each hyperpolarization. We then measured the maximum amplitude of the slow transient inward current after the return to −40 mV (Fig. 4). These data were then fit with a sigmoid curve (Igor Pro), from which two parameters were identified, including the midpoint and slope. There was a relatively long time dependence for I_Trans-LTS deinactivation (midpoint, 7.4 ± 0.4 s; slope, 2.4 ± 0.2 s⁻¹; n = 3; Fig. 4B).

We determined the voltage dependence of the I_Trans-LTS deinactivation by varying the prestep voltage across a range (−75 to −50 mV) of membrane potentials, while maintaining the prestep duration (8 s) and subsequent step potential (−45 mV; midpoint, −60.9 ± 2 mV; slope, −5.3 ± 0.5 mV⁻¹, n = 3). This midpoint value was well within the normal LG neuron membrane potential range (−55 to −70 mV) during the gastric mill retraction phase (Saideman et al., 2007b). Thus, based on the time and voltage dependence of this transient current in LG, and the LG neuron membrane potential trajectories during the gastric mill rhythm (Saideman et al., 2007a,b; this study), it likely exhibits considerable inactivation during the course of each gastric mill protraction phase and deinactivation during the retractor phase. These correlations support the hypothesis that the CabPK-activated slow transient inward current helps enable the LG neuron to generate a periodic burst during a pyloric-timed membrane potential depolarization produced by the combination of I_MI and the periodic (AB-mediated) removal of synaptic inhibition from Int1 (see below).

Both CabPK-activated transient inward currents were extracellular Ca²⁺ dependent. Replacing most of the extracellular Ca²⁺ with Mn²⁺, a Ca²⁺ channel antagonist (Turrigiano et al., 1996), consistently resulted in no measureable fast (n = 4) or slow transient inward currents (peak I_Trans-LTS at −50 mV: CabPK alone, −1.6 ± 0.1 nA; CabPK with 0.1 mm Ca²⁺/10.9 mm Mn²⁺, 0 ± 0 nA; CabPK post-reduced Ca²⁺, −0.8 ± 0.02 nA; n = 4; Fig. 5A). This manipulation had only a moderate effect on I_MI (Fig. 5A), due to the divalent cation sensitivity of this current being approximately equivalent for Ca²⁺ and Mn²⁺ (Golowasch and Marder, 1992). In addition, replacing extracellular Na⁺ with a nonpermeant ionic species (NMDG⁺) also consistently resulted in no measureable I_Trans-LTS (maximum amplitude: control, −3.8 ± 0.9 nA; NMDG saline, 0 ± 0 nA, n = 7; Fig. 5B). In contrast, in all four of these NMDG⁺ experiments where there was a discernible I_Trans-LTF peak in the control recordings, this peak persisted in the NMDG⁺ condition (data not shown). In the three experiments where there was no distinguishable I_Trans-LTF peak in the control recording, it was not possible to determine whether it was influenced by the NMDG⁺ substitution (Fig. 5B).

In sum, these results suggested that I_Trans-LTS is permeable to both Na⁺ and Ca²⁺, is a Ca²⁺-sensitive I_Na, or is an I_CAN, although we also did not rule out the possibility that NMDG⁺ acts instead as an inhibitor of this current. I_CAN was identified previously in C. borealis, both in the stomatogastric nervous system and cardiac ganglion, where it exhibited a reversal potential (V_rev) of approximately −30 mV and was insensitive to changes in extracellular Na⁺ but sensitive to caffeine application (10⁻² m), which stimulates intracellular Ca²⁺ release, and the I_CAN antagonist FFA (10⁻⁵ m; Zhang et al., 1995; Kadiri et al., 2011; Ransdell et al., 2013). However, bath-applied FFA did not alter any of the CabPK-activated currents (n = 2). Insofar as I_Trans-LTS exhibited a V_rev > 0 mV, sensitivity to extracellular Na⁺ and insensitivity to FFA, it was not likely to be an I_CAN.

CabPK-activated transient inward currents enable postinhibitory rebound in the LG neuron

To determine how the CabPK-activated currents might contribute to LG neuron burst generation during the CabPK–gastric mill rhythm, we examined intrinsic properties in LG. Specifically, we found that brief hyperpolarizing current injections into LG were followed by passive responses during saline superfusion but elicited a PIR burst during CabPK superfusion. Under control conditions (saline), we depolarized LG to a membrane potential that was comparable to its CabPK-mediated baseline potential (approximately −50 mV) using either direct depolarizing current injection or DClamp I_MI injection. Despite this depolarized baseline potential, following a period of hyperpolarization there was no evidence of PIR (n > 10; Fig. 6). In contrast to its passive response during saline superfusion, LG neuron hyperpolarization from its CabPK-mediated depolarized resting potential was consistently followed by a PIR burst (Fig. 6). Specifically, during CabPK superfusion, injecting a modest hyperpolarizing current (−1 nA) into LG, which caused a 5–10 mV hyperpolarization, consistently elicited a PIR burst when the current injection was terminated (PIR burst: duration, 5.14 ± 0.2 s; number of spikes: 8.22 ± 0.2; n = 9). We used hyperpolarizing durations (5 s) and amplitudes that were similar to those experienced by LG during the gastric mill retraction phase. The trough of the subthreshold LG neuron oscillations during retraction ranged from −55 to −65 mV across experiments (Saideman et al., 2007a,b).

Figure 6.

CabPK enables the LG neuron to generate PIR bursts. Left, During saline superfusion, the LG neuron membrane potential was held depolarized by constant depolarizing current injection, during which it was hyperpolarized for 5 s by current injection (−1 nA). After the hyperpolarization, the LG neuron membrane potential returned directly to its original, depolarized baseline. Middle, In the same LG neuron recording, during CabPK superfusion, a hyperpolarizing current injection (amplitude, −1 nA; duration, 5 s) from the CabPK-mediated depolarized baseline was followed by a PIR burst (duration, 8.5 s). Note that the last two spikes were excluded from the PIR duration due to their large interspike intervals. Right, In the same preparation, during CabPK application, Int1 activity was suppressed by constant hyperpolarizing current injection and then released from hyperpolarization to fire action potentials for 5 s. This Int1 activity inhibited LG, causing a hyperpolarization comparable to that in the middle trace. When Int1 activity was again suppressed, LG generated a PIR burst (duration: 8.9 s). The last spike was excluded from the PIR burst duration due to the large interspike interval.

The LG neuron also readily exhibited PIR bursts during CabPK application after an episode of synaptic inhibition from Int1 (n = 5; Fig. 6). To establish Int1 mediated PIR in LG, Int1 activity was suppressed via hyperpolarizing current injection and periodically released from this hyperpolarization to fire action potentials for 5 s, comparable to its active period during the gastric mill rhythm. The resulting inhibition in LG caused it to hyperpolarize by 10.2 ± 1.5 mV (n = 5), comparable to its response to Int1 during gastric mill retraction (Saideman et al., 2007a,b). At the end of each inhibitory episode, LG generated a PIR burst comparable to those resulting from hyperpolarizing current injection (PIR burst duration, 5.3 ± 1 s; number of spikes, 8.2 ± 0.6; n = 5; p > 0.5 for both parameters).

PIR bursts are often driven at least partly by the hyperpolarization-activated inward current (I_h; McCormick and Bal, 1997; Sekirnjak and du Lac, 2002; Robinson and Siegelbaum, 2003; Sangrey and Jaeger, 2010; Engbers et al., 2011; Felix et al., 2011). However, I_h did not appear to contribute to the CabPK-enabled PIR bursts in LG insofar as neither hyperpolarizing current injection nor synaptic inhibition from Int1 revealed any evidence of a depolarizing sag potential during saline superfusion (n > 10) or CabPK application (n = 18/20; Figs. 6, 7). Similarly, there was no evidence in our voltage-clamp experiments for a sag current (n > 10). However, the CabPK-activated I_Trans-LTS, with its voltage- and time-dependent properties of inactivation and deinactivation, was a candidate for the ionic current underlying PIR burst generation.

Figure 7.

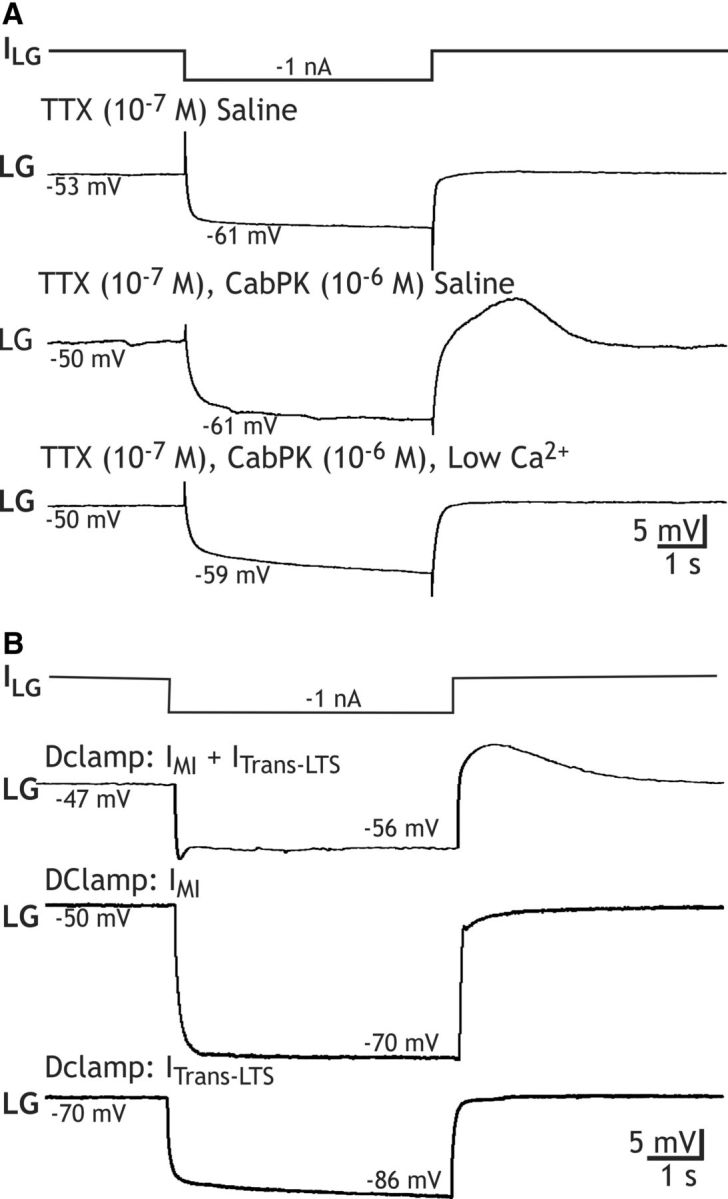
PIR in the LG neuron persists in the presence of TTX during either CabPK application or dynamic-clamp coinjection of artificial I_M plus I_Trans-LTS. A, Top, In the presence of TTX saline, a 5 s hyperpolarization in the LG neuron from a depolarized baseline was followed by a direct return to the depolarized baseline. Middle, During CabPK superfusion in TTX saline, a comparable 5 s hyperpolarization in LG was followed by PIR, albeit without action potentials. Here, the depolarized baseline resulted from the influence of CabPK. Bottom, CabPK superfusion in TTX saline containing 0.1× normal Ca²⁺, substituted with equimolar Mn²⁺, did not enable PIR after the same hyperpolarizing step as above. All recordings were from the same LG neuron. B, Top, Dynamic clamp injection of artificial I_MI (g_MI, 80 nS) plus I_Trans-LTS (g_Trans-LTS, 100 nS) in TTX saline enabled PIR in the LG neuron after a hyperpolarizing step. The initial dip in the LG neuron membrane potential occurred in all (n = 4) of these responses to hyperpolarizing current injection during the dynamic-clamp coinjections but not during the individual injections (e.g., see below). Middle, bottom, In contrast, separate dynamic-clamp injection of I_MI (middle) or I_Trans-LTS (bottom) in TTX saline did not enable PIR in the LG neuron. Note that, in the bottom recording without artificial I_MI, the LG neuron resting potential is not depolarized.

We first assessed the contribution of this CabPK-activated transient inward current to PIR in LG by simplifying the preparation with TTX (10⁻⁷ m) saline to silence all neurons. There was no evidence for a PIR response after LG was hyperpolarized in TTX saline either from its resting potential (−59.1 ± 1.1 mV; n = 18) or from a depolarized membrane potential (−47.4 ± 1 mV; n = 13; Fig. 7A). In contrast, during CabPK (10⁻⁶ m) application under this condition, LG again exhibited a maintained depolarization (−48.4 ± 1.2 mV, n = 18) from which it displayed PIR in response to hyperpolarizing pulses (−1 nA), albeit without associated action potentials (n = 18; Fig. 7A). Thus, this CabPK-mediated PIR did not require activation of TTX-sensitive I_Na. However, these PIR events were briefer than the PIR bursts that occurred during normal CabPK saline (2.0 ± 0.1 s; n = 18; p < 0.01), suggesting that a TTX-sensitive I_Na might prolong this response.

We tested the role in PIR generation played by the I_MI-associated depolarization in the LG neuron during CabPK application. To this end, during CabPK application in TTX saline, we injected constant amplitude hyperpolarizing current to return the LG neuron membrane potential to its pre-CabPK resting potential. That is, we eliminated the effect of CabPK-activated I_MI, which underlies the steady LG neuron depolarization (see above). From that resting potential, we again injected hyperpolarizing current pulses as above. Doing so reduced the PIR amplitude to ∼25% of the control amplitude (control: V_m = −51.1 ± 2 mV; PIR amplitude, 7.2 ± 0.4 mV; hyperpolarized: V_m = −59.1 ± 2 mV; PIR amplitude, 1.8 ± 0.7 mV; n = 7; p < 0.01), supporting the hypothesis that the I_MI-mediated depolarization in LG neuron strengthens PIR generation mediated by activation of the transient inward current (see below).

We next assessed whether this CabPK-enabled PIR event in TTX saline was Ca²⁺-sensitive by applying CabPK after replacing most of the Ca²⁺ (0.1× normal) in the saline with an equimolar concentration of Mn²⁺. Under these conditions, the PIR amplitude was reversibly reduced (precontrol, 7.5 ± 0.7 mV; reduced Ca²⁺/added Mn²⁺ saline, 0.4 ± 0.1 mV; n = 6, p < 0.01; Fig. 7A). These results suggested that the CabPK-elicited PIR was mediated by activation of the CabPK-activated low-threshold inward currents.

We tested the hypothesis that the CabPK-activated I_MI plus I_Trans-LTS was sufficient to enable PIR in LG. To this end, in TTX saline, we injected into LG a dynamic-clamp version of these two currents. This manipulation did indeed enable LG to express PIR in response to the same hyperpolarizing current injections used in the presence of CabPK (PIR amplitude, 8.7 ± 1.5 mV; PIR duration, 4.5 ± 0.03 s; n = 4; Fig. 7B). Performing the same manipulation using only the DClamp version of I_MI or I_Trans-LTS did not elicit PIR (n = 4; Fig. 7B). The absence of PIR during the latter manipulation likely resulted from the absence of a depolarized LG neuron resting potential, which in turn limited the activation of the transient inward current after the hyperpolarizing current injection. Thus, the ability of CabPK to enable the LG neuron to generate PIR bursts apparently results from its coactivation of I_MI, to depolarize LG, and I_Trans-LTS, to provide the drive for the PIR burst.

CabPK-activated inward currents in the LG neuron are necessary for gastric mill rhythm generation

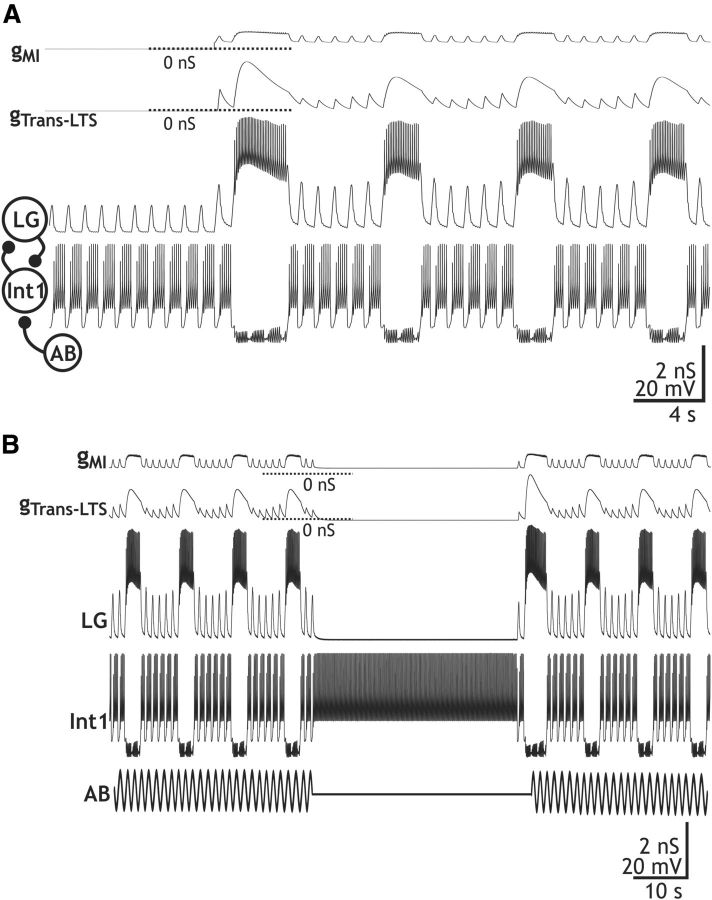
We tested the ability of the identified CabPK-activated inward currents in the LG neuron to enable gastric mill rhythm generation in a computational model, after which we tested the predictions of the model in the biological system. We developed a computational model of the CabPK–gastric mill rhythm generator (LG, Int1, and AB neurons) in which LG contained CabPK-activated I_MI plus I_Trans-LTS (see Materials and Methods; Table 2). This model was based on one of three previously published models (CabPK Mechanism 1) that were focused on distinct candidate mechanisms for CabPK-mediated gastric mill rhythm generation (Kintos et al., 2008). As shown in Figure 8A, our model produced gastric mill rhythm-like alternating bursting in LG and Int1. The model rhythm exhibited a cycle period (10.8 ± 2 × 10⁻⁴ s), LG neuron burst duration (2.75 ± 1 × 10⁻⁴ s), and LG neuron interburst duration (8.09 ± 1 × 10⁻⁴ s) similar to the biological CabPK–gastric mill rhythm (cycle period, 11.96 ± 1.1 s; LG neuron burst duration, CabPK, 3.2 ± 0.3 s; LG neuron interburst duration, 8.8 ± 1.1 s; n = 12). Additionally, the average protraction and retraction duty cycles (DCs; fraction of the cycle) were comparable (protraction DC: model, 0.25; biological, 0.27; retraction DC: model, 0.75; biological, 0.73). Note that, during the model rhythm, g_MI and g_Trans-LTS followed the LG neuron voltage trajectory (Fig. 8A), insofar as their activation was voltage dependent. The deinactivation (h) state of g_Trans-LTS also tracked the LG neuron membrane potential, rising during the retractor phase when LG was rhythmically hyperpolarized by Int1 inhibition.

Figure 8.

CabPK-like gastric mill rhythm generation output from a computational model that includes models of the LG, Int1, and AB neurons. A, Output of the computational model showing the rhythmic alternating bursting in LG and Int1 neurons that commences upon activating the CabPK-activated conductances (g_Trans-LTS; g_MI). The AB neuron influence is evident in the fast rhythmic Int1 hyperpolarizations and the associated subthreshold depolarizations (removal of Int1 inhibition) in the LG neuron. Note that the CabPK-activated conductances all track the membrane potential changes in LG, while g_Trans-LTS also exhibits time-dependent processes, including inactivation during the LG neuron burst and an increasing level of activation (due to deinactivation) during the LG neuron interburst. Most hyperpolarized membrane potentials: Int1, −60.5 mV; LG, −58.4 mV. Filled circle, inhibition. B, Suppressing the AB inhibition of Int1 terminates the ongoing gastric mill rhythm in the computational model of the CabPK–gastric mill rhythm generator, as occurs in the biological system (Bartos et al., 1999). When the AB neuron activity was temporarily terminated (horizontal line, middle of the AB trace), Int1 activity changed from a fast rhythmic pattern to tonic firing, while the LG neuron membrane potential exhibited a steady hyperpolarized potential. Note that, due to the hyperpolarized LG neuron membrane potential, g_Trans-LTS was at 0 nS while g_MI was maintained at a reduced level. Most hyperpolarized membrane potentials: Int1, −47.7 mV; LG, −58.4 mV.

The model CabPK–gastric mill rhythm was also comparable to the biological rhythm in that it was suppressed by eliminating the AB inhibition of Int1 (Fig. 8B). In the biological system, this manipulation terminates the CabPK–gastric mill rhythm, but not the MCN1–gastric mill rhythm (Bartos et al., 1999; Saideman et al., 2007b). As discussed above, during the gastric mill rhythm each fast rhythmic depolarization (disinhibition) in the LG neuron results from the fast rhythmic AB inhibition of Int1 unmasking the depolarizing drive in LG due to CabPK-activated I_MI and I_Trans-LTS. When the AB inhibition of Int1 is suppressed, Int1 fires tonically (Bartos et al., 1999). Selectively silencing AB in the model CabPK–gastric mill rhythm-generating circuit did cause Int1 to fire tonically and eliminated the rhythmic disinhibitions in LG that normally provide the trigger for each LG burst (Fig. 8B). Silencing AB also resulted in the Int1 inhibition dominating the LG neuron membrane potential, keeping LG too hyperpolarized to activate sufficient g_MI and g_Trans-LTS (Fig. 8B).

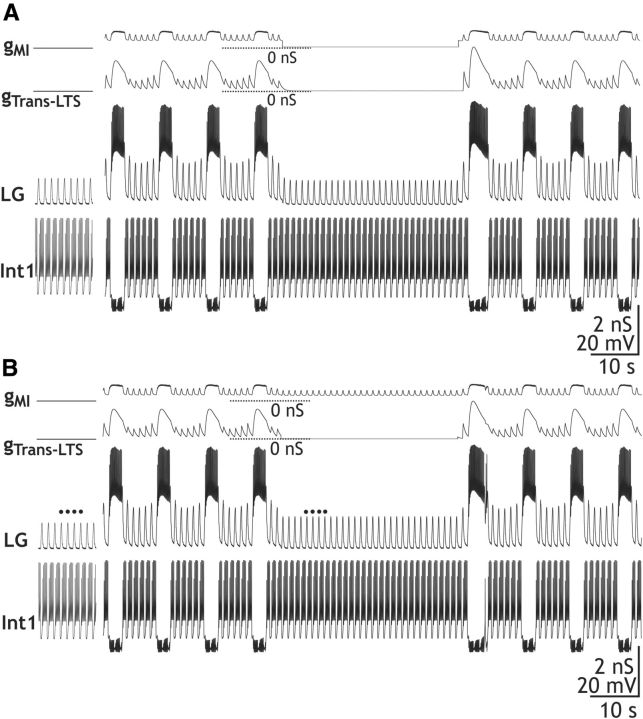
Removing either I_MI or I_Trans-LTS from the model LG neuron eliminated gastric mill rhythm generation, supporting the hypothesis that these currents are necessary for this process (Fig. 9A,B). When either the model g_MI or g_Trans-LTS was removed (i.e., set to 0 nS), the pyloric-timed LG neuron membrane potential oscillation peak amplitude was reduced, preventing LG from reaching action potential threshold and terminating the model gastric mill rhythm (Fig. 9A,B). The peak amplitude of these subthreshold oscillations in LG was larger after selectively removing g_Trans-LTS (12.92 ± 3.4 mV; Fig. 9B) than after selectively removing g_MI (7.32 ± 1.6 mV; Fig. 9A). This result was not surprising, given that with I_MI absent the subthreshold oscillations peaked at a membrane potential close to threshold for I_Trans-LTS activation (Fig. 3).

Figure 9.

Selective elimination of either g_MI or g_Trans-LTS is sufficient to suppress the gastric mill rhythm in a computational model of the CabPK–gastric mill rhythm generator. A, Eliminating g_MI in the middle of an episode of the model CabPK–gastric mill rhythm terminated that rhythm, until g_MI was reinstated. Note that, when g_MI was eliminated, g_Trans-LTS was also reduced to nearly 0 nS due to the less depolarized peak of the subthreshold oscillations in the LG neuron. B, Eliminating g_Trans-LTS terminated the ongoing model gastric mill rhythm until this conductance was reactivated. It did not, however, eliminate g_MI. As a result, the peaks of the subthreshold oscillations remained larger than before the onset of the CabPK influence (black dots). However, g_MI alone was not sufficient to enable the LG neuron to fire a burst.

We evaluated the predictions of the computational model in the biological system using dynamic-clamp current injections into LG. We tested the necessity of I_MI and I_Trans-LTS for CabPK–gastric mill rhythm generation by selectively nullifying each one during the CabPK–gastric mill rhythm. We performed each such manipulation by using the dynamic-clamp to provide negative versions of each conductance, enabling injection of artificial I_MI or I_Trans-LTS that was approximately equal in amplitude and opposite in sign to the CabPK-activated version of that same current (DeLong and Nusbaum, 2010).

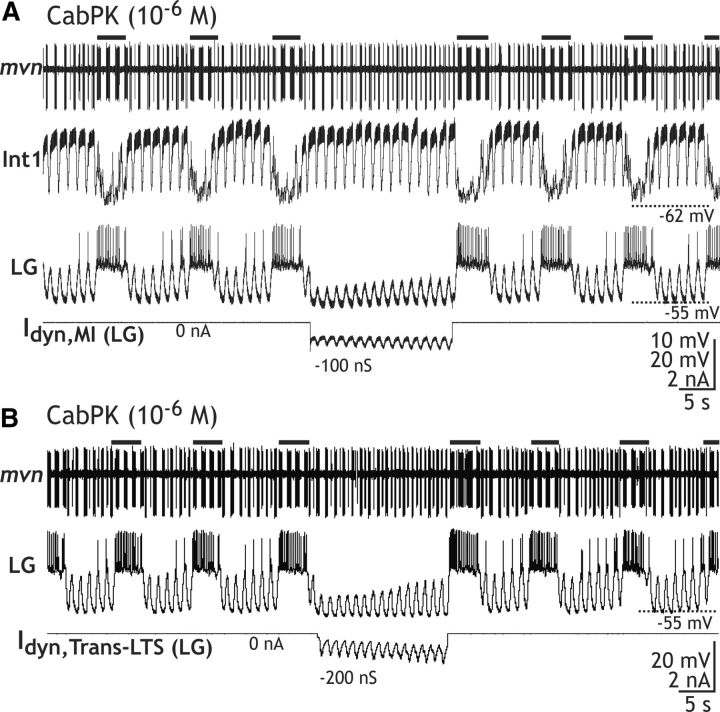
As was the case during the comparable manipulations in our computational model (Fig. 9), moderate levels of negative conductance injection (range, 50–200 pS) of either g_MI or g_Trans-LTS caused only a modest reduction in the peak depolarization of the pyloric-timed oscillations in LG, but it was sufficient to arrest LG neuron bursting and terminate the ongoing gastric mill rhythm for the duration of the manipulation (g_MI, n = 7; g_Trans-LTS, n = 5; Fig. 10). In most experiments, we tested a twofold range of negative conductance values and found that they all effectively suppressed the ongoing rhythm. These manipulations not only suppressed rhythmic bursting in LG, but they eliminated the entire gastric mill rhythm. For example, the combined pyloric- and gastric mill-timed patterns of the IC (inferior cardiac) and VD neurons were replaced by an exclusively pyloric rhythm-timed pattern (n = 3 of 3 preparations; Fig. 10). The gastric mill rhythm consistently resumed when the dynamic-clamp injection was terminated (Fig. 10). Thus, both CabPK-activated I_MI and I_Trans-LTS in the LG neuron were necessary for gastric mill rhythm generation.

Figure 10.

Selectively nullifying CabPK-activated g_MI or g_Trans-LTS via dynamic-clamp injection of a negative version of that conductance suppressed an ongoing CabPK–gastric mill rhythm. A, B, Injecting into the LG neuron a negative version of g_MI [I_{dyn,MI (LG)}] (A) or g_Trans-LTS [I_{Trans-LTS (LG)}] (B) reduced the amplitude of the LG neuron subthreshold oscillations and prevented its bursting. During this time, Int1 activity remained pyloric timed, while the IC (mvn: small unit) and VD (mvn: large unit) neuron activity switched from exhibiting gastric mill- and pyloric-timed bursting to exclusively pyloric-timed activity. Black bars, Gastric mill protraction phase-timed IC neuron bursting. Both panels are from the same preparation.

CabPK-activated inward currents in the LG neuron are sufficient for gastric mill rhythm generation

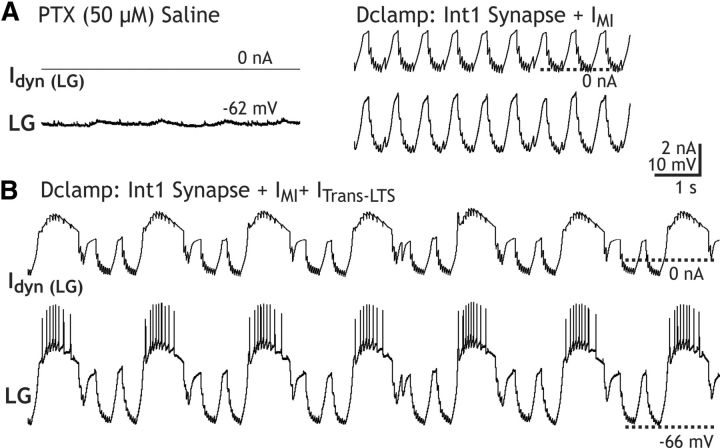
To determine whether the CabPK-activated I_MI and I_Trans-LTS in the LG neuron were sufficient for gastric mill rhythm generation, as was the case in the computational model, we first combined a dynamic-clamp injection of I_Trans-LTS into the LG neuron with bath application of the muscarinic agonist OXO (10⁻⁵ m), an I_MI activator in pyloric circuit neurons (Swensen and Marder, 2000, 2001). We established via voltage-clamp experiments that OXO consistently activated I_MI in the LG neuron as well (n = 5). In parallel current-clamp experiments in which hyperpolarizing current steps were injected into LG during OXO superfusion, PIR was not elicited (n = 5). The OXO-activated I_MI characteristics in the LG neuron were comparable to those resulting from CabPK and CCAP application (e.g., a relatively steady and small-amplitude inward current at potentials more hyperpolarized than −60 mV (−0.3 ± 0.04 nA, n = 5), and a similar V_m for peak amplitude (−7.6 ± 3.8 mV, n = 5), although the peak amplitude was lower relative to these peptides (−1.2 ± 0.27 nA, n = 5; DeLong et al., 2009a; this paper). OXO (10⁻⁵ m) superfusion consistently increased the amplitude of the subthreshold pyloric-timed oscillations in LG by 5–10 mV (n = 10), by selectively increasing their depolarized peak V_m (peak V_m: control, −54.2 ± 1.7 mV; OXO, 45.8 ± 2 mV; n = 10, p < 0.01; trough V_m: control, −55.2 ± 1.8 mV; OXO, −55.7 ± 1.9; n = 10, p = 0.13), without activating LG neuron bursting (Fig. 11A). This result was comparable to that occurring during CabPK applications with dynamic-clamp nullification of I_Trans-LTS, when the only CabPK-activated inward current influencing the LG neuron membrane potential was I_MI (Fig. 10B).

Figure 11.

Gastric mill rhythm-equivalent bursting in the LG neuron during application of the I_MI activator OXO plus dynamic-clamp injection of I_Trans-LTS. A, Left, During saline superfusion and no dynamic-clamp injection, the LG neuron membrane potential exhibited small-amplitude pyloric-timed oscillations. Right, OXO application increased the amplitude of these oscillations, but they remained subthreshold. These subthreshold oscillations exhibited a more depolarized peak, presumably due to OXO-activated I_MI, and a more hyperpolarized trough, presumably due to OXO excitation of Int1 (Norris et al., 1994). The oscillation frequency also increased, because OXO also excites the pyloric CPG (Bal et al., 1994). B, Dynamic-clamp injection of I_Trans-LTS (g_Trans-LTS, 100 nS) during OXO superfusion elicited gastric mill-equivalent bursting in the LG neuron.

During OXO (10⁻⁵ m) superfusion, injecting I_{dyn,Trans-LTS} (50–100 nS; peak current, 1–3 nA) enabled LG to generate gastric mill rhythm-like bursting (n = 5; Fig. 11B). This rhythmic bursting in LG exhibited characteristics that were similar to those occurring during the CabPK–gastric mill rhythm (n = 12), such as its intraburst firing frequency (OXO/DClamp, 3.9 ± 0.6 Hz; CabPK, 2.7 ± 0.2 Hz; p = 0.14), burst duration (OXO/DClamp, 2.3 ± 0.3 s; CabPK, 3.2 ± 0.3 s; p = 0.17), and interburst duration (OXO/DClamp, 6.4 ± 0.8 s; CabPK, 8.8 ± 1.1 s; p = 0.41). These results were consistent across a twofold range of dynamic-clamp conductances (e.g., 50–100 nS) within the same experiments.

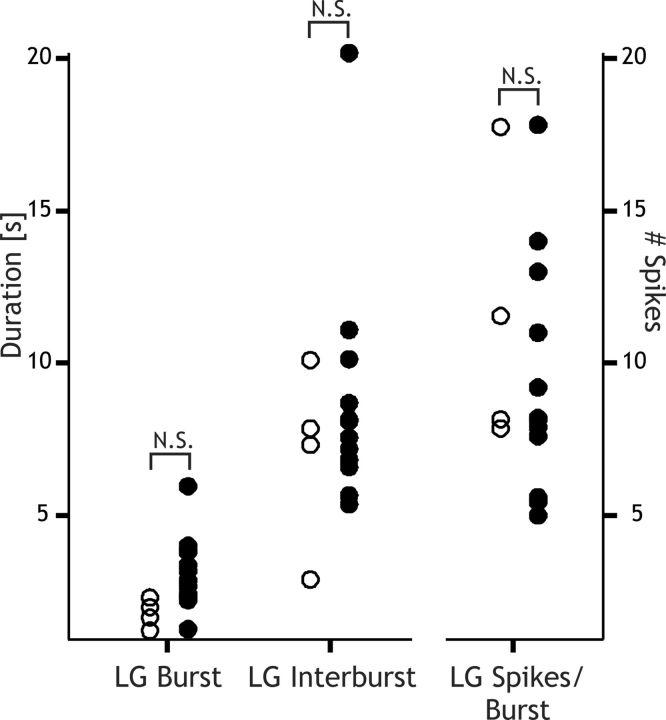
In the above OXO experiments, it remained possible that rhythm generation resulted in part from additional OXO actions on other neurons (e.g., Int1, AB) necessary for gastric mill rhythm generation. Therefore, to determine whether the CabPK-activated inward currents in LG were likely to be truly sufficient to enable a gastric mill rhythm-like pattern in LG, we coinjected into the biological LG neuron dynamic-clamp versions of I_MI, I_Trans-LTS plus the Int1-mediated synaptic inhibition. These experiments were performed in PTX saline to isolate the LG neuron. These dynamic-clamp coinjections consistently elicited gastric mill rhythm-like bursting in LG (n = 4; Fig. 12). The resulting cycle period (8.92 ± 1.7 s, p > 0.05), LG neuron burst duration (1.83 ± 0.2 s, p > 0.05), interburst duration (7.09 ± 0.8 s, p > 0.05), and the number of spikes per burst (11.38 ± 0.9, p > 0.05) were all similar to the above-reported values during the CabPK–gastric mill rhythm (Fig. 13). These experiments therefore supported the hypothesis that the CabPK-activated I_MI plus I_Trans-LTS in the LG neuron were sufficient to enable gastric mill rhythm-equivalent alternating bursting in the core gastric mill rhythm generator neurons LG and Int1.

Figure 12.

Dynamic-clamp coinjection of all CabPK–gastric mill rhythm generator conductances into the LG neuron elicits gastric mill rhythm-like bursting in the LG neuron. A, Left, In PTX saline with no dynamic-clamp injection, the LG neuron maintained a steady resting potential of −62 mV. Right, Dynamic-clamp coinjection of the inhibitory synapse from Int1 (200 nS) plus CabPK-activated I_MI (80 nS) in PTX saline elicited subthreshold, pyloric rhythm-like oscillations in LG. B, Dynamic-clamp coinjection into LG of the rhythmic inhibitory synapse from Int1 (200 nS), CabPK-activated I_MI (80 nS), plus CabPK-activated I_Trans-LTS (100 nS) in PTX saline elicited gastric mill rhythm-like bursting in LG.

Figure 13.

The range of the gastric mill rhythm-related parameters in the LG neuron are comparable during the biological CabPK–gastric mill rhythm and when artificial versions of synaptic inhibition plus the CabPK-activated conductances are coinjected into LG. Distribution of mean values is shown for the LG neuron burst duration, interburst duration, and number of spikes per burst during CabPK–gastric mill rhythms (filled circles: n = 11) and dynamic-clamp-elicited gastric mill rhythm-like bursting in LG (n = 4). All error bars (SEM) are smaller than the associated circles. N.S., Not significantly different (p > 0.05).

Discussion

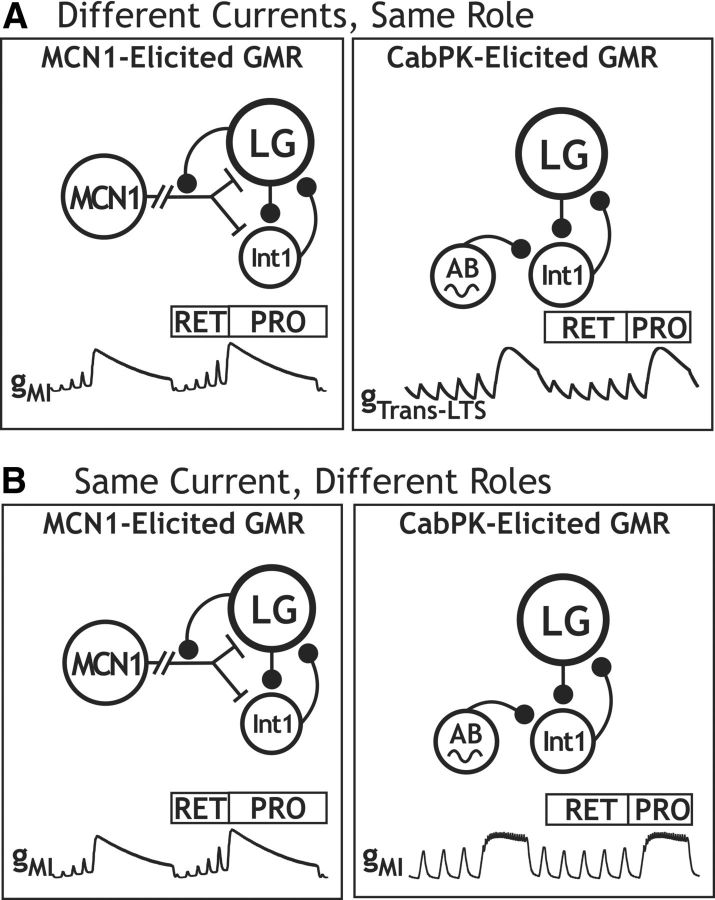
We have identified the cellular mechanisms underlying CabPK neuropeptide activation of a rhythmic motor pattern, thereby establishing that these mechanisms are distinct from those by which a previously studied modulatory pathway activates the same motor pattern. Specifically, bath applying CabPK or stimulating the projection neuron MCN1 configure different gastric mill circuits yet elicit the same gastric mill motor pattern (Fig. 1B; Saideman et al., 2007b). Here we demonstrated that CabPK peptide-elicited gastric mill rhythm generation results from its persistent recruitment of at least two voltage-dependent inward currents (I_MI, I_Trans-LTS) in the rhythm generator neuron LG. These currents conjointly enable LG to rhythmically generate a PIR burst and thereby produce an alternating activity pattern with the rhythm generator neuron Int1, which they then impose on the other gastric mill motor neurons via their synaptic actions (Fig. 1B).

Our computational model and dynamic-clamp manipulations support the hypothesis that the CabPK-elicited rhythmic LG neuron bursting results from I_MI depolarizing LG closer to its spike threshold, enabling the voltage- and time-dependent properties of I_Trans-LTS to periodically generate a PIR burst. The projection neuron MCN1 also activates the gastric mill rhythm generator via I_MI activation in LG (DeLong et al., 2009a). However, the MCN1-activated I_MI grows and decays during the gastric mill retractor and protractor phases, respectively, due to continual neuropeptide release from MCN1 during retraction and presynaptic feedback inhibition of that release during protraction. This MCN1-mediated rhythmic buildup of I_MI is sufficiently strong to enable LG to periodically reach spike threshold and generate a self-terminating burst (Coleman et al., 1995; Bartos et al., 1999; DeLong et al., 2009a).

Different processes can potentially enable the same rhythmic motor pattern to be elicited by different modulatory inputs. These processes include convergent activation of the same direct input to a circuit (Di Prisco et al., 2000; Korn and Faber, 2005; Derjean et al., 2010), convergent modulation of the same properties in the same network neurons (Doi and Ramirez, 2010), divergent modulation in network neurons of multiple baseline intrinsic and synaptic conductances, which functionally compensate for one another (MacLean et al., 2003; Prinz et al., 2004a; Goaillard et al., 2009; Grashow et al., 2010; Norris et al., 2011), or configuration of different circuits by activating distinct conductances that enable different intrinsic properties in network neurons (Saideman et al., 2007b; this article). The crab gastric mill system appears to provide the first example of the latter of these mechanisms.

Despite MCN1 and CabPK configuring different rhythm-generating circuits, at their core both circuits include the reciprocally inhibitory neurons LG and Int1. These two neurons establish the protractor and retractor phases, respectively, and in each case the pivotal rhythm-generating event is LG neuron activation, presumably because Int1 is spontaneously active (Bartos et al., 1999; Saideman et al., 2007b). However, despite these similarities, and the fact that MCN1 and CabPK each recruit I_MI, they enable different active properties in LG. These different properties result from the distinct temporal dynamics of I_MI activation by these two pathways, the likelihood that MCN1 activates more I_MI than CabPK (see below), and the fact that only CabPK appears to activate I_Trans-LTS (Bartos et al., 1999; DeLong et al., 2009a; this article).

PIR bursts often involve the complementary influence of multiple voltage-dependent inward currents, as during CabPK modulation of the LG neuron (McCormick and Bal, 1997; Sekirnjak and du Lac, 2002; Angstadt et al., 2005; Sangrey and Jaeger, 2010; Wang et al., 2011; Engbers et al., 2011; Felix et al., 2011; Zheng and Raman, 2011). One inward current that often contributes to the initial PIR depolarization is I_h (McCormick and Bal, 1997; Sekirnjak and du Lac, 2002; Robinson and Siegelbaum, 2003; Pirtle et al., 2010; Sangrey and Jaeger, 2010; Engbers et al., 2011; Felix et al., 2011). The I_h-mediated rebound depolarization facilitates activation of other voltage-dependent inward currents that elicit or strengthen the PIR burst. These latter currents often have time- and voltage-dependent properties similar to those of CabPK-activated I_Trans-LTS. In many neurons, the additional PIR-generating current is some type of I_Ca (McCormick and Bal, 1997; Angstadt et al., 2005; Sangrey and Jaeger, 2010; Wang et al., 2011; Engbers et al., 2011; Felix et al., 2011). The role of I_h in PIR bursts is similar to that of CabPK-activated I_MI in LG, which depolarizes the LG neuron after a period of inhibition and enables sufficient I_Trans-LTS activation to generate the PIR burst. Also, similar to the CabPK comodulation of I_MI and I_Trans-LTS, the complementary PIR-generating currents in some other systems can be comodulated (Harris-Warrick et al., 1995; Angstadt et al., 2005; Wang et al., 2011).

MCN1 and CabPK activation of the gastric mill rhythm generator involves both divergent actions of the same ionic current (I_MI) and a conserved function mediated by distinct ionic currents (I_MI, I_Trans-LTS; Fig. 14). As discussed above, I_MI is the burst-generating conductance during MCN1 rhythm generation, whereas during CabPK rhythm generation there is insufficient I_MI to directly enable LG neuron bursting. In this latter condition, I_MI instead facilitates burst generation by I_Trans-LTS. The shared role of I_MI and I_Trans-LTS during MCN1 and CabPK rhythm generation, respectively, results from each current exhibiting a phase-dependent growth and decay process that is pivotal to determining the LG neuron burst (protraction) and interburst (retraction) durations (Fig. 14; Bartos et al., 1999; DeLong et al., 2009a; this article). The growth and decay process for I_MI during MCN1 stimulation results from its synaptic regulation, as discussed above. In contrast, the availability of CabPK-activated I_Trans-LTS grows and decays during gastric mill retraction and protraction, respectively, due to its voltage- and time-dependent properties. During retraction, when the LG neuron is hyperpolarized by rhythmic synaptic inhibition from Int1, I_Trans-LTS exhibits a buildup of deinactivation, which increases its availability, while during protraction it first enables and then limits the LG neuron burst duration due to its depolarization- and time-dependent inactivation.

Figure 14.

MCN1 stimulation and CabPK superfusion activate different conductances to perform the same function, and activate the same conductance to perform different functions, during gastric mill rhythm generation. A, Rhythmic LG neuron burst generation results from the rhythmic buildup and decay of MCN1-activated g_MI (left) and CabPK-activated g_Trans-LTS (right). During MCN1 stimulation, the buildup occurs during retraction and results from continual MCN1 activation of g_MI, while the decay during protraction results from LG neuron presynaptic inhibition of MCN1 transmitter release. During CabPK application, the buildup during retraction results from the accumulation of deinactivation in g_Trans-LTS, while the decay during protraction results from the time-dependent inactivation of this conductance. B, The g_MI in LG is the burst-generating conductance during the MCN1–gastric mill rhythm, whereas it provides a sustained but subthreshold depolarizing drive that facilitates PIR burst generation by I_Trans-LTS during the CabPK–gastric mill rhythm. Note that the different g_MI trajectories during protraction result from g_MI being both voltage- and synaptic inhibition-dependent during the MCN1–gastric mill rhythm, whereas during the CabPK–gastric mill rhythm it is only voltage-dependent. RET, Retraction; PRO, protraction.

Despite these differences in the rhythm-generating process, during both gastric mill rhythms the LG neuron burst initiates during a pyloric rhythm-timed depolarization that results from AB neuron inhibition of Int1 (Bartos et al., 1999; Saideman et al., 2007b). However, these pyloric-timed depolarizations are necessary only for CabPK rhythm generation (Saideman et al., 2007b). This is because, when the pyloric rhythm is suppressed during MCN1 stimulation, the MCN1-activated I_MI amplitude continues to grow during each prolonged retraction phase until it eventually becomes large enough to enable LG to escape from Int1 inhibition and generate a burst (Bartos et al., 1999). In contrast, CabPK-activated I_MI alone is insufficient to enable the LG neuron to depolarize and trigger I_Trans-LTS activation in the presence of persistent Int1 inhibition.

The phase transitions occurring during rhythmic alternating bursting by reciprocally inhibitory neurons commonly result from the inhibited neuron either escaping from continuing inhibition (“escape” mode) or waiting until it is released from that inhibition (“release” mode) (Skinner et al., 1994; Marder and Calabrese, 1996; McCormick and Bal, 1997). Each mode can also mediate the same transition under different conditions (Bartos et al., 1999; Sorensen et al., 2004; Kristan et al., 2005). During the MCN1–gastric mill and CabPK–gastric mill rhythms, the protraction-to-retraction transition appears to occur via the release mechanism, as the LG neuron burst self-terminates and releases Int1 from inhibition. In contrast, for reasons discussed above, during the retraction-to-protraction transition the CabPK rhythm only operates via the release mode, whereas the MCN1 rhythm can operate either in its normal release mode or, if the pyloric rhythm is very slow or suppressed, in the escape mode.

A neural network might have the ability to configure distinct circuits generating the same activity pattern because it needs to generate the same core behavior under different conditions. These differently configured circuits, however, might be differentially sensitive to particular inputs. This, for example, is evident for the pyloric pacemaker neuron AB influence on these two gastric mill circuits (i.e., it is a necessary rhythm-generating component only for the CabPK–gastric mill circuit). Such differential sensitivity likely also occurs in circuits that generate a consistent output pattern despite extensive, albeit compensatory, changes in the baseline intrinsic and synaptic conductances of circuit neurons (Prinz et al., 2004a; Grashow et al., 2009, 2010; Calabrese et al., 2011; Guttierez et al., 2013). Two interesting tests of this hypothesis for the gastric mill circuit will be the influence of the gastro-pyloric receptor neuron, a muscle proprioceptor, and the peptide hormone CCAP on the CabPK-gastric mill rhythm. Both of these inputs regulate the MCN1–gastric mill rhythm via actions that involve MCN1, which does not participate in the CabPK rhythm (Beenhakker et al., 2005; DeLong et al., 2009a,b).

This study highlights an alternative consequence to the well established flexibility in neural circuit output imparted by their neuromodulatory inputs. Here, neuromodulation configures distinct circuits/mechanisms that generate a conserved output rather than generating distinct outputs. As part of this process, different modulatory pathways activate the same ionic current in the same neuron but use it in different ways, and they use different currents in the same neuron to perform the same function (Fig. 14). Whether the conserved output pattern resulting from these distinct mechanisms belies latent differences in responsiveness to the same perturbation remains to be determined.