Network Visualization of Conformational Sampling during Molecular Dynamics Simulation

Abstract

Effective data reduction methods are necessary for uncovering the inherent conformational relationships present in large molecular dynamics (MD) trajectories. Clustering algorithms provide a means to interpret the conformational sampling of molecules during simulation by grouping trajectory snapshots into a few subgroups, or clusters, but the relationships between the individual clusters may not be readily understood. Here we show that network analysis can be used to visualize the dominant conformational states explored during simulation as well as the connectivity between them, providing a more coherent description of conformational space than traditional clustering techniques alone. We compare the results of network visualization against 11 clustering algorithms and principal component conformer plots. Several MD simulations of proteins undergoing different conformational changes demonstrate the effectiveness of networks in reaching functional conclusions.

1. Introduction

Molecular dynamics (MD) simulation is a widely used approach for investigating the dynamics of biomolecules [1]. With increases in computer processing power and the advent of enhanced sampling techniques, an extensive range of conformational changes encompassing several timescales may be probed with MD simulation. As a result, increasingly large data sets must be analyzed in order to elucidate the relevant conformational states of a particular system and the interpretation of a trajectory may become exceedingly complex. Therefore, it is valuable to develop techniques that permit efficient data reduction so as to accurately describe the conformational space sampled in a given trajectory.

One commonly used approach for analyzing the conformational space sampled during MD simulation is clustering [2,3]. Clustering of large MD trajectories requires a criterion that measures the similarity between ensemble members, such as the root-mean-square deviation (RMSD) of atomic coordinates. Once such a measure has been selected, similar structures can be clustered through a pairwise comparison of trajectory frames. In this way, simulations with tens of thousands of frames can be reduced to just a handful of representative snapshots associated with populations, uncovering information that may not be easily discerned from the full set of trajectory frames. The data garnered from traditional clustering methods includes fractional cluster populations, cluster dispersion, and representative conformations. Yet potentially more information can be extracted by means of visualizing the clustering of simulation data using network analysis.

Network analysis is a form of graph theory that can be used to represent complex systems as a collection of “nodes” connected to one another by links, or “edges” [4]. The structure of a network – its connectivity and topology – provides useful information for revealing interactions and inherent relationships within the system. Such information has been used to study a variety of systems such as the World Wide Web and metabolic pathways [4]. Protein structure can also be modeled as a network, with amino acids playing the role of the nodes and an edge connecting two nodes if the residues are in contact. This application of network analysis has been used to identify a subset of residues essential for forming the transition state during protein folding [5,6] as well as fundamental features that may govern native protein folds [7]. Networks have also been used to investigate evolutionary relationships between protein domain structures [8].

With respect to biomolecular dynamics simulation, networks are often applied to study the conformational space and folding free energy landscapes of polypeptides [9–12] (see Caflisch (2006) [13] for a review). In these studies, trajectory snapshots are grouped into “conformations,” or structures that exhibit similar features (e.g., secondary structure elements), that define nodes. Links represent transitions between conformations. Given sufficient sampling in a trajectory, the probability of visiting each conformation can be used to calculate the free energy. The network approach is especially useful in this context because it circumvents the need to project the free energy along an arbitrarily chosen reaction coordinate (e.g., the radius of gyration or fraction of native contacts). Such projections hide the complexity of the free energy surface, especially the heterogeneity of the unfolded ensemble [13].

In a study focusing on the folding free energy landscape of a three-stranded anti-parallel β-sheet peptide, network analysis revealed hierarchical organization of the free energy minimum as well as identified conformations of the transition state ensemble and two folding pathways [11]. Other studies constructed graphical free energy surfaces describing the conformational space of an alanine dipeptide [10] and the native state of a 10-residue β-hairpin polypeptide [12]. Krivov and Karplus [14,15] visualized folding free energy surfaces with “transition disconnectivity graphs” by grouping conformational states from an equilibrium trajectory into free energy minima and determining the barriers that join them from the transition rates between the basins. This approach was used along with conformational space networks to analyze the conformational dynamics of the aspartic protease β-secretase during its catalytic cycle [16]. The application of networks in biomolecular dynamics has extended to several other protein systems [17–24]. For example, networks constructed from the clustering of contact maps permitted detailed examination of alternate folding pathways of an outer membrane drug target simulated with a Gō model [17]. Yang and coworkers clustered conformations generated from a Gō model [23] and from many all-atom MD trajectories [22] to construct networks reporting on the transition dynamics leading to Src kinase activation. Networks assembled from oligomeric conformational states helped to uncover early aggregation events of amyloidogenic steric zipper peptides [20]. Moreover, transition networks were recently employed in a novel method to identify hub-like behavior in protein folding [18].

In the present work, we discuss the use of network visualization for the analysis of conformational ensembles generated from MD simulation as an alternative approach to traditional clustering methods. In each of the aforementioned studies, the grouping of similar conformations into a single node reduces the number of representative structures in order to simplify the description of the ensemble and to clarify the character of transition pathways between conformational states. We instead explore a different approach to visualize the conformational ensemble about the native state of a protein as a network. Instead of grouping several conformations, i.e. without making any presumption, each frame from an MD trajectory represents one node. Nodes representing similar conformations (e.g., as determined by the RMSD) are connected to one another by an edge in the network. Once the connections between the nodes in the network have been assigned, the graphical arrangement of nodes can be accomplished by employing a network layout algorithm, with the goal of properly reflecting the conformational space sampled by a trajectory. The resulting network is a particularly powerful tool for visualizing complex MD data sets.

The focus of our approach differs from previously mentioned studies. It is not suitable for direct inference of transition pathways per se since edges between nodes represent conformational similarity and the actual transitions between them are not guaranteed. However, our approach excels in its versatility and simplicity for presenting the character of conformational ensembles while using a variety of visual annotations. For example, the network could be annotated to infer the over-time relationship between conformational populations (see the Cyanovirin-N example below for details).

We outline the methodology for utilizing network visualization in the interpretation of conformational ensembles obtained from MD. Several open source software packages are available for network visualization [25–30], and we use the program Cytoscape [27] to integrate simulation data into these representations. Network visualization with Cytoscape is commonly used to study genetic interaction networks [27] and its application to the interpretation of conformational ensembles obtained from MD simulation has been more limited [17,20,21,31– 34]. To examine the validity of our approach, we compare network visualization against 11 clustering algorithms and to principal component (PC) conformer plots. Several examples of proteins undergoing distinct conformational changes demonstrate the effectiveness of network representations in understanding the conformational space explored by MD trajectories. Network annotations increase the information content of the layout and are especially useful for visualizing the relationships between representative structures from clustering, experimental structures, and the simulated ensemble so as to reach functional conclusions.

2. Characterizing Conformational Similarity in an MD Ensemble

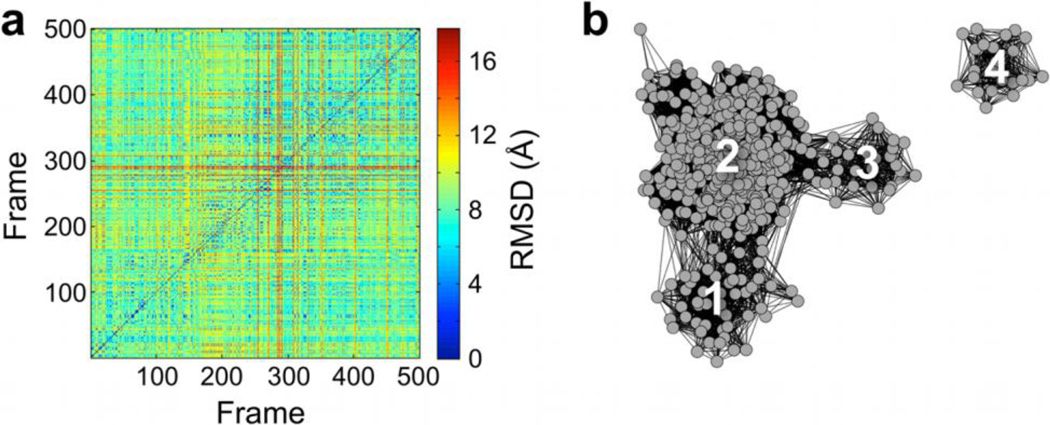
A commonly used measure to characterize both global and local conformational change during an MD simulation is the RMSD. The definition of RMSD needs to be selected according to the nature of the conformational space being discussed. Studies reporting on large-scale motions (e.g., relative domain movements) may use backbone or Cα pairwise RMSD measurements, while those focusing on changes in local conformation (e.g., side-chain torsional dynamics) may employ all heavy atom RMSD measurements. Capturing either type of motion also often necessitates alignment of rigid regions of a molecule before measuring the RMSD of more flexible segments. A pairwise RMSD measurement between all simulation frames provides a distance metric by which to determine conformational similarity within the ensemble. The resulting pairwise matrix (N × N, where N is the number of frames extracted from simulation) contains all of the information about how the ensemble members are related to one another by the RMSD measure (Figure 1a).

Figure 1.

Pairwise RMSD matrix for an MD trajectory represented as (a) a colormap and (b) a network layout.

Traditional clustering algorithms group MD frames in a desired number of clusters based upon a distance metric (e.g., the RMSD). The main information from clustering procedures includes relative population size, the spread of the individual clusters, as well as a representative member for each population. The representative member for each cluster corresponds to the MD structure that most closely resembles all of the other trajectory snapshots within that cluster. Although one can analyze the RMSD between representative structures, clustering algorithms do not give direct information about how individual clusters are interconnected. Therefore, it would be valuable to show the relationships between these separate populations.

Figure 1b shows the network representation of the conformational space sampled during MD simulation. The graph has the potential to yield additional information compared to traditional clustering algorithms alone. In a network, each simulation frame is treated as a node, and nodes can be connected or disconnected from one another, depending on a similarity measure. Network visualization reports on both the size of individual clusters as well as the connectivity between them, which is not self-evident from simple cluster analysis.

In our analyses, this similarity measure is the pairwise RMSD. We require the implementation of an RMSD cutoff such that any two nodes related by an RMSD value less than the cutoff in the pairwise matrix are connected by an edge in the network. Thus, an edge connecting two nodes signifies structural similarity of the corresponding molecular configurations. The information about the connectivity between all nodes is first imported into Cytoscape. Several network layout algorithms are implemented in Cytoscape, which enable the user to arrange the positions of the nodes to delineate the graph connectivity, as shown in Figure 1b. (This representation was constructed using data from simulation of a small heat shock protein (unpublished data) and the force-directed layout algorithm, both of which are discussed below in more detail.)

3. Practical Considerations for Constructing the Network Layout

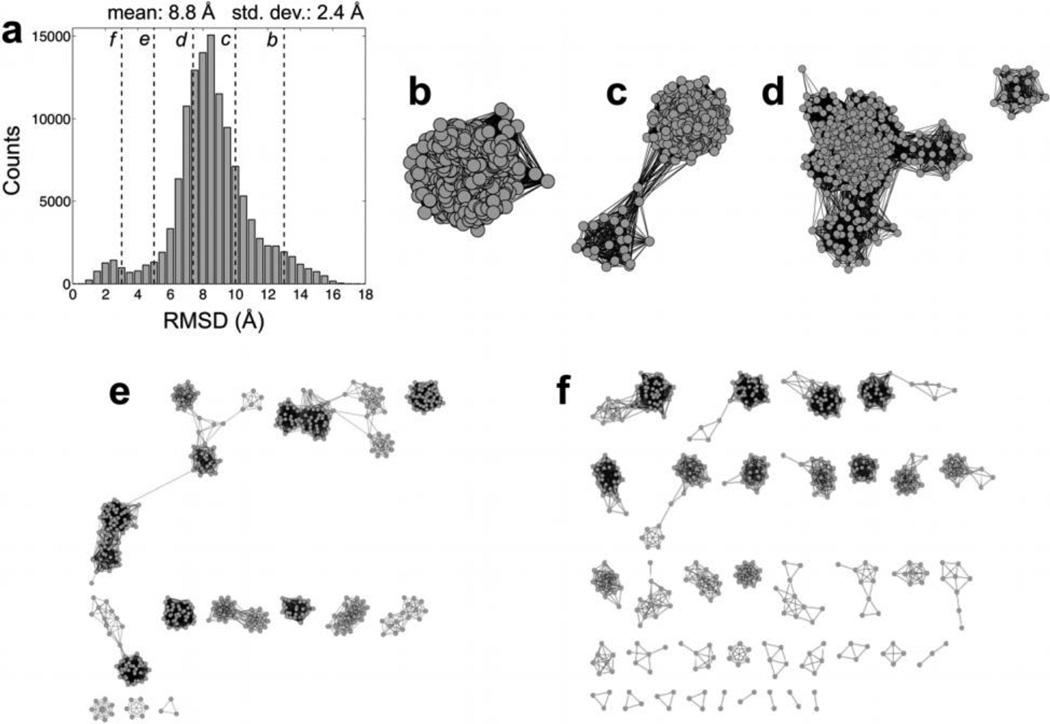
One of the main considerations in constructing a suitable network layout for representing the conformational space visited by an MD trajectory is selecting the value of the RMSD cutoff from the pairwise distribution (Figure 2a). If the cutoff is too large, almost all of the nodes are connected to one another and the network will appear mostly, if not all, as one large cluster (Figure 2b and c). On the other hand, a cutoff that is too small produces a layout in which most nodes are disconnected from every other node (Figure 2e and f) and connectivity between the clusters cannot be retrieved. Even if the number of nodes is significantly increased (e.g., by ten times) while employing a low RMSD cutoff, the connectivity between populations is still not evident (Figure 3). In each case, the major conformational states can no longer be distinguished. The goal then is to choose a cutoff that allows for the sequestration of nodes into individual clusters, while maintaining sufficient connectivity between clusters in the layout, such that the layout reports on the major conformational states present within the ensemble as well as their relationships to one another (Figure 2d). We find that choosing a cutoff within one standard deviation less than the mean of the pairwise RMSD distribution generally works well (Figure 2a). This value may be refined through an iterative process in which a cutoff is chosen, and then a network layout is generated and evaluated for its ability to distinguish between different clusters.

Figure 2.

(a) Frequency distribution of pairwise RMSD values calculated from an MD trajectory (500 snapshots), with the vertical dashed lines indicating the RMSD cutoffs used to construct the networks in panels (b-f): (b) 13, (c) 10, (d) 7.4, (e) 5, and (f) 3 Å.

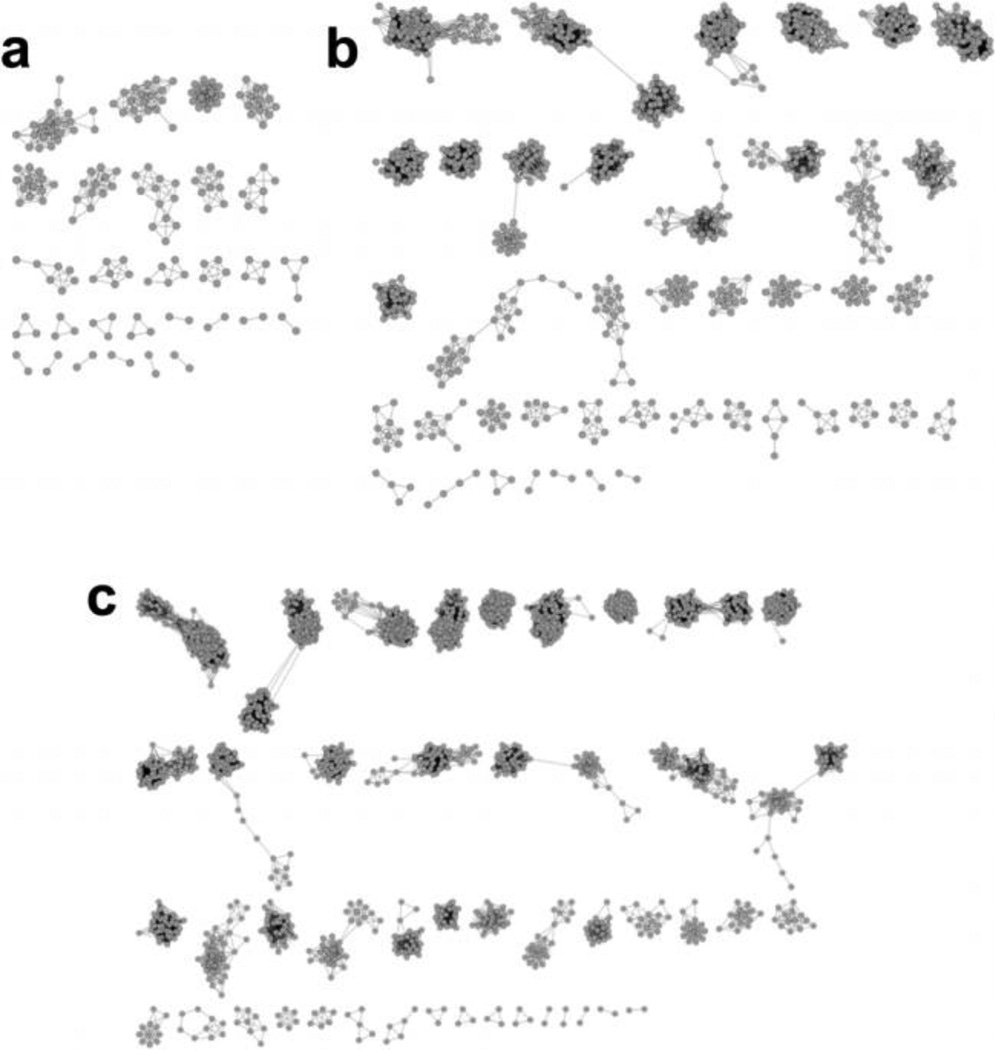
Figure 3.

Networks constructed by applying a 3 Å RMSD cutoff (as in Figure 2f) with (a) 200, (b) 1000, and (c) 2000 snapshots.

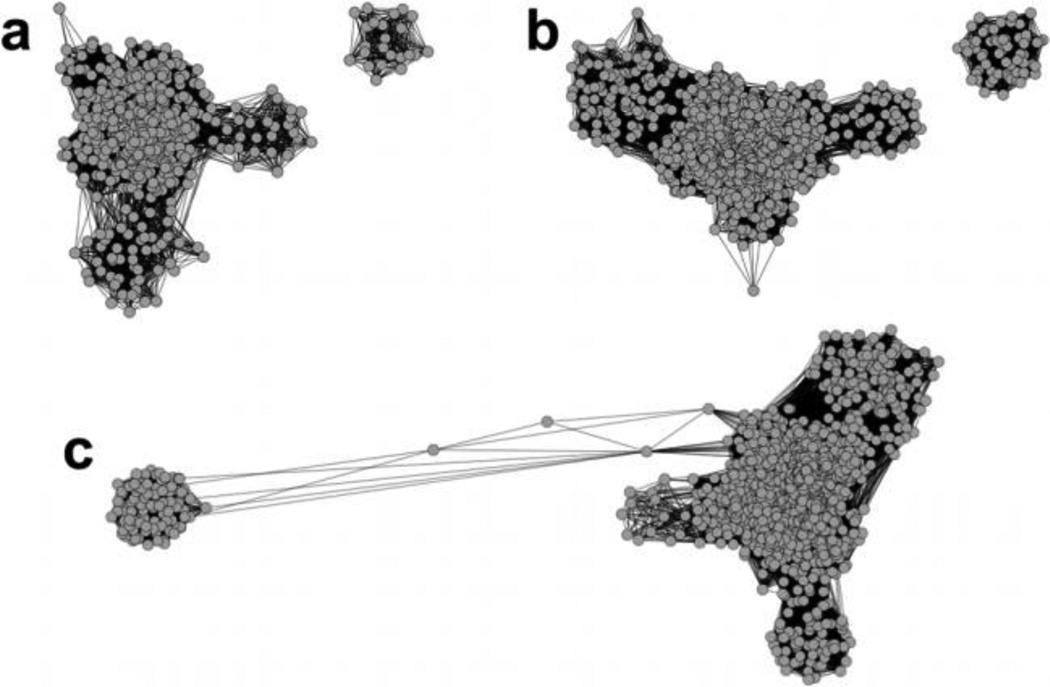
Network visualization becomes computationally demanding as the number of simulation frames used to construct the layout increases due to the large amount of graphical objects that need to be displayed (both nodes and edges). Thus, the number of frames chosen to create the layout should be reasonably low (i.e., a few hundred). (See Cline et al. [27] for an overview of hardware requirements to construct networks with Cytoscape.) This would be a problem if a large amount of simulation frames was necessary to yield the proper topology of a layout. However, given that a trajectory is well equilibrated, we observe that the overall network topology and connectivity is conserved when the total number of frames is varied for the same trajectory (Figure 4). It should be noted that the position of the nodes in the Cartesian space has no significance in the network; rather the connectivity among the nodes and the topology is the only information that the network visualization provides. With a large number of frames (Figure 4c), the network detects two nodes between the main body and the separate cluster of the layout. (For the two other networks, no such bridges are detected.) Connections involving these nodes are satisfied by relatively long edges, which are a result of the optimization model of the network layout algorithm. The long distance in Cartesian space does not indicate a large conformational difference in RMSD. Thus, these three networks represent nearly identical topology of the conformational ensemble. Therefore, the number of nodes may be maintained at a manageable amount without losing information.

Figure 4.

Networks constructed with (a) 500, (b) 1000 and (c) 1500 snapshots from an MD trajectory. The sampling density increases by a factor of two and three in (b) and (c), respectively.

Cytoscape offers a variety of network layout algorithms. The algorithm we find to be well suited for the purpose of visualizing networks produced from the pairwise RMSD matrix of an MD trajectory is the force-directed layout algorithm [35]. An example of a network constructed with this algorithm is shown in Figure 1b. This algorithm treats a network as a pseudo-physical system in which each node is assigned a like charge and the edges connecting the nodes are modeled as springs with the same spring constant and equilibrium length. The nodes are distributed in space by minimizing the energy of charge repulsion and spring attraction between the nodes, yielding the intrinsic structure of the network. When groups of nodes are highly connected to one another, the spring attractions are sufficient to overcome local charge repulsions, and the nodes combine into a cluster. Separate clusters are observed when multiple groups of nodes each have a large number of connections among one another, but a small number of connections between the groups. Note that the resulting layout is not a unique solution for the optimization process, and thus every execution of the algorithm may result in a different layout. However, we observe that the important features of the graph (e.g., the cluster size and relative connectivity between populations) are reproducible after each execution (Figure S1). Node attributes, such as size, color, and shape, are easily adjustable in Cytoscape so as to enhance the information content of the network, highlighting properties that may be unique to a particular collection of nodes.

4. Correspondence Between Network Visualization and Traditional Clustering Algorithms

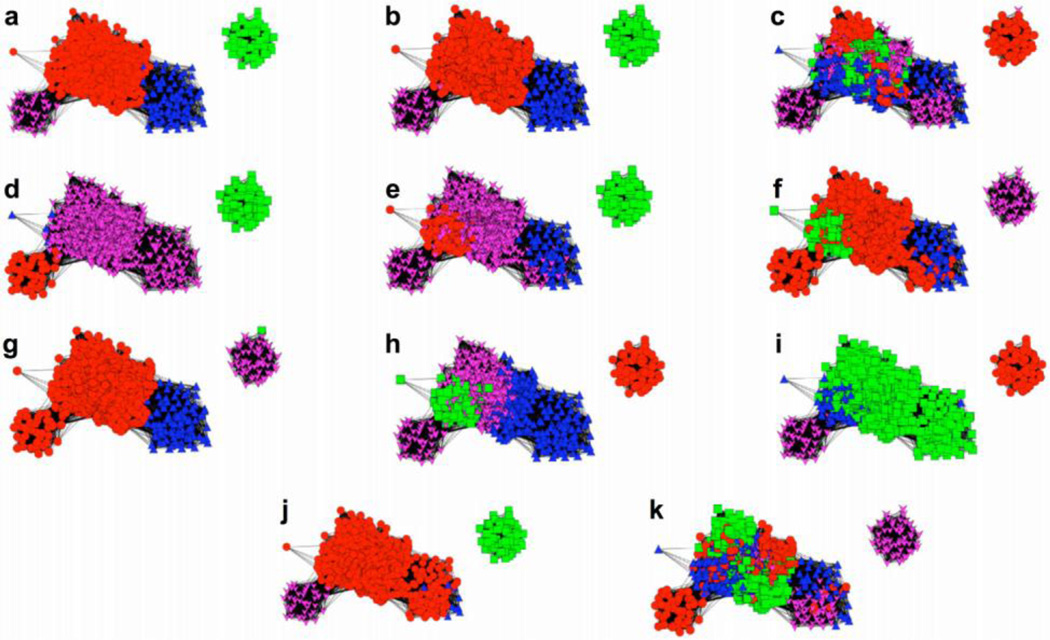
We examined the agreement between conformational states depicted by network visualization and the results from traditional clustering algorithms. Eleven clustering algorithms [2,36,37] were compared to the force-directed layout to determine which ones best match the network. The populations determined by the clustering algorithms are mapped onto the network as different colors to assess the level of agreement between the two approaches (Figure 5).

Figure 5.

Comparison of the results from 11 clustering algorithms with a network constructed using 1000 frames from MD simulation and the force-directed layout algorithm: (a) FAG-EC, (b) average linkage, (c) Bayesian, (d) centripetal, (e) centripetal complete, (f) complete linkage, (g) edge, (h) hierarchical, (i) k-means, (j), single linkage, and (k) SOM. A threshold parameter of one and a minimum complex size of two were used for the FAG-EC algorithm.

Visual inspection suggests four clusters are present in the network layout. We first used the Cytoscape plug-in ClusterViz [38] to implement the fast agglomerate edge clustering (FAG-EC) algorithm [37], which does not require prior knowledge about the number of clusters present in the data. FAG-EC assigned four clusters, which correspond well with the natural topology of the layout (Figure 5a). It should be noted that the FAG-EC algorithm uses the network connectivity as clustering criteria and RMSDs between frames are not taken into account.

We then queried the remaining 10 clustering algorithms [2,36] for four clusters and the results were mapped onto the network layout. The average linkage algorithm produced the most natural distribution of the cluster members onto the network (Figure 5b), identifying one larger population and three smaller ones in agreement with the FAG-EC method (Figure 5a). Each of the remaining nine algorithms identified the single detached cluster, but either misses one of the other clusters in the core entirely or distributes their cluster members over multiple populations within the network. Cluster members are especially mixed throughout the core of the layout when using the Bayesian and self-organizing maps (SOM) algorithms (Figure 5c and k). Thus, for the case presented in Figure 5, all clustering algorithms other than average linkage and FAG-EC lead to cluster assignments that disagree with the force-directed layout algorithm. (For a review of the overall performance of each clustering algorithm with respect to MD simulation, see Shao et al. [2])

Additionally, there is complete agreement between the members of each cluster determined by the FAG-EC and average linkage algorithms for the case presented in Figure 5a and b. This observation indicates, at a given RMSD cutoff, that the FAG-EC algorithm, as implemented in Cytoscape, can be quickly applied to determine the number of clusters that should be specified as input for the average linkage algorithm. The correspondence between FAG-EC and average linkage upholds when mapping the clustering algorithm to another network (Figure S2). However, depending on the system, the results from these two clustering algorithms are not always the best match with network topology. For simulations of the luciferase mobile loop (discussed below), the FAG-EC and average linkage algorithms failed to delineate major conformational populations in the network. Instead, the k-means algorithm yielded the most natural distribution of clusters onto the network (Figure S3). This observation highlights an advantage of network analysis – the ensemble can be visualized directly from the trajectory without the need to select a suitable clustering algorithm.

5. Comparison of Networks to PC Conformer Plots

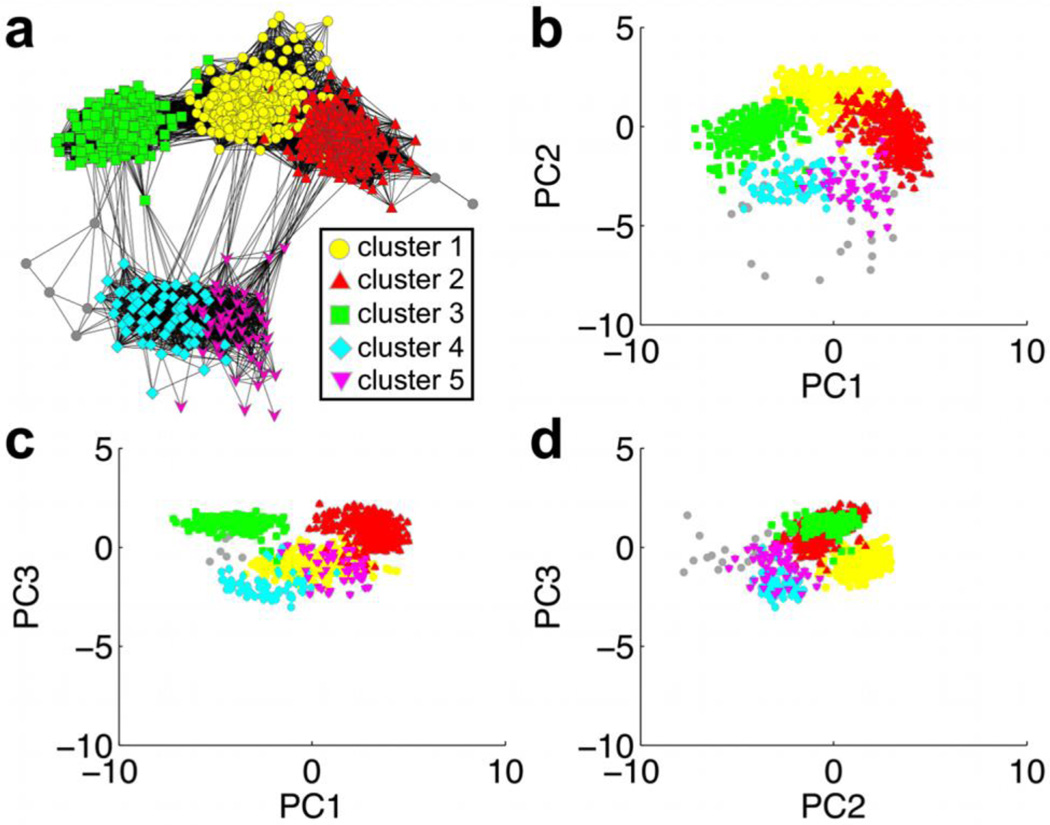
We next compare network visualization against conformer plots in which we project the MD trajectory onto two PCs. Connectivity between nodes in the network is analogous to spatial proximity of points in PC space. The clusters determined from average linkage clustering are mapped onto both the network and the PC plots in order to determine the correspondence between the two approaches (Figure 6). Each cluster is denoted by the same color in the network and in the PC plots, and the PCs with the three largest eigenvalues are considered. For the two dominant modes (PC1 and PC2), the conformer plot exhibits a similar distribution of clusters as does the network, indicating that the latter provides a reliable description of conformational space (Figure 6A and B). The separation between clusters is more evident in the network, e.g. between clusters 1 and 3 and between the larger clusters (1–3) and the smaller ones (4 and 5). In addition, clusters 1 (yellow) and 2 (red) are not well separated in the PC1 vs. PC2 plot. Conformations in these two clusters are different along other PCs, as clearly seen in the plots comprising PC2 and PC3 (Figure 6c and d). The network layout is better suited to capture the conformational diversity: each of the conformer plots represents the projection of high-dimensional conformational space onto a two dimensional (2D) space described by two PCs, while the network connectivity is directly defined from the comparison of the three-dimensional (3D) conformations. Constructing a 3D conformer plot (i.e., PC1 vs. PC2 vs. PC3) results in a more complex plot than the 2D case (Figure S4a). Comparison of an additional network with PC conformer plots also yields similar trends (Figures S4b and S5). Thus, while multiple conformer plots may be needed to report on both the individual populations and the relationship between them, the network representation provides a simple approach to delineate conformational similarity between clusters. Moreover, an advantage of networks is that the distance between nodes and clusters is known (RMSD < cutoff), whereas the closeness of points in PC space may not be as straightforward to interpret. “Similarity” in the network can be defined in various ways depending on the system, such as RMSD after pre-alignment or RMSD in dihedral angles, which is not attainable by PC analysis. Based on these observations, we argue that networks can serve as an alternative approach to conformer plots. In the next section, we illustrate how network visualization can aid in interpreting MD simulation of several different proteins.

Figure 6.

Comparison of network visualization and PC conformer plots: (a) network, (b) PC1 vs. PC2, (c) PC1 vs. PC3, (d) PC2 vs. PC3. The five dominant clusters from the average linkage algorithm are mapped onto the network and PC plots by color. Grey nodes and points represent snapshots that were not assigned to one of the five major clusters. The covariance matrix and projections for PC analysis were computed with the AmberTools program ptraj (http://ambermd.org/) [39].

6. Examples of Network Visualization to Analyze MD Trajectories

In this section we present several examples that highlight the usefulness of network visualization in analyzing large MD trajectories. In particular, we demonstrate how multiple layers of information can be embedded in a network by annotation of the nodes. Through the manipulation of node size, shape, color and labeling, as well as the inclusion of experimental and representative structures into the network, a rich multi-dimensional view of functionally relevant conformational relationships within the native state ensemble can be achieved.

6.1 Conformational dynamics of a binding site residue in Cyanovirin-N in solution versus in the crystal

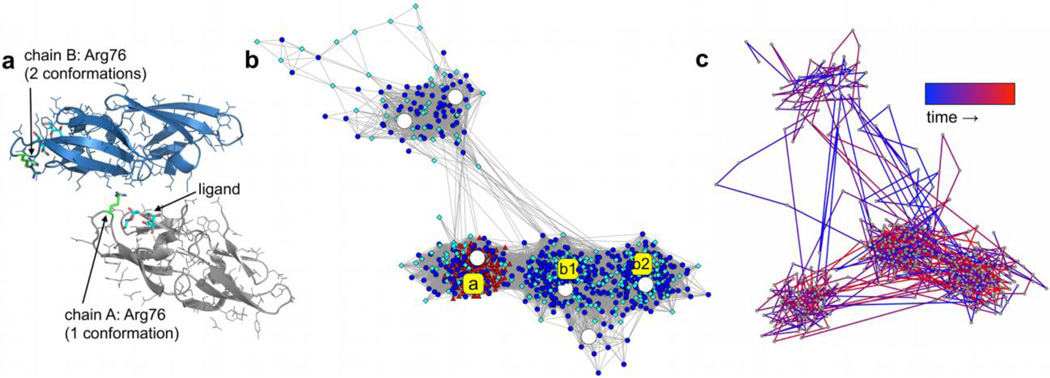
Cyanovirin-N (CVN) prevents the attachment and fusion of HIV to host cell receptors by binding with high affinity to mannose-rich moieties of glycoproteins on the viral envelope [40]. A recent X-ray structure of CVN in complex with di-mannose suggests the functional role of Arg76 located near the binding site [41]. Arg76 is observed in three different conformations in two independent chains (A and B) in the crystal. The residue partially covers the ligand in chain A and also participates in crystal packing, whereas in chain B Arg76 is observed in two alternate conformations that are relatively free from the ligand and does not participate in crystal contacts (Figure 7a). To investigate the observed conformations of Arg76, solution and crystal MD were performed [34].

Figure 7.

(a) Packing interface in the crystal of the CVN:di-mannose complex (PDB: 2RDK [41]) involving chains A (gray) and B (blue) with Arg76 (green) and the di-mannose ligand (cyan) indicated in both chains. (b) Network constructed from snapshots of Arg76 from solution (circular blue nodes) and crystal MD (red triangles and cyan diamonds correspond to snapshots from chains A and B, respectively) as well as the X-ray conformations (a, b1, and b2; yellow squares) and six representative structures from average linkage clustering of the solution trajectory (large white circles). (c) Over-time transitions for 500 frames from solution simulation [34].

For the network presented in Figure 7b, we combine snapshots from solution and crystal MD simulations (950 total frames) for the pairwise RMSD calculation. Also included in the pairwise calculation are the three X-ray conformations of Arg76 as well as six representative structures from average linkage clustering of the simulated solution ensemble. Node color, size, and shape were changed in order to easily identify the X-ray (large yellow squares – a, b1, and b2) and representative (large white circles) conformations. For the pairwise calculation, the backbone coordinates of Arg76 and the closest residue of the neighboring di-mannose ligand were first aligned before measuring the RMSD of the side-chain heavy atoms. An RMSD cutoff of 0.75 Å and the force-directed layout algorithm were used to construct the network. Arg76 samples several conformations in solution simulation (blue circles), and the three largest populations are in excellent agreement with the X-ray conformations and three of the representative structures. The resulting network highlights differences in the MD ensembles generated in solution and in the crystal. The conformational space sampled by Arg76 of chain B in the crystal (cyan diamonds) agrees well with the solution ensemble, whereas Arg76 of chain A was trapped in its single X-ray conformation during crystal MD (red triangles). This indicated that the conformation of Arg76 was selected by crystal packing in chain A and, taken together with the lack of a single conformation of the residue in solution, an alternate mode for CVN-ligand binding was proposed [34].

In addition to characterizing conformational similarity within an MD ensemble, the network can also be used to examine the over-time conformational sampling by a trajectory. To highlight this application, Figure 7c shows a network constructed from 500 solution MD snapshots of Arg76 (blue circular nodes in Figure 7b). The pairwise RMSD calculation was performed in the same manner as described above. Any two snapshots that are adjacent in time but related by an RMSD greater than the cutoff are also connected in the layout. As a result, the spring coefficient for the force-directed layout algorithm was lowered from its default value of 10⁻⁶ to 10⁻⁷ in order to obtain a similar degree of separation as the network shown in Figure 7b. Only the edges representing transitions between two time-consecutive MD frames are shown and are colored as a gradient, with blue and red denoting earlier and later transitions, respectively. Transitions between conformational populations are observed throughout the course of simulation, indicating that sufficient conformational sampling was achieved.

6.2 Dynamics of a mobile loop about the binding site of luciferase

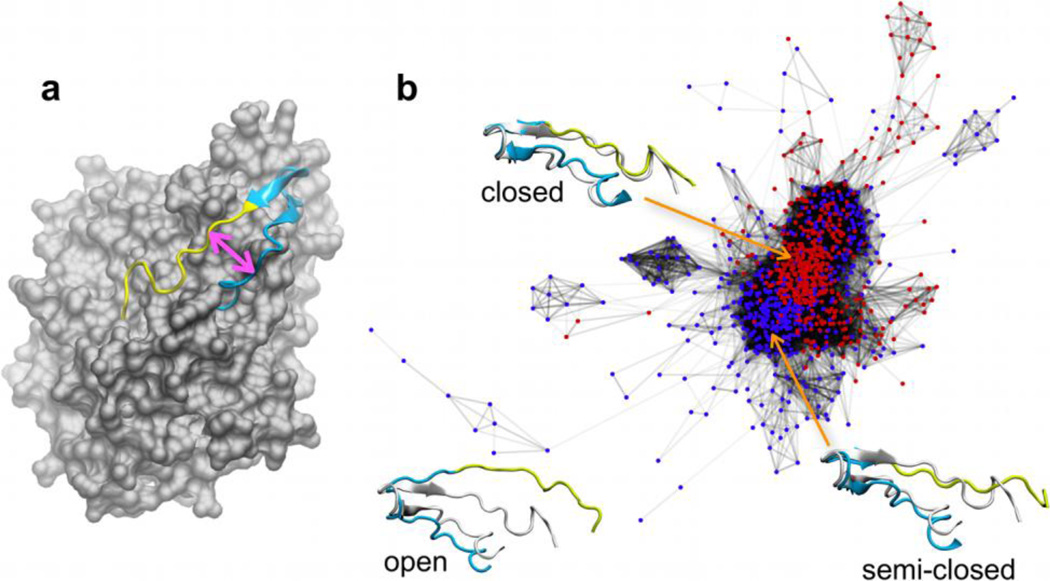
Luciferase catalyzes a light emitting chemical reaction in bioluminescent bacteria and a mobile loop about the active site appears to play an important role in substrate (flavin) binding [42,43]. The loop is observed in two different conformations of the heterodimeric flavin-bound crystal structure [44] of luciferase (“open” and “closed,” defined by the distance between the two anti-parallel loop regions, Figure 8a). Based on the available X-ray data, the contributions of the loop conformations to the catalytic mechanism were unclear. To examine the crystallographically observed loop conformations and to gain insight into loop dynamics important for substrate binding, replica exchange molecular dynamics (REMD) simulations [45,46] of luciferase in the presence and absence of ligand were performed [33].

Figure 8.

(a) Location of the mobile loop in luciferase (gray) with the flavin-distal region (cyan) and the flavin-proximal region (yellow) indicated. The space between these two regions (pink double-headed arrow) is used to denote closed and open loop conformations. (b) Network constructed with snapshots from the ligand-bound (red nodes) and ligand-free (blue nodes) REMD trajectories [33], with closed, semi-closed, and open representative loop structures from k-means clustering shown against to the closed complex (gray) from panel (a).

The network in Figure 8b depicts the conformational space sampled by the luciferase mobile loop in the flavin-bound (red nodes) and flavin-free (blue nodes) REMD trajectories. The pairwise calculation was performed for 1000 frames from REMD (500 from both trajectories) by first aligning the Cα atoms of the globular region of the protein and then taking the RMSD for the Cα atoms of the loop. A 2.75 Å RMSD cutoff and the force-directed layout algorithm were employed. The topology of the layout shows a relatively low level of distinction between populations due to the continuous motion of the flexible loop. Average linkage clustering did not delineate individual populations within the core of the network, identifying the layout primarily as one cluster (Figure S3). K-means clustering was instead chosen to calculate representative structures since it yielded clusters in better agreement with the topology of the core than did other algorithms (Figure S3).

The network indicates that flavin binding shifts the conformational ensemble toward closed states – the fully closed representative conformation lies among nodes only from the ligand-bound trajectory while the “semi-closed” conformation is located within a group of nodes unique to the ligand-free trajectory. Ligand-free and ligand-bound nodes are mixed in other regions of the core of the network, suggesting that the loop is inherently flexible since similar conformations are sampled regardless of the presence or absence of substrate. Structures located on the fringe of the network correspond to more open conformations. Based on network connectivity, a model for loop opening and closure was proposed [33].

6.3 Active conformation of a small heat shock protein

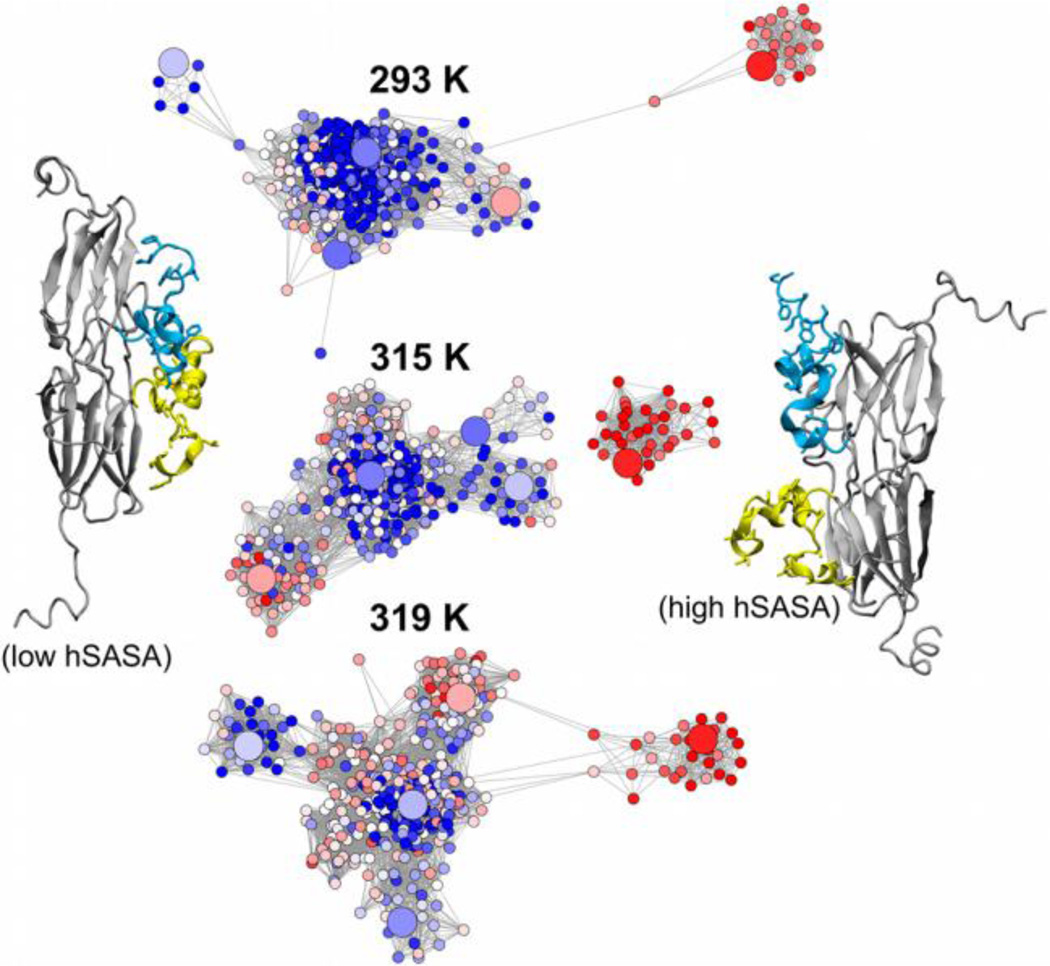
The small heat shock proteins (sHSPs) protect unfolded proteins from aggregation during conditions that promote cellular stress [47]. Under heat stress, the Ta16.9 sHSP dissociates from an oligomeric state into functional dimers, exposing hydrophobic regions of its disordered N-terminal arms that are implicated in substrate recognition [48]. REMD simulation of the Ta16.9 dimer was performed to report on functionally relevant conformations of the arms (unpublished data).

Networks were constructed for the REMD trajectories at multiple temperatures (293, 315, and 319 K) (Figure 9). For each network, 400 simulation frames and five representative structures from average linkage clustering (larger circular nodes in the layout) were considered for the pairwise RMSD calculation, which was performed for the Cα atoms of the flexible N-terminal arms while aligning to the more rigid domains of the protein. A 7.4 Å RMSD cutoff and the force-directed layout algorithm were then applied. Distinct conformations of the N-terminal arms are observed during simulation. To analyze the effect of temperature on the exposure of the hydrophobic surface of the arms, the hydrophobic solvent accessible surface area (hSASA) for the N-terminal arm residues is projected onto the layout as a color gradient. At elevated temperatures, the population of N-terminal arm conformations with higher hydrophobic exposure (higher hSASA, red nodes) increases relative to conformations in which the hydrophobic surface area of the arms is largely unexposed (lower hSASA, blue nodes). This correlation between the temperature and exposure of the hydrophobic surface of the N-terminal arms may explain the hydrophobic interaction between Ta16.9 sHSP and substrate under higher temperature stress conditions.

Figure 9.

Networks reporting on the conformational sampling of the Ta16.9 sHSP dimer N-terminal arms (cyan and yellow in the cartoon representations) at 293, 315, and 319 K during REMD simulation. Nodes are colored by the hSASA of the arms, which ranges from ~1400 Ų to 3100 Ų (blue, white, and red nodes correspond to low, medium, and high values of hSASA, respectively) and larger nodes denote representative structures from average linkage clustering. N-terminal arm conformations with low and high hSASA values are depicted to the left and right of the networks, respectively.

6.4 Open-closed transitions of the lambda Cro dimer

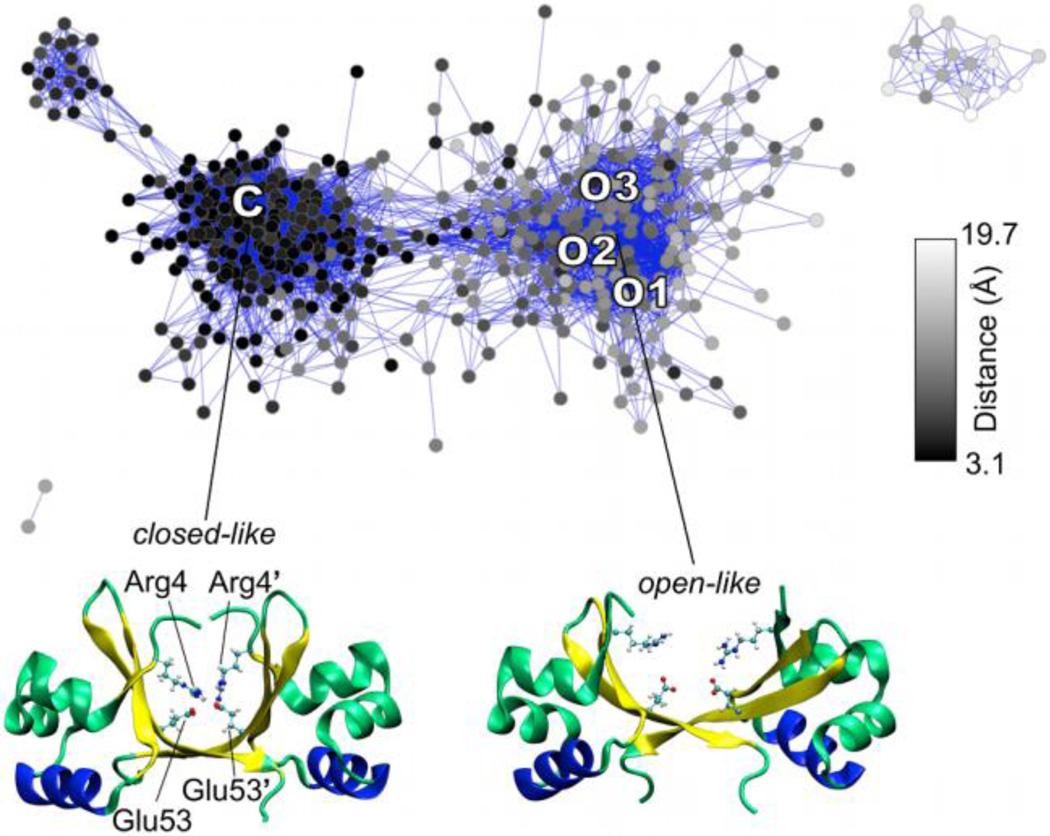
The dimeric Cro transcription factor from bacteriophage lambda is a prototypical system for studying gene regulation [49]. Variation among the Cro crystal structures ranges from an apo closed [50] to a DNA-bound open [51] global conformation. Two new open-like X-ray structures were recently solved in the absence of DNA [52], bringing into question its dominant solution form and DNA-binding mechanism. To address these issues, REMD simulation was performed to elucidate the conformational space available to the protein in solution [31].

A network was constructed from Cro REMD simulation to report on the dominant dimer solution states (Figure 10). Five hundred trajectory snapshots and the four X-ray structures (“C”, “O1–3”) were included in the pairwise RMSD calculation for non-terminal Cα atoms. A 1.7 Å cutoff along with the force-directed layout algorithm were used. The network shows that both closed- and open-like dimers that are in good agreement with the X-ray structures dominate the solution ensemble. Relatively little connectivity between the two major populations in the network suggests a two-state open-closed transition, which appears to be controlled by intersubunit salt-bridging between Arg4 and Glu53 of the neighboring monomer. The inter-residue distance (as defined between the centers of mass of Nη1/Nη2 of Arg4 and Oε1/Oε2 of Glu53’) was mapped as a color gradient onto the network to highlight the relationship between the formation of the salt bridge and conformational sampling. (Since Cro is a homodimer, the interaction between Arg4’ and Glu53 may also form.) Black nodes correspond to the shortest inter-residue distances and are located almost exclusively in the population of closed-like dimers, whereas gray and white nodes indicate larger distances and primarily correspond to open-like dimers. Thus, the network illustrates the correlation between the formation of the salt bridge and the sampling of closed conformations. The role of the Arg4-Glu53 intersubunit salt bridge in the open-closed transition as well as the accessibility of open-like dimers in solution supported a conformational selection model for Cro-DNA binding [31].

Figure 10.

Network constructed from REMD simulation of the lambda Cro dimer [31] with the closed (C) and open (O1, O2, and O3) X-ray structures indicated on the layout. Black and gray/white nodes denote conformations with shorter and longer distances between the Arg4 and Glu53’ intersubunit salt bridge residues, which are highlighted in the closed- and open-like structures shown below the network.

7. Conclusion

Network visualization can serve as an effective tool for uncovering the inherent conformational relationships in large MD trajectories. Networks report on both the size of and connectivity between major conformational states, which offers a coherent picture of conformational space that a simple clustering analysis cannot provide. Whereas the application of networks in previous studies, particularly for protein folding, first clusters trajectory snapshots into conformations, the approach presented in this study constructs a network representative of the native state ensemble without any presumptions of the conformational space. The application of an RMSD cutoff in combination with the force-directed layout algorithm results in a distinct network topology. Although network visualization is sensitive to the choice of the RMSD cutoff, a reasonable estimate of the cutoff may be obtained from the pairwise distribution of RMSD values and quickly refined by iteratively constructing the layout. The number of major conformational states can be gauged from the resulting network topology and used to guide the choice of a clustering algorithm. Moreover, network visualization can serve as an alternative to PC conformer plots. For the protein MD examples presented, networks reveal the relationship of experimental and representative structures to the simulated conformational ensemble and are instrumental in arriving at new functional insights.

Highlights.

• Network visualization aids analysis of large molecular dynamics trajectories.

• Networks reveal the connectivity between dominant conformational states.

• Compare network visualization against clustering and principal component analysis.

• Networks facilitate functional conclusions for several protein simulations.