The Tumor Radiobiology of SRS and SBRT: Are More than the 5 R’s Involved?

Abstract

Stereotactic radiosurgery (SRS) and stereotactic body radiotherapy (SBRT), also known as stereotactic ablative radiotherapy (SABR), are rapidly becoming accepted practice for the radiotherapy of certain tumors. Typically SRS and SBRT involve the delivery of one or a few large dose fractions of 8 to 30 Gy per fraction: a major paradigm shift from radiotherapy practice over the past 90 years when, with relatively large amounts of normal tissues receiving high doses, the goal was to maximize tumor response for an acceptable level of normal tissue injury. The development of SRS and SBRT have come about because of technological advances in image guidance and treatment delivery techniques that enable the delivery of large doses to tumors with reduced margins and high gradients outside of the target, thereby minimizing doses to surrounding normal tissues. Because the results obtained with SRS and SBRT have been impressive they have raised the question of whether classic radiobiological modeling, and the linear-quadratic (LQ) model, are appropriate for large doses per fraction. In addition to objections to the LQ model, the possibility of additional biological effects resulting from endothelial cell damage and/or enhanced tumor immunity, have been raised to account for the success of SRS and SBRT. In this review, we conclude that the available preclinical and clinical data do not support a need to change the LQ model nor invoke phenomena over and above the classic 5 R’s of radiobiology/radiotherapy with the likely exception that for some tumors high doses of irradiation may produce enhanced antitumor immunity. Thus, we suggest that for most tumors the standard radiobiology concepts of the 5 R’s are sufficient to explain the clinical data, and the excellent results obtained from clinical studies are the result of the much larger biologically effective doses (BEDs) that are delivered with SRS and SBRT.

Introduction

Stereotactic radiosurgery (SRS) and stereotactic body radiotherapy (SBRT), also known as stereotactic ablative radiotherapy (SABR), are novel and increasingly popular ways of delivering radiotherapy. SRS, usually limited to brain lesions, is an extreme example of SBRT in that the entire dose is typically given in a single fraction. SBRT is defined as treatment of tumors outside of the brain with 1–5 dose fractions. The generally outstanding results already obtained with SRS and SBRT, together with certain preclinical data, have led to the suggestion that the large single doses of SRS, or high doses per fraction in SBRT, produce greater anti-tumor efficacy than would be predicted from the survival curves of the tumor cells or from the accumulated clinical experience with fractionated radiotherapy. We will critically examine these claims using both preclinical and clinical data.

However we must first consider why single dose radiotherapy can even be considered based on the fact that it is a major paradigm shift from the practice of radiotherapy that has developed over the past 90 years when the goal was to maximize tumor response for an acceptable level of normal tissue injury. It is uncontested that fractionation of the radiation dose is superior to single doses in achieving such differential sparing of normal tissue compared to tumor. The reason that SRS and SBRT can essentially ignore this classic fractionation paradigm is the result of technological advances in image guidance and treatment delivery techniques that enable the delivery of large doses to tumors with reduced margins with high gradients outside of the target, thereby minimizing doses to relatively large volumes of surrounding normal tissue. This practice has now raised the question of whether these large doses per fraction produce greater anti-tumor efficacy than predicted by classical radiobiology, or the 5 R’s.

Factors Affecting Tumor Response to Irradiation (the 5 Rs)

Loss of reproductive ability, due to double strand breaks (DSB) in DNA, is the primary means by which radiation kills cells: any cell that is incapable of reproducing indefinitely is by definition considered “dead”, although it may still be metabolically active for some time. The response of tumors to radiation has therefore been largely characterized in terms of factors that influence the ability of radiation to damage DNA, and that affect a population of cells in tumors to recover from such damage.

Almost a century of research on the biological basis of radiotherapy has revealed five factors that are critical in determining the net effect of radiation therapy on tumors. These are:

1. Repair of sublethal cellular damage.

2. Repopulation of cells following radiation.

3. Redistribution of cells within the cell cycle.

4. Reoxygenation of the surviving cells.

5. Radiosensitivity (intrinsic).

The first four of these factors were described initially by Withers (1), but the list was subsequently increased to five by Steel based on emerging data that the responsiveness of tumors to radiotherapy correlated with the intrinsic radiosensitivity of the cells in vitro (2). These five factors can work in opposite directions depending on the particular tumor and the way in which the radiation is delivered. For example, if a given dose of radiation is divided into a set of (typically daily) fractions, redistribution and reoxygenation facilitate increased overall cell kill by redistributing the resistant survivors into more sensitive states over time. However, repair and repopulation produce increased cell survival by allowing for recovery of cells following individual radiation doses and allowing proliferation between radiation doses. Modern fractionation schemes are based on manipulating these effects so as to maximize tumor cell kill while avoiding normal tissue toxicities, particularly those arising in late responding tissues. Tumors are generally considered early-responding tissues, although given the heterogeneity of neoplastic tissues this is not universal.

For many years after the publication of the first mammalian radiation survival curve by Puck and Marcus (3) using colony formation as the criterion for cell survival, investigators fitted survival curve data using the multi-target model which describe cell survival (S) in terms of the dose (D), a parameter D₀, representing the slope of the exponential portion of the curve, and the extrapolation number n as follows:

$$\text{S}=1-{(1-{\text{e}}^{-\text{D}/\text{D}0})}^{\text{n}}$$

This equation produced a good fit to most experimental data over a wide range of cell killing. However, the equation does not describe any realistic cell biology for cell killing by irradiation. Nonetheless, it is notable for the fact that experimental data obtained over 2–3 logs of survival can be readily extrapolated to the very high levels of cell kill expected for doses of 15–30 Gy given in SRS because the curve quickly becomes a straight line on a semi-log plot, so extrapolation to high doses is simple and reasonable.

However, when investigators developed techniques to measure cell killing at low radiation doses (producing 80–90% survival) they quickly found that this equation, which predicts zero cell killing at small radiation doses (zero initial slope to the survival curve) did not fit the experimental data at these low doses. This, plus the fact that another model, the linear-quadratic (LQ) model, which derives from biological considerations of how cells could be killed by ionizing radiation, did fit the data at low doses, led to the replacement of this equation by the LQ equation as follows:

$$\text{S}={\text{e}}^{-({\alpha }_{\text{D}}+{\beta }_{\text{D}2})}$$

This equation represents a model in which cell killing is caused by either 1 or 2 radiation tracks (4, 5), which is consistent with extensive experimental data that cells die by chromosome breakage producing dicentrics along with an acentric fragments (which require breaks in two adjacent chromosomes) or by terminal deletions. Further the model has become successfully used by the radiation oncology community to calculate changes in dose per fraction or in number of fractions to achieve the same radiation effects on normal tissues as a standard fractionation regime. The only parameter needed to perform these calculations is the value of α/β, which, based on extensive preclinical and clinical data, is typically considered to be ~3 Gy for late responding tissues and ~10 Gy for early responding tissues including most tumors, though especially for tumors there is much uncertainty in the values and can be very high particularly for lung tumors (6).

So successful has been the LQ model that it has been used as the basis of clinical trials of hyperfractionation based on the predicted superiority of regimes with small doses per fraction (< 2 Gy) in terms of reducing late effects for the same level of early effects (including tumor response) (7). Typical among such trials is a European head and neck trial (EORTC 22791) in which treatment with a seven week course consisting of twice daily 1.15 Gy fractions to a total dose of 80.5 Gy was compared with a conventional seven week course administering 2 Gy daily for five days a week (8). As predicted by the LQ model, late effects between the groups were comparable, while acute reactions were elevated (but manageable) and the 5-year local control rate was significantly higher in the hyperfractionated arm.

In general, clinical results have validated the LQ model over a modest dose range of 1–5 Gy/fraction and in particular the lower α/β ratio for late responding normal tissues relative to acute effects and most tumors (with the likely exception of prostate cancer (9, 10)). However, implicit in modeling of tumor response by the LQ equation is that full reoxygenation occurs between each dose fraction. It would therefore seem difficult to justify large single doses of radiation as the LQ equation, as well as the detrimental effect of the lack of interfraction reoxygenation, would predict that such doses would produce far less tumor cell kill for the same level of normal tissues damage (11). However there is little doubt that the clinical results with SBRT, particularly for early stage NSCLC, have been impressive (12). Possible reasons for the efficacy of high dose per fraction radiotherapy are:

1. Advances in image guidance and dose delivery enable the delivery of large doses to tumors with much smaller volumes of normal tissue irradiated, thus overcoming the need in some situations to be concerned with normal tissue injury.

2. The LQ model may not accurately predict cell killing at high doses. It might be suggested that the model may over predict cell killing at high doses so the damage to late responding normal tissues (which have smaller α/β values and therefore a more “curvy” dose response curve) may be less than predicted by the model, thereby allowing bigger doses than predicted by the model to be used in practice.

3. There are anti-tumor effects of high radiation fractions that are not predicted by classical radiobiology including enhanced anti-tumor immunity and secondary effects deriving from injured vasculature.

4. Many tumors may not be hypoxic so there would be no benefit of reoxygenation between doses in a multi-fraction regime.

The first of these is undoubtedly true. Below we examine the evidence for the other possibilities.

Is the Linear-Quadratic Model Adequate to Describe Cell Killing at High Doses?

Clinical data from prospective randomized trials is of course the gold standard in medicine, but in the absence of good clinical outcome data, biological models should be exploited to carefully and systematically guide the selection of new or alternate treatment regimens. The ideal biological model should be accurate over the entire dose range of interest and have a small number of adjustable biological parameters that are well characterized.

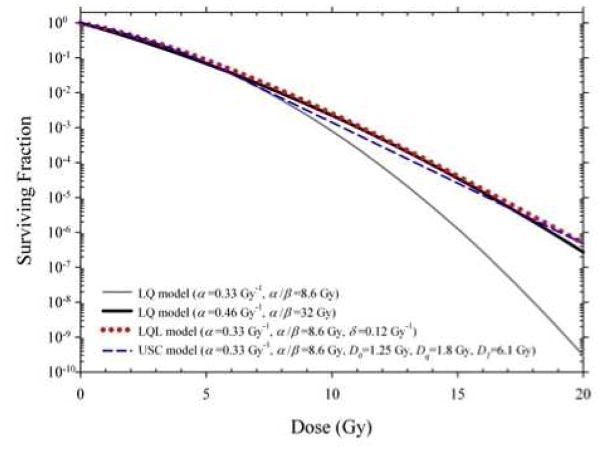
The validity of the LQ model at high doses per fraction is controversial and has been critically examined by many investigators (13–18). It is well known that the LQ is only an approximation to more sophisticated kinetic reaction rate models (5, 19, 20) which, when fit only to the low dose data, can provide a better prediction of in vitro clonogenic survival data at larger doses. LQ predictions begin to deviate, for example, from Repair-Misrepair (RMR) and Lethal-Potentially Lethal (LPL) model predictions above ~5 Gy for high dose rates (4, 14). However, the LQ model has been shown to fit experimental survival data well up to ~10 Gy (14) and may even be appropriate for single fraction doses as large as ~15–20 Gy when fit over the entire dose range (15). Several empirical or semi-empirical modifications have recently been proposed (14, 17, 21, 22) which introduce additional high-dose terms to synthetically straighten the survival curve at high doses. By doing so, any plausible underlying biological mechanisms of the original LQ model are lost. In a recent review of the history of the use of biologically effective dose (BED), Jack Fowler (23) questioned the need for a straightening of the simple LQ curve beyond an arbitrary threshold dose and suggested that instead this straightening could be achieved by assuming a higher α/β. There is a good biological rationale for higher α/β values in rapidly proliferating and hypoxic tumors. Figure 1 shows a visual comparison of model predictions for the LQ, Linear-Quadratic-Linear (LQL) (14, 22), and Universal Survival Curve (USC) (17) models. Substantial overlap in model predictions is achievable by simply assuming a higher α/β for the LQ model.

Figure 1. The perceived overprediction of cell killing at high doses by the LQ model is resolved by assuming a higher α/β value.

Comparison of predictions of the Linear-Quadratic (LQ), Linear-Quadratic-Linear (LQL) (14, 22), and Universal Survival Curve (USC) (17) models. LQL and USC model predictions are similar assuming an α/β of 8.6 Gy..

While an alternate “high-dose” model may provide a superior visual fit to a specific in vitro cell survival dataset fit over a restricted dose range, it remains to be shown if any of these models with additional high-dose terms can provide significantly better fits to multiple datasets. In addition, the utility of an empirical model decreases with the introduction of additional adjustable parameters. For example, the number of variable model parameters increases to three and five in the LQL and USC models, respectively, compared to only two parameters in the simpler LQ model. It would not be surprising at all if a 5-parameter model could provide a statistically superior fit to an in vitro dataset compared to a 2-parameter model. Yet, this has not been definitively demonstrated to the knowledge of the authors. Two important questions remain unanswered at this time: (1) can an alternate high-dose model provide a statistically superior fit to the data considering an increase in the number of adjustable parameters and (2) is there any evidence that any of these alternate models provide better estimates of clinically-relevant endpoints than the conventional LQ model?

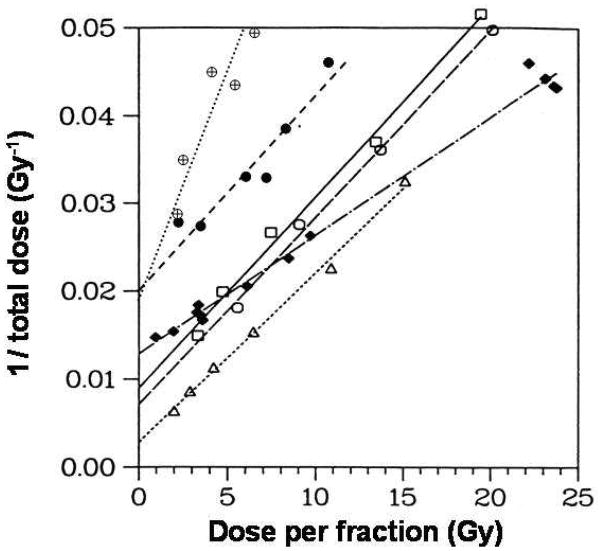
There is compelling in vitro and in vivo normal tissue evidence that the LQ model provides reasonable results at high doses (15). In particular, Fig 2 shows iso-effect results for late-responding damage to the rat spinal cord (24), for acute damage in mouse skin (25), and for early and late damage to the murine small intestine (26) up to very high single doses. All the quantitative in vivo endpoints are consistent with the LQ model, over a wide range of doses per fraction, including those of interest to SBRT, including the data for single fractions of ~20 Gy. In addition, clinical outcome data for local tumor control can be used to compare biological models over a wide range of doses and fractionations. Recently, Mehta et al. (27) analyzed the available local control data for early-stage non-small cell lung cancer (NSCLC) patients undergoing 3D conformal radiotherapy (3D-CRT) and SBRT. They found that the clinical data could not distinguish between the LQ and USC models suggesting that it may be difficult with tumor response to distinguish between the LQ model and LQ modification models.

Figure 2. Isoeffect data for response in normal tissues fit the LQ model.

Data for different regions (□,○,△) of the rat spinal cord (24), for acute skin reactions (◆) in mice (25), and for early (●) and late (⊕) murine intestinal damage (26). The LQ model predicts straight lines for these plots. From (15) with permission.

We conclude from the above that the LQ model is reasonably predictive of in vitro and in vivo normal tissue dose-response relations in the dose per fraction range of 1.8 to 20 Gy and it is not currently possible to identify an alternate high-dose model that performs better than the LQ for predicting cell killing. There is also insufficient clinical evidence at this time that the LQ needs to be modified or replaced at high doses. If alternative models do not provide a better fit to the clinical data (even with additional adjustable parameters), then there is no justification for using them regardless of how well they fit an in vitro cell survival curve. However, no model describing dose-time patterns can be fully complete or correct. Some of the main perceived mechanistic uncertainties of the LQ model have been discussed in detail by Brenner (15) so we will only summarize the conclusions reached in that review. Brenner concluded that though the mechanistic basis for the LQ model is usually attributed to pairwise production of chromosome aberrations, this does not have to be the case, and the model does accommodate other cell killing mechanisms such as apoptosis and lethal mutations. One important objection often raised as to the generality of the LQ model at high doses is whether repair might saturate at high doses. Two arguments suggest this is not the case. First for normal tissues, as mentioned above, the dose response curves fit the LQ model up to at least 20 Gy. Second, the rate and extent of DSB repair is similar in cells after 1 Gy (determined by γ-H2AX loss) and after 80 Gy (determined by pulsed field gel electrophoresis) (28). Thus, in the absence of any data to the contrary it would appear that saturation of repair up to doses that could conceivably be used in radiotherapy is not important.

However, given the preponderance of evidence that the LQ model fits both in vitro and in vivo normal tissue dose responses, there remains the major question of the response of tumors to irradiation, and it is this question that is the focus of the claims that high dose per fraction SBRT provides results superior to those expected from standard fractionation. We review below this question, which essentially comprises three major challenges to the validity of standard radiobiology to high dose irradiation of tumors.

Biological Challenges to the 5 Rs for SRS/SBRT

As noted earlier, there have been several biological effects that suggest that doses per fraction above 10 Gy give greater antitumor efficacy than predicted from standard radiobiological modeling as follow:

1. Endothelial cell damage may enhance the cytotoxic effect of irradiation on tumor cells

The joint laboratories of Zvi Fuks and Richard Kolesnick published in 2003 an influential paper (29) (and expanded later (30)) proposing that the radiation sensitivity of tumors to dose fractions of 10 Gy or more was governed by the sensitivity of the tumor endothelial cells to apoptosis: the same tumors in mice sensitive to radiation-induced endothelial cell apoptosis were more sensitive to radiation than those in mice resistant to endothelial cell apoptosis (Fig 3A). However, data in the same publication suggests there could be another explanation, namely that the composition of the bone marrow could have affected the radiation response. Fig 3B shows that the tumors in wild-type (amase^+/+) mice could be converted from sensitive to resistant by a bone marrow transplant from endothelial apoptosis resistant (amase^−/−) mice. The authors proposed that the endothelial cells in the bone marrow transplanted mice had derived from the new bone marrow, but more recent studies of others has cast doubt on this possibility (31, 32), or have suggested that incorporation of bone marrow cells into tumor endothelium is mostly very low (33). This suggests that it is the asmase^−/− character of the bone marrow, not the endothelial cells of the tumor, that is responsible for the tumor resistance in this model. Another challenge to the endothelial cell apoptosis theory is that no other lab has independently confirmed the data, rather, most publications have shown only modest changes to the vasculature with a gradual loss of tumor endothelial cells after irradiation (34, 35). We therefore conclude that without further confirmation the concept that rapid post-irradiation endothelial damage amplifies tumor cell kill may not be generally applicable to SBRT.

Figure 3. Tumor response is affected by the genetics of the host;

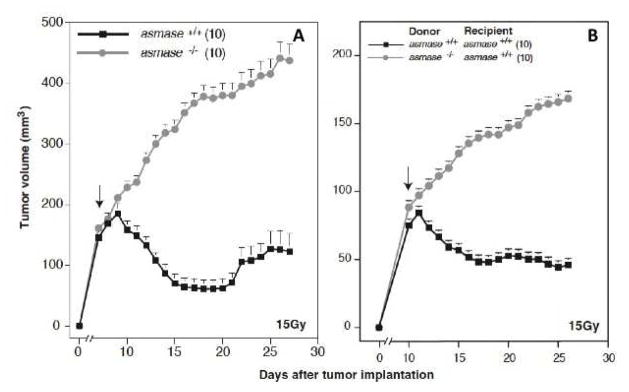
A. Response of the MCA/129 fibrosarcoma to 15 Gy either in wild-type (asmase +/+) (endothelial apoptosis sensitive) or asmase−/− (apoptosis resistant) mice. B. Response of the MCA/129 fibrosarcoma in asmase +/+ mice that had been bone marrow transplanted with bone marrow from asmase +/+ or asmase −/− mice. These data suggest that it may be the asmase −/− bone marrow, rather than the asmase −/− tumor endothelium, that confers tumor radioresistance. Adapted from (29) with permission.

2. Vascular damage at high doses produces secondary cell killing

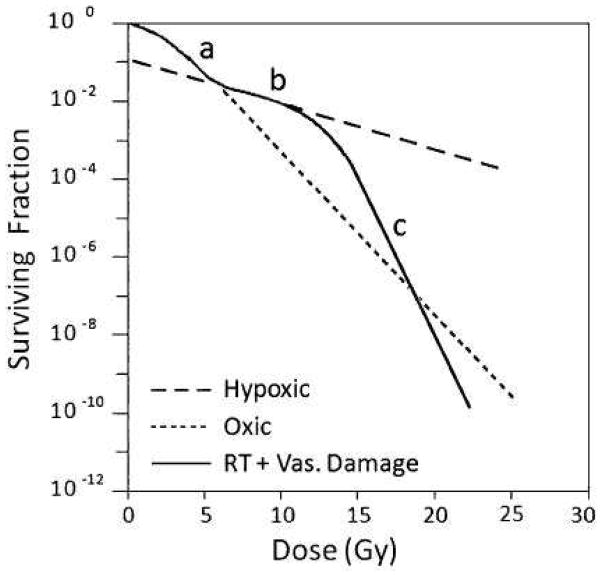
This theory, suggested by Song and colleagues (36), suggests that radiation doses higher than about 10 Gy induce vascular damage leading to indirect tumor cell death. The concept is illustrated in Fig 4. Though this is an attractive hypothesis there are only fragmentary data to support it (37) (Fig 5A). There are also extensive early data from Barendsen and Broese on the survival of cells in a rat rhabdomyosarcoma as a function of time after single doses of both 10 and 20 Gy that shows no evidence of this increasing cell kill as a function of time after irradiation (38) (Fig 5B). We thus conclude that there needs to be considerable more experimental evidence that this potential mechanism plays a role in the sensitivity of tumors after high dose per fraction radiotherapy.

Figure 4. An illustration of how indirect death due to vascular damage could contribute to total clonogenic cell kill in tumors irradiated with large single doses of radiation.

The model assumes 10% of the tumor cells are maximally radioresistant hypoxic cells. The dotted lines indicate the response of oxic (- - - - -) and hypoxic (– – – –) tumor cells. The response at doses 0–5 Gy is dominated by oxic cells (a), while that at 5–12 Gy is dominated by hypoxic cells (b). As radiation dose is increased above 12 Gy, it is suggested that indirect cell death due to vascular damage (c) can enhance total cell kill. From (60) with permission

Figure 5. Conflicting data on whether large single doses produce indirect cell kill.

A: Data on the Walker 256 tumor showing falling cell survival following a single dose of 10 Gy (originally published in 1978 and reproduced recently (60) with permission) B (upper) Gross response of the rat rhabdomyosarcoma to 10 or 20 Gy (lower): Data on the cell survival from the same tumors as a function of time after irradiation. Note there is no evidence for a fall in cell survival over the first 4 days after irradiation, prior to the rapid growth of the surviving cells From (38) with permission.

3. Enhanced antitumor immunity after tumor irradiation

There is now clinical evidence that for melanoma, irradiation by SBRT of a tumor at one site contributes to an antitumor immunological rejection of a metastatic lesion at a distant site- a so-called “abscopal effect” (39, 40). So far the data have been reported for only two patients so there are many questions to be resolved. These include whether this phenomenon is produced only at high single doses (or high doses per fraction), and whether other tumors besides melanoma experience this effect. On the first of these questions the preclinical data suggest that though radiation enhances the antigenicity of tumors (41–43) it has been reported by the Demaria lab that this is greater for fractionated irradiation than for single doses (44). However, none of the radiation schedules tested in this study was comparable to standard fractionation: of the schedules tested (20 Gy ×1, 8 Gy ×3, and 6 Gy ×5 fractions in consecutive days), the fractionated 8 Gy was the most effective with the 6 Gy intermediate and the 20 Gy the least effective. Thus all of these schedules could be considered to be similar to SBRT. Another preclinical study from the Weichselbaum laboratory (45) has reported a similar enhancement of antitumor immunity by local tumor irradiation but in this case there was a greater effect of 20 Gy ×1 than 5 Gy ×4 over 2 weeks. Of interest is that the Demaria study in mice and in the clinical study with melanoma mentioned above the radiation was combined with anti-CTLA-4 antibody: in the case of the preclinical study there was no indication of enhanced antitumor immunity by the radiation alone though in the Weichselbaum study (45) antitumor immunity was achieved by irradiation alone. These data are clearly exciting and illustrate the fact that much more information is needed in this field to be able to recommend the best doses per fraction and timing of the radiation regimen to optimize this effect. Also of major importance is just how general the phenomena of enhanced antitumor immunity by high dose/fraction radiotherapy will be across the spectrum of tumors undergoing radiotherapy.

Preclinical data with tumors do not support enhanced efficacy of high dose radiation

A number of investigators have addressed the question of whether tumor control at high single doses can be predicted from in vitro survival curves obtained at low doses (46–48). In general these have been successful – i.e. the dose to control 50% of the tumors (TCD50) is consistent with the sensitivity of the tumor cells determined at low to moderate doses. The most compelling of these data are from the laboratory of Gerweck who determined the in vitro sensitivity of six tumor cell lines, as well as the number of cells needed to transplant the tumors (TD50) and showed that these two parameters could predict the in vivo TCD50 (Fig 6). Importantly four of the six tumors were from tumors that had originated spontaneously in mice and were transplanted into their respective hosts. Thus an immunological component could have been involved. The other two were human tumors transplanted into nude mice.

Figure 6. The radiation dose to control 50% of the tumors (TCD50) is well predicted from the radiosensitivity of the cells in vitro and the number of cells needed to transplant the tumor (TD50).

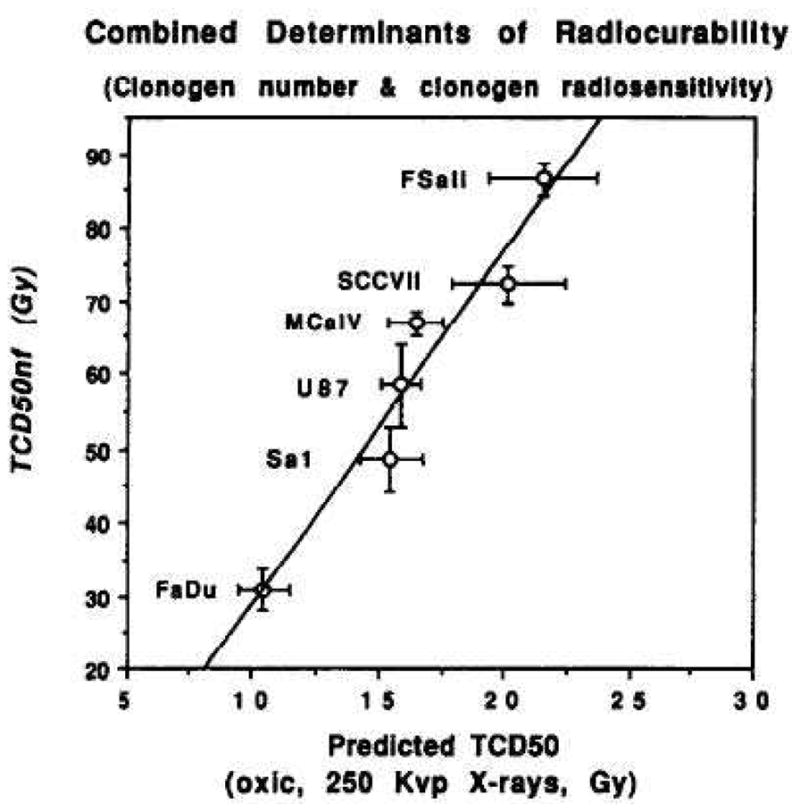
The observed TCD50 under air breathing conditions as a function of the predicted TCD50s, calculated from tumor cell radiosensitivity (in the 0–12 Gy range) and tumor clonogen number (from the TD50). Error bars are 1 SD. From (48) with permission.

These data demonstrating that the TCD50 to large single doses (>20 Gy) can be predicted from the radiation survival curve at low doses (<10 Gy) do not support any extra cell kill due to endothelial damage, vascular collapse or enhanced immunity.

Tumor Hypoxia is likely to be more Important for SRS/SBRT than for Conventional Fractionation

It has been known for some 60 years that hypoxic cells are resistant to killing by ionizing radiation (49). A cell population deprived of oxygen requires approximately a threefold larger radiation dose to produce the same amount of cell kill as a cell population exposed to physiological oxygen conditions. Hypoxia has been observed in many human cancers: Approximately 90% of all solid tumors have median oxygen concentrations less than the typical values of 40 to 60 mmHg found in normal tissues with many cancers having median oxygen levels below 10 mmHg (50), which would make the cells more resistant than normal tissues to irradiation. A number of investigators have now demonstrated unequivocally that the extent of tumor hypoxia has a negative impact on the ability of radiotherapy to locally control certain tumors (51, 52). This is despite the fact that fractionation of radiation mitigates the protection afforded by tumor hypoxia because of the phenomenon of reoxygenation (53), the process by which the hypoxic cells surviving a given radiation dose become oxygenated prior to the next radiation dose most likely as a result of fluctuating tumor blood flow (54).

Given the fact that tumor hypoxia has been demonstrated to negatively impact the efficacy of radiotherapy, at least for some tumors, it is reasonable to ask what impact it would have for SBRT/SABR. There are both preclinical and modeling studies that demonstrate that tumor hypoxia will be an even greater detrimental factor for SRS.

First the preclinical data. Some 30 years ago Fowler and colleagues measured control of transplanted mouse mammary tumors for the same level of skin damage (an early responding normal tissue) for a variety of fractionation schemes including single doses. They showed that large single doses of radiation were notably inferior in achieving tumor control for a given level of skin reaction (hence providing justification for fractionation in radiotherapy). Further this inferiority could be entirely overcome if the resistance of the hypoxic cells in the tumors was eliminated by pretreatment of the mice with a large dose of the hypoxic cell radiosensitizer misonidazole (55). In other words, fractionation is effective in improving tumor control for a given level of early responding normal tissue damage because it partially overcomes the resistance of hypoxic cells due to reoxygenation between doses. The LQ model predicts a further benefit of fractionation for tumor response relative to late responding tissues.

Second, up-to-date modeling of the influence of hypoxia on tumor response confirms that fractionation will produce more antitumor effect for the same biological effect on normal tissues (11) This is shown in Fig 7. In this study, the effect of tumor hypoxia, modeled as a continuous distribution of oxygen tensions (and radiosensitivity) from the blood vessels to the most hypoxic regions, on the survival of tumor cells is calculated for the same BED for oxygenated cells (or the cells of normal tissues). The reader is reminded that BED is an LQ model based estimate of the effective biological dose that corrects for the effect of dose fractionation (56). The conclusions from this study are:

Figure 7. Modeling (using the 5 R’s) predicts loss of efficacy of tumor cell kill for the same level of normal tissue toxicity as the dose/fraction increases.

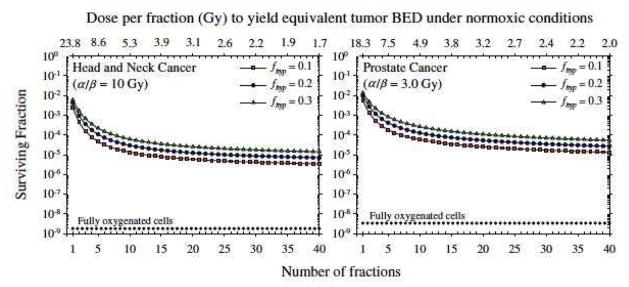
Predicted surviving fraction of tumor cells for different size dose fractionations assuming full reoxygenation between fractions, Dependence of predictions on the assumed hypoxic fraction of the tumor, f_hyp, is shown. It is evident that there is less cell kill predicted for very few fractions compared to standard fractionation for the same BED (response of well-oxygenated normal tissues). From (11) with permission.

1. Tumor hypoxia makes a large difference to the calculated level of cell killing even for highly fractionated irradiation and the value of α/β or the “hypoxic fraction” has relatively less effect. This is consistent with the clinical data.

2. As the number of fractions decreases the expected tumor cell survival increases (i.e. less tumor response) for the same BED or the same normal tissue damage. The worst situation is with a single dose, which gives a survival of approximately 10⁻² compared to 10⁻⁵ with 30 daily fractions.

3. A logical consequence of the predicted increased importance of tumor hypoxia to the response of tumors to SBRT is that hypoxic cell radiosensitizers, which largely failed with fractionated irradiation, become a realistic option to improve the clinical outcome (11, 57).

Thus, both preclinical data and modeling studies show that tumor hypoxia is more of a detrimental factor for single dose treatments that for fractionated irradiation. Are there clinical data that can be used to address this question?

We recently analyzed tumor control data for non-small cell lung cancer and for brain metastases treated both with single doses and fractionated SBRT as well as conventional radiotherapy (Brenner et al, 2013, in preparation). The results of this analysis suggest that tumor control was significantly less for single doses than fractionated irradiation for the same BED. This is consistent with the predicted loss of tumor response because of tumor hypoxia of single doses compared to fractionated radiotherapy for the same BED.

Clinical Data Suggest that Radiobiological Modeling with the Linear-Quadratic Equation is Adequate to Explain the Efficacy of SRS and SBRT

In a recent editorial (58), we suggest that dose escalation, not “new biology,” can account for the efficacy of SBRT with early-stage NSCLC. We used the term “new biology” to describe any of the above mentioned novel radiobiological mechanisms that could potentially make SBRT more effective than would be predicted from clinical experience with fractionated radiotherapy. Mehta and colleagues (27) recently reviewed the available local control data for early-stage NSCLC patients undergoing 3D-CRT and SBRT. Fig 8A shows the NSCLC tumor control probability (TCP) data as a function of BED, replotted in Brown et al. (58) to clearly distinguish the data for single fraction SBRT, multi-fraction SBRT, and conventional 3D-CRT. A monotonic relationship between TCP and BED is clearly observed for the 3D-CRT and SBRT data. Regardless of fractionation, higher TCPs are obtained by delivering higher tumor BEDs. Thus, there is currently no evidence from the available NSCLC data in the literature that SBRT and 3D-CRT produce different probabilities of tumor control when corrected for tumor BED.

Figure 8. Tumor control probability (TCP) as a function of biologically effective dose (BED) for stage I NSCLC.

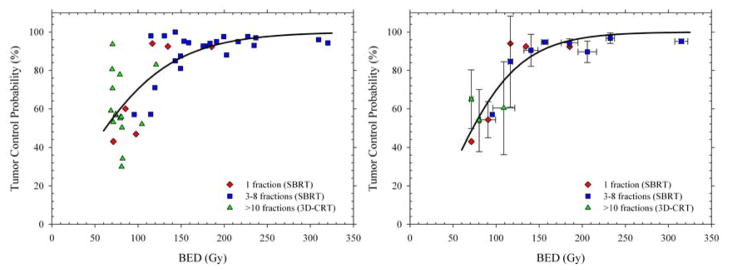
Left panel: Symbols show local control rates (≥2 years) from a pooled analysis reported by Mehta et al. (27) with symbols distinguishing conventional and SBRT fractionations. Right panel: Weighted mean TCP probabilities calculated to compensate for the different numbers of patients in each study. Solid lines show LQ-based fits to the data which show that, within the limits of clinical data, the efficacy of single doses, a few SBRT fractions, and conventional radiotherapy produce the same overall TCP for the same BED. From (58) with permission.

Based on the observations that (1) TCP increases monotonically with BED, and (2) the TCP vs. BED relation is similar for 3D-CRT, single-fraction and multi-fraction SBRT, we can say with some confidence that the great success of SBRT is due to the fact that the new stereotactic radiotherapy technologies provide dose distributions that permit the clinician to prescribe BEDs of 100 Gy or more (59). These high tumor BEDs are simply unachievable with conventional dose delivery techniques. The higher TCPs for SBRT can therefore be fully explained by the much higher tumor doses delivered, and are entirely consistent with predictions of the linear-quadratic model. For non-small cell lung cancer, there is no need to invoke a “new biology” to explain the high cure rates. We have also reached the same conclusions for brain metastases (Brenner et al. 2013, in preparation).