The Origins and Structure of Quantitative Concepts

Abstract

‘Number’ is the single most influential quantitative dimension in modern human society. It is our preferred dimension for keeping track of almost everything including distance, weight, time, temperature, and value. How did ‘number’ become psychologically affiliated with all of these different quantitative dimensions? Humans and other animals process a broad range of quantitative information across many psychophysical dimensions and sensory modalities. The fact that adults can rapidly translate one dimension (e.g., loudness) into any other (e.g., handgrip pressure) has been long established by psychophysics research (Stevens, 1975). Recent literature has attempted to account for the development of the computational and neural mechanisms that underlie interactions between quantitative dimensions. We review evidence that there are fundamental cognitive and neural relations among different quantitative dimensions (number, size, time, pitch, loudness, and brightness). Then, drawing on theoretical frameworks that explain phenomena from crossmodal perception, we outline some possible conceptualizations for how different quantitative dimensions could come to be related over both ontogenetic and phylogenetic timescales.

Introduction

Humans and other animals process information from many continuous psychophysical dimensions across sensory modalities and perceptual variables, including number, size, event duration, speed, visual and auditory brightness, pitch, and loudness. These dimensions constitute “quantities” or “magnitudes”¹ because they are (at least roughly) interpretable as amounts, as in the case of number, size, and duration, visual brightness, and loudness, or because changes in stimulus values can be readily interpreted as amounts, as in the case of auditory brightness and pitch. Discrimination data collected from many such dimensions conform to Weber’s law: successful discrimination of two stimuli along a given continuum depends on their ratio rather than absolute values. This is the principal signature of analog magnitude representations, in which values of increasing quantity are correlated with an increase in uncertainty (Moyer & Landauer, 1967; Gallistel & Gelman, 1992, 2000; Gallistel, 1990; Stevens, 1975; see also Cantlon, Platt, & Brannon, 2009, for review). This commonality in psychophysical performance suggests that, at some level, the neural computations required of each dimension are similar. In fact, a growing body of evidence suggests that different magnitudes—even those that might not be intuitively grouped at first glance—are related.

We begin by presenting the historical origins of currently discussed proposals for functional and neural architectures of magnitude representation. We then consider evidence that many dimensions of magnitude are related in the adult mind and brain, including space, time, number, pitch and brightness. We include a brief overview and critique of the evidence discussed in previous reviews (Bueti & Walsh, 2009; Cantlon et al., 2009; Lourenco & Longo, 2011) as well as more recent, related findings; in addition, we include potentially related literature not previously discussed to illustrate the scope and complexity of the evidence to be explained.

The section that follows describes biologically plausible, computational analogies for processes that could account for the development of composite or overlapping magnitude representations. Because little is known about the development of these representations, we base our discussion on theoretical frameworks that have shaped investigations of multisensory integration and cross-modal transfer. Previous characterizations of the development of composite magnitude representations leave many assumptions and linking hypotheses unstated. We lay out some the assumptions and predictions of the candidate hypotheses to frame current evidence and guide future research. This allows us to illustrate that some of the implicit assumptions about relations among magnitudes may not be valid. In particular, we show that asymmetries of interference between two dimensions of magnitude (eg., space interferes with time more than time interferes with space) are consistent with many conceptualizations of magnitude relations and therefore do not offer a way of adjudicating among them.

In the final portion of the paper, we consider how either evolution or learning and development may implement these processes and the multiple representational levels at which composite representations may occur, incorporating evidence from developmental studies as well as highlighting areas where research is needed.

Origins of Current Debates

The question of how quantitative cognition is functionally organized in the brain began with neuropsychological investigations of patients with numerical and arithmetic impairments (e.g., Gerstmann, 1940). Neurological patients with parietal lesions can be impaired in making numerical judgments while other cognitive abilities such as object categorization and recognition remain intact (Cipolotti, Butterworth, & Denes, 1991; Dehaene & Cohen, 1997). Furthermore, studies of patients with semantic dementia (and anterior temporal lobe atrophy) have shown that numerical skills can be spared in cases where other semantically demanding tasks such as picture categorization or picture naming are impaired (Cappelletti, Kopelman, Morton, & Butterworth, 2005). Those data show that it is possible to isolate numerical cognition from other components of cognition through damage to one (albeit large) part of the brain: parietal cortex. Because those initial studies did not test magnitude representations for dimensions other than number, the question of whether the dissociation between ‘number’ and other semantic domains is unique to numerical magnitudes cannot be resolved at present. In fact, it is not always the case that numerical deficits neatly segregate from other deficits: individuals with relatively focal lesions to intraparietal cortex commonly exhibit simultaneous deficits in arithmetic, spatial, and abstract perceptual judgments (Figure 1; Gerstmann, 1940; Takayama, Sugishita, Akiguchi, & Kimura, 1994). The functional relationships among those associated impairments have not been studied and so it cannot be concluded that there is representational interdependence between arithmetic and visuospatial judgments. However, a long tradition of cognitive-science research supports the possibility that judgments of other perceptual intensities or magnitudes (e.g., size, time, brightness, loudness) could exhibit a similar pattern of impairment to numerical performance in these cases of neural impairment.

Figure 1.

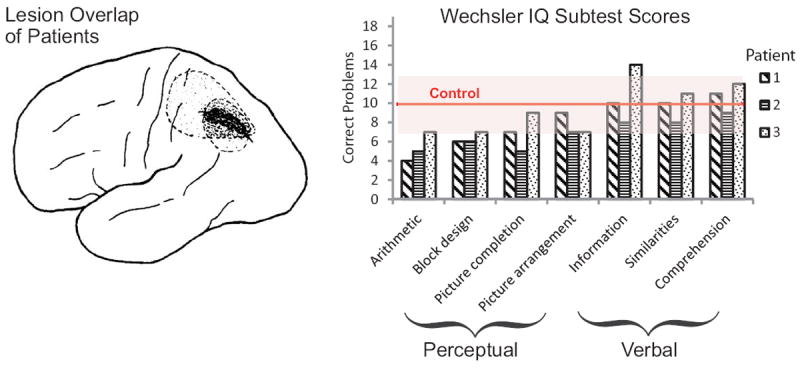
Left: Lesion overlap at the intraparietal sulcus of three patients with isolated acalculia. Right: Performance of acalculic patients on subtests of WAIS subtests demonstrates impairment to arithmetic ability, as well as more subtle impairments in perceptual and spatial reasoning, but no impairment on verbal tasks. (Takayama et al., 1994). (Figure reprinted with permission from the American Medical Association.)

The idea that other magnitudes might share a common neural code was initially proposed by Gallistel and Gelman (2000). In their review of behavioral data from humans and other animals, they argued that discrete number should be represented with an analog magnitude code. Because animals must combine discrete number with continuous quantities in making decisions (for example, in assessing food patches based on the number of potential food items and the space over which the food is spread), reconciling these incompatible formats necessitates conversion to a common code: the analog format.

Drawing on this suggestion, Walsh (2003) proposed that space, time, and other quantities—primarily number—share an abstract, undifferentiated magnitude code present at birth. His key claim is that an interconnected magnitude representation of time, space, and number emerges because of the critical role of magnitude information in the action system. The argument is that the common neural location of magnitude information and motor control in parietal cortex is what binds those computations. Although neural location could be an important factor in determining what cognitive representations are associated, a potentially more important factor is their functional origins in development. According to Walsh, the generalized magnitude system becomes differentiated in postnatal development, developing into specialized magnitude subsystems that share neural resources (in parietal cortex), though exactly how they are shared over development and to what extent each dimension is functionally differentiated remains unspecified.

One problem for understanding how magnitude dimensions are related over development is that a substantial amount of behavioral and neural evidence from human adults and non-human animals is consistent with a number of theoretical possibilities for how magnitude relations develop or evolved. These possibilities include innate relations, learned correlational relationships, and both verbal/cultural and nonverbal analogies. We review the evidence in the next section.

Inferences about the Canonical Domains of Space, Time, and Number

Evidence for interactions among representations of space, time, and number comes from tasks that elicit representations in two of these dimensions simultaneously. In a now classic study of the interaction between time and number, Meck and Church (1983) found that rats are similarly sensitive to both number and duration (holding the other variable constant). In addition, they found that administration of methamphetamines increases the speed of the mechanism governing judgments of both dimensions indicating that the animals’ representations of time and number are subject to common constraints at some level of processing (Figure 2). Similarly, a recent study in human adults suggests that a click train can accelerate a common internal clock in sequential line, duration, and numerosity bisection tasks (Droit-Volet, 2010). Experiments in pigeons (Roberts, 1995; Roberts, Coughlin, & Roberts, 2000) and Stroop-like experiments in humans (Dormal, Seron, & Pesenti, 2006) have shown similar behavioral signatures (but see Roitman, Brannon, Andrews, & Platt, 2007, for evidence of a possible asymmetry in representations of number and duration). Taken together, these findings suggest that a common mechanism underlies judgments of both dimensions in these nonverbal tasks.

Figure 2.

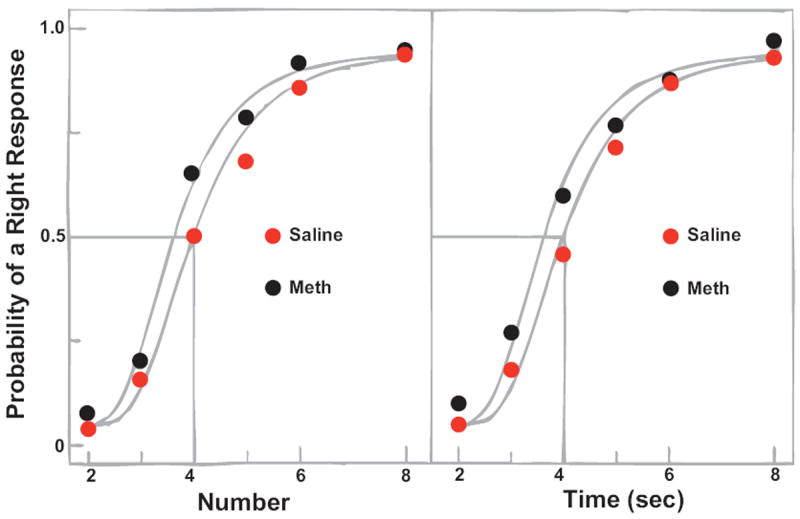
Psychophysical functions from Meck & Church (1983). Median probability of a right response as a function of number (left) and duration (right). The methamphetamine condition (black circles) shifted the curves above the baseline (saline—red circles) condition by about 10% for judgments of both number and duration. (Figure reproduced according to the republishing guidelines of the American Psychological Association.)

Reaction time experiments also provide evidence of the interaction between number and space. In one early study, Henik and Tzelgov (1982) showed that when Arabic numerals are pitted against physical size (eg., 9 5), judgments of which numeral is larger (in size or number) showed congruency effects between the attended and unattended dimensions. Another classic signature is the so-called SNARC effect (Spatial-Numerical Association of Response Codes; Dehaene, Bossini, & Giraux, 1993). According to the most popular construal, adults map representations of number onto a horizontal mental number line, explaining the observation of faster processing times for larger numerical values on the right side of the line. This type of mapping between space and number is also evident in cases of spatial neglect wherein adult neurological patients with parietal cortex damage can exhibit asymmetries in their estimates of the ‘center’ both during line bisection and numerical bisection tasks (Zorzi, Priftis, & Umlita, 2002). Thus the neural origin of space-number association appears to depend on parietal cortex. But, this is at least partly a learned association. The space-number mapping is known to emerge following exposure to counting behaviors and formal training in school (Opfer, Thompson, & Furlong, 2010; Berch, Foley, Hill, & Ryan, 1999; van Galen & Reitsma, 2008) and is flexible in bilinguals who learn two different spatial writing directions (Shaki & Fischer, 2008), strongly implicating culture in shaping this type of representation. However, it is unclear whether the culturally mediated mapping of number onto space builds on a biological disposition to preferentially map number onto space (e.g., deHevia & Spelke, 2010). One recent set of experiments suggests that space does not have a privileged psychological relationship with number in adulthood. Nuñez, Doan, and Nikoulina (2011) tested how well adult participants mapped number to non-spatial formats. In these experiments, participants mapped number onto non-spatial formats such as squeezing, bell striking, and vocalizing as well as spatial ones. Though the non-spatial mappings were found to be slightly different from the spatial mappings (they were logarithmically rather than linearly spaced and less precise), the authors suggest that there might not be anything biologically or conceptually special about the space-number relationship. However, an open issue is whether higher precision in the spatial judgments relative to non-spatial judgments is due to innate biases or extensive cultural experience with mapping dimensions onto space.

Much of the recent evidence for an interaction between representations of time and space in adults and animals comes from experiments that explore how language use might shape the development of concepts. Across languages, the use of spatial language to describe time suggests that conceptualization of time is dependent on physical conceptions of space, though the exact way in which languages tend to conceptualize time in terms of space varies across cultures. For instance, according to Boroditsky (2000; 2001), Mandarin speakers are more likely to think about time in a vertical orientation than English speakers, in line with the metaphors present in the language. Failures to replicate these results have rendered the original findings controversial (January & Kako, 2007; Chen, 2007; see Boroditsky, Fuhrman, & McCormick, 2011, for a response). Nonetheless, evidence from linguistic metaphors (e.g., Lakoff & Johnson, 1980; 1999) may suggest a link between space and time independently of whether the link is at a deep representational level or a superficial linguistic response level.

Results from tasks that presumably do not depend on language use suggest that the dependence of representations of time on space extends beyond the domain of language. Nonverbally presented magnitudes with no temporal component (i.e., static stimuli) modulate estimates of duration; larger, brighter, and more numerous stimuli are perceived to last longer than smaller stimuli of equal duration (Xuan, Zhang, He, & Chen, 2007). Eagleman (2008) suggests that these heuristic estimates of duration from size, brightness, and number directly reflect the amount of neural energy required for visual stimulus encoding, implying that the perception of interval duration is heavily influenced by aspects of stimulus encoding that are only indirectly related to timing (see also Pariyadath & Eagleman, 2007). The implications of those studies are not settled: either duration perception largely piggy-backs on the computational machinery of other magnitudes or the weight given to other magnitudes in overlapping representations is so large that it masks the input from true timing mechanisms. Under either interpretation, interactions between time, brightness, number, and size are fundamental.

A possibly related behavioral signature is an asymmetry of interference: in adult humans, judgments of line length interfere with judgments of duration more than duration judgments interfere with judgments of line-length (Casasanto & Boroditsky, 2008). In one recent study, Merritt, Casasanto, and Brannon (2010) found that while adults’ nonverbal judgments of duration are affected by the simultaneous representation of line length in a dual task, the effect of duration on judgments of line length are considerably smaller, consistent with previous findings. In rhesus macaques, duration and line length seem to interfere with each other equally, suggesting that the magnitude code the monkeys accessed is equally distributed between spatial and temporal representations. Thus there appears to be a spatially biased temporal representation in humans but not in monkeys. However, even though both the humans and monkeys were trained to complete the task without verbal labels, human participants may still have linguistically encoded the durations (subvocally or otherwise) into English spatial terms (i.e., “short” and “long”). So, the uniquely human pattern of interference might arise at the level of lexical representation or response selection rather than a language-independent magnitude system. The results from the monkeys show that this asymmetry between time and size is a uniquely human phenomenon and therefore is unlikely to be purely a signature of interval timing as proposed by Eagleman (2008). Thus we potentially can rule out the claim that the use of size, brightness, and number as a proxy for interval duration (described earlier) is the root cause of asymmetrical interference effects between space and time in humans.

The relationship between space and time has also been found at the neural level. Single-neuron data from neurophysiology studies of monkeys broadly indicate that the same neural substrate represents space, time, and number (Leon & Shadlen, 2003; Nieder, 2005; Roitman, Brannon, & Platt, 2007). Moreover, some data even suggest that a single parietal neuron can represent more than one type of magnitude. In one study (Tudusciuc & Nieder, 2007), monkeys were trained to perform a line length-matching task and a numerical matching task. During stimulus presentation or a subsequent delay, single neurons in parietal area VIP responded selectively to visual stimuli based on their numerosity or length. Although some neurons responded only to numerosity and others only to line length, a subset of cells (~20%) responded to the magnitudes of both the line lengths and the numerical values. In an adjacent parietal region (LIP), single neurons have been shown to be sensitive to quantities such as duration and number (Leon & Shadlen, 2003; Roitman et al., 2007). These and other studies, including fMRI studies of adults, have led some researchers to argue for a “distributed but overlapping” representation of different magnitudes at the neural level (Pinel, Piazza, Le Bihan, & Dehaene, 2004; Tudusciuc & Nieder, 2007). Moreover, Pinel et al. (2004) found that the amount of functional overlap between brain regions recruited during Stroop-like tasks predicted the size of the interference effects observed (Figure 3). Simply put, different types of magnitude representation including size, number, and time (and possibly brightness) share some neural resources in parietal cortex but not others.

Figure 3.

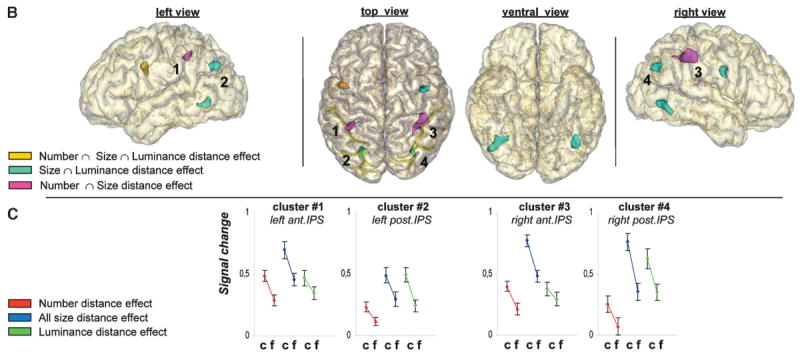
Top: Neural overlap among combinations of the dimensions of number, size and luminance. Bottom: The distance effect: neural signal differences in the intraparietal sulcus (IPS) between close (c) and far (f) pairs of number stimuli, size stimuli, and luminance stimuli (Pinel et al., 2004). (Figure reprinted with permission from Cell Press).

Taken together, these findings tend to emphasize the relations between the dimensions of space, time, and number. The fact that there are so many studies that report a relationship between those dimensions (and not others) has led to arguments that there is a biologically privileged relationship among the dimensions of space, time, and number (Dehaene, Izard, Spelke, & Pica, 2008; Srinivasan & Carey, 2010; Walsh, 2003; Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999). However, as mentioned above, there is some evidence for fundamental interactions among quantitative dimensions beyond space, time, and number, such as interactions between time and brightness (Xuan et al., 2007). In the next section we review further evidence.

Beyond Space, Time, and Number

There is some evidence that dimensions such as loudness, brightness, and pitch--dimensions other than those that are allegedly privileged (space, time, and number)--interact at the representational level. For example, adults are equally facile at scaling any kind of continuum to digital number as they are with scaling to loudness (Stevens, 1975). Further, we already described evidence that among adult humans, brighter stimuli (in addition to larger and more numerous stimuli) are mistakenly estimated as lasting longer in duration than darker stimuli (Xuan et al. 2007). In addition, cross-dimensional mapping effects show up in Stroop-like paradigms for dimensions beyond space, time, and number. Marks (1987) showed that presentation of irrelevant auditory pitch information in visual brightness judgments (dark vs. light) and irrelevant visual brightness information in auditory pitch judgments (low vs. high) affect adults’ reaction times. In that experiment, irrelevant stimuli that were congruent (dark and low; light and high) facilitated responses and those that were incongruent (dark and high; light and low) interfered with responses. In this section, we focus in particular on interactions found between non-canonical domains (e.g., auditory pitch and luminance) and canonical domains (number, space and time).

Interactions with Non-Canonical Domains

i. Luminance/Brightness and Loudness

Pinel et al. (2004) report interactions between stimulus luminance and the canonical domains of number and space in magnitude comparison tasks. Irrelevant luminance information interfered with Arabic numeral and size comparisons, as indicated by a significant increase in response times on trials where the irrelevant dimension was incongruent with the relevant dimension. In addition, irrelevant information about physical size (but not number) interfered with luminance comparisons. The authors report that symmetrical interference only occurred between size and luminance. In combination with the finding that the amount of functional overlap in activation in parietal cortex parallels the size of interference effects (see Figure 2), this study suggests that size, number, and luminance share computational resources and that, at least in the adult state, the representations of some pairs of magnitudes might be more closely related than others. Although it might not be intuitive that number and size should interact with luminance, one line of vision research suggests that they should: of two objects at equal depth, the brighter object will be perceived as closer (eg., Farnè, 1977). This presumably is because the amount of retinal surface area stimulated by light reflected from an object increases as an object approaches. Thus, representations of subjective size and luminance may be linked to the perception of object distance.

Luminance interacts with perceived duration as well. With absolute duration held constant, humans, pigeons and rats perceive bright lights as lasting longer than dim lights (Brigner, 1986; Wilkie, 1987; Kraemer, Brown, & Randall, 1995, Xuan et al., 2007). Goldstone, Lhamon, & Sechzer (1978) report an effect of loudness on perceived tone duration as well as brightness on light duration in a magnitude comparison task (Figure 4). These results do not provide evidence for whether duration might also modulate brightness or loudness perception. However, at a broad level, these findings from pigeons, rats, and humans implicate fundamental interactions between time and brightness.

Figure 4.

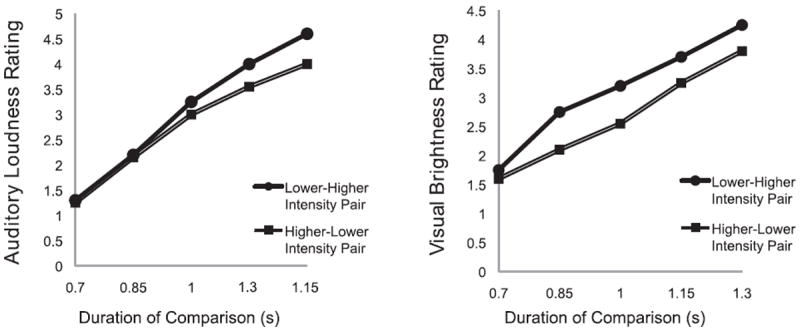
Figures redrawn from Goldstone et al. (1978). Y-axis is the “average category response” rating, where 1 = “shorter” and 5 = “longer” than a 1-second standard duration. X-axis indicates the duration of the comparison value (in seconds). Higher/lower intensity in the figure legend refers to the order of brightness or loudness value presentation. High-Low pairs induce a bias to rate durations slightly lower, on average, than Low-High pairs. (Figure reproduced with permission from the Psychonomic Society.)

ii. Pitch

A mapping similar to the SNARC effect occurs in the mapping of pitch height onto vertical space in adults (aptly dubbed the ‘SMARC effect’; Rusconi, Kwan, Giordano, Ulmità, & Butterworth, 2005). In this experiment, subjects were required to indicate whether a given pitch was lower or higher than a standard by pressing the space bar or 6; each key stood for the “higher” response half the time. For example, pressing 6 for a “lower” response would result in longer response times, while pressing the same key for a “higher” response would result in faster responses. A similar signature of pitch-space representation has been observed in infants (Walker, Bremner, Mason, Spring, Mattock, Slater & Johnson, 2009). Mapping of pitch height onto vertical space in infants, musicians, and non-musicians alike may also result from peripheral filtering of the acoustic signal by the pinnae; shifting pitch height corresponds to shifting spectral peaks in the head-related transfer function (HRTF) for vertical space (Roffler & Butler, 1967; Butler, 1969; Butler, 1971; for an explanation relating these results to the HRTF, see Moore, 2003). Thus, the mapping of pitch height onto space might be explained at more than one level of representation—a consequence of learning the fundamental acoustic cues to object height or a higher-level, shared magnitude code.

Other evidence for the mapping of pitch onto a spatial representation, either through a common magnitude code or some other mechanism, comes from individuals with congenital amusia. Congenital amusia is an impairment of fine-grained pitch discrimination, pitch-change direction (Ayotte, Peretz, & Hyde, 2002; Peretz & Hyde, 2003), and impaired short-term memory for non-verbal, auditory sequences (Williamson, McDonald, Deutsch, Griffiths, & Stewart, 2010; Tillmann, Schulze, & Foxton, 2009). It has been found to be correlated with impaired performance on spatial tasks (Douglas & Bilkey, 2007). In addition, impaired memory for changes in pitch-height direction reduces interference with spatial judgments in dual tasks in which both pitch and spatial judgments are made, suggesting that the representation of pitch height may share computational resources in individuals with typical pitch-processing capabilities (Douglas & Bilkey, 2007; but see Tillmann, Jolicœur, Ishihara, Gosselin, Bertrand, Rossetti, and Peretz, 2010).

Some studies also report interactions between duration and pitch. In the auditory kappa effect, tones are perceived as longer when their pitch is higher (Brigner, 1988; Cohen, Hansel & Sylvester, 1954; see also Lourenco & Longo, 2011). In addition, the pitch difference between two tones increases the perceived duration of the silence between them (Crowder & Neath, 1995; Shigeno, 1986) and the length of an intervening tone (Henry & McAuley, 2009). Moreover, amusics fail to show an auditory kappa effect at small pitch intervals (<4 semitones; Pfeuty & Peretz, 2010). In the auditory tau effect, the pitch of the second tone in a three-tone sequence is affected by its timing; for example, when the middle tone is closer in time to the first tone it is also perceived as closer in pitch (Henry, McAuley, & Zaleha, 2009; Christensen & Huang, 1979; Shigeno, 1986; Cohen et al., 1954). These studies indicate interactions between representations of pitch, space, and time.

Neuropsychological data that address the issue of neural overlap between representations of pitch and other magnitudes are currently sparse. Ideally, such tests would be administered within-subjects in cases of focal damage to a parietal locus that has caused a magnitude-related, performance impairment. One study that was conducted in that way showed that patients with damage to right posterior parietal cortex can exhibit impairments in judging the relative duration of two tones but remain unimpaired in judging tone pitch (Harrington et al., 1998). However, 2 out of the 10 patients in that study presented with comorbid impairments of pitch and duration judgment. The study shows that pitch and duration judgment are neurally dissociable processes in individuals with right posterior parietal lesions but that mutual impairment can occur in some of those cases. Interestingly, in patients with more anterior lesions, more than half of the individuals exhibited mutual impairment of pitch and duration judgments. Thus, pitch and duration judgments are commonly dissociated following posterior cortical lesions but they are associated in cases of more anterior lesions. However, since the pitch judgment task was intended as a control task in that study, it is difficult to determine the nature of the association between duration and pitch judgments in the group with anterior lesions. Future studies that are intended to test for comorbid impairments in magnitude judgments would ideally include control tasks that allow performance to be functionally dissected.

iii. Melodic Contour

Ordinal relations among exemplars from one dimension are easily compared to ordinal relations from another dimension. In the domain of pitch height, ordinal relations among successive musical notes form melodic contour (Marvin & Laprade, 1987). A more imprecise definition of contour is the “up” and “down” motion between successive notes (Dowling & Fujitani, 1970; Dowling, 1978)). One study reports that similar contour relations may be found in other auditory patterns such as loudness and brightness, which is correlated with the portion of the frequency spectrum with the greatest concentration of energy (McDermott, Lehr, & Oxenham, 2008). Adults can match contours across auditory dimensions and recognize familiar melodies in dimensions other than pitch. The authors suggest that contour extraction is a generalized feature of auditory memory and may have a centralized processing mechanism. Further work is needed to assess whether contour extraction is based on ordinal computations from a generalized analog magnitude system such as the one that may underlie the processing of ordinal relations for space, time and number. The representation of ordinal relations, including relative judgments of number, size, time, loudness, brightness, and pitch (i.e., mental comparisons) might be functionally interdependent and share mechanisms or, they could be functionally parallel and rely on mechanisms that are not shared but rather operate in a similar way. In fact, this conclusion could also apply to much of the data that shows associations among dimensions such as number, space, and time: the data are often ambiguous as to whether their relationship is one of functional interdependence or a functional parallel.

Summary of Evidence From Human Adults and Animals

Based on the above evidence, several open but empirically tractable issues can be identified. One issue is the extent to which the representations of different magnitudes and their associated computations are distinct. Another issue is to define what a more comprehensive description of the functional architecture of the magnitude system(s) should look like. A final issue is what level of representation interference effects arise and whether asymmetries of interference reflect unequal distribution of computational resources. Most extant studies are consistent with many views of magnitude relations including innate constraints on certain magnitude relations and statistical, correlational, or associative learning or tuning of abstract magnitude representation during learning.

In order to understand what taxonomic distinctions exist among magnitudes, it is important to consider how associations among magnitudes might originate and develop in the mind and brain and therefore what their functional relations could be. In the following section we consider existing ideas about magnitude representation within the larger context of theories of ‘abstraction’ in development. We extend frameworks from crossmodal perception to the conceptual structure of abstract relations among magnitudes. The frameworks presented here are not mutually exclusive and could even be complementary. Here, we describe two broad mechanisms for how magnitude dimensions could become related.

The Formation of Magnitude Relations

Little is known about the development of generalized magnitude representations. We borrow hypotheses and evidence from research on the development of multisensory perception to help frame research questions concerning the relations between magnitudes. This approach is justifiable because multisensory representations of abstract percepts (eg., object location, typically modeled as a weighted combination of visual and auditory cues) are similar to generalized magnitudes in the sense that information from separate sources can be bound together and/or influence composite representations that factor in information from more than one source.

A. Types of Relationships among Magnitudes

In principle, there are two possible types of cross-dimensional magnitude representation: (1) connections between pairs or groups of magnitudes that arise from simple association and (2) more general, abstract, higher-level representations. In the multisensory-integration and cross-modal perception literature, these higher-level representations are often referred to as amodal because they refer to a property that does not belong to any one sensory modality alone. In the case of magnitudes, we refer to this type of representation as adimensional because information is abstracted away from magnitude dimensions rather than stimulus modalities. Both types of representation may be present at birth or built and tuned across development.

i. Simple Associations or Conditional Probabilities

The binding of correlated events across senses and cognitive domains (assumed to be innately separate) has been the historically dominant explanation of the development of multisensory percepts and abstract concepts (e.g., Piaget, 1952; 1954). At a minimum, an associative account requires that infants and children construct representations of correlations among percepts via a direct connection: stimulation of one dimension at a certain magnitude leads to activation of a regular value of magnitude in another dimension, and this mapping is established on the basis of previous observations. At the computational level, this is analogous to the storage of the conditional probabilities among individual instances of magnitude observations. In the simplest case, this would be stored as the probability of observing a magnitude level on dimension Y given the observed magnitude on dimension X, p(Y ∣ X), and/or the reverse, p(X ∣ Y). As we alluded to earlier, postnatal learning need not be the only process that explains the construction of such mappings; infants may come with innate, prior expectations about any given conditional probability. Conditional probabilities can also explain asymmetrical relations between any two variables: p(Y ∣ X) may not be equal to p(X ∣ Y). This means that, contrary to general assumptions in the literature, an associative account of this type does not require symmetrical associations between dimensions.

How plausible is this type of mechanism? There is no doubt that infants possess powerful associative-learning and statistical-learning mechanisms that build representations of conditional probabilities. Infant methodologies that use reinforcement schedules, like the conditioned head turn procedure (see Werker, Polka & Pegg, 1997, for a review) and paradigms that involve anticipatory eye movements (McMurray & Aslin, 2004), would not work without associative learning. Infants’ (and adults’) sensitivity to transitional probabilities between adjacent and non-adjacent syllables and tones provides evidence that associations can be used to abstract conditional rules and auditory patterns (Saffran, Aslin, & Newport, 1996; Aslin, Saffran, & Newport, 1998; Saffran, Johnson, Aslin, & Newport, 1999; Newport & Aslin, 2004; Creel, Newport, & Aslin, 2004). Some studies suggest that similar signatures of transitional-probability learning can be found within a variety of modalities (eg., visual sequences of objects, Kirkham, Slemmer, & Johnson, 2002), across modalities (Yu & Smith, 2011), and that this type of learning can apply to multiple perceptual and cognitive domains (Thiessen, 2011).

Although associative learning is a powerful mechanism that can result in complex representations in infants, it has limitations for explaining more abstract ordinal and arithmetic interactions among magnitudes. As mentioned earlier, in order for different magnitude dimensions to be related or compared to one another, the process must require abstraction from the stimuli themselves (Gallistel & Gelman, 2000). A process of abstracting magnitudes also would allow different dimensions to be combined together, such as to compute rate from number and time or density from number and surface area. The abstraction away from absolute magnitude to normalized, relative magnitude implies the use of a code or representation that is common to all magnitude dimensions, which could arise in the second type of model—abstract, adimensional representations.

ii. Amodal and Adimensional Representations

An abstract magnitude representation can be thought of as a representation in which the intensity of a stimulus is represented as “a lot” or “a little” independently of the dimension from which the intensity initially derives. Current conceptualizations of analog magnitude representation assume that type of abstractness wherein the values of a given dimension are encoded as relative (normalized) values such as “a lot” or “a little” in addition to absolute values(e.g., see Cantlon et al., 2009, for review; Srinivasan & Carey, 2010). By virtue of being encoded in a common analog magnitude format, intensities and quantities theoretically provide the necessary level of abstraction for encoding the correlations or redundancies among various magnitudes in the natural environment. At the computational level, generalized representations of the correlations among multiple dimensions might be tuned as one or more composite variables that receive weighted inputs from each individual dimension. We base our conceptualization of these adimensional variables on various descriptions and models of amodal representations from the multisensory-integration and cross-modal perception literature.

A large body of evidence suggests that amodal representations of multisensory inputs exist early in development. Eleanor Gibson (1969) sought to explain cross-modal matching behavior in multiple domains (eg., for intensity across several modalities, Stevens, Mack, & Stevens, 1960; for higher-order figural properties, Rudel & Teuber, 1964; and for case studies of letter identification after vision restoration, Gregory & Wallace, 1963) and cross-modal transfer (eg., for non-conventional shape, Caviness, 1964). Her approach assumes initial separateness of modalities and dimensions, but asserts the possibility that more abstract representations of information presented across multiple modalities or dimensions also are present early in infant development and may be (at least initially) more important than modality-specific representations. In this view, an abstract, amodal representation of intensity or amount of stimulation is present from birth or very early in infancy and thus represents an innate component of multisensory perception. Gibson thought of amodal representations as dividing into two possible types, both of which rely on information redundancy. Her discussion of amodal relations includes two types: (1) intersensory redundancy (e.g., timing information about hammer strikes can be sampled from both the auditory and visual modalities) and also (2) relative intensity (e.g., “sharpness, bluntness, and jerkiness”; Gibson, 1969, p. 219).

Since Gibson, evidence for amodal representations in infancy has come from demonstrations of information transfer across modalities in infants (from oral to visual, Gottfried, Rose, & Bridger, 1977; from tactile to visual, Gottfried et al., 1977; Meltzoff & Borton (1979), though see Maurer, Stager, & Mondlach, 1999) as well as demonstrations of cross-modal equivalence (eg., continuity/discontinuity and ascendancy/descendency, Wagner, Winner, Cicchetti, & Gardner, 1981). Across those demonstrations of amodal representation, the transfer of information from one modality to the next is not necessarily equally strong in either direction (eg., in visual-tactile transfer, Bushnell & Weinberger, 1987). As for correlational representations between magnitudes, this finding indicates that symmetrical relationships between different dimensions need not be assumed for adimensional magnitude representations. An asymmetry in mappings between magnitudes also does not indicate that one dimension is more or less fundamental than the other since we see that asymmetrical relations emerge among basic sensory modalities.

Some studies suggest that similar behavioral signatures from crossmodal perception exist for various types of magnitude. For example, Jordan and Baker (2010) found that 3- to 5-year-old children succeed at number matching tasks when given redundant auditory and visual numerical information, but perform at chance levels when given only unimodal information. In addition, redundant, multisensory information increases the precision of 6-month-olds’ numerical discrimination (Jordan, Suanda, & Brannon, 2008). These data demonstrate that redundant, multimodal information about magnitude dimensions is more powerful than unimodal information. Moreover, Lewkowicz and Turkewicz (1980) demonstrated that 3- and 4.5-week-old infants respond to matched relative intensity levels of auditory loudness and visual brightness. These data are important because they show that very young infants find correspondences between different magnitude dimensions, even across modalities. The result supports the argument that adimensional representations of magnitude (in this case loudness and brightness) are fundamental in development.

Little is known about the computations that underlie the development of amodal representations or the format of their original state. To address the hypothesis that multisensory representations are tuned over time from unisensory inputs, Yildirim and Jacobs (2012) developed a nonparametric Bayesian model with multisensory feature variables (without specifying the number of features in advance) that are tuned in the course of learning. These multisensory feature variables are latent in the sense that they are unobserved: they must be estimated from the values of the observed unisensory inputs. As higher-level representations are tuned to integrate information from unisensory inputs, they allow for improved inference in both the latent variable(s) and the unisensory domains. Moreover, training with multisensory input leads to better performance in simulated unisensory tasks than training in unisensory input only, and can predict values of missing unisensory inputs from latent variables. These results match known benefits of multisensory perception and training in multisensory environments.

If adimensional variables are computed in the same manner, we might expect similar benefits to arise in uni-dimensional judgments following learning. If subjects train on a task with multiple magnitudes, this will lead to improved inference in tasks involving only one magnitude. In addition, such an account would predict transfer of stimulation from one magnitude dimension to all magnitude dimensions tied to the same adimensional magnitude. This account also predicts the existence of neurons that respond to multiple magnitudes at birth (an innate capacity to represent correlational information) and that mature, adimensional neurons are tuned to weight unidimensional inputs relative to their precision.

A way of conceptualizing how adimensional variables of this sort might be constructed at the representational level is principle component analysis (PCA), a method that reduces high-dimensional data sets to low-dimensional sets of composite variables by grouping clusters of correlated variables. Groups of correlated unidimensional variables are mapped onto one principal component to implement dimensionality reduction. Each individual dimension’s contribution to the value on the principal component is weighted relative to its distance from the principal component. The functional implication of this PCA-type representation is that a large amount of unrelated but structurally similar magnitude information could be compressed into a smaller amount of related magnitude information in which any commonalities among magnitude dimensions are represented only once. Interference effects arise naturally in this architecture from the information loss associated with collapsing correlated dimensions onto the same principal component. Asymmetries in interference would arise from the different amount of weight given to each dimension in estimating a particular stimulus’ value on the principal component.

Artificial neural networks, which implement PCA and its variants, have modeled emergent properties of real neurophysiological systems. In one example, a recent type of neural network used for dimensionality reduction called deep networks (Hinton & Salakhudtinov, 2006) has successfully modeled neurophysiological and behavioral data from visual numerosity estimation and comparison tasks (Stoianov & Zorzi, 2012). However, like Yildirim and Jacobs’ model (2012), PCA and its more sophisticated variants have important limitations. For example, in classical PCA, the researcher must specify the number of principal components to find in advance of performing the computation. In short, every model must start with some constraints in the form of specifying prior information about the latent components to be found. This suggests that part of the challenge of investigating the development of generalized magnitude representations is the specification of the initial state of the representations.

B. Current Evidence and Predictions

Current behavioral evidence that supports either an associative or amodal/adimensional view of magnitude relations is limited. Independently of hypotheses concerning the precise nature of an abstract magnitude code, it has been proposed that certain dimensions map spontaneously onto some dimensions but not others in infancy and childhood because they share a privileged relationship from birth (eg. de Hevia & Spelke, 2010; Dehaene, Izard, Spelke, & Pica, 2008; Srinivasan & Carey, 2010). In particular, these studies have argued for privileged relations between space and number and space and time. These studies do not aim to distinguish among associations, statistical correlations, or adimensional representations of magnitudes, though the developmental primacy and generality of the findings suggest that at least one of these processes is engaged within the first months of life. Identical thresholds across space, time, and number in six-month-olds suggest the development of a shared substrate for time, size, and number (Brannon, Lutz & Cordes, 2006; vanMarle & Wynn, 2009; reviewed in Feigenson, 2007 and Cantlon et al. 2009). Similar results have been reported for older children (5 and 8 yrs) and adults (Droit-Volet, Clément, & Fayol, 2008). However, it is clear from the psychophysics of magnitude estimation (Stevens, 1975) that adults can, at the very least, map relational information from any one dimension onto any other dimension. How do infants reach that adult state?

In children, the precision of numerical discrimination judgments gets finer from ages 6 to 8 years; quantitative comparisons in non-numerical magnitudes (e.g., luminance and bar height) follow this same developmental trajectory (Holloway & Ansari, 2008). Similar results, mentioned above, have been found among infants for the discrimination trajectories of size, time, and number over the first year of development (see Feigenson, 2007). These data suggest that the mechanism and/or constraints underlying the development of these comparisons are common across continua.

Beyond shared constraints, there is evidence that different types of magnitudes are encoded relationally as early as infancy. Infants seem to spontaneously map stimuli from one of these magnitude dimensions to another. In one example, infants showed evidence of this spontaneous mapping when habituated to positively correlated number/line-length pairs (de Hevia & Spelke, 2010). One recent study showed that 9-month-olds were equally likely to transfer an experimentally learned association between one dimension and color-pattern cues to another dimension (Lourenco & Longo, 2010). For example, if infants learned that large objects were black and had stripes while small objects were white with dots, they expected a congruent association between those color/shape patterns and the dimensions of number and duration. The generality of these effects with other continuous dimensions such as brightness, loudness, duration, or density is not yet known, though one study suggests that it may not hold across all magnitude dimensions. Srinivasan and Carey (2010) show that 9-month-old infants more easily bind line length to tone duration than to tone amplitude when such mappings are positively correlated.

To explain these findings, Srinivasan & Carey (2010) propose that two dimensions may share some degree of computational and neural resources. At one extreme, termed functional overlap, two dimensions may innately share computational and neural resources such that cross-dimensional mapping should be spontaneous even in infancy and early childhood. At the other extreme, termed structural similarity (borrowed from Gentner & Markman, 2005), the two dimensions may share a representational format (e.g., ordered analog magnitude), and may therefore be mapped analogically; however, these dimensions cannot (or may not yet appear to) map onto each other spontaneously in children and infants because they share minimal computational and neural resources at those developmental time points.

Innately privileged relations between certain magnitudes are also indicated in the universality of their association. The ability to map numbers onto space (number lines) for example is widespread among human cultures. The Mundurucu, an Amazonian people who lack a rich linguistic system of discrete number, can map nonverbal numerical magnitude onto horizontal lines just as do Western subjects (Dehaene et al., 2008). The finding supports the conclusion that mappings between space and number are not culturally determined because Mundurucu do not generally use numerical symbols in reading and reciting. However, this finding does not necessarily indicate the presence of an innate bias to map numbers to space in humans (Cantlon, Cordes, Libertus, & Brannon, 2009; van Dijck & Fias, 2011), and could represent an underlying preference for spatial representations in general.

Fundamental interactions between space and number are also observed in Stroop-like effects between magnitudes throughout development. Monkeys and 3-year-old children simultaneously and automatically represent both number and cumulative surface area in judgments of visual dot arrays (Cantlon & Brannon, 2007; Cantlon, Safford, & Brannon, 2009). Performance for both groups is better when number and cumulative area are congruent between the arrays than when they are incongruent, suggesting a convergence of the dimensions at some point in the processing stream. Similar results of congruity effects between number and area have been found in Stroop-like tasks with 5-year-old children and adults (Gebius, Kadosh, de Haan, & Henik, 2009; Hurewitz, Gelman, & Schnitzer, 2006). These data from monkeys and young children demonstrate convergence of magnitude representations for number and space during stimulus processing. However, the data do not indicate at what level of representation mappings between dimensions occur.

Some evidence from childhood suggests that the full array of conceptual mappings between dimensions emerges gradually over development. For example, 3-year olds reliably match high-pitched sounds to smaller and brighter balls in a categorization task (Mondloch & Maurer, 2004). Three- and four-year-old children, but not two-year-olds, match louder sounds with larger visual stimuli; however, mapping between the dimension of surface darkness (as distinct from luminance) and size is less consistent (Smith & Sera, 1992). Six- and eight-year-olds can spontaneously map higher-order relational patterns among objects between different dimensions (eg., small-big-small to light-dark-light); 4-year-olds can perform such mappings, but only following within-dimension mapping trials (Kotovsky & Gentner, 1996; Gentner & Medina, 1998). Broadly speaking, these studies suggest that some higher-order relations that depend on the ordinal nature of different magnitudes can be accessed at young ages. Performance-competence issues related to the explicit nature of the mapping task render the poor performance of young children on mapping between certain dimensions difficult to interpret. Moreover some data from infants showing early mappings between dimensions such as pitch and space (Walker et al., 2009) and loudness and brightness (Lewkowicz & Turkewicz, 1980) are at odds with a conclusion of gradual mappings between dimensions over development. However, at face value, the data implicate experience-related changes in cross-dimensional mapping concepts during childhood.

In summary, some evidence from interdimensional mapping in infancy and across cultures is consistent with the existence of innate relations between magnitudes. However, there is currently a question as to which dimensions are related to one another and when. Moreover, further evidence is needed to show whether these relations are amodal/adimensional, or separate but associated. In an experimental setting, an amodal/adimensional architecture predicts that training in multiple dimensions will result in improved inference in the unidimensional domains. Finally, some evidence described above indicates that infants and children benefit from redundant magnitude information and it is generally known that congruent magnitude information (such as surface area and number) results in better performance than incongruent magnitude information in children, adults, and non-human primates. However, whether there is a critical role for redundant cross-dimensional magnitude information in the development of magnitude concepts is not known.

Trajectory of Developing Magnitude Representations

In previous studies, the developmental origins of relations among magnitudes have been studied independently of the mechanisms that are responsible for altering those relations over the course of development. In this section, we describe mechanisms that are hypothesized to influence the developmental course of ‘abstract’, amodal representations during infancy and we discuss their significance for the development of magnitude representation. Virtually no evidence from cross-sectional studies is available concerning the time-course of magnitude mappings across development. However, we can make predictions about what the course of development might look like based on evidence from the time-course of cross-modal perception—if, in fact, the neural underpinnings of coordinating information across magnitudes are principally similar to those of cross-modal perception (as suggested in Spector & Maurer, 2009).

Neonates and very young infants seem to successfully coordinate information from different modalities, fail at similar tasks in the following months, and gradually regain those computational capacities before the end of the first year of life (Figure 5; eg., face-voice synchrony, Pickens, Field, Nawrocki, Martinez, Soutollo, & Gonzalez, 1994; tactile to visual transfer as demonstrated by novelty preference, Streri, 1987 and Streri & Pêcheux, 1986). Maurer and colleagues claim that this U-shaped function characterizing the development of multi-modal integration and cross-modal matching cannot be fully explained by either coordination of innately separate unisensory inputs or a progression from undifferentiated to differentiated representations of redundant information across the senses alone (Maurer & Maurer, 1988; Maurer & Mondloch, 2004).

Figure 5.

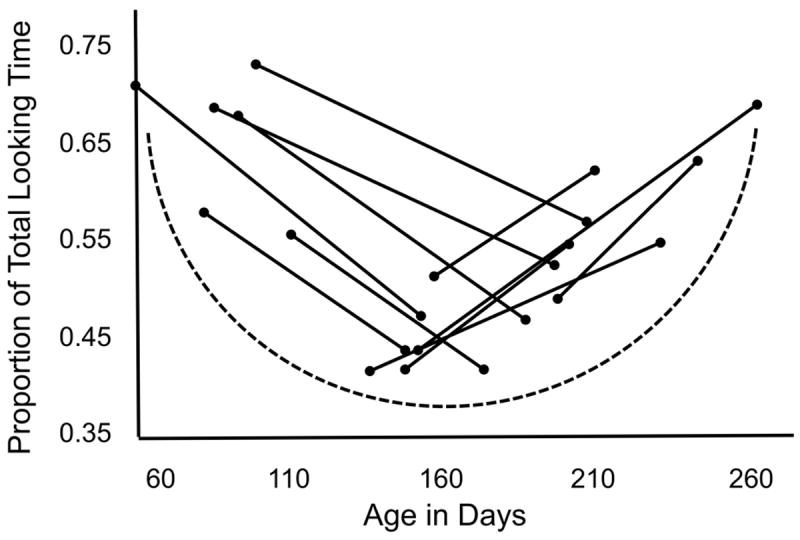
Figure redrawn from Pickens et al. (1994) demonstrating a U-shaped curve (drawn for illustrative purposes) for cross-modal matching of synchronized faces and voices in infants studied longitudinally. Dependent measure on the y-axis is the proportion of total looking time to matching/synchronized face/voice pairs. (Figure reproduced with permission from Elsevier.)

To explain those phenomena, it has been proposed that infants experience something akin to synesthesia near birth; this hypothesis has been formulated in strong (Maurer & Maurer, 1988; Spector & Maurer, 2009) and weak (reviewed in Maurer & Mondloch, 2004) versions. Originally motivated in part by evidence for increased differentiation among sensory areas associated with neural pruning in the first year of life (Neville, 1995), the strong version claims that a percept experienced in one modality automatically stimulates a parallel percept in another modality. Over the course of the first year of life, these synesthetic percepts become weaker as either overabundant neural connections between different functional areas of the brain become pruned or inhibited but they form the basis for systematic (quasi-synesthetic) associations in non-synesthetic adults (Spector & Maurer, 2009). Magnitudes, under a similar conceptualization, might be related via cross-activation of dimension-dedicated mechanisms. The weak version of the hypothesis, traceable to a much older proposal (eg., von Hornbostel, 1938; Hayek, 1952), states that newborn infants do not differentiate between senses; however, over time, infants begin to differentiate information coming from different senses and subsequently learn to coordinate information from each modality. Importantly, the strong and weak versions are not necessarily mutually exclusive. Whatever the case, the neural process hypothesized to underlie differentiation is pruning and the process hypothesized to underlie subsequent coordination of information from separate senses is coordination. By extension, under a process such as this, magnitude representations would initially be neurally undifferentiated at birth; across development, pruning would lead to increased differentiation among magnitude dimensions and to subsequent coordination.

Researchers have supported the neonatal synesthesia hypothesis either with evidence for infant mappings of dimensions that do not have a straightforward, information-redundancy explanation or by explicitly documenting the decrease in synesthetic associations over development. For example, the presence of particular shapes influences the color preferences of infants at 2 months but not 8 months, consistent with the predictions of neural pruning or inhibition of connections between the areas that process shape and color (Wagner & Dobkins, 2011). Associations between continuous psychophysical dimensions are also present early in life and may be supported by an innate, synesthesia-like component. For instance, infants at 4 months of age prefer to look at a ball that is bouncing in congruent motion with an auditory pitch (the ball goes up when the pitch goes up) over a ball that is bouncing incongruently with pitch; in addition, they prefer to look at a shape that is getting sharper as the pitch paired with it gets higher (Figure 6; Walker et al., 2009).

Figure 6.

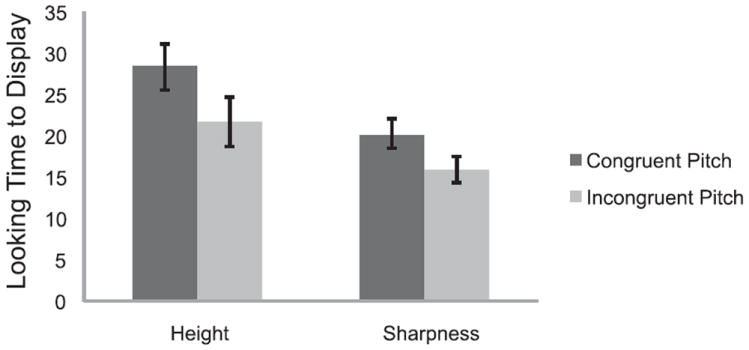
Mean total looking times to displays with a bouncing ball (congruent or incongruent pitch height to object height mapping) or an object decreasing or increasing in sharpness (congruent or incongruent pitch height to sharpness mapping. Measurements taken from Walker et al. (2009). Error bars ±1 SE. (Figure drawn with permission from Walker).

The proposal that differentiation among magnitudes is mediated by processes of pruning or inhibition, predicts (1) neural changes (eg., in functional connectivity and white-matter integrity in relevant brain regions such as intraparietal cortex) correlated with behavioral changes across the first year of life and into childhood and (2) that occasionally adults would demonstrate vestigial associations among the magnitude dimensions hypothesized to be intimately connected at birth. There is at least some evidence for the second prediction: digit-color synesthetes show a decrease in the subjective brightness of the induced color experience as the magnitude of the numerical inducer increases (Cohen Kadosh, Henik, & Walsh, 2007); this is similar to reports of a connection between luminance and number in non-synesthetes (Cohen Kadosh, Cohen Kadosh, & Henik, 2007). Moreover, there is some evidence that the mechanism underlying spatial-sequence synesthesia, in which tokens from number sequences, alphabets, and other series take on explicit spatial locations, parallels the SNARC effect in non-synesthetes (Eagleman, 2009).

Evolutionary Perspectives on Adimensional Magnitude Representation

Ultimately, any account of generalized, adimensional magnitudes must be placed in an evolutionary context. If these adimensional representations of magnitude are innate, where did they come from? Both the developmental and evolutionary history of the relations between magnitude systems will have important consequences for interactions among magnitudes in adults. Walsh’s (2003) view of the differentiation of space, time, and number leaves the job only to development. However, both descent with modification—the gradual differentiation of dedicated modules across evolution from more primitive ones originally dedicated to other purposes (e.g., Marcus, 2006)—and culturally-mediated repurposing of cortical areas designed to perform related computations during development (Dehaene & Cohen, 2007) may play a role in shaping how adults process magnitude information.

Perceptual and cognitive systems are shaped by natural selection to address the demands of interacting with and representing the natural world. So, evolution could shape those systems in such a way that innate mechanisms are in place to encode environmental statistics that are stable across long periods of time and more fluid mechanisms are in place for learning across shorter timescales such as development (Simoncelli and Olshausen, 2001; Yang & Purves, 2004). If a process like correlational learning among magnitudes is to be tuned across evolution, then correlations among magnitudes should exist in the natural environment. We can think of a few intuitive examples: long travel distances are generally associated with greater travel durations; in natural light, close and/or large objects impact the brightness of a visual scene more than objects that are small and/or far away; greater numbers are loosely associated with greater spatial extent, and (for foragers) number of fruit to be harvested is correlated with greater foraging time. However, it is unclear how to go about collecting statistics from the natural environment to characterize the empirical correlations among magnitudes.

One potentially informative first question to ask about evolution is how did different but related magnitudes emerge in the first place? According to descent with modification, separate, but closely related, magnitude representations may have emerged via duplication, expansion, or other modifications of previously existing machinery. One view of the functional organization of magnitudes that maps onto this idea is that space serves as the foundational domain for all other magnitudes, particularly those that are hypothesized to be more conceptually abstract—such as number and time. This view finds some loose correspondence in metaphor theory, in which linguistic metaphors that use ‘space’ to talk about other domains are taken as indirect evidence of ‘space’s’ conceptual primacy (e.g., Clark, 1973; Lakoff & Johnson, 1980; 1999). Piaget (1969) also proposed that children conceptualize duration solely in terms of space, only to later differentiate duration from space. Other investigators have failed to find sufficient evidence to support such a strong claim in toddlers and preschoolers (eg., Friedman & Seely, 1976; Levin, 1977, Levin, 1978; Levin & Gilat, 1983). Yet, these findings do not rule out the possibility that spatial representations are evolutionarily primary.

The notion that ‘space’ could ground other continuous magnitude representations is not far-fetched from an evolutionary perspective. Location and motion are among the only dimensions that can be represented by the most primitive forms of vertebrate “eyes”. Depressed sheets of light-sensitive cells, the most primitive “eye”, can get very little form or object information however they get a good representation of location and motion direction (Lamb, Collin, & Pugh, 2007; Land & Fernald, 1992). Numerical information, in contrast, would require some ability to segregate objects. A similar argument for the primacy of space can be made from an even more primitive sensory system than vision – chemoreception. Modern animals from can use this sense to represent simple one-dimensional spatial maps of chemical gradients without access to object form or individuation (Adams-Hunt & Jacobs, 2007).

Evolutionary forces could have caused relations among magnitudes to form in the sense that one dimension evolved from another, leaving functional similarities in their neural and computational operations. If many magnitude representations emerged from modification of the functional substrates that code for space, we might expect functional parallels between the spatial module and its evolutionary descendants as well as parallels among the descendants, although the degree of overlap would likely be heterogeneous and difficult to quantify. Confirmation of such an evolutionary process would require comparative work across multiple species of non-human primates as well as more distantly related animals and the possibility of genetic anomalies that selectively impair processing of multiple magnitudes thought to be dependent on, or genetically descended from, spatial processing. Congenital disorders affecting the evolutionarily primary magnitude system could also cluster with impairments of related magnitude systems if genetic physical and functional interdependencies from a common evolutionary history still remain. For instance, people with developmental dyscalculia, who have difficulty processing number magnitudes, show weaker interference effects from the physical size of the number than normal controls (Rubinsten & Henik, 2006), suggesting an impaired ability to relate digital number and physical size. In addition, this population performs less well on time discrimination tasks with lower scores on a standardized screening test (Cappelletti, Freeman, & Butterworth, 2011). However, more work is needed to determine whether a broader set of magnitude abilities is impaired.

Adjudicating Among Theories & Conclusion

The most important point that we hope to have captured in this review is that questions regarding the source and functions of different types of magnitude representation in the mind and brain are tractable for the fields of cognitive neuroscience and development, thanks to the empirical and theoretical foundation that was laid by prior cognitive and neuropsychological research. Increasingly detailed models of associational or adimensional architectures will help adjudicate among hypotheses about the development and organization of magnitude representations. These two conceptualizations of magnitude relations are based on literature from crossmodal perception, which has relevance in the domain of magnitude representation. This way of framing magnitude representation offers amendments to existing interpretations of behavioral signatures, such as asymmetries in cross-dimensional mappings, and new predictions for the interactions among dimensions as a function of learning.

Current evidence demonstrates the existence of interactions or neural overlap among magnitudes and that these interactions vary in strength. This evidence is consistent with theories of interaction and overlap that emphasize either a strong innate component or a strong learned component. Under our characterization of associational or correlational representations of magnitudes, innate mappings may be subject to modification by early experience and learned mappings are likely subject to innate constraints. The evolution of relations among magnitudes and the trajectory of magnitude relations across development require specification to paint a richer picture of the underlying computations and neural architecture.

Building on these models, future experiments could clarify the extent of functional overlap among dimensions and the relative contributions of pruning and construction to the developmental course of overlapping magnitude representations. Such knowledge will help constrain and refine explicit models of representation. Clarification of the possible levels at which interactions between dimensions might arise will help evaluate the assumptions underlying interpretations of mapping ‘strength’ and symmetry.

First, we have to understand the degree to which neural processes and representational content are shared among dimensions. Measurements of neural overlap are helpful for distinguishing whether magnitude representations with the same behavioral signatures (e.g., Weber’s law) are functionally interdependent (same behavior, same neural substrate) or functionally parallel (same behavior, different neural substrate). Further, without linking overlapping neural signatures to more explicit models of representation, it is impossible to fully understand the functional origins of those neural signatures.

The development of neural processes for magnitude processing can also uniquely reveal functional distinctions and relations between dimensions. For example, a lack of neural overlap between dimensions in adulthood does not imply a lack of neural overlap in infancy. If a lack of neural overlap is to be taken as evidence for distinct magnitude representations, it would have to be shown that it is also lacking in development. Otherwise, the possibility that non-overlapping magnitude representations have a common developmental foundation remains open. Overlap early in development (even if absent in adulthood) will likely have functional consequences for the structure of the non-overlapping adult representations. And, of course, even if magnitude representations do not overlap in infancy, the possibility remains that they had a common evolutionary origin (perhaps still evident in non-human animals). The developmental and evolutionary origins of relations among magnitudes are thus critical for understanding the origins of magnitude representations, and they too represent different levels at which interactions among magnitude representations could have arisen (Tinbergen, 1963).

In terms of the development of magnitude relations, future research could determine the relative contributions of pruning and construction to the overlap among representations of different magnitudes. Pruning (or masking) would predict decreased associations among magnitudes with increased precision for discriminating within and between dimensions over development. Construction would predict increased associations among magnitudes over development. A combination of the forces of pruning and construction on development could take the form of a U-shaped trajectory of magnitude discrimination wherein associations among magnitudes initially decrease (pruning) and then subsequently increase (construction), as is found for cross-modal perception.

Second, at what level of processing do interactions between magnitudes occur and what are the evolutionary and cultural influences that shape that level? The levels at which magnitude representations can interact and the number and types of continua to which such an underlying magnitude code applies beyond space, time, and number—for example, brightness, loudness, and pitch—are currently underspecified. At the algorithmic level of analysis, ‘levels’ can refer to stages of processing such as encoding, comparison, and response selection in the Sternbergian sense (Sternberg, 1966, 1969a, 1969b; 2012). Interactions among magnitude representations occur at these levels of processing that may also be subject to varying evolutionary and cultural influences; for example, as we discussed above regarding Cassasanto & Boroditsky (2008) and Merritt et al. (2010), higher-level, linguistic re-encoding of line durations with the terms ‘long’ and ‘short’ could account for some of the interference effects reported in adult humans. In principle, different types of behavioral signatures of interactions may have come from different levels of processing; for example, the interaction between space and number might occur during working memory for the SNARC effect (van Dijck & Fias, 2011) but at encoding for Stroop-like interference.

The salience of each dimension on its own, as shaped by cultural forces, also can influence the nature of the observed overlap at different levels of processing. For example, if number and space are each culturally prominent dimensions in the human experience then they might appear to have a stronger mapping than space and brightness, given that brightness is less prominent than space or number in this example. The salience of each individual dimension can influence the symmetry of the relations between magnitudes and the natural clustering of dimensions in the environment can also influence the symmetry of the correlations. Therefore, it is important to consider subjects’ sensitivity to mapping each dimension alone in assessments of cross-dimensional magnitude representations. Given the above points, the existence or non-existence of asymmetries of interference or facilitation between magnitude representations may not be enough to adjudicate among competing hypotheses of the origins of magnitude relations.

We have described two general frameworks for clarifying and building hypotheses about overlapping magnitude representations: associations among absolute magnitudes and composite, abstract magnitudes. A benefit of their generality is that these types of representation can be implemented across both evolutionary and developmental time scales. Moreover, they lend themselves to computationally precise predictions about behavior and neural activity.