Abstract
ObjectiveTo provide a tutorial for using propensity score methods with complex survey data.
Data SourcesSimulated data and the 2008 Medical Expenditure Panel Survey.
Study DesignUsing simulation, we compared the following methods for estimating the treatment effect: a naïve estimate (ignoring both survey weights and propensity scores), survey weighting, propensity score methods (nearest neighbor matching, weighting, and subclassification), and propensity score methods in combination with survey weighting. Methods are compared in terms of bias and 95 percent confidence interval coverage. In Example 2, we used these methods to estimate the effect on health care spending of having a generalist versus a specialist as a usual source of care.
Principal FindingsIn general, combining a propensity score method and survey weighting is necessary to achieve unbiased treatment effect estimates that are generalizable to the original survey target population.
ConclusionsPropensity score methods are an essential tool for addressing confounding in observational studies. Ignoring survey weights may lead to results that are not generalizable to the survey target population. This paper clarifies the appropriate inferences for different propensity score methods and suggests guidelines for selecting an appropriate propensity score method based on a researcher’s goal.
Keywords: Survey research, primary care, health care costs
Causal inference—answering questions about the effect of a particular exposure or intervention—is often elusive in health services research. Administrative and survey data capture information on the standard course of treatment or experiences, which allows researchers to measure the effects of treatments or programs that cannot feasibly be evaluated with a randomized trial. In our motivating example, we cannot randomize the type of physician (general practitioner or a specialist) from whom an individual receives primary care, but we can use existing observational datasets to assess the effect of specialist versus generalist care on health care spending. Furthermore, complex survey data frequently yield nationally representative samples. The fundamental challenge in using these data for causal inference is addressing potential confounding while still retaining the representativeness of the data. Confounding occurs when there are variables that affect both whether an individual receives the intervention of interest as well as the outcome.
Propensity score methods are statistical methods used to address potential confounding in observational studies (Rosenbaum and Rubin 1983). Broadly, the goal of propensity score methods is to improve the comparability of treatment groups on observed characteristics, to reduce bias in the effect estimates. Primary propensity score methods include matching, weighting, and subclassification (Stuart 2010). Although propensity score methods help reduce confounding, they cannot fully “recreate” a randomized experiment—randomization ensures balance on both observed and unobserved variables, whereas propensity score methods only ensure balance on observed variables.
While propensity score methods for observational studies in general have been well described, there are few guidelines regarding how to incorporate propensity score methods with complex survey data. Few researchers, with the exception of Zanutto (2006) and Zanutto, Lu, and Hornik (2005), have focused on the complexities of how to use propensity score methods with complex survey data and appropriately interpret the results.
To assess current practice, we conducted a limited systematic review of the peer-reviewed literature to identify studies that used propensity score analysis and complex survey data in the health services field. For 2010 and 2011, we identified 28 articles in PubMed that contained the key word “propensity score” and related to complex surveys in health services research. These studies demonstrated a variety of methodological approaches and interpretations of effect estimates. Of the 28 studies, 16 (57 percent) did not incorporate the survey weights into the final analysis. Of these 16 papers, 6 incorrectly described their results as “nationally representative” or reflective of a “population-based” sample. Only one of these explicitly stated that not incorporating the survey weights “compromises external validity, such that outcomes are not generalizable to national figures” (McCrae et al. 2010). Seven (25 percent) of the 28 studies stated that they included the survey weights in the final outcome regression model. Five (18 percent) studies performed propensity score weighting and multiplied the propensity score weights and the survey weights, with varying approaches to interpreting the final results. This heterogeneity in the recent literature suggests a variety of approaches and some possible misunderstandings in how to appropriately apply and interpret results from propensity score methods with complex survey data. More broadly, failure to properly account for the complex survey design is a common analytic error. In a review of statistical (but not propensity score) methods used in studies involving three youth surveys, Bell and colleagues (2012) found that nearly 40 percent of reviewed studies did not adequately account for the complex survey design.
Survey samples obtained using a complex survey design offer researchers the unique ability to estimate effects that are generalizable to the target population (often, the national population). As this is a major advantage of survey data, we primarily focus on propensity score methods that incorporate survey weights to retain the generalizability of the final effect estimates using survey design-based analysis. Statistical analyses that do not include the survey weights will not necessarily be generalizable to the target population if the survey weights are correlated with the independent or dependent variables and may be biased for estimating population effects (Pfeffermann 1993). We provide an illustration of this phenomenon in our simulation study below. Although formal statistical generalizability is not always a goal, as we observed in our review of published studies, a common error is to ignore survey weights when using propensity score methods yet describe results as applicable to the original target population, which can lead to misleading conclusions.
When assessing the effect of a treatment on an outcome, there are two causal estimands commonly of interest in observational studies: the average treatment effect on the treated (ATT) and the average treatment effect (ATE). The ATT is the average effect for individuals who actually received the treatment. The ATE is the average effect for all individuals, treated and control. In our motivating example (Example 2 below), the ATT represents the comparison of health care spending between individuals who had a specialist as a primary provider (the “treatment” group) and spending for the same individuals, if instead they had a generalist (the “control” group). In contrast, the ATE represents the difference in health care spending if everyone in the sample had a specialist compared to if everyone had a generalist. In a randomized experiment, the ATT and ATE are equivalent because the treatment group is a random sample of the full sample; in an observational study the ATT and ATE are not necessarily the same.
When using survey data that represent a target population, there is a further distinction in that it is possible to estimate both sample and population ATTs and ATEs. The Sample ATT and ATE (denoted SATT and SATE, respectively) are the corresponding ATEs in the unweighted survey sample. The Population ATT and ATE (denoted PATT and PATE) are the corresponding estimands for the survey’s target population, accounting for the sampling design. See Imai, King, and Stuart (2008) for a more technical discussion of these estimands.
The objective of this paper was to provide a tutorial for appropriate use of propensity score methods with complex survey data. We first assess the performance of various methods for combining propensity score methods and survey weights using a simple simulation. We then present results from the Medical Expenditure Panel Survey (MEPS), estimating health care spending among adults who report a generalist versus a specialist as their usual source of care. We highlight relevant interpretations of various analytic approaches and offer a set of guidelines for researchers to select the most appropriate propensity score methods for their study, given their desired estimand.
General Propensity Score Methodology
The propensity score is defined as the probability that an individual received the treatment, based on his or her observed characteristics. Propensity score methods rely on two fundamental assumptions, collectively termed “strong ignorability” by Rosenbaum and Rubin (1983). The first component of strong ignorability is that there is sufficient overlap (positivity): every individual could potentially be assigned to any treatment group and the distributions of baseline covariates among treatment groups overlap, such that no combinations of covariates is unique to a single treatment group. The second component is that of unconfounded treatment assignment, meaning that treatment status is independent of the potential outcomes after conditioning on the observed covariates. Broadly, this assumes that the set of observed pretreatment covariates is sufficiently rich, such that it includes all variables directly influencing both the treatment status and outcome (i.e., there are no unobserved confounders).
Propensity scores are typically estimated using logistic regression or nonparametric methods such as random forests or generalized boosted models (McCaffrey, Ridgeway, and Morral 2004; Stuart 2010). We focus on three common approaches for using propensity scores: k : 1 matching, subclassification, and weighting, first describing their standard use and then discussing extensions to complex survey data.
Propensity score matching pairs each treated individual with k (typically 1–5) control individuals with the closest propensity score to the treated individual. This approach discards control subjects who are not “good” matches (Stuart 2010). This approach is appropriate when the ATT, not the ATE, is of primary interest.
Propensity score subclassification groups individuals (both treated and control) with similar propensity score values into subclasses or strata. Typically at least five subclasses are used (Cochran 1968). Generally, regression analysis is conducted within each subclass and then effect estimates averaged across subclasses to generate the final effect estimate (Lunceford and Davidian 2004). Subclassification can be used to estimate either the ATE or ATT (Stuart 2010). To estimate the ATT, subclass-specific estimates are weighted by the proportion of all treated individuals in each subclass; to estimate the ATE, subclass-specific estimates are weighted by the proportion of all individuals (treated and control) in each subclass.
Propensity score weighting uses the propensity score to calculate weights, similar in spirit to sample selection weights in survey sampling. The propensity score weight is incorporated into the analysis to weight the sample to the relevant “population” of interest; weighting can estimate the ATT or ATE. To estimate the ATT, each treated individual receives a weight of 1, while control individuals are weighted by e/(1 − e), where e is the propensity score. This weights the control group to look like the treatment group and is sometimes called “weighting by the odds.” To estimate the ATE, the treatment group weights are 1/e, while the control group weights are 1/(1 − e), weighting each group to the combined sample; this is often called “inverse probability of treatment weighting” (IPTW; Lunceford and Davidian 2004).
Incorporating Survey Weights with Propensity Score Methods
We now discuss ways to incorporate complex survey designs with propensity score methods. Consistent with previous work in this area, and given a focus in nonexperimental studies on bias reduction, we primarily discuss methods to incorporate the survey weight with propensity score methods (Zanutto, Lu, and Hornik 2005; Zanutto 2006) and include brief reference to other complex survey design elements. Thinking about the weights, there are two stages at which the survey weights could be incorporated into propensity score methods: (1) when estimating the propensity score and (2) when using the propensity score to estimate the treatment effect.
In Stage 1, we recommend including the survey weight as a predictor in the propensity score model. The survey weight may capture relevant factors, such as where individuals live, their demographic characteristics, and perhaps variables related to their probability of responding to the survey (Korn and Graubard 1991; Pfeffermann 1993). Ideally we might include these variables themselves (along with strata or cluster indicators) in the propensity score model, but this is not always feasible. In particular, the survey weight may be particularly important to use in this way when the individual variables that make up the weight (e.g., sampling strata or other characteristics of individuals) are not available separately, for example, when confidentiality concerns prevent the release of stratum indicators, or when degrees of freedom concerns prohibit their inclusion (e.g., when there are a large number of strata or clusters). Including the weight may thus help satisfy the assumption of unconfounded treatment assignment. A similar strategy is recommended by Lumley (2010) in the context of estimating weights to adjust for nonresponse.
A separate question is whether the propensity score model needs to be a weighted regression or account for the complex survey design elements. In keeping with Zanutto’s (2006) recommendation, we argue that the propensity score model does not need to be survey-weighted, as we are not interested in generalizing the propensity score model to the population. In fact, propensity scores are inherently an in-sample concept as the goal is to make the observed treated and control groups as similar as possible (rather than in generating a model of treatment assignment that would relate to the target population). Similarly, because we do not use the variance estimates from the propensity score model (we only obtain the predicted probabilities), it is not crucial to incorporate the clustering and stratification information in the model estimation.
At Stage 2, the decision to incorporate survey design elements in the final outcome model (and how to do so) depends, in part, on the study goal (Figure 1). The goal of many analyses of complex survey data is to make population-level inferences (the PATE or PATT). As such, it is imperative to account for survey design elements (especially weights) in the final outcome model if the association of interest may vary between the population and the sample. Alternatively, if the goal is to estimate effect estimates for the survey sample itself (the SATE or SATT), the survey weights are not needed. All outcome models should account for clustering and stratification to yield accurate variance estimates, due to the resulting nonindependence of individuals.
Figure 1.
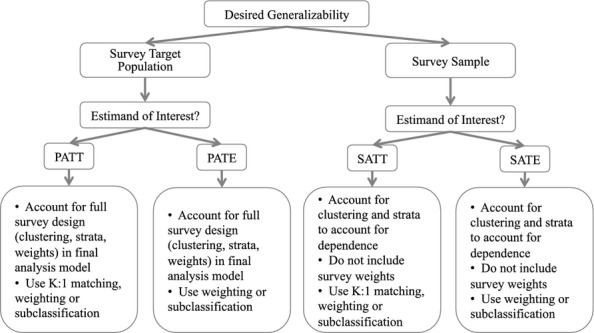
Recommended Decision Tree for Researchers Interested in Causal Estimand Using Complex Survey Data
The following approaches may be used to combine survey weighting and propensity score methods when interest is the PATT or PATE. When using propensity score matching, the effect estimate is generated from a survey-weighted regression that accounts for the complex survey design within the matched sample (applications seen in DiBonaventura et al. 2010; Kuo, Bird, and Tilford 2011). When using subclassification, subclass-specific effect estimates are generated from a survey-weighted regression that accounts for the complex survey design within each subclass. These subclass-specific effects are then combined using the survey-weighted subclass size (applications in Roberts et al. 2010 and Zanutto 2006). To estimate the PATE, the weighting ratio (for a given subclass) is the number of people in the population in that subclass divided by the total number of people in the population. To estimate the PATT, the weighting ratio (for a given subclass) is the number of people in the population who were treated in that subclass divided by the total number of people in the population who were treated. When using propensity score weighting, the propensity score weights and survey weights are multiplied to form a new weight; the effect estimate is generated from a weighted regression that incorporates the complex survey design elements and the composite weight (application seen in Cook et al. 2009). This approach is conceptually similar to methodology for addressing differential censoring in the context of propensity score weighting: inverse probability of censoring weights is multiplied by propensity score weights and this composite weight is used in the final analysis (Cole et al. 2003, 2010; Cain and Cole 2009). It is also similar to the multiplication of survey sampling weights by nonresponse adjustment weights, as is commonly performed in survey analysis (Groves et al. 2004).
Example 1: Simulation Study
We first describe a simple simulation study used to assess the performance of propensity score methods with complex survey data. Data were simulated with the following structure: a single normally distributed covariate X, a binary treatment indicator variable, a survey sampling weight (which depended on X and which of three survey strata the subject was in), and a pair of normally distributed potential outcomes. The covariate X was related to survey stratum membership, sampling probability, treatment assignment, and the size of treatment effects. The simulation design thus included stratification and survey weights but, for simplicity, did not incorporate clustering. Each simulated dataset contained 90,000 observations in the population from which samples of size 9,000 were drawn; 2,000 simulations were performed. This simulation study was conducted in R, and the MatchIt package was used to conduct the propensity score methods (Ho et al. 2011). The simulation design code is provided in Appendix SA1.
We compared the following methods for estimating the treatment effect: a naïve estimate (ignoring both survey design elements and propensity scores), weighted regression accounting for survey design elements, propensity score methods (ignoring survey weights and survey strata), and propensity score methods accounting for survey design elements. We assessed the performance of methods for estimating the PATT (weighting, subclassification, and 1 : 1 matching) and for estimating the PATE (weighting, subclassification). Appendix SA2 presents the regression models and Stata commands used for each estimand of interest.
For each method, we estimated the absolute bias, calculated as the absolute value of the difference between the estimated and true effects. In addition, we estimated the 95 percent confidence interval coverage rate, namely the percentage of 95 percent confidence intervals that contained the true treatment effect.
When estimating the PATE, methods that combine propensity scores and survey design elements achieve the smallest absolute bias and best confidence interval coverage (Figure 2). Using propensity score methods without survey design elements yields large bias and very low coverage. In general, in conjunction with survey design elements, propensity score subclassification and weighting perform very similarly.
Figure 2.
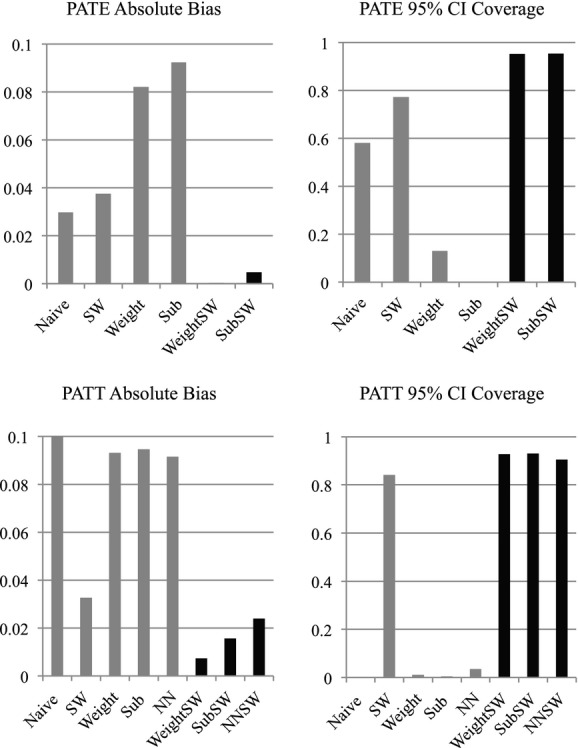
Estimated Absolute Bias and 95 percent Confidence Interval Coverage Rates When Estimating the PATE and PATT. (Methods that combine propensity score methods and survey weights are depicted with black bars. Naïve, no survey weight or propensity score; SW, survey weight; Weight, Propensity weight; Sub, Propensity score subclassification; NN, 1 : 1 matching; WeightSW, Survey weight and propensity weight; SubSW, subclassification and survey weight; NNSW, 1 : 1 matching and survey weight)
Similarly, when estimating the PATT, methods that combine propensity scores and survey design elements also perform most favorably, yielding the smallest absolute bias and best coverage rates (Figure 2). Again, using propensity score methods without accounting for the sampling weights yields bias and very poor coverage. In general, propensity score matching, subclassification, and weighting perform similarly, although propensity score weighting shows smallest absolute bias.
Overall, this simulation study shows that combining propensity score methods and methods that incorporate survey design elements can yield unbiased effect estimates with excellent coverage for both PATE and PATT estimands. However, ignoring either the survey design elements (e.g., weights) or propensity scores when trying to estimate the PATE or PATT may yield very misleading results.
Example 2: The Association between Usual Source of Care and Health Care Expenditures
In this example, we discuss a real-world example to highlight the appropriate conclusions that can be drawn from each propensity score approach. In this example, we estimate the PATE, PATT, SATE, and SATT of having a specialist physician as one’s usual source of care on annual health care costs. Our data are drawn from the 2008 MEPS Household Component, which is a nationally representative survey of the U.S. civilian noninstitutionalized population (Ezzati-Rice, Rohde, and Greenblatt 2008). All final outcome models adjusted for the MEPS’s strata and clusters when estimating the variance; relevant analyses also included the sampling weight. Propensity scores were calculated in R using the MatchIt package (Ho et al. 2011) and exported to Stata for analysis. The outcome models were fit in Stata version 12 using the svyset command (StataCorp 2011), which calculated the standard errors using Taylor series linearization. The study design and methods are discussed in further detail in Appendix SA3.
Findings
Table 1 presents the descriptive characteristics of the sample and the standardized biases. Standardized bias is a way of quantifying the balance between the treatment and control groups for each covariate; it is the difference in the means (or proportions) between the treated group and control group divided by the standard deviation in the treated group (Austin and Mamdani 2006; Stuart 2010). In 2008, 5,304 respondents representing 63 million people reported having a usual source of care. In the sample, 216 individuals reported having a specialist physician as their usual source of care. Compared with individuals in the sample with a family physician or general practice physician as their usual source of care, these respondents were older, less healthy, had lower incomes, were more likely to be on public insurance, had less education, and were less likely to identify as White. An unweighted bivariate comparison (Table 1) indicated that individuals with a primary care physician spent less, on average, than those who saw a specialist as their usual source of care ($5,261.37 compared to $10,664.38). After accounting for the complex survey design, we found some covariate differences between the two groups diminished; however, there continued to be statistically significant differences on education, health status, marital status, and type of insurance coverage. In addition, after accounting for the complex survey design, average expenditures by type of usual source of care widened: individuals with a primary care physician spent $5,274.18 annually compared to $10,899.97 for those who saw a specialist.
Table 1.
Descriptive Characteristics of Adults Who Have a Primary Care Physician or Specialist as a Usual Source of Care, Medical Expenditure Panel Survey (MEPS) 2008
| Sample Means (No Survey Adjustment) | Population Means* (Accounting for Survey Weights) | |||||
|---|---|---|---|---|---|---|
| Specialist Physician | Primary Care Physician | Standardized Difference in Means | Specialist Physician | Primary Care Physician | Standardized Difference in Means | |
| N | 216 | 5,088 | 2,517,828 | 61,110,686 | ||
| Covariates | ||||||
| Age >64 (%) | 36.11 | 22.25 | 0.29 | 40.71 | 22.91 | 0.37 |
| White (%) | 52.78 | 56.11 | −0.07 | 70.02 | 74.21 | −0.08 |
| Black (%) | 20.37 | 17.96 | 0.06 | 11.46 | 10.24 | 0.03 |
| Hispanic (%) | 12.04 | 17.33 | −0.16 | 8.79 | 9.42 | −0.02 |
| Other (%) | 14.81 | 8.59 | 0.175 | 9.73 | 6.13 | 0.10 |
| Poor (%) | 39.81 | 31.98 | 0.16 | 33.42 | 24.95 | 0.17 |
| Education (years) | 12.56 | 12.78 | −0.07 | 12.72 | 13.15 | −0.15 |
| SF-12—PCS | 44.02 | 47.68 | −0.29 | 44.35 | 48.11 | −0.30 |
| SF-12—MCS | 49.73 | 50.58 | −0.08 | 50.29 | 51.05 | −0.07 |
| Self-reported health | ||||||
| Excellent | 10.80 | 14.58 | −0.13 | 13.61 | 15.27 | −0.05 |
| Very good | 26.39 | 33.96 | −0.17 | 26.57 | 35.96 | −0.21 |
| Good | 35.65 | 33.22 | 0.05 | 34.64 | 33.20 | 0.03 |
| Fair | 21.30 | 14.09 | 0.18 | 20.45 | 12.24 | 0.20 |
| Poor | 6.02 | 4.15 | 0.08 | 4.73 | 3.34 | 0.06 |
| Insurance | ||||||
| Private (%) | 59.72 | 69.81 | −0.21 | 61.20 | 74.35 | −0.27 |
| Public (%) | 31.94 | 21.93 | 0.21 | 30.90 | 18.52 | 0.27 |
| Uninsured (%) | 8.33 | 8.25 | 0.00 | 7.90 | 7.13 | 0.03 |
| Female (%) | 52.31 | 55.94 | −0.07 | 50.69 | 53.43 | −0.06 |
| Married (%) | 48.15 | 59.91 | −0.24 | 48.88 | 60.32 | −0.23 |
| MSA (%) | 84.72 | 85.10 | 85.21 | 84.60 | ||
| Region | −0.01 | 0.02 | ||||
| Northeast (%) | 14.35 | 20.13 | −0.16 | 19.14 | 23.88 | −0.14 |
| Midwest (%) | 18.98 | 21.74 | −0.07 | 17.71 | 23.16 | −0.14 |
| South (%) | 42.13 | 41.47 | 0.01 | 40.32 | 38.42 | 0.04 |
| West (%) | 24.54 | 16.67 | 0.18 | 22.82 | 14.53 | |
| Outcome | ||||||
| Medical spending | $10,664.38 | $5,261.37 | 0.26 | $10,899.97 | $5,274.18 | 0.28 |
Univariate statistics calculated using Stata’s survey set command using MEPS SAQWT08F survey weight. No propensity score adjustment applied.
Propensity score methods improved the balance between the two groups. As Figure 3 illustrates, the distribution of standardized biases for covariates used in the propensity score model narrowed from the unmatched sample (labeled “All”) when using 1 : 1 matching, 5 : 1 matching, subclassification, and weighting. When estimating PATE and PATT, we included the survey weight as a predictor in the propensity score model. When estimating the PATE, subclassification provided better overall balance than weighting. When estimating the PATT, 5 : 1 matching outperformed 1 : 1 matching, and subclassification provided better balance than weighting. The overall performance of these methods was similar when estimating the SATE and SATT. The SATE and SATT propensity score models did not include the survey weights as a covariate.
Figure 3.
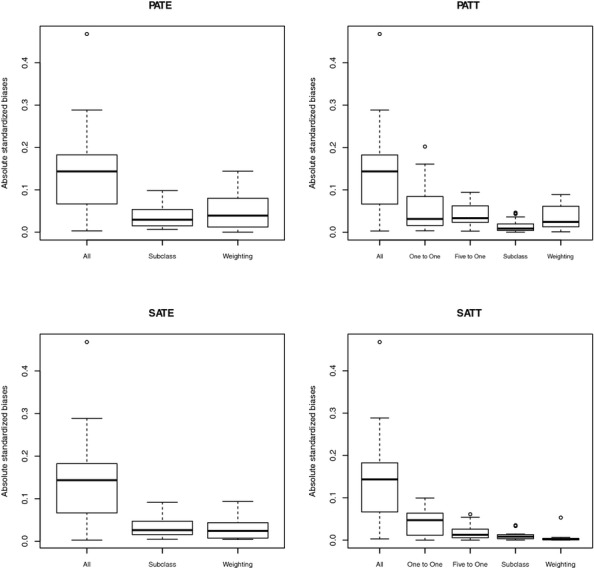
A Comparison of the Absolute Standardized Differences in Means for Covariates When Estimating the PATE, PATT, SATE, and SATT Using Different Propensity Score Methods
Table 2 reports the estimated PATE, PATT, SATE, and SATT. PATE estimates ranged from $2,477 using weighting to $2,765 using subclassification. We found that the various propensity score methods produced a wide range of estimates for the ATT. The PATT estimates ranged from $1,758 using weighting to $3,614 using 5 : 1 matching; the SATT estimates ranged from $1,118 using 1 : 1 matching to $3,193 using 5 : 1 matching. Weighting and subclassification estimates were more similar for the ATE. The PATE estimates ranged from $2,477 using weighting to $2,765 using subclassification; the SATE estimates ranged from $2,573 using subclassification to $2,948 using weighting. All estimates, except for those from the 1 : 1 matched sample, were statistically significant at the 5 percent level.
Table 2.
Results of Estimated Difference in Annual Health Care Spending among Adults Who Have a Specialist as Their Usual Source of Care Compared to a Primary Care Physician (Medical Expenditure Panel Survey 2008)
| Inference | Propensity Score Method | Estimated Difference | p-Value |
|---|---|---|---|
| PATE | |||
| 1 : 1 matching | NA | ||
| 5 : 1 matching | NA | ||
| Subclassification | $2,765.64 | <.001 | |
| Weighting | $2,477.02 | <.001 | |
| PATT | |||
| 1 : 1 matching | $2,544.76 | .086 | |
| 5 : 1 matching | $3,614.43 | <.001 | |
| Subclassification | $3,414.36 | <.001 | |
| Weighting | $1,759.60 | .003 | |
| SATE | |||
| 1 : 1 matching | NA | ||
| 5 : 1 matching | NA | ||
| Subclassification | $2,573.13 | <.001 | |
| Weighting | $2,948.03 | .000 | |
| SATT | |||
| 1 : 1 matching | $1,118.09 | .448 | |
| 5 : 1 matching | $3,193.53 | <.001 | |
| Subclassification | $2,723.21 | <.001 | |
| Weighting | $2,015.33 | .002 |
Interpretation
We now provide exemplar interpretations of the PATE, PATT, SATE, and SATT using propensity score weighting. The PATE is the population ATE and is arguably the most common estimand of interest. It is the average difference in outcomes under the treatment and control conditions in the survey’s target population. In our example, the PATE represents the average impact on health care spending of having a specialist (rather than a general practitioner) as one’s usual source of care among noninstitutionalized adults in the United States. Our results indicate that having a specialist as one’s usual source of care was associated with nearly a $2,477 increase in health care spending for U.S. adults. This result suggests that shortages of primary care physicians may result in higher spending if Americans turn to specialists as their usual source of care.
The PATT is the population ATT, which is the effect of the treatment among those in the population who would actually receive the treatment. In our example, the PATT represents the impact on health care spending of having a specialist (rather than a general practitioner) as one’s usual source of care among noninstitutionalized U.S. adults who had a specialist as their usual source of care. We found that among U.S. adults who selected a specialist as their usual source of care, having a specialist resulted in $1,759 higher health care spending than if those individuals had a primary care physician as their usual source of care. This finding suggests that having a primary care physician as one’s usual source of care is associated with lower spending even among those individuals who would select a specialist and thus may have a theoretically higher likelihood to use medical care services due to personal preferences or illness.
The SATE is the sample ATE, which is the average difference in outcomes under the treatment and control conditions among all survey respondents (treated and control). In our example, the SATE represents the average impact on health care spending of having a specialist (rather than a general practitioner) as one’s usual source of care among MEPS survey respondents. We found that having a specialist as one’s usual source of care was associated with an additional $2,948 in annual health care spending among survey respondents. The SATT is the sample ATT, which is the average difference in outcomes under the treatment and control conditions for survey respondents in the treatment group. In our example, the SATT represents the average impact on health care spending of having a specialist (rather than a general practitioner) as one’s usual source of care among MEPS survey respondents who had a specialist as their usual source of care. We found that among those survey respondents who chose a specialist as their usual source of care, the estimated effect was an additional $2,015 in annual health care spending.
Discussion
In this paper, we sought to illustrate how researchers can use propensity score methods with complex surveys. Propensity score methods are effective at reducing confounding arising in observational studies. While computationally straightforward, propensity score methods should be applied carefully and effect estimates interpreted thoughtfully, especially with complex survey data.
The simulation study in Example 1 focused on identifying appropriate analysis methods that yield unbiased effect estimates and are generalizable to the survey’s target population. As this simulation study demonstrated, only methods that combine propensity scores and survey design elements meet these criteria. Final outcome analyses that did not incorporate either propensity scores or survey weights yielded significant absolute bias and poor 95 percent confidence interval coverage rates. Analyses that only incorporated propensity scores performed the poorest, with the highest bias and worst coverage rates. Of note, numerous studies in our review of the literature used propensity scores, but not survey weights, and interpreted their effect estimates as generalizable to the target population. Our simulation study shows that this is not necessarily an appropriate interpretation.
In Example 2, we explored the four different estimands (PATE, PATT, SATE, and SATT) and illustrated the appropriate interpretation of each. We find that the estimated effect size varied by propensity score method and estimand. This variation between methods may be a result of the relatively small treated group size (N = 216). More important, we show that the inferences that can be drawn from these approaches are considerably different. When using SATT, the inference is narrowed to the effect of specialists on those 216 survey subjects who selected a specialist; for PATE, the estimated effect can be interpreted as the difference in spending for all noninstitutionalized adults in the United States.
When using complex survey data to estimate causal effects, researchers are faced with a number of study design options. We recommend that researchers approach this problem systematically to ensure that the desired estimand is estimated and proper inference is drawn. First, researchers should decide if they are interested in the ATE or the ATT.
Second, researchers must identify to which group (i.e., the target population of the original survey, the survey sample itself, or some other subgroup) they would like to generalize their effect estimates. While we present four possible estimands, we expect that many researchers use complex survey data to take advantage of the opportunity to generalize to the target population and thus are interested in the PATE or PATT.
Third, survey weights should be used as a predictor in the propensity score model. We also suggest including strata, clustering, and primary sampling unit information if available and feasible. There is a substantial literature to guide researchers in estimating the propensity score model and several software packages to assist in model diagnostics (e.g., MatchIt and twang in R, psmatch2 and pscore in Stata).
Fourth, a propensity score method appropriate to the estimand of interest should be selected. For PATT or SATT estimation, propensity score weighting, subclassification, or matching is appropriate. For PATE or SATE, either propensity score weighting or subclassification may be used. One common recommendation is to select the method (within each of these sets) that yields the best covariate balance between treatment and control groups (Stuart 2010).
Fifth, in the outcome analysis, survey weights should be incorporated if the goal is to make inferences about the target population (PATE or PATT). For all estimands, strata and clustering should be accounted for in the final analysis (using standard survey commands) to obtain accurate variance estimates. When matching, the outcome regression is conducted within the matched data. For subclassification, the outcome regression is conducted within each propensity score-defined subclass and then subclass-specific estimates are combined using population totals for PATT or PATE and sample totals for SATT or SATE. For propensity score weighting, the outcome regression is estimated within the total sample. When estimating the SATE or SATT, the model is run using weights that are simply the propensity score weights; when estimating the PATE or PATT, the weights are the product of the survey weight and propensity score weight.
Lastly, it is important to be precise when interpreting the study results. Effect estimates from national surveys will only be nationally representative if survey design elements and survey weights are appropriately incorporated in the propensity score analysis.
Further work in this area is warranted. Our simulation design was intentionally simple; simulations that include a more complex survey design, additional covariates, model misspecification, or nonlinear propensity score estimation may reach different conclusions. In addition, while we investigated three common propensity score methods, we do not fully assess the relative performance of these methods. Furthermore, the performance of other potential ways of combining propensity scores and complex survey designs has yet to be explored, such as the possibility of conditioning on the weight rather than using weighted models and design-based analysis (Gelman 2007). Several technical issues such as how to treat extreme weights and variance estimation for propensity score methods in complex survey contexts should be investigated. Finally, while we argue that including survey weights is not necessary for SATT and SATE results (in terms of interpretation), future empirical and theoretical work could explore if any adjustment is necessary to reflect individuals’ varying sampling probabilities.
Conclusion
This paper presents guidance to researchers who are interested in estimating causal effects using complex survey data. We present a simulation and real-world example to illustrate common pitfalls, advantages, and disadvantages in these methods. We recommend that researchers consider carefully their desired estimand of interest and population target. We found that propensity score models and outcome models that accounted for the survey sampling weights are more appropriate for making population-level inferences.
Acknowledgments
Joint Acknowledgment/Disclosure Statement: This research was supported by the National Institute of Mental Health (K25 MH083846, Principal Investigator Stuart) and Alvin R. Tarlov and John E. Ware Jr. Doctoral Dissertation Award from the Health Assessment Laboratory (Eva DuGoff). We are grateful for the helpful comments of two anonymous reviewers.
Disclosures
None.
Disclaimers
None.
Supporting Information
Additional Supporting Information may be found in the online version of this article:
Appendix SA1: Simple Simulation Design R Code.
Appendix SA2: Analysis Models by Estimation Method and Stata Commands.
Supplementary Methods and Discussion on Example 2: The Association between Usual Source of Care and Health Care Expenditures.
Author Matrix.
References
- Austin PC, Mamdani MM. A Comparison of Propensity Score Methods: A Case-Study Estimating the Effectiveness of Post-AMI Statin Use. Statistics in Medicine. 2006;25:2084–106. doi: 10.1002/sim.2328. [DOI] [PubMed] [Google Scholar]
- Bell BA, Onwuegbuzie AJ, Ferron JM, Jiao QG, Hibbard ST, Kromrey JD. Use of Design Effects and Sample Weights in Complex Health Survey Data: A Review of Published Articles Using Data from Three Commonly Used Adolescent Health Surveys. American Journal of Public Health. 2012;102(7):1399–405. doi: 10.2105/AJPH.2011.300398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cain LE, Cole SR. Inverse Probability-of-Censoring Weights for the Correction of Time-Varying Noncompliance in the Effect of Randomized Highly Active Antiretroviral Therapy on Incident AIDS or Death. Statistics in Medicine. 2009;28:1725–38. doi: 10.1002/sim.3585. [DOI] [PubMed] [Google Scholar]
- Cochran WG. The Effectiveness of Adjustment by Subclassification in Removing Bias in Observational Studies. Biometrics. 1968;24(2):295–313. [PubMed] [Google Scholar]
- Cole SR, Hernan MA, Robins JM, Asastos K, Chmiel J, Detels R, Ervin C, Feldman J, Greenblatt R, Kingsley L, Lai S, Young M, Cohen M, Muñoz A. Effect of Highly Active Antiretroviral Therapy on Time to Acquired Immunodeficiency Syndrome or Death Using Marginal Structural Models. American Journal of Epidemiology. 2003;158(7):687–94. doi: 10.1093/aje/kwg206. [DOI] [PubMed] [Google Scholar]
- Cole SR, Jacobson LP, Tien PC, Kingsley L, Chmiel JS, Anastos K. Using Marginal Structural Measurement-Error Models to Estimate the Long-Term Effect of Antiretroviral Therapy on Incident AIDS or Death. American Journal of Epidemiology. 2010;171:113–22. doi: 10.1093/aje/kwp329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook BL, McGuire TG, Meara E, Zaslavsky AM. Adjusting for Health Status in Non-Linear Models of Health Care Disparities. Health Services and Outcomes Research Methodology. 2009;9(1):1–21. doi: 10.1007/s10742-008-0039-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiBonaventura MD, Wagner JS, Yuan Y, L’Italien G, Langley P, Ray Kim W. Humanistic and Economic Impacts of Hepatitis C Infection in the United States. Journal of Medical Economics. 2010;13(4):709–18. doi: 10.3111/13696998.2010.535576. [DOI] [PubMed] [Google Scholar]
- Ezzati-Rice T, Rohde F, Greenblatt J. Sample Design of the Medical Expenditure Panel Survey Household Component, 1998–2007. Methodology Report No. 22. Rockville, MD: Agency for Healthcare Research and Quality; 2008. [Google Scholar]
- Gelman A. Struggles with Survey Weighting and Regression Modeling. Statistical Science. 2007;22(2):153–64. [Google Scholar]
- Groves RM, Fowler FJ, Jr, Couper MP, Lepkowski JM, Singer E, Tourangeau R. Survey Methodology. Hoboken, NJ: Wiley; 2004. [Google Scholar]
- Ho DE, Imai K, King G, Stuart EA. MatchIt: Nonparametric Preprocessing for Parametric Causal Inference. Journal of Statistical Software. 2011;42(8):1–28. [Google Scholar]
- Imai K, King G, Stuart EA. Misunderstandings between Experimentalists and Observationalists about Causal Inference. Journal of the Royal Statistical Society Series A-Statistics in Society. 2008;171:481–502. [Google Scholar]
- Korn EL, Graubard BI. Epidemiologic Studies Utilizing Surveys – Accounting for the Sampling Design. American Journal of Public Health. 1991;81(9):1166–73. doi: 10.2105/ajph.81.9.1166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo DZ, M. Bird T, Tilford JM. Associations of Family-Centered Care with Health Care Outcomes for Children with Special Health Care Needs. Maternal and Child Health Journal. 2011;15(6):794–805. doi: 10.1007/s10995-010-0648-x. [DOI] [PubMed] [Google Scholar]
- Lumley T. Complex Surveys: A Guide to Analysis Using R (Wiley Series in Survey Methodology) Hoboken, NJ: Wiley; 2010. [Google Scholar]
- Lunceford JK, Davidian M. Stratification and Weighting via the Propensity Score in Estimation of Causal Treatment Effects: A Comparative Study. Statistics in Medicine. 2004;23(19):2937–60. doi: 10.1002/sim.1903. [DOI] [PubMed] [Google Scholar]
- McCaffrey DF, Ridgeway G, Morral AR. Propensity Score Estimation with Boosted Regression for Evaluating Causal Effects in Observational Studies. Psychological Methods. 2004;9:403–25. doi: 10.1037/1082-989X.9.4.403. [DOI] [PubMed] [Google Scholar]
- McCrae JS, Lee BR, Barth RP, Rauktis ME. Comparing Three Years of Well-Being Outcomes for Youth in Group Care and Nonkinship Foster Care. Child Welfare. 2010;89(2):229–49. [PubMed] [Google Scholar]
- Pfeffermann D. The Role of Sampling Weights When Modeling Survey Data. International Statistical Review. 1993;61(2):317–37. [Google Scholar]
- Roberts AL, Gilman SE, Fitzmaurice G, Decker MR, Koenen KC. Witness of Intimate Partner Violence in Childhood and Perpetration of Intimate Partner Violence in Adulthood. Epidemiology. 2010;21(6):809–18. doi: 10.1097/EDE.0b013e3181f39f03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum PR, Rubin DB. The Central Role of the Propensity Score in Observational Studies for Causal Effects. Biometrika. 1983;70(1):41–55. [Google Scholar]
- StataCorp. Stata Statistical Software: Release 12 (Release) College Station, TX: StataCorp LP; 2011. [Google Scholar]
- Stuart EA. Matching Methods for Causal Inference: A Review and a Look Forward. Statistical Science. 2010;25(1):1–21. doi: 10.1214/09-STS313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanutto EL. A Comparison of Propensity Score and Linear Regression Analysis of Complex Survey Data. Journal of Data Science. 2006;4:67–91. [Google Scholar]
- Zanutto E, Lu B, Hornik R. Using Propensity Score Subclassification for Multiple Treatment Doses to Evaluate a National Antidrug Media Campaign. Journal of Educational and Behavioral Statistics. 2005;30(1):59–73. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix SA1: Simple Simulation Design R Code.
Appendix SA2: Analysis Models by Estimation Method and Stata Commands.
Supplementary Methods and Discussion on Example 2: The Association between Usual Source of Care and Health Care Expenditures.
Author Matrix.


