On the ergodicity of supercooled molecular glass-forming liquids at the dynamical arrest: the o-terphenyl case

Abstract

The dynamics of supercooled ortho-terphenyl has been studied using photon-correlation spectroscopy (PCS) in the depolarized scattering geometry. The obtained relaxation curves are analyzed according to the mode-coupling theory (MCT) for supercooled liquids. The main results are: i) the observation of the secondary Johari-Goldstein relaxation (β) that has its onset just at the dynamical crossover temperature T_B (T_M > T_B > T_g); ii) the confirmation, of the suggestion of a recent statistical mechanical study, that such a molecular system remains ergodic also below the calorimetric glass-transition temperature T_g. Our experimental data give evidence that the time scales of the primary (α) and this secondary relaxations are correlated. Finally a comparison with recent PCS experiments in a colloidal system confirms the primary role of the dynamical crossover in the physics of the dynamical arrest.

The so-called dynamic arrest phenomenon (DA), accompanied by a remarkable dynamic slowing down at the glass transition temperature T_g, marks a dramatic change in the properties of a physical system¹. The clarification of the microscopic origin of the DA slowing down represents an hot topic of much current research. The phenomenon is customarily studied by exploring the transport coefficients (e.g., viscosity η, self-diffusion constant D_s, and relaxation time τ) temperature dependence of the supercooled liquid into a metastable state below its melting temperature T_M. The study of the way of their approaching to these limiting values may provide information about the nature of the process. A special situation regards these coefficients, and τ in particular, as T decreases below T_M, it can change by several orders of magnitude (more than 15), surpassing the time required for experimental accessibility. In some cases, this behaves, as proposed by the mode-coupling theory (MCT)² the breaking of the system's ergodicity in the amorphous glass phase at or below the glass transition temperature.

Considering the various open questions on the related basic processes, the DA constitutes an exciting and challenging research topic today while strongly debated also with conflicting opinions³,⁴,⁵,⁶,⁷,⁸,⁹,¹⁰. One of these deals with a possible “DA criticality”: i.e., whether transport parameters reflect an underlying phase transition to a state in which these quantities diverge at a finite temperature (the “dynamic divergence”). Another one instead focuses on the occurrence, or not, of the system non-ergodicity inside the glass phase originally observed in hard colloidal solutions and explained according to the MCT theory¹¹,¹². For this latter argument it has been recently proposed that grafted polydisperse colloids¹³ and molecular liquids with internal degrees of freedom remain ergodic at all temperatures⁵,¹⁴ and therefore statistical mechanics can be applied to describe the arrest process.

The parametrization of transport coefficients inside the supercooled regime, has been extensively treated in the recent years by means of the empirical Vogel-Fulcher-Tammann (VFT or super Arrhenius) form: η = η₀ exp (BT₀/(T − T₀)). That indicates a finite diverging temperature (associated with the Kauzmann temperature T_K⁴,¹⁵). Furthermore, the VTF was used to classify liquids in two separate categories: “fragile” or “strong” glass former¹⁶. Whereas “strong” liquids exhibit pure Arrhenius T–dependence: ln(η/η₀) = E/k_BT, the “fragile” ones have a marked VFT behavior. The so called steepness index, 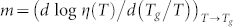, can be used to measure the system fragility. The VFT has been treated as a “universal” feature¹⁷, despite the fact that it has been questioned¹⁸: recent studies, in fact, propose that the validity of this form must be reconsidered because different experimental and theoretical reasoning show that it lacks physical meaning⁵,⁷,⁸,¹⁸,¹⁹.

In addition to the VFT validity, various recent studies⁶,⁸,¹⁹ also suggest the necessity to study the supercooled liquid dynamics in a broader range of temperatures at least two dynamic regimes are necessary. Hence, an intriguing phenomenon occurring at a temperature (T_B) well above T_g: the so called fragile to strong dynamic crossover (FSDC) becomes of great interest. Lately, T_B has been also recognized as a milestone on the way with which systems approach DA since a lot of exceptional processes disclose their properties there.

Thus, several significant phenomena should be explored, such as: (i) the increasing broadening of the structural relaxation time distribution that can be described by means of a stretched exponential 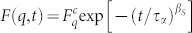accompanied in some cases by the loss of ergodicity observed when F(q, t) approaches an almost constant value for long times¹¹,¹²; (ii) the splitting of the high T relaxation into the primary (α) and the Johari-Goldstein β_JG relaxation times (also named secondary or β_slow)²⁰; (iii) the violation of the Stokes-Einstein (SE) relation with a fractional behavior and the decoupling between the translational and the rotational diffusion (for T < T_B). In the high T-regime, as evidenced by the SE, the translational diffusion, D_s, tracks the inverse of the shear viscosity (η⁻¹) whereas for T < T_B D_s declines far less rapidly by decreasing T as D_s ~ η^−ξ, with 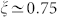; instead D_Rot (or the rotational correlation time) remains proportional to the inverse of the shear viscosity down to T_g²¹,²²,²³,²⁴,²⁵,²⁶. For this reason any experimental technique that looks only to the D_Rot cannot observe the violation; (iv) for a broad set of supercooled systems τ(T_B) = 10^−7±1 sec and η(T_B) ≈ 10³ Pa sec are near-universal¹⁹,²⁷ and if we consider the T – P phase diagram: τ(T_B, P_B), η(T_B, P_B) = const for a given glass former; (v) it is believed that the dynamical crossover is closely related to the appearing of dynamical heterogeneities (DH), although some pure Arrhenius systems show them²⁸. DH refers to the presence of transient spatially separated regions with vastly different relaxation times²¹,²²,²³,²⁹. (vi) usually a fragile to less fragile (or strong) transformation occurs when passing T_B¹⁹; (vii) and finally the hopping extended MCT (EMCT) identifies T_B with the MCT critical temperature T_c²,³⁰,³¹. T_B can be evaluated by means of different methods, such as by means of a plot based on the T-derivative of the α-relaxation time³².

Exploration of all these phenomena can help to stress more the importance of the dynamical crossover⁶,³³ and its universality¹⁹.

Different approaches for estimating T_B have been recently proposed: one is based on the MCT¹⁹,³¹, the second employs the constraints of the Adam–Gibbs theory⁸,³³ and the most recent one explores the apparent enthalpy space properties⁶. All of them stress the basic importance of the dynamical crossover in the DA physics. The dynamic crossover concept can be considered of true interest not only for the way in which a system arrests its dynamics but also for the new science frontiers towards the mesoscales. In fact very recently the crossover has been explicitly considered as a way with which multiscale materials can model the mesoscale, i.e. how the understanding of mechanisms at the microscale can enable predictions of functional behavior at the macroscale³³. For these reasons T_B appears to be of central interest in material science.

As already mentioned, a recently proposed statistical mechanical theory of the glass transition from molecular liquids with internal degrees of freedom suggests that supercooled liquids can remain ergodic also at the DA¹⁴. To substantiate this idea, we have modeled the liquid OTP (ortho-terphenyl) by taking into account its internal degrees of freedom.

Furthermore, we explore, by detecting the depolarized light scattering (DLS), using a photon correlation spectroscopy (PCS) method, the OTP dynamics below the dynamical crossover temperature T_B (also for T < T_g). The measured correlators are studied in the current MCT frames with the following main objectives: a) to obtain a careful verification on whether the primary α-relaxation together with the secondary Johari-Goldstein β_JG-relaxation can be observed; b) to explore whether the system maintains the ergodicity near and below the calorimetric glass transition temperature, and whether the dynamical crossover exists with this property; c) to accurately compare the obtained data with the related findings recently observed in colloidal systems¹³.

Results

It is well known that in the DLS regime the field autocorrelation function is the convolution of the translational and diffusional modes³⁴. For a scattering geometry in which the scattering plane is the x – y one, whereas the incident field propagates along x with a z linear polarization, the correlation is:

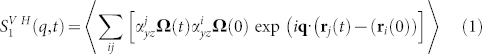where α is the molecular polarizability tensor, Ω the orientation vector and r_j represents the position of the j–th molecule and the brackets is the ensemble average. 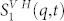, and hence the 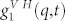, includes dynamical correlations in both orientation and position between all pairs of molecules. To be precise, whereas the translational motion is represented by the exponential terms (in other words the density-density correlation) the rotational ones are in the remaining part. It is important to stress that the 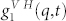includes information on the dynamical coupling between translations and rotations of the scattering element³⁴. On these bases the present PCS experiment measures both the mutual translational and the rotational diffusion.

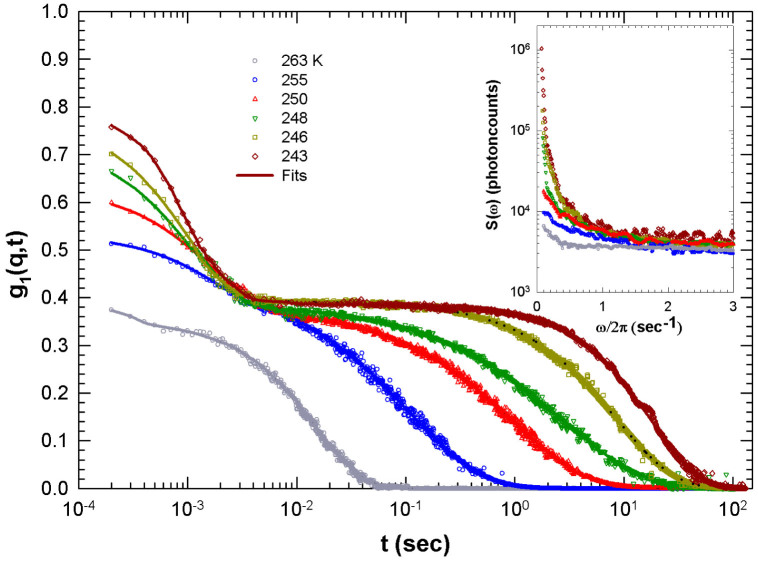
Figure 1 illustrates the measured g₁(q, t) for T = 263, 255, 250, 248, 246 and 243 K, whereas in the inset are reported the measured spectral PSD at the same temperatures; in both cases data also below the calorimetric T_g are reported. All the g₁(q, t) curves are characterized by a bimodal relaxation and also by the decay to zero in finite times, even below T_g. Hence, the system ergodicity is fully preserved, for T < T_B also below the calorimetric T_g. The OTP evolution towards a very slow dynamics is also observable, in the same T–region, by the marked S(q, ω) increases in the lowest frequency region by decreasing T (inset).

Figure 1. The correlator g₁(q, t) for T = 263, 255, 250, 248, 246 and 243 K. The inset reports the power spectral density (PSD), S(q, ω), measured at the same temperatures.

All the g₁(q, t) curves are characterized by a bimodal relaxation and also by the decay to zero in finite times and show that the system relaxation times span about 6 decades. Ergodicity is preserved below the glass transition temperature T_g as proposed by the theory⁵,¹⁴.

The g₁(q, t) curves have been analyzed, according to the MCT, as the superposition of a short-time decay (the β contribution) and a long-time stretched tail (the α-decay), weighted for the non-ergodicity factor f_c. In principle, also two stretched forms can be used, a situation avoided for the parameters redundancy. From the data fitting (continuous lines in Figure 1) we obtain f_c, the times τ_α and τ_β, and the stretched exponent β_S, that will be discussed in the following section.

Discussion

The OTP together with water, is certainly the most studied supercooled liquid, and can be considered as the prototype of molecular glass forming materials, therefore up to now, it represented a test system of the MCT suggestions (see e.g.2). For this reason it has been extensively studied with many different experimental approaches³⁵ including: light (PCS³⁶, DLS³⁷,³⁸, optical Kerr effect (OKE), combinations of different light scattering approaches like the double grating monochromators (DM) and tandem Fabry-Pérot interferometry (TFPI)³⁵), neutrons³⁹, viscoelasticity⁴⁰, dielectric relaxation (DE)²⁰,⁴¹,⁴², calorimetry⁴³ and nuclear magnetic resonance (NMR)²⁵,⁴⁴. In considering these studies and a recent NMR experiment⁴⁵, the characteristic temperatures of the system are: 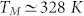, 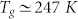and T_B ~ 285 K. For our study, we stress again that our main interest is to find out what happens for T < T_B.

As it is well known, the ideal MCT clearly evidences the existence of a precursor phenomenon exhibiting anomalous (“glassy”) dynamics, connected to a “critical temperature” T_c, at the transition from liquid to amorphous solid well prior to T_g. The ideal MCT theory uses, to interpret experimental data inside the supercooled phase, closed equations of motion by measuring the so called correlator (the density-fluctuation correlation functions F(q, t) at a given wave-vector q²). In these terms, T_c is explained as a singularity resulting from a bifurcation phenomenon in the long-time limit of the correlator, for which the observables posses two different behaviors above and below it; a limit that is zero for the liquid phase but positive for the ideal glass. It is called glass form factor (or non-ergodicity parameter f_c) and behaves discontinuously, with the loss of the ergodicity and a diverging behavior in transport (the MCT divergence) if an order parameter such as T passes the critical value T_c. Thus, f_q exhibits a singularity as a function of the distance 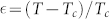for . The same situation can be detected by studying the system with the volume fraction φ as an order parameter, and at φ_c both the non-ergodicity and the MCT divergence are observable. In this latter case avoiding crystallization, by introducing size polydispersity, hard spheres (like colloidal particles¹¹,¹²,¹³) have been largely used to study the DA by means of the MCT. These systems, as it is well known at thermal equilibrium become very viscous and eventually form an amorphous solid⁴⁶ at large φ, in analogy to the glass transition of molecular liquids²⁹.

The molecular caging has been considered as a logic feature characterizing these dynamics, hence T_c represents a crossover between two different dynamic behaviors located inside the interval T_M − T_g. Above T_c, F(q, t) decays to zero according to precise scaling laws (also supporting the arrest universality). Below T_c the interactions of density fluctuations arrest the previous region via cage-effects. As previously said, a crucial and actual question is to clarify the molecular origin of the dynamic evolution of the system in the region between T_c and T_g. The MCT scaling form commonly used to analyze the transport parameters and to calculate T_c inside the arrest region is in τ_α(T) case:

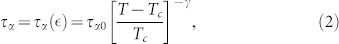where γ is a non-universal exponent. The same law holds for φ (τ ~ (φ_c − φ)^−γ), φ_c ≈ 0.57–0.59 are the most accepted values for the location of the colloidal glass transition; it has been also widely believed that a truly nonergodic state is obtained at larger φ. Eq. 2 describes well transport data of supercooled fluids in the region 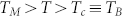, and thus in the temperature region from the liquid stable phase to the coupled fluid phase, i.e., the moderately supercooled state. In the same region MCT characterizes the measured structural relaxations as the bimodal decay (primary α- and secondary β-processes) in F(q, t) observing the way in which molecules explore all the available cage space. In the quasielastic scattering (QES) time regime, the two contributions are superimposed, with the β contribution at the lowest time (β_fast). Indicating 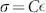as the so called separation parameter, the MCT proposes precise scaling laws and exponents for both these relaxations (see e.g. ref. 2). The ideal MCT divergence is represented by these scaling law forms.

The MCT has been intensively studied by means of experimental and simulation approaches in molecular systems and colloids. There is however a difference in these systems: for the same molecular glass formers the transition from an ideal MCT regime to an activated one has been experimentally demonstrated²⁹. Hence, it was possible to consider proper extended MCT models². For colloidal hard spheres the situation remains essentially unclear for the limited range of the corresponding dynamical data. If compared with the 15 orders of magnitude for which the molecular fluids dynamic data are measurable, for colloids is in fact available a much smaller range, typically five decades or less. To be precise, one must note the experimental time window available for these two classes of systems; whereas in the case of molecular materials the α-relaxation can be explored in a time relaxation interval ranging from 10⁻¹³ to 10² sec, for colloidal systems this range can be actually, by means of a proper use of the dynamical light scattering technique (DLS)¹³, 10⁻⁴ to 10⁴ sec. In the past by means of traditional DLS the range for colloids was very limited: 10⁻⁴ to 1 sec¹².

The MCT also considers the possibility of more qualitative approaches by assuming that the long time decays (α-) of the density correlation function are caused by the presence of a hierarchical multi-exponential temporal relaxation observable as a stretched exponential. Such an approach can help us to illustrate how a liquid does become a glass in a spatially heterogeneous fashion. A Laplace transform resolves 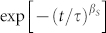into a weighted linear superposition of pure exponentials: 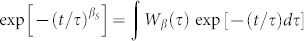, where W_β is the weight function. As T decreases below T_B, β_S decreases, causing a broadening in W_β(τ) that reasonably can be interpreted as an evidence for DH: many different dynamical regions that have a simple exponential relaxation. These distinct regions of space change independently in structure and contents with time exhibiting strong dynamic correlations where transport parameters can decouple so that the Stokes-Einstein relation is violated and their structural relaxation time can differ by orders of magnitude from the average over the entire system. Rotational and translational dynamics average differently over these space-time heterogeneities; whereas the translational motion is very sensitive to the relaxation of these structures, being directly coupled with them, the local molecular rotation is relatively more independent. Near the arrest, the time required for reequilibration of local environments is two or more orders of magnitude larger than the corresponding rotational correlation time.

From a more precise theoretical point of view, the dynamical crossover and these two broad classes of behavior, the Arrhenius and the more intriguing non-Arrhenius variation, are more correctly described in the frame of energy landscape (or the so-called inherent structures)⁴,³³. Whereas the Arrhenius behavior is observed when a single particle hops over barriers of uniform height, the cooperative structural arrest is observed when the barriers have a broad frequency (and thus correlation time) distribution of heights. In addition, whereas the potential-energy surface associated with ‘strong' T–dependence should be relatively smooth, the corresponding one giving rise to fragile behavior should be quite rough. Hence, the fast dynamics of supercooled liquids corresponds to an intrabasin motion and the long-time slow dynamics to an interbasin one (the hopping). At the lowest T the multibasin dynamics, i.e., the arrest behavior, is favored. Each of these basins is characterized by a temperature dependent weight factor and the T decreasing implies not only their progressive numerical reduction but also a decreasing of their weight up to negligible values. At this stage the only relevant dynamics is the molecule hopping from a cluster to another, i.e., a process with only one typical energy scale: the Arrhenius energy. In this framework the crossover phenomenon — the transition from gradual to accelerated variations in behavior — can be expected whenever different existing mechanisms compete, and the dominance of one over the other depends on the local environment (or the driving force).

The existence of a temperature marking dynamical changes of fragile supercooled liquids below T_M, has been already considered in the past⁷,⁸,³⁷,⁴⁰,⁴⁷. By considering these suggestions, recently it has been proposed that 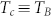⁶,¹⁹,³¹. A way to explain these findings on microscopic bases, as proposed by the energy landscape model, is the extended MCT (EMCT)². By considering a Lennard-Jones system it is showed that, for the self diffusion coefficient, T_B just occurs near the critical temperature of the idealized version of the theory as due to the change in the dynamics from the one determined by the cage effect to a second one dominated by hopping processes³⁰,⁴⁸.

In the EMCT frame, the scale decoupling is explained by assuming that the relaxation is due to two diffusional contributions: i.e. a very long time thermally activated hopping process (D^hop) and the cage affected one typical of the ideal MCT (D^id); thus the self-diffusion coefficient can be represented as D_s ≈ D^hop + D^id, with the calculated values characterized by the dynamical crossover at T ≈ T_c from D ≈ D^id to D^hop·D^id, characterizing the kinetic glass transition (the first step of the DA) must vanish at T_c/T = 1 with a power law D^id ~ |T − T_c|^γ just reflecting the predictions by the idealized theory. Hence, the dynamical behavior of the supercooled liquid for T < T_c, towards T_g (and below it) is dominated by the hopping process with only one energy barrier (the second DA step).

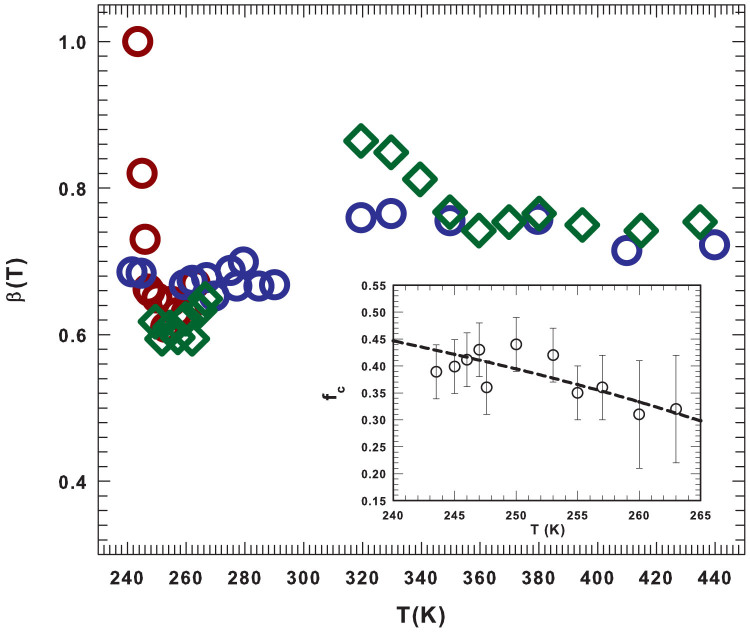
Before discussing the relaxation times we measured, we consider, in Figure 2, the obtained non-ergodicity factor f_c and the stretched exponent β_S by comparing, in the frame of the MCT, our results with the previous ones obtained for OTP. We aim to stress that the overall behavior of these quantities (new and early reported data) is fully coherent with the theory.

Figure 2. The OTP non-ergodicity factor f_c (inset) and the stretched exponent β_S obtained from the correlators and compared with the previous one obtained in the MCT frame.

The Debye-Waller factor f_c is reported for different temperatures in the range 243 < T < 263 K. The dashed line represents the MCT scaling law prediction, as the temperature decreases below T_B: f_c ~ |T_B − T|^1/2. Together with actual data for β_S (dark red circles) the figure reports the values of the stretched exponent measured in previous experiments: PCS (open green diamonds³⁶) and TFPI/DM (blue circles³⁵).

The inset of Figure 2 illustrates the f_c behavior for different temperatures in the range 243 < T < 263 K. We found that f_c has a value of about 0.4 and appears to be T–dependent; these behaviors in the same T-range have also been observed in other literature³⁶. The MCT predicts that this parameter increases, as the temperature decreases for T < T_B, according to |T_B − T|^1/2. The data reported in the figure appear to agree with such scaling law (dashed line) although the reported data are far from T_B and the experimental error is fairly large in order to draw a definitive conclusion on this respect. However, there is, near T_g, a sudden slowing down in which f_c becomes T-independent. This result agrees with the main findings of a recent neutron scattering experiment on a “strong” molecular glass forming system⁴⁹.

Finally we consider the T–dependence of β_S. In Figure 2 we plot the data of the stretched exponent measured in the actual study together with data coming from previous experiments. In the T range studied we report our data (dark red circles), PCS data (open green diamonds³⁶) and TFPI/DM data (blue circles³⁵); and for comparison data measured well above T_B, in the range T > 320 K are also reported. As it can be observed there is a difference in the measured average values above and below the crossover: for 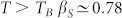whereas for T < T_B we have 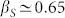. According to the other reported experimental data, the behavior is consistent with the MCT time-temperature superposition principle², no temperature dependence in this stretching parameter is observed above T_B. Below the dynamical crossover the situation is different, data coming out from the present and the two mentioned PCS experiments seem to have comparable and constant behavior by decreasing T up to about 250 K; below it and on approaching T_g our data are instead characterized by a marked increase towards 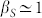, indicating the recovering of a single exponential temporal behavior. Such a situation (if confirmed) seems to indicate that the relaxation time decays also have to obey to the same precise two-stage activation process indicated by the T- behavior of transport parameters, in a way fully consistent with the hopping process of the EMCT.

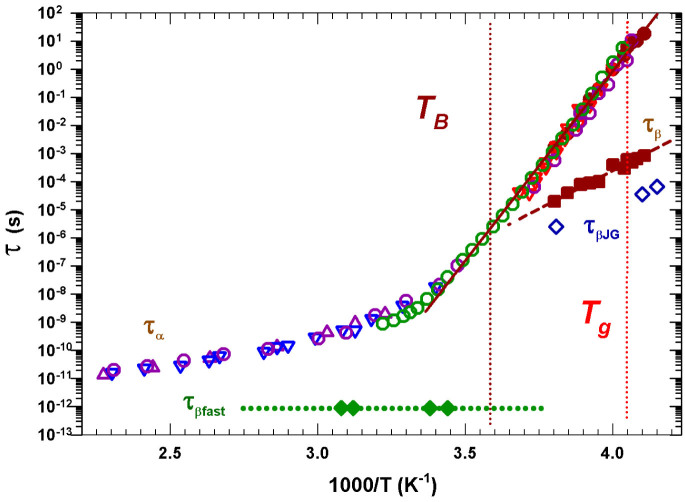
Figure 3 reports τ_α and τ_β obtained in our experiments (dark red full circles and squares, respectively) and compared with the literature data coming out from several experiments like dielectric relaxation (DE - green circles⁴¹,⁴²), PCS (reversed red triangles⁵⁰), depolarized light scattering from the measurement of the Raileigh-Wing contribution (DLS - dark pink circles³⁸) and the combination of a tandem Fabry-Perot interferometer with a double monochromator (TFPI/DM - dark pink triangles and reversed blue triangles³⁵). Figure 3 also reports both the Johari Goldstein (JGR) relaxation (τ_βJG) as blue open diamonds and the fast one (τ_βfast) as green closed diamonds, respectively measured by means of DE²⁰ and neutron scattering⁵¹. Our data measured in the range 263 > T > 243 K show these behaviors: 1) a general agreement is observable in τ_α(T) (dark red full circles) in the large temperature range reported in the figure, although collected data come out from different studies; within statistical errors data are mutually consistent and the dynamical crossover at T_B can be easily observed; 2) a bifurcation from the α process appears close to T_B, (at the relaxation time of ~ 10⁻⁷ sec) where τ_β (dark red full squares) has its onset showing an Arrhenius T-dependence that persists also inside the glass state. Some experimental points of the cage relaxation time τ_βfast, are reported as reference. It has been measured in the OTP by means of neutron scattering⁵¹ and has an order of magnitude of 10⁻¹² sec. In the actual study, the window of the used experimental time allows only the τ_βJG measurement.

Figure 3. The OTP τ_α and τ_β here measured (dark red full symbols), compared with literature data: dielectric relaxation (DE - green circles⁴¹,⁴²), PCS (reversed red triangles⁵⁰), DLS from the measurement of the Raileigh-Wing contribution (dark pink circles³⁸) and the combination of a tandem Fabry-Perot interferometer with a double monochromator (TFPI/DM - dark pink triangles and reversed blue triangles³⁵).

The figure also reports both the Johary Goldstein (JGR) relaxation (τ_βJG) as blue open diamonds and the fast one (the τ_βfast order of magnitude is of 10⁻¹² sec) as green closed diamonds, respectively measured by means of DE²⁰ and neutron scattering⁵¹. Our data measured in the range 263 > T > 243 K show that a bifurcation from the α process occurs close to T_B (at the relaxation time of ~ 10⁻⁷ sec), where τ_β has its onset with an Arrhenius T-dependence that persists also inside the glass state.

From Figure 3 one can also observe that τ_β and τ_βJG, measured by means of the DE technique (the most used to observe such a relaxation) have a similar temperature behavior, although there is a difference in the two relaxation times of about one order of magnitude. Both τ_β and τ_βJG are however, localized in the time interval 10⁻⁶–10⁻³ sec in the temperature region between T_B and T_g. This suggests that the measured τ_β may represent just the JGR, a molecular process, that is supposedly to be an universal feature in glassy dynamics with strong connections to the structural α-relaxation in all glass formers⁵². On this aspect, there is a certain experimental evidence that this latter bears nontrivial connections in dynamic and thermodynamic properties to the structural α–process. A satisfactory proof of this was obtained, by using the NMR spectroscopic technique, for some glass former liquids (including the OTP) by showing that these two relaxations are correlated⁵³.

In the DE spectra the JGR appears as a peak if it is resolved, but manifests itself as an excess wing on the high frequency flank of the primary relaxation when not resolved⁵². However, in spite of the invoked ubiquity, and on the different experimental techniques used, there are some small molecular glass formers that give no evidence of such a phenomenon. Possible reasons of this can be the instrumental resolution for the thermodynamical conditions (e.g. proper pressure and temperature value) or for the secondary relaxation that is sandwiched between the more intense α- and a faster secondary γ-relaxation (local and non-cooperative, characterized by a very fast dynamics) (see e.g. the references reported in ref. 52).

Eq. 1 explains why the observed secondary relaxation may be the JGR; as previously mentioned the function 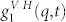measures the dynamical correlations in both orientation and position between all pairs of molecules. Whereas the corresponding translational mutual diffusion is reflected in the α–process, the roto-translational coupling gives rise to the JG contribution. In principle the 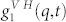contains all the possible molecular dynamics and, depending on the probe used and under special experimental conditions, can be separately measured. In other words these modes, characterized by characteristic dynamics covering wide temporal (and frequency) intervals can be selected by the proper choice of the experimental window. Our choice to probe the system, only in the temperature region below T_B (where there is a slowing down in the system dynamics) in the temporal window from 2 × 10⁻⁴ to 100 sec, where both the principal α– and of the JG relaxations have been previously measured with different techniques, gives us the possibility to observe and detail with the PCS this latter one. In addition, the fact that the ensemble average, in Eq. 1, for pure fluids, cannot, in principle, be factorized in two separate modes gives us a proof that the two observed relaxations are coupled.

All the PCS data here reported for the OTP stress the significant role in the dynamical arrest of the dynamical crossover. Although all the observed processes related with the crossover temperature evidence that for many aspects T_B is more relevant than T_g⁶,¹⁹, here we have a confirmation on this that comes out from the preservation of the system ergodicity experimentally observed here and for polydisperse grafted colloids also above the MCT glass transition concentration (φ_c)¹³.

The hypothesis that molecular glass formers fluids are characterized by a cutoff mechanism suppressing the MCT divergence was originally proposed for compressible fluids⁵⁴ by means of a field-theory approach. At the same time, for the same systems the transition from an ideal MCT regime to an activated one has been experimentally demonstrated²⁹. In connection with the JGR, we have to stress that M. Goldstein recently suggestioned that the JG relaxation, like the primary α–, can involve transitions between different energy basins, and that a closer connection between this relaxation and the phenomenon of dynamic heterogeneity should be possible⁵⁵.

In recent years the viewpoint that colloids posses the property of the MCT divergence suppressions, has been a subject of special interest. It has been debated that extended MCT, in particular the one represented by an activated hopping mechanism, could be used to clarify why the ideal MCT transition can be avoided². More properly, it has been realized that the same dynamical events cut off the idealized mode-coupling transition in all the systems characterized by different statistics: stochastic, Newtonian and Brownian⁵⁶,⁵⁷, suggesting that the same behavior must hold true for molecular and colloidal systems. i.e., for all of them the supercooled liquid dynamics takes place in the two-steps above described: the kinetic glass transition that ends at T_c and an activated hopping process below this latter temperature. In all cases, on approaching T_c from T_M, the idealized MCT provides a good description of this transition, i) the relaxation time shows a power law temperature dependence with an exponent that is close to that predicted and the behavior of the measured non-ergodicity parameter agrees well with that proposed by the theory.

We must stress that from these studies emerge that the kinetic glass transition does not coincide with the ergodicity-breaking and the ergodicity is maintained by varying the concentration, also in the activated hopping region. According to these mentioned studies on the MCT frame, the grafted colloids¹³ and our molecular material have identical behaviors, and the correlator g₁(q, t) remains ergodic for all the studied conditions. Hence, the MCT transition is generally avoided in colloidal materials, just as in molecular glass formers. However, there is a difference with the findings of previous experiments on hard colloids characterized by an evident non-ergodicity¹². In comparing the two DLS experimental results in similar systems, it is evident that the non-ergodicity of the older study can be apparent mainly due to the time window used. If observed under the same experimental conditions the recent data, in which the ergodicity is maintained also for φ > φ_c, will show the identical non-ergodicity of the previous ones. However, in both the old and the new colloid studies, there are still two substantial differences: a) the first one is essentially a hard sphere system characterized by a pure repulsive interaction, while the grafted colloid has an interaction with two contribution: a repulsive hard sphere plus an attractive tail; b) in the two experiments there is a difference in the polydispersity, of the used colloids. On this issue some comments⁵⁸,⁵⁹ to the results of ref. 13 must be considered. The first comment focuses on the physics of colloidal hard spheres above the MCT φ_c. It reports that “whatever the nature of the observed processes, in this range, they are not excluded by MCT”⁵⁸ and states that the ergodicity restoring observed in the grafted colloids study can be explained by MCT as well as by considering nonstationary processes explicitly treating different species in the particle size distribution⁶⁰. The second comment⁵⁹ instead suggests that the ergodicty observed in ref. 13 is only a polydispersity effect that shifts φ_c at higher values than that predicted by the ideal MCT; furthermore, the MCT fits well the calculated correlators and only fails to explain the final decay at the highest studied densities.

In our experiment on the OTP we have observed the Johari-Goldstein relaxation that has its onset at the dynamical crossover temperature T_B (or the MCT T_c)⁴⁰,⁶¹. We also have shown as, in the frame of the present scattering experiment, the primary, τ_α, and this latter, τ_βJG, are correlated. In any case the ergodicity is maintained in the OTP as far as in the grafted colloidal solution. Finally we stress that, in our interpretation, such as the case of OTP and the grafted colloid dynamics, studied in ref. 13, they can be driven by the FSDC, with the only difference that in this latter case, instead of T, the control parameter is the volume fraction φ. In these terms the observed apparent singularity at φ_c suggests that this concentration value is, like T_B = T_c in the OTP case, a FSDC concentration: φ_B. From the theoretical point of view, just in the MCT terms, such interpretation for attractive colloid (like the grafted) is correct², hence φ_B can separate two dynamical behavior before (φ < φ_B) and after it (φ > φ_B). In the first case the measured τ_α has to obey the MCT scaling law and in the second one a concentration activated process takes place. Such an interpretation well agrees with the main finding of the ref. 13: the first stage of the dynamical slowing down can be described by an MCT divergence at a critical volume fraction φ_c, upon further compression a crossover to another dynamical stage is observed. A definitive confirmation of this is in the observation, obtained from the measurement of the colloidal four-point dynamical susceptibility, that the process is accompanied by a similar crossover for the growth of dynamical correlations¹³.

In conclusion, we report a set of new dynamical relaxation measurement results in the supercooled OTP, above and below the calorimetric glass transition temperature T_g, that firmly establishes the absolute relevance of the dynamical crossover temperature T_B in the dynamics and thermodynamics of the dynamical arrest phenomenon. The comparison of these data with the main findings of the recent study on grafted colloids¹³ highlights that molecular and colloidal systems behave, on this respect, at the same way. This is another support to the idea that T_B plays an essential role for the understanding of the dynamical arrest process in glassy liquids.

Methods

In order to study the OTP dynamics below T_B we use a special PCS experimental setup for light scattering working in both the heterodyne and homodyne detection mode. In the first case with the modulation of the reference beam through a controlled optical delay of amplitude and frequency, the frequency resolution is improved. The setup, that works in the I_{V H} depolarized scattering geometry (DLS) is specially designed to explore the slow relaxation processes of supercooled glass-forming systems in the sub-Hertz frequency domain⁶². The system measures directly, at a given wave-vector q, the scattered power spectral density (PSD), S(q, ω), proportional to the squared modulus of the Fourier transform of the scattered electric field normalized autocorrelation function, 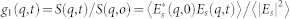. The reference beam modulation allows the separation in the PSD, at the modulation frequency, of the scattering signal from the unwanted zero-frequency contributions.

The advantage of this detection mode is that it gives g₁(q, t) independently of the statistics of the scattered field, on the contrary of the homodyne mode that gives the intensity correlation function g₂(q, t) = 〈I(q, 0)I(q, t)〉/〈I〉², related to g₁(q, t) through the Siegert's relation g₂(q, t) = 1 + |g₁(q, t)|², only valid for Gaussian statistics.

The general layout of the experimental setup, used at a scattering angle ϑ_s = 90° (|q| = 4πn/λ₀sen(ϑ_s/2) being n the system refractive index and λ₀ the vacuum light wavelength), is detailed in ref. 62. The laser light, of a HeNe laser with 10 mW power, linearly polarized orthogonal to the scattering plane, is separated into two beams (by a beam splitter transmitting 97%): one is focused into the sample cell, while the other beam was used as local oscillator. In order to ensure the g₁(q, t) measure, the intensity of this latter is adjusted to be one order of magnitude greater than that of the scattered one. An analyzer selects the scattered beam polarization in the V H geometry. Optical collection is obtained by a unimode optical fiber with a proper geometry in order to have a single coherence area and hence the maximum of the optical beating. The photoncounts are sampled and stored in a data buffer to obtain the power spectral density from the squared modulus of the Fourier transform of the sampled data. The Fourier transform calculation is performed in real time with a sampling frequency that can go up to 50 kHz with a maximum of 2²² times and averaging for more than 1.4·10⁴ sec. The stored data can be used to calculate directly the |g₁(q, t)|².The apparatus was optically tested by using a water solution of colloidal particles obtaining a spectral resolution lower than 0.03 Hz.

We have focused our interest in the OTP dynamics only for T < T_B also below T_g, more precisely in the range 263–243 K, by maintaining a thermal stability of 0.02 K by two sets of separate experiments (ϑ_s = 90°). A first set of experiments was devoted to explore by means of separate measurements of g₁(q, t) and g₂(q, t) the validity of the Siegert's relation in a large part of the T region of interest up to 250 K (i.e. ~ 35 K below T_B and some degrees, near T_g). We observe that for a typical overall experimental time of about 2 hours the system has for these correlation functions a Gaussian statistics. Because at the lowest temperatures very long experimental times (averaging times) are necessary and in order to improve the signal/noise ratio we have considered to work only in the homodyne mode (for the experiments in the interval 250 to 243 K the averaging time was doubled up to more than 1.4·10⁴ sec).

Author Contributions

N.L., V.V. and N.M. carried out the PCS measurements. F.M., C.C., V.V. and N.M. performed data analysis. F.M., N.M. and S.H.C. supervised the research project. All authors discussed the results and reviewed this manuscript.