A review of statistical methods for testing genetic anticipation: looking for an answer in Lynch syndrome

Abstract

Anticipation, manifested through decreasing age of onset or increased severity in successive generations, has been noted in several genetic diseases. Statistical methods for genetic anticipation range from a simple use of the paired t-test for age of onset restricted to affected parent-child pairs, to a recently proposed random effects model which includes extended pedigree data and unaffected family members [Larsen et al., 2009]. A naive use of the paired t-test is biased for the simple reason that age of onset has to be less than the age at ascertainment (interview) for both affected parent and child, and this right truncation effect is more pronounced in children than in parents. In this paper, we first review different statistical methods for testing genetic anticipation in affected parent-child pairs that address the issue of bias due to right truncation. Using affected parent-child pair data, we compare the paired t-test with the parametric conditional maximum likelihood approach of Huang and Vieland [1997] and the nonparametric approach of Rabinowitz and Yang [1999] in terms of Type I error and power under various simulation settings and departures from the modeling assumptions. We especially investigate the issue of multiplex ascertainment and its effect on the different methods. We then focus on exploring genetic anticipation in Lynch syndrome and analyze new data on age of onset in affected parent-child pairs from families seen at the University of Michigan Cancer Genetics clinic with a mutation in one of the three main mismatch repair (MMR) genes. In contrast to the clinic-based population, we re-analyze data on a population-based Lynch syndrome cohort, derived from the Danish HNPCC-register. Both datasets indicate evidence of genetic anticipation in Lynch syndrome. We then expand our review to incorporate recently proposed statistical methods that consider family instead of affected pairs as the sampling unit. These prospective censored regression models offer additional flexibility to incorporate unaffected family members, familial correlation and other covariates into the analysis. An expanded dataset from the Danish HNPCC-register is analyzed by these alternative set of methods.

1 Introduction

Genetic anticipation is a term that refers to an earlier age of onset or increased disease severity in successive generations. Trinucleotide repeat expansions are a well-known explanation of this phenomenon in some Mendelian disorders, though alternative mechanistic explanations have also been suggested [La Spada, 1997, Fraser, 1997]. While investigating anticipation and assessing the findings of a study, one has to be cautious about multiple sources of biases that can affect the results and the choice of appropriate statistical techniques. The “naive” approach to test for anticipation is a paired t-test comparing the difference in mean ages of onset of affected children and affected parents. Unfortunately, as demonstrated by Heiman et al. [1996], truncation bias occurs with older generations having longer follow-up time and later generations not being followed throughout the entire “at-risk” period. This can dramatically increase the type I error of a t-test. A nonparametric alternative, like the matched-pairs signed-rank Wilcoxon test, is another potential choice but is still subject to the same truncation bias [Westphalen et al., 2005]. A sensible but crude way to minimize truncation bias is to limit the analysis to older birth cohorts (e.g., with affected parents and children both born before 1920) [Westphalen et al., 2005, Picco et al., 2001, Nilbert et al., 2009], which allows adequate follow-up time for both generations. But this entails a loss of sample size and consequently a loss of power for detecting anticipation effects. This restriction does not make full utilization of the data available in many newer cohorts.

Apart from truncation bias, other factors that could influence findings on genetic anticipation are secular trends, such as a change in diagnostic techniques or reporting protocols, or the introduction of new environmental toxicants/carcinogens that could affect specific birth cohorts. Also prevalent is ascertainment bias where findings are derived from multiplex families ascertained for genetic studies. Such families are enriched with early-onset cases and preferentially selected due to the presence of multiply affected individuals, as opposed to a population-based sample of affected parent-child pairs.

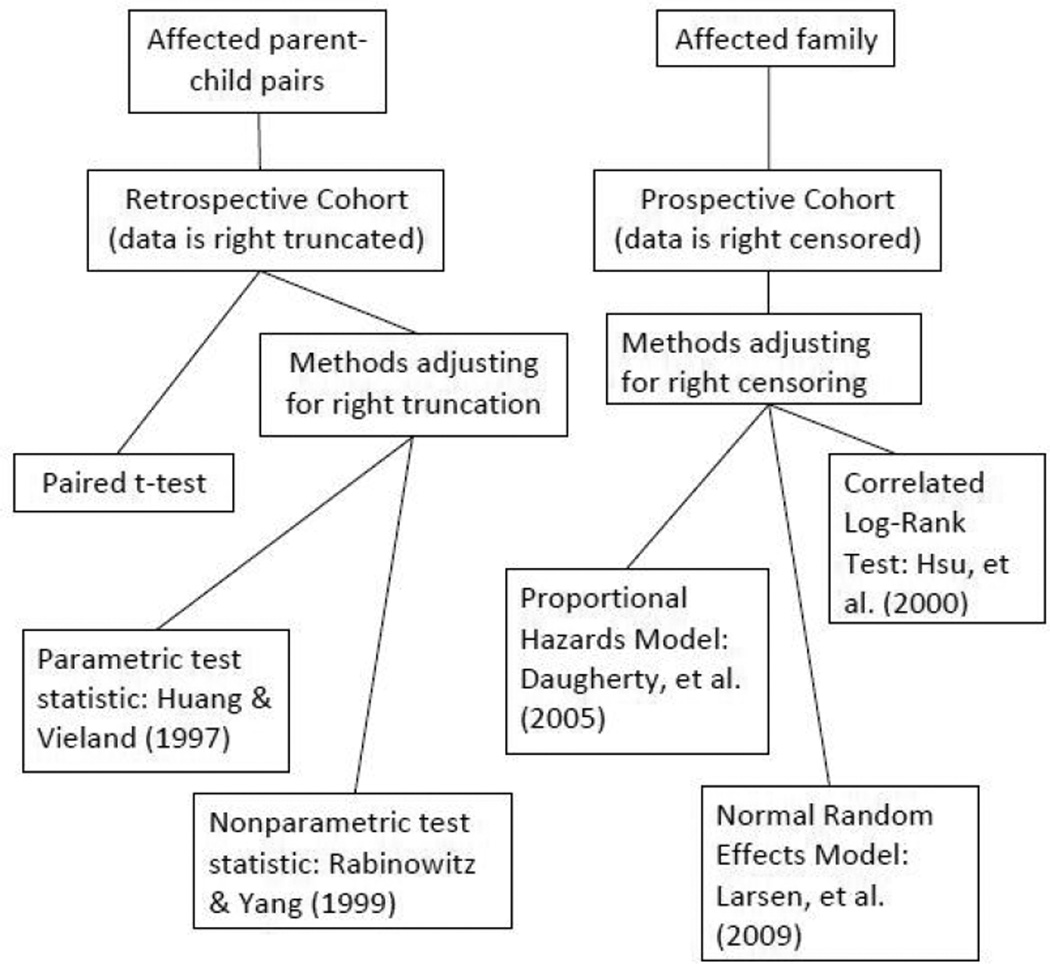
The objective of this paper is twofold. We first review an array of statistical approaches to evaluate genetic anticipation as measured by differences in age of onset in successive generations. The primary study design we consider is that which samples affected parent-child pairs from existing cohorts. To this end, we present simulation results that compare the naive paired t-test with parametric and nonparametric approaches that account for bias due to right truncation [Huang and Vieland, 1997, Rabinowitz and Yang, 1999]. We present comparison of these methods under random ascertainment as well as multiplex ascertainment and summarize recommendations in terms of adopting these methods for a given analysis. We then consider another study design which includes all at-risk family members in a predefined cohort (affected and unaffected) and follows them prospectively. The variable of interest is age of diagnosis and we review survival methods to evaluate risk by relative type [Daugherty et al., 2005, Larsen et al., 2009]. Censoring events are age at death, age at last follow-up visit or censored at age 85 years. Here, missing data is not right truncated but right censored, which is accounted for in the survival regression models. Figure A.1 in the Appendix gives a simple schematic representation of the two different sampling strategies and the corresponding statistical methods with references.

Figure A.1.

A schematic classification of statistical methods for testing genetic anticipation with corresponding references.

We then turn our attention to assess evidence of anticipation in hereditary nonpolyposis colorectal cancer (HNPCC)/Lynch syndrome in two family cohorts potentially representing two distinct sets of multiplex ascertainment probabilities. One is a population-based cohort of all Danish families identified with pathogenic mutations in the mismatch repair (MMR) gene. Nilbert et al. [2009] reported evidence of anticipation in this cohort. The other is an aggregation of families seen at the genetic counseling clinic at the University of Michigan Comprehensive Cancer Center (UMCCC), with identified mutations in the MMR gene. The UMCCC data has not been previously analyzed for anticipation and is a clinical setting where multiplex ascertainment could influence the findings. The few studies prior to the one by Nilbert et al. [2009] have reached contradictory results on anticipation in Lynch syndrome [Tsai et al., 1997, Westphalen et al., 2005, Stella et al., 2007]. Our results shed light on the existing body of literature on anticipation in Lynch syndrome and the dependence of the inference on the choice of statistical techniques. For illustration purposes, we also employ the second class of survival regression methods described above to analyze data from an expanded cohort of the Danish HNPCC (Lynch syndrome) register which evaluates age-at-onset times for proven MMR mutation carriers (affected/unaffected by a cancer associated with Lynch syndrome). This enables us to contrast this study design and the appropriate statistical methods with the ones involving affected parent-child pairs. The paper thus presents a comprehensive overview of statistical design and analytic tools to evaluate genetic anticipation and contributes new data to the assessment of anticipation in Lynch syndrome families.

The rest of the paper is organized as follows. In Section 2, we restrict our attention to the most common format of data on affected parent-child pairs and discuss statistical methods to handle the right truncation bias. Section 2.1 presents simulation results comparing existing choices within this class of methods in the absence and presence of familial ascertainment. Section 2.2 analyzes data on two Lynch syndrome cohorts using affected parent-child pairs. Section 3 discusses the second class of statistical models that considers all at-risk affected and unaffected family members and employs a prospective censored regression model. Section 3.1 analyzes expanded family data from the Danish HNPCC-register with this second class of methods. The concluding section is subdivided into two subsections to emphasize the two major contributions of the paper. Section 4.1 presents an integrated overview of the different statistical approaches, putting them in the perspective of different sampling mechanisms and study designs and furnishing a recommendation for a research investigator. Section 4.2 then summarizes the data analysis results on genetic anticipation in Lynch syndrome, findings which still conflict across studies and demonstrate a poorly understood phenomenon from a biological perspective. [Vasen et al., 1994, Rodríguez-Bigas et al., 1996, Tsai et al., 1997, Westphalen et al., 2005, Nilbert et al., 2009, Larsen et al., 2009].

2 Methods for affected parent-child pairs

Let (T_Pi, T_Ci) be the ages of onset and (C_Pi, C_Ci) the ages at ascertainment or ages at interview of the ith parent and child, respectively. While there is no real physical constraint to the relationship between (T_Pi, T_Ci) and (C_Pi, C_Ci), we only observe those pairs which satisfy the condition

$$\{C_{P_i}>T_{P_i},C_{C_i}>T_{C_i}\}.$$ (1)

These are the pairs that can be recognized as “affected” at the time of retrospective assessment of the cohort. Let the term “parent-child pair” hereafter refer to any pair which satisfies (1). As mentioned before, comparing the sample means of T_P and T_C via the paired t-test ignores that the data are conditionally observed given (1) and thus leads to biased inference if follow-up times for the cohort are not sufficiently long. Huang and Vieland [1997] consider a conditional likelihood reflecting (1) and propose a parametric Wald-type test for this problem. Their method assumes a joint bivariate normal distribution for (T_Pi, T_Ci) and is based on the asymptotic normality of the conditional maximum likelihood estimate (MLE). Using the work of Huang and Vieland [1997] and Vieland and Huang [1998], we briefly review the construction of the likelihood.

Assume that (T_Pi, T_Ci) and (C_Pi, C_Ci) are conditionally independent given (1). Let f, F denote the joint probability distribution function (PDF) and cumulative distribution function (CDF) corresponding to (T_Pi, T_Ci), and g, G denote the joint PDF and CDF of (C_Pi, C_Ci). The conditional likelihood of the i-th parent-child pair is given by,

$$L_i=\frac{f(t_{p_i},t_{c_i})g(c_{p_i},c_{c_i})}{\text{Pr}(T_{P_i}\le C_{P_i},T_{C_i}\le C_{C_i})}1[t_{p_i}\le c_{p_i},t_{c_i}\le c_{c_i}].$$

Here 1[A] is the indicator function which assumes the value 1 if event A is true, and is zero otherwise. When g is left unconstrained (that is, when its governing parameters are not constrained to be the same as those of f), Huang and Vieland [1997] show that the likelihood is proportional to

$$L_i\propto \frac{f(t_{p_i},t_{c_i})}{F(c_{p_i},c_{c_i})}.$$ (2)

That is, as long as g is estimated nonparametrically, maximizing $L={\prod }_{i=1}^n{L}_i$ is equivalent to maximizing the conditional log-likelihood $\text{log}(L)={\sum }_{i=1}^n\text{log}\frac{f(t_{p_i},t_{c_i})}{F(c_{p_i},c_{c_i})}$. We consider three test statistics which invoke the general form of this likelihood.

1. The parametric test statistic (HV)

[Huang and Vieland, 1997]: HV assumes that f is a bivariate normal distribution and maximizes log(L) with respect to the mean vector and covariance matrix of the distribution. Anticipation exists when the difference in the means of the parents and the children is greater than zero. An estimate of this effect is obtained by evaluating the difference of the MLEs, µ̂_TP – μ̂_TC, with proper standard errors being estimated from the inverse of the observed Fisher information matrix. Wald-type test statistics are then constructed, which are standard normal under the null hypothesis of no anticipation. The HV approach can be thought of as an adjustment to the t-test for right truncation, both methods assuming normality.

2. An alternative nonparametric test statistic (RY1)

[Rabinowitz and Yang, 1999]: RY1 uses the quadruples (T_Pi, T_Ci, C_Pi, C_Ci) to test the null hypothesis that F is symmetric, without assuming a particular form of the distribution F. RY1 is based on all parent-child pairs for which max(T_Pi, T_Ci) ≤ min(C_Pi, C_Ci). This eliminates the bias due to truncation because every pair which satisfies the condition will be observed. Hence,

$$\text{Pr}(T_{C_i}\le T_{P_i}|\text{max}(T_{P_i},T_{C_i})\le \text{min}(C_{P_i},C_{C_i}))=1/2,$$

under the null hypothesis of no anticipation. For n parent-child pairs, the statistic

$$\sum _{i=1}^n(1[T_{C_i}<T_{P_i}]-1/2)1[\text{max}(T_{P_i},T_{C_i})\le \text{min}(C_{P_i},C_{C_i})]$$ (3)

is approximately normal with mean 0 and variance ${\sum }_{i=1}^{n}1[\text{max}(T_{P_i},T_{C_i})\le \text{min}(C_{p_i},C_{C_i})]/4$. RY1 can be thought of as a modification to theWilcoxon signed-rank test in the presence of right truncation.

3. A second nonparametric test statistic (RY2)

[Rabinowitz and Yang, 1999]: RY2 compares parents and children across different pairs. For any i₁, i₂, the following holds, assuming no anticipation:

$$\text{Pr}(T_{C_{i_1}}\le T_{P_{i_2}}|\text{max}(T_{C_{i_1}},T_{P_{i_2}})<\text{min}(C_{C_{i_1}},C_{P_{i_2}}),\text{max}(T_{P_{i_1}},T_{C_{i_2}})<\text{min}(C_{P_{i_1}},C_{C_{i_2}}))=1/2.$$

The estimator sums over all pairwise comparisons where the event happens and compares it 1/2:

$$\sum _{i_1=1}^n\sum _{i_2=1}^n(1[T_{C_{i_1}}<T_{P_{i_2}}]-1/2)1[A],$$

where

$$A=\{\text{max}(T_{C_{i_1}},T_{P_{i_2}})<\text{min}(C_{C_{i_1}},C_{P_{i_2}});\text{max}(T_{P_{i_1}},T_{C_{i_2}})<\text{min}(C_{P_{i_1}},C_{C_{i_2}})\}.$$

.

This statistic will also have mean 0 under the null hypothesis with variance expression provided in [Rabinowitz and Yang, 1999].

Remark 1

The efficiency loss of RY1 comes via a reduction of sample size, as the conditioning event which eliminates the bias due to truncation will also eliminate data and restrict inference to a smaller subset (see Section 4.1 for a further discussion of this issue). The extent of this reduction in sample size will depend on how severe the truncation is. RY2 attempts to compensate for this loss of data by making comparisons between parent-child pairs. When this between-pair comparison is justifiable, i.e., when the parent-child pairs are exchangeable, this will increase the effective sample size and, consequently, the power of the test.

Remark 2

In a more recent report, Tsai et al. [2005] propose a generalized paired t-test and a Wilcoxon signed-rank test that very similar in spirit to RY1: they restrict analysis to comparable parent-child pairs which satisfy max(T_Pi, T_Ci) ≤ min(C_Pi, C_Ci) and apply the standard paired t-test and Wilcoxon signed-rank test to this subset. Due to its similarity to RY1, we refrain from including this as a separate method for comparison purposes. One contribution of Tsai et al. [2005] is to extend the generalized t-test to a random effects model that incorporates family level correlation and introduce a general mixed model framework to test for a difference in mean ages of onset across generations; this is more robust and general than a t-test.

2.1 Simulation Study

Our simulation study was designed to compare the performance of the above three test statistics (HV, RY1, and RY2) with the paired t-test under three different ascertainment schema described below. Note that these methods only use data from affected parent-child pairs. Previously, Vieland and Huang [1998] provided an extensive discussion on the effect of the ascertainment scheme on the behavior of HV in terms of Type I error and power but so far no such simulation results are available for the nonparametric methods RY1 and RY2 under varying selection mechanisms. Also, even for an unbiased random ascertainment, there does not exist any simulation study directly comparing HV, RY1 and RY2 simultaneously in terms of power and Type I error. We first describe the simulation design under each ascertainment scheme and then summarize our simulation findings.

1. Random Ascertainment (RA)

RA draws a simple random sample of parent-child pairs from the population of eligible pairs. That is, every parent-child pair for which both individuals have developed the disease at time of ascertainment has an equal probability of selection, regardless of the size of the pedigree. Simulation of RA is straightforward. The ages of onset, (T_P, T_C), are assumed to be bivariate normal. (C_P, C_C), the pair of ascertainment ages, is assigned to (c₁, c₂), where c₁ is a continuous uniform random variable, and c₂ = c₁ – d₁, where d₁ is also a continuous random variable with parameters such that c₂ is guaranteed to be positive. Sample parent-child pairs are randomly drawn in this manner, and those which satisfy condition (1) are included in the simulated dataset until n such pairs have been selected.

2. Generalized Single Ascertainment (GSA)

[Hodge and Vieland, 1996]: GSA samples entire pedigrees and, within a pedigree, randomly selects a single parent-child pair. A crucial component of this scheme is that the selection probability of a pedigree is strictly proportional to the number of parentchild pairs it contains. Hodge and Vieland [1996] prove, and Vieland and Huang [1998] confirm by example, that if pairs are ascertained with probability proportional to the number of parent-child pairs in the pedigree, then the correct likelihood is proportional to the conditional likelihood given the truncation. This shows that whether the data come from a true random sample of all possible parent-child pairs (an unlikely situation) or from GSA, maximizing the conditional likelihood is valid and will yield unbiased estimates.

To simulate GSA, we follow the prescribed methods in Appendix B of Vieland and Huang [1998] to generate simple pedigrees. Three ages at ascertainment are drawn (c₁, c₂, c₃), representing a grandparentparent-child triad. As described in RA, c₁ is a continuous uniform random variable, c₂ = c₁ – d₁, and c₃ = c₁ – d₁ – d₂, where d₁ and d₂ are also continuous uniform random variables with parameters such that c₂ and c₃ are guaranteed to be positive. One of the two possible parent-child pairs (either (c₁, c₂) or (c₂, c₃)) is selected with equal probability and assigned to (C_P, C_C). After drawing a single random bivariate normal pair (T_P,T_C), if (1) is satisfied, the pair is included in the dataset, otherwise not. Thus those pedigrees which have two affected parent-child pairs are twice as likely to be selected as those with one pair; this is the condition which satisfies GSA. (Although (c₁, c₂) and (c₂, c₃) are selected with equal probability, the fraction of young pairs in the resulting dataset will be less than 0.5, since (c₂, c₃) will fail to satisfy (1) more often than (c₁, c₂).)

3. Multiplex Ascertainment (MA)

In MA, pedigrees with more affected parent-child pairs are ascertained with a larger probability that is not directly proportional to the number of affected parent-child pairs. Vieland and Huang [1998] argue that this results in samples with younger affected individuals: a pedigree with young affected individuals will also have many affected individuals, since the disease tends to present earlier in that pedigree. Thus a sampling scheme which preferentially selects pedigrees with multiply affected individuals will have the byproduct of having selected many young pairs. This will artificially create a difference in mean ages of onset between the parent and the child, even if there is none. This artificial difference is in addition to that created by the truncation bias. To simulate MA, then, we “enrich” our sample with young pairs. Three ages of ascertainment are drawn, as in GSA. One of the two pairs is selected (the probability of which determines the level of “enrichment” of young pairs in the dataset), and random draws of (T_P, T_C) are made until condition (1) is satisfied.

For each of the sampling schema, our choice of distributional parameters was governed by previous simulation studies from Rabinowitz and Yang [1999] and Vieland and Huang [1998]. Under each simulation configuration, we generated 5000 simulated datasets, each with 50 parent-child pairs, and tested the null hypotheses of no genetic anticipation against a one-sided alternative that the mean age of onset in parents exceeds the mean age of onset in children. In each setting, we calculated the proportion of times the null hypothesis was rejected in 5000 replications. When data were generated under the null distribution, this proportion provided an estimate of Type I error, whereas under the alternative, it provided an empirical estimate of power.

Table 1 provides the simulation results under RA. In terms of Type I error, the most honest test is RY1, which is close to its nominal value of α = 0.05 for each set of generating parameters. HV and RY2 stay just above their nominal size, while the paired t-test fares poorly. The Type I error rate of the paired t-test depends crucially on the amount of truncation; it converges to its nominal value as the ascertainment distributions increase and the age-of-onset distributions remain fixed. This is the rationale behind restricting analysis to older birth cohorts. Under the alternative, RY1 is the most underpowered, with only about 35% of simulations able to detect a difference of 5 years under the assumption of uncorrelated ages of onset. RY2 does slightly better and HV the best. Of course, the t-test is the most powerful, which is to be expected given its high rate of false positives.

Table 1.

Estimated Type I error rates and Power (corresponding to 5000 simulations with 50 parent-child pairs per simulation) with nominal significance level α = 0.05 under Random Ascertainment for 4 test statistics. (T_P, T_C) are the respective ages of onset for the parent and child, with BVN the bivariate normal distribution with parameters (µ_p, µ_c, σ_p,σ_c ρ(T_p,T_c)). The ascertainment ages (C_P,C_C) are determined by c₁~ Unif (80, 90) and d₁ ~ Unif(20,30) as described in Section 2. Powers in bold come from tests which asymptotically fail to maintain nominal level of significance. Powers in italics come from tests which are asymptotically unbiased, but, due to small sample size, have Type I error rates significantly greater than 0.05.

(TP, TC)~	t-test	HV1	RY12	RY22
	Type I Error
BV N (55, 55, 100, 100, 0.0)	0.858	0.085	0.054	0.067
BV N (55, 55, 100, 100, 0.5)	0.562	0.069	0.048	0.062
BV N (55, 55, 100, 100, 0.7)	0.387	0.064	0.049	0.058
	Power
BV N (55, 50, 100, 100, 0.0)	0.996	0.642	0.353	0.543
BV N (55, 45, 100, 100, 0.0)	1.000	0.988	0.826	0.966
BV N (55, 50, 100, 100, 0.5)	0.999	0.912	0.673	0.853
BV N (55, 45, 100, 100, 0.5)	1.000	1.000	0.993	1.000
BV N (55, 50, 100, 100, 0.7)	1.000	0.993	0.891	0.979
BV N (55, 45, 100, 100, 0.7)	1.000	1.000	1.000	1.000

¹Huang and Vieland [1997]

²Rabinowitz and Yang [1999]

Remark 3

For all 4 tests, as the correlation between the ages of onset increases, performance improves. To understand this phenomenon, note that “large” values of T_C are the primary cause of a pair being truncated: in the first three rows of Table 1, Pr(T_C > C_C) ≈ 0.32, whereas Pr(T_P > C_P) ≈ 0.002. This truncation inflates the difference in the observed means, even when no such difference exists between the true means. When T_C is uncorrelated with T_P, knowing that a pair was ascertained does not provide much information about T_P. But, as the correlation increases, small T_C become associated with small T_P the bias from truncation decreases, and, under the null, test statistics converge to the correct asymptotic distribution faster. Under both the null and non-null scenario, presence of a positive correlation leads to increased precision for estimating the mean differences for a fixed n. The fact that HV is most sensitive (among the three asymptotically unbiased statistics HV, RY1 and RY2) to changes in ρ can be understood further by observing that the computation of HV involves calculating ρ̂, the estimated correlation between T_P and T_C, by maximizing a profile likelihood. We noted in our simulation that this estimator ρ̂ generally becomes more precise as ρ departs from the null value of zero: the estimated mean squared error of ρ̂ when ρ = 0 is 2.92 × 10⁻² but is 1.98 × 10⁻² when ρ = 0.5, providing a estimated relative efficiency of 68%. Moreover, in small samples, ρ is slightly overestimated when the true value is 0, causing the variance of the difference in mean age of onset to be underestimated and the null hypothesis of no anticipation to be rejected more often than desired. On the other hand, RY1 and RY2, which do not directly use an estimate of ρ in their calculation and are non-parametric tests, remain less affected.

Table 2 displays the estimated Type I error rates and power under GSA. As before, RY1 is consistently close to its nominal significance level, and RY2 and HV do reasonably well. The paired t-test, again, falsely rejects the null many more times than its nominal size suggests. Power rankings are also as before, with RY1 performing the worst and HV almost as powerful as the t-test. As was the case under RA, greater correlation decreases Type I error and increases power.

Table 2.

Estimated Type I error rates and Power (corresponding to 5000 simulations with 50 parent-child pairs per simulation) with nominal significance level α = 0.05 under Generalized Single Ascertainment for 4 test statistics. (T_P,T_C) are the respective ages of onset for the parent and child, with BVN the bivariate normal distribution with parameters (µ_pµ_c,σ_p,σ_c,ρ(T_p,T_c)). The ascertainment ages (C_P,C_C) are determined by c₁ ~ Unif (80, 90) and d₁, d₂ ~ Unif(20,30) as described in Section 2. Powers in bold come from tests which asymptotically fail to maintain nominal level of significance. Powers in italics come from tests which are asymptotically unbiased, but, due to small sample size, have Type I error rates significantly greater than 0.05.

(TP, TC)~	t-test	HV1	RY12	RY22
	Type I Error
BV N(55, 55, 100, 100, 0.0)	0.906	0.078	0.051	0.065
BV N(55, 55, 100, 100, 0.5)	0.653	0.049	0.051	0.063
BV N(55, 55, 100, 100, 0.7)	0.444	0.044	0.050	0.055
	Power
BV N(55, 50, 100, 100, 0.0)	0.994	0.635	0.330	0.521
BV N(55, 45, 100, 100, 0.0)	1.000	0.988	0.778	0.951
BV N(55, 50, 100, 100, 0.5)	1.000	0.799	0.633	0.834
BV N(55, 45, 100, 100, 0.5)	1.000	0.997	0.984	1.000
BV N(55, 50, 100, 100, 0.7)	1.000	0.931	0.854	0.968
BV N(55, 45, 100, 100, 0.7)	1.000	0.997	0.999	1.000

¹Huang and Vieland [1997]

²Rabinowitz and Yang [1999]

Table 3 simulates multiplex ascertainment, varying the level of enrichment of young pairs for a fixed set of generating distributions. As before, RY1 commits the expected number of Type I errors. The paired t-test performs very poorly, rejecting the null hypothesis with probability 1 for sufficient levels of enrichment. The number of false positives HV yields increases with increasing enrichment. Unlike the prior ascertainment schema, this inflation cannot be solely attributed to small sample sizes; as shown by Vieland and Huang [1998], the method does incur inflated Type I error under multiplex ascertainment. Besides the t-test, HV is the most powerful test statistic. Both the nonparametric test statistics lose power precipitously with increasing enrichment. In this setting, since the t-test and HV do not maintain nominal Type I error, we present two combined measures of precision, the accuracy (ACC) and positive predictive value (PPV), defined as

$$\text{ACC}=\frac{1-\text{Type I error}+\text{Power}}{2},\text{PPV}=\frac{\text{Power}}{\text{Power}+\text{Type I Error}}.$$

Table 3.

Estimated Type I error rates, Power, Accuracy and Positive Predictive Value (corresponding to 5000 simulations with 50 parent-child pairs per simulation) with nominal significance level α = 0.05 under Multiplex Ascertainment for 4 test statistics. ‘Percent Young’ is the level of enrichment of young pairs. For all rows, the ages of onset for the parent and child are generated from (T_P, T_C) ~ BVN (55, 55,100,100,0) (Type I Error) or BVN (55,45,100,100,0.0) (Power). The parameters associated with the ascertainment distributions are c₁ and (d₁, d₂) as described in Section 2, with c₁ ~ Unif(80,90), and d₁, d₂ ~ Unif(20, 30). Powers in bold come from tests which asymptotically fail to maintain nominal level of significance. Powers in italics come from tests which are asymptotically unbiased, but, due to small sample size, have Type I error rates significantly greater than 0.05.

Percent Young	t-test	HV1	RY12	RY22	t-test	HV1	RY12	RY22
	Type I Error				Power
0.1	0.975	0.066	0.049	0.061	1.000	0.989	0.776	0.953
0.3	0.999	0.060	0.046	0.064	1.000	0.973	0.685	0.900
0.5	1.000	0.068	0.052	0.068	1.000	0.926	0.563	0.796
0.7	1.000	0.102	0.048	0.053	1.000	0.848	0.391	0.536
0.9	1.000	0.160	0.052	0.020	1.000	0.745	0.201	0.079
	Accuracy				Positive Predictive Value
0.1	0.513	0.962	0.864	0.946	0.506	0.937	0.941	0.940
0.3	0.501	0.957	0.820	0.918	0.500	0.942	0.937	0.934
0.5	0.500	0.929	0.756	0.864	0.500	0.932	0.915	0.921
0.7	0.500	0.873	0.672	0.742	0.500	0.893	0.891	0.910
0.9	0.500	0.796	0.575	0.523	0.500	0.823	0.794	0.798

¹Huang and Vieland [1997]

²Rabinowitz and Yang [1999]

Note that here the ACC and PPV measures are used not in the sense of a diagnostic test but rather as a combined metric of Power and Type I error, just as mean squared error is a combined measure of bias and variance in the context of estimation. For example, these measures have recently been used to assess properties of statistical tests for genetic association which do not strictly maintain Type I error level in the context of combining individual and family-based studies [Mirea et al., 2010]. All three test statistics, HV, RY1, and RY2, outperform the paired t-test in terms of these metrics. HV performs best for all levels of enrichment; its strength is most evident in terms of its accuracy for high levels of enrichment. The loss of power is not nearly as dramatic as for the nonparametric tests, and this outweighs its increase in Type I error. Between RY1 and RY2, RY2 would be preferred in terms of both metrics.

Remark 4

In Tables 1–3, we noted that HV has the highest power, while the nonparametric tests, RY1 and RY2, lack power in spite of adhering to nominal Type I error rates under a wide spectrum of scenarios. Recall that in all these simulation settings we generated the age-of-onset distribution from a bivariate normal distribution. Thus the parametric modeling assumption of HV was exactly satisfied by the generated data. To assess the sensitivity of HV in terms of model misspecification, we generated ages of onset from a bimodal distribution, governed by a two component mixture of Normals (results not shown). Under this setting, HV has slightly inflated error rates compared to the more robust RY statistics but still retains its power advantages in most cases. This trade off between robustness and efficiency is expected in comparing any parametric method with its nonparametric counterpart.

2.2 Example: Application to Lynch syndrome data from affected parent-child pairs

In addition to the above simulation studies, we applied these methods to two cohorts of families with genetic predisposition to Lynch syndrome (previously better known as hereditary nonpolyposis colorectal cancer (HNPCC), but first known as a cancer family syndrome [Warthin, 1913], characterized by the early onset of gastrointestinal, uterine and other cancers). In 1991, the Amsterdam criteria were developed for inclusion of families in HNPCC studies to identify causal genes [Vasen et al., 1991, 1999]. The genetic basis of Lynch syndrome is germline mutation in MMR genes, with four genes known so far to be causally responsible for Lynch syndrome (hMSH2, hMLH1, hMSH6 and hPMS2). The possibility for anticipation has been suggested, sometimes by anecdotal observation or subjective observation of the data [Menko et al., 1993, Vasen et al., 1994, Rodríguez-Bigas et al., 1996] and sometimes by formal statistical analysis [Westphalen et al., 2005, Nilbert et al., 2009]. In a carefully done analysis in Tsai et al. [1997] consisting of 475 pairs selected from 308 families identified through the Hereditary Colorectal cancer registry at John Hopkins University, no evidence of anticipation was noted. However the nature and definition of our cohort is quite different from the Tsai et al. study where only 14 out of the 475 pairs were from 7 families identified with germline mutations in hMSH2 or hMLH1.

Our first dataset consisted of 74 families, each with an identified deleterious MMR mutation, seen at the genetic counseling clinic at the UMCCC. The index cases presented to the clinic between 1999 and 2009. Thus the clinic data is very likely to be subjected to multiplex ascertainment as discussed in Section 2.1. Cancers that qualified as a part of Lynch syndrome were colorectal cancer, endometrial cancer, epithelial ovarian cancer, upper urothelial cancer, gastric cancer, cancer of the small intestine, and malignant brain tumors. Out of these 74 families, 57 had at least one affected parent-child pair, leading to 181 affected parent-child pairs in the database. For patients with multiple cancers, the first was used to establish the age of onset. Due to missing age-of-onset information, some pairs were deleted from the current analysis, and the final analysis was restricted to 136 parent-child pairs with complete age-of-onset information coming from 47 MMR-positive families. The maximum number of pairs coming from a single family was 15 with an average of 3.53 pairs coming from each pedigree. The final dataset consisted of 190 individuals. The date of ascertainment was taken as the date of interview with the proband. For relatives with missing date of birth, age at ascertainment was estimated from a prediction model based on the proband/index person’s year of birth and relationship to the proband/index person. Construction of the family cancer history was based on interviews with the proband by a trained genetic counselor and cross-verified by interviews with other family members. Absence of confirmatory medical records to verify ages of onset was an obvious limitation of this cohort. We will refer to this cohort as UMLYNCH from now on.

The other dataset we considered comes from the Danish HNPCC-register on all Danish families identified with hereditary colorectal cancer from 1991 until December 2006. The Lynch syndrome cohort was defined as 151 families with pathogenic MMR gene mutations. Out of these 151 families, 92 families contained at least one affected parent-child pair. The final cohort consisted of 400 individuals making up 290 parent-child pairs. Unverifiable cancers were ignored, and, for patients with multiple cancers, the first was used to establish the age of onset. Nilbert et al. [2009] analyzed this data in a prior paper using the paired t-test and HV but did not apply the methods of Rabinowitz and Yang [1999]. We will refer to this cohort as DLYNCH from now on. In comparison to UMLYNCH, DLYNCH has more complete age-of-onset information and the advantage of having verified medical history data. From Table 4, the mean age at diagnosis for all individuals in UMLYNCH was 47.1 yrs, compared to 46.8 yrs in DLYNCH.

Table 4.

Summary of UMLYNCH and DLYNCH with numbers of individuals, mean ages of diagnosis (aod) and standard errors (SE) by cancer type and mutation status. Cancers in the ‘Other’ category include brain tumors, ovarian, rectal, cancer of the small intestine, stomach, endometrial, cancer of the ureter, and upper urothelial cancer.

		UMLYNCH		DLYNCH
		n	mean aod (SE)	n	mean aod (SE)
All Individuals		190	47.1(13.7)	400	46.8(12.3)
Cancer	·Colorectal	130	45.7(13.7)	266	46.4(13.1)
	·Other	60	50.1(13.3)	134	47.7(10.6)
Mutation	·hMSH2	27	44.9(15.3)	207	46.5(11.4)
	·hMLH1	18	42.7(11.6)	134	44.6(13.0)
	·hMSH6	1	70.0(NA)	59	52.9(12.1)
	·Unknown	144	47.8(13.5)	0
Total Pairs (n)			136		290

Remark 5

Since the objective of this article is to provide a review and comparison of existing methods, our simulation studies only considered the originally proposed test statistics (t-test, HV, RY1, RY2) and generated independent parentchild pair data with one pair per family. However, the data analysis results presented in this section are modifications of the original test statistics in the sense that they make adjustments for the correlation that may potentially exist between multiple pairs sampled from the same family, which is the case for both UMLYNCH and DLYNCH cohort. For the parametric methods (t-test and HV), we used robust sandwich estimators of the standard errors based on the score residuals summed over each family. For the nonparametric methods (RY1 and RY2) we extended the original variance formulae to accommodate between-pair correlation within the same family (assumed to be constant across families). More specifically, from the theory of U-statistics, both RY1 and RY2 can be asymptotically represented in the form ${\sum }_i^n{u}_i$ (with i indexing each pair and n being the total number of pairs) where exact expressions for u_i and the corresponding variance approximations under the independence assumption are provided in Rabinowitz and Yang [1999]. The original unadjusted variance estimates assume that Var $u_i={\sigma }_u^2$ for i = 1…, n and Cov (u_i,u_j) = 0 for i ≠ j. Thus, $\widehat{\text{Var}}{\sum }_i^n{u}_i=n{\widehat{\sigma }}_u^2$. We introduce a familial correlation structure by letting $\text{Cov}(u_i,u_j)={\rho }_u{\sigma }_u^2$ when i and j come from the same family, which implies that

$$\widehat{\text{Var}}\sum _i^n{u}_i={\widehat{\sigma }}_u^2[n+2{\widehat{\rho }}_u\sum _{k=1}^{\#\text{FAMILIES}}(\begin{array}{c}\#\text{PAIRS IN FAMILY}k\\ 2\end{array}\left)\right],$$

with the convenion that $\left(\begin{array}{c}1\\ 2\end{array}\right)=0$. This serves to adjust for the artificial increase in sample size due to incorrectly assuming between-pair independence. The estimates ${\widehat{\sigma }}_u^2$ and ρ̂_u are obtained from the empirical variance and cross-correlation of û_i, with û_i as described in Rabinowitz and Yang [1999].

Table 5 provides the correlation-adjusted version of the set of four test statistics discussed in Section 2. We first discuss the analysis that includes all pairs. The paired t-tests, even with robust standard errors, as might be expected, display high levels of significance, with observed differences in mean ages of onset of 9.89 years for UMLYNCH (P < 0.0001) and 8.72 yrs for DLYNCH (P < 0.0001). Similar evidence is obtained by RY2 (P = 0.0067 in UMLYNCH and P < 0.0001 in DLYNCH). HV gives only slight evidence of genetic anticipation in UMLYNCH (P = 0.0294) compared to DLYNCH (P < 0.0001), and RY1 applied to UMLYNCH shows no significance (P = 0.5) whereas DLYNCH shows significance (P = 0.0046). This last observation is explained by the fact that in UMLYNCH, only 62 pairs qualified in the construction of RY1, limiting the power and reliability of the analysis (as discussed in Remark 1 of Section 2). Results from DLYNCH show greater levels of significance than UMLYNCH for all the tests we considered, which is explained by the larger sample size of DLYNCH.

Table 5.

Four analytical methods¹ applied to UMLYNCH and DLYNCH. ‘Only CRC’ considers those parent-child pairs where both had colorectal cancer and, for DLYNCH, ‘MSH2’, ‘MLH1’ and ‘MSH6’ stratify by mutation type.

Subset	UMLYNCH						DLYNCH
	Difference		Test StatisticsSignificance				Difference		Test StatisticsSignificance
	pairs(n)	in means	t-test	HV2	RY13	RY23	pairs(n)	in means	t-test	HV2	RY13	RY23
Entire cohort	136	9.89	5.65***	1.89	0.00	2.47*	290	8.72	7.77***	4.10***	2.60*	4.67***
Only CRC	62	11.19	4.53***	1.82	−0.10	2.28	130	11.01	6.68***	4.25***	2.01	3.85***
MSH2							153	7.58	5.13***	2.85*	2.09	2.86*
MLH1	Not Analyzed Due to Missingness						92	10.10	4 28***	2.51*	1.21	3.74***
MSH6							41	9.76	4 29***	1.74	1.05	2.08

¹With adjustments to the variance estimates for correlation of multiple pairs coming from the same family.

²Huang and Vieland [1997]

³Rabinowitz and Yang [1999]

^***indicates a p-value less than 0.0001,

^**less than 0.001, and

^*less than 0.01.

Considering only those pairs where both individuals had colorectal cancer, the difference in mean ages of onset increased in both datasets (11.19 yrs in UMLYNCH, 11.01 yrs in DLYNCH); with one exception (HV in DLYNCH), the significance level dropped slightly across the board due to the reduced sample size in this subgroup. In UMLYNCH, mutation status was known for 46 out of 190 individuals. Since this is a small number of subjects, stratified analysis by gene-specific mutation type was not feasible. In DLYNCH, where complete data was available on mutation status, the gene most commonly mutated was hMSH2 (153/290 pairs). The difference in mean ages of onset in successive generations restricted to hMSH2 mutation carriers was 7.58 yrs, and all three test statistics (HV, RY1, RY2) displayed only marginal statistical significance (0.01 < P < 0.05). Among those with a mutation in the hMLH1 gene, the difference in mean ages of onset was larger, 10.10 yrs, and HV and RY1 were less significant; however, RY2 was actually considerably more significant (P < 0.0001). The hMSH6 group had a difference of 9.76 yrs and was least significant due to only 41 pairs.

For the sake of completeness, the data analysis results using the test statistics as proposed in the original articles and discussed in Section 2, without adjusting for correlation among pairs coming from the same family are presented in Table ?? and, as expected, they are inflated relative to the adjusted results in Table 5. Appendix Table ?? provides the inverse variance-weighted pooled estimates [DerSimonian and Laird, 1986] combining UMLYNCH and DLYNCH estimates from the full cohort corresponding to Table ??. The pooled estimates from the t-test, HV and RY2 still show strong statistical significance, whereas RY1 fails to reach significance. The same finding holds for adjusted estimates presented in Table 5 when pooled.

3 Use of censored regression models: Inclusion of affected and unaffected family members

Anticipation is a phenomenon which can be addressed via study designs beyond a retrospective comparison of mean ages of onset of affected parent-child pairs in a (possibly truncated) cohort. The second genre of methods and thus study designs considers a well-defined cohort of all at-risk affected and unaffected individuals and applies censored regression models and classical survival analysis techniques to test for a generational effect.

Hsu et al. [2000] proposed two nonparametric matched and unmatched test statistics based on multivariate survival analytic techniques that consider both affected and unaffected family members and potential correlation between the ages of onset within a family. For unaffected individuals, Hsu et al. consider age at last follow-up or age at death and include this information while differentiating the age-of-onset distribution in two successive generations. The method proposed by Hsu et al. [2000] cannot incorporate other covariates. However, their idea of including all affected/unaffected pairs is further extended into a general survival regression framework in the following two more recent papers. The advantages of these censored regression models are the flexibilities to incorporate other covariates, environmental factors, screening practices or secular trends as needed. They are also easily amenable to incorporate familial correlation using standard techniques for correlated failure time data [Kalbfleisch and Prentice, 2002].

1. Normal random effects model (REM)

Larsen et al. [2009] employ a normal random effects model in the following study setting. Pedigrees known to be carriers for mutations in one of the MMR genes are identified, and all at-risk members of these families (affected or unaffected) are followed until disease diagnosis or time of censoring. The paper uses a superset of DLYNCH. Let t_ij be the age to disease diagnosis for the jth individual in the ith family. Larsen, et al. posit the following model,

$$T_{ij}=u_i+\mathit{\beta }{X}_{ij}+\gamma Z_{ij}+{\epsilon }_{ij},$$ (4)

where u_i is a family specific random effect, Z_ij is the generation of the j-th individual in the i-th family (with the oldest individual in a family being denoted as first generation with Z_ij = 1), γ is the fixed effect of generations, and ε_ij is the residual with mean zero and a given variance component. All random effects u and ε are assumed to be independent. When γ = 0, there is no change in time to disease diagnosis across generations. Random family effects account for within family correlation, and fixed effects for other covariates can be added to the model, as the term βX_ij represents in (4). The likelihood is adjusted for censoring indicators, assuming censoring is non-informative with respect to age of onset.

2. Cox proportional hazards model (CPH)

Daugherty et al. [2005] use a Cox proportional hazards model under the following study design: families with at least one affected individual are first ascertained, and all parents and children of affected individuals are followed until the cancer event (disease diagnosis) or time of censoring. Let t_ij again be the age of onset for member j in family i. The following marginal proportional hazards model is assumed:

$$\lambda (t_{ij}|X_{ij},Z_{ij})={\lambda }_0(t_{ij})\text{exp}({\mathit{\beta }}^{*}{X}_{ij}+{\gamma }^{*}{Z}_{ij}).$$ (5)

The term λ_o is the baseline hazard function, X_ij are other relevant measured covariates for a given individual and Z_ij is a binary indicator of relative type (0 for offspring and 1 for parent). Evaluating H₀ : γ^* = 0 evaluates the relative hazard between parents and offspring. Estimation of β^* and γ^* are carried out via a working independence assumption, but, by using a robust sandwich estimate of the covariance matrix, within-family correlations can be accounted for. Despite these strengths, however, the model answers the question of anticipation at the generational level and not the familial level; that is, all parents are assumed to have the same hazard function and all children another. This is problematic for two reasons. First, the degree of anticipation in one family may be different than the degree of anticipation in another, yet both are constrained to have the same hazard. The matched statistic of Hsu et al. [2000] addresses this issue of heterogeneity of hazards across families. Second, when three consecutive generations are considered, the middle individual plays the role of a child in one parent-child pair and that of a parent the other. The same individual will thus have two predicted hazards, one as a child and one as a parent according to this model. This also artificially inflates the sample size. To overcome this second limitation of their approach, we slightly modify the model, letting Z_ij denote the generation of person j in family i (as in REM). This slightly changes the interpretation of γ^*, which now becomes the hazard ratio between two successive generations.

3.1 Application of censored regression models to expanded Danish cohort

For illustration purposes of the second class of methods as well as to understand the differences in defining the study cohort, we return to the Danish HNPCC registry and consider the same dataset analyzed in Larsen et al. [2009]. The dataset consists of 816 individuals who are mutation positive for one of the three MMR genes, coming from 155 pedigrees. Lynch associated cancer developed in 568 individuals by December 2007. Z_ij took values in {1, 2, 3, 4}, with Z_ij = 1 corresponding to the oldest member of a family. Excluding censored individuals, the mean ages of onset were 53.0 years, 45.2 years, 40.0 years and 25.0 years in generations 1,2, 3, and 4, respectively.

Let X_ij = 1[individual j in family i is male] in (4) and (5), so that β, here 1-dimensional, characterizes the increase (or decrease) in age at diagnosis between males and females, and β^*, also 1-dimensional, gives the log hazard ratio between males and females, all other factors being equal. See Larsen et al. [2009] for details of the derivation of the likelihood of (4), where censored observations must be taken into account. Maximization of the likelihood can be accomplished via standard optimization routines or via a grid search, and standard errors can be calculated by inverting the Hessian of the maximum likelihood estimates. Standard software packages will estimate parameters and standard errors for (5), this being the regular partial likelihood of the Cox proportional hazards model. Table 6 gives parameter estimates and test statistics under both REM and CPH model.

Table 6.

Analysis of expanded DLYNCH data of all at-risk individuals from MMR carrier families using a normal random effects model (REM) and Cox proportional hazards model (CPH). For REM, u_i is the family-wise random intercept, γ is the effect of generation on time to diagnosis, and β is the expected difference between males and females in time to diagnosis. For CPH, γ^* is the log hazard ratio corresponding to generation, and β^* is the log hazard ratio corresponding to gender. Gender is coded as Male=1 and Female=0, whereas generation can take values 1,2,3 and 4, with 1 representing the oldest generation in a family.

Parameter	REM1 Estimate(SE)	Wald p-value	Parameter	CPH2 Estimate(Robust SE)	Wald p-value
E(ui)	55.03(1.36)	< 0.0001	γ* (Generation)	0.22(0.07)	0.0014
γ (Generation)	−3.28(0.61)	< 0.0001	β* (Gender)	−0.17(0.08)	0.0300
β (Gender)	1.22(0.93)	0.1870
Var(ui)	11.17(4.77)
Var(εij)	135.76(8.92)

¹Larsen et al. [2009]

²Daugherty et al. [2005]

REM estimates of γ indicate that each generation within a family, adjusting for gender, develops Lynch syndrome about 3 years sooner than the previous generation; this effect is highly significant (P < 0.0001). As mentioned before, we modified the CPH approach of Daugherty et al. [2005] slightly by defining Z_ij not as a dichotomous classifier but as the generation of the jth individual in the ith family. CPH estimates γ^*, the difference in the log-hazards between two consecutive generations, to be 0.222 (P = 0.001). The hazard for generation k + 1 is about e⁰²²² = 1.25 times higher than the hazard for generation k, k = 1,2,3. The gender effect is not significant in REM and only marginally so in CPH, but both indicate that men with Lynch Syndrome tend to be diagnosed with cancer at a later age than women. The interpretation/magnitudes of γ and γ^* are not directly comparable (as is also the case with β and β^*), although, in both cases, the null hypothesis of no genetic anticipation H₀ : γ(or γ^*) = 0 is rejected.

4 Discussion

Since the paper has a two-pronged objective of reviewing analytical choices to assess genetic anticipation and adding new evidence to the context of Lynch syndrome, we separate the two discussion items and summarize our findings.

4.1 Choice of statistical methods

The primary objective of the paper is to provide the reader with a sense of the gamut of statistical techniques that can be used to assess genetic anticipation, depending on their choice of cohort. We clearly delineate contrasting statistical issues when one assesses generational effects on age of onset using just affected parent-child pairs versus affected and unaffected family members at risk. Collecting data under the first design is probably easier, because gathering information on unaffected relatives often requires substantial work. However, the censored regression models are more powerful, since each family contributes the additional information of its unaffected members. The second class of methods falls under the well-developed realm of regression models for censored data and allows the immediate extension to inclusion of covariates and correlations among ages of onset.

The simulation study in the paper is also the first one to compare the parametric and nonparametric methods that address the issue of truncation bias. We evaluate the performance of these alternatives under different ascertainment schema and model misspecification. Using solely Type I error as a metric, RY1 is consistently the preferred test statistic across all ascertainment schema, among any set of generating parameters we considered. However, as demonstrated in Tables 1 to 3, its power, even for an effect as large as a difference in 10 years in mean age of onset, can be unacceptably small. We notice this limitation in our data analysis as well, where RY1 appears to have a non-significant/less significant result in contrast to HV and RY2. This is because many parent-child pairs get excluded from the construction of the RY1 test statistic. For example, in the last row of Table 3, over 5000 simulations, an average of 5.58 pairs (out of 50) satisfied 1[max(T_Pi, T_Ci) ≤ min(C_Pi, C_Ci)] (see expression (3) above). Thus the hypothesis was typically accepted or rejected based on only 5 or 6 parent-child pairs, with all the others being excluded from the sample. In some simulations, no parentchild pairs satisfied the criterion for being retained and RY1 is not defined in that case. The highest level of enrichment simulated in Table 3 was 90%. HV has inflated Type I errors of approximately 16% in this instance. Although these extreme levels of enrichment do inflate HV’s Type I error, for a modest level of enrichment (50–60%), the Type I error is still within an acceptable range. RY2 also maintains Type I error, but under extreme enrichment, (90%) it is very conservative with Type I error rate lower than nominal level (0.02).

In terms of power, because we generated data from the Bivariate normal distribution in Tables 1–3, HV was superior as expected. However, the nonparametric RY methods are valid over any distributional form of the age-of-onset distribution in terms of Type I error rates. Among the two nonparametric methods, RY2 has better power properties than RY1 across all simulation settings. Given the operating characteristics of these procedures across simulation settings, we recommend calculating HV and RY2, and examining the results of both procedures, so as to strike a balance between bias and efficiency. If there is the possibility of multiplex ascertainment strongly influencing the results, or major violation of the normality assumption, one should trust RY2 more than the HV method in order to avoid the chance of yielding false positives.

Remark 6

A referee suggested comparing the methods in Section 1 (affected parent-child pairs) with methods in Section 2 (all affected and unaffected family members at risk). Since the two classes of methods are based on two different designs, it is hard to structure a realistic simulation study that will be meaningful to compare across all six tests (Design 1: t-test, HV, RY1, RY2; and, Design 2: REM and CPH) based on generated pedigree data. Note that REM and CPH always maintains Type I error as they are valid statistical tests under the given survival regression model. To provide an approximate sense of relative power across the six tests, we resampled the extended DLYNCH data with pedigree sizes of 25, 50 and 75 respectively and applied the Section 1 methods to the affected parent-child pairs from the sampled families and applied Section 2 methods to the entire sampled family. The results are presented in Appendix Table ??. We note that HV, RY2 and REM are the most powerful statistical tests. Since REM uses data from all family members and is a likelihood-based parametric approach, it is the most powerful method. The CPH and RY1 appear to be less powerful tests in this context. The loss of power in CPH as compared to REM may be attributed to the use of robust sandwich estimator of variance to account for familial correlation in CPH, whereas REM is a model-based approach, modeling the age-of-onset times directly via a normal random effects model.

4.2 Looking for an answer in Lynch syndrome?

In the context of Lynch syndrome, new evidence in favor of genetic anticipation is added through the analysis of UMLYNCH. UMLYNCH arguably falls under more severe multiplex ascertainment than DLYNCH; a likely catalyst for probands/index persons to present at the clinic is multiply affected family members with early age of onset. On the other hand, DLYNCH data is a richer, populationbased database of larger size, with cancers verified through medical records, clinical records and death certificates, as well as complete characterization of mutation status. Despite these differences, there is a surprising amount of agreement between UMLYNCH and DLYNCH cohorts in terms of the mean age of onset, their mean differences across generations and effect sizes in terms of genetic anticipation. We analyzed the datasets by all four methods, after adjusting for correlation between pairs coming from the same family, and the generally significant results with P < 0.01 (except HV and RY1 in UMLYNCH) are indeed reassuring. Our simulation results (Table 3) indicate that under multiplex ascertainment, RY1 and RY2 are valid procedures, maintaining correct Type I error rates with RY2 having more power to detect a given effect size. Thus, using RY2, the risk of false positives from an inflated Type I error due to multiplex ascertainment is not a concern in our analysis of UMLYNCH and DLYNCH. The analysis of the expanded DLYNCH data also presents strong evidence in favor of genetic anticipation in Lynch Syndrome by both a random effects and a proportional hazards model.

There are other considerations that add complexity to the situation. While age of onset is an important indicator for anticipation, there may also be anticipation exhibited through more aggressive disease severity. In Lynch syndrome, for example, this can be measured by the number of cancers/tumors or the stage of the tumor. Ideally, the measured response then would be multivariate, taking into account all of these outcomes via a multivariate response model. As mentioned in the introduction, bias in estimates may result from a change in screening practices over time. For the case of Lynch syndrome, an increase in the rate of colonoscopies or a decrease in the mean age of first colonoscopy may lower the mean age at diagnosis apart from the effects of genetic anticipation. For retrospective data, this may mean stratifying analysis by time relative to the introduction of the colonoscopy as a common diagnostic tool. A model-based approach to this bias would be the inclusion of an indicator variable for whether the individual was diagnosed before or after the introduction of the colonoscopy. Incorporating detailed colonoscopy records would be a critical contribution towards arriving at the truth. In the Danish registry, information on all colonoscopies were not available, but if an adenoma had been identified at screening, this information was entered in the population-based pathology register and at-risk individuals were censored at this time.

Another addition to the regression-based approaches in Section 2 would be the expansion of the random effects model; a referee pointed out that a constant random intercept alone might not properly account for familial correlations of larger datasets, and each family may have an individual random slope for generational effects. Changing the fixed effect γ to a random effect γ_i in (4) would allow for additional flexibility in the model, and family-wise predictions of γ_i may be of clinical interest. We are currently investigating this model from a Bayesian perspective.

Finally, detecting anticipation statistically does not necessarily suggest a plausible mechanistic explanation to genetic anticipation in Lynch syndrome. Before the biological basis of anticipation had been demonstrated in several specific disorders, the phenomenon was thought to be due to sampling bias, epigenetic effects, gene conversion, or recombinant events. Since then, the biological basis for anticipation in a number of neurodegenerative disorders has been shown to be attributable to trinucleotide repeat instability, with expansion of repeats clearly correlated with an earlier age of onset. While molecular instability due to MMR gene mutation is a natural hypotheses for anticipation in Lynch syndrome, there is no mechanistic data to support this. Recently, telomere shortening has been suggested as the mechanism for anticipation [Vulliamy et al., 2004]. Anticipation has been hard to study in cancer genetic syndromes. However, new evidence from studies of Li-Fraumeni syndrome (LFS) suggest telomere shortening as an alternative mechanism [Tabori et al., 2007]. Accelerated telomere attrition has been reported in affected carriers with LFS compared with unaffected carriers as well as compared with normal wild-type controls, leading investigators to speculate that defects in TP53 allow cells with shorter telomeres to escape senescence and proliferate. If this type of selection for shorter telomeres applies to both somatic and germline tissues, then one would expect that shorter telomeres would be identified at birth in each successive generation. Whether this hypotheses is tenable for Lynch syndrome is a question that still remains to be answered. The National Comprehensive Cancer Network’s guidelines recommend initiating colonoscopy at age 20 to 25 or 10 years before the earliest diagnosis in carrier families, and these new data clearly support enhanced surveillance for mutation carriers at a young age. Except for the Tsai et al. [1997] paper, all published data have so far presented evidence in favor of genetic anticipation in Lynch syndrome. Further mechanistic studies are needed to arrive at the true answer to this important question.

Appendix

Table A.1.

Four analytical methods¹ applied to UMLYNCH and DLYNCH. ‘Only CRC’ considers those parent-child pairs where both had colorectal cancer and, for DLYNCH, ‘MSH2’, ‘MLH1’ and ‘MSH6’ stratify by mutation type.

Subset	UMLYNCH						DLYNCH
	Difference		Test StatisticsSignificance				Difference		Test StatisticsSignificance
	pairs(n)	in means	t-test	HV2	RY13	RY23	pairs(n)	in means	t-test	HV2	RY13	RY23
Entire cohort	136	9.89	7.42***	3.11**	0.00	3.05*	290	8.72	9.84***	4.73***	2.97*	5.39***
Only CRC	62	11.19	5.06***	2.74*	−0.18	2.85*	130	11.01	8.54***	4.41***	2.65*	4.89***
MSH2							153	7.58	6.38***	3.33**	2.51*	3.59**
MLH1	Not Analyzed Due to Missingness						92	10.10	6.18***	2.89*	1.21	3.75***
MSH6							41	9.76	4.32***	1.90	1.13	2.00

¹With no adjustments to the variance estimates for correlation of multiple pairs coming from the same family. These results are obtained by direct use of the test statistics as proposed in the original papers.

²Huang and Vieland [1997]

³Rabinowitz and Yang [1999]

^***indicates a p-value less than 0.0001,

^**less than 0.001, and

^*less than 0.01.

Table A.2.

Pooled estimator from combining the UMLYNCH and DLYNCH estimators for genetic anticipation (from Table A.1 – not adjusted for within-family correlation); the method for pooling used was that prescribed by DerSimonian and Laird [1986] for combining estimates across studies with different sample sizes, using the inverse variances as weights.

	n	t-test	HV	RY1	RY2
UMLYNCH	136	7.42***	3.11**	0	3.05*
DLYNCH	290	9.84***	4.73***	2.97*	5.39***
POOLED	426	12.29***	5.64***	1.39	3.79***

Table A.3.

Estimated proportion of rejection with 2500 resampled datasets with n = 25, 50, 75 pedigrees from the expanded DLYNCH dataset containing 155 families. The first four estimates under Design 1 are based on affected parentchild pairs sampled from the selected families, whereas the two tests under Design 2 use all affected and unaffected family members. The tests that may not maintain Type I error under multiplex ascertainment are presented in bold font.

n	Method:	Design 1				Design 2
		t-test	HV	RY1	RY2	REM	CPH
25		0.956	0.615	0.330	0.693	0.703	0.525
50	Rejection Rate:	0.999	0.826	0.505	0.876	0.905	0.628
75		1.000	0.925	0.671	0.947	0.971	0.764