Multi-analyte quantification in bioprocesses by Fourier-transform-infrared spectroscopy by partial least squares regression and multivariate curve resolution

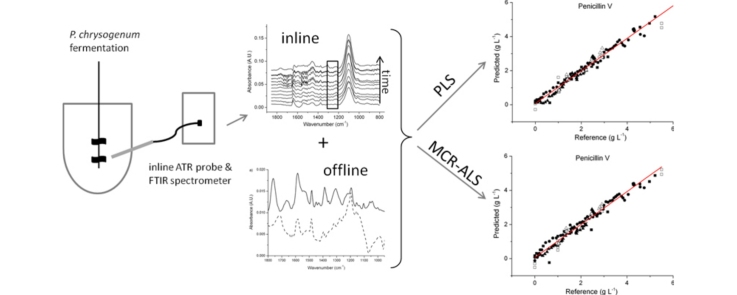
Graphical abstract

Highlights

• •Selective quantification using inline fiber optic ATR probe and midIR spectroscopy.
• •Comparison of performance and ease of interpretation of PLS and MCR-ALS.
• •General workflow for reliable quantification by FTIR spectroscopy in bioprocesses.

Abstract

This paper presents the quantification of Penicillin V and phenoxyacetic acid, a precursor, inline during Pencillium chrysogenum fermentations by FTIR spectroscopy and partial least squares (PLS) regression and multivariate curve resolution – alternating least squares (MCR-ALS). First, the applicability of an attenuated total reflection FTIR fiber optic probe was assessed offline by measuring standards of the analytes of interest and investigating matrix effects of the fermentation broth. Then measurements were performed inline during four fed-batch fermentations with online HPLC for the determination of Penicillin V and phenoxyacetic acid as reference analysis. PLS and MCR-ALS models were built using these data and validated by comparison of single analyte spectra with the selectivity ratio of the PLS models and the extracted spectral traces of the MCR-ALS models, respectively. The achieved root mean square errors of cross-validation for the PLS regressions were 0.22 g L⁻¹ for Penicillin V and 0.32 g L⁻¹ for phenoxyacetic acid and the root mean square errors of prediction for MCR-ALS were 0.23 g L⁻¹ for Penicillin V and 0.15 g L⁻¹ for phenoxyacetic acid. A general work-flow for building and assessing chemometric regression models for the quantification of multiple analytes in bioprocesses by FTIR spectroscopy is given.

1. Introduction

The advantage of spectroscopic methods over classical analytical methods employed for bioprocess analysis is the simultaneous determination of multiple target analytes through multivariate data analysis. Data are acquired in situ, without the need for sample preparation and can be provided in real-time making it well suited for process monitoring. Especially attenuated total reflection (ATR) Fourier-transform-infrared (FT-IR) spectroscopy has become increasingly interesting as a process analytical tool (PAT) for inline and online monitoring of (pharmaceutical) bioprocesses [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14]. Dissolved substrate components, as well as desired and undesired metabolites can be quantitatively determined using multivariate data analysis methods, i.e. chemometrics, like principal component analysis (PCA), partial least squares (PLS) regression and multivariate curve resolution (MCR) [15], to name a few. Landgrebe et al. [16] give a good overview of bioprocesses and specific analytes monitored by online mid- and near-infrared spectroscopy. Lourenço et al. [17] give a more general review of optical spectroscopy methods employed for bioprocess monitoring, including a brief introduction to chemometric methods. ATR-probes designed for process control/monitoring are commercially available and are fit for measurements in harsh and variable process environments, i.e. are autoclavable and made from biocompatible materials.

In this work we concentrated on Penicillin V (PenV), a commonly used beta-lactam antibiotic [18], [19]. It is produced in industrial-scale bioprocesses by Penicillium chrysogenum. Bioprocess design and control for filamentous fungi still rely greatly on empirical methods. Here, a science-based approach, as facilitated by online and inline sensors combined with simplified mechanistic models, would be beneficial since it helps increase process economics and decrease development time [20]. Accurate determination of optimal harvest time of the bioprocess is crucial to product quality and productivity. Routine measurements of PenV and phenoxyacetic acid (POX) concentrations are typically performed offline by high performance liquid chromatography (HPLC) analysis.

Guzman et al. [21] showed that prediction of termination times of a biotransformation batch process by monitoring the hydrolysis of Penicillin V to phenoxyacetic acid and 6-aminopenicillanic acid using online ATR FT-IR spectroscopy in a bypass system and PLS regression was superior to standard procedures, like offline HPLC analysis. We aim at quantitative determination of the precursor phenoxyacetic acid and product, Penicillin V in fed-batch fermentations of P. chrysogenum. Here we present a method that allows for determination of precursor and product inline as well as real-time determination of the optimal harvest time, making sampling unnecessary and thus minimizing possible errors. We compared two different chemometric methods, PLS and MCR-ALS, for prediction of POX and PenV concentrations from FT-IR spectra.

PLS regression is a calibration method that is suitable for numerous, strongly correlated x-variables [22] as presented by FT-IR spectra. It projects the X data onto a set of “latent variables” that are good predictors of Y using a least-squares approach. These latent variables are often hard to interpret or relate to spectra of pure components. While for PLS regression a reliable reference method is necessary, MCR-ALS is based on the assumption that the multivariate data matrix (X or D), e.g. FT-IR spectra taken at different times of a chemical reaction, can be approximated as a linear combination of unfolded (pure) component spectra (S) weighed by their respective concentration profiles (C) plus the residuals that cannot be explained by the model (E). The unfolded spectra S can be given a chemical meaning when comparing them to measured pure component spectra, thus allowing for evaluation of model quality. Reference data is not necessary for this type of modeling, however, a good estimation of starting concentrations helps. Furthermore, application of different constraints, such as non-negativity for concentrations, or combination with hard models, e.g. a hard equilibrium model describing the acid-base equilibria of simple molecules for quantitative analysis of pH-modulated mixture samples [23], can improve the MCR-ALS model.

2. Material and methods/experimental

2.1. Fermentation of P. chrysogenum

Four fed-batch fermentations of P. chrysogenum (strain: BCB1) were carried out similar to a recently described protocol except for POX addition [24]. Since accurate determination of the optimal harvest time was the goal, POX was not added continually, but in a pulsed way, so depletion could be observed more than once during a fermentation run. In order to allow applicability of the FT-IR probe with 25 mm Ingold^® design however, fed-batch cultivations were performed in a 15 L autoclavable, fully automated and controlled stirred bioreactor (Infors, Switzerland) instead of the previously described 7.5 L glass reactor system [24]. For all fed-batch cultivations, process duration was in the range of 140–160 h.

2.2. FT-IR spectroscopy

FT-IR spectra were recorded with a 1.5 m DiComp AgX (silver halide) fiber optic probe connected to the portable process spectrometer ReactIR 15 (both Mettler Toledo, Switzerland) equipped with a liquid-nitrogen-cooled mercury-cadmium-telluride (MCT) detector. The probe was equipped with a diamond ATR element and a special adapter was designed and built in-house to couple the probe to a 25 mm Ingold^® port available in the bioreactor. The ReactIR 15 is a sealed instrument, thus no purging with dry air was required. Spectra were acquired using the dedicated software IcIR 4.2 (Mettler Toledo, Switzerland), with the resolution set to 8 cm⁻¹ in the spectral range of 900–4000 cm⁻¹, as the co-addition of 256 scans. Basic data manipulation, like single point baseline correction, was also performed in IcIR 4.2.

The applicability of ATR FT-IR spectroscopy for determination of POX and PenV in complex media matrices was assessed offline. Single analyte and binary solutions of POX and PenV were prepared in 20 mM phosphate buffer adjusted to pH = 6.5 which is the pH level maintained throughout PenV production in the fermentation (for concentration levels see Supplementary data Table A). Phenoxyacetic acid (99%, Sigma Aldrich, USA) and phenoxymetylpenicillin potassium salt (Penicillin V potassium, kindly provided by Sandoz GmbH, Austria) were weighed in and diluted and mixed to the desired final concentrations. The standard solutions and supernatant samples from previous fermentations were measured offline against a water background by depositing a drop of the solution onto the horizontally aligned ATR surface. Inline, spectra were acquired every 2–5 min against a medium background, resulting in approximately 2000 spectra for each fermentation run.

2.3. Reference analysis

Analysis of penicillin V and phenoxyacetic acid was performed by isocratic HPLC using a ZORBAX C-18 column (Agilent Technologies, USA) and 28% ACN, 6 mM H₃PO₄, 5 mM KH₂PO₄ as elution buffer (all reagents: Sigma Aldrich, USA). The bioreactor was coupled to the HPLC via a 0.2 μm pore size ceramic probe (iba e.V. Heiligenstadt, Germany). Samples of the medium were drawn from the bioreactor at constant flow and were sampled from a flow-through cell as often as possible during pulsed addition of POX (approx. every 15–20 min) and every 3 h during the decrease of POX. The sampling delay was 1 h 15 min in runs 1 to 3 and 15 min for run 4, respectively (a sampling line with thinner diameter was available in this run). The HPLC method was optimized to ensure good separation of peaks, and an automatic dilution step was introduced to keep analyte concentrations within the calibration range.

Additionally, samples were drawn from the bioreactor every 12 h and HPLC measurements were performed offline. These were in good agreement with the online measurements (data not shown). The relative standard deviation of the HPLC determination alone is small: 0.9% relative standard deviation (RSD) for 3.4 g L⁻¹ POX and 1.3% RSD for 0.8 g L⁻¹ PenV. When coupling the HPLC online with the bioreactor, the error is expected to increase for several reasons: Due to inferences from media components, the integration method had to be adjusted. Since a relatively small sample volume is drawn for every point in time (i.e. continuously), time resolution is slightly blurred by sampling from the flow-through cell. Furthermore, because of the long sampling line, degradation of the analytes could occur and matching the HPLC measurement times with the acquisition times of FT-IR spectra becomes difficult. We therefore estimated the total error of the method to be roughly 5%.

2.4. Multivariate calibration

To build multivariate calibration models, the three spectra acquired closest to the times of HPLC measurements (see Section 2.3) were averaged and imported into Matlab^®. A total of 196 spectra with reference data were available for regression. To break co-linearity between POX and PenV and to correct for potential errors in HPLC reference measurements, single analyte and binary standards were included in the model to increase robustness as previously reported [9]. Furthermore, POX addition was performed continuously for run 1, as would be done in the industrial process, and in a spiked manner for runs 2 to 4, i.e. POX was added quickly to a predetermined concentration after its depletion.

2.4.1. PLS regression

PLS regression models were built using the PLS toolbox 6.2 (Eigenvector Research, Inc., USA) using the SIMPLS algorithm [25]. Suitable spectral regions for calibration were identified from the pure PenV and POX spectra, taking into account interferences of the fermentation broth (for spectral regions used see Table 1). Preprocessing consisted of calculation of first derivative (Savitzky-Golay (Sav-Gol), order 2, window size 11) of spectral data and mean centering of both, spectral and concentration data. Cross-validation of PLS models was performed using random subsets (10 data splits, 3 iterations).

Table 1.

Model parameters and figures of merit for the POX and PenV PLS models.

Model	Calibration range (g L−1)	Data included	Wavenumber region (cm−1)	Preprocessing steps	Latent variables	RMSECV (g L−1)	r2 CV
POX-PLS	0–3.47	Offline: fermentation, standards; fermentations 1–4	1188–1352 & 1747–1817	Mean centering, first derivative (Sav-Gol, order 2, window 11)	6	0.31	0.90
PenV-PLS	0–5.55	Offline: fermentation, standards, fermentations 1 & 3–4	1184–1501 & 1672–1855	Mean centering, first derivative (Sav-Gol, order 2, window 11)	7	0.22	0.97

2.4.2. MCR-ALS calibration

The multivariate calibration algorithm MCR-ALS has been extensively described in the literature [15], [26] so, only a brief description of it is given here.

The bilinear decomposition of the augmented matrix D is performed according to the expression:

$$\text{D}=\text{C}{\text{S}}^{\text{T}}+\text{E}$$ (1)

in which the rows of D contain the spectra measured for different samples (pure and mixture standards and fermentation samples), the columns of C contain the relative concentrations of the intervening species, the columns of S their related unfolded spectra, and E is a matrix of residuals not fitted by the model.

Decomposition of D is achieved by iterative least-squares minimization of the Frobenius norm of E, under suitable constraining conditions during the ALS procedure. MCR-ALS requires initialization with system parameters as close as possible to the final results. In the present work we employed the SIMPLISMA (simple to use interactive self-modeling mixture analysis) methodology [27] in all cases.

During the iterative recalculations of C and S^T, a series of constraints are applied to give physical meaning to the obtained solutions, and to limit their possible number for the same data fitting. In this paper, the correspondence among species in the experiments was used as restriction together with a correlation constraint, in which the concentrations of the analytes in calibration samples at each ALS iteration are forced to be correlated to previously known reference concentration values of the analyte in these samples. More details about the implementation of this constraint in previous works can be found elsewhere [28], [29]. This latter constraint has been successfully applied in the determination of several compounds in the presence of unexpected interferences using first-order instrumental data [30].

Correlation constrained MCR-ALS was implemented using a MATLAB code which is available on request from R. Tauler (e-mail: Roma.Tauler@idaea.csis.es).

3. Results and discussion

3.1. Workflow

The following, generally applicable workflow for optimal model building and calibration of inline spectroscopic measurements for multi-analyte quantification was followed:

Feasibility study:

• 1.Pure analyte spectra were recorded in order to assess general IR absorbance characteristics and identify possible cross-correlations. Generally, the chemical and physical environment of the pure analytes should be comparable to that expected in the process, i.e. similar pH, temperature, etc.
• 2.Then, matrix effects of the (bio)process medium were investigated by spiking real process samples with the analyte of interest (POX).

  Multivariate model building:

• 3.Given accurate and sensitive reference analytics in place, inline measurements were performed at the process and PLS model building based on synthetic standards and inline measurements was performed.
• 4.Finally, to verify reasonable model building, model validity for each analyte was ensured by selectivity analysis. At this stage, unless acceptance criteria are met, further orthogonal measurements should be included for calibration in order to break undesired cross-correlations.
• 5.If selectivity cannot be achieved satisfactory with PLS, or not enough calibration samples are available, MCR-ALS, which calculates spectral traces of modeled factors, should be used to ensure that the target analyte is modeled by one of the factors. We have built MCR-ALS models for the analytes of interest and compare their performance to that of PLS regression.

3.2. Investigation of feasibility

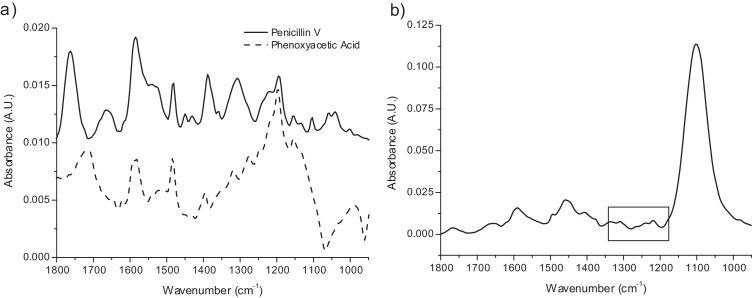
To ensure the applicability of ATR FT-IR spectroscopy as a means for quantification of POX and PenV, spectra of synthetic single and binary solutions were acquired. Fig. 1(a) shows the pure component spectra of solutions of PenV and POX in 20 mM phosphate buffer (pH = 6.5). Spectral overlap between the two analytes is, as expected, high, but there are some distinct differences that can help to break the co-linearity around 1775 cm⁻¹ and in the range between 1100 and 1400 cm⁻¹. In Fig. 1(b) a spectrum of a typical fermentation sample acquired offline is shown. The spectrum is governed by a large absorption peak around 1100 cm⁻¹ which is due to (SO₄²⁻) introduced from ammoniumsulphate addition and sulphuric acid for pH control. Characteristic spectral features of PenV (bands between 1800 and 1750 cm⁻¹, 1270 and 1340 cm⁻¹ and 1200 and 1250 cm⁻¹) and POX (bands between 1200 and 1250 cm⁻¹) are visible; they are however relatively weak. Spiking of samples drawn before the addition of POX had been started, thus without any POX or PenV content, showed that the appropriate bands appeared and were proportional to POX concentration (Fig. 2(a)). The difference spectrum of the sample spiked to 1 g L⁻¹ POX final concentration (Spiked 1) and the unspiked sample is highly similar to that of 1 g L⁻¹ POX in 20 mM phosphate buffer (Fig. 2(b)). This strong correlation shows that the spectral features are conserved in the complex fermentation broth matrix and indicate that the determination of POX from fermentation broth spectra is feasible.

Fig. 1.

(a) Reference attenuated total reflection (ATR) spectra of Penicillin V (10 g L⁻¹) and phenoxyacetic acid (3 g L⁻¹) in 20 mM phosphate buffer adjusted to pH = 6.5. Pure phosphate buffer was used as a background. Spectral similarities of the two analytes are obvious, however some differences, especially around 1350 cm⁻¹ and 1750 cm⁻¹, are present. (b) Offline ATR spectrum of a typical fermentation broth sample. Between 1200 and 1350 cm⁻¹ typical features of POX and PenV can be seen (black box), their absorbances are however very low compared to other components, e.g. (SO₄²⁻) which absorbs around 1100 cm⁻¹.

Fig. 2.

(a) Spectra of fermentation broth without POX (Broth, dotted line), fermentation broth spiked to a final POX concentration of 1 g L⁻¹ (Spiked 1, dash-dot line) and spiked to a final concentration of POX of 2 g L⁻¹ (Spiked 2, solid line). The spectral range in which POX-specific bands can be seen is indicted by the black box. (b) Difference spectrum of Spiked 1 (1 g L⁻¹ POX) and the Broth spectrum (solid line) and spectrum of 1 g L⁻¹ POX in 20 mM phosphate buffer (dashed line). The correlation between the spectra is very good, especially in the region between 1200 and 1400 cm⁻¹ (spectra are offset for clarity).

The potential of multianalyte determination by mid-IR spectroscopy and chemometric modeling also poses a challenge: cross-correlations with interferents and modeling of general temporal, rather than concentration changes. Therefore, a validation of the generated chemometric models is very important, especially in complex, variable matrices that are present in bioprocesses.

3.3. PLS regression

The PLS regression models built for POX and PenV were based on prior knowledge of the spectral ranges relevant for the two analytes. The spectral ranges were chosen based on the wavenumber regions where specific bands of POX and PenV were identified and little interference from the fermentation broth was expected. Different spectral ranges were tested, i.e. PLS models built, and the spectral regions that performed best for each analyte and for which selectivity ratios indicated specificity (see below) were chosen. The relative changes in the observed wavenumber regions over the course of a single fermentation can be seen in Supplementary data Fig. B, a PCA scoreplot of all data used for calibration can be seen in Supplementary data Fig. C. Apart from variations in the spectral range employed for model construction, different preprocessing steps (raw spectra, first and second derivative (Sav-Gol) spectra) were tested. For both analytes, first derivative spectra gave the best results, since baseline shifts could thus be omitted. The relatively small signal to noise ratio for the analytes of interest made second derivate spectra unsuitable for modeling. The wavenumber regions used for the respective analytes were different. Details about the PLS-models for POX and PenV are given in Table 1. The POX PLS-model was based on all offline spectra and the spectra obtained in fermentation runs 1–4. In fermentation run 2 one HPLC outlier was omitted and two were omitted from fermentation run 3 (comparison with previous and subsequent HPLC results and approximate calculation of POX concentration). For the PenV PLS-model data from fermentation run 2 were omitted, since no PenV was produced during this run. Models including these data performed worse in cross-validation than when the data were predicted using models built omitting the data, i.e. the RMSECV was higher than the RMSEP. We concluded that the introduction of these additional data lead to an introduction of noise to the model increasing the RMS error. The calibration curve of POX concentrations determined by HPLC vs. the values predicted from cross-validation for the POX PLS model is shown in Fig. 3(a). The RMSECV for POX was determined as 0.31 g L⁻¹; the RMSECV normalized to the calibration range is 9% which is slightly worse than the estimated error of reference analysis (5%). Fig. 3(b) shows the calibration curve for PenV; the respective RMSECV was determined as 0.22 g L⁻¹ and the normalized RMSECV (to calibration range) is 4%, which is in the range of the expected error of the reference method.

Fig. 3.

(a) Calibration curve for POX. (b) Calibration curve for PenV. Reference concentrations determined by HPLC or gravitmetrically are plotted vs. the POX concentrations predicted by the cross-validated PLS model. The origin of the data is indicated by different marker symbols.

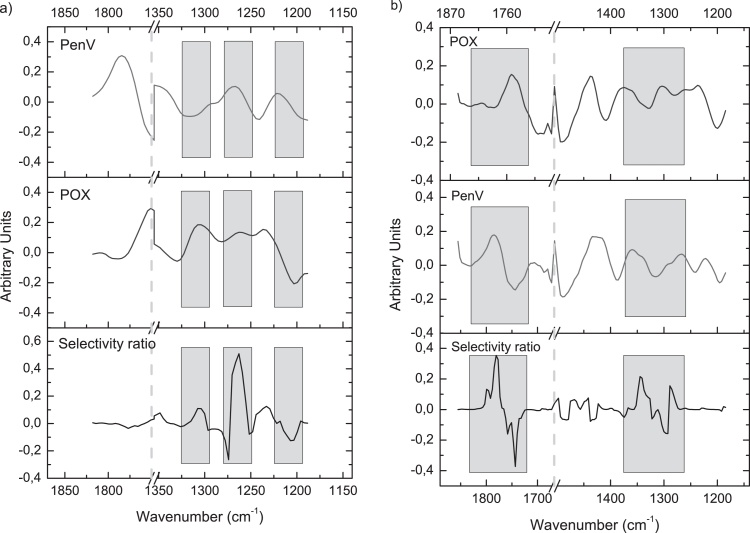
As a means to check the validity of the developed PLS models, the selectivity ratio, which is the ratio of explained to residual variance for each variable, i.e. wavenumber, was calculated [31]. A high selectivity ratio indicates wavenumber regions that have a strong impact on the prediction, and the type of correlation is inferred from the regression vector (i.e. positive or negative). By comparing spectral regions that have a high selectivity ratio with spectral features of the target analyte and potential interferents, the correctness/validity of the model can be checked. In Fig. 4(a) the preprocessed, i.e. first derivative and mean centered, pure analyte spectra of PenV, the strongest interferent, and POX and the selectivity ratio of the POX-PLS model are shown. Wavenumber regions with a high positive or negative selectivity ratio are highlighted in gray. The highest selectivity ratio is found around 1265 cm⁻¹, which coincides with a maximum for both POX and PenV. Selectivity for POX can be attributed to the positive correlation around 1310 cm⁻¹, where for the POX spectrum a maximum is located, while the PenV spectrum shows a local minimum, and the negative correlation around 1205 cm⁻¹. Here, the first derivative, mean centered POX spectrum has a minimum as well, while the PenV spectrum is close to zero. Fig. 4(b) shows the same plots for the PenV-PLS model. Again, the first derivative, mean centered spectra of PenV and POX are compared to the selectivity ratio multiplied by the sign of the regression vector. Good agreement between the selectivity ratio and the PenV spectrum can be seen in the region between 1725 and 1825 cm⁻¹. For the second region with large selectivity ratios (1250–1380 cm⁻¹), the curve is also very similar to the PenV spectrum. No matches between the POX spectrum and the selectivity ratio of the PenV-PLS model can be observed.

Fig. 4.

(a) Selectivity ratio multiplied by the sign of the correlation vector (bottom) for POX-PLS model compared to the first derivative, mean centered spectra of POX and PenV (vector normalized). (b) Selectivity ratio multiplied by the sign of the correlation vector (bottom) for PenV-PLS model compared to the first derivative, mean centered spectra of POX and PenV (vector normalized). A high absolute value of the selectivity ratio points to spectral regions that have a strong influence on the model, while the sign indicates whether the correlation is positive or negative.

3.4. MCR-ALS models

The MCR-ALS models built for POX and PenV were based on prior knowledge of the spectral ranges relevant for the two analytes derived from single analyte spectra. The wavenumber regions which resulted in the best performance of the MCR-ALS models for both POX and PenV were smaller than those used in the PLS models (see Table 2). As for the PLS models, mean centered first derivative (Sav-Gol, polynomial order 2, window size 11) spectra gave the best results. For concentration prediction from spectra acquired during the fermentation runs, the concentration information from offline fermentation samples, single analyte standards and binary standards was used for calibration. Calibration curves of MCR-ALS predicted concentrations vs. concentration measured using reference analysis obtained for POX and PenV are shown in Fig. 5. As for the PLS models, good correlations with a high r² value were found. The root-mean-square-error of prediction (RMSEP) for POX was determined as 0.16 g L⁻¹ (normalized to calibration range: 4.6%), which is significantly lower than the RMSECV of the PLS-POX model and in the range of the estimated reference method error. The higher goodness of fit is also reflected in a higher r² of the calibration curve, namely 0.97, for the MCR-ALS model than for the PLS model (r² = 0.90). For PenV the RMSEP was determined as 0.23 g L⁻¹ (normalized to calibration range: 4.1%), making the performance of the MCR-ALS model similar to the PLS model and the estimated reference method error.

Table 2.

Parameters and figures of merit for the POX and PenV MCR-ALS models.

Model	Calibration range (g L−1)	Calibration data	Data predicted	Wavenumber region (cm−1)	Preprocessing steps	Factors	RMSEP (g L−1)	r2 prediction
POX-MCR-ALS	0–3.0	Offline: fermentation, standards	Single analyte standards; fermentations 1–4	1281–1352 & 1747–1817	Mean centering, first derivative (Sav-Gol, order 2, window 11)	5	0.16	0.97
PenV-MCR-ALS	0–5.55	Offline: fermentation, standards	Offline: fermentation, standards; fermentations 1 & 3–4	1307–1352 & 1747–1817	Mean centering, first derivative (Sav-Gol, order 2, window 11)	5	0.23	0.95

Fig. 5.

Calibration curves for the MCR-ALS models for POX (a) and PenV (b). Values predicted using the MCR-ALS models are plotted against values obtained by reference analysis.

Since MCR-ALS is a method that, for a given number of components, calculates concentration profiles and spectral traces that best describe the spectral changes of the data, these spectra can be directly compared to (preprocessed) pure analyte spectra. Fig. 6 shows the spectral traces calculated by MCR-ALS for both the POX (a) and PenV (b) and the respective pure analyte spectra. For both, PenV and POX, good agreement between the respective single analyte spectrum and the spectral trace of one of the components can be seen. Component 1 of the POX MCR-ALS model correlates well with the POX spectrum and component 5 of the PenV MCR-ALS model correlates well with the PenV spectrum.

Fig. 6.

MCR spectra traces for the MCR-ALS model for POX (a) and for PenV (b). The preprocessed single analyte spectrum of the target analyte (dashed line) for each model is plotted over the calculated spectral traces. For the POX MCR-ALS model, the spectral trace of component 1 (bottom of graph a) is in good agreement with the POX spectrum. The spectral trace of component 5 (top of graph b) of the PenV MCR-ALS model is highly correlated to the PenV spectrum.

4. Conclusions

Comparing PLS with MCR-ALS, similar model performances were reached. While, in principle, step 3 may be omitted for MCR-ALS, predictive accuracy proved to be superior when using standard spectra as a means to calibrate the model. Since PLS is the more established method for spectral calibration and does not require as much expertise and not as many input parameters as for MCR-ALS, we recommend it as a starting point. If selectivity analysis is not satisfactory, MCR-ALS modeling should be used, as the spectral traces of the modeled components are calculated directly and can be compared to target analyte spectra. In cases where only a limited number of calibration spectra is available, e.g. due to lack of reliable reference analysis, MCR-ALS should be the method of choice, as the algorithm basically does not require reference concentrations. Furthermore, in some cases the performance of MCR-ALS is better than that of PLS, as is the case for POX in this work.

Applying the suggested workflow, concentrations of PenV and POX were successfully predicted inline. This is a step toward accurate determination of optimal termination time of the bioprocess. To increase the accuracy of predictions, two things have to be considered: the performance of chemometric models is always limited by the accuracy of the reference analysis and by the signal-to-noise ratio (SNR) of the spectroscopic system in use. With respect to an improved SNR, the elimination of the silver halide fiber in favor of a monolithic sensor design seems to be a promising approach. This could be realized either using External Cavity Quantum Cascade Lasers (EC-QCLs) coupled with waveguides and small pyro-electric detectors, or the use of pulsed mid-IR sources in combination with a multi-reflection ATR-element and line (Bragg) filter detectors. Both approaches use dispersive measurement principles, therefore also eliminating the need for potentially bulky and vibration sensitive interferometers.

Appendix A. Supplementary data

The following are the supplementary data to this article: