A Bayesian Integrative Genomic Model for Pathway Analysis of Complex Traits

Abstract

With new technologies, multiple types of genomic data are commonly collected on a single set of samples. However, standard analysis methods concentrate on a single data type at a time and ignore the relationships between genes, proteins, and biochemical reactions that give rise to complex phenotypes. In this paper, we propose a novel integrative model to incorporate multiple types of genomic data into an association analysis with a complex phenotype. The method combines path analysis and stochastic search variable selection into a Bayesian hierarchical model that simultaneously identifies both direct and indirect genomic effects on the phenotype. Results from a simulation study and application of the Bayesian model to a pharmacogenomic study of the drug gemcitabine demonstrate greater sensitivity to detect genomic effects in some simulation scenarios, when compared to the standard single data type analysis. Further research is required to extend and modify this integrative modeling framework to increase computational efficiency to best capitalize on the wealth of information available across multiple genomic data types.

INTRODUCTION

With the wealth of data being produced by new technologies, it is becoming common to collect multiple types of genomic data on a set of samples. Currently, standard analysis methods concentrate on a single data type, or experiment, at a time. Few statistical methods have been developed to maximize the use of the enormous amount of genomic data to unravel the etiology of complex disease and drug-related phenotypes. Joint analysis of multiple types of genomic data would likely provide novel insights, especially when the etiology of the disease or phenotype is complex [Reif et al., 2004].

A few methods have been proposed to integrate multiple forms of genomic data, sometimes referred to as “integrative genomics” or “genomic convergence” [Hauser et al., 2003; Schadt et al., 2005]. Other approaches involve a multistep procedure to identify potential key drivers of complex traits by integrating genetic variation and mRNA gene expression data [Li et al., 2009; Niu et al., 2010]. Schadt et al. [2005] describe a multistep method that uses conditional correlation measures and a likelihood-based causality model selection to model the relationship between DNA variation, mRNA expression, and clinical traits. Another type of integrative analysis involves approaches that complete a comprehensive analysis, as opposed to a multistep procedure. However, these approaches have mostly been described in the context of a small number of genomic variables, such as those contained within a pathway. Nock et al. [2007] proposed an approach based on structural equation modeling (SEM), whereas Conti et al. [2003] used a Bayesian approach to model the complex relationship within a small, biological pathway of interest.

Similar to these comprehensive approaches, we propose a modeling framework that combines Bayesian pathway analysis [Congdon, 2007] and Bayesian variable selection using stochastic search variable selection (SSVS) [Fridley, 2009; George and McCulloch, 1993] into a novel modeling framework to identify both direct and indirect genomic effects on a complex phenotype. The novel Bayesian integrative genomic model is illustrated using data from mRNA expression and single nucleotide polymorphisms (SNPs) within the gemcitabine drug pathway from a pharmacogenomic study of the drug gemcitabine. We also present simulation studies to assess the ability of the proposed model to detect simulated effects. Finally, we compare results from the Bayesian integrative genomic model to results from the standard “one-at-a-time” analysis using both the pharmacogenomic data and simulated data.

METHODS AND MATERIALS

PHARMACOGENOMIC STUDY OF GEMCITABINE

To understand the pharmacogenomics of gemcitabine drug therapy, the Coriell Human Variation Panel lymphoblastoid cell lines have been utilized extensively [Li et al., 2009; Niu et al., 2010]. EBV-transformed B lymphoblastoid cells were derived from approximately 60 Caucasian American (CA), 60 African American (AA), and 60 Han Chinese-American (HCA) subjects. Gemcitabine cytotoxicity data for the cell lines were collected at drug dosages 1,000, 100, 10, 1, 0.1, 0.01, 0.001, and 0.0001 uM. The quantitative phenotype IC50 (effective dose that kills 50% of the cells) was estimated using a four parameter logistic model [Gallant, 1987], and was used as the drug-response phenotype. A large value of IC50 indicates that a cell line is resistant to the drug, whereas a small value indicates a cell line is sensitive to the drug.

Genotyping of SNPs on the Illumina's Infinium Human-Hap 550K and 510S BeadChips for the cell lines was completed at the Genotyping Shared Resources at the Mayo Clinic in Rochester, Minnesota. Quality control was completed by excluding SNPs with Hardy-Weinberg Equilibrium (HWE) P-value < 0.001 (minimum P-value between exact test for HWE by race [Guo and Thompson, 1992; Wigginton et al., 2005] and stratified test for HWE [Schaid et al., 2006]), minor allele frequency <5%, or call rate <95% from further analyses. Missing genotypes within the gemcitabine pathway were imputed prior to analyses using the program fastPHASE [Scheet and Stephens, 2006]. This resulted in 15 genes within the gemcitabine pathway containing 265 SNPs.

Whole genome expression data for the cell lines was obtained with Affymetrix U133 Plus 2.0 expression array chip, which contains over 54,000 probe sets. The mRNA expression array data were normalized on the log₂ scale using GCRMA methodologies [Bolstad et al., 2003; Irizarry et al., 2003; Wu et al., 2004]. This data contained 20 probe sets for genes within the gemcitabine pathway. The goal of this study is to complete a comprehensive integrative analysis of both genetic variation (in the form of SNPs) and mRNA gene expression variation to determine their collective impact on gemcitabine response as measured by the IC₅₀.

STANDARD ANALYSIS APPROACH

The standard analysis approach for the analysis of multiple types of genomic data is to complete, for each data type, the univariate association of the genomic variable with the phenotype. Following the analysis of each genomic data type with the phenotype, to understand these association results, expression quantitative trait loci (eQTLs) analysis is then completed to determine the association of each SNP with the level of gene expression. P-values for each effect type are adjusted according to Bonferroni's multiple testing procedure. Throughout this paper, we will refer to this analysis approach as the standard all-pairwise correlation analysis, denoted as APCA.

BAYESIAN INTEGRATIVE MODEL

To model the joint relationship of mRNA gene expression and SNP genotypes on a quantitative phenotype (e.g. drug cytotoxicity), we propose the following Bayesian integrative model. Let Y_i be the phenotypic value for subject i (i = 1, …, N), and let SNP_i = (SNP_i1, SNP_i2, …, SNP_iK)^T represent the SNP genotypes of subject i where SNP_ik is the genotype (under additive coding in terms of the number of minor alleles) for SNP k (k = 1, …, K). Next, let GE_i = (GEi1, …, GE_iJ)^T represent a vector of gene expression values for subject i, where GE_ij is the standardized mRNA expression value for gene j (j = 1, …, J) for subject i. The first step in specifying the Bayesian integrative model is to specify the direct effects of the SNPs and mRNA expression on the quantitative phenotype, where the phenotype follows a normal distribution whose mean is a function of both the SNP genotypes and the mRNA expression levels. Let $Y_i~N({\mu }_{Yi},{\sigma }_Y^2)$ for i = 1, …, N, where μ_yi = b₀ + b^TSNP_i + c^TGE_i , b = (b₁, …, b_K)^T represents a vector of K direct SNP effects with b_k representing the direct effect of SNP k on the phenotype, c = (c₁, …, c_J )^T represents a vector of J mRNA expression effects with c_j representing the direct effect of the mRNA expression value for gene j on the phenotype.

Next, we model the effect of SNPs on the phenotype via the mRNA expression levels. In assessing the association between the SNPs and the mRNA expression levels, there are two possibilities (1) assessment of only cis-acting SNPs (i.e. SNPs within the 5′ r 3′ genomic region of a gene); or (2) to assess both cis- and trans-acting SNPs (i.e. SNPs not near or within the 5′ or 3′ genomic region of the gene). Incorporating only cis-relationships in a model reduces the model complexity, which eases model evaluation; however, this limits the types of relationships that can be discovered and assessed. For models examining both cis- and trans-relationships between SNPs and mRNA expression (i.e. all possible SNP-mRNA pairs), for every subject i 1, …, N and gene j = 1, …, J, let $G{E}_{ij}~N({\mu }_{GE\mathit{ij}},{\sigma }_{GEj}^2)$ where ${\mu }_{GE\mathit{ij}}=a_{j0}+{\underset{¯}{a}}_j^T{\underset{¯}{SNP}}_i$ and a_j = (a_j1, …,a_jK)^T where a_jka_j1 represents the effect of SNP k on mRNA expression value for gene j.

In contrast, for models examining only cis-acting SNPs, let SNP_ij be the subset of SNP_i containing SNPs within gene j and N_j be the number of SNPs within gene j (i.e. length of the vector SNP_ij) with $G{E}_{\mathit{ij}}~N({\mu }_{GE\mathit{ij}},{\sigma }_{GEj}^2)$ where ${\mu }_{GE\mathit{ij}}=a_{j0}+{\underset{¯}{a}}_j^T{\underset{¯}{SNP}}_{\mathit{ij}}$ and a_j = (a_j1, …, a_jNj)^T, where a_jk represents the cis-acting effect of SNP k on the mRNA expression for gene j. The effect of SNPs on mRNA expression modeled in this fashion could be indirect effects of SNPs on the phenotype acting through mRNA expression, or less desirable, eQTLs not related to the phenotype. For the remainder of this paper, we will not make the distinction between SNP effects on mRNA expression that are associated or not associated with the phenotype. The effects of SNPs and mRNA on the phenotype are referred to as “direct” effects.

PRIOR DISTRIBUTIONS FOR THE INTEGRATIVE MODEL

Bayesian approaches to model selection and shrinkage are useful for regression-based analysis of genomic data since the uncertainty in model choice can be incorporated into the inferences for genomic effects. Additionally, Markov chain Monte Carlo (MCMC) and stochastic search methods efficiently interrogate the model space without fitting all possible models. To model SNP effects on mRNA expression and a quantitative phenotype, we use SSVS for Bayesian model averaging with “shrinkage” of SNP effects toward zero [Conti et al., 2003; Conti and Gauderman, 2004; Fridley, 2009; George and McCulloch, 1993; Kim et al., 2004]. Under this SSVS prior model for the SNP effects, the prior distribution of each SNP coefficient is a mixture of two normal distributions that represent two cases: the SNP is selected for inclusion in the model or the SNP is not selected for inclusion in the model. Coefficients for SNPs included in the model have a normal prior distribution centered at zero with a large variance, while coefficients for SNPs not included in the model have a normal prior distribution centered at zero but with a small variance (and thus will be estimated close to zero).

For modeling the direct SNP effects (b_k `s), let φ = (φ<sub>1</sub>, φ<sub>2</sub>, …,φ<sub>K</sub>) be a vector of latent indicator variables for every SNP k = 1, …, K, where φ<sub>k</sub> = 1 if SNP<sub>k</sub> is included in the modeling of the phenotype or φ<sub>k</sub> = 0 if SNP<sub>k</sub> is omitted from modeling the phenotype. Next, the latent indicators are modeled as φ<sub>k</sub>|p<sub>b</sub> ~ Bernoulli (p<sub>b</sub>) with p<sub>b</sub> ~ Beta(α<sub>1</sub>, β<sub>1</sub>). To determine appropriate prior values for the parameters α<sub>1</sub> and β<sub>1</sub>, we followed an approach similar to one outlined by Chen et al. [2004]. We assumed a priori that only 10% of the K SNPs will be related to the phenotype, which suggests the mode of the prior distribution is 0.1. We further assumed that the prior mean will be 0.12, 20% larger than the prior mode, resulting in values of α<sub>1</sub> = 4.8 and β<sub>1</sub> = 35.2, where α<sub>1</sub> = (mean − 2 × mode × mean)/(mean − mode) and β<sub>1</sub> = [(1 − 2 × mode)(1 − mean)]/(mean − mode). Other possible priors for p<sub>b</sub> include p<sub>b</sub> ~ Uniform(0,1) or fixing p<sub>b</sub> to a constant (e.g. p<sup>b</sup> = 0.10). Similarly, for indirect SNP effects on the phenotype via the mRNA expression levels (ajk `s), let γ_j = (γ_j1, γ_j2, …, γ_jK) be a vector of latent indicator variables, where γ_jk = 1 if SNP K is included in the modeling of the mRNA expression level for gene j or γ_jk = 0 if SNP K is omitted from the modeling of mRNA gene expression level for each gene j = 1, …, J.

Using this prior SSVS model for the=SNP effects, the conditional distributions for the direct SNP effects (b_k `s) and the indirect SNP effects on the phenotype via mRNA gene expression (a<sub>jk</sub> `s) given their respective latent indicators are then given by

$$b_k\mid {\phi }_k~(1-{\phi }_k)N(0,w^2)+{\phi }_{k}N(0,z^2{w}^2)\text{for}j=1,\dots ,J\text{and}{a}_{\mathit{jk}}\mid {\gamma }_{\mathit{jk}}~(1-{\gamma }_{\mathit{jk}})N(0,w^2)+{\gamma }_{jk}N(0,z^2{w}^2)\text{for}j=1,\dots ,\mathrm{J}$$

for k = 1, …, K, where z and w are constants specified such that w² is small and z² w² is large. For our analyses, we chose to shrink coefficient estimates less than δ = 0.005 to zero and chose z = 50. This results in the value of w equal to 0.00179, using the formula $w=\sqrt{\frac{z^2-1}{2z^2\log \left(z\right)}}\times \delta$ [Gilks et al., 1996]. The reader is referred to George and McCulloch [1993] and Wakefield and Bennett [1996] for further insight and guidance on choice of z and w.

For the remaining parameters in the Bayesian integrative genomic model, diffuse proper prior distributions were placed on the model parameters. In particular, b₀ ~ N(0, 1,000), ${\sigma }_Y^{-2}~\mathit{Gamma}(0.01,0.01)$, ${\sigma }_{G{E}_j}^{-2}~\mathit{Gamma}(0.01,0.01)$, a₁₀, …, a_J0 ~ N(0, 1,000), c ~ MVN(μ_GE, V), μ_GE ~ MVN(μ, V_μ) and V ~ Wishart(R, J) with μ = (0, …, 0)^T and R = 0.1*I, where J is the number of gene expression variables in the model and I is the identity matrix.

SIMULATION STUDY

To assess the ability of the Bayesian integrative model to detect both direct and indirect effects, a simulation study was completed, with the simulation scenarios depicted in Figure 1. The first simulation scenario, Scenario A (Fig. 1A), includes two SNP effects on the phenotype and on the gene expression of the corresponding gene with the gene expression of these genes also associated with the phenotype. Scenario B (Fig. 1B) has two cis-SNP effects on gene expression with the gene expression associated with the phenotype. The third simulation scenario, Scenario C (Fig. 1C), consists of a SNP with both a direct-SNP effect on the phenotype and a cis-acting effect on gene expression, with the gene expression of this gene also associated with the phenotype. In addition to these effects, the gene expression of a second gene is also associated with the phenotype. The last simulation scenario is the null scenario (Scenario D) with no genomic effects on the phenotype (Fig. 1D).

Fig. 1.

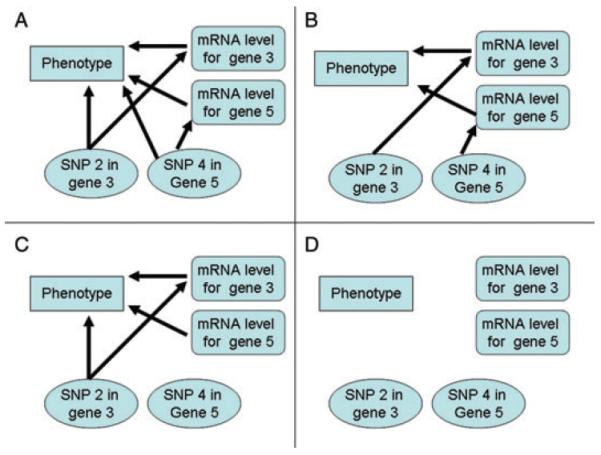
Diagram depicting the four simulation scenarios. (A) Scenario A includes two cis-acting SNP effects on gene expression and the phenotype; (B) Scenario B has two cis-acting SNPs on gene expression, with the gene expression associated with the phenotype; (C) Scenario C consists of a cis-acting SNP effect on gene expression and the phenotype with the expression of this gene also associated with the phenotype, along with the gene expression of a second gene associated with the phenotype; (D) Scenario D is the null scenario (no genomic effects on the phenotype).

Genotypic data for SNPs within five genes were simulated based on the genotypic data collected on 60 Caucasian cell lines from the gemcitabine pharmacogenomic study. SNPs were tagged using Haploview (http://www.broad.mit.edu/mpg/haploview/) [Barrett et al., 2005] using a threshold for r² of 0.64 and minor allele frequency of 0.05. This resulted in seven SNPs within Gene 1, 15 SNPs within Gene 2, five SNPs within Gene 3, eight SNPs within Gene 4, and four SNPs within Gene 5, with a total of 39 SNPs in the five genes. Haplotype frequencies were estimated using the haplo.em function within the haplo.stats R library (http://cran.r-project.org/web/packages/haplo.stats/index.html). For each cell line, the haplotype with the greatest estimated frequency was used as the “true” haplotype, creating an underlying population of 120 haplotypes. Six hundred haplotypes were simulated using the hapsim library in R (http://cran.r-project.org/web/packages/hapsim/index.html) based on this underlying haplotype population. These simulated haplotypes were then assigned to 300 simulated individuals.

Conditioned on the simulated genotypic data, mRNA expression data for five genes were simulated for each individual according to $G{E}_{\mathit{ij}}~N({\underset{¯}{a}}_j^T{\underset{¯}{SNP}}_i,{\sigma }_{GE}^2=1)$. Finally, a quantitative phenotype for each individual was simulated based on both SNP and mRNA values according to $Y_i~N({\underset{¯}{b}}^T{\underset{¯}{SNP}}_i+{\underset{¯}{c}}^T{\underset{¯}{GE}}_i,{\sigma }_Y^2=10)$. For the simulation scenarios, non-zero coefficients for gene expression effects on the phenotype (c) were chosen to be 0.4, whereas non-zero coefficients for SNP direct (b) and indirect (a_j) effects were set to 0.88 and 0.3, respectively. For the simulations, Gene 3 and Gene 5 were considered to have mRNA expression effects on the phenotype; SNP 2 in Gene 3 and SNP 4 in Gene 5 were consider to have genetic effects on the phenotype, with these two SNPs also having cis-acting effects on Gene 3 and Gene 5, respectively. The various scenarios are also depicted in Figure 1 and Table I. For each simulation, the mRNA expression data were standardized for each gene prior to analysis. Data for each scenario were simulated with n = 300 subjects and 50 replicates.

TABLE I.

Parameter values used in the simulation scenarios. Scenarios A, B, and C had genomic effects, while Scenario D was the null scenario (no genomic effects simulated)

		Scenario
Effect type	Parameter	A	B	C	D
Direct SNP	SNP 2 in Gene 3; b24	0.88	0	0.88	0
	SNP 4 in Gene 5; b39	0.88	0	0	0
Indirect SNP	cis-acting SNP 2 in Gene 3; a3,2	0.3	0.3	0.3	0
	cis-acting SNP 4 in Gene 5; a5,4	0.3	0.3	0	0
Direct mRNA	Gene 3; c3	0.4	0.4	0.4	0
	Gene 5; c5	0.4	0.4	0.4	0

Following the simulation of the synthetic datasets, each simulated data set was analyzed using both the standard APCA and the Bayesian integrative model assessing only cis-relationships. Each simulated data set included simulated mRNA expression data for five genes and genotypes for 39 SNPs within the five genes. For the APCA, significant effects were identified using a two-sided, Bonferroni-corrected P-value to account for multiple testing. For the Bayesian integrative model, SNP effects were considered significant (or selected) using the median model decision rule [Barbieri and Berger, 2004; Swartz et al., 2008] (i.e. P(γ_jk| data) ≥ 0.50 for indirect SNP effects or P(φ_k| data) ≥ 0.50 for direct SNP) and significant gene expression effects were identified according to their 95% posterior credible interval (i.e. if posterior credible interval does not contain zero). In addition to using the median model decision rule to determine if SNP effects were significant, we also considered significance of the SNP effects if the P(γ_jk | data) ≥ 0.25 or 0.35 and P(φ_k| data) ≥ 0.10, 0.15, or 0.25. While power and type I error rates are not clearly defined in the Bayesian framework, each coefficient was either declared to be significant or not. Power for the Bayesian integrative model was defined as the proportion of truly non-zero coefficients that were declared significant, while the type I error rates were defined as the proportion of truly zero coefficients declared significant.

RESULTS

SIMULATION STUDY

The type I error rate estimates and power estimates for Bayesian integrative model and APCA are presented in Tables II and III, respectively. Due to the difference in significance testing and philosophy of these two approaches, it is not possible to complete a fair “head-to-head” comparison of the approaches. For example, in the Bayesian analysis, the choice of prior can impact the error rates, along with there being no concept of adjustment for multiple testing. Therefore, we present the results for these two approaches in separate tables, noting the difference in interpretation of the results from these two contrasting approaches.

TABLE II.

Power and type I error rate estimates for the Bayesian integrative model for the three genetic models (Scenarios A, B, and C) and a null simulation scenario (Scenario D). Estimates are based on 50 simulations

Relationship assessed	Type I error rates					Power
		Scenario					Scenario
	Parameter	A	B	C	D	Parameter	A	B	C
Phenotype and mRNA expression	c's	0.053	0.053	0.060	0.068	c3	0.62	0.50	0.72
						c5	0.80	0.64	0.56
Indicator for SNP and mRNA expression relationshipa	γ					γ3,2 (SNP 24)
	0.25	0.053	0.045	0.043	0.013	0.25	0.84	0.78	0.68
	0.35	0.000	0.000	0.000	0.000	0.35	0.02	0.00	0.00
	0.50	0.000	0.000	0.000	0.000	0.50	0.00	0.00	0.00
						γ5,4 (SNP 39)
						0.25	0.90	0.96	–
						0.35	0.00	0.00	–
						0.50	0.00	0.00	–
Indicator for SNP and phenotype relationshipb	φ					φ 24
	0.10	0.999	0.998	0.999	0.997	0.10	1.00	–	1.00
	0.15	0.039	0.005	0.027	0.011	0.15	0.70	–	0.56
	0.25	0.001	0.000	0.000	0.000	0.25	0.60	–	0.00
	0.50	0.000	0.000	0.000	0.000	0.50	0.00	–	0.00
						φ 39
						0.10	1.00	–	–
						0.15	0.64	–	–
						0.25	0.06	–	–
						0.50	0.00	–	–

^aSignificance determined if P(γ| data) > 0.25, 0.35, or 0.50.

^bSignificance determined if P(φ| data) > 0.10, 0.15, 0.25, or 0.50.

TABLE III.

Power and type I error rate estimates for the APCA for the three genetic models (Scenarios A, B, and C) and a null simulation scenario (Scenario D). Estimates are based on 50 simulations and the Bonferroni adjusted P-values

Relationship assessed	Type I Error Rates				Power
	Scenario					Scenario
	A	B	C	D	Parameter	A	B	C
Phenotype and mRNA expression	0.000	0.000	0.000	0.000	c3	0.18	0.14	0.26
					c5	0.30	0.16	0.16
SNP and mRNA expression	0.001	0.001	0.001	0.000	a3,2	0.04	0.02	0.04
					a5,4	0.10	0.00	–
Phenotype and SNP	0.002	0.000	0.000	0.000	b24	0.10	–	0.06
					b39	0.12	–	–

For the Bayesian integrative model, the type I error rates ranged from 0.000 to 0.068 for the effects determined significant based on 95% credible intervals, while the type I error rates for the APCA approach had error rates that ranged from 0.000 to 0.002. The more conservative error rates for APCA are attributed to the Bonferroni adjustment for multiple testing, where effects were determined to be significant if the Bonferroni adjusted P-value was less than 0.05. However, as depicted in Table II, the choice of significance threshold for the SNP effects modeled with the SSVS mixture prior (e.g. P(γ| data) > 0.25, 0.35, or 0.50) greatly impacts the error rates. As the threshold in the posterior probability of the indicator given the data is lower, more variables are selected resulting in an increase in the type I error rate. In addition, the posterior distribution of the indicator variables is tied to the choice of normal priors used in the SSVS (e.g. choice of z and w) and the prior used for modeling p_b and p_b (e.g. p_b~Unif(0,1) or p_b ~ Beta(α₁, β₁)). If more “stringent” priors for the SNP effects were used, a larger amount of “shrinkage” would be completed resulting in fewer variables selected for the model.

Power estimates for the Bayesian integrative model, broken down for the various parameters and simulation scenarios are presented in Table II. Power for the mRNA effects on the phenotype (c₃ and c₅) ranged from 0.50 to 0.80. We have chosen to focus the rest of our discussion of power on the SNP effects, where significance is determined by P(γ| data) > 0.25 or P(φ| data) > 0.15, as these thresholds produced reasonable type I error rates. For the direct effects of SNPs on the phenotype, the power ranged from 0.56 to 0.70, while for the indirect SNP effects via mRNA, the power ranged from 0.68 to 0.96. The power for the standard APCA approach is presented in Table III. In contrast, power (controlling for type I error rate after adjustment for multiple testing at the 0.05 level) for the standard APCA approach was considerably lower, mostly due to the adjustment for multiple testing. The highest power was for detecting mRNA expression effects on the phenotype, as only five genes were tested (power ranged from 0.14 to 0.30). The power of detection for either SNP-phenotype association or cis-acting SNP-mRNA associations ranged from 0.00 to 0.12, with multiple testing adjustments for 39 SNP association tests. In an attempt to make a “fair” comparison of power for the APCA method and the Bayesian integrative model for detecting SNP effects (direct or indirect), the power must be observed where the type I error rates are similar. In this case, the significance for SNP effects would be determined using P(γ| data) > 0.35 and P(φ| data) > 0.25. Using this condition, both methods had low power to detect SNP-mRNA associations, along with the effect of SNP 4 in gene 5 on the phenotype (Bayesian power = 0.06, APCA power = 0.12 for Scenario A). However, for Scenario A, power to detect a SNP effect for SNP 2 in gene 3 was 0.60 for the Bayesian analysis and 0.10 for APCA.

PHARMACOGENOMIC STUDY OF GEMCITABINE

Next, we applied the Bayesian integrative model and the standard APCA approach to the gemcitabine study using the 171 cell lines that had both SNPs (265 SNPs in 15 genes) and mRNA expression variables (20 probe sets) measured within the gemcitabine pathway. All analyses were adjusted for race and gender, with the phenotype gemcitabine IC50 transformed to the log scale. To enable the assessment of both cis- and trans-acting SNPs on mRNA gene expression in the Bayesian integrative model, we further reduced the dimension of the genotype data and the complexity of the model space as follows. We partitioned SNPs within a gene into bins based on their correlation using a hierarchical clustering method [Rinaldo et al., 2005] with a liberal threshold of 0.05, followed by principal components analysis [Gauderman et al., 2007; Mardia et al., 1979] for SNPs within each bin. The first principal component for each bin of SNPs was used in the model as the “genotypic” variable, as opposed to the individual SNP genotypes. This dimension reduction approach resulted in 38 genotypic factors used in both the Bayesian integrative model and the APCA.

Significant associations of the phenotype IC50 with the genetic factors and mRNA expressions are presented in Table IV for both the Bayesian integrative model and the APCA approaches. Based on results from the simulation study, we chose to determine significant SNP effects if P(γ_jk| data) ≥ 0.25 for indirect SNP effects and P(φ_k| data) ≥ 0.15 for direct SNP. After using the Bonferroni adjustment to account for multiple testing within each effect type, the APCA identified three direct gene expression effects, zero direct SNP effects, and three indirect SNP effects. The Bayesian integrative model identified two direct gene expression effects (both were among the three identified by the APCA), zero direct SNP effects, and five indirect SNP effects (including the three identified by the APCA).

TABLE IV.

Associations detected in the gemcitabine study using the Bayesian integrative model or the all-APCA approaches. Results from different prior model specifications for p_a and p_b are presented for the Bayesian integrative model. Effects determined to be significant at the 0.05 level from the APCA (after adjustment for multiple testing) are included with bolded P-values. For the Bayesian integrative model, genomic variables are included if (1) the 95% credible interval for the direct mRNA expression effects did not contain zero; (2) the P(γ_jk | data) ≥ 0.25 with the Beta prior for the indirect SNP effect; or (3) the P(φ_k| data) ≥ 0.15 with Beta prior for the direct SNP effect

Effect type	mRNA gene expression variation	Genetic variation	APCA p-value	p ~ Beta posterior probability or 95% CI	p ~ Uniform posterior probability or 95% CI	p = 0.2 posterior probability or 95% CI
SNP—mRNA association or indirect SNP effect	SLC28A1	CMPK1	4.94e–4	0.35	0.22	0.65
	SLC28A2	NT5C1B	5.77e–3	0.25	0.13	0.53
	CMPK1	CMPK1	4.06e–4	0.37	0.20	0.70
	CDA	RRM2	3.97e–3	0.28	0.17	0.51
	NT5C3L	NT5C3L	1.42e–18	1.00	1.00	1.00
mRNA expression-—IC50 association or direct mRNA effect	SLC29A1	—	2.79e–3	(−0.225, 0.066)	(−0.225, 0.065)	(−0.226, 0.067)
	DCK	—	2.65e–3	(−0.266, −0.004)	(−0.267, −0.003)	(−0.267, −0.003)
	NT5C3	—	9.75e–6	(0.035, 0.266)	(0.034, 0.266)	(0.035, 0.267)

Table IV also includes results from a sensitivity analysis for the prior distribution of the latent variable inclusion probabilities. Alternative priors examined included p_a and p_b~Uniform(0,1) and p_a = p_b = 0.2. The analysis in which p_a and p_b~Uniform(0,1) was most conservative (posterior inclusion probabilities indirect SNP effects range from 0.13 to 1.00), while the analysis where p_a = p_b = 0.2 was the most liberal (posterior inclusion probabilities for indirect SNP effects range from 0.51 to 1.00). The top results (ranked by posterior probability) were similar across the three prior distributions used to model p_a and p_b, with the most significant effect for expression of NT5C3L detected by all models (P = 1.42e–18, posterior probability of selection of 1.00 for all three prior models).

DISCUSSION

Phenotypes related to an individual's response to a drug are likely the products of complex networks involving genetic variation, mRNA, proteins, etc. along with external environmental factors. Advances in technology are now allowing the acquisition of these multiple types of genomic data from a single set of samples. When combined with statistical methods appropriate for analyzing such complex networks, this data may generate substantial new insights into the genomic basis of complex traits and phenotypes, such as response to cancer therapeutics. In this paper, we proposed a novel Bayesian integrative model that combines ideas of path analysis with SSVS for a comprehensive modeling strategy. Results from applying this model to the pharmacogenomic study of the drug gemcitabine and simulation studies show the Bayesian integrative model is able to capture the relationship between SNP variation, mRNA expression variation, and the complex phenotype, if one exists.

In the specification of the prior model, we chose to use SSVS priors only for the SNP effects (direct and indirect) and not the mRNA effect, due to the small number of expression probe sets (in relation to the number of SNPs) included in the analysis. The model could be extended to also include SSVS priors on the mRNA expression effects. However, this would add an additional layer of complexity and computation time. Additional care in model specification and interpretation of results from this more complex model would also be needed, particularly in the context of the SNP indirect effects on the phenotype via mRNA.

Implementing the Bayesian integrative model for a comprehensive analysis offers several advantages. First, prior biological knowledge can be easily incorporated into the model thought the prior model specification. The incorporation of biological information will aid in the integrative model's ability to detect biologically relevant loci related to complex traits. Second, inference for a function of effects, such as the collective indirect effect of SNP k on the phenotype (${\sum }_{j=1}^J{a}_{\mathit{jk}}{c}_j$), can be conducted easily using MCMC and posterior credible intervals. Third, uncertainty related to selection of important genotype variables is accounted for as a form of Bayesian model averaging. The implementation of the Bayesian integrative model via MCMC is straightforward, however it comes with a high computational cost. The computational burden of the MCMC simulation limits the number of SNP or mRNA expression variables that can be included in association studies. Similar to previous proposed approaches involving SEM [Nock et al., 2007] or Bayesian approaches [Conti et al., 2003], our Bayesian integrative model is only able to handle a few hundred SNP and mRNA expression variables, such as those within a given pathway. However, as demonstrated with the gemcitabine study presented in this paper, one can reduce the dimensionality of genetic datasets to create manageably complex models. To follow-up the results from the Bayesian integrative model, standard regression techniques can be applied using the significant, possibly modified, genotype or gene-expression variables identified.

In conclusion, this paper presented a novel Bayesian integrative model for modeling the complex relationship between genetic variation in the form of SNPs and mRNA expression variation, and their collective impact on a complex phenotype. Further research is needed to develop integrative analysis approaches for the study of complex diseases and phenotypes. In particular, further research is required to extend and modify this integrative modeling framework to increase computational efficiency and extend this model to other data types to capitalize on the wealth of information available across multiple genomic data types.