Abstract
Purpose: The investigation of cortical porosity is an important aspect of understanding biological, pathoetiological, and biomechanical processes occurring within the skeleton. With the emergence of HR-pQCT as a noninvasive tool suitable for clinical use, cortical porosity at appendicular sites can be directly visualized in vivo. The aim of this study was to introduce a novel topological analysis of the cortical pore network for HR-pQCT data and determine the influence of resolution on measures of cortical pore network microstructure and topology.
Methods: Cadaveric radii were scanned using HR-pQCT at two different voxel sizes (41 and 82 μm) and also using μCT at a voxel size of 18 μm. HR-pQCT and μCT image sets were spatially coregistered. Segmentation and quantification of cortical porosity (Ct.Po) and mean pore diameter (Ct.Po.Dm) were achieved using an established extended cortical analysis technique. Topological classification of individual pores was performed using topology-preserving skeletonization and multicolor dilation algorithms. Based on the pore skeleton topological classification, the following parameters were quantified: total number of planar surface-skeleton canals (N.Slabs), tubular curve-skeleton canals (N.Tubes), and junction elements (N.Junctions), mean slab volume (Slab.Vol), mean tube volume (Tube.Vol), mean slab orientation (Slab.θ), mean tube orientation (Tube.θ), N.Slabs/N.Tubes, and integral (total) slab volume/integral tube volume (iSlab.Vol/iTube.Vol). An in vivo reproducibility study was also conducted to assess short-term precision of the topology parameters. Precision error was characterized using root mean square coefficient of variation (RMSCV%).
Results: Correlations to μCT values for Ct.Po were significant for both the 41 and 82 μm HR-pQCT data (41: r2 = 0.82, p < 0.001, 82: r2 = 0.75, p < 0.001). For Ct.Po.Dm, only the 41 μm data were significantly predictive of μCT values (r2 = 0.72, p < 0.01) Data at both HR-pQCT voxel sizes were strongly predictive of the μCT values for N.Slabs (41: r2 = 0.93, p < 0.001; 82: r2 = 0.84, p < 0.001), N.Tubes (41: r2 = 0.94, p < 0.001; 82: r2 = 0.84, p < 0.001), and N.Junctions (41: r2 = 0.93, p < 0.001; 82: r2 = 0.78, p < 0.001), though proportional bias was evident in these correlations. Weak correlations were seen for iSlab.Vol/iTube.Vol at both voxel sizes (41: r2 = 0.52, p < 0.01; 82: r2 = 0.39, p < 0.05). Slab.Vol was significantly correlated to μCT data at 41 μm (r2 = 0.60, p < 0.01) but not at 82 μm, while Tube.Vol was significantly correlated at both voxel sizes (41: r2 = 0.79, p < 0.001; 82: r2 = 0.68, p < 0.01). In vivo precision error for these parameters ranged from 2.31 to 9.68 RMSCV%.
Conclusions: Strong correlations between μCT- and HR-pQCT-derived measurements were found, particularly in HR-pQCT images obtained at 41 μm. These data are in agreement with our previous study investigating the effect of voxel size on standard HR-pQCT metrics of trabecular and cortical microstructure, and extend our previous findings to include topological descriptors of the cortical pore network.
Keywords: HR-pQCT, micro-CT, resolution, cortical porosity, structure
INTRODUCTION
Cortical bone strength is critical to skeletal integrity, particularly at appendicular sites where the cortex is responsible for the majority of axial load transfer.1, 2 The mechanical properties of cortical bone are influenced by many factors, including geometry, porosity, tissue composition, mineral distribution, lamellar organization, and collagen fibril orientation. Among these factors, porosity has been demonstrated to be a major determinant of strength, stiffness, and fracture toughness of cortical tissue.3, 4, 5, 6, 7, 8, 9 Cortical bone porosity is responsive to disease, therapy, and metabolic alterations. Further, cortical pore structure is dynamic, becoming increasingly interconnected and convoluted as age progresses.10, 11, 12, 13, 14 Cortical pore structure12, 13, 15, 16, 17 and its relationship to biomechanical parameters18 and fracture19, 20 have been studied extensively in the human femoral neck and shaft. At this site spatial clustering of remodeling osteons leads to merging of osteonal canals, producing “giant canals.”21 These large, asymmetric giant canals have a topology unique from discrete, tubular osteonal canals. Pore structure and distribution produce heterogeneous local strain and stress fields within cortical bone.22 Therefore it is likely that these giant canals serve as focal stress concentrations. As discrete canals intersect to become interconnected voids, whole bone fragility may be influenced. Clusters of remodeling osteons and giant canals are in fact more prevalent in fracture cases, suggesting that the structural realignment of porosity may be a mechanism of hip fracture.13, 19 Therefore the investigation of cortical microstructure is an important aspect of understanding biological, pathoetiological, and biomechanical processes occurring within the skeleton.
Structure of cortical porosity has been well-characterized through ex vivo evaluation techniques.17, 19, 23, 24, 25 Early efforts to create 3D representations of cortical porosity networks grew out of the realization that these networks are complex and difficult to interpret in two dimensions. Three-dimensional reconstructions of serial sections led to a new understanding of the branching patterns and remodeling processes of the cortex.10, 11 Today micro computed tomography (μCT)—particularly with a synchrotron radiation source—enables 3D visualization of cortical porosity in biopsy or cadaver specimens at spatial resolutions reaching the nanometer level.26, 27 Data produced by these techniques have been quantified using 3D structural parameters adapted from established analogs in trabecular bone morphology16, 18, 28, 29, 30 Applied to Volkmann's and Haversian canals, trabecular thickness becomes canal diameter (Ca.Dm) and is the most commonly assessed porosity structure parameter; however, Ca.Dm cannot capture topological shifts such as may occur as discrete tubular canals merge to create wide, planar pores.
With the emergence of high resolution peripheral quantitative computed tomography (HR-pQCT) as a noninvasive tool suitable for clinical use, 3D microstructure at appendicular sites can be directly visualized in vivo.31, 32, 33, 34 The current generation of HR-pQCT scanners provide volumetric data with voxel sizes of 41 and 82 μm (88 and 128 μm spatial resolution, respectively, 10% MTF).35 At these resolutions larger canals and resorption spaces can be visualized directly. Since the standard HR-pQCT analysis protocol mainly provides morphometric measures of trabecular microstructure (trabecular number, thickness, and separation), a number of analysis techniques have been developed to expand microstructural characterization of both trabecular and cortical compartments. One such technique is an extended cortical analysis that quantifies cortical porosity (Ct.Po) and pore diameter (Ct.Po.Dm).36, 37 Another approach to classify the nature of the trabecular network termed individual trabecula segmentation (ITS) analysis involves the spatial decomposition of the trabecular network into plate and rod elements.38, 39 This allows for the classification of individual trabeculae as either plate-like or rod-like and provides topological parameters for trabecular structure that are more descriptive than those generated by the standard clinical analysis. While HR-pQCT has become a useful tool for analyzing bone microstructure for in vivo studies, the gold standard remains μCT. Implementing novel analysis techniques for HR-pQCT, therefore, first requires validation by comparison to μCT.
The aim of this study is to introduce a novel topological analysis of the cortical pore network for HR-pQCT data and determine the influence of resolution on measures of cortical pore network microstructure and topology. Similar to the ITS analysis developed for the trabecular network, the analysis presented here classifies individual pores based on the topology of their skeletons, and calculates individual pore size, shape, and orientation. It does so by first applying a skeletonization algorithm to the cortical pore volume and subsequently assigning topological labels to each voxel. In order to validate and characterize the resolution dependence of the algorithm, specimens were scanned using HR-pQCT at two different voxel sizes (41 and 82 μm) and also using μCT at a voxel size of 18 μm.
METHODS
Specimens
Radii were obtained from 17 human cadavers (9 male, 8 female; 60–93 years of age). All specimens were received fresh frozen from National Disease Research Interchange (NDRI, Philadelphia, PA) and were kept frozen until 12 h before scanning. Specimens were obtained under a protocol that excluded donors with a known history of osteoporosis or other primary or metastatic diseases affecting bone. All specimens had partial soft tissue covering sections of the radius.
HR-pQCT imaging
Intact specimens were imaged using a clinical HR-pQCT scanner (XtremeCT, Scanco Medical AG, Brüttisellen, Switzerland) with the x-ray source potential of 60 kVp and a current of 900 μA. The remaining parameters for each scan varied depending on the desired voxel size. For images with an isotropic voxel size of 82 μm, 750 projections were acquired at a 100 ms integration time/projection. The 126 mm field of view (FOV) was then reconstructed across a 1536 × 1536 matrix, yielding the 82 μm voxel size. For images with an isotropic voxel size of 41 μm, 1000 projections were acquired at a 200 ms integration time/projection and subsequently reconstructed across a 3072 × 3072 matrix. The size of the detector was 3072 × 256; therefore, the projection images at 41 μm had no binning while the projection images at 82 μm were subjected to 2 × 2 binning.
Specimens were scanned at the standard in vivo radius imaging site, starting 9.5 mm proximal to the distal endplate and covering a distance of 9.02 mm in the proximal direction. Images consisted of 110 slices (yielding a voxel size of 9.02 mm/110 slices = 82 μm) and 220 slices (41 μm). The linear attenuation values generated from the reconstructions were converted to hydroxyapatite (HA) mineral densities using calibration data derived from a phantom provided by the manufacturer.
μCT imaging
After HR-pQCT imaging, specimens were dissected (soft tissue removed) and radii were cut using a diamond blade precision saw (IsoMet 1000, Buehler, Lake Bluff, IL) to a length overlapping the HR-pQCT imaging region. Marrow was removed using successive cycles of water jet treatment and Terg-a-zyme detergent (Alconox, New York, NY) followed by sonication. Specimens were then submerged in saline and vacuum degassed. Images were acquired using a desktop in vitro μCT system (μCT-40, Scanco Medical AG, Brüttisellen, Switzerland) with the x-ray source potential set to 70 kVp and a current of 114 mA. 1023 projections were acquired at a 400 ms integration time/projection, and the resulting projections were reconstructed across a 2048 × 2048 matrix, yielding an isotropic voxel size of 18 μm. Calibration of reconstructed linear attenuation values was performed using an HA phantom supplied by the manufacturer.
Image analysis
Periosteal contouring
For the HR-pQCT images, contours identifying the periosteal perimeter of the bone were drawn semiautomatically using an edge-finding algorithm previously described in the literature.31 All contours were examined manually and modified as necessary to ensure proper segmentation of bone. For the μCT images, periosteal contours were created semiautomatically by first identifying the periosteal perimeter using the edge-finding algorithm referenced above on every 25th slice and then interpolating throughout the whole sample.
Registration
In order to ensure that the same volume of interest (VOI) was analyzed across all image sets, the HR-pQCT and μCT image sets were spatially coregistered. For each specimen, the μCT image set was chosen as the fixed frame of reference, and each corresponding HR-pQCT image set was transformed accordingly by applying a 3D rigid transformation. For the purpose of determining the transformation, all grayscale images and periosteal contours were resampled using Image Processing Language (IPL v5.08b, Scanco Medical AG) to a voxel size of 82 μm to standardize image dimensions. Grayscale images were then aligned using Rview (http://rview.colin-studholme.net), a program that calculates a transformation matrix based on normalized mutual information.40 This transformation was applied to the HR-pQCT periosteal contours; the resulting transformed contours were subsequently overlaid with the corresponding μCT contours in IPL to extract the common region among all images. This contour consisting of the union between all three image sets was then inverse transformed and resampled as necessary to define the registered VOI for each HR-pQCT resolution.
Because of imprecision in the tissue cutting process, the full HR-pQCT volume was not available for analysis in the μCT data set. Those samples that had less than a 50% overlap of slices were discarded, resulting in a total of 14 samples that were suitable for analysis. All subsequent analysis was performed on the registered VOI of each specimen.
Cortical porosity segmentation
Segmentation of cortical porosity was achieved using an extended cortical analysis described in detail in Refs. 36 and 37. The first step in this process is the creation of a cortical mask. For the HR-pQCT data, this process initially requires a segmented image of the whole bone. This is done through application of a Laplace-Hamming (L-H) filter to the grayscale image followed by a fixed threshold binarization. The parameters for this process differed for each HR-pQCT voxel size; specific values have been documented in a previous study.35 The resulting segmented image and the periosteal contour generated previously were then used to create an endosteal contour through a series of dilations and erosions and the application of a connectivity filter.36 The cortical compartment was identified by subtracting the endosteal contour from the periosteal contour. For the μCT data, computational constraints prevented the automatic generation of endosteal contours. Specifically, the memory required to perform the series of dilation operations was beyond the capability of available workstations, so contours were created manually.
Application of the cortical mask generated above to a binary image of the bone provides an initial estimate of cortical porosity. For HR-pQCT images, the cortical mask was applied to the binary image created using a L-H filter and fixed threshold as described in previous publications.35, 36 For μCT images, the binary image was created by applying an automatically selected adaptive-iterative threshold to the original grayscale image.
The porosity segmentation is further refined by application of a 2D connectivity filter to exclude voids belonging to endosteal marrow space or extra-osseal compartments along with a hysteresis region-growing process to include intracortical pore voxels that were not identified by the initial porosity estimate.36 Parameters for the connectivity filter that were dependent on voxel size were scaled as necessary for each resolution data set.35
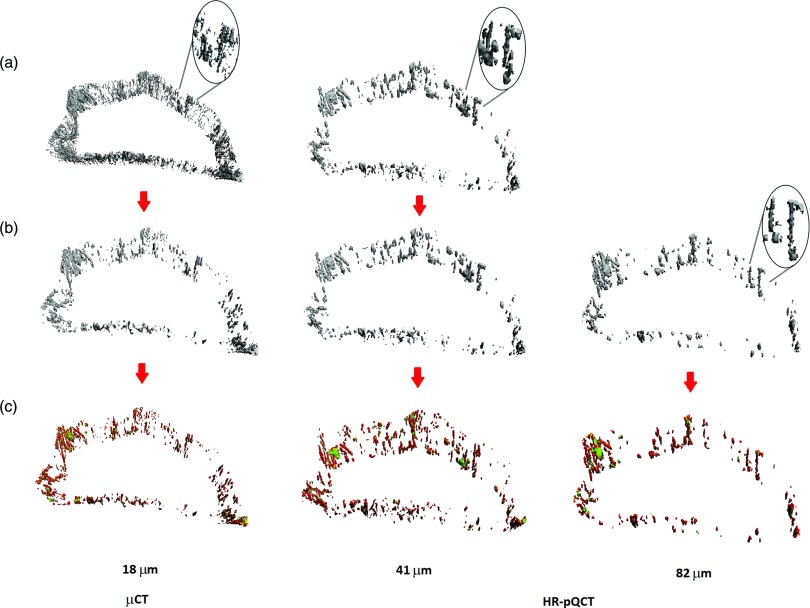
Due to the disparity in resolution between the HR-pQCT and μCT images, the level of pore structure captured using μCT vastly differed from that captured using HR-pQCT. To account for this difference in resolution, pores with a diameter smaller than 82 μm were removed from the μCT and the 41 μm HR-pQCT images prior to analysis [Fig. 1b]. A fixed diameter threshold was applied to the μCT and 41 μm HR-pQCT porosity thickness maps generated using a direct 3D sphere-filling technique.41 No diameter threshold was applied to the 82 μm porosity images. All further analysis was performed on the size-thresholded porosity images, and all results are presented for this subset of data.
Figure 1.
Representative volume renderings of the cortical porosity segmentation and the results of the pore topology analysis. (a) The initial cortical pore volume. (b) The cortical pore volume after application of a size threshold to remove all pores below 82 μm in diameter (initial cortical pore volume for the 82 μm HR-pQCT scan). (c) The topologically classified pore volume (green = slabs; red = tubes).
Cortical porosity skeletonization and classification
In order to define the topology of the pore network, the binary image of cortical porosity was skeletonized based on the MB-3D algorithm of Manzanera et al.42 The MB-3D algorithm is a medial surface, topology preserving technique previously implemented in trabecular bone analysis using μCT (Ref. 43) and magnetic resonance imaging.44, 45 MB-3D generated a skeleton with a thickness of up to two voxels, which was converted to a one-voxel-thick skeleton using conditional erosion.43 Each voxel was then labeled as surface, curve, or junction based on the topological numbers of Malandain et al.46 The one-voxel-thick labeled skeleton was further refined by iteratively removing one-voxel thick layers from surface edges, where the number of iterations was given by the slenderness parameter (s-value),43 and a new topological classification was performed at each iteration. The intent of this erosion was to reduce slender planes into curve elements. For the 82 μm HR-pQCT images, an s-value of 2 was chosen based on visual inspection of the resulting classified skeleton. The s-values used for the 41 μm HR-pQCT data and the μCT data were upscaled as necessary (41 μm: s = 4, μCT, s = 9), and the resulting skeletons were also visually inspected to ensure proper classification. Finally, the labeled slab/tube skeleton was propagated back to the initial volume using a dilation algorithm that minimizes directional bias, namely multicolor dilation43 [Fig. 1c]. All algorithms were implemented in-house45 using MATLAB (R2010b, The MathWorks, Inc.).
Parameter quantification
Based on the cortical pore binary volumes, cortical porosity (Ct.Po) and the mean and standard deviation of cortical pore diameter [Ct.Po.Dm (mm) and Ct.Po.Dm.SD (mm), respectively] were calculated as described in our previous publications.36 Briefly, Ct.Po was defined as the fraction of pore volume over the sum of the pore and cortical bone volume. Ct.Po.Dm was calculated based on a porosity thickness map generated via 3D sphere-filling.
Based on the pore skeletonization and classification, the total number of planar surface-skeleton canals (N.Slabs), tubular curve-skeleton canals (N.Tubes), and junction elements (N.Junctions) were calculated. The volume of each slab and tube was calculated from the propagated image, and mean slab volume [Slab.Vol (mm3)] and mean tube volume [Tube.Vol (mm3)] were quantified. The orientation of each element was defined as the angle from the longitudinal axis of the image volume (approximately colinear with the longitudinal axis of the forearm). Mean slab orientation [Slab.θ (degree)] and tube orientation [Tube.θ (degree)] were calculated. To investigate the overall structure of the cortical pore network, two ratios were calculated: N.Slabs/N.Tubes and integral (total) slab volume/integral tube volume (iSlab.Vol/iTube.Vol). Elements with an orientation of exactly 0° or 90° were excluded from all calculations, as these were associated with imaging and reconstruction artifacts.
In vivo reproducibility study
To evaluate the precision of the cortical microstructure analysis techniques and metrics described in Sec. 2D an existing reproducibility data set was retrospectively analyzed. The UCSF institutional review board for human research approved the study. The cohort consisted of 20 postmenopausal, osteopenic women 62 ± 7 years of age. All subjects were imaged on the clinical HR-pQCT scanner using the standard in vivo 82 μm nominal resolution protocol at the distal radius site.33 Each subject was imaged twice with complete repositioning between acquisitions. The analysis described above was applied and quantitative metrics were calculated for each image.
Statistical analysis
Means and standard deviations for each structural parameter were calculated. To facilitate comparison between the HR-pQCT and μCT images, the difference of each HR-pQCT value with respect to the μCT value was also calculated. Regression analysis was performed between each pair of μCT and HR-pQCT values (μCT vs 41 μm HR-pQCT, μCT vs 82 μm HR-pQCT), and the corresponding linear equations, correlation coefficients, and normalized root mean square error (CV(RMSE)) were tabulated. Bland-Altman plots were generated to qualitatively assess the agreement between μCT and HR-pQCT values. To identify parameters that showed significant resolution dependence, a repeated measures one-way analysis of variance (RMANOVA) was performed for each parameter across all voxel sizes. Those that showed resolution dependence were analyzed further using a post-hoc paired t-test. Precision error for the in vivo reproducibility study was characterized using root mean square coefficient of variation (RMSCV%). All statistical analysis was performed using JMP (Version 7.0, SAS Institute Inc., Cary, NC).
RESULTS
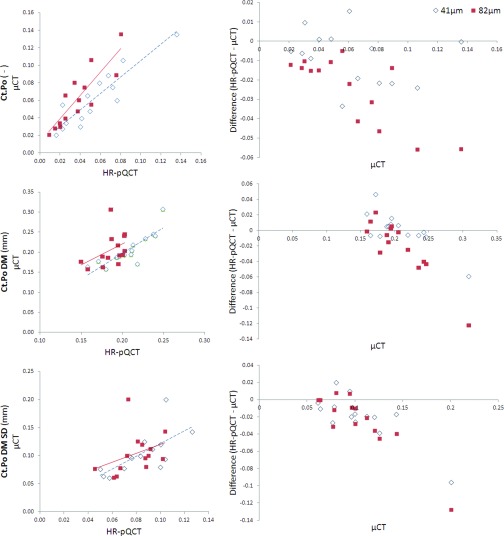
Regression data for cortical porosity measures are summarized in Table 1 and the associated Bland-Altman plots are shown in Fig. 2. Correlations for Ct.Po were significant for both the 41 and 82 μm HR-pQCT data (41: r2 = 0.82, p < 0.001, 82: r2 = 0.75, p < 0.001). For Ct.Po.Dm, only the 41 μm data were significantly predictive of μCT values (r2 = 0.72, p < 0.01); the correlation for the 82 μm data was nonsignificant. Ct.Po.Dm.SD was weakly correlated at 41 μm (r2 = 0.48, p < 0.01) and not correlated at 82 μm.
Table 1.
Regression data for microstructural and topological parameters.
| Voxel size (μm) | Slope | Intercept | r2 | CV(RMSE) | p value |
|---|---|---|---|---|---|
| Ct.Po | |||||
| 41 | 0.88 | 0.00 | 0.82 | 0.260 | 0.001 |
| 82 | 0.57 | 0.00 | 0.75 | 0.290 | 0.001 |
| Ct.Po.DM (mm) | |||||
| 41 | 0.56 | 0.09 | 0.72 | 0.07 | 0.001 |
| 82 | 0.18 | 0.15 | 0.19 | 0.08 | 0.12 |
| Ct.Po.DM.SD (mm) | |||||
| 41 | 0.42 | 0.04 | 0.48 | 0.20 | 0.006 |
| 82 | 0.16 | 0.06 | 0.13 | 0.20 | 0.21 |
| N.Slabs | |||||
| 41 | 0.22 | −68 | 0.93 | 0.26 | 0.001 |
| 82 | 0.04 | 11 | 0.84 | 0.33 | 0.001 |
| N.Tubes | |||||
| 41 | 0.22 | −61 | 0.94 | 0.22 | 0.001 |
| 82 | 0.05 | 47 | 0.84 | 0.29 | 0.001 |
| N.Slabs/N.Tubes | |||||
| 41 | −1.58 | 1.41 | 0.08 | 0.11 | 0.34 |
| 82 | 0.99 | −0.14 | 0.02 | 0.18 | 0.67 |
| iSlab.Vol/iTube.Vol | |||||
| 41 | 0.66 | 0.04 | 0.52 | 0.31 | 0.003 |
| 82 | 0.61 | 0.04 | 0.39 | 0.39 | 0.02 |
| N.Junctions | |||||
| 41 | 0.18 | −11.1 | 0.93 | 0.25 | 0.001 |
| 82 | 0.0 | −4.2 | 0.78 | 0.53 | 0.001 |
| Slab.Vol (mm3) | |||||
| 41 | 2.90 | 0.002 | 0.60 | 0.24 | 0.001 |
| 82 | 3.90 | 0.009 | 0.16 | 0.40 | 0.16 |
| Tube.Vol (mm3) | |||||
| 41 | 3.91 | 0.002 | 0.79 | 0.09 | 0.001 |
| 82 | 6.91 | 0.008 | 0.68 | 0.10 | 0.001 |
| Slab.θ (deg) | |||||
| 41 | −0.07 | 62 | 0.00 | 0.07 | 0.85 |
| 82 | −0.20 | 66 | 0.02 | 0.09 | 0.65 |
| Tube.θ (deg) | |||||
| 41 | −0.14 | 45 | 0.02 | 0.09 | 0.59 |
| 82 | 0.12 | 30 | 0.02 | 0.09 | 0.65 |
Figure 2.
Regression and Bland-Altman plots for cortical porosity parameters. Regression data are summarized in Table 1. Slight proportional bias is evident in the Bland-Altman plots for Ct.Po (82 μm only), Ct.Po DM, and Ct.Po DM SD.
Ct.Po was underestimated by HR-pQCT at both voxel sizes (Table 2), with the 41 μm data providing the greatest accuracy. The Bland-Altman plot for the 82 μm Ct.Po data displayed proportional bias with a pattern of stronger underestimation at higher values. Ct.Po.Dm at 41 μm was not significantly different from that measured using μCT. In contrast, Ct.Po.Dm at 82 μm was significantly lower than the μCT values and displayed proportional bias with a pattern of stronger underestimation at higher values.
Table 2.
Mean ± SD for cortical pore microstructure and topology parameters.1
| μCT (18 μm) | HR-pQCT (41 μm) | HR-pQCT (82 μm) | |
|---|---|---|---|
| Ct.Po | 0.062 ± 0.033 | 0.054 ± 0.0322 | 0.037 ± 0.0213 |
| Ct.Po.DM (mm) | 0.207 ± 0.04 | 0.208 ± 0.027 | 0.186 ± 0.017 |
| Ct.Po.DM.SD (mm) | 0.104 ± 0.036 | 0.084 ± 0.0222 | 0.079 ± 0.0162 |
| N.Slabs | 2144 ± 1706 | 397 ± 3843 | 106 ± 823 |
| N.Tubes | 3697 ± 2970 | 770 ± 6873 | 233 ± 1633 |
| N.Slabs/N.Tubes | 0.58 ± 0.01 | 0.49 ± 0.063 | 0.43 ± 0.083 |
| iSlab.Vol/iTube.Vol | 0.39 ± 0.14 | 0.30 ± 0.134 | 0.28 ± 0.144 |
| N.Junctions | 4873 ± 4142 | 772 ± 8133 | 179 ± 1513 |
| Slab.Vol (mm3) | 0.0017 ± 0.0007 | 0.007 ± 0.00263 | 0.0161 ± 0.00673 |
| Slab.Vol.SD (mm3) | 0.0099 ± 0.0067 | 0.0285 ± 0.01753 | 0.0436 ± 0.02983 |
| Tube.Vol (mm3) | 0.0025 ± 0.0005 | 0.0119 ± 0.00233 | 0.0258 ± 0.00433 |
| Tube.Vol.SD (mm3) | 0.003 ± 0.0009 | 0.0122 ± 0.0033 | 0.0234 ± 0.00453 |
| Slab.θ (deg) | 60.2 ± 3.3 | 57.6 ± 3.9 | 54.2 ± 4.94 |
| Slab.θ.SD (deg) | 32.0 ± 3.4 | 30.6 ± 3.1 | 25.7 ± 5.63 |
| Tube.θ (deg) | 47.7 ± 3.6 | 38.2 ± 3.33 | 35.4 ± 3.13 |
| Tube.θ.SD (deg) | 27.0 ± 5.2 | 22.7 ± 12 | 21.6 ± 1.13 |
Statistical significance of differences between μCT and HR-pQCT determined by RMANOVA and post-hoc t-tests.
p < 0.05.
p < 0.001.
p < 0.01.
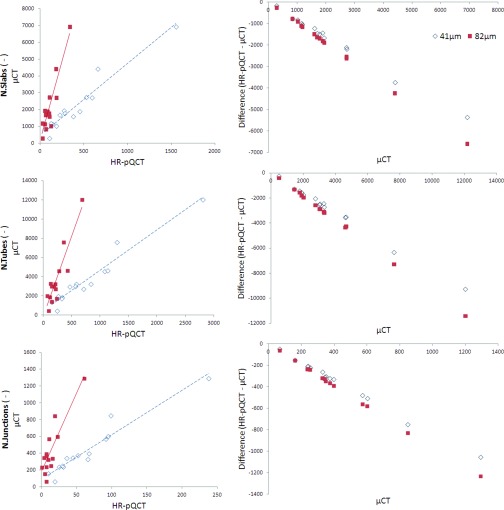
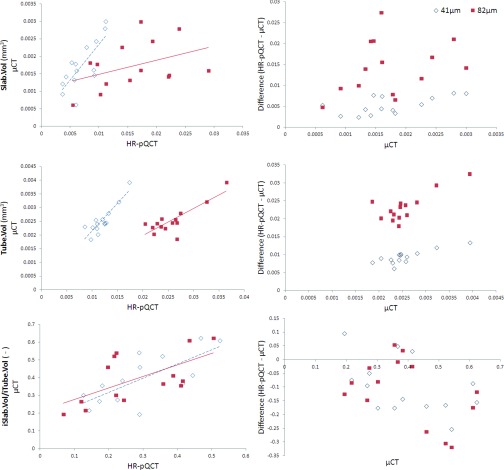
Regression data for the topology parameters are summarized in Table 1 and the associated Bland-Altman plots are shown in Figs. 34. Both HR-pQCT voxel sizes were strongly predictive of the μCT values for N.Slabs (41: r2 = 0.93, p < 0.001; 82: r2 = 0.84, p < 0.001), N.Tubes (41: r2 = 0.94, p < 0.001; 82: r2 = 0.84, p < 0.001), and N.Junctions (41: r2 = 0.93, p < 0.001; 82: r2 = 0.78, p < 0.001). While correlations for N.Slabs/N.Tubes were not significant at 41 and 82 μm (possibly due to the very small range of values for this parameter across samples), weak correlations were seen for iSlab.Vol/iTube.Vol at both voxel sizes (41: r2 = 0.52, p < 0.01; 82: r2 = 0.39, p < 0.05). Slab.Vol was significantly correlated to μCT data at 41 μm (r2 = 0.60, p < 0.01) but not at 82 μm, while Tube.Vol was significantly correlated at both voxel sizes (41: r2 = 0.79, p < 0.001; 82: r2 = 0.68, p < 0.01). Orientation parameters measured using HR-pQCT were not correlated with μCT values. CV(RMSE) was minimized for all topology parameters using the 41 μm data.
Figure 3.
Regression and Bland-Altman plots for topology parameters. Regression data are summarized in Table 1. Strong proportional bias is evident in the Bland-Altman plots.
Figure 4.
Regression and Bland-Altman plots for volume parameters. Regression data are summarized in Table 1. Slight proportional bias exists in the Bland-Altman plot for Tube.Vol only.
For all topological parameters, the 41 μm data minimized differences between HR-pQCT and μCT (Table 2). N.Slabs, N.Tubes, N.Junctions were underestimated by HR-pQCT at both voxel sizes. For these parameters, Bland-Altman plots showed strong proportional bias, with the degree of underestimation increasing at higher values. N.Slabs/N.Tubes and iSlab.Vol/iTube.Vol were also underestimated at 41 and 82 μm. Slab.Vol and Tube.Vol were significantly overestimated at 41 and 82 μm. Bland-Altman plots showed a fixed offset for Slab.Vol and iSlab.Vol/iTube.Vol, but a trend towards a proportional bias for Tube.Vol, with overestimation increasing at larger values.
In vivo precision error for cortical pore topology parameters ranged from 2.31 to 9.68 RMSCV% (Table 3).
Table 3.
RMSCV% for cortical pore topology parameters derived from in vivo repeat scans at 82 μm.
| RMSCV% | |
|---|---|
| N.Slabs | 5.01% |
| N.Tubes | 4.46% |
| N.Slabs/N.Tubes | 2.31% |
| iSlab.Vol/iTube.Vol | 9.68% |
| N.Junctions | 9.58% |
| Slab.Vol (mm3) | 9.03% |
| Slab.Vol.SD (mm3) | 14.07% |
| Tube.Vol (mm3) | 4.23% |
| Tube.Vol.SD (mm3) | 6.95% |
| Slab.θ (deg) | 4.24% |
| Slab.θ.SD (deg) | 5.94% |
| Tube.θ (deg) | 2.61% |
| Tube.θ.SD (deg) | 3.15% |
DISCUSSION
The objectives of this study were to introduce topological analysis of the cortical pore network in the context of HR-pQCT image data and to investigate the resolution-dependence of pore microstructure and topology parameters. Topological analysis of the pore network facilitates the classification of individual pores based on their skeleton topology, quantification of individual pore volume and orientation, and direct assessment of pore network connectivity, total pore number, and distribution. In conjunction with established cortical microstructure parameters describing overall pore volume and mean pore diameter, these techniques and measurements augment our capability to evaluate microstructural changes within the cortex. To assess resolution-dependence of pore microstructure and topology parameters, cadaveric specimens were imaged using μCT at 18 μm nominal resolution and HR-pQCT at 41 and 82 μm nominal resolutions. Strong correlations between μCT- and HR-pQCT-derived measurements were found, particularly in HR-pQCT images obtained at 41 μm. These data are in agreement with our previous study investigating the effect of voxel size on standard HR-pQCT metrics of trabecular and cortical microstructure, and extend our previous findings to include topological descriptors of the cortical pore network.
Topologic classification of the pore network facilitates a number of potentially important analyses. First, topological analysis in combination with finite element analysis can be used to determine the impact of pore topology on local stress distribution and whole-bone strength. Second, topological classification can facilitate investigation of morphological mechanisms of pore network expansion, for example, through a preferential increase in number and volume of slab canals as we have documented in the case of disuse.47 Third, topological classification may aid in the identification of pores belonging to the Haversian system vs marrow space to define the endosteal envelope for more precise classification of trabecular and cortical compartments. Fourth, decomposition of the network allows the calculation of pore volume, a more robust measure of pore size than Ca.Dm or Ct.Po.Dm, which are limited by the smallest dimension. Fifth, identification of junctions by topological analysis facilitates the calculation of pore network connectivity (N.junctions per unit volume). An alternative approach to measuring connectivity—using the Euler number to estimate the number of connections that can be removed without separating one part of the structure48—is not well suited for the analysis of cortical porosity, where the structure cannot be regarded as a tightly packed mesh of closed loops.28 Finally, decomposition of the pore network enables the calculation of true pore number (and number of each topological subset). The alternative, derived from the mean distance transform of the pore skeleton, provides a single mean value in units of 1/mm, and can be confounded by boundary effects due to the narrow cortical envelope relative to intercanal distances.
As with the cortical porosity measures, the results generated from the pore skeletonization analysis were most accurate using the 41 μm data. Along with previously published data examining the resolution dependence of trabecular microstructure parameters,35 the results presented here display a clear pattern of increasing accuracy with smaller HR-pQCT voxel sizes. These results further support the implementation of a smaller HR-pQCT voxel size than the current clinical standard of 82 μm. However, a number of factors must be taken into account when proposing clinical scans at 41 μm, including radiation dose, scan time, and scan quality. The radiation dose for in vivo 41 μm scans will be higher (approximately 7.5 μSv (Ref. 35) compared to 3 μSv for 82 μm scans) but still within a very low range in comparison to natural background radiation exposure and other ionizing radiation imaging techniques. HR-pQCT imaging at 41 μm produces lower signal to noise ratio (52.4 in comparison to 61.8 for 82 μm scans35) and requires a longer scan time (5.6 min in comparison to 2.8 min for 82 μm scans). Importantly, in terms of applicability to clinical in vivo studies, a longer scan increases the probability of patient motion. Motion artifacts can lead to significant errors in microstructural measures at 82 μm;49 this problem would likely be exacerbated for scans at 41 μm. Unfortunately there are no data comparing motion artifacts, overall scan quality, and reproducibility in 41 and 82 μm in vivo scans. The data presented in this work and in our previous publication underscores the importance of evaluating these issues.
Correlation coefficients between HR-pQCT and μCT values for topological parameters were found to be similar to or better than those for standard metrics of cortical microstructure. Correlations for N.Slabs, N.Tubes, and N.Junctions were higher than that found for Ct.Po. Correlations for Slab.Vol and Tube.Vol were similar to that found for Ct.Po.Dm, with the correlation for Tube.Vol at 82 μm significantly higher than the correlation for Ct.Po.Dm at 82 μm. However, correlations between HR-pQCT and μCT values for cortical microstructure and topology were lower than previously reported correlations for trabecular microstructure,34, 35 driven by the small dimensions of cortical porosity relative to HR-pQCT resolution. In addition, strong proportional bias exists for some of the topological parameters. In particular, N.Slabs, N.Tubes, and N.Junctions are increasingly underestimated by HR-pQCT as the number of elements increases. A sample with many elements will have a more complex microstructure, which will be simplified at lower resolutions and appear as fewer, larger elements. The overestimation of Slab.Vol and Tube.Vol by HR-pQCT reflects this phenomenon.
Despite the exclusion of voxels representing Ct.Po.Dm less than 82 μm, N.Slabs and N.Tubes were underestimated by HR-pQCT. This appears to be a result of a simplified pore network representation in the HR-pQCT images, where multiple pores and junctions appear as a single large unified pore. Accordingly, Slab.Vol and Tube.Vol were overestimated by HR-pQCT. These trends are consistent with the resolution dependence for canal number and canal volume found by Cooper et al.15 in cortical bone samples imaged at 5, 10, and 15 μm voxel sizes. In our analysis, larger voxel sizes also resulted in a bias towards identifying more canals as tubes. Ratios comparing the relative proportions of slabs and tubes (iSlab.Vol/iTube.Vol and N.Slabs/N.Tubes) were significantly lower at 41 and 82 μm compared to the μCT data. This bias is most likely driven by artifacts influencing pore segmentation, which in the HR-pQCT images may lead to attenuated pore structures, resulting in classification of more pores as tubes.
Correlations for canal orientation were nonsignificant at both HR-pQCT voxel sizes. While resolution may influence this, inconsistencies in specimen placement during HR-pQCT and μCT scanning may also play a role. Orientation was defined relative to the axes of the image volume. The registration process created a set of common masks rather than transforming the images themselves; images were not transformed to a common reference frame. Therefore, the calculated canal orientation is dependent on the position of the specimen during imaging. Correlations for canal orientation may improve if variance in specimen positioning is reduced, or if orientation is calculated with respect to true anatomical axes rather than image axes.
Reproducibility of the topological metrics of pore microstructure calculated from patient scans using the standard 82 μm imaging protocol was comparable to the level of in vivo precision reported previously for established metrics of trabecular and cortical microstructure.33, 36, 50 However, in vivo precision at 41 μm nominal resolution will be affected by lower signal-to-noise and increased motion artifacts, and must be assessed prior to applying this technique to in vivo scanning at 41 μm.
A clear limitation of HR-pQCT-based evaluation of the cortical pore network is that HR-pQCT cannot resolve cortical porosity at the level of the smallest Haversian and Volkmann canals. However, the power of HR-pQCT indices of cortical porosity to discriminate fracture status, menopausal status, race, and age51, 52, 53, 54 have demonstrated the practical utility of evaluating resolvable microstructure. Additionally, in cohorts experiencing pathologic porosity increases, pore sizes are considerably larger than the resolution limit of HR-pQCT.2, 33 In determining the resolution-dependence of pore microstructure and topology parameters, voxels representing pores with Ct.Po.Dm less than 82 μm were excluded from analysis. This was done because the development and application of this analysis technique is in the context of resolvable microstructure rather than complete microstructure. Further, acknowledging the hierarchical nature of cortical pore microstructure, we aim to focus on the analysis of large and possibly pathological pores rather than small pores, lacunae, or canaliculi. The correlations obtained from this size-limited subset of porosity are consistent with those reported in an earlier study of standard HR-pQCT trabecular and cortical microstructure parameters in which the full level of porosity was analyzed.35 At 41 μm, the correlation for Ct.Po based on the size-limited subset of porosity (r2 = 0.82, p < 0.001) was similar to the value calculated using the full porosity image (r2 = 0.84, p < 0.001); at 82 μm, the correlation for Ct.Po slightly strengthened using the size-limited subset (subset: r2 = 0.75, p < 0.001; full: r2 = 0.61, p < 0.05). At 41 μm, the correlation for Ct.Po.Dm was strengthened when evaluating the size-limited subset (subset: r2 = 0.72, p < 0.01; full: r2 = 0.36, p < 0.05); at 82 μm, however, correlations for Ct.Po.Dm were nonsignificant for both the subset and the full pore image. The results presented here might change if different exclusion criteria were applied. Exclusion based on canal volume, for example, is another approach to account for the inherent resolution difference between HR-pQCT and μCT images.
Additional limitations of this specimen study include the advanced age of specimen donors and the nonphysiologic preparation of specimens. All specimens were drawn from an elderly population, potentially limiting the applicability of results to younger cohorts. Radii were isolated prior to imaging, therefore most soft tissue as well as the ulna were not present during the scan. This limits the ability of the ex vivo scans to simulate in vivo data.
This ex vivo validation study establishes the accuracy and voxel size dependence of pore microstructure and topology analysis as a basis for application to in vivo studies. With the advent of HR-pQCT, in vivo imaging and evaluation of cortical microstructure has become an area of much interest and activity. The literature to date has established the accuracy, reproducibility, and utility of HR-pQCT in characterizing cortical porosity in various populations and conditions. However, little effort has been focused on understanding the pathoetiology associated with microstructural changes in longitudinal HR-pQCT studies. As porosity increases, is pore size simply increasing? Or are new pores being formed? As pore size or number increases, do pores become more interconnected? Is increased porosity driven by expansion of the Haversian system, the marrow cavity, or both? The answers to these questions are critical for understanding the mechanisms underlying cortical microstructure changes, as well as the biomechanical impact of these changes. In this context, the accurate quantification of porosity structure measures is very important in determining bone health and strength.
ACKNOWLEDGMENTS
This publication was supported by NIH K01 AR056734, NIH R01 AR060700, and NIH RO1 AG17762. The authors have no conflicts of interest.
References
- MacNeil J. A. and Boyd S. K., “Load distribution and the predictive power of morphological indices in the distal radius and tibia by high resolution peripheral quantitative computed tomography,” Bone 41, 129–137 (2007). 10.1016/j.bone.2007.02.029 [DOI] [PubMed] [Google Scholar]
- Burghardt A. J., Kazakia G. J., Ramachandran S., Link T. M., and Majumdar S., “Age- and gender-related differences in the geometric properties and biomechanical significance of intracortical porosity in the distal radius and tibia,” J. Bone Miner. Res. 25, 983–993 (2010). 10.1359/jbmr.091104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCalden R. W., McGeough J. A., Barker M. B., and Court-Brown C. M., “Age-related changes in the tensile properties of cortical bone. The relative importance of changes in porosity, mineralization, and microstructure,” J. Bone Jt. Surg., Am. Vol. 75, 1193–1205 (1993). [DOI] [PubMed] [Google Scholar]
- Currey J. D., “The effect of porosity and mineral content on the Young's modulus of elasticity of compact bone,” J. Biomech. 21, 131–139 (1988). 10.1016/0021-9290(88)90006-1 [DOI] [PubMed] [Google Scholar]
- Schaffler M. B. and Burr D. B., “Stiffness of compact bone: Effects of porosity and density,” J. Biomech. 21, 13–16 (1988). 10.1016/0021-9290(88)90186-8 [DOI] [PubMed] [Google Scholar]
- Yeni Y. N. and Norman T. L., “Fracture toughness of human femoral neck: Effect of microstructure, composition, and age,” Bone 26, 499–504 (2000). 10.1016/S8756-3282(00)00258-1 [DOI] [PubMed] [Google Scholar]
- Wachter N. J., Krischak G. D., Mentzel M., Sarkar M. R., Ebinger T., Kinzl L., Claes L., and Augat P., “Correlation of bone mineral density with strength and microstructural parameters of cortical bone in vitro,” Bone 31, 90–95 (2002). 10.1016/S8756-3282(02)00779-2 [DOI] [PubMed] [Google Scholar]
- Ural A. and Vashishth D., “Effects of intracortical porosity on fracture toughness in aging human bone: A microCT-based cohesive finite element study,” J. Biomech. Eng. 129, 625–631 (2007). 10.1115/1.2768377 [DOI] [PubMed] [Google Scholar]
- Yeni Y. N., Brown C. U., Wang Z., and Norman T. L., “The influence of bone morphology on fracture toughness of the human femur and tibia,” Bone 21, 453–459 (1997). 10.1016/S8756-3282(97)00173-7 [DOI] [PubMed] [Google Scholar]
- Stout S. D., Brunsden B. S., Hildebolt C. F., Commean P. K., Smith K. E., and Tappen N. C., “Computer-assisted 3D reconstruction of serial sections of cortical bone to determine the 3D structure of osteons,” Calcif. Tissue Int. 65, 280–284 (1999). 10.1007/s002239900699 [DOI] [PubMed] [Google Scholar]
- Tappen N. C., “Three-dimensional studies on resorption spaces and developing osteons,” Am. J. Anat. 149, 301–317 (1977). 10.1002/aja.1001490302 [DOI] [PubMed] [Google Scholar]
- Cooper D. M., Thomas C. D., Clement J. G., Turinsky A. L., Sensen C. W., and Hallgrimsson B., “Age-dependent change in the 3D structure of cortical porosity at the human femoral midshaft,” Bone 40, 957–965 (2007). 10.1016/j.bone.2006.11.011 [DOI] [PubMed] [Google Scholar]
- Bell K. L., Loveridge N., Reeve J., Thomas C. D., Feik S. A., and Clement J. G., “Super-osteons (remodeling clusters) in the cortex of the femoral shaft: Influence of age and gender,” Anat. Rec. 264, 378–386 (2001). 10.1002/ar.10014 [DOI] [PubMed] [Google Scholar]
- Chen H., Zhou X., Shoumura S., Emura S., and Bunai Y., “Age- and gender-dependent changes in three-dimensional microstructure of cortical and trabecular bone at the human femoral neck,” Osteoporosis Int. 21, 627–636 (2010). 10.1007/s00198-009-0993-z [DOI] [PubMed] [Google Scholar]
- Cooper D., Turinsky A., Sensen C., and Hallgrimsson B., “Effect of voxel size on 3D micro-CT analysis of cortical bone porosity,” Calcif. Tissue Int. 80, 211–219 (2007). 10.1007/s00223-005-0274-6 [DOI] [PubMed] [Google Scholar]
- Bousson V., Peyrin F., Bergot C., Hausard M., Sautet A., and Laredo J. D., “Cortical bone in the human femoral neck: Three-dimensional appearance and porosity using synchrotron radiation,” J. Bone Miner. Res. 19, 794–801 (2004). 10.1359/jbmr.040124 [DOI] [PubMed] [Google Scholar]
- Thompson D. D., “Age changes in bone mineralization, cortical thickness, and haversian canal area,” Calcif. Tissue Int. 31, 5–11 (1980). 10.1007/BF02407161 [DOI] [PubMed] [Google Scholar]
- Basillais A., Bensamoun S., Chappard C., Brunet-Imbault B., Lemineur G., Ilharreborde B., Ba Tho M. C. Ho, and Benhamou C. L., “Three-dimensional characterization of cortical bone microstructure by microcomputed tomography: Validation with ultrasonic and microscopic measurements,” J. Orthop. Sci. 12, 141–148 (2007). 10.1007/s00776-006-1104-z [DOI] [PubMed] [Google Scholar]
- Bell K. L., Loveridge N., Jordan G. R., Power J., Constant C. R., and Reeve J., “A novel mechanism for induction of increased cortical porosity in cases of intracapsular hip fracture,” Bone 27, 297–304 (2000). 10.1016/S8756-3282(00)00318-5 [DOI] [PubMed] [Google Scholar]
- Jordan G. R., Loveridge N., Bell K. L., Power J., Rushton N., and Reeve J., “Spatial clustering of remodeling osteons in the femoral neck cortex: A cause of weakness in hip fracture?” Bone 26, 305–313 (2000). 10.1016/S8756-3282(99)00272-0 [DOI] [PubMed] [Google Scholar]
- Bell K. L., Loveridge N., Power J., Garrahan N., Meggitt B. F., and Reeve J., “Regional differences in cortical porosity in the fractured femoral neck,” Bone 24, 57–64 (1999). 10.1016/S8756-3282(98)00143-4 [DOI] [PubMed] [Google Scholar]
- Hoc T., Henry L., Verdier M., Aubry D., Sedel L., and Meunier A., “Effect of microstructure on the mechanical properties of Haversian cortical bone,” Bone 38, 466–474 (2006). 10.1016/j.bone.2005.09.017 [DOI] [PubMed] [Google Scholar]
- Ferretti M., Muglia M. A., Remaggi F., Cane V., and Palumbo C., “Histomorphometric study on the osteocyte lacuno-canalicular network in animals of different species. II. Parallel-fibered and lamellar bones,” Ital. J. Anat. Embryol. 104, 121–131 (1999). [PubMed] [Google Scholar]
- Nyssen-Behets C., Duchesne P. Y., and Dhem A., “Structural changes with aging in cortical bone of the human tibia,” Gerontology 43, 316–325 (1997). 10.1159/000213871 [DOI] [PubMed] [Google Scholar]
- Raum K., Leguerney I., Chandelier F., Talmant M., Saied A., Peyrin F., and Laugier P., “Site-matched assessment of structural and tissue properties of cortical bone using scanning acoustic microscopy and synchrotron radiation muCT,” Phys. Med. Biol. 51, 733–746 (2006). 10.1088/0031-9155/51/3/017 [DOI] [PubMed] [Google Scholar]
- Schneider P., Stauber M., Voide R., Stampanoni M., Donahue L. R., and Muller R., “Ultrastructural properties in cortical bone vary greatly in two inbred strains of mice as assessed by synchrotron light based micro- and nano-CT,” J. Bone Miner. Res. 22, 1557–1570 (2007). 10.1359/jbmr.070703 [DOI] [PubMed] [Google Scholar]
- Thurner P. J., Chen C. G., Ionova-Martin S., Sun L., Harman A., Porter A., Ager J. W. 3rd, Ritchie R. O., and Alliston T., “Osteopontin deficiency increases bone fragility but preserves bone mass,” Bone 46, 1564–1573 (2010). 10.1016/j.bone.2010.02.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper D. M., Turinsky A. L., Sensen C. W., and Hallgrimsson B., “Quantitative 3D analysis of the canal network in cortical bone by micro-computed tomography,” Anat. Rec. Part B 274B(1), 169–179 (2003). 10.1002/ar.b.10024 [DOI] [PubMed] [Google Scholar]
- Chappard C., Bensalah S., Olivier C., Gouttenoire P. J., Marchadier A., Benhamou C., and Peyrin F., “3D characterization of pores in the cortical bone of human femur in the elderly at different locations as determined by synchrotron micro-computed tomography images,” Osteoporosis Int. 24, 1023–1033 (2013). 10.1007/s00198-012-2044-4 [DOI] [PubMed] [Google Scholar]
- Schneider P., Voide R., Stampanoni M., Donahue L. R., and Muller R., “The importance of the intracortical canal network for murine bone mechanics,” Bone 53, 120–128 (2013). 10.1016/j.bone.2012.11.024 [DOI] [PubMed] [Google Scholar]
- Laib A., Hauselmann H. J., and Ruegsegger P., “In vivo high resolution 3D-QCT of the human forearm,” Technol. Health Care 6, 329–337 (1998). [PubMed] [Google Scholar]
- Boutroy S., Bouxsein M. L., Munoz F., and Delmas P. D., “In vivo assessment of trabecular bone microarchitecture by high-resolution peripheral quantitative computed tomography,” J. Clin. Endocrinol. Metab. 90, 6508–6515 (2005). 10.1210/jc.2005-1258 [DOI] [PubMed] [Google Scholar]
- Kazakia G. J., Hyun B., Burghardt A. J., Krug R., Newitt D. C., de Papp A. E., Link T. M., and Majumdar S., “In vivo determination of bone structure in postmenopausal women: A comparison of HR-pQCT and high-field MR imaging,” J. Bone Miner. Res. 23, 463–474 (2008). 10.1359/jbmr.071116 [DOI] [PubMed] [Google Scholar]
- MacNeil J. A. and Boyd S. K., “Accuracy of high-resolution peripheral quantitative computed tomography for measurement of bone quality,” Med. Eng. Phys. 29, 1096–1105 (2007). 10.1016/j.medengphy.2006.11.002 [DOI] [PubMed] [Google Scholar]
- Tjong W., Kazakia G. J., Burghardt A. J., and Majumdar S., “The effect of voxel size on high-resolution peripheral computed tomography measurements of trabecular and cortical bone microstructure,” Med. Phys. 39, 1893–1903 (2012). 10.1118/1.3689813 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burghardt A. J., Buie H. R., Laib A., Majumdar S., and Boyd S. K., “Reproducibility of direct quantitative measures of cortical bone microarchitecture of the distal radius and tibia by HR-pQCT,” Bone 47, 519–528 (2010). 10.1016/j.bone.2010.05.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buie H. R., Campbell G. M., Klinck R. J., MacNeil J. A., and Boyd S. K., “Automatic segmentation of cortical and trabecular compartments based on a dual threshold technique for in vivo micro-CT bone analysis,” Bone 41, 505–515 (2007). 10.1016/j.bone.2007.07.007 [DOI] [PubMed] [Google Scholar]
- Liu X. S., Sajda P., Saha P. K., Wehrli F. W., Bevill G., Keaveny T. M., and Guo X. E., “Complete volumetric decomposition of individual trabecular plates and rods and its morphological correlations with anisotropic elastic moduli in human trabecular bone,” J. Bone Miner. Res. 23, 223–235 (2008). 10.1359/jbmr.071009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saha P. K., Xu Y., Duan H., Heiner A., and Liang G., “Volumetric topological analysis: A novel approach for trabecular bone classification on the continuum between plates and rods,” IEEE Trans. Med. Imaging 29, 1821–1838 (2010). 10.1109/TMI.2010.2050779 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Studholme C., Hill D. L. G., and Hawkes D. J., “An overlap invariant entropy measure of 3D medical image alignment,” Pattern Recogn. 32, 71–86 (1999). 10.1016/S0031-3203(98)00091-0 [DOI] [Google Scholar]
- Hildebrand T. and Rüegsegger P., “A new method for the model-independent assessment of thickness in three-dimensional images,” J. Microsc. 185, 67–75 (1997). 10.1046/j.1365-2818.1997.1340694.x [DOI] [Google Scholar]
- Manzanera A., Bernard T. M., Preteux F., and Longuet B., “Medial faces from a concise 3D thinning algorithm,” in Proceedings of the 7th IEEE International Conference on Computer Vision (IEEE, Washington, DC, 1999), pp. 337–343.
- Stauber M. and Muller R., “Volumetric spatial decomposition of trabecular bone into rods and plates—A new method for local bone morphometry,” Bone 38, 475–484 (2006). 10.1016/j.bone.2005.09.019 [DOI] [PubMed] [Google Scholar]
- Magland J. F. and Wehrli F. W., “Trabecular bone structure analysis in the limited spatial resolution regime of in vivo MRI,” Acad. Radiol. 15, 1482–1493 (2008). 10.1016/j.acra.2008.05.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carballido-Gamio J., Folkesson J., Baum T., Link T., Majumdar S., and Krug R., “3D. Geodesic topological analysis of trabecular bone micro-architecture of the proximal femur,” presented in International Society for Magentic Resonance in Medicine, Montreal, Canada, 2011.
- Malandain G., Bertrand G., and Ayache N., “Topological segmentation of discrete surfaces,” Int. J. Comput. Vis. 10, 183–197 (1993). 10.1007/BF01420736 [DOI] [Google Scholar]
- Tjong W., Nirody J., Carballido-Gamio J., Burghardt A., Patsch J. M., Majumdar S., and Kazakia G., “Longitudinal analysis of cortical pore structure using HR-pQCT,” presented in American Society for Bone and Mineral Research, Minneapolis, MN, 2012.
- Odgaard A. and Gundersen H. J., “Quantification of connectivity in cancellous bone, with special emphasis on 3-D reconstructions,” Bone 14, 173–182 (1993). 10.1016/8756-3282(93)90245-6 [DOI] [PubMed] [Google Scholar]
- Pialat J. B., Burghardt A. J., Sode M., Link T. M., and Majumdar S., “Visual grading of motion induced image degradation in high resolution peripheral computed tomography: Impact of image quality on measures of bone density and micro-architecture,” Bone 50, 111–118 (2012). 10.1016/j.bone.2011.10.003 [DOI] [PubMed] [Google Scholar]
- MacNeil J. A. and Boyd S. K., “Improved reproducibility of high-resolution peripheral quantitative computed tomography for measurement of bone quality,” Med. Eng. Phys. 30, 792–799 (2008). 10.1016/j.medengphy.2007.11.003 [DOI] [PubMed] [Google Scholar]
- Nicks K. M., Amin S., Atkinson E. J., Riggs B. L., Melton J. L., and Khosla S., “Relationship of age to bone microstructure independent of areal bone mineral density,” J. Bone Miner. Res. 27, 637–644 (2012). 10.1002/jbmr.1468 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macdonald H. M., Nishiyama K. K., Kang J., Hanley D. A., and Boyd S. K., “Age-related patterns of trabecular and cortical bone loss differ between sexes and skeletal sites: A population-based HR-pQCT study,” J. Bone Miner. Res. 26, 50–62 (2011). 10.1002/jbmr.171 [DOI] [PubMed] [Google Scholar]
- Nishiyama K. K., Macdonald H. M., Buie H. R., Hanley D. A., and Boyd S. K., “Postmenopausal women with osteopenia have higher cortical porosity and thinner cortices at the distal radius and tibia than women with normal aBMD: An in vivo HR-pQCT study,” J. Bone Miner. Res. 25, 882–890 (2010). 10.1359/jbmr.091020 [DOI] [PubMed] [Google Scholar]
- Stein E. M., Liu X. S., Nickolas T. L., Cohen A., Thomas V., McMahon D. J., Zhang C., Yin P. T., Cosman F., Nieves J., Guo X. E., and Shane E., “Abnormal microarchitecture and reduced stiffness at the radius and tibia in postmenopausal women with fractures,” J. Bone Miner. Res. 25, 2572–2581 (2010). 10.1002/jbmr.152 [DOI] [PMC free article] [PubMed] [Google Scholar]