A neural network model to predict knee adduction moment during walking based on ground reaction force and anthropometric measurements

Abstract

The external knee adduction moment (KAM) is a major variable for the evaluation of knee loading during walking, specifically in patients with knee osteoarthritis. However, assessment of the KAM is limited to locations where full motion laboratories are available. The purpose of this study was to develop and test a simple method to predict the KAM using only force plate and anthropometric measurements. Three groups of 28 knees (asymptomatic, mild osteoarthritis, and severe osteoarthritis) were studied. Walking trials were collected at different speeds using a motion capture system and a force plate. The reference KAM was calculated by inverse dynamics. For the prediction, inter subject artificial neural networks were designed using 11 inputs coming from the ground reaction force and the mechanical axis alignment. The predicted KAM curves were similar to the reference curves with median mean absolute deviation (MAD) of 0.36%BW*Ht and median correlation coefficient of 0.966 over 756 individual trials. When comparing mean group curves, the median MAD was 0.09%BW*Ht and the median correlation coefficient 0.998. The peak values and the angular impulses extracted from the predicted and reference curves were significantly correlated, and the same significant differences were obtained among the three groups when the predicted or when the reference curves were used for 95% of the comparisons. In conclusion, this study demonstrated that a simple method using a generic artificial neural network can predict the KAM curve during walking with a high level of significance and provides a practical option for a broader evaluation of the KAM.

1. INTRODUCTION

The external knee adduction moment (KAM) is an important marker of knee loading and the primary predictor of load distribution across the tibial plateau during the stance phase of gait (Schipplein and Andriacchi 1991). The magnitude of the KAM and the knee adduction angular impulse, which is the time integral of the KAM curve (Schipplein and Andriacchi 1991), are important variables for the evaluation of knee function. For example, the KAM has been shown to be a strong predictor of the presence (Baliunas et al., 2002; Gok et al., 2002; Schnitzer et al., 1993), severity (Creaby et al., 2010; Mündermann et al., 2004; Sharma et al., 1998), pain (Hurwitz et al., 2000; Kim et al., 2004; Kito et al., 2010; Thorp et al. 2007), and rate of progression (Miyazaki et al., 2002) of medial compartment knee osteoarthritis. These KAM variables have also been shown to be associated with the development of future chronic knee pain (Amin et al., 2004), distribution of bone in the proximal tibia (Hurwitz et al., 1998; Throp et al., 2006a), and clinical outcomes following surgery (Prodromous et al., 1985). Although the KAM is an important marker for knee function, this measure is not readily available for large clinical trials or routine clinical evaluations. In fact, the KAM is obtained by inverse dynamics calculation (Andriacchi et al., 2004) which requires a full gait laboratory equipped with a motion capture system and a force plate as well as extensive time to prepare the subject and process the data. Therefore, there is a need for simpler methods to estimate the KAM.

Recently, Hunt and Bennell (2011) proposed a regression model including body mass, tibial angle, and walking speed to predict the maximum KAM value achieved during stance. Although promising for clinical settings, this method only predicted raw KAM magnitudes, whereas KAM curves or normalized KAM values are necessary for some applications. Other studies (Goulermas et al., 2005; Rouhani et al., 2010) have shown that artificial neural networks (ANNs) (Bishop, 2007; Duda et al., 2001) are powerful tools to predict time series in biomechanics when no explicit relationship is known between the measurements and the data of interest. In particular, Liu et al. (2009) proposed an ANN to predict the hip, knee, and ankle sagittal moments during a vertical jump using the measurements from a force plate. Therefore, it might be possible to design an ANN to predict the normalized KAM curve during walking using only a force plate and the anthropometric characteristics of the subject. With a generic ANN (i.e., a network that is not subject dependent), this method would be very valuable because the instrumentation could be reduced to a single force plate and the subject would only be required to step on the force plate in street clothes without additional apparatus.

The purpose of this study was to develop and evaluate a simple method using an ANN to predict the KAM during the stance phase of gait based only on force plate and anthropometric measurements. The KAM predicted with this method in the case of inter subject training was compared to a reference KAM obtained by inverse dynamics. Furthermore, the outcome sensitivity of this prediction method was evaluated by comparing the KAM between three groups of knees with different disease conditions.

2. MATERIALS AND METHODS

Subjects

Three groups of twenty-eight knees each from 69 subjects were selected for this study (Table 1). They consisted of a group of asymptomatic knees, a group of knees with mild osteoarthritis (OA), and a group of knees with severe OA. Kellgren/Lawrence grades (Kellgren and Lawrence, 1957) of 1 or 2 were considered mild OA, whereas grades of 3 or 4 were considered severe OA. For each knee, the mechanical axis alignment, which is the angle between the loading axes of the thigh and shank segments in the frontal plane, was measured during quiet standing using an optoelectronic system (Dyrby and Andriacchi, 2004; Mündermann et al., 2008). This study was approved by the Institutional Review Board and informed written consent was obtained from all participants prior to data collection.

Table 1.

Population information.

	Asymptomatic	Mild OA	Severe OA
Gender	12M, 16F	13M, 15F	14M, 14F
Side	14R, 14L	14R, 14L	18R, 10L
Age* (year)	36 ± 14	57 ± 9	61 ± 10
Height (m)	1.72 ± 0.08	1.71 ± 0.07	1.71 ± 0.08
Weight* (kg)	66 ± 12	78 ± 16	85 ± 13
BMI* (kg/m2)	22 ± 2	27 ± 5	29 ± 4
MA* (deg)	3.8 ± 2.7	5.6 ± 3.0	1.1 ± 5.3
Speed (m/s) slow*	1.1 ± 0.2	1.0 ± 0.3	1.0 ± 0.1
normal*	1.4 ± 0.2	1.3 ± 0.2	1.2 ± 0.2
fast*	1.8 ± 0.2	1.7 ± 0.3	1.5 ± 0.2

Data are presented as mean ± one standard deviation.

^(*)A star indicates a significant difference between asymptomatic, mild OA, and severe OA groups (one way ANOVA; p<0.01). MA refers to the mechanical axis alignment.

Experimental protocol

For each knee, three successful walking trials of 10 m were recorded at each of self-selected normal, slow, and fast speeds. A trial was considered successful if the subject stepped with the appropriate foot on a force plate (Bertec, Columbus, OH) embedded in the floor. Nine infrared cameras (Qualisys Medical, Gothenburg, SE) were used to measure the trajectory of 21 reflective markers fixed on the leg of interest following the protocol of Dyrby and Andriacchi (2004). Data were collected at 120 Hz and marker trajectories were low-pass filtered (Butterworth, 2^nd order, 5Hz).

The reference KAM was calculated by an inverse dynamics approach (Andriacchi et al., 2004). The inertial properties of the segments were defined according to Dempster and Gaughran (1967) and the point cluster technique was used to calculate the segment kinematics based on the marker trajectories (Andriacchi et al., 1998). The KAM was expressed as an external moment relative to the tibial anatomical frame (Dyrby and Andriacchi, 2004). Ground reaction forces were normalized to percent bodyweight (%BW) and KAM to percent bodyweight and height (%BW*Ht). The force plate was used to determine stance phase and all ground reaction forces and KAM data were normalized to 101 time points (t= 0 to 100%) during this phase.

Prediction method

A feedforward multi-layer perceptron (MLP) ANN with one hidden layer was used in this study. The hidden layer consisted of hyperbolic tangent sigmoid transfer functions, whereas the output layer was a linear transfer function. This network structure was chosen because it is one of the most efficient to predict time-series (Hagan et al., 1996; Schalkoff, 1997) and because it was successfully used for the prediction of dynamic signals in biomechanics (Goulermas et al., 2005; Liu et al., 2009; Rouhani et al., 2010). Based on previous studies that predicted knee loading (Liu et al., 2009; Hunt and Bennell, 2011), 12 inputs were selected for this ANN (Table 2).

Table 2.

Description of the 12 inputs of the neural network.

Variable	Unit	Description
Fx, Fy, Fz	%BW	ground reaction force expressed as three components along the x, y, and z axes of the lab
Vx, Vy, Vz	m/s	relative velocity of the subject’s center of mass obtained by single integration of the ground reaction force and expressed as three components along the x, y, and z axes of the lab
Dx, Dy, Dz	m	relative displacement of the subject’s center of mass obtained by double integration of the ground reaction force and expressed as three components along the x, y, and z axes of the lab
StDu	s	stance duration
t	%	time point expressed as percentage of stance duration
MA	deg	mechanical axis alignment of the knee

A cross-validation strategy was used in this study because it simulates the use of a generic ANN (i.e., a network that has been trained with other subjects than the subjects used for the prediction). The cross-validation was done at the knee (and not at the trial or time point) level to avoid optimistic evaluation bias due to the possible association between data intra-knee. This procedure consisted of: 1) selecting one knee and creating a new ANN using the 9 trials of the 83 other knees; 2) predicting the KAM during the 9 trials for the selected knee using the ANN; 3) comparing the predicted KAM with the reference KAM obtained by inverse dynamics. This three-step process was repeated for all 84 knees in the dataset. For each repetition, the ANN was trained by error back-propagation using the Levenberg-Marquardt algorithm (Hagan et al., 1996) based on 75′447 (83 knees* 9 trials* 101 time points) vectors of 12 inputs and 75′447 target KAM values.

To determine how many neurons to include in the hidden layer, first the cross-validation described above was performed with an increasing number of neurons. The mean absolute deviation (MAD)(Eq.1) was then calculated for all 756 trials, and the number of neurons resulting in the minimum median MAD value was selected (Rouhani et al., 2009). Based on this analysis, the optimal number of neurons was set to 7.

$$\mathit{MAD}=\frac{1}{101}\sum _{t=0}^{100}\mid \widehat{\mathit{KAM}}\left(t\right)-\underset{¯}{\mathit{KAM}}\left(t\right)\mid$$ (Eq.1)

where $\widehat{\mathit{KAM}}\left(t\right)$ corresponds to the predicted KAM(t) and corresponds to the reference KAM at time point t.

Data Analysis

For each trial, the predicted KAM curve was compared to the reference KAM curve using the MAD and the normalized MAD (MAD%) (Eq.2); additionally the curve patterns were compared using the Pearson correlation coefficient (R). Two-way analysis of variance (ANOVA) tests with knee condition and walking speed as the grouping factors were performed to determine if the results were significantly different among the three groups of knees or among the three speeds. For this analysis, a Fisher transformation was applied to the correlation coefficients.

$$\mathit{MAD}\%=\frac{\mathit{MAD}}{\text{range}\left(\underset{¯}{\mathit{KAM}\left(t\right)}\right)}\ast 100$$ (Eq.2)

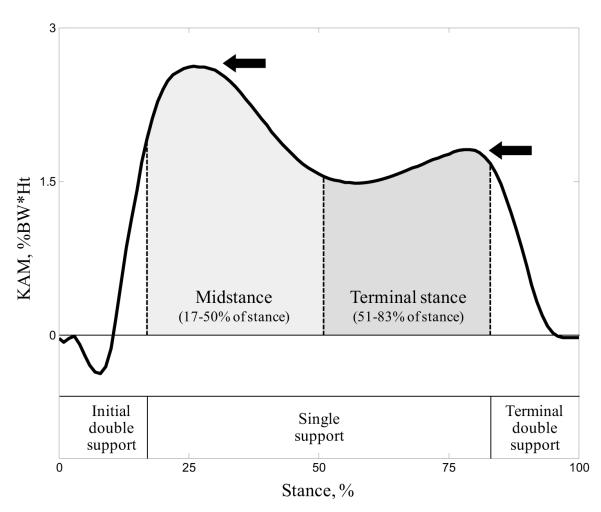
Four well-established discrete parameters were extracted from the KAM curves to describe the loading pattern: the adduction peaks during midstance and terminal stance and the angular impulses during midstance and terminal stance (Fig. 1). The angular impulses were calculated according to Thorp et al. (2006b) using the phase definitions of Perry and Burnfield (2010). The results from the three trials were averaged to reduce the data to one mean value per knee, walking speed, and parameter. Two-way ANOVA tests with knee condition and walking speed as the grouping factors were performed to determine if the error between predicted and reference parameters were significantly different among the three groups of knees or among the three speeds. The Pearson correlation coefficient was then used to test the association between the predicted and reference parameters. Finally, in order to determine if the prediction method could distinguish groups with similar sensitivity as the reference method, one-way ANOVA tests with knee condition as the grouping factor were performed for each parameter and method. Since the KAM is speed dependent (Mündermann et al., 2004), the association and sensitivity analyses were performed separately for each speed. Statistical analysis was done with Matlab (Mathworks, MA) and the significance level was set a priori to p<0.01. ANOVA tests were followed by post hoc Tukey tests when necessary.

Figure 1.

Illustration of the discrete parameters extracted from a KAM curve to describe the loading pattern. The arrows indicate the adduction peaks and the shaded areas indicate the adduction angular impulses. The stance phases are defined according to Perry and Burnfield (2010).

3. RESULTS

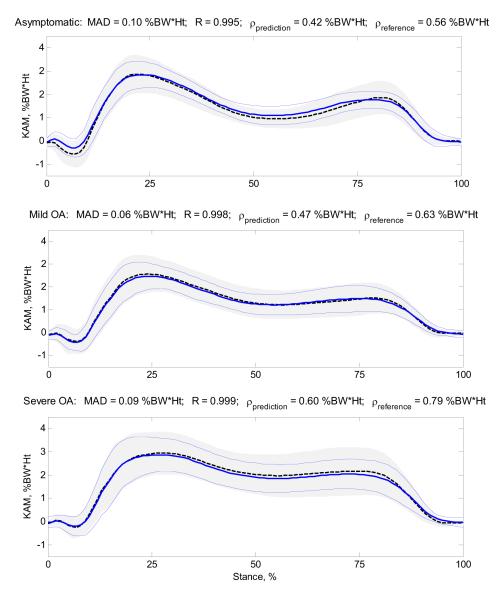
The amplitudes and patterns of the predicted KAM curves were similar to the reference curves. Over the 756 trials analyzed in this study, the median MAD, MAD%, and correlation coefficient were 0.36%BW*Ht, 10.1%, and 0.966, respectively (Table 3). The MAD values were significantly smaller for the asymptomatic and mild OA groups compared to the severe OA group (p=0.003), and the MAD% values were significantly higher for slow compared to fast walking speed (p<0.001). When comparing mean group curves instead of individual trials, the similarity between prediction and reference was higher with median MAD, MAD%, and correlation coefficient of 0.09%BW*Ht, 2.8%, and 0.998, respectively (Fig. 2, Table 4). The intra group variability was reduced for the prediction compared to the reference method. This can be observed in Figure 2 where the areas defined by ± one standard deviation around the mean group curves are smaller for the prediction method. This observation is confirmed by the smaller average standard deviations of the 84 curves of each group around their mean curve (ρ values) for the prediction method.

Table 3.

Comparison of the predicted and reference individual KAM curves.

		Asymptomatic	Mild OA	Severe OA
MAD	slow	0.34 [ 0.26 ; 0.43 ]	0.34 [ 0.25 ; 0.50 ]	0.35 [ 0.24 ; 0.61 ]
	normal	0.34 [ 0.26 ; 0.51 ]	0.35 [ 0.23 ; 0.50 ]	0.36 [ 0.24 ; 0.68 ]
	fast	0.36 [ 0.29 ; 0.46 ]	0.41 [ 0.28 ; 0.51 ]	0.46 [ 0.27 ; 0.67 ]
MAD%	slow	10.7 [ 7.9 ; 14.2 ]	11.7 [ 8.4 ; 16.6 ]	10.7 [ 6.4 ; 16.6 ]
	normal	9.5 [ 6.4 ; 13.8 ]	10.9 [ 7.5 ; 14.8 ]	11.3 [ 6.9 ; 17.1 ]
	fast	8.4 [ 5.7 ; 10.2 ]	9.9 [ 7.2 ; 13.2 ]	11.0 [ 6.3 ; 15.0 ]
R	slow	0.956 [ 0.933 ; 0.973 ]	0.964 [ 0.937 ; 0.986 ]	0.973 [ 0.945 ; 0.987 ]
	normal	0.969 [ 0.932 ; 0.981 ]	0.963 [ 0.922 ; 0.977 ]	0.967 [ 0.944 ; 0.983 ]
	fast	0.968 [ 0.940 ; 0.978 ]	0.962 [ 0.939 ; 0.976 ]	0.969 [ 0.932 ; 0.981 ]

For each knee condition and walking speed, data are presented as median [25^th percentile; 75^th percentile] over 84 curves. MAD refers to the mean absolute deviation in %BW*Ht, MAD% refers to the mean absolute deviation in percentage of the KAM range, and R refers to the correlation coefficient.

Figure 2.

Mean (± one standard deviation) KAM curves for the asymptomatic, mild OA and severe OA groups at normal walking speed. The continuous lines correspond to the predicted KAM, whereas the dashed lines and the shaded areas correspond to the reference KAM. The mean absolute deviation (MAD) and correlation coefficient (R) values at the top of the graphs correspond to the difference between the mean of the predicted KAM curves and the mean of the reference KAM curves. The average standard deviations over the 101 time points (ρ) are also reported for both methods to characterize the intra group variability.

Table 4.

Comparison of the predicted and reference group KAM curves.

		Asymptomatic	Mild OA	Severe OA
MAD	slow	0.20	0.04	0.05
	normal	0.10	0.06	0.09
	fast	0.09	0.12	0.17
MAD%	slow	7.2	1.6	1.8
	normal	2.9	1.9	2.8
	fast	2.1	3.5	4.5
R	slow	0.991	0.998	0.999
	normal	0.995	0.998	0.999
	fast	0.996	0.997	0.999
ρ prediction	slow	0.42	0.45	0.57
	normal	0.42	0.47	0.60
	fast	0.51	0.57	0.67
ρ reference	slow	0.50	0.59	0.75
	normal	0.56	0.63	0.79
	fast	0.67	0.75	0.84

See Figure 2 for an illustration of the results at normal walking speed. MAD, ρ_prediction, and ρ_reference values are in %BW*Ht, and MAD% values are in percentage of the KAM range.

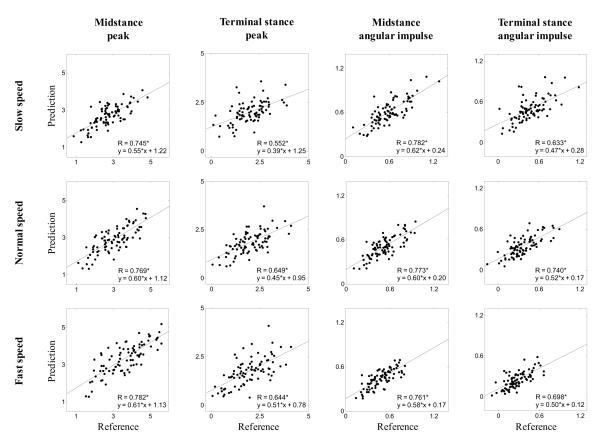
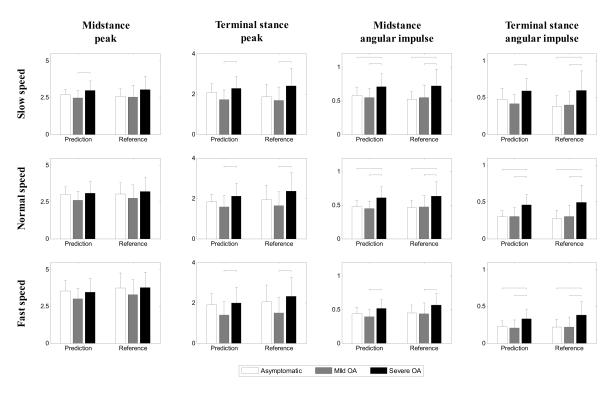
The errors between the parameters extracted from the predicted and reference KAM curves were not statistically different among knee conditions or walking speeds, except for the angular impulse during terminal stance where the errors were lower for the asymptomatic than for the severe OA group (p=0.005). The predicted and reference parameters were significantly correlated (p<0.001), and in all the cases, the slope of the regression line was smaller than one, indicating that the prediction method decreased the absolute inter subject variability (Fig. 3). Regarding mean group parameters, the differences between prediction and reference method were in median 0.12%BW*Ht for the peaks and 0.02%BW*Ht*s for the angular impulses (Fig. 4). Again, the intra group variability was reduced for the prediction method as indicated by the smaller standard deviations. Moreover, the same significant differences were obtained among the three groups regardless of whether the predicted or the reference KAMs were used, except for two comparisons at slow walking speed.

Figure 3.

Plot of the predicted parameters (y) vs. the reference parameters (x) for the three walking speeds. A star (*) indicates a significant correlation (p<0.001). Peak values are in %BW*Ht, and angular impulse values are in %BW*Ht*s.

Figure 4.

Mean (+ one standard deviation) value for the four parameters by knee condition (n=28) calculated from both the predicted and the reference KAM curves. The horizontal bars indicate significant differences between knee conditions (p<0.01). Peak values are in %BW*Ht, and angular impulse values are in %BW*Ht*s.

4. DISCUSSION

The results demonstrated that the KAM during walking can be predicted based on the measurements from a force plate and the anthropometric characteristics of the subject using a generic ANN. The errors of prediction for individual curves were moderately dependent on knee condition or walking speed, suggesting that the ANN was able to generalize the relation between the inputs and the KAM across participants and speeds. Nevertheless, the predictions seemed a little less accurate for the severe OA group and slow walking speed which are situations with higher relative discrepancy of KAM between subjects. Therefore, in the future, it might be beneficial to increase the number of training data for these situations. Although similar to the reference, the predicted KAM might not be similar enough to replace the inverse dynamics values when highly accurate KAM curve is required for a particular analysis. However, the prediction might be used as a substitute for the inverse dynamics calculation if the objective is to differentiate knee loading among subjects or time points as indicated by the significant associations between the parameters extracted from the predicted and the reference KAM curves. The slope of the regression lines between the predicted and reference parameters were smaller than one, indicating that the mapping functions reduced the absolute inter-subject variability. This observation agreed with previous studies that have reported a smoothing effect for predictions based on ANNs (Lui et al., 2009). Finally, it is worth mentioning that the results were equivalent for the parameters consisting of peak values or angular impulses, confirming that the method was able to predict both the amplitude and the pattern of the KAM curves.

The prediction method appears to be most efficient for characterizing groups of knees relative to individual trials, as the similarity between the prediction and the inverse dynamics curves increased noticeably. This result agreed with the association plots (Fig. 3) and, as expected, showed that averaging trials decreases the random error of prediction. Also in accordance with the association plots, the intra-group variability was lower for the predicted KAM compared to the reference KAM for all groups and speeds. However, this decrease of inter-subject variability did not affect the groups comparison since the same significant differences were obtained when the predicted or when the reference KAMs were analyzed, except for two comparisons at slow walking speed involving the severe OA group. As discussed above, it might be beneficial to increase the number of training data for this knee condition and walking speed. All together, these results demonstrated excellent outcome sensitivity for the prediction method and thus suggested that this method could be a valuable tool for the analysis of large cohorts, because the measurement procedure is reduced to asking the subjects to step on a force plate. Compared to an inverse dynamics approach, this method does not require the measurement of the lower leg kinematics, eliminating the need for a motion capture system and decreasing both preparation and post processing times.

Recently, Hunt and Bennell (2011) proposed a regression model using body mass, tibial angle, and walking speed to predict the maximum raw KAM value achieved during stance. In comparison, this new method substituted the speed sensor for a force plate, but could predict KAM curves and normalized KAM values. Moreover, the present study enrolled subjects with healthy and pathological knees and evaluated the ability of the method to differentiate among groups. Finally, although for a different application, this study supports the conclusion of Liu et al. (2009) by actually showing that a generic ANN and a force plate can be used to predict joint moments for a heterogeneous population.

A multi-layer perceptron ANN with one hidden layer was selected because this method was shown to provide better prediction than linear regression for gait variables (Goulermas et al., 2005; Rouhani et al., 2010). To understand the nonlinearities inherent to this KAM application, the cross-validation was also done with a classic linear regression instead of the ANN. Although very similar, the results were better with the ANN (Table 5) supporting the selection of this prediction method. Nevertheless, other ANNs were recently highlighted for biomechanics (Ferreira et al., 2009; Goulermas et al., 2008) and further research is required to determine if they could improve the prediction. Similarly, further research should investigate alternative sets of inputs. This study aimed to predict the KAM curves, but other algorithms could be more appropriate if only specific parameters (e.g., peak values) or subject classification were of interest. Furthermore, this study did not consider intra-subject training because this configuration strongly limits the number of possible applications. However, previous publications have shown that prediction is better with intra-subject compared to inter-subject training (Findlow et al., 2008; Rouhani et al., 2010), and we can expect similar results for the KAM.

Table 5.

Bench testing of the artificial neural network with a classic linear regression method.

		ANN	LR
Individual curves	median MAD **	0.36	0.41
	median MAD% **	10.1	11.4
	median R **	0.966	0.953
Group curves	median MAD *	0.09	0.17
	median MAD% *	2.8	5.5
	median R **	0.998	0.978
Association analysis	median R	0.742	0.705
Sensibility analysis	number of divergent comparisons	2	4

ANN refers to the artificial neural network described in this article and LR refers to the classic least square linear regression method using pseudo inverse. The results presented under “Individual curves” correspond to the results reported in Table 3 for all knee conditions and walking speeds (756 individual curves). The results presented under “Group curves” correspond to the results reported in Table 4 for all knee conditions and walking speeds (9 mean curves). The results presented under “Association analysis” correspond to the results reported in Figure 3 for all parameters and walking speeds (12 regressions). The results presented under “Sensibility analysis” correspond to the results reported in Figure 4 for all parameters and walking speeds. Stars indicate significant difference between ANN and LR (t test;

^*p<0.01,

^**p<0.001). MAD values are in %BW*Ht, and MAD% values are in percentage of the KAM range

While this study has shown that an ANN can predict the KAM based on force plate and anthropometric measurements, it did not help to understand the relationship between the inputs and the KAM. ANNs are great tools to learn complex processes, but they are not optimal to derive explicit causal relationships between inputs and outputs. Another limitation is that the same dataset was used to determine the number of hidden neurons and to evaluate the method. While the results were only slightly dependent on the number of neurons, it would have been better to use two separate datasets to avoid possible optimistic bias. However, preliminary analyses showed that 14 knees per group were not enough to train the ANN. Therefore, the results should be confirmed with another dataset. Finally, it is worth mentioning that the mechanical axis alignment is a common measurement for patients with knee pathology. In this study it was measured using an optoelectronic system to standardize the measurement between healthy subjects and OA patients. However, alternative methods using single knee radiography or simple measurement devices (e.g., caliper) exist (Hinman et al., 2006).

In conclusion, this study described a simple method using an artificial neural network to predict the KAM curve based on the measurements from a force plate and the anthropometric characteristics of the subject. The parameters extracted from the predicted curves were significantly correlated to the parameters extracted from the reference KAM curves obtained by inverse dynamics. Furthermore, for all comparisons except two, the prediction method reported the same outcome sensitivity as the reference method. In this study, inter-subject training was used in order to evaluate the performance that would be obtained with a generic network. Once a generic network is created, it is enough to know the anthropometric characteristic of a subject and to have a force plate measurement during walking to predict the KAM. Therefore, this method may be a valuable tool for the analysis of large cohorts and a step toward routine evaluation of the KAM.