Random forest fishing: a novel approach to identifying organic group of risk factors in genome-wide association studies

Abstract

Genome-wide association studies (GWAS) has brought methodological challenges in handling massive high-dimensional data and also real opportunities for studying the joint effect of many risk factors acting in concert as an organic group. The random forest (RF) methodology is recognized by many for its potential in examining interaction effects in large data sets. However, RF is not designed to directly handle GWAS data, which typically have hundreds of thousands of single-nucleotide polymorphisms as predictor variables. We propose and evaluate a novel extension of RF, called random forest fishing (RFF), for GWAS analysis. RFF repeatedly updates a relatively small set of predictors obtained by RF tests to find globally important groups predictive of the disease phenotype, using a novel search algorithm based on genetic programming and simulated annealing. A key improvement of RFF results from the use of guidance incorporating empirical test results of genome-wide pairwise interactions. Evaluated using simulated and real GWAS data sets, RFF is shown to be effective in identifying important predictors, particularly when both marginal effects and interactions exist, and is applicable to very large GWAS data sets.

Introduction

Many genetic variations have been successfully identified for common complex diseases by genome-wide association studies (GWAS).^{1, 2} There is converging evidence that interactions can have an important role in common disease etiology.^{3, 4, 5, 6} However, most published GWAS studies investigated only the marginal effects of individual single-nucleotide polymorphisms (SNPs) and not genome-wide interactions, because there is a dearth of methodology to directly handle the vast number of possible interaction effects in GWAS data.

Although traditional exhaustive test of all pairwise interactions is feasible in GWAS,⁷ it is computationally prohibitive for higher-order interactions. Adding to the problem, are hard statistical issues. First, complex interaction models have high degrees of freedom, hence, compromised power of the test. Second, the extreme number of tests to examine all interactions would be detrimental for any multiple-testing correction method.

The method of statistical learning⁸ is a promising approach for high-dimensional problems. Many statistical learning techniques were introduced to genetic analysis in recent years, including multifactor dimensionality reduction,⁹ multivariate adaptive regression splines,¹⁰ and random forest (RF).^{11, 12} RF is an ensemble method that combines the result of many classification and regression trees to make a prediction. The trees were built after introducing two levels of randomization: randomly sampling subjects to grow each tree and randomly selecting candidate variables to determine splitting criteria at each node of the tree (see Supplementary Materials). Each variable is assigned a measure of predictive importance by RF, entailing both marginal and interaction effects involving this variable. Use of the importance measure precludes the need to explicitly model every possible interaction terms; and makes interaction analysis of many variables less strenuous. RF was shown to perform well by simulation,¹³ and in genetic studies with moderate number of variables, including microarray data analysis^{14, 15} and association analyses with no more than hundreds of SNPs.^{13, 16, 17} It can effectively select the few important variables out from a large number of irrelevant ones (noise), and be used when the number of variables is much larger than the number of observations.

Recent advances such as Random Jungle (RJ)¹⁸ have made it possible to construct large RFs from genome-wide data. However, direct application of RF to GWAS still poses a real challenge, and only a few studies were reported in the literature.^{14, 17, 19, 20, 21} The difficulty lies in the poor quality of estimates of variables' importance when huge forests are constructed indiscriminately from the whole data, where the majority of the variables are noise. This obstacle must be overcome for GWAS applications of RF to be practically useful.

Herein, we propose a novel method called ‘random forest fishing' (RFF) to address the problems. Instead of fitting RF with all GWAS variables, RFF repeatedly fits RF with relatively small sets of variables to limit the noise, and uses the fitted results to iteratively update a core list of important variables. This updating algorithm searches through the vast parameter space for a globally important group of variables that gives good prediction of the phenotype. To improve search efficiency and accuracy, features of genetic programming (GP) and simulated annealing (SA) are incorporated. In the following sections, we present the concept and details of RFF, including how to use empirical information of genome-wide pairwise interactions to guide RFF search. The performance of RFF is then evaluated using simulated and real genome-wide data sets.

Materials and Methods

Idea of RFF

The soul of RFF is ‘fishing'. Namely, it makes use of an intuitive idea that: ‘known' important factors can help draw out other predictors that interact with them. If a variable contributes to the disease mainly through interaction, it manifests effects only when its interacting partners are also present, that is, this variable is most detectable when its interacting partners are used as ‘baits'.

The main steps of the RFF procedure are as follows:

1. Start the analysis with some initial bait sets. At the very beginning, with limited knowledge of which variables might be important, the initial bait sets may include randomly selected SNPs, top SNPs from single SNP tests, SNPs with known function or in candidate genes.

2. Sample from remaining GWAS SNPs to form a pool of variables for RF evaluation. The number of variables in a pool is kept the same as the bait set size. RF models are fitted with variables from the union of the pool and the baits. If any important variables were present, they are more easily picked up in this small variable subset. If all baits were random noise, the initial RF fittings would hone in on detectable marginal effects.

3. Update the bait set. Based on estimated variable importance from the RF fitting in step (2), top ones are retained as the new bait set for the next iteration. In the updated bait set, noisy and weak baits are replaced by more important variables from the pool to improve the prediction accuracy of the whole group.

4. Evaluate the ‘fitness' of new bait set against the stopping rule. The fitness is measured using prediction accuracy of the RF model based on the new set. The prediction accuracy in RF is the proportion of correct predictions for binary trait, and the fraction of explained phenotype variance for quantitative trait. If the fitness stopped improving, or a maximum number of iterations were reached, stop and output the best bait set as the final ‘best variable set'. Otherwise, repeat steps (2) and (3) to continue updating bait sets.

Through the iterative process, globally important variables are eventually captured in the bait set and further used to ‘fish out' (prioritize) their interacting partners. This constitutes a search strategy to find an organic group of important variables, using collective prediction accuracy of the set as objective for optimization.

To improve the search efficiency and effectively determine the number of important variables for output at the end, the RFF search heuristics combines strengths of three techniques: elements of SA to bring down randomness by iteratively shrinking bait/pool sizes; features of genetic algorithm to traverse the huge parameter space; and a dictionary based on empirical pairwise interaction test results for guided search to promote variables more likely involved in interactions.

Elements of SA in RFF

SA is a heuristic search algorithm for global optimization, using iterative random movements that mimic physical process of ‘cooling down' to the state of minimum energy (approximate optimum solution).²² During iteration, a new random perturbation close to the current solution is evaluated and accepted with some probability depending on its fitness and a global parameter T called ‘temperature'. This parameter controls the degree of randomness away from the current solution, and gradually decreases during the entire process. A ‘slow cooling' protocol allows SA to traverse enough portions of the parameter space to successfully find the optimal solution in the end.

In RFF iteration, ‘slow cooling' is achieved by gradually decreasing bait/pool sizes between iterations. By starting at ‘high temperature' with relatively large bait and pool sets, RFF quickly traverses the GWAS SNPs in large chunks, and allows strong marginal effects being captured in earlier iterations. With strong effects captured in baits set, later iterations decrease pool sizes to reduce the number of noise variables included for RF fitting. As a result, subtler effects such as interactions will start to stand the chance of being captured and retained across iterations. Similar to standard SA, the decrease of bait size must be slow enough to allow RFF to evaluate a representative sample of sets at current size before moving on to smaller ones.

In practice, it is reasonable to start with bait set size larger than an estimated number of risk factors, gradually finishing at a bait size below it. Also, to allow every variable ample chance of being included in the pools for fishing, the sum of all pool sizes should be several times larger than the total number of GWAS SNPs. The average times that a SNP would be randomly sampled and evaluated during the entire fishing process, as estimated by the ratio of the total pool size to the total number of variables, is termed the overall SNP coverage. In all experiments reported below, the rate of decreasing baits sizes were chosen so that, on average, RFF always evaluated about the same number of variables from all pools combined over any interval of a given length for pool set sizes (see Supplementary Materials).

Features of GP in RFF

GP²³ is a computation method inspired by biological evolution, and terms like ‘mutation' and ‘crossover' are used in their algorithmic sense. In RFF, GP is applied to construct a certain number of RFs in parallel (called populations) at each iteration (generation) to further enhance computational efficiency. In each generation, a fixed number of bait sets of the same size are maintained. Mutation and crossover produce candidates of bait sets for the next generation: for mutation, the bait sets are each merged with a new pool set; for crossover, the bait sets are randomly paired and merged. The updated bait sets then comprise the top-K most important variables by RF evaluation of the candidate sets, where the size K of the new bait sets is determined by the cooling scheme of SA. Competition and selection are introduced based on predictive capacity of the candidates to obtain fittest population for the next generation.

GA enhances the power of RFF because good predictors will prevail multiple bait sets in a generation and are less likely lost, and improves computational efficiency as good predictors propagate among bait sets.

Pairwise interaction-guided search in RFF

In the vanilla RFF, variable pools are generated giving all variables equal chances. When most variables are noise, the chance that these randomly generated pools contain any interacting partners of the baits is infinitesimally small, likely resulting in wasted RF evaluations. Such waste could be reduced if we introduce some bias toward interacting partners of the baits, by using pairwise interactions as guidance. More specifically, pairwise interaction tests are performed first, and then variables having significant interactions with baits are given more chance to be included in fishing pools.

Software implementation of RFF

The new RFF algorithm is implemented in a standalone C++ program and also as an R²⁴ package, with the flexibility of using any of the several existing software as the RF engine, including: the original Fortran program by Breiman and Cutler,¹¹ the randomForest R package by Liaw and Wiener,²⁵ and the more recent RJ C++ program by Schwarz and colleagues.¹⁸ The first two have been in wide use in different fields of statistical learning before the advent of GWAS studies. The RJ was designed for GWAS scale analysis, with greatly improved memory management and computation efficiency (7 × faster than the Fortran or R RF on a single CPU, and 159x faster using parallel computation on 40 CPUs¹⁸). Although both randomForest and RJ were tested in analyses presented below, only RJ was used by RFF for analyzing real GWAS data.

Data simulation

GWAS data were simulated by modeling interactions among multiple risk SNPs. All interaction models were fully described using penetrance tables that specify the probabilities of disease status for every possible multi-locus genotype. Together with genotype frequencies, the penetrance table determines all genetic effects (marginal and any-order multilocus interactions). In our tests, the disease prevalence equals 0.05, with six contributing risk loci. We consider five scenarios, each characterized by the marginal effects of the six loci disease. (S1): no marginal effect for all six loci; (S2-1): two rarest loci have moderate marginal effects (OR=1.5 in recessive model); (S2-2): two most common loci have moderate marginal effects (OR=1.5); (S3-1) two rarest loci have strong marginal effect (OR=4); and (S3-2) two most common loci have strong marginal effect (OR=4). The minor allele frequencies (MAFs) and marginal effects of the six SNPs are listed in Table 1. For each of the five scenarios, 10 penetrance tables conformal to the marginal effects were randomly selected and used for simulation. Marginal and interacting effects accounts for a total heritability of around 0.12 in all 50 models. In scenario S1, all genetic contributions come from interactions; in the other four scenarios, interactions account for 53.2–98.8% of the total heritability (Table 1).

Table 1. Five scenarios of disease models used by the simulation tests.

	Genotype relative risk ratio						Heritability explained by interactions (%)
Scenario	SNP1	SNP2	SNP3	SNP4	SNP5	SNP6
S1	1:1:1	1:1:1	1:1:1	1:1:1	1:1:1	1:1:1	100
S2-1	1:1:1.5	1:1:1.5	1:1:1	1:1:1	1:1:1	1:1:1	98.6–98.8
S2-2	1:1:1	1:1:1	1:1:1	1:1:1	1:1:1.5	1:1:1.5	96.3–96.8
S3-1	1:1:4	1:1:4	1:1:1	1:1:1	1:1:1	1:1:1	91.6–92.8
S3-2	1:1:1	1:1:1	1:1:1	1:1:1	1:1:4	1:1:4	53.2–58.1
MAF	0.05	0.1	0.2	0.3	0.4	0.5

Genetic effects of each disease SNP are described by genotype relative risk ratios (i.e., risk for minor-allele-homozygotes: risk of heterozygotes/risk of major-allele-homozygotes). SNP1, SNP2, … and SNP6 are the six disease variants. Scenarios with marginal effects are in boldface.

In the simulation, SNPs with MAF ≥1% were selected from those shared by HapMap²⁶ CEU panel and Affymetrix 50K Human Gene Focused Array, and their genotypes were simulated using an in-house R package simGWA that extends an existing C++ program GWAsimulator²⁷ so as to correctly specify disease models with complex interactions. Simulated data have LD patterns resemble that of GWAS studies in Caucasians using the 50K arrays. The final data sets contained genotypes of 40 011 SNPs for 500 cases and 500 controls, with 100 replicates generated for each of the 50 models. Extra data were simulated for a few scenarios for larger samples sizes (2000 cases and 2000 controls) when required to demonstrate appreciable power.

Simulation test of RFF

The simulated data sets were used to evaluate several fishing strategies by RFF, using: (1) tests without pairwise interaction guidance (RFF.nointx); (2) empirical guidance by results of pairwise interaction tests, using a low SNP coverage of 4x (RFF.intx1); (3) same guidance as (2), using a high coverage of 24x (RFF.intx2); (4) theoretical guidance by ‘synthetic' interactions over a set of designated SNPs, using a coverage of 4x (RFF.intx3). Two kinds of ‘synthetic' interactions were made to mimic real studies: background noise interactions were produced by allowing each SNP to randomly interact with four other SNPs on average (following Poisson distribution) and a dense cluster of interactions over a designated set of SNPs by linking any two designated SNPs with interaction at an elevated chance of 60%. For power analyses of the five scenarios, the designated set in RFF.intx3 are the six risk SNPs so as to introduce an ideal guidance; to demonstrate that guided RFF is immune to chance clustering of irrelevant interactions, we also tested RFF.intx3 using a designated set of six random SNPs.

Test power is approximated by the frequency of observing a risk locus in the final best variable set returned by 1000 RFF tests (10 models × 100 replicate data sets) for each of the five scenarios. In all simulation tests, RFF was performed using the R package with randomForest as RF engine with the bait sizes being gradually decreased from 100 to 3. There are other tunable parameters used by the RF engine and the RFF fishing process, all of which are described in Supplementary Tables 2 and 3 of Supplementary Materials together with their values used in this paper.

Other statistical tests

The performance of RFF is compared with single SNP χ² test and two other interaction analysis methods: conventional RF using RJ, and pairwise SNP–SNP interaction test using PLINK²⁸ (‘--fast-epistasis'). In results by RJ, SNPs are ranked by their importance values; in results by PLINK, SNPs are ranked by their highest interaction test statistics with any other SNPs.

Power for these tests is defined as the frequency of observing a risk locus among the top-K variables, where K equals the size of the best variable set returned by RFF.

Real GWAS data analysis

To demonstrate that RFF is indeed capable of analyzing real GWAS data, it is applied to a pilot GWAS data set from a real study of hypertensive heart disease (HHD). The HHD data set contains 75 cases and 75 controls, genotyped using the Affymetrix Mapping 500 K Array Set. Genotype data underwent quality control for array quality (missing rate <0.05, mean heterozygosity between 0.25 and 0.3) and for SNP marker quality (call rate >0.99 for SNPs with MAF <0.05, call rate >0.95 for all other SNPs, and Hardy–Weinberg test P-value>10⁻⁶). After quality control, 389 344 SNPs, in a sample of 70 cases and 70 controls were used for RFF analysis. RFF search started with 10 parallel bait sets each with 2500 random SNPs. The bait sizes gradually decreased to 50 SNPs after 624 generations, at an overall SNP coverage of 10x. Empirical guidance was applied using fast-epistasis test results by PLINK. RFF was performed using the C++ package with RJ as the RF engine. We also compared RFF results with those by the other methods described above, with an additional run of RJ using tuning parameters as in Goldstein et al²¹ (details in Supplementary Materials).

Results

RFF analysis results of simulated data

All RFF tests returned relatively small sets of important predictors (Table 2), out of the total of 40 011 SNPs in the test data. The average sizes of returned bait sets are about 30, and most sets are less than or equal to 50 (97.77–99.20%).

Table 2. Size distributions of final best variable sets returned by RFF in simulation tests.

	Minimum	Maximum	Mean	≤50
RFF.nointx	4	66	30	97.77%
RFF.intx1	3	81	28.31	98.31%
RFF.intx2	4	56	32.14	99.20%
RFF.intx3	3	66	23.12	98.46%

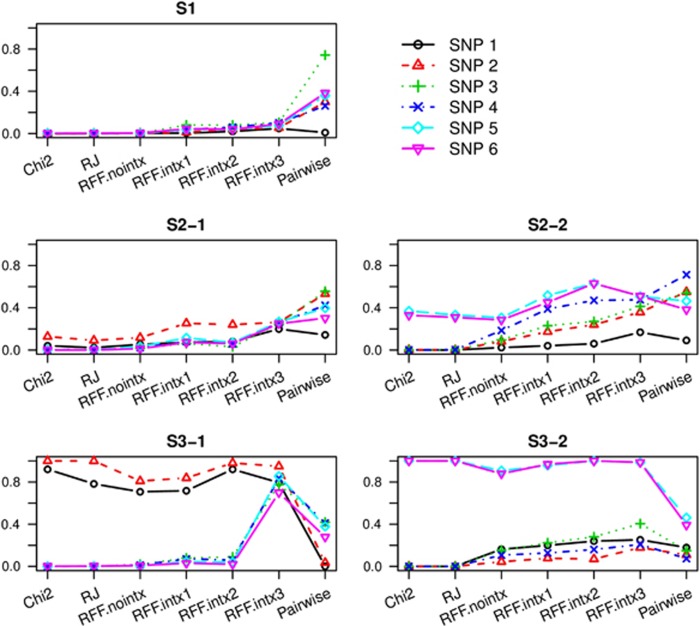
The performances of RFF were first compared with the single SNP test and the conventional RF (using RJ). As seen in Figure 1 (and Supplementary Figure 3), the χ² test only detected the SNPs with marginal effects. Conventional RF, when applied blindly to the vast number of SNPs in the simulated GWAS data, were no more powerful than singe SNP χ² test for capturing risk SNPs.

Figure 1.

Power for detecting each risk SNPs using 500 cases and 500 controls. The power to detect the six risk SNPs are shown for the five scenarios. ‘Chi2' represent χ² tests; ‘RJ' for Random Jungle test; ‘Pairwise' for pairwise SNP–SNP interaction test by PLINK fast-epitasis. In all tests, we declared the top 31 SNPs as ‘detected' to estimate the power. ‘RFF.nointx' and ‘RFF.intx' are RFF tests without and with guidance by interactions. ‘RFF.intx1' and ‘RFF.intx2' used empirical guidance based on the pairwise interaction tests, with SNP coverage of 4 and 24, respectively; and ‘RFF.intx3' used theoretical guidance based on synthetic interactions clustered over the six risk SNPs.

In contrast, all RFF methods show some increase in power for detecting weak risk SNPs that contributes to disease only through interactions. For vanilla RFF without interaction guidance, the increase in power is only obvious in S2-2 and S3-2, where there are two SNPs with moderate to strong marginal effects. More improvements were seen for RFF.intx1 with empirical guidance, for which power was increased cross-the-board for all SNPs with or without marginal effects. Moreover, increasing SNP coverage (RFF.intx2) added additional power to the test, most obvious in S2-2 and S3-2. Using ideal theoretical guidance by synthetic interactions in RFF.intx3, substantial power increase was observed for most scenarios. For the best scenario S3-1, power to detect every single risk SNPs is ≥60%, and power to capture three out of four weak SNPs is ≥80% (Figure 2).

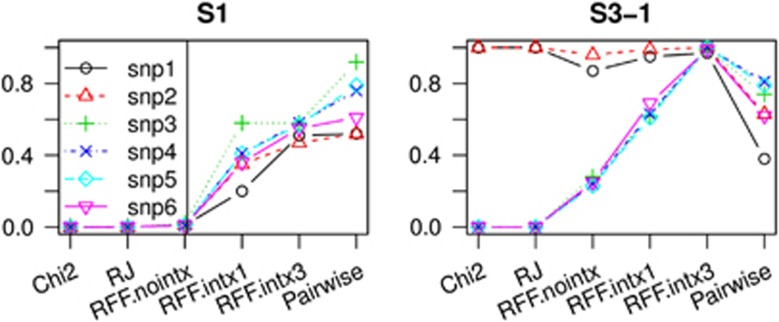
Figure 2.

More appreciable power in S1 and S3-1 using 2000 cases and 2000 controls. Other details are same as in Figure 1 caption.

Although RFF performed generally better in the comparisons shown above, it was under-powered because of the relatively small sample size. More practically appreciable power improvement by RFF was shown by the additional tests using a larger sample size of 4000, where power was improved by vanilla RFF and guided RFF. The results for worst scenario S1 and best scenario S3-1 are shown in Figure 2. In S1, the guided RFF had power of ∼40% (RFF.intx1) to over 50% (RFF.intx3) to detect most of the risk SNPs, even though none of these SNPs had marginal effect. In S3-1, RFF.intx1 had over 61% of power to detect every risk SNPs, and RFF.intx3 over 97%. In contrast, single SNP test and the conventional RF still detected only strong marginal effects.

In Figure 1 (and Supplementary Figure 3), comparisons were also made to the pairwise interaction test by PLINK. As expected, the pairwise interaction test performs the best among all methods when there is weak marginal effect (S2-1) or not at all (S1). However, as some marginal effects become stronger, RFF test begins to show its advantage. In scenario S2-2, three of the risk SNPs have better power using RFF.intx2. In scenarios S3-1 and S3-2, the advantage of RFF.intx3 was most pronounced. For a sample size of 4000, under best scenario S3-1, all six risk SNPs showed better power by RFF.intx3.

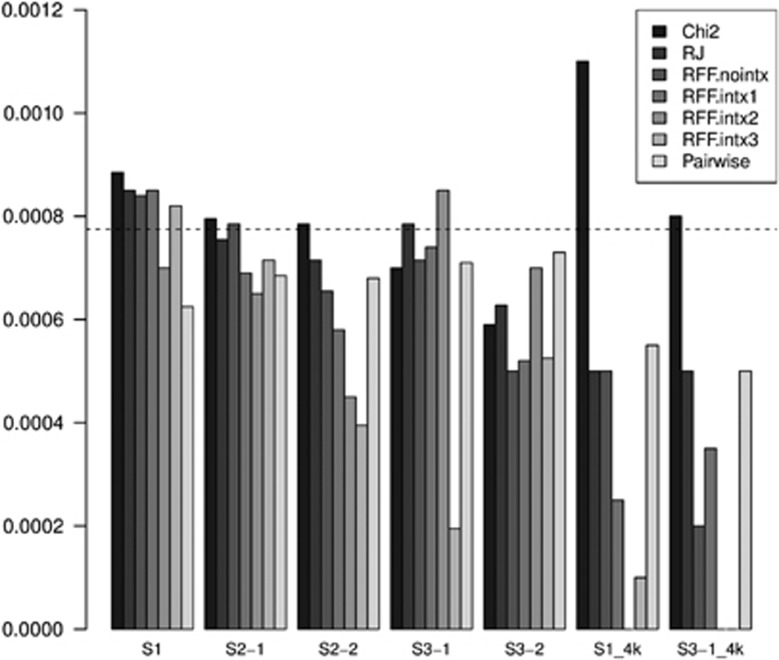
The false positive rates (FPRs) of all tests were evaluated by counting the occurrences of irrelevant SNPs among the top SNPs (for χ² tests, conventional RF and pairwise interaction tests) or final best variable set (for RFF). ‘Irrelevant' SNPs are defined by SNPs not on any of the chromosomes that have a risk SNP. The expectation of observing such random SNPs among the top 31 SNPs would be 31/40 011=7.7 × 10⁻⁴. Almost all tests have FPR around this value (Figure 3).

Figure 3.

False positive rates. The false positive rates of the tested methods are displayed side by side (in different shade) for each of the five scenarios with the ‘default' sample size of 1000 (500 cases, 500 controls), and for the two low-powered scenarios with an increased sample size of 4000 (2000 cases, 2000 controls; with ‘_4k' affixed to their scenario labels).

We note that guided RFF was immune to chance clustering of irrelevant interactions: when applied to the 4000-subject samples in S1 and S3-1 with a dense cluster of ‘synthetic' interactions falsely introduced over six random SNPs, there was no power increase for detecting them.

RFF analysis results of real GWAS data

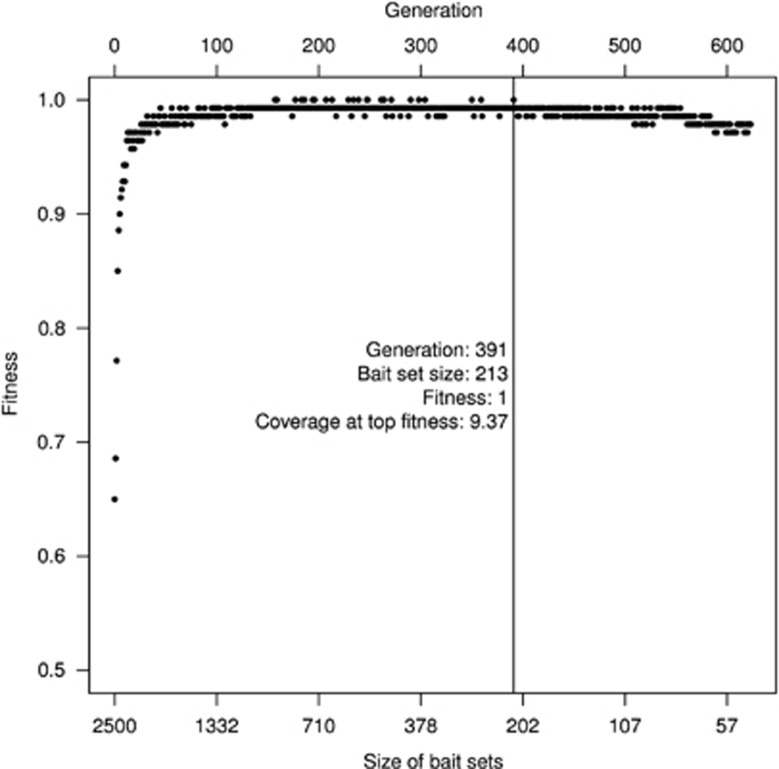
Application of guided RFF to real GWAS data of the HHD study made some interesting findings. Figure 4 shows how fitness of the bait set changed as the generation evolved. The fitness rose from 0.65 in the first generation and reached 1 in generation 157. It dropped again after generation 391 as bait size became too small. The smallest set with highest fitness rate was returned by RFF as the final best variable set. It contained 213 SNPs, assigned to 196 genes according to Affymetrix's annotation. We applied functional annotation tool from DAVID (Database for Annotation, Visualization and Integrated Discovery),²⁹ and found ‘enriched' association with three disease traits, including ‘atherosclerosis', ‘coronary lipoprotein', and ‘long QT syndrome', and in several pathways involved in hypertension etiology(see Supplementary Table 4). On the other hand, none of the 213 SNPs reached GWAS significance threshold (1.3 × 10⁻⁷) by single SNP tests (209 SNPs with P-value ≥1 × 10⁻⁴).

Figure 4.

Random forest fitness (RFF; prediction rate) of variable sets as RFF generation evolves. The fitness values of RF constructed at each generation are plotted against the decreasing size of baits/pool sets (fishSize). The vertical line indicates the generation with the smallest variable set size at which the maximum fitness was achieved.

When compared with the top 213 SNPs from the other tests, RFF had 92 in common with single SNP χ², 1 with the pairwise interaction test, 95 with RJ using default parameter values, and 105 with RJ using tuned parameter values (Supplementary Tables 5 and 6). There were a total of 40 genes assigned to the RFF-found SNPs that were not in top 213 by any of the other tests; and functional annotation of the 40 genes by DAVID suggested enrichment in ‘atrasentan phamacokinetics'. This was quite interesting because atrasentan is a selective endothelin-A receptor antagonist mostly used for their vasoconstrictive properties to treat hypertension.³⁰

Discussion

We showed a practical approach to analyzing GWAS data to detect risk SNPs involving high-order interactions by applying the novel idea of RFF. RFF inherits the feature of RF in capturing both marginal and joint effects of multiple variables, and overcomes its limitation in dealing with extremely noisy data. We presented evaluation analyses using SNPs as predictors of binary disease traits. However, RFF is not limited to genetic markers — covariates such as sex, age, and other environment factors may be included for potentially important gene–environment interactions. Similarly, if population substructure is a concern in analysis, variables accounting for the effects of the substructures (eg, principal components from EIGENSTAT) may be treated in a similar manner like other covariates. The disease phenotype is also not limited to dichotomous traits — quantitative traits can be tested using regression-based RF. Compared with standard RF, the new method is more suited for massive data such as GWAS where majority of variables are noise and interaction effects are abundant.

One advantage of RFF is the improved estimate of variable importance under extremely high level of noise. It achieves this through the iterative process that encourages stronger marginal effects being detected in earlier stages and lets their interaction partners with weaker marginal effects being fished out in later stages when noise is much reduced. Although strong marginal effects prescribe excellent power for RFF, this dependency on marginal effects is far less than for standard RF. As the simulation result shows, even in the situation when none of the risk SNPs has any marginal effect, with enough sample size, the power to identify them can still be high. Compared with other methods, RFF showed more balanced power between risk SNPs with detectable marginal effects and those involved mainly through interactions. It has good power in situations where both marginal and interaction effects are important, which is usually the case for complex diseases.

Another advantage of RFF is the flexibility it allowed to introduce a guidance mechanism. We showed that guided search using empirical pairwise interactions downplayed the need for a strong marginal effect and improved the search efficiency; more importantly, using wrong guidance did not increase the power of detecting random SNPs (it may affect the search speed, though). Therefore, in practice, one may apply various kinds of guidance based on domain/expert knowledge without worrying about inflated false discoveries. For example, because cholesterol levels are known risk factors of coronary heart disease, one may introduce synthetic interactions among cholesterol-related candidate genes to help quickly fish out relevant coronary heart disease variants.

The use of iterative process to approximate an optimal solution by RFF is similar in spirit to some recent extensions of RF. The ‘backward elimination'^{14, 15} iteratively discard the least important variables and refit RF over all remaining variables until finding a ‘non-redundant' subset; another RF application¹⁷ selects the most important variables by repeatedly fitting RF to chunks of 5000 randomly selected variables and then eliminating those with least importance averaged over all constructed RFs. The RFF is different in: (1) it always limits the number of predictors piped into RF to reduce ‘fitting to noise' for more reliable estimates of variable importance; and (2) it forces slowly decreasing bait/pool sizes to accommodate relevant variables that arrive late in the iterative process.

Our RFF implementation allows for ‘plug-in' of existing RF engines in real GWAS studies. In our tests, the RFF C++ program with RJ as RF engine used ∼3 h on a single CPU to finish analyzing 500K GWAS data in 140 subjects. For very large data sets, RFF may be easily parallelized by distributing RF fitting on a large number of computer nodes and evaluating their fitness in parallel to update the bait sets.

In summary, the new RFF method can be applied to identify organic group of important risk factors in GWAS studies without directly modeling obscure interaction effects. Further analyses may be applied over the identified group to study details of relationships among the risk factors and how they contribute jointly to the disease (eg, by explicit modeling of high-order interactions or network analysis). Results from the RFF application to the real study of HHD should be viewed with caution, pending replication in large samples. Nonetheless, the evaluation demonstrated that the RFF method is capable to meaningfully handle real GWAS data and as such to facilitate analysis of genome-wide interactions studies to improve our understanding of many complex diseases.

The authors declare no conflict of interest.