Reconciling clinical importance and statistical significance

Upon revisiting our published work on the genetic architecture of adult height,¹ we noted the following sentence: ‘Height was measured with a stadiometer to the nearest 0.1 cm.' Genetic association studies generally do not utilize information regarding precision of phenotypic measurements. We suggest that doing so addresses a long-standing issue between clinical importance and statistical significance. In this specific instance, we suggest that effects smaller than 0.1 cm are clinically insignificant, as they are not measurable; the issue then becomes how to incorporate this limit into statistical approaches in human genetics investigations such as genome-wide association studies (GWAS).

One solution to this problem is based on classical measurement error. Assume that the observed value of the outcome (dependent variable) y^* is equal to the true, underlying value of y plus a random component e. In ordinary least squares (OLS), the true model y=Xβ+ɛ becomes y^*=Xβ+e+ɛ. Assuming that (1) the two errors are uncorrelated, (2) the expected values of both errors are 0, and (3) both error terms are uncorrelated with the independent variable, the OLS estimate 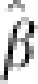is a consistent and unbiased estimate of β. However, the variance of 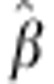increases from 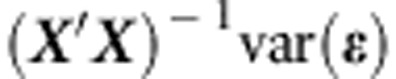to 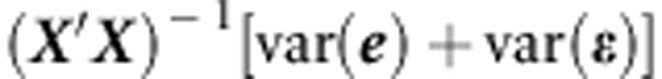. Consequently, test statistics accounting for measurement error will be smaller. Critically, claims of statistical significance will be limited by the precision of the measurement of the outcome.

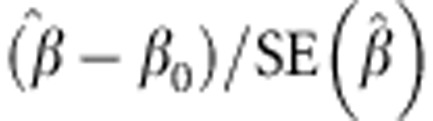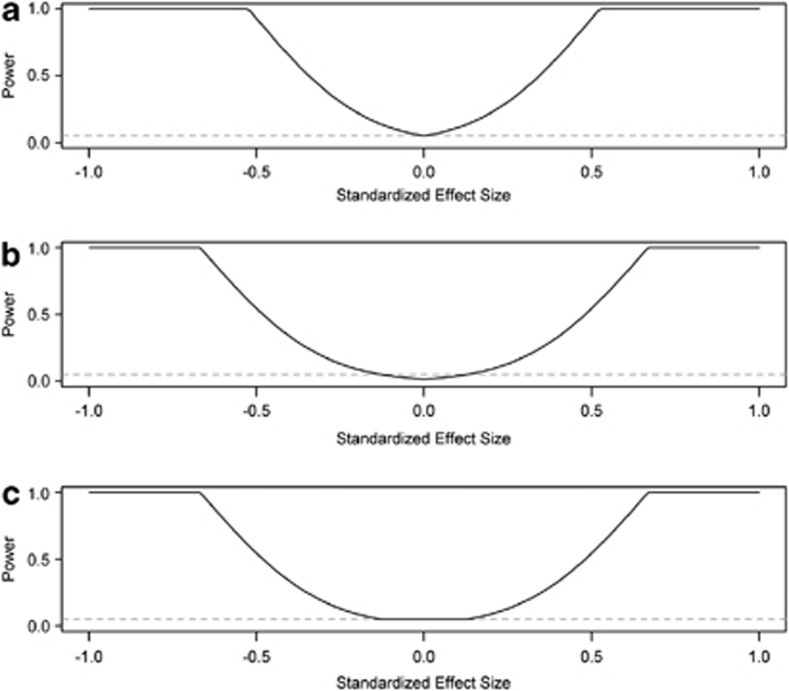
A second solution to this problem is to use protected inference.² Classical inference is based on testing what is called a point null hypothesis: in GWAS, a normally distributed test statistic can be formulated as with the point null value β₀=0. In slightly simplified terms, 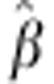is called consistent if it converges to the true value of β with enough data, ie, a suitably large sample size. However, the probability mass of any point in a continuous distribution is 0. Consequently, statistical significance can be attained for trivial effects by simply increasing the sample size (Figure 1a). Under protected inference, the null hypothesis is an interval rather than a point. We suggest two ways to implement protected inference. We can control the false positive error rate at the borders of the null interval, allowing the test to become overly conservative within the null interval (Figure 1b). Alternatively, we can control the false positive error rate at a fixed value across the entire null interval (Figure 1c). We recommend this latter approach, formulating the test statistic as 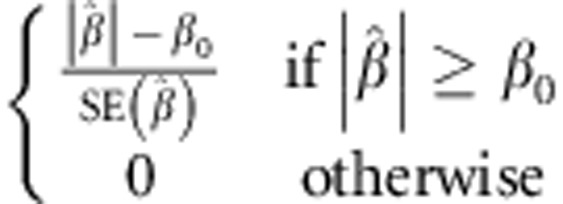, with β₀ now corresponding to the limit of precision, eg, 0.1 cm for our stadiometer. Either way, protected inference prevents arbitrarily large sample sizes from yielding statistical significance for trivial effects.

Figure 1.

Power in classical vs protected inference. The gray dashed lines represent the significance level α=0.05. (a) Classical inference involves testing the point null hypothesis that the effect size is 0. (b) Protected inference involves testing a null interval hypothesis. In this implementation of protected inference, the false positive error rate is controlled at the borders of the null interval. (c) In this alternative implementation of protected inference, the false positive error rate is fixed across the entire null interval.

Another way to address measurement error is through use of repeated measures. In a repeated measures design, the dependent variable is measured multiple times for each individual to account for within-individual variability. However, each measurement is still limited by the precision of the instrument, so that repeated measures designs will not protect against trivial effects.

Returning to our example, we standardized our measurement error (0.1 cm corresponded to 0.0103 SD) and compared it with the standardized effect sizes reported for 180 loci for human height identified by meta-analysis of GWAS.³ The smallest effect reported in their follow-up (Stage 2) analysis was 0.010 SD, suggesting that the detection of genetic loci influencing human height is near its limit; increasing the sample size will have limited utility until the precision of the measurement of height improves.

Clinical importance ought to have much to do with statistical significance. The use of statistical models that account for the precision of measured traits, either through measurement error models or null interval testing, will eliminate the problem of trivial effects, thereby helping to reconcile clinical importance and statistical significance.

The authors declare no conflict of interest.