Integrating multiple lines of evidence into historical biogeography hypothesis testing: a Bison bison case study

Abstract

One of the grand goals of historical biogeography is to understand how and why species' population sizes and distributions change over time. Multiple types of data drawn from disparate fields, combined into a single modelling framework, are necessary to document changes in a species's demography and distribution, and to determine the drivers responsible for change. Yet truly integrated approaches are challenging and rarely performed. Here, we discuss a modelling framework that integrates spatio-temporal fossil data, ancient DNA, palaeoclimatological reconstructions, bioclimatic envelope modelling and coalescence models in order to statistically test alternative hypotheses of demographic and potential distributional changes for the iconic American bison (Bison bison). Using different assumptions about the evolution of the bioclimatic niche, we generate hypothetical distributional and demographic histories of the species. We then test these demographic models by comparing the genetic signature predicted by serial coalescence against sequence data derived from subfossils and modern populations. Our results supported demographic models that include both climate and human-associated drivers of population declines. This synthetic approach, integrating palaeoclimatology, bioclimatic envelopes, serial coalescence, spatio-temporal fossil data and heterochronous DNA sequences, improves understanding of species' historical biogeography by allowing consideration of both abiotic and biotic interactions at the population level.

1. Introduction

A main goal of historical bioegeography is to determine drivers of species distributions and demography through time. Doing so, however, is challenging, as multiple types of biotic and abiotic processes affect population dynamics, and, ideally, all these processes should be considered when making inferences about a species's past distribution and demography. Carstens & Richards [1] combined advances in bioclimatic envelope models (BEMs), statistical phylogeography and coalescence in an attempt to integrate disparate processes into a common modelling framework. Their workflow began by developing hypotheses in the form of demographic models that characterize potential past distributions of species using BEMs as a guide, and then testing those alternatives using coalescent methods [1]. Despite opportunities for integration of multiple lines of evidence, the vast majority of the many subsequent studies are still limited along multiple dimensions. These limitations include: using only modern genetic data and modern occurrence data to train and test demographic models about the past (e.g. [1]); using only a single approach or method to build BEMs (e.g. [2]); considering only climate as a potential driver of species' distribution and demography (e.g. [3]); using ancient DNA but only modern occurrence data (e.g. [4]), and quantifying only coarse parameters of overall range extent when population-level scales are likely to be very important (e.g. [5]). We argue that demographic modelling approaches should also incorporate characterizations of species niches with differing degrees of data completeness, including both abiotic and biotic drivers, and use spatially explicit, mathematically rigorous and temporally precise model sets.

Late Pleistocene and Holocene subfossil deposits, characterized by dramatic biotic and climatic changes, and rich in heterogeneous, high-quality data, provide an ideal temporal window for developing synthetic, model-based approaches (e.g. [5]). Such datasets are becoming further enriched by advances in data generation from fossil material, including increased accuracy and precision of radiocarbon dating and the recovery of ancient DNA. Such advances, coupled with growing population-genetic modelling toolkits, have provided Quaternary scientists with unprecedented views of genetic diversity over space and time, showing, for example, that Late Pleistocene extinctions account for only part of the major loss of diversity during this period [6–8]. At the same time, BEMs have vastly enhanced our understanding of past species' distributions [9–12], which can then be further used as inputs into biogeographic hypotheses. By combining rich data on fossil localities and radiocarbon datasets, it is possible to use BEMs to estimate the realized climatic envelope, an n-dimensional space of climatic variables where populations have been maintained or have thrived, over multiple time periods [13,14].

Herein, we develop a multi-step, methodological workflow, which rigorously tests drivers of distributional and demographic changes, utilizing the American bison (Bison bison) as a focal case study group. Bison populations were once extremely large, probably spanning most of western North America [7]. It remains unclear to what extent the changing climate and interactions with humans may have contributed to their decline [5,7,15]. For example, bison were almost hunted to extinction in the nineteenth century, leaving populations today founded from as few as 30 to 50 individuals [16]. We explore in particular the following key questions. Are BEM-predicted changes in bison population structure and size supported by genetic data? Does incorporating biotic interactions between bison and humans improve demographic model support?

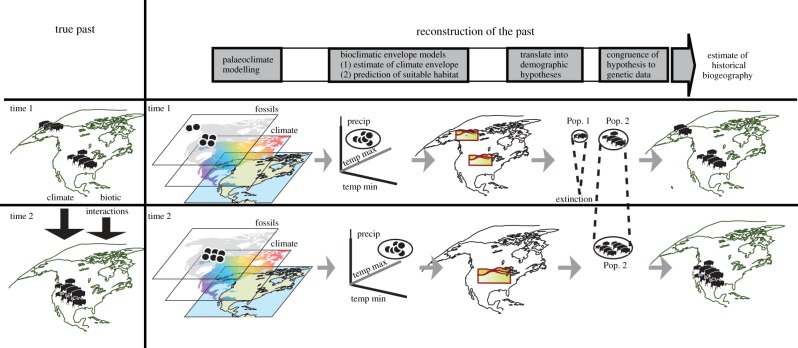
Bison have one of the largest datasets of accelerator mass spectrometry-dated fossils and ancient DNA available for any Late Pleistocene species. Given these abundant data, bison are ideal for seeking a consensus among multiple lines of spatial ecological, palaeontological, demographic and distributional evidence. Figure 1 illustrates how time-calibrated and georeferenced fossils, ancient DNA and palaeoclimate reconstructions can be used to best determine whether changes in species bioclimatic envelopes are associated, temporally, with changes in effective population size and population structure.

Figure 1.

A workflow for reconstructing a species's historical biogeography by integrating multiple data types. We show how fossils, palaeoclimate data along with radiocarbon dating and BEM techniques can be used to develop a hypothesis testing framework to be assessed with ancient and modern DNA datasets. The goal of combining several data types over multiple time frames is to improve estimates of historical biogeography so that they are closer to the species's true history. (Online version in colour.)

2. Material and methods

(a). Step 1: estimating the bioclimatic envelope of bison through time

Estimating a species's bioclimatic envelope is an important first step for reconstructing and understanding its past distribution [13,17]. We included climate data from multiple time periods, which allowed us to compare estimates of bison BEMs calculated independently ‘within’ each time period against ‘pooled’ estimates obtained using the full fossil record. The ‘within period’ analysis refers to climatic niches calibrated using only data from within each time period. The ‘pooled period’ used all the data to create a conglomerate of the climatic niche conditions experienced by the species throughout the Late Quaternary, which was then projected to each time slice. The advantage of this approach is that it limits possible spatial and environmental bias, but it requires accepting that niches are conserved over time (but see [18]).

Two palaeoclimatic simulations were performed to represent the climatic conditions during the Marine Isotope Stage 3 (MIS 3): the warmer middle part, around 42 thousand years ago (ka) and the colder later part, around 30 ka. We also used one simulation for the Last Glacial Maximum (LGM; approx. 21 ka) and one for the Mid-Holocene (approx. 6 ka). Carbon dioxide levels were specified at 200 ppm for the MIS 3 and LGM simulations [19], and 280 ppm for the Mid-Holocene simulation [20]. The 0 ka simulation is pre-industrial and built using the same general circulation model, to ensure temporal and spatial comparability of our climatic surfaces and BEM outputs. Sea surface temperatures (SSTs) for the MIS 3 and LGM simulations were taken primarily from CLIMAP [21], with modifications from GLAMAP-2000 and other sources [22]. SSTs for the Mid-Holocene simulation were prescribed at present-day values [23]. In all cases, insolation was calculated using orbital parameters [24,25]. All simulations were spun up to equilibrium; results are 10-year averages. Areas known to be under ice sheets given palaeoclimate models were masked as unsuitable habitat. Although palaeoclimatic simulations based on different AOGCMs might differ, previous studies comparing the effect of AOGCM (GENESIS v. 2 versus HadCM3) on modelled ranges show that trends in range size are highly correlated for six different megafauna species, including the bison [5]. Together, these climate data provided five time periods (42, 30, 21, 6 and 0 ka) for estimating BEMs.

A comprehensive set of fossil and historic bison localities was assembled from multiple sources [7,26]. Fossils were calibrated using the IntCal09 calibration curve [27], available through OxCal online (http://c14.arch.ox.ac.uk/). Georeferencing was accomplished using Google Earth and according to best practices as defined in Chapman & Wieczorek [28] (see the electronic supplementary material, table S1).

Fossils were considered contemporaneous with a climate layer if the calibrated estimate of the radiocarbon-dated fossil was within ±3000 years, following Nogues-Bravo et al. [9]. We note that the bin of ±3000 years may not be appropriate for all climate layers and should not be considered as a hard and fast rule of our suggested framework. Three climate predictors were used: average minimum temperature of the coldest month (t_min), average maximum temperature of the warmest month (t_max) and mean annual precipitation sum (pre). Following ensemble forecasting methodologies [29], we fitted models with a fully factorial combination of predictor variables allowing an exploration of the resulting range of uncertainties [30].

All models were fitted with BIOENSEMBLES, a platform for computer-intensive ensemble forecasting of bioclimatic models (e.g. [30]). Models included three presence-only methods (BIOCLIM, DOMAIN and Mahalanobis [31]), two presence-background methods (MaxEnt [32] and GARP [33]) and four presence–absence methods (GLM, GAM, MARS and GBM). As we do not have true absences in our data, we generated randomly selected pseudo-absences across the cells in the region of interest without records of bison while keeping prevalence constant at 0.13 (the value found in the pooled dataset).

We randomly split the fossil and contemporaneous distributions data into 75% for calibration and 25% for evaluation, repeating the procedure 10 times. Every model run yielded a projection; ‘True Skill Statistics’ (TSS) measured the matching between predictions and observations in the 25% evaluation data. TSS-weights, indicating model performance, were obtained for every model run and eventually used to weight the different models for their ability to predict the data. For each dataset (five periods and one ‘pooled’ set), bison data were modelled using nine model types × seven variable combinations × 10 cross-validated samples for a total of 630 model runs per dataset (i.e. 3780 model runs in total).

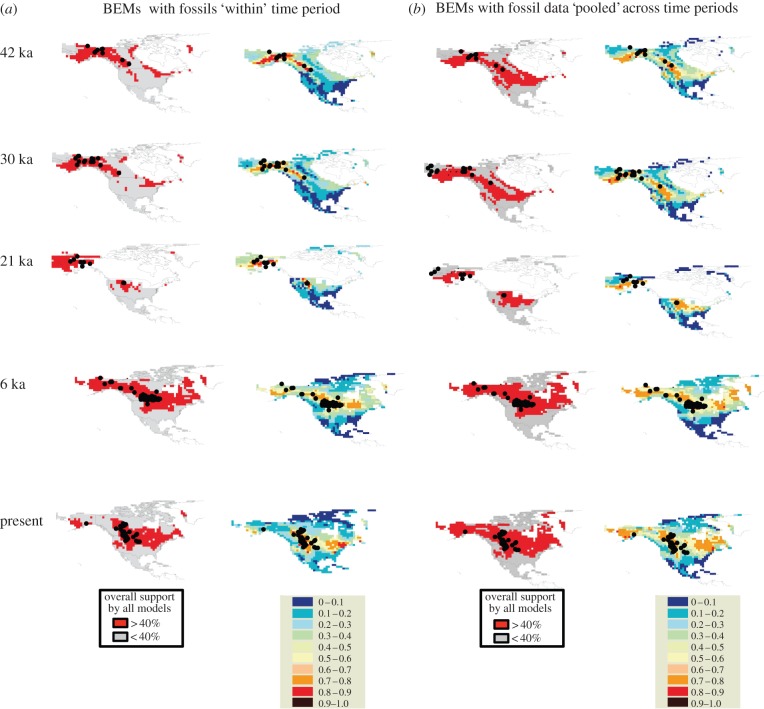
To generate a consensus across all individual model projections, first we removed all poorly performing projections (i.e. with TSS < 0.4 in the evaluation data) [34]. Then, we overlaid the remaining projections and considered a site suitable if models agreed at least 40% of the time. This is an arbitrary measure of agreement among models that is less conservative than the 50% consensus threshold used in several forecasting studies (e.g. [30,35]), and which provided reasonable results in tests using artificial data (F. G. Guilhaumon & M. B. Araújo 2012, unpublished data; see also [36]). With presence–absence methods and MaxEnt, we used the 0.13 prevalence value as the cut-off to convert probabilities or continuous suitability scores (from 0 to 1) into estimates of presence and absence [37,38]. With the distance-based presence-only methods, we used thresholds usually fixed in the literature at 0.95 for BIOCLIM and DOMAIN, and 0.75 for Mahalanobis, while for GARP we used default options to set the threshold internally. Specific details on the parametrization of each model are provided (see the electronic supplementary material, table S2). We used the binary thresholded results (figure 2) from both the ‘within’ and pooled’ probability of occurrences to help calibrate coalescence models.

Figure 2.

BEMs predicting suitable habitat for B. bison over five time periods: 42, 30, 21, 6 and 0 ka. The areas for which over 40% of models resulted in suitable habitat are shown in dark shading on the left side of each panel and the overall probability of an area containing suitable bison habitat is shown on the right of each panel. (a) The ‘within period’ refers to climatic envelopes calibrated and projected within each period of time. (b) The ‘pooled period’ uses all the data for each period to create a summary environmental niche space that is projected to each time slice. Fossil localities are shown as black dots. (Online version in colour.)

(b). Step 2: demographic model set-up for bison

The first step to create demographic models from the BEMs involved examining the number of separate populations at each time slice and the relative geographic extents of those populations through time. Criteria for defining a population were: (i) a continuous set of cells separated from other such continuous groups by modelled unsuitable habitats; (ii) clear evidence that bison had existed at locations at some point in the past; and (iii) that enough fossil evidence and ancient DNA were available to generate population parameters usable for demographic model testing.

The approach so far only considers climate drivers in the creation of demographic models. However, biotic interactions (e.g. predation) can dramatically impact demography, and this is especially true with regard to bison. Archaeological evidence supports increased human occupation [39], decreased numbers of bison fossils [39] and bison hunting from Alaska to New Mexico [40–42] starting around 10 ka. Most evidence of large-scale bison hunting, including communal bison hunting with use of corrals and jumps, occurred in the Mid-Holocene, beginning at approximately 5–6 ka (reviewed by Bamforth [43]). For example, the oldest corral site is in Scoggin, Wyoming and dates to approximately 5.2 ka [43]. Furthermore, jump sites, which date back to a similar time period, became increasing frequent after approximately 3.2 ka [43]. Together, evidence of bison hunting suggests that most large-scale hunting occurred after approximately 5 ka and into the Late Holocene. The arrival of European settlers on bison populations during historic times is perhaps an even greater impact on Bison demography. The introduction of firearms and the European horse in approximately AD 1700 resulted in large-scale slaughter for private and commercial interests, which ultimately almost drove the species to extinction by the end of the nineteenth century [43,44]. We used all the information above to create alternative demographic models that represent either ‘within’ or ‘pooled’ BEM results, along with different biotic interactions. The models are described in more detail in the Results section, as well as in figure 3 and table 1.

Figure 3.

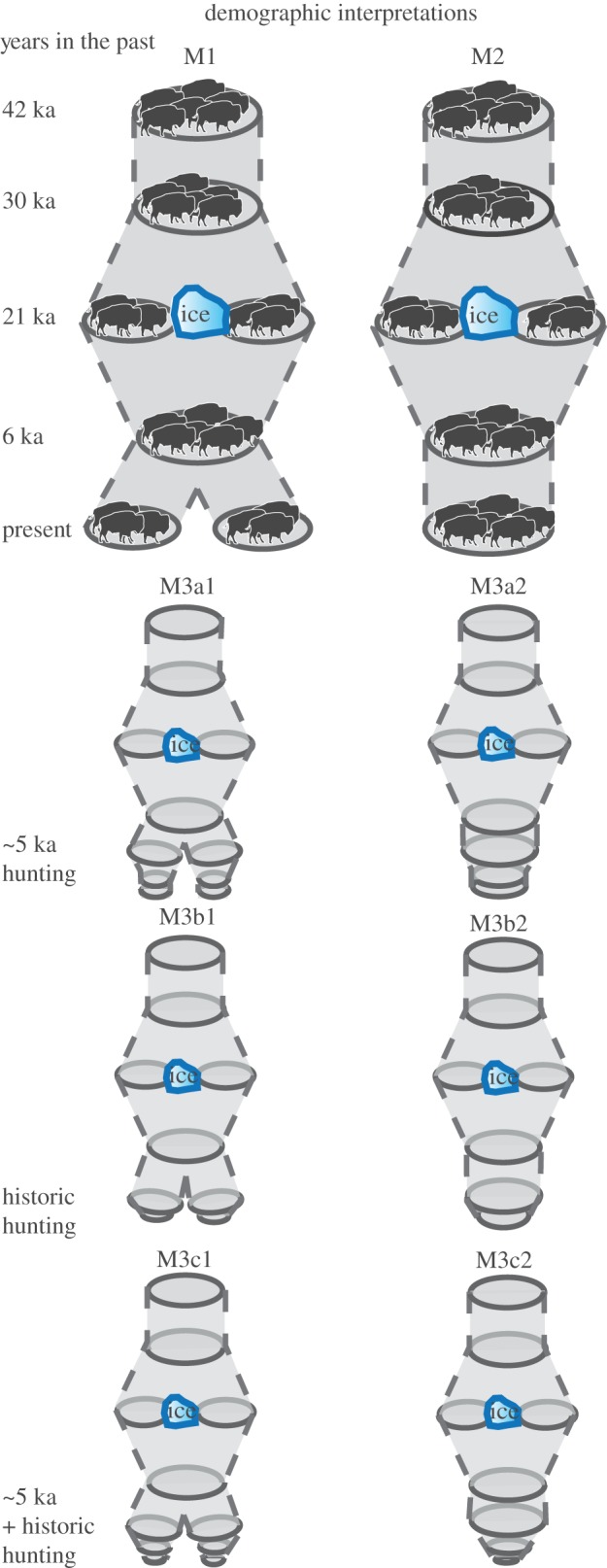
Demographic models based on BEMs (M1 and M2) and a combination of BEMs and additional data (M3 variants). Each model illustrates the number of populations (number of discs) and relative size (width of disc) through time. Model 3 includes six variants that include large-scale bison hunting by Native Americans starting around 5 ka (M3a), large-scale bison hunting by European settlers (M3b) and a combination of both hunting events (M3c). Each hunting scenario is included in a model based on M1 (e.g. M3a1, M3b1 and M3c1) or M2 (e.g. M3a2, M3b2 and M3c2). (Online version in colour.)

Table 1.

Description of demographic models tested with modern and ancient genetic data. Model 1 is based on BEMs calculated independently ‘within’ each time period, whereas model 2 is based on a conglomerate of ‘pooled’ climatic niche conditions experienced by the species throughout the Quaternary. Model 3 variants are based on models 1 and 2, but include potential bison population declines owing to hunting by humans.

	model 1	model 2
BEMs demographic model	single population between 42 and 30 ka; population splits between 30 and 21 ka; population merge between 11 and 8 ka, and split between approximately 5 and 1 ka	single population between 42 and 30 ka; population splits between 30 and 21 ka; population merge between 11 and 8 ka
BEM + end Pleistocene/Mid–Late Holocene decline (M3a)	BEM Model 1 + population decline between approximately 5 and 0.9 ka (M3a1)	BEM Model 2 + population decline between approximately 5 and 0.9 ka (M3a2)
BEM + historic decline (M3b)	BEM Model 1 + population decline between the approximately 0.3 ka and the present (M3b1)	BEM Model 2 + population decline between approximately 0.3 ka and the present (M3b2)
BEM + end Pleistocene/Mid–Late Holocene decline + historic decline (M3c)	BEM Model 1 + population decline between approximately 5 and 0.9 ka + decline between the approximately 0.3 ka and the present (M3c1)	BEM Model 2 + population decline between approximately 5 and 0.9 ka + decline between approximately 0.3 ka and the present (M3c2)

(c). Step 3: genetic data and analysis

Ancient DNA sequence data for bison were originally published and analysed by Shapiro et al. [7] and Drummond et al. [15]. To estimate the probability of each of the three demographic models, we used 615 bp of control region mitochondrial DNA sequence data for 159 North American, contemporary, historic and radiocarbon-dated bison samples spanning 60 000 years [7].

We used the software program Bayesian Serial Simcoal (BayeSSC) [45] to simulate 500 000 iterations of the different demographic scenarios (see the electronic supplementary material, input files for prior distributions) and the ‘abc’ R package [46] to estimate demographic parameters and determine the best-supported demographic model. We chose an approximate Bayesian computational (ABC) setting [47] to determine which demographic model was best supported. In general, estimates obtained with full likelihood-based approaches should be more reliable than ABC estimates because they use information from the complete data rather than summarized statistics. However, ABC is more flexible, can compute multi-population demographic models in a reasonable amount of time and computational power, and can be used for direct model selection [47,48]. To model demographic scenarios using BayeSSC, populations were grouped in different statistics groups using age ranges (in generations) that reflected the BEM time frames described in step 1 (i.e. 42, 30, 21, 6, 0 ka ±3000 years) and the time frames between BEMs (before 45 ka, 33–39 ka and 9–18 ka). For time periods with two populations, fossils were either assigned to the northern or southern population depending on their location (see the electronic supplementary material, tables S1 and S3, and input files).

We chose segregating sites, nucleotide diversity and pairwise Fst as summary statistics for the analysis. This adds up to a total of 28 summary statistics. In general, more information can be added by increasing the number of summary statistics; however, too many summary statistics add stochastic noise to the analysis, and thus increase the error estimating the distance between empirical to simulated data during the regression step [47,49]. We thus used an algorithm introduced by Blum & Francois [50], which is based on nonlinear regression and uses neural networks to optimize the dimensionality. The choice of the tolerance level used in the analysis can have a strong impact on the demographic model results, and thus we used different levels in our analysis. We used tolerance levels of 0.002, 0.004 and 0.008, thereby accepting the 1000, 2000 and 4000 closest values, respectively, for the ABC parameter estimations. Expected deviance according to the deviance information criterion (DIC) [51], implemented in the R package ‘abc’, was applied to infer the best-supported demographic model. We simulated the respective demographic models with 1000 iterations using the parameters of each iteration separately (sampled from the posterior distribution) as fixed model parameters. The summary statistics were then used to calculate DIC values.

To determine meaningful upper limits for the modern population size, we first performed initial runs using broad uniform priors ranging up to 30 000 000. Excessively broad priors can destabilize ABC parameter estimation. We simulated 1000 datasets and performed an ABC analysis, which showed that the higher values resulted in unreasonably high estimates of genetic diversity and that the ABC analysis clearly favoured smaller modern population size values. Thus, the upper limit for the modern population size was refined to 100 000, which resulted in a much higher effective number of simulations. This estimate was used in the full 500 000-iteration simulations.

3. Results

(a). Step 1: estimating the bioclimatic envelope of bison through time

Both ‘within period’ and ‘pooled period’ BEMs showed similar trends but with some key differences (figure 2). Overall, bison appear to have relatively continuous ranges across temperate and boreal North America from 42 ka to present, with habitat expanding after the LGM at 21 ka, when the Laurentide ice sheet began to retreat. The most notable difference between the two sets of suitable habitat predictions was the separation of northern and southern populations between 6 ka and the present day in the ‘within period’ BEMs (M1), while the ‘pooled period’ BEMs suggested panmixia during this time period.

(b). Step 2: demographic model parameterizations

We generated three main demographic model sets: (i) those based solely on climatic drivers from the ‘within time-period BEMs’; (ii) those based solely on climatic drivers from the ‘pooled BEMs’; and (iii) those that deviate from the BEMs (both ‘within’ and ‘pooled’) at certain time periods given the evidence of human impacts, including presumed impacts of Native American ‘jump’ and ‘corral’ hunting from approximately 5 to 0.9 ka and the massive impact of European settlement and hunting from approximately 0.3 ka to present. The first two models, M1 and M2, are consistent with the BEM results, and show single populations at 42 and 30 ka, and split at the LGM owing to the ice sheet covering large portions of North America. Populations re-merge in the Holocene for both M1 and M2. The models differ in that in M1 populations split again between 6 ka and the present, while in M2 there is no split. The models M3a1 (based on M1) and M3a2 (based on M2) include a bison population bottleneck resulting from human hunting between 5 and 0.9 ka (figure 3 and table 1). Models M3b1 and M3b2 include a bottleneck during historic times, reflecting intesive, large-scale hunting by European settlers from 300 years ago to the present. Finally, models M3c1 and M3c2 include both potential hunting-caused bottlenecks.

(c). Step 3: genetic data and analysis

The DIC analyses inferred the best support for the M3b2 model (using a tolerance level of 0.008; see table 2; electronic supplementary material, table S4). This model includes the historic bottleneck and is based on M2, thus including only one panmictic modern population. The second-best-supported model is M2 (tolerance: 0.002), followed by M3a2 (tolerance: 0.002).

Table 2.

DIC values for the ABC model selection. Models are ranked according to their support. Model description can be found in table 1. The no. of accepted values indicates the number of values accepted in the nonlinear regression step.

model	no. of accepted values	DIC
M3b2	4000	8.978
M2	1000	9.093
M3a2	1000	9.324
M3c1	1000	9.366
M1	1000	9.366
M3a1	1000	9.531
M3c1	2000	9.565
M3c2	4000	9.631
M2	2000	9.645
M3c1	4000	9.650
M3a2	4000	9.679
M3b2	1000	9.742
M2	4000	9.793
M3b1	4000	9.798
M1	4000	9.878
M3a1	4000	9.951
M3b1	1000	10.171
M1	2000	10.207
M3a1	2000	10.713
M3b1	2000	10.839
M3c2	2000	11.273
M3c2	1000	199.855
M3a2	2000	199.855
M3b2	2000	199.855

4. Discussion

(a). Best-supported model

In our case study, we integrated multiple lines of evidence to determine the patterns, and perhaps some of the processes, that have led to bison demographic and distribution shifts through time. Our demographic models included population subdivisions and reconnection over time rather than simply considering range-wide estimates of area, such as did Lorenzen et al. [5]. Of the demographic models we generated, the best-supported model was based on a combination of climate and potential influences of bison hunting by humans during historic (later than 0.3 ka) times (M3b2). The decrease in population size of bison in historic times can be reasonably attributed to decimation of bison populations by European settlers, a well-documented event [52,53]. It is notable that despite variation in importance of human impacts, the three best models were based on the ‘pooled’ BEM outputs, supporting the view of negligible climate niche evolution during the Late Quaternary (e.g. [54]) and the advantage of characterizing species climatic niches with as much fossil data as possible [9].

Overall, these results highlight the complexity of integrating multiple data types and attempting to invoke causation from various drivers. Additionally, integration of these data types is particularly challenging given that each step has assumptions and data limitations that may compromise the ability to make proper inferences. We think it is essential to detail those challenges for each step as our main goal is to critically assess and advance methods for rigorous hypothesis testing and falsification frameworks.

(b). Challenges in constructing bioclimatic envelope models over time (step 1)

We observed differences in BEM results across methods in our study, and also highlight that our results are different compared with those of Lorenzen et al. [5]. Overall, there was less suitable habitat predicted using the ‘within period’ approach, which was to be expected because the bioclimatic ‘envelope’ characterized was a subset of the envelope characterized with all data. A more substantial difference in projected suitable habitat was observed by Lorenzen et al. [5]. Lorenzen and colleagues predicted a decrease in suitable habitat for bison at 6 ka, while our results showed a clear increase in suitable bison habitat for this time period, a result also found by Martinez-Meyer et al. [10]. These differences may be driven by our use of additional fossil locality data for Holocene North American bison from Harington [26], illustrating the pitfalls of incomplete sampling that is nearly ubiquitous for fossil datasets [11,55]. Additionally, in our study, we masked ice sheets during the LGM as unsuitable habitat to further improve the accuracy of our BEMs.

Another consideration when constructing BEMs is that the palaeoclimate data are modelled based on incomplete pollen and isotope records interpolated across very coarse geographic scales (in our case, the grain of the climate data layers was approx. 48 000 km²). Further, bioclimatic modelling choices may add additional sources of uncertainty [56,57]. Here, we have used an ensemble modelling approach to account for differences generated from modelling approaches, and thresholds based on current best practices. We recognize, as has been shown in the literature, that such choices impact model results [38], and future efforts can better quantify uncertainties based on differences in those choices.

(c). Challenges in constructing demographic models (step 2)

The translation of distribution predictions into demographic models requires several major assumptions about suitable habitat, population size and gene flow. First, it is assumed that suitable habitat predictions reflect actual distributions rather than potential distributions. However, BEMs represent potential distributions, but actual distributions are most likely to link to demographic estimates generated from genetic data. Second, changes in effective population size (N_e—as estimated by genetics data) may lag or not reflect changes in census size (N_c—as counted on the landscape) [58]. Third, when a population subdivides at some point in the past, but reunites in the future, the two previously distinct populations may not interchange genetic information after contact, as presumed in our demographic models. A challenge for the future is to investigate how past potential distributions relate to demographic events and evolutionary processes such as introgression or reinforcement likely to be recorded in the genetic signal.

Another major issue is whether the five time periods covered by the BEMs were the most important for driving demographic changes in bison. Of particular concern is the lack of a climate reconstruction for the tumultuous climatic time period at the Pleistocene/Holocene transition. The transition between the Late Pleistocene Younger Dryas cold period (approx. 12.9–11.7 ka) and the onset of Holocene warming was rapid [59–62], and associated with the extinction of iconic North American Late Pleistocene megafauna [39,63]. During that climatically chaotic time period, human populations were expanding across North America after their initial arrival around 15 ka [64]. This time period would have been important for a robust model of bison historical demography.

Finally, the time periods covered by the BEMs left large temporal gaps and included large bins (±3000 years) around each time period. Future research should explore the breadth of time bins for different palaeoclimate periods because ±3000 years may not be appropriate in some cases. Recent advances in climate modelling allow for climate reconstructions for tighter and sequential time periods, which will be likely to improve our ability to iteratively test results and better correlate suitable habitat and genetic demographic signals.

(d). Challenges testing the demographic models with genetic data (step 3)

The use of ABC methods to estimate parameter values such as population size and timing of bottlenecks helps us to get around some of the limitations of hypothesis testing in that it is possible to explore a broad range of priors for each demographic model (i.e. hypothesis) without being limited to a strict interpretation of population-genetic parameters. However, even with the use of ABC approaches, it is still necessary to select a set of informative summary statistics useful for comparing the simulated and empirical datasets in order to assess the fit of the model to the data (see [46,65–67]).

A final challenge with genetic data is a lack of power. In our case study, we estimate values for population-genetic parameters using a single-gene ancient DNA dataset. Population-genetic estimates based on a single gene with small sample sizes (approx. n = 10–15) covering many time periods will carry a large amount of uncertainty and, in the case of mitochondrial DNA, only represent the biogeographic history of the maternal lineage. In general, we found a lack of power given our genetic data during important climatic time frames (e.g. LGM and Mid-Holocene), which is partly limited by opportunistic sampling of the fossil record. Temporal genetic data from multiple genes will provide much better power in discriminating among alternative demographic models. Genomic ancient DNA datasets will allow evolutionary biologists to refine estimates of effective population size and migration rates through time.

5. Overall conclusion

Combining datasets from multiple sources (e.g. climate, fossil and DNA), while powerful and needed, can also lead to compounding uncertainty with progress through the workflow (see electronic supplementary material, figure S1). While it is tempting to believe that more data will help untangle the thorny problems of inferring past events, it is possible that what is required is not more data, but the right kind of data with limited biases and uncertainties. For example, the addition of large archaeological datasets documenting human presence, such as in Nogues-Bravo et al. [9] and Lorenzen et al. [5], is another important data type to include in studies of species biogeography. These data may be helpful for understanding time periods when species' demographies may become strongly decoupled from their previous distributions owing to biotic interactions (e.g. high kill rates by humans).

The approach championed here is to consider multiple datasets over multiple time periods with direct translation of suitable habitat predictions into demographic models that can be contrasted with demographic models that diverge from climate at particular time points where evidence of other biotic or abiotic drivers exist. We believe that despite the challenges, full utilization of multiple data types (e.g. DNA, fossils and palaeoclimate) considered over multiple time periods is essential for taking the next steps towards more realistic models and tests of species' historical biogeography.

Funding statement

We thank the National Evolutionary Synthesis Center (NESCent) for funding a catalysis meeting (26–29 May 2010) to develop these methods and workflow. M.B.A. acknowledges the Imperial College London's Grand Challenges in Ecosystems and Environment initiative and the Danish NSF for support of his work. A.C. and J.L.M. acknowledge funding by the Australian Research Council. E.G.D. acknowledges the National Science Foundation. D.N.B. thanks det Frie Forskningsrads forskerkarriere program Sapere Aude and the Danish National Research Foundation for its support of the Center for Macroecology, Evolution, and Climate.