How body mass and lifestyle affect juvenile biomass production in placental mammals

Abstract

In mammals, the mass-specific rate of biomass production during gestation and lactation, here called maternal productivity, has been shown to vary with body size and lifestyle. Metabolic theory predicts that post-weaning growth of offspring, here termed juvenile productivity, should be higher than maternal productivity, and juveniles of smaller species should be more productive than those of larger species. Furthermore because juveniles generally have similar lifestyles to their mothers, across species juvenile and maternal productivities should be correlated. We evaluated these predictions with data from 270 species of placental mammals in 14 taxonomic/lifestyle groups. All three predictions were supported. Lagomorphs, perissodactyls and artiodactyls were very productive both as juveniles and as mothers as expected from the abundance and reliability of their foods. Primates and bats were unproductive as juveniles and as mothers, as expected as an indirect consequence of their low predation risk and consequent low mortality. Our results point the way to a mechanistic explanation for the suite of correlated life-history traits that has been called the slow–fast continuum.

1. Introduction

Species vary consistently in the speed at which they progress through their life histories. This allows them to be arrayed quantitatively along a ‘slow–fast’ continuum [1–10]. Life histories that are fast in one part of a lifecycle tend to be fast in others. The mechanistic basis of these associations has been elusive [10]. However, recent developments in metabolic theory suggest that the speed of progress through the life history depends on the rates at which individuals produce biomass, and these in turn depend on metabolic rates and mechanisms of energy and material allocation between maintenance, growth and reproduction [11,12].

Individual mammals produce net new biomass in two phases. First, the mother fuels production during the early stages of the life history prior to weaning, initially by supplying energy and materials for embryonic growth and development across the placenta during gestation, and then by providing nutrients in milk during lactation. Second, the juvenile fuels its own production from weaning to maturity by foraging and allocating a fraction of the assimilated food to growth. We refer to these as maternal and juvenile production, respectively. The rate at which adult female mammals allocate biomass to produce offspring varies with intrinsic biological attributes, such as body size and diet, and extrinsic ecological conditions, such as food availability and predation risk [13]. Much less is known, however, about the lifestyle factors that influence the growth rates of juveniles after weaning. There have been many studies of embryonic, pre-weaning and post-weaning growth in the context of ontogenetic development [14–19], but few treatments, especially of juvenile growth, in the explicit context of a metabolic theory of life history and ecology.

Metabolic theory predicts a close, mechanistic linkage between the rate of metabolic energy expenditure and the rate of production. This is because the synthesis of net new biomass is fuelled by the assimilation and processing of energy and materials. Mass-specific metabolic rates have long been known to vary negatively with body size and positively with temperature, and mechanistic models of assimilation and biosynthesis predict quantitatively how body size and temperature affect ontogenetic growth rates in both endothermic and ectothermic animals [20–23]. In addition to body size, rates of metabolism and production also depend on ‘lifestyle’, a suite of correlated traits that affect the acquisition and allocation of metabolic resources [13,24,25].

On this basis, we predict the following.

• (i) Juvenile productivity will scale negatively with adult body mass. In endothermic birds and mammals, where body temperature is nearly constant, mass-specific rates of maternal production, here called productivity, scale with body size as R_iM^b, where R_i is a normalization constant that differs among taxonomic and lifestyle groups, M is body mass and b is a scaling exponent [13,26]. Mass-specific productivity is lower in larger organisms than in smaller ones, with b usually in the range of −0.25 to −0.35. This size-dependence has been interpreted as reflecting a fundamental constraint of body size on metabolic rate and consequently on the rate of biomass production [27].

• (ii) Juvenile productivity will be generally greater than maternal productivity. At least two factors are relevant. First, juveniles are smaller than adults, so the above allometric scaling relationships predict that they will have higher mass-specific rates of metabolism and productivity. Second, during lactation, maternal productivity fuels growth of the offspring by supplying milk, which must be ingested and assimilated. This means that the lactating offspring is in effect operating one trophic level higher than its mother, with a trophic transfer efficiency of the order of 0.5 based on data on grey and other seals [28,29]. Trophic transfer losses end at weaning and this contributes to juvenile productivity being greater than maternal productivity.

• (iii) Juvenile and maternal productivity will be positively correlated across species of mammals. After accounting for the effect of body size, most of the residual variation in metabolic rate and maternal productivity can be attributed to differences in lifestyle [13]. This is because rates of both metabolism [25] and production [13] vary with extrinsic environmental factors that affect acquisition and allocation of metabolic resources. So, for example, mammals that feed on abundant green vegetation and marine animal prey tend to have high rates of maternal production, whereas those that have low risk of predation because they are volant, arboreal, fossorial or large tend to have low rates. After weaning, juveniles tend to have similar ecological niches to adults, and these lifestyles should similarly constrain how metabolic resources are acquired from the environment and allocated to growth by juveniles.

We evaluated the above predictions by compiling and analysing a dataset on biomass production of juvenile and adult placental mammals. We calculated maternal productivity as the rate of biomass allocation to offspring prior to weaning. We calculated juvenile biomass production from juvenile growth after weaning when juveniles were foraging independently.

2. Material and methods

Maternal productivity was calculated as the mass-specific rate of production of offspring biomass by a female on an annual basis, so as (offspring mass at weaning) × (litter size) × (number of litters per year)/(adult mass), following [30]. The units are grams per gram per year. This measure is the same as that used by Sibly & Brown [13] except that offspring mass is taken not at birth but at weaning, the end of maternal allocation.

In choosing a measure of juvenile productivity our first consideration was to have the same units as maternal productivity, i.e. grams per gram per year. Mass-specific growth rate, here called relative growth rate, is a suitable measure. Second, we needed to take into account how juvenile mammals grow. Post-weaning growth of most mammals is well fitted by the von Bertalanffy growth equation, illustrated in figure 1, which describes the relationship between body mass, m, and age, t, as

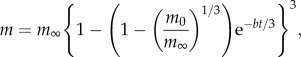2.1

where m₀ is neonate mass at t = 0, m_∞ is the asymptotic maximum body mass at maturity and b is the Bertalanffy rate constant, measured in units of time⁻¹. Relative growth rate can be obtained from equation (2.1) by differentiation, giving

2.2

Figure 1.

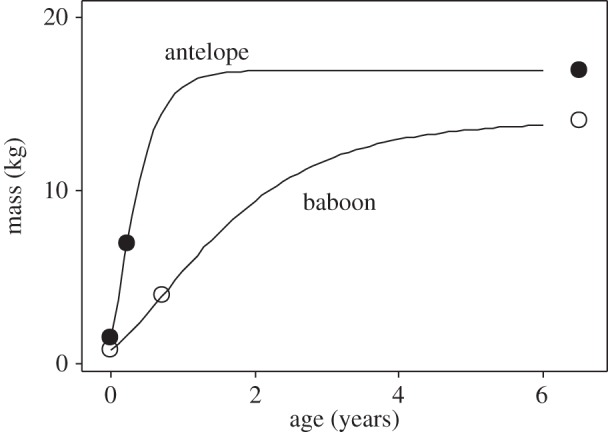
Growth of an antelope, Gazella dorcas, and a baboon, Papio hamadryas, showing how growth curves can be derived using data for body mass and time for just three key points in the life history: birth, weaning, and adult. Bertalanffy growth constants were calculated from these data using equation (2.4) and then equation (2.1) was used to draw the growth curves shown.

Equation (2.2) shows that relative growth rate is directly proportional to the Bertalanffy time constant, but also varies with juvenile size. Evaluating equation (2.2) at 10, 50 and 90% of adult size, we obtain values of relative growth rate of 1.15 b, 0.26 b and 0.04 b, respectively. So as weaning size varies systematically with adult size [30,31], it is necessary to control for weaning size when measuring juvenile productivity. In this paper, we estimate relative growth rate at 50% of adult size, when most species (79%) have weaned their offspring (median mass at weaning = 32% of mass at maturity), and we use this as our measure of juvenile productivity. When juvenile mass is 50% of adult size, 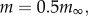and inserting this value into equation (2.2) gives

2.3

The parameter b is usually obtained by fitting equation (2.1) to data for post-weaning growth measured under ideal conditions in the laboratory. However, if four values—body masses of neonates (m₀), weanlings (m_w) and adults (m_∞), together with age at weaning (t_w)—are known, then the Bertalanffy growth constant can be obtained by rearranging equation (2.1) to estimate b:

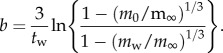2.4

Although b in equation (2.4) is calculated only from four measurements, these values are very closely correlated with values of b estimated by fitting equation (2.1) to detailed data for growth trajectories of placental mammal species (r₈₈ = 0.98, p < 0.001; J. M. Grady 2013, unpublished data) other than capital breeders (seals (Phocidae) and baleen whales (Mysticeti)), which were therefore excluded from the present analysis.

Our measures of juvenile and maternal productivity described above require species-specific data for litter size, number of litters per year, neonate, weanling, and adult mass and age at weaning. We obtained data for female placental mammals from Ernest [32], with additional data on bats from Jones et al. [33]. Following the study of Sibly & Brown [13], we divided the Carnivora into Fissipedia (terrestrial carnivores) and Pinnipedia (here sea lions and walruses). One bat species, Miniopterus schreibersii, was excluded because in the dataset weaning mass exceeded adult mass so b could not be calculated using equation (2.4). The dataset consisted of 270 species in 14 groups, comprising Artiodactyla (deer and antelope, 23 species), Chiroptera (bats, 19), Fissipedia (terrestrial carnivores 43), Insectivora (shrews and moles, 10), Lagomorpha (rabbits and hares, 13), Macroscelidea (elephant shrews, 2), Odontoceti (toothed whales, 2), Odobenidae and Otariidae (sea lions and walruses, 8), Perissodactyla (horses and rhinos, 2), Primates (43), Proboscidea (elephants, 1), Rodentia (mice and squirrels, 102), Sirenia (sea cows, 1) and Tubulidentata (aardvark, 1).

We accounted for shared ancestry in our statistical treatment of these data using the mammalian supertree of Fritz et al. [34]. For our t-tests and correlations, we used a phylogenetic generalized least squares approach [35] implemented in the program BayesTraits [36]. Tests of correlation in a phylogenetic context use a likelihood ratio (D) test to compare a model of evolution where two traits are allowed to independently evolve along the branches of a phylogenetic tree (covariance = 0), to a model where the covariance between the traits is estimated [35]. We estimate the parameter λ [35] in all analyses to determine the strength of the phylogenetic signal. The parameter λ varies between 0 and 1, where 1 is very strong phylogenetic and 0 is no phylogenetic signal. If λ = 0, the results are equivalent to tests without accounting for shared ancestry among species. For our phylogenetic generalized linear models (GLMs), we used the R package MCMCglmm [37] which incorporates the phylogenetic structure in the same way as quantitative genetic techniques integrate pedigrees—the phylogeny can be thought of as an inbred pedigree [38]. MCMCglmm estimates parameters by Markov chain Monte Carlo (MCMC) sampling and as such needs prior information. We used very weakly informative priors for all fixed effect (normal distribution, μ = 0 and σ² = 10¹⁰) and parameter-expanded priors on the random effect (phylogeny) [37]. The strength of phylogenetic signal is reported in MCMCglmm analyses as phylogenetic heritability, H², but this is identical to λ [38] so here we use λ to refer to phylogenetic signal throughout. The MCMC chains were run for 100 000 000 iterations after convergence sampling every 10 000 to minimize autocorrelation between successive samples. We report the means of the posterior distributions and 95% confidence intervals (CI).

3. Results

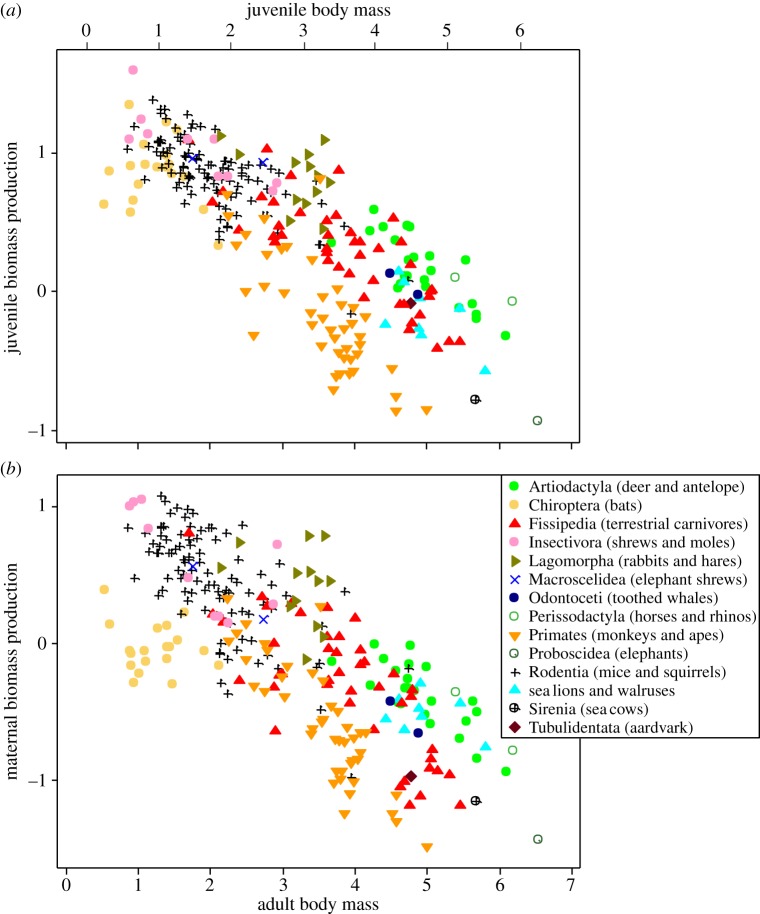
Juvenile and maternal productivities are plotted in relation to adult body mass in figure 2. Data points are for species and are colour-coded by taxon/lifestyle group. Note that productivity is measured in the same units in both graphs, i.e. year⁻¹, so the two measures are directly comparable. The patterns in figure 2a,b generally support our predictions.

• (i) Juvenile productivity scales negatively with adult body mass: both juvenile and maternal productivity scale negatively with body mass in the entire dataset (slope −0.28, t = 14.4, λ = 0.73, p = 10⁻³⁵ and slope −0.31, t = 12.3, λ = 0.82, p = 10⁻²⁸, respectively). They are similarly negatively correlated within lifestyle groups where there is good resolution because the range of body mass exceeds two orders of magnitude, in all five of the lifestyle groups for juveniles (p < 0.05), and in four out of five for adults (p < 0.05; electronic supplementary material, table S1).

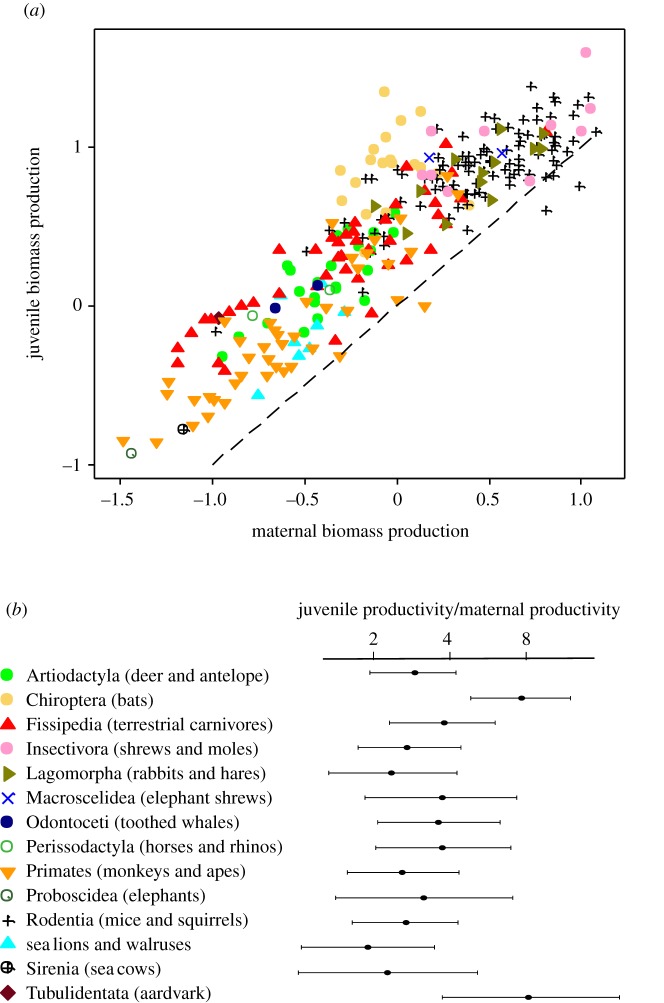
• (ii) Juvenile productivity is higher than maternal productivity: a relevant comparison is shown in figure 3a, which shows that juvenile rates exceeded maternal rates in 264 of 270 species and all lifestyles. Quantitatively, juvenile rates exceeded maternal rates by an average factor of 3, ranging from around two in lagomorphs, sea lions and walruses and sea cows to around eight in bats and Tublidentata (figure 3b).

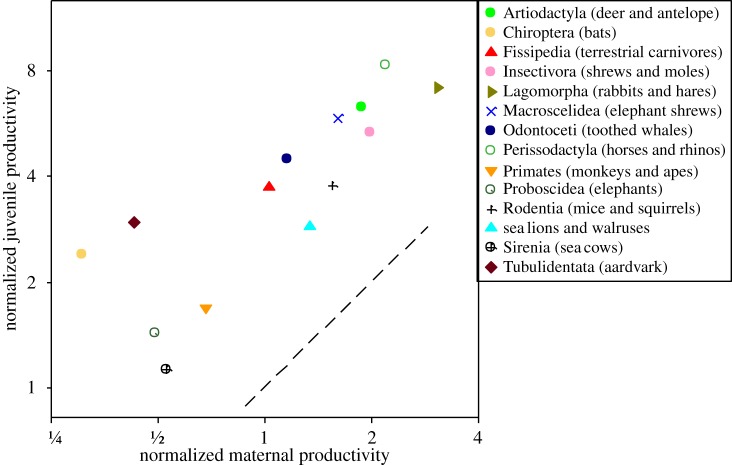
• (iii) Juvenile and maternal productivities exhibit similar variation with lifestyle across species of mammals: support can be seen by comparing figure 2a,b. In both panels, the lagomorphs and perissodactyls are higher than the bats and primates. More accurate and precise quantification is possible by controlling for the effects of body size and phylogeny. We used a phylogenetic GLM to fit parallel lines through the lifestyle groups in figure 2, following Sibly & Brown [13]. The common slope was −0.30 (CI = −0.35 to −0.25), λ = 0.73 (CI = 0.64–0.79). The elevations (normalization coefficients) were calculated at median body size (609 g). These are referred to as normalized productivities and are shown in figure 4. As expected, there is a strong correlation (r = 0.81, D₁ = 14.92, λ = 1, p < 0.001).

Figure 2.

Maternal and juvenile productivities shown in relation to adult body mass in grams in log–log plots. (a) Juvenile biomass production, measured as per cent increase per year as in equation (2.3). (b) Annual biomass production by adult females, expressed in units of grams produced per gram of mother per year, i.e. year⁻¹. In both plots, each point refers to a single species and points are colour-coded by order, except that Carnivora species are split into terrestrial carnivores (Fissipedia) and marine carnivores (here just the income-breeding sea lions and walruses). The same species are plotted in both panels. A scale for juvenile body mass, referred to in the Discussion, has been inserted above (a).

Figure 3.

Juvenile productivity in relation to maternal productivity. (a) shows all the data, symbols as in figure 2, one point per species, log–log scales. Dashed line shows where juvenile and maternal productivities are equal. (b) shows juvenile production rate as a multiple of maternal production rate. Points are phylogenetically weighted means for each taxonomic/lifestyle group and bars indicate confidence intervals divided by 1.96, similar to standard errors.

Figure 4.

Normalized juvenile productivity plotted against normalized maternal productivity for each of the lifestyle groups after allowing for body mass variation and phylogeny. Symbols as in figure 3b. Dashed line shows where juvenile and maternal productivities are equal.

4. Discussion

Metabolic theory provides a unifying mechanistic framework for understanding energy allocation to growth across all phases of the life history. In placental mammals, energy and materials allocated to produce new biomass comes from two sources: first mothers fuel growth of dependent offspring during gestation and lactation, and then juveniles fuel their own growth from weaning to maturity. Rates of maternal and juvenile productivity are closely correlated across species, suggesting that fundamental constraints on structure and function largely set the pace of the life history. Both maternal and juvenile productivities are inversely correlated with body size, showing the pervasive effects of metabolic processes and allometric scaling.

Maternal productivity is about 50% lower than that of a newly weaned offspring. This is because lactation introduces an additional trophic level—the mother feeds to produce the milk the offspring feeds on to produce flesh. This inefficiency ends when the offspring is weaned and starts foraging for itself. So post-weaning juveniles are able to be more productive than reproducing females of equivalent size and lifestyle. To assess how much more productive, it is necessary to measure productivity relative to body mass of the producer. So a scale for juvenile body mass has been inserted at the top of figure 2a (shifted to the right, because juvenile productivity is assessed at 50% adult body mass). The normalization procedure in figure 4 shows that this makes juveniles 1.23 times more productive than adults (1.23 = 10^{−0.30 × log 0.5}). Together with the twofold advantage gained by eliminating lactation, this is sufficient to account for the juvenile/adult productivity ratios seen in many of the lifestyle groups in figure 3. However, ratios are higher in the Chiroptera and Tubulidentata, so other factors may sometimes operate as well. Juveniles often must expend more energy than adults on abiotic stresses (e.g. thermoregulation) and biotic challenges (e.g. immune responses), and these costs may vary between lifestyle groups. In addition, ontogenetic shifts in energy allocation from production to maintenance may play a role (see [39]). It will be interesting to see what factors can account for the pattern of variation in the juvenile/maternal productivity ratio seen in figure 3b.

The slope of the lines through the lifestyle groups in figure 2 is −0.30, steeper than the −0.25 expected from metabolic theory. This suggests that larger animals allocate proportionately less energy to production than smaller animals. Energy not used for production fuels maintenance and survival (e.g. [40]), so the slope of −0.30 reflects a life-history trade-off between production and survival, with larger animals allocating more to survival as discussed by Hamilton et al. [30].

After controlling for body size, some of the remaining variation across species in both maternal and juvenile productivity is related to lifestyle and environment, especially food supply and predation risk (figure 4). Specifically, lagomorphs, artiodactyls and perissodactyls have exceptionally high productivities for mammals. This high productivity was interpreted by Sibly & Brown [13] as a direct consequence of diet: abundant and reliable foods allow high rates of ingestion and allocation to offspring, and consequently fast life histories [5,6]. Bats, primates, elephants, aardvarks and sea cows have exceptionally low juvenile and maternal productivities and hence slow life histories. Sibly & Brown [13] interpreted this as an indirect consequence, through ‘ecological compensation’, of the low mortality rates which result from reduced susceptibility to predation.

We suggest that an energy-based approach provides a unifying framework for understanding patterns of variation in mammal life histories in terms of the uptake and use of the energy that fuels production. The rate of using energy for production is constrained by body size and lifestyle, but body size has an additional subtle effect because larger animals increasingly prioritize survival over production. Overall, some mammals with certain body sizes and lifestyles are more productive than others, but higher productivities are balanced by increased mortality rates (e.g. ‘live fast die young’ strategies [8]). Rates of productivity and mortality must equilibrate in the long term, because average population growth rates must be close to zero. This is the principle of ecological compensation [40]. It means that in stable populations the rate of energy added owing to production must match the rate of energy loss because of mortality. So our results point the way to a mechanistic energetic explanation for the suite of correlated life-history traits that has been called the slow–fast continuum.

Funding statement

For financial support, we thank the National Science Foundation Research Coordination Network, grant DEB 0541625 (R.M.S. and J.H.B.) and National Institutes of Health, grant T32EB009414 (J.M.G. and J.H.B.).