A Comprehensive Assessment of Regional Variation in the Impact of Head Micromovements on Functional Connectomics

Abstract

Functional connectomics is one of the most rapidly expanding areas of neuroimaging research. Yet, concerns remain regarding the use of resting-state fMRI (R-fMRI) to characterize inter-individual variation in the functional connectome. In particular, recent findings that “micro” head movements can introduce artifactual inter-individual and group-related differences in R-fMRI metrics have raised concerns. Here, we first build on prior demonstrations of regional variation in the magnitude of framewise displacements associated with a given head movement, by providing a comprehensive voxel-based examination of the impact of motion on the BOLD signal (i.e., motion-BOLD relationships). Positive motion-BOLD relationships were detected in primary and supplementary motor areas, particularly in low motion datasets. Negative motion-BOLD relationships were most prominent in prefrontal regions, and expanded throughout the brain in high motion datasets (e.g., children). Scrubbing of volumes with FD > 0.2 effectively removed negative but not positive correlations; these findings suggest that positive relationships may reflect neural origins of motion while negative relationships are likely to originate from motion artifact. We also examined the ability of motion correction strategies to eliminate artifactual differences related to motion among individuals and between groups for a broad array of voxel-wise R-fMRI metrics. Residual relationships between motion and the examined R-fMRI metrics remained for all correction approaches, underscoring the need to covary motion effects at the group-level. Notably, global signal regression reduced relationships between motion and inter-individual differences in correlation-based R-fMRI metrics; Z-standardization (mean-centering and variance normalization) of subject-level maps for R-fMRI metrics prior to group-level analyses demonstrated similar advantages. Finally, our test-retest (TRT) analyses revealed significant motion effects on TRT reliability for R-fMRI metrics. Generally, motion compromised reliability of R-fMRI metrics, with the exception of those based on frequency characteristics – particularly, amplitude of low frequency fluctuations (ALFF). The implications of our findings for decision-making regarding the assessment and correction of motion are discussed, as are insights into potential differences among volume-based metrics of motion.

1. INTRODUCTION

Resting-state functional magnetic resonance imaging (R-fMRI) has emerged as a mainstream imaging modality with myriad applications in basic, translational and clinical neuroscience (Fornito and Bullmore, 2012; Fox and Raichle, 2007; Kelly et al., 2012; Van Dijk et al., 2010). Beyond impressive demonstrations of accuracy, reliability and reproducibility for measures of intrinsic brain function (Damoiseaux et al., 2006; Guo et al., 2012; Shehzad et al., 2009; Thomason et al., 2011; Zuo et al., 2010a), this approach has gained popularity due to its sensitivity to developmental, aging and pathological processes (e.g., Andrews-Hanna et al., 2007; Fair et al., 2008; Greicius, 2008; Zuo et al., 2010c), ease of data collection in otherwise challenging populations, and amenability to aggregation across studies and sites (ADHD-200-Consortium, 2012; Biswal et al., 2010; Mennes et al., 2012; Tomasi and Volkow, 2012). Despite exponential growth in usage over the last decade, R-fMRI methodologies are still confronted with significant challenges.

Head motion presents a particularly formidable challenge for R-fMRI. Recent work has demonstrated that the combined impact of “micro” head movements, as small as 0.1mm from one time point to the next, can introduce systematic artifactual inter-individual and group-related differences in R-fMRI metrics (Power et al., 2012a, b; Satterthwaite et al., 2012; Van Dijk et al., 2012). Such movements are well below quality control thresholds typically employed by most investigators, increasing the potential for artifactual findings - particularly in studies of hyperkinetic populations, such as young children or individuals with Attention-Deficit/Hyperactivity Disorder (Power et al., 2012a, b; Satterthwaite et al., 2012; Van Dijk et al., 2012). Consequently, the issue has sparked substantial debate (http://sfari.org/news-and-opinion/news/2012/movement-during-brain-scans-may-lead-to-spurious-patterns).

Several potential solutions to the challenges of overcoming motion in R-fMRI data have been proposed (e.g., Van Dijk et al., 2012). A first and obvious solution is to minimize motion; in this regard, head restraint devices (e.g., dental rests/bite bars, vacuum packing) and practice sessions with MRI simulators prior to scanning (de Bie et al., 2010; Lueken et al., 2012; Raschle et al., 2009) are sensible. Real-time feedback strategies are also possible, though less common - likely due to the need for online motion detection and concerns about potential biases that can be introduced into one’s data by such feedback (Zaitsev et al., 2006). Most promising is the proposed development of MRI acquisition strategies that are robust to motion – which already exist for structural imaging (Brown et al., 2010; Kuperman et al., 2011; White et al., 2010) and are under development for functional imaging (Maclaren et al., 2012; Ooi et al., 2011; Speck et al., 2006). However, even when successful, these solutions will not improve our ability to use already collected data – resulting in a dramatic loss of existing resources for guiding future endeavors.

With respect to post-acquisition motion correction, brain images are first realigned to correct motion-related changes in position. However, motion-induced artifacts remain due to partial voluming, magnetic inhomogeneity and spin history effects (Friston et al., 1996). A number of strategies exist to correct for residual motion artifacts, which can be used individually or in combination. Two primary approaches are advocated: 1) to model the impact of motion artifacts on BOLD signal and remove the fitted response (i.e., the predicted impact of motion), and 2) to scrub (i.e., remove or regress out) motion contaminated time points (i.e., volumes). With regard to modeling, a common practice is to regress time series data on the three translation and three rotation parameters for head movement estimated by motion realignment procedures (e.g. Fox et al., 2005; Vincent et al., 2007; Weissenbacher et al., 2009); the temporal derivatives of these six parameters can be included as well (e.g. Andrews-Hanna et al., 2007; Power et al., 2012a; Van Dijk et al., 2012). Although appealing and widely used in the R-fMRI literature, modeling-based approaches appear to be inadequate in attenuating the impact of micromovements on synchronies in the BOLD signal (Power et al., 2012a; Satterthwaite et al., 2012; Van Dijk et al., 2012). A recent study by Satterthwaite et al. (2013) systematically examined the ability of several orders of motion regression models (3, 9, 18, and 36 parameters) to remove motion-related signal. The authors demonstrated an advantage for higher order models, though residual artifact remained regardless of the model used. The best performing model (36 parameters) was based on work by Friston et al. (1996), who proposed an autoregressive model to account for the cumulative effects of motion on spin magnetization. When considering spin magnetization, the current position is important, as the excitation of spins depends on an interaction between the local magnetic field and the Fourier transform of the slice-selective pulse (Friston et al., 1996). However, the prior location can be equally important, as the spin excitation history can produce differences in local saturation. Accordingly, to account for present and past displacements, Friston et al. suggested a 24-parameter autoregressive model that included current and past position parameters, along with the square of each parameter.

An alternative approach for carrying out individual subject-level correction is to scrub contaminated volumes from time series data prior to deriving R-fMRI metrics. This is performed variably across laboratories and typically involves the removal (Mazaika et al., 2009; Power et al., 2012a) or regressing out (Lemieux et al., 2007; Power et al., 2012b; Satterthwaite et al., 2013) of single time points characterized by a sudden, sharp movement, or segments of motion-corrupted data in an otherwise usable time series. Realizing the artifactual contributions of micromovements to R-fMRI findings, Power and colleagues recently called for the rigorous scrubbing of any time frames in which micromovements occur, as well as their neighboring time points, proposing framewise displacement (FD) > 0.2mm as the threshold for frame removal (Power et al., 2012a, b). Recent work has suggested that the combination of scrubbing and modeling based approaches brings about the greatest reduction in motion-induced artifact (Power et al., 2012b, Satterthwaite et al., 2013) – this combination can be accomplished in a single, integrated regression model (i.e., by modeling motion parameters and spike regressors for each scrubbed time point). However, scrubbing approaches also have potential limitations. Scrubbing can lead to removal of large (>50%) proportions of time points from a single participant’s R-fMRI data, and can result in significant variation in the remaining numbers of time points (and therefore, degrees of freedom) from one subject to the next. Such variation can impact findings for inter-individual or group-differences in R-fMRI metrics. From an implementation perspective, the removal of non-contiguous time points alters the underlying temporal structure of the data, precluding conventional frequency-based analyses (e.g., the fast Fourier transform [FFT]-based amplitude of low frequency fluctuations [ALFF] measure, and fractional ALFF, [fALFF]), and requiring a more complicated and slower discrete Fourier transform (DFT) instead (Babu and Stoica, 2010).

Beyond individual-level correction approaches, correction for motion artifacts in group-level regression analyses is possible – primarily through inclusion of individual average motion estimates as a nuisance regressor (Satterthwaite et al., 2012; Van Dijk et al., 2012). As shown in Satterthwaite et al. (2012), the inclusion of individual motion estimates as a nuisance regressor at the group level permits the differentiation of inter-individual differences in R-fMRI measures that are attributable to motion and that are those related to variables of interest (e.g., age). One limitation is that variance shared by both motion and the variable of interest will be removed – potentially leading to underestimation of relationships with the variable of interest. Additionally, sufficiently large datasets are necessary to appropriately model the impact of motion and other nuisance signals.

In light of concerns regarding the insidious effects of micromovements, there is a strong impetus to definitively resolve the artifactual contributions of motion to R-fMRI findings. However, optimal decision-making requires a comprehensive assessment of the problem, as well as evaluation and comparison of the impact of proposed solutions. As detailed in Table 1, the goals of the present work are multifold. First, we build on prior demonstrations of regional differences in the magnitude of FD effects, by providing a comprehensive voxel-based examination of the impact of motion on the BOLD signal (i.e., motion-BOLD relationships), revealing regional variation. We use recently developed voxel-wise metrics of framewise displacement (FD_vox) (Satterthwaite et al., 2013; Wilke, 2012) to accomplish this goal, and carry out our analyses in both high and low motion datasets to determine possible dependencies of our findings on motion severity.

Table 1.

Summary of objectives, materials, methods and key novel findings.

Objective	Analytic Method	Data Employed	Key Novel Findings
1Demonstrate Regional Variation in the Impact of Motion on the BOLD Signal (Figures 1, 2, S1, S2, S3)	Calculate the correlation between BOLD signal and voxel-specific head motion and then perform one-sample t-test.	All datasets	High motion datasets exhibited more pronounced negative motion-BOLD relationships (esp. prefrontal areas). Low motion datasets exhibited more pronounced positive motion-BOLD relationships (esp. primary and supplementary motor areas).
2Evaluate the Ability of Motion Correction Strategies to Decrease the Impact of Motion on the BOLD Signal at Individual-Level (Figures 3, 4, S4)	After applying the individual-level motion correction strategies on the functional data (after realignment), calculate the correlation between corrected BOLD signal and voxel-specific head motion. Calculate the mean positive correlation and mean negative correlation as summary measures for each participant, and then perform paired t-test to compare strategies.	Cambridge Adults (n = 158; 18 participants removed due to motion)	Only ‘scrubbing’ (FD < 0.2mm) removed negative motion-BOLD relationships. Positive motion-BOLD relationships tended to cluster in primary and supplementary motor areas and remained even after scrubbing, thus may reflect to motion-related neural activity.
3Evaluate the Ability of Motion Correction Strategies to Decrease Residual Relationships Between Motion and R-fMRI Metrics at Group-Level (Figures 5, 6, S5–S10)	Calculate R-fMRI metrics after motion correction strategies, and then evaluate their correlation with motion across participants. Wilcoxon signed-rank test were used to test the distribution of residual motion effects (absolute correlation) across motion correction strategies.	Cambridge Adults (n = 158)	None of the individual-level motion correction approaches successfully bypass the need for group-level correction for inter-individual differences in R-fMRI related to motion. Z-standardization on subject-level maps reduced relationships between motion and inter-individual differences
4Examine the Influence of Global Signal Regression (GSR) on the Impact of Motion on the BOLD signal and R-fMRI metrics (Figures 7, S11)	Repeat the analyses in objective 4 and 5, taking in account GSR as well as WM/CSF signal regression.	Cambridge Adults (n = 158)	GSR introduced negative motion-BOLD relationships at individual level. However, GSR was highly effective in removing inter-individual differences related to motion.
5Examine the Impact of Motion and Motion Correction Strategies on Test-Retest Reliability (Figures 8, S12)	Calculate R-fMRI metrics after motion correction strategies, then evaluate the test-retest reliability via intra-class correlation (ICC). Wilcoxon signed-rank test were employed to compare the reliability across motion correction strategies.	NYU TRT (high motion dataset [n = 11] vs. low motion dataset [n = 11])	Motion appears to reduced test-retest reliability for correlation-based metrics Motion did artifactually increase the reliability of frequency-based metrics (ALFF >> fALFF); correction approaches reduced these increases.
6Compare Framewise Displacement (FD) Metrics (Figure 9)	Plot the difference between FDvol and meansp FDvox as a function of meansp FDvox for all time points and all participants. Plot the temporal mean of FDvol (mean FDvol) and temporal mean of meansp FDvox (mean [meansp FDvox]).	Cambridge Adults (N = 176)	Overall, there was high concordance among volume-based metrics of FD. Failure to account for rotation can lead to substantial underestimation of FD. The metric by Jenkinson et al. (2002) uniquely accounted for regional variation in motion.

Second, we examine the ability of motion correction strategies to decrease motion-BOLD relationships for a given subject, as well as their ability to eliminate artifactual inter-individual differences related to motion in group-level analyses for a broad array of voxel-wise R-fMRI metrics. Additionally, we provide insights into the impact of nuisance signal correction approaches (Chang and Glover, 2009; Fox et al., 2009; Jo et al., 2010; Weissenbacher et al., 2009) (e.g., global signal (GS) regression, white matter (WM) and cerebrospinal fluid (CSF) signal regression) on motion-BOLD relationships and artifactual inter-individual differences related to motion. We also examine the impact of motion and motion correction strategies on TRT reliability for these R-fMRI metrics. The above analyses are carried out using the following R-fMRI metrics: seed-based correlation (Biswal et al., 1995), ALFF/fALFF (Zang et al., 2007; Zou et al., 2008; Zuo et al., 2010a), regional homogeneity (ReHo, Zang et al., 2004; Zuo et al., 2013), voxel-mirrored homotopic connectivity (VMHC, Anderson et al., 2011; Zuo et al., 2010c) and degree centrality (DC, Buckner et al., 2009; Zuo et al., 2012).

Finally, given the growing number of FD metrics (Jenkinson et al., 2002; Power et al., 2012a; Van Dijk et al., 2012), we compare frequently employed metrics to verify their relative equivalence. If not equivalent, the FD metrics themselves can become a source of variability in findings across studies – even when using the same data. We explain differences among the metrics in terms of their underlying assumptions regarding brain morphology, the spatial uniformity of head motion and the contributions of rotation. All analyses conducted in the present work are carried out on publicly available datasets with publicly available algorithms, thereby facilitating efforts to replicate and extend our findings.

2. MATERIALS AND METHODS

2.1. Participants and Imaging Protocols

We implemented our analyses on publicly available pediatric (Power et al. (2012) and NYU typically developing children datasets) and adult (Power et al. (2012), Beijing and Cambridge datasets) imaging datasets from the 1000 Functional Connectomes Project and the International Neuroimaging Data-sharing Initiative. We assessed TRT reliability based on the NYU TRT dataset; all data are available at http://fcon_1000.projects.nitrc.org. The corresponding institutional review boards approved or provided waivers for the submission of anonymized data obtained with written informed consent from each participant.

Participant and scanning parameter details for each dataset are provided in Table 2. Participants were instructed to simply rest while awake in a 3 T scanner, and R-fMRI data were acquired using an echo-planar imaging (EPI) sequence. For spatial normalization and localization, a high-resolution T1-weighted magnetization prepared gradient echo image (MPRAGE) was also obtained for each participant.

Table 2.

Participant and scanning parameter details for each dataset analyzed in the current study.

Dataset	N	Sex (M/F)	Age mean/SD	TR (ms)	TE (ms)	Flip Angle (°)	Slice number	Time points
Cambridge	176*	70/106	20.9/1.9	3000	30	85	47	119
Beijing	176*	70/106	21.2/1.9	2000	30	90	33	235**
NYU Children	89	55/34	11.7/3.2	2000	33	90	33	176
NYU TRT	25	9/16	30.7/8.8	2000	25	90	39	197
J. Power Children	22	11/11	8.5/1	2500	27	90	32	Varied***
J. Power Adolescents	29	22/7	12.1/1.1	2500	27	90	32	Varied
J. Power Adults	26	4/22	23.5/1.4	2500	27	90	32	Varied

^*There were 180 participants in the Beijing Enhanced dataset and 198 participants in the Cambridge dataset. After removing 4 participants (due to inadequate field of view or bad DARTEL spatial normalization) from the Beijing dataset, 176 participants from Cambridge dataset were selected to group-match the Beijing dataset for sex and age.

^**There were no dummy scans and no deletion of first scans from the data released in the Beijing Enhanced dataset; accordingly the first 5 time points from 240 time points were discarded in preprocessing to allow signal equilibrium and participant adaptation to scanner noise. Thus 235 time points were analyzed.

^***There were 1 – 2 scanning sessions for each participant, while 1 – 6 BOLD runs within each session and 76 – 164 time points for each run (for more details: http://fcon_1000.projects.nitrc.org/indi/retro/Power2012.html). We concatenated all the runs and sessions for each subject for analyses after slice timing correction. Of note, the concatenation caused large spikes in FD at the transition time points between runs, thus the transition time points have been removed before subsequent mean FD calculation and examination of motion-BOLD relationship.

2.2. Preprocessing

Unless otherwise stated, all preprocessing was performed using the Data Processing Assistant for Resting-State fMRI (DPARSF, Yan and Zang, 2010, http://www.restfmri.net), which is based on Statistical Parametric Mapping (SPM8) (http://www.fil.ion.ucl.ac.uk/spm) and Resting-State fMRI Data Analysis Toolkit (REST, Song et al., 2011, http://www.restfmri.net). All volume slices were corrected for different signal acquisition times by shifting the signal measured in each slice relative to the acquisition of the slice at the mid-point of each TR. Then, the time series of images for each subject were realigned using a six-parameter (rigid body) linear transformation with a two-pass procedure (registered to the first image and then registered to the mean of the images after the first realignment). Individual structural images (T1-weighted MPRAGE) were co-registered to the mean functional image after realignment using a 6 degrees-of-freedom linear transformation without re-sampling. The transformed structural images were then segmented into gray matter (GM), WM and CSF (Ashburner and Friston, 2005). The Diffeomorphic Anatomical Registration Through Exponentiated Lie algebra (DARTEL) tool (Ashburner, 2007) was used to compute transformations from individual native space to MNI space and vice-versa.

2.3. Voxel-Specific Head Motion Calculation

Wilke (2012) suggested that head motion impacts voxels differentially depending on their distance from the center of the gradient coil. In contrast to the assumption that each rotation (pitch, roll, yaw) has the same effects at all voxels, we computed voxel-specific head motion by taking location-related differences in rotation into account, as recently performed by Satterthwaite et al. (2013). Below, we detail the formulas used to perform voxel-specific head motion calculations here; the implementation is freely available in the open-source toolbox DPARSF.

Based on the six head motion parameters (x, y, z translations and α, β, γ rotations) derived in the realignment step, we can calculate a matrix T_t that corresponds to the rigid-body transformation of the image at time point t to the position of the reference image I₀ (usually the first time point or the mean image after an initial motion correction) (Ashburner and Friston, 2004).

$$T_t=\left[\begin{array}{cccc}1& 0& 0& x\\ 0& 1& 0& y\\ 0& 0& 1& z\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \text{cos}\alpha & \text{sin}\alpha & 0\\ 0& -\text{sin}\alpha & \text{cos}\alpha & 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}\text{cos}\beta & 0& \text{sin}\beta & 0\\ 0& 1& 0& 0\\ -\text{sin}\beta & 0& \text{cos}\beta & 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}\text{cos}\gamma & \text{sin}\gamma & 0& 0\\ -\text{sin}\gamma & \text{cos}\gamma & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$ (1)

Conversely, $T_t^{-\mathit{1}}$ is the rigid-body transformation of the reference image I₀ to the position of the image at time point t.

For a voxel V_ijk,0 at reference time point 0, its corresponding coordinates C_xyz,0 in (mm) are:

$$C_{xyz,\mathit{0}}=M_{\mathit{0}}{V}_{ijk,\mathit{0}}$$ (2)

where M₀ is the voxel-to-world mapping affine matrix (geometric coordinates of the index voxel) for reference image I₀.

After head motion transformation, voxel V_ijk,0 will have new coordinates C_xyz,t at time point t:

$$C_{xyz,t}=T_t^{-\mathit{1}}{M}_{\mathit{0}}{V}_{ijk,\mathit{0}}$$ (3)

We can then calculate the voxel specific translations in x, y, z:

$$H{M}_{ijk,t,\mathit{0}}=C_{xyz,t}-C_{xyz,\mathit{0}}=T_t^{-\mathit{1}}{M}_{\mathit{0}}{V}_{ijk,\mathit{0}}-M_{\mathit{0}}{V}_{ijk,\mathit{0}}$$ (4)

Specifically, we can obtain the voxel-specific total displacement relative to the reference image (TD_vox):

$$T{D}_{vox,t}=\sqrt{H{M}_{vox,x,t}^2+H{M}_{vox,y,t}^2+H{M}_{vox,z,t}^2}$$ (5)

And the voxel-specific distance relative to the previous image (i.e., voxel-based framewise displacement FD_vox):

$$F{D}_{vox,t}=\sqrt{{(H{M}_{vox,x,t}-H{M}_{vox,x,t-1})}^2+{(H{M}_{vox,y,t}-H{M}_{vox,y,t-1})}^2+{(H{M}_{vox,z,t}-H{M}_{vox,z,t-1})}^2}$$ (6)

The voxel-specific head motion is a nonlinear combination of the volume-wise translations and rotations, as well as the voxel’s position. Here, the voxel-specific movement is handled via a combination of affine matrices for each rotation and translation, $T_t^{-\mathit{1}}$.

We also compared the volume-based framewise displacement (FD_vol) proposed in previous studies with the spatial mean FD_vox across voxels (mean_sp FD_vox, an analogue of FD_vol):

$${\text{FD}}_{\text{vol},\mathrm{t}}(\text{Power})=|{\mathrm{x}}_{t-1}-x_t|+|y_{t-1}-y_t|+|z_{t-1}-z_t|+50•\frac{\pi }{180}•(|{\alpha }_{t-1}-{\alpha }_1|+|{\beta }_{t-1}-{\beta }_t|+|{\gamma }_{t-1}-{\gamma }_1|)$$

where 50 mm denotes the assumed radius of the head (Power et al., 2012a). ${\text{FD}}_{\text{vol},\mathrm{t}}(\text{Van Dijk})=\sqrt{x_t^2+y_t^2+z_t^2}-\sqrt{x_{t-1}^2+y_{t-1}^2+z_{t-1}^2}$ (Van Dijk et al., 2012) ${\text{FD}}_{\text{vol},\mathrm{t}}(\text{Jenkinson})=\sqrt{\frac{1}{5}{R}^2\mathit{\text{Trace}}(A^{T}A)+{(b+Ac)}^T(b+Ac)}$ (Jenkinson et al., 2002) where R=80 mm denotes the assumed radius of the head (as used in FSL), c indicates the coordinates for the center of the volume, and A, b are defined as:

$$\left[\begin{array}{ll}A\hfill & b\hfill \\ 0\hfill & 0\hfill \end{array}\right]=T_t{T}_{t-1}^{-1}-I$$

2.4. The Differential Impact of Region-Specific Motion on the BOLD Signal

Having calculated regional differences in the magnitude of framewise displacements, we next examined regional differences in the impact of a given amount of head motion on the BOLD signal after realignment. We calculated the Pearson’s correlation coefficient between FD_vox and the BOLD signal at each voxel while partialling out linear and quadratic trends to account for low-frequency drifts in the BOLD signal. After Fisher’s r-to-z transformation, the correlation maps were converted to MNI space (3mm³ cubic voxels) and smoothed with a 4.5 mm Gaussian smoothing kernel. One-sample t-tests were performed to detect consistent relationships between head motion and the BOLD signal across subjects. To compare the whole-brain pattern across datasets, we present unthresholded images in the main text, but include figures illustrating only statistically significant results in the Supplementary Materials (Gaussian random field theory correction for multiple comparisons was applied, thresholding at Z > 2.3 and cluster-level p < 0.05).

2.5. Head Motion Correction Strategies

We used various strategies to further correct head motion effects on R-fMRI BOLD signal at the individual level. Of note, we examined the head motion correction models separately from global signal regression (GSR) as well as from regression of WM and CSF signals. This differs from the approach taken by Satterthwaite et al. (2013), who employed global, WM and CSF signal regression in their comparisons of head motion regression models. Specifically, we examined the following motion correction strategies:

1. Regression of realigned data on 6 head motion parameters (i.e., three translations and three rotations) (rigid-body 6-parameter model);

2. Regression of realigned data on 6 head motion parameters and their first temporal derivatives (derivative 12-parameter model);

3. Regression of realigned data on 6 head motion parameters and autoregressive models of motion: 6 head motion parameters, 6 head motion parameters one time point before, and the 12 corresponding squared items (Friston et al., 1996) (Friston 24-parameter model);

4. Regression of realigned data on voxel-specific head motion parameters in a Friston autoregressive style (Friston et al., 1996): the 3 voxel-specific translation motion parameters in x, y, z, the same 3 parameters for one time point before, and the 6 corresponding squared items (voxel-specific 12-parameter model);

5. Scrubbing after regression (volume removing): Removing time points using a threshold of framewise displacement (FD: FD_vol proposed by Power et al., 2012a) > 0.2 mm as well as 1 back and 2 forward neighbors (Power et al., 2012b). The “scrubbing” procedure was performed after each of Strategies 1–4. The multiple regression of nuisance variables was fit to all data as done by Power et al. (2012a).

6. Scrubbing within regression (spike regression): Identifying “bad” time points using a threshold of FD>0.2mm as well as 1 back and 2 forward neighbors as done in Power et al. (2012b), then modeling each “bad” time point as a separate regressor in the regression models (Lemieux et al., 2007; Satterthwaite et al., 2013) in addition to Strategies 1–4. The residual is equivalent to performing regression only within the “good” data (Power et al., 2012b).

As scrubbing (Strategies 5 and 6) can result in a removal of a large number of time points (Power et al., 2012a, b; Satterthwaite et al., 2013) and too few remaining time points may lead to unreliable results, we set a 3-minute criterion and removed subjects who had less than 3 minutes of data remaining after scrubbing. We used a 3-minute rather than a 5-minute (Power et al., 2012a) or 4-minute (Satterthwaite et al., 2013) minimum criterion to ensure that enough subjects remained to permit the examination of test-retest reliability after “scrubbing.” In the NYU TRT dataset, 11 subjects had at least 3 minutes of data remaining for each of the 3 sessions after scrubbing, while only 5 subjects would have remained if we had required 4 minutes (Table S1)¹. In a recent study (Zuo et al., 2013), good inter-session reliability was found for functional homogeneity analyses even with scan durations as brief as 3 minutes. In addition, a supplementary analysis was performed to test the impact of scan length after scrubbing on the reliability of R-fMRI measures (see Supplementary Results and Figure S15). This analysis indicated that 3 minutes of scrubbed data exhibits high reliability (intraclass correlation (ICC)>0.7) with the full-duration, unscrubbed time series (7.8 minutes).

For regression models, linear and quadratic trends were also included as regressors to account for low-frequency drifts in the BOLD signal. Temporal filtering (0.01 – 0.1 Hz) was applied to the data with each correction method prior to calculating derivatives, except for frequency-based R-fMRI indices (ALFF and fALFF).

2.6. Global Signal Regression (GSR)

GSR, a commonly used, yet controversial practice in the R-fMRI field yields substantial increases in negative correlations (Murphy et al., 2009; Weissenbacher et al., 2009) and may distort group differences in iFC (Saad et al., 2012). Here, we evaluated the effects of head motion correction strategies on analyses performed with and without GSR. According to the Frisch–Waugh–Lovell theorem (Frisch and Waugh, 1933; Lovell, 1963, 2008), a single model multiple regression is equivalent to a three-step version in which 1) a subset of regressors (here, the motion parameters) is regressed out from the response (here, the BOLD signal) and 2) this subset of regressors is regressed out from any remaining regressors (here, the GS), then 3) the residuals of response obtained in Step 1 (i.e., the BOLD signal orthogonal to motion) are regressed on the residuals of remaining regressors obtained in Step 2 (i.e., the GS orthogonal to motion). The residuals and beta values produced by Step 3 are equivalent to those that would be obtained using a single multiple regression model. Thus, we extracted the GS after head motion regression (which is equivalent to regressing out motion from GS extracted beforehand), and then regressed it out from the residuals of head motion regression, which is equivalent to regressing out head motion and GS (extraction after realignment) in a single model. We also evaluated the effects of regression on WM and CSF signals, as well as GS together with WM and CSF signals.

2.7. A Broad Array of R-fMRI-based Intrinsic Brain Function Indices

We explored whether and how a broad array of R-fMRI based indices of intrinsic brain function are affected by head motion and various motion correction strategies. The R-fMRI indices examined were:

1. Amplitude measures: amplitude of low frequency fluctuations (ALFF) (Zang et al., 2007) and fractional ALFF (fALFF) (Zou et al., 2008). ALFF is the sum of amplitudes within a specific low frequency range (0.01 – 0.1 Hz in the current study), while fALFF is the ratio of the ALFF of a given low frequency band (here, 0.01 – 0.1Hz) to the sum of amplitudes across the entire frequency range detectable in a given signal. ALFF indexes the strength or intensity of low frequency oscillations, while fALFF represents the relative contribution of specific oscillations to the whole detectable frequency range. Subject-level Z-score maps were acquired by subtracting the mean value for the entire brain, and then dividing by the whole brain standard deviation¹.

2. Regional homogeneity (ReHo) (Zang et al., 2004). ReHo assesses the degree of regional synchronization among fMRI time courses. ReHo is defined as the Kendall’s coefficient of concordance (KCC, Kendall and Gibbons, 1990) of the time series of a given voxel with those of its nearest neighbors (26 in the current study). A larger ReHo value for a given voxel indicates higher regional coherence. Subject-level Z-score maps were created by subtracting the mean value for the entire brain from each voxel, and dividing by the corresponding standard deviation (Zuo et al., 2013).

3. Voxel-mirrored homotopic connectivity (VMHC) (Zuo et al., 2010c). VMHC corresponds to the functional connectivity between any pair of symmetric inter-hemispheric voxels - that is, the Pearson’s correlation coefficient between the time series of each voxel and that of its symmetrical inter-hemispheric counterpart. The resultant VMHC values were transformed into z values using Fisher’s r-to-z transformation.

4. Seed-based correlation analysis (SCA). Consistent with previous motion studies (Satterthwaite et al., 2012; Van Dijk et al., 2012), we extracted the mean time series for the posterior cingulate cortex (PCC: 0, −53, 26; 10mm diameter sphere) from smoothed functional volumes in MNI space, and then calculated the Pearson’s correlation coefficient between each time course and every other voxel in the native brain space. These correlation values were transformed into z values using Fisher’s r-to-z transformation.

5. Network degree centrality (Buckner et al., 2009; Zuo et al., 2012). Degree centrality is the number or sum of weights of significant connections for a voxel. Here, we calculated the weighted sum of positive correlations by requiring each connection’s statistical significance to exceed a threshold of p < 0.001. Subject-level Z-score maps were created by subtracting the mean degree centrality value for the entire brain from each voxel, and dividing by the corresponding standard deviation.

Indices 1, 2, 4 and 5 were calculated in native space, and corresponding maps were then registered into MNI space with 3mm³ cubic voxels by using transformation information acquired from DARTEL. A smoothing kernel of 4.5mm was applied after registration. Measure 3 (VMHC) was a notable exception, as the measure requires that data are first registered in MNI space and smoothed (FWHM = 4.5mm) prior to calculation.

2.8. Assessing The Impact of Motion Correction Strategies

To evaluate the ability of motion correction strategies to decrease the impact of motion on the BOLD signal at an individual level, we calculated the correlation between the residual BOLD signal obtained after motion correction strategies (described in Section 2.5) and voxel-specific head motion (FD_vox) for each subject (as described in Section 2.4). To statistically compare these different correction strategies, we extracted the mean positive correlation (i.e., the sum of all positive Fisher’s z values across the brain divided by the total number of voxels) and mean negative correlation for each subject. Paired t-tests were used to compare the mean positive correlation (and mean negative correlation) of the subjects across motion correction strategies.

At the group-level, to examine head motion effects on our targeted array of R-fMRI-based intrinsic brain function measures, we calculated the correlation between head motion indexed by mean FD_vox (temporal mean for each voxel) and each of the R-fMRI indices across participants. We plotted the spatial distribution of these group-level motion correlations (converted into z value with the same significance) for each motion correction strategy. To examine whether certain motion correction strategies yield less extreme correlations in the distribution, we performed the Wilcoxon signed-rank test on the absolute value of motion correlations across strategies.

2.9. Test-Retest Reliability of R-fMRI Measures with Head Motion Correction Strategies

To evaluate the effects of different head motion correction strategies on the TRT reliability of R-fMRI indices, we computed intra-class correlations (ICC) (Shrout and Fleiss, 1979) for each of the R-fMRI indices, using the NYU TRT dataset.

$$ICC=\frac{M{S}_b-M{S}_w}{M{S}_b+M{S}_w}$$

Where MS_b is the between-subject mean square and MS_w is the within-subject mean square for each index.

There were three scans in the NYU TRT dataset; the first scan (scan 1) was collected 5 – 16 months (mean±SD = 11±4) before two subsequent scans (scan 2 and 3), which were collected in a single session 45 minutes apart. We evaluated inter-session reliability as the ICC between scan 1 and the average of scans 2 and 3. Scans 2 and 3 were averaged to improve the estimation of long-term reliability (Shehzad et al., 2009; Zuo et al., 2010a).

Between-subject differences in head motion have been found to be stable (Van Dijk et al., 2012). We also found relatively high TRT reliability (inter-session ICC = 0.73) for motion (indexed by mean [mean_sp FD_vox]). To address the question of whether high TRT reliability of head motion artificially increases the TRT reliability of R-fMRI metrics, we selected 11 low motion subjects from the NYU TRT dataset (all of these subjects survived the 3-minute criterion for each of the 3 sessions after scrubbing) to create a low motion dataset, as well as 11 high motion subjects with the highest mean motion across the 3 sessions (all of these subjects had at least one session that did not survive the 3-minute criterion after scrubbing) to create a high motion dataset. We then performed TRT reliability analyses on the low motion dataset and high motion dataset separately, and applied the Wilcoxon signed-rank test to compare the distributions of TRT reliability between the datasets.

3. RESULTS

3.1. Regional Variation in the Impact of Motion on the BOLD Signal

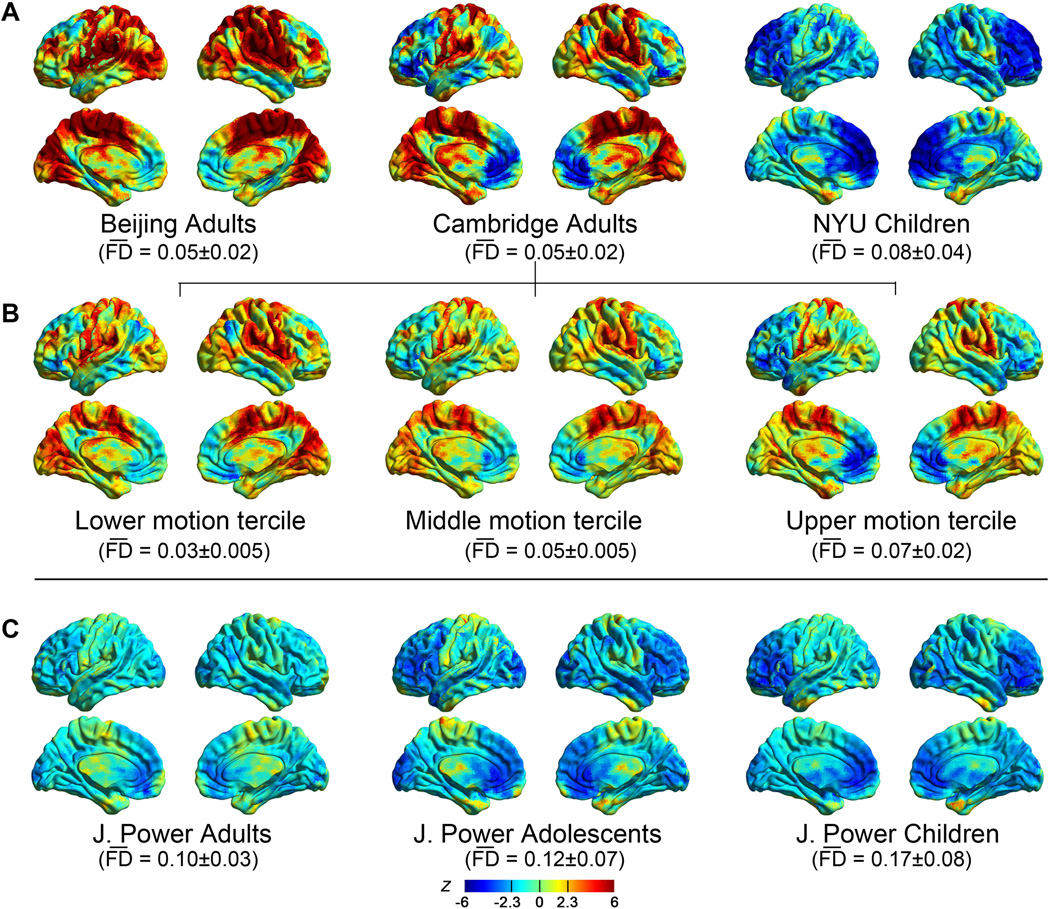
We examined regional differences in the impact of head motion on the BOLD signal (i.e., motion-BOLD relationships), building upon prior work (Satterthwaite et al., 2013) demonstrating regional differences in the magnitude of framewise displacements. Replicating previous findings, voxel-specific metrics of framewise displacements (FD_vox) revealed regional differences in the magnitude of motion, with the specific pattern depending on the nature of the movement (e.g., pitch, roll, yaw) (Figure 1A). Consistent with the findings of Satterthwaite et al. (2013), motion tended to be greatest in prefrontal cortex and least in inferior parietal and superior temporal cortex (Figure 1B), likely reflecting the characteristic pattern of pitch (i.e., head nodding) - the most common in-scanner head movement.

Figure 1.

The voxel specific head motion measure. (A) Voxel-based framewise displacement (FD_vox) pattern of different rotations (pitch, roll and yaw) and the mean FD_vox (averaged across time) pattern for a representative participant. (B) The group mean and coefficient of variation (CV) across the Cambridge dataset of mean FD_vox. Consistent with the mean FD_vox in panel A, the greatest motion was found in the prefrontal cortex and the least motion was found in the parietal cortex. Surface maps were created with BrainNet Viewer (www.nitrc.org/projects/bnv/).

To investigate the motion-BOLD relationships, we first examined the relationship between FD_vox and the BOLD signal at each voxel on an individual basis, and then tested for the presence of consistent patterns across subjects. As shown in Figure 2A (but see Figure S1 for thresholded maps), medial and lateral prefrontal cortex exhibited a negative relationship between FD_vox and BOLD signal, while primary and supplementary motor as well as visual cortex showed positive relationships. Interestingly, negative correlations in prefrontal regions are more prominent in the child dataset (NYU children), which is characterized by relatively greater head motion, while positive correlations in the motor area were more prominent in adult datasets (Beijing and Cambridge), which are characterized by relatively lower head motion (see the head motion distribution in Figure S2). A similar age-group dependent pattern of results was noted in the Power et al. (2012) sample that consisted of children, adolescents and adults (Figure 2C), though with more diffuse negative relationships (i.e., greater number of voxels exhibiting negative relationships). Importantly, relative to Cambridge and Beijing adult datasets, the Power et al. datasets contained more motion (Figure S2), regardless of age, suggesting that more diffuse negative relationships may indeed reflect greater participant motion. To determine the extent to which these negative correlations corresponded to the degree of motion as opposed to participant age, we divided the Cambridge and NYU Children datasets into terciles according to mean motion (indexed by mean [mean_sp FD_vox]) (Figures 2B and S3A). As expected, in both datasets, the lowest head motion tercile demonstrated positive correlations in motor areas, while the highest head motion tercile demonstrated negative correlations in prefrontal regions and weaker positive relationships.

Figure 2.

The correlation between the BOLD signal (after realignment) and voxel-specific head motion. (A) One-sample t-test on all the individual’s Fisher’s Z-score maps for the relationship between FD_vox and BOLD signal within the Beijing adults, Cambridge adults and NYU Children datasets. (B) We examined the motion-BOLD relationship by dividing the Cambridge dataset (N=176) into 3 terciles according to mean [mean_sp FD_vox]: lower tercile (n=59), middle tercile (n=58) and upper tercile (n=59). (C) The motion-BOLD relationships in J. Power’s data from adults, adolescents and children (the transition time points between runs have been removed before correlation calculation due to the large spikes in FD caused by concatenation). ***denotes mean [mean_sp FD_vox], the group mean and standard deviation are listed below each dataset.

Given that pitch (rotation around the x axis) was the predominant head motion across samples, we were not surprised to note the high degree of congruence between the hemispheres with respect to motion-BOLD relationships. Homotopic areas appear to exhibit highly similar head motion and may disproportionately and spuriously increase iFC between symmetric brain regions, and possibly contribute to the well-documented ubiquity of homotopic connectivity (Anderson et al., 2011; Salvador et al., 2005; Stark et al., 2008; Zuo et al., 2010c). This concern was explored further and addressed in the supplementary materials (see supplementary results and Figure S16). Specifically, replication of analyses performed by Stark et al. (2008) demonstrated that homotopic connections maintained their superior strength relative to intrahemispheric and heterotopic connections regardless of motion correction strategy.

3.2. The Ability of Motion Correction Strategies to Decrease the Impact of Motion on the BOLD Signal at the Individual Level

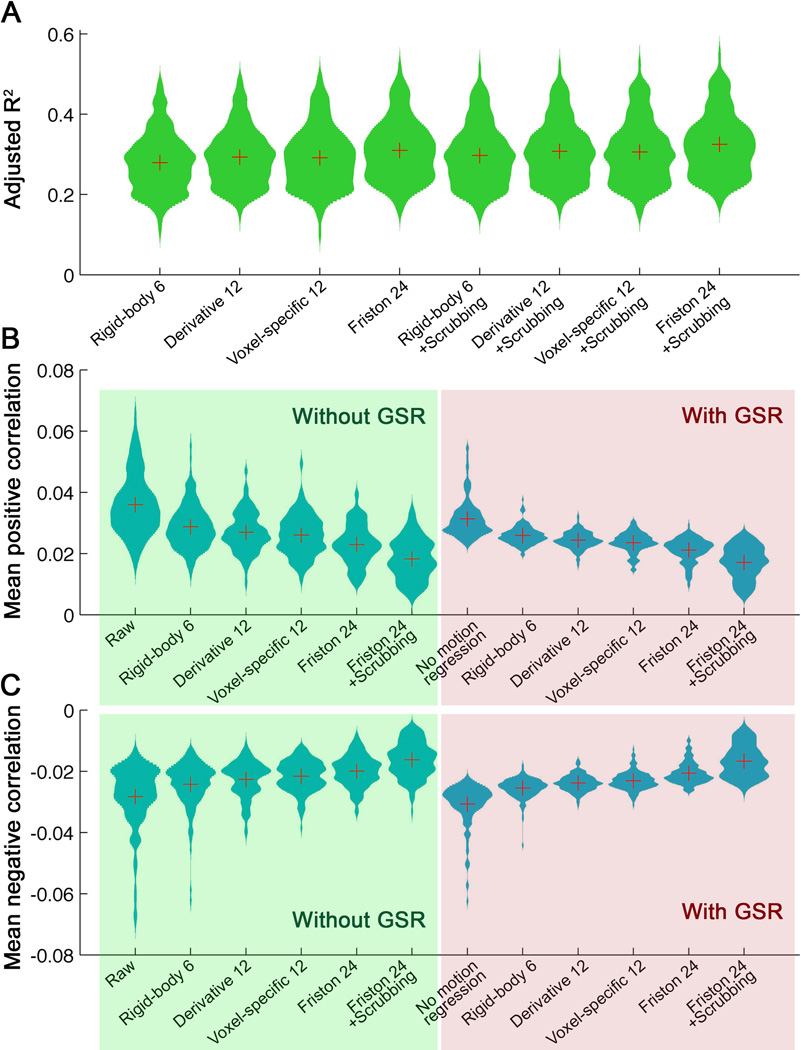
We examined the ability of various motion correction strategies to reduce the positive and negative motion-BOLD relationships described in Section 3.1. All of the modeling-based approaches demonstrated some ability to reduce motion-BOLD relationships (Figure 3), with the Friston-24 approach showing the greatest reductions in both positive (t = −9.9, p < 0.0001, versus next best: voxel-specific 12 model; see Figure 4B) and negative (t = 7.0, p < 0.0001, versus next best: voxel-specific 12 model; see Figure 4C) motion-BOLD relationships. Examining the BOLD signal after head motion correction models, the Friston 24 approach produced the least motion-related spikes (a representative subject is shown in Figure S4). Examination of the proportion of variance explained (an approach previously employed by Satterthwaite et al., 2013) further supported this conclusion (t = 10.4, p < 0.0001, versus next best: derivative 12 model) (Figure 4A). However, none of the approaches examined completely eradicated positive or negative motion-BOLD relationships (Figure 3).

Figure 3.

The effects of motion correction strategies on the correlation between BOLD signal and voxel-specific head motion in the Cambridge dataset. The first column (“Raw”) demonstrated one-sample t-test on all the individual’s Fisher’s Z-score maps for the relationship between FD_vox and BOLD signal obtained with the uncorrected data. Columns 2–4 demonstrated the motion-BOLD relationships after motion regression models (rigid-body 6, derivative 12, voxel-specific 12 and Friston 24). Row 2 demonstrated the motion-BOLD effects by combined scrubbing within the motion regression models (each bad time point defined a single regressor, i.e., spike regression). Row 3 demonstrated the results with scrubbing performed after the regression models (i.e., volume removing). To facilitate comparison with scrubbing strategies, 18 subjects that failed to meet the 3-minute criterion after scrubbing were removed, thus all the analyses here were based on the remaining 158 subjects.

Figure 4.

Comparison of head motion correction procedures on the motion-BOLD relationship (within-subject level) in the Cambridge dataset (n=158). (A) The adjusted R² across head motion correction procedures (the spatial mean adjusted R² extracted for each participant). (B) The mean positive correlation (i.e., the sum of all positive Fisher’s z values across the brain divided by the total number of voxels) across different motion correction strategies. (C) The mean negative correlation across different motion correction strategies. The red “+” denotes the mean of each distribution.

In contrast to modeling-based approaches, scrubbing approaches effectively removed negative motion-BOLD relationships in their entirety. However, prominent albeit reduced positive relationships remained in motor and dorsomedial visual areas even after scrubbing (Figure 3). These findings were independent of the specific implementation of scrubbing employed; although, the addition of spike-regression-based scrubbing to the Friston-24 approach appeared to best account for motion-related variations in the BOLD signal, based on the proportion of variance explained (t = 7.84, p < 0.0001, versus next best: Friston 24 model) (Figure 4A). We thus selected this strategy as the representative scrubbing approach used in all subsequent group-level analyses.

3.3. The Ability of Motion Correction Strategies to Decrease Residual Relationships Between Motion and R-fMRI Metrics at Group-Level

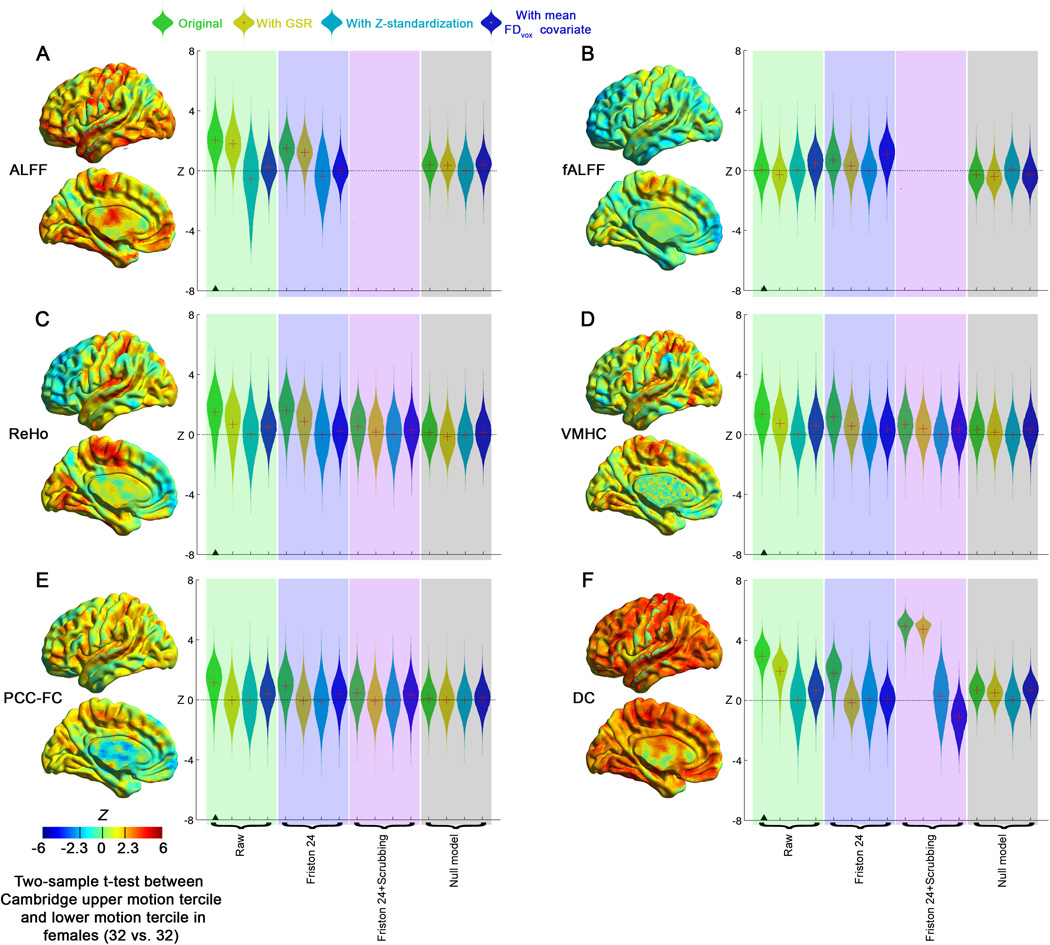
Group-level results from fALFF, ReHo and DC metrics were relatively robust across different motion correction strategies (Figures 5, S5, S6). The use of a Z-standardization with these metrics (i.e., within-subject mean centering and variance normalization) largely explains their relative robustness to motion and the impact of differing strategies (see Supplementary results and Figure S7 for demonstration of this point). A notable exception was for DC following Friston 24 + scrubbing approach, which produced a marked increase in the distribution of voxels exhibiting significant relationships between motion and centrality across subjects (Wilcoxon signed-rank test Z = 59.8, p < 0.0001, versus Friston 24) (Figures 5, S5, S6, Table S2); as depicted in Figure S7, these relationships increased drastically when the Z-standardization was not applied (Z = 226.8, p < 0.0001). This reflects an increase in the likelihood of extreme correlation values for the connectome produced by scrubbing; see Supplementary Results and Figure S14 for demonstration of increases in maximum and minimum correlation values that result from decreases in the number of degrees of freedom associated with volume-censoring. Use of Z-standardization appears to make findings robust to biases in likelihood of high correlation values introduced by scrubbing, due to mean centering (see Figure S7).

Figure 5.

The impact of head motion correction procedures on the relationships between R-fMRI measures (A: ALFF; B: fALFF; C: ReHo; D: VMHC; E: PCC-FC and F: DC) and motion (mean FD_vox) across subjects (between-subject level) in the Cambridge dataset (n=158). The green shadow denotes analyses without GSR, while the pink shadow denotes analyses with GSR. “?” denotes the condition on which the surface map was generated. The red “+” denotes the mean of each distribution. “*” denotes that the relevant R-fMRI measure has been Z-standardized.

Consistent with prior work noting the susceptibility of ALFF to artifactual contributions of motion and pulsatile effects (Zuo et al., 2010a), we found significantly more voxels exhibiting prominent relationships with motion for ALFF, relative to fALFF (Wilcoxon signed-rank test Z = 91.9, p < 0.0001, on uncorrected data) (Figures 5, S5, S6). The higher order Friston-24 model was successful in reducing the distribution of voxels exhibiting relationships with motion (Wilcoxon signed-rank test Z = −26.0, p < 0.0001, versus next best: voxel-specific 12 model) (Table S2). Of note, post-scrubbing data cannot be used for ALFF and fALFF analyses using traditional fast Fourier approaches, as scrubbing alters the temporal structure of the data.

Selection of motion correction strategy appeared to impact inter-individual relationships between motion and simple bivariate correlation based metrics (e.g., VMHC and functional connectivity with PCC (PCC-FC)) the most (Figure 5). For both VMHC and PCC-FC, there was a positive bias in their relationship with motion across subjects, with application of the Friston-24 model producing the greatest decreases in artifactual relationships among modeling-based approaches (VMHC: Z = −66.6, p < 0.0001, versus next best: voxel-specific 12 model; PCC-FC: Z = −51.1, p < 0.0001, versus next best: voxel-specific 12 model). The addition of spike-regression-based scrubbing to the Friston-24 approach reduced these relationships further (VMHC: Z = −160.7, p < 0.0001; PCC-FC: Z = −129.6, p < 0.0001; versus Friston 24). In considering potential non-motion related contributions to our findings, we repeated our analyses with age and sex as covariates, obtaining identical patterns of findings (data not shown due to their similarity). Of note, similar to other R-fMRI metrics, artifactual relationships with motion appeared to be mitigated by application of Z-standardization (mean-centering and variance normalization) to each participant’s data (see supplementary Figure S7).

In summary, the Friston 24 model performed the best among the modeling-based approaches for all measures but fALFF. The addition of scrubbing to the Friston 24 model yielded further reductions in motion effects for ReHo, VMHC and PCC-FC (see Table S2A for Wilcoxon signed-rank test summary statistics).

Given the suggestion of the continued need for group-level correction after individual-level motion correction (Satterthwaite et al., 2012; Van Dijk et al., 2012), we decided to compare the upper and lower motion terciles for the Cambridge dataset (Section 3.1). Before doing so, we noted the presence of significant differences in sex ratios between the two terciles (25% male in lower tercile, 58% male in upper tercile; χ² = 11.15 p < 0.001). In light of this, we re-created upper and lower motion terciles using females only (n = 32 / group) to avoid potential confounds associated with sex; age did not differ. Marked reductions in residual relationships were noted by taking mean FD_vox as a covariate, as would be expected, particularly for correlation-based metrics (PCC-FC, VMHC) (see Figure S8). A small number of voxels did exhibit persistent relationships with motion, suggesting that additional covariates may be needed to more comprehensively remove any and all dependencies. To ensure that these relationships were truly related to motion, we mixed subjects of the motion terciles together and created two “null groups” equated for motion and age. Distributions for comparison of these groups were tightly centered around zero (see Figure S9). In Figure 6, the key findings related to the impact of individual and group level motion corrections on motion-related group differences in R-fMRI metrics, as well as the Z-standardization and global signal regression (discussed in next section) are depicted; the distribution for the null group comparison is included as well¹.

Figure 6.

The impact of GSR, Z-standardization, group-level covariate of mean FD and head motion correction procedures on the motion-related group difference in R-fMRI measures (A: ALFF; B: fALFF; C: ReHo; D: VMHC; E: PCC-FC and F: DC). Two-sample t-test was performed between upper motion tercile (n=32) and lower motion tercile (n=32) of Cambridge females (who survived the 3-minute criterion). The “null model” was defined by performing two-sample t-test between two “null” groups (mixing the motion terciles and equating for motion and age). “?” denotes the condition on which the surface map was generated. The red “+” denotes the mean of each distribution.

Given the growing usage of both individual- and group-level corrections in the literature, we further explored the potential benefits of combining group-level correction with the best performing models (Friston 24 and Friston 24 + scrubbing; see Figure S10 and Table S5A). Adding mean FD as covariate to the Friston 24 model, was generally beneficial for the non-Z-standardized VMHC and PCC-FC (Z = −120.8 and Z = −94.5; with FD Cov vs. without FD Cov), as well as the Z-standardized measures such as ALFF, ReHo and DC (Z = −65.4, Z = −47.0 and Z = −78.6; with FD Cov vs. without FD Cov). Importantly, when group-level correction with mean FD was carried out, the previous benefits of adding scrubbing (i.e., spike regression) to the Friston 24 model for ReHo, VMHC and PCC-FC were nearly extinguished (Z = 0.9, Z = 18.8 and Z = −6.1; scrubbing + FD Cov vs. FD Cov). Overall, these findings suggest the value of combining group- and modeling-based individual-level corrections, though not scrubbing.

3.4. The Influence of Global Signal on the Impact of Motion on the BOLD Signal and R-fMRI Metrics

GSR remains commonly used in the literature, despite concerns about its effect on the distribution of intrinsic functional connectivity and resultant increases in negative correlations (Murphy et al., 2009; Saad et al., 2012; Weissenbacher et al., 2009). While our primary analyses were conducted without GSR, we also evaluated the influence of GSR on the impact of motion on the BOLD signal and R-fMRI metrics.

At the individual subject-level, positive motion-BOLD correlations were substantially reduced with GSR (significant for all motion correction strategies, e.g., Friston 24 with GSR vs. Friston 24 without GSR: t = −4.4, p < 0.0001), and markedly less variation in the magnitude of positive motion-BOLD relationships was observed across voxels (Figure 4). The magnitudes of negative motion-BOLD relationships increased with GSR (significant for all the combinations of motion corrections strategies, e.g., Friston 24 with GSR vs. Friston 24 without GSR: t = −2.3, p < 0.01; see Figure 4) – particularly in medial and lateral prefrontal cortex; these negative motion-bold correlations could not be removed with scrubbing (Figure 7). Correction for WM+CSF signal without GSR produced no such change in motion-BOLD relationships (Figure 7), which is consistent with a previous report that WM regressors explained little of the variance of the R-fMRI BOLD signal (Jo et al., 2010).

Figure 7.

Comparison of nuisance regressions (with or without the regression of global, WM and CSF signals) on the FD_vox-BOLD relationship in Cambridge dataset (n=158). Row 1 corresponds to regression combined with the Friston 24 model. Row 2 corresponds to regression combined with the Friston 24 + scrubbing model. Column 1 corresponds to no regression of global, WM or CSF signals. Column 2 corresponds to regression of WM and CSF signals. Column 3 corresponds to regression of global signal. Column 4 corresponds to regression of global, WM and CSF signals.

At the group level, relationships with motion were drastically reduced for the bivariate correlation-based VMHC and PCC-FC metrics - to a far greater extent than the application of any motion correction techniques (Wilcoxon signed-rank test: significant for all the combinations of motion corrections strategies, e.g., Friston 24 with GSR vs. Friston 24 without GSR: VMHC - Z = −170.5, p < 0.0001; PCC-FC - Z = −142.2, p < 0.0001) (Figures 5 and S11, Table S2B). The motion relationships with ALFF, fALFF, ReHo and DC across subjects were relatively less affected by GSR. This is not surprising, as Z-standardization (i.e., within-subject mean centering and variance normalization) was applied in accord with common practice (e.g., Buckner et al., 2009; Zou et al., 2008; Zuo et al., 2010a; Zuo et al., 2012). However, GSR is still beneficial for ALFF, ReHo and DC, as residual relationships with motion were reduced with GSR applied (Friston 24 with GSR vs. Friston 24 without GSR: ALFF - Z = −13.9, p < 0.0001; ReHo - Z = −53.8, p < 0.0001; DC - Z = −83.8, p < 0.0001). Once again, simple WM/CSF regression did not produce such marked changes in motion relationships (Figure S11).

Similar to our findings for data analyzed without GSR, we found that model-based correction at the individual level provided additional benefits for all measures (with the exception of fALFF). The Friston-24 model was found to be optimal for ALFF, ReHo and DC; for PCC-FC, Friston-24 had less of an advantage over the lower order 12-parameter models (see Table S2B for Wilcoxon Signed-Rank test summary statistics). We also repeated our examination of the value of combining group-level and individual level corrections, now with GSR analyses. Once again finding added benefits for the combination of group-level correction with mean FD and individual-level correction with the Friston-24 model, though notably less robust than what was observed when GSR was not applied (see Table S5B).

In summary, global signal regression, Z-standardization, and group-level covariate regression of mean FD all emerged from the present work as effective means of mitigating inter-individual relationships between R-fMRI metrics and motion. We provide a summary figure to facilitate comparison of the impact of motion and nuisance correction strategies (Figure 6 and Table S6).

3.5. The Impact of Motion and Motion Correction Strategies on Test-Retest Reliability of R-fMRI Metrics

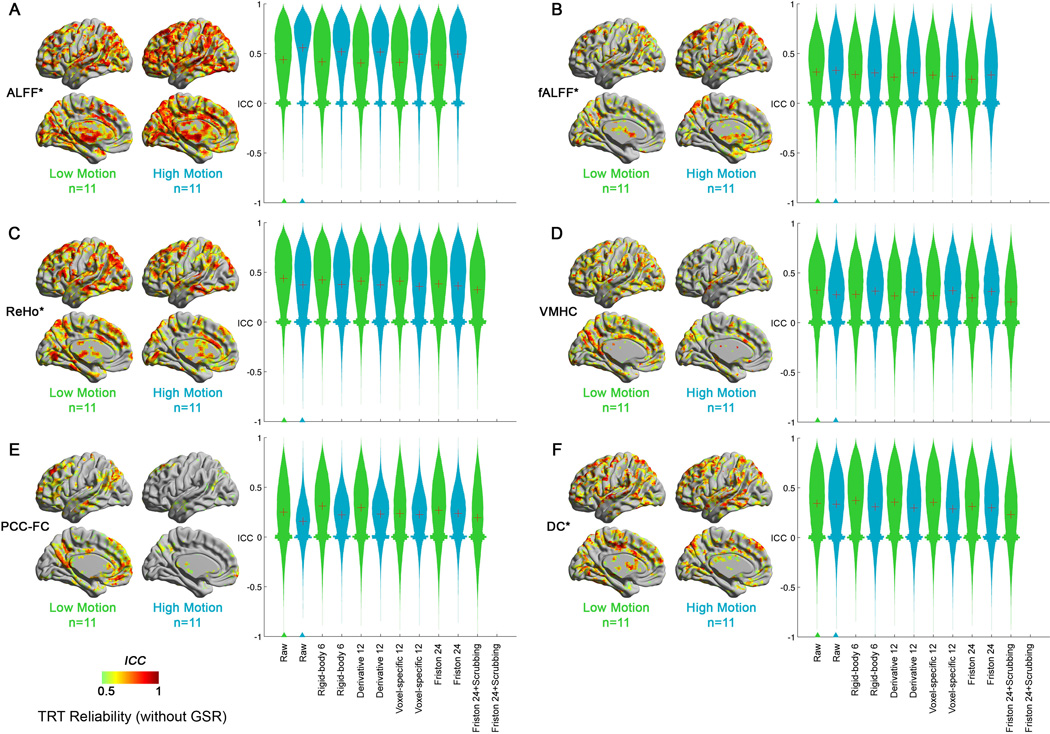
For most regional metrics except ALFF and fALFF, high motion reduced TRT. By contrast, ALFF exhibited much higher TRT reliability in the high motion dataset than in the low motion dataset (Wilcoxon signed-rank test on uncorrected data: Z = 88.3, p < 0.0001) (Figure 8). This is consistent with the findings on group-level motion effects as well as findings from prior work emphasizing the susceptibility of ALFF to artifactual contributions (Zuo et al., 2010a). For fALFF, the high motion dataset demonstrated slightly higher TRT reliability than the low motion dataset (Wilcoxon signed-rank test on uncorrected data: Z = 7.6, p < 0.0001), but the difference was much smaller than for ALFF, reflecting fALFF’s greater resistance to noise. For the artificially high TRT reliability obtained for ALFF and fALFF in the high motion datasets, the Friston 24 model decreased TRT reliability versus uncorrected data (ALFF: Z = −104.5, p < 0.0001; fALFF: Z = −59.8, p < 0.0001) (Table S7).

Figure 8.

The impact of head motion and head motion correction strategies on test-retest (TRT) reliability of R-fMRI measures (A: ALFF; B: fALFF; C: ReHo; D: VMHC; E: PCC-FC and F: DC) without GSR in the NYU TRT dataset (low motion: n=11; high motion: n=11). Of note, the scrubbing strategies cannot be applied on the high motion dataset, as they have less than 3-minute data after scrubbing. “?” denotes the condition on which the surface map was generated. The red “+” denotes the mean of each distribution. “*” denotes that the relevant R-fMRI measure has been Z-standardized. ICC: intra-class correlation.

For ReHo, VMHC, PCC-FC and DC, the high motion dataset demonstrated lower TRT reliability than the low motion dataset (ReHo: Z = −45.7, p < 0.0001; VMHC: Z = −35.3, p < 0.0001; PCC-FC: Z = −69.4, p < 0.0001; DC: Z = −6.6, p < 0.0001; on uncorrected data). Thus, head motion does not always inflate TRT reliability for all R-fMRI metrics, but instead decreases TRT reliability for non-frequency-based measures, especially PCC-FC. Of note, application of the Friston 24 model helped to increase the TRT reliability in the high motion dataset for VMHC and PCC-FC versus uncorrected data (VMHC: Z = 54.7, p < 0.0001; PCC-FC: Z = 138.5, p < 0.0001). In the high motion dataset, a fair examination of the impact of scrubbing in addition to the Friston 24 strategy was precluded, as none of the participants had a sufficient number of time points after scrubbing (i.e., cannot surviving the 3-minutes criterion).

Of note, an important caveat regarding the Friston-24 correction has emerged from our TRT reliability analyses. Namely, that although beneficial for high motion dataset, the higher order model can actually lower reliability for low motion dataset (Figure 8 and Table S7). Further examination of the impact of the model on the terms of the ICC calculation, revealed that while reducing between-subject variance as expected, within subject variance remained unaffected or actually increased for some R-fMRI measures (i.e., ReHo and VMHC); over-fitting may be an explanation for these increases.

GSR did not substantively change the pattern of differences between high motion and low motion datasets for ALFF, fALFF and ReHo, though, in general, TRT reliability was reduced (see Figure 8 for results obtained without GSR, and Figure S12 for those with GSR) in consistent with prior work (Zuo et al., 2013); these findings were independent of motion correction strategy. For PCC-FC, GSR increased the TRT reliability for the high motion dataset (Friston 24 with GSR vs. Friston 24 without GSR: Z = 45.0, p < 0.0001) and thus alleviated the difference in TRT reliability between the high and low motion datasets.

3.6. Comparing Framewise Displacement Metrics: Testing the Assumptions

Given the growing number of available FD metrics (Jenkinson et al., 2002; Power et al., 2012a; Van Dijk et al., 2012), we compared volume-based metrics of framewise displacement (FD_vol), with a particular focus on understanding the impact of their varying assumptions regarding brain morphology and the uniformity of head motion. To accomplish this goal, we used the voxel-wise head motion (FD_vox) metric as the point of reference, as it does not involve any of these assumptions. Regional variation was observed in the relationship between volume-based and voxel-specific (FD_vox) motion metrics, with the spatial pattern differing markedly depending on the specific volume-based measure employed (see Figure 9A). The range of voxel-wise correlation strengths between FD_vox and the FD_vol proposed by Van Dijk et al. (2012) (0.4 – 0.7) was generally lower than that observed with other metrics (Power et al: 0.7 – 0.86; Jenkinson et al: 0.7 – 0.93), likely reflecting the fact that the Van Dijk et al. FD_vol measure does not take rotation into account.

Figure 9.

A comparison between FD_vol and FD_vox(A) The group mean across the Cambridge dataset of the correlation between FD_vox and the FD_vol (Power), FD_vol (Van Dijk) as well as the FD_vol (Jenkinson). (B) The difference between FD_vol and spatial mean FD_vox across the brain (mean_sp FD_vox) as a function of mean_sp FD_vox for all time points and all participants in the Cambridge dataset. (B) The temporal mean of FD_vol (mean FD_vol) and temporal mean of mean_sp FD_vox (mean [mean_sp FD_vox]). r_Pearson: Pearson’s correlation coefficient; τ_Kendall: Kendall’s rank correlation coefficient; slope: the slope of the fitted regression line (intercept is 0).

To provide a more comprehensive mapping of disparities, we plotted differences between FD_vol and mean_sp FD_vox observed for all subjects and time points (see Figure 9B). This allowed us to verify the consistency of the directionality of these disparities, as well as the similarity between FD_vol (Jenkinson) and mean_sp FD_vox. Finally, we compared mean FD for the three FD_vol measures (Power, Van Dijk, Jenkinson) with the voxel-based analogue - mean [mean_sp FD_vox] (Figure 9C). The mean FD_vol (Power) and mean FD_vol (Jenkinson) both exhibited near perfect correlation with mean [mean_sp FD_vox] (Power: r_Pearson = 0.98; Jenkinson: r_Pearson = 0.99) across subjects, though Jenkinson’s measure exhibited stronger rank-based consistency (Power: τ_Kendall = 0.87; Jenkinson: τ_Kendall = 0.97) and a slope near 1. The Van Dijk et al. measure also demonstrated a high degree of correlation (r_Pearson = 0.85), though lower consistency (τ_Kendall = 0.66).

4. DISCUSSION

The present work provided a comprehensive examination of the impact of head motion and motion correction strategies on the BOLD signal, R-fMRI metrics, and their reliability. Voxel-wise motion metrics revealed marked regional variation in the impact of motion on the BOLD signal, with positive motion-BOLD relationships being revealed in primary and supplementary motor areas, and negative motion-BOLD relationships emerging in prefrontal areas. The latter were driven primarily by large-movements and were effectively eliminated by scrubbing. At the group-level, relationships between the R-fMRI metrics and mean FD persisted regardless of the motion correction strategy employed, suggesting that the group-level correction outlined by Van Dijk et al. (2012) and Satterthwaite et al. (2012) is necessary. Despite concerns that GSR may introduce negative motion-BOLD relationships at the individual level, GSR reduced relationships between motion and inter-individual differences more than any motion-correction approach. Mean centering and variance normalization procedures (Z-standardization), commonly applied to metrics such as ALFF, fALFF, ReHo and DC, showed similar advantages. Finally, we demonstrated the negative impact of motion on TRT reliability for correlation-based R-fMRI metrics, and the ability of motion-correction approaches to appropriately improve TRT reliability. Below, we discuss our findings and their implications in greater detail.

4.1. Motion Artifact vs. Motion-Related Neural Activity

A basic assumption in the functional MRI literature is that motion-BOLD relationships are strictly artifactual. This hypothesis was recently tested by Power et al. (2012a) through an examination of high motion frames, and the authors concluded that motion-induced signal changes were unlikely to reflect motor-related neural activity. Our findings suggest an intriguing hypothesis – that some component of motion-related activity in primary and supplementary motor cortex, as well as motor-sensitive visual areas (e.g., dorsomedial visual areas implicated in analyzing self-motion relative to the environment (Rosa et al., 2009; Rosa and Tweedale, 2001)), may reflect the neural correlates of moving one’s head in the scanner. Positive motion-BOLD relationships within these areas are prominent even in low motion datasets, and remain robust in the face of various motion correction strategies, even in the absence of notable head motion after scrubbing at FD_vol (Power) < 0.2. This suggests that positive motion-BOLD relationships may not be purely artifactual – however, both simulation and experimental work is required to confirm this hypothesis.

In contrast to positive motion-BOLD relationships, negative motion-BOLD relationships, which tend to cluster in prefrontal areas, appeared to be associated with large framewise displacements, and to become more diffuse in higher motion datasets (e.g., Power et al., 2012 datasets; NYU children dataset). This is consistent with previous findings (Satterthwaite et al., 2013) in that spikes in head motion generally induce BOLD signal decreases. These negative relationships tended to dominate over positive motion-BOLD relationships in high motion datasets, and were reduced by modeling-based motion correction strategies and eliminated by scrubbing at FD > 0.2mm - further supporting the conclusion they may be artifacts induced by head motion. Of note, global signal regression reduced the ability of scrubbing approaches to eliminate negative relationships.

4.2. Motion-Related Differences Among Subjects and Groups: Contrasting the Impact of Head Motion & Nuisance Correction Strategies

Comparison of the impact of motion correction strategies on motion-related differences in R-fMRI metrics across individuals demonstrated the inability of subject-level correction strategies to completely remove between-subject differences related to motion. Complicating the issue further, the presence of motion-related differences among individuals and the effectiveness of motion correction strategies varied depending on the specific R-fMRI measure being examined.

Global signal regression proved to be more effective in removing relationships between motion and correlation-based R-fMRI metrics across subjects than any correction strategy that explicitly models motion. GSR has a standardization effect, as it shifts the center of the correlation distribution for iFC towards zero (Murphy et al., 2009). Given prior demonstrations that motion appears to increase connectivity across the brain (Satterthwaite et al., 2013), and will hence increase mean connectivity, the zero-centering effect of GSR likely explains its effectiveness in reducing motion effects. Consistent with this notion, we found that Z-standardization, which explicitly mean-centers the distribution, also outperformed all other motion correction approaches with respect to the removal of motion-relationships across individuals. Nevertheless, GSR may not be an entirely attractive solution for handling motion-related relationships, as it can introduce negative relationships with motion at the individual subject level. Similar to its role in iFC analyses, GSR reduces the positive correlation between BOLD signal and FD_vox, while enhancing the negative correlation between BOLD signal and FD_vox. This concern adds to those previously raised in the literature regarding the ability of GSR to artifactually exaggerate negative functional connectivity and to alter inter-individual differences (Murphy et al., 2009; Saad et al., 2012; Weissenbacher et al., 2009). In sum, GSR mitigates the effects of motion-related differences among subjects, consistent with the expectation that the global mean is in part related to motion. However, investigators must weigh up the pros and cons of GSR when deciding whether to employ it in the context of testing specific hypotheses.

Although not a focus of examination in the present work, it is worth noting that metrics employing within-subject Z-standardization (i.e., within-subject mean centering and variance normalization) exhibited markedly diminished relationships with motion, even without GSR. Although similar in its ability to mitigate motion relationships, Z-standardization is not equivalent to GSR in definition or the intent for which it is used in the literature for metrics such as ALFF, fALFF, ReHo and DC (e.g., enforcement of normality, removal of floor noise levels) (Buckner et al., 2009; Zou et al., 2008; Zuo et al., 2013; Zuo et al., 2010a; Zuo et al., 2012). Likewise, the interpretation of voxel-wise findings with GSR and Z-standardization are somewhat different, given that Z-standardization is explicitly relative (e.g., “increased ALFF relative to global mean with unit global SD of ALFF”, as opposed to “increased ALFF”), a way of standardizing brain metrics by eliminating inter-individual differences in global brain features and thus producing more regionally comparable metrics across participants. Of note, Z-standardization demonstrated an advantage for ALFF in particular – which is arguably the most noise-susceptible measure (Zuo et al., 2010a). Future work should consider the utility of mean-centering and variance normalization approaches in overcoming global effects induced by factors such as motion on a broader range of R-fMRI metrics.

4.3. Considerations Regarding Test-Retest Reliability

Test-retest reliability is an important criterion for establishing the utility of a measure for examination of inter-individual variation. Both neural and artifact (e.g., motion, physiological signals) signals can impact to TRT reliability. In this regard, a natural concern for R-fMRI would be the possibility that motion artifacts, which appear to have moderate TRT reliability, may be artifactually driving the reports of moderate to high TRT reliability in the literature. Prior work found that regressing out motion does not reduce TRT reliability (Van Dijk et al., 2012; Zuo et al., 2013), mitigating this concern. Our results provide additional evidence by comparing TRT reliability for a subset of subjects characterized by high motion vs. low motion. With the exceptions of ALFF and to a lesser degree fALFF, R-fMRI metrics exhibited greater TRT reliability in the low motion subset than the high motion subset (PCC-FC differed the most). In the case of ALFF, this finding is not surprising, as prior work found greater influence of motion on ALFF than on its normalized variant – fALFF (Zuo et al., 2010b). The Friston 24 model is helpful for decreasing the artificially high TRT reliability in ALFF/fALFF, as well as increasing the comparatively low TRT reliability in VMHC and PCC-FC for the high motion dataset. Unfortunately, scrubbing methods could not be evaluated in the high motion dataset, as insufficient data remained to be evaluated. Finally, it is worth noting that consistent with our prior assertion that GSR effectively reduces motion-related noise, for PCC-FC, GSR increased TRT reliability for the high motion dataset.

4.4. Volume-Based Metrics: Similar But Not Identical

Although similar in their base definitions, differences among current volume-based metrics of the relative contributions of angular rotation and uniformity of motion effects across the brain yield predictable disparities in results. For example, the FD_vol measure employed by Van Dijk et al. (2012) does not take into account angular rotations while other approaches do (a separate Euler angle metric is provided instead by Van Dijk et al.). Additionally, Van Dijk et al. (2012) subtract the root-mean-square (RMS) of the translation parameters for the current time point from the RMS for the previous time point; this calculation may cancel large extents of head motion crossing zero between two time points, e.g., x_i-1 = 1, y_i-1 = 2, z_i-1 = 3; while x_i = −1, y_i = −2, z_i = −3¹. Not surprisingly, their metrics tend to provide the smallest estimates of motion. In contrast, Jenkinson et al. (2002) and Power et al. (2012a) both take into account angular rotation, though with different strategies. Power et al. (2012a) assumes that all voxels undergo equivalent displacements along a sphere (radius = 50mm) in response to a given rotation. The measure proposed by Jenkinson et al. (2002) is similar in that it also assumes the brain to be a sphere (radius = 80mm), but differs in that it takes into account variations in head motion among voxels prior to integrating over the sphere². As a result, even though Jenkinson et al. (2002) assume a larger brain, their framewise displacement estimates tend to be more conservative. In trying to reconcile the differences in the findings between these two approaches, we note that the FD_vol measure of Jenkinson et al. was found to be near equivalent to the volume-based measure derived from the voxel-wise FD_vox metric – which makes no assumptions about brain size or uniformity. The Power et al. measure tended to consistently overestimate motion relative to this measure. In summary, among the volume-based metrics, our analyses lead us to recommend the measure by Jenkinson et al. (2002) as preferable due to its consideration of voxel-wise differences in its derivation.

Despite their importance for characterizing regional head motion, the utility of voxel-wise metrics for more general applications in R-fMRI remains unclear. Similar to Satterthwaite et al. (2013), we found that correction with voxel-wise motion metrics offered insufficient advantage over the more easily computed Friston 24 model. This does not preclude the possibility that future developments of motion-correction attempts may have greater success in using the rich information encapsulated by voxel-specific indices. The failure of voxel-specific metrics to enhance motion correction may highlight the need to consider spin history effects from more principled perspectives grounded in physics (e.g., Bloch equations, partial voluming).

4.5. What to Do about Motion?

The question of “what to do about motion” remains open and its answer depends in part on the intended level of analysis. Among the individual-subject level options for motion correction, scrubbing approaches were superior in removing both the artifactual negative motion-BOLD relationships within individuals, and relationships between motion and R-fMRI metrics across individuals. The inability of modeling-based approaches to effective mitigate motion-BOLD relationships makes scrubbing approaches increasingly attractive¹ – particularly for studies employing single subject statistics or relatively small sample sizes which precludes adequate group-level modeling of motion. However, some key caveats regarding the aggressive scrubbing of time points need to be considered. First as demonstrated in our work, decreases in the degrees of freedom associated with the censoring of time-points are not without cost. As demonstrated in our supplementary analyses, reductions in the number of time points are associated with increases in the likelihood of high correlation scores. If not properly accounted for, such changes can become a source of systematic noise, particularly in the context of group comparisons, where one group may have significantly fewer remaining time points after scrubbing than the other.

Further, while the collection of longer time series data from participants can appear to be a solution to the challenge of removing too many time points, recent work suggests potential flaws in an inherent assumption of scrubbing - namely, that all time points are equal, i.e., that functional connectivity is stationary and non-dynamic. The field is increasingly appreciating time-related fluctuations in patterns of functional connectivity (Allen et al., in press; Chang and Glover, 2010; Kang et al., 2011; Smith et al., 2012); most recently, Allen et al. (in press) demonstrated the presence of up to seven connectivity “states” within the course of a 5 minute fMRI scan for single individuals. The scrubbing of time points can unintentionally bias estimates of an individual’s functional connectivity patterns towards one state over another, particularly if one or more of the states are associated with an increased risk of motion. Further investigation is required to clarify such concerns.

Our findings suggest that regardless of whatever correction one employs at the individual level, inclusion of the mean FD as a nuisance covariate is generally necessary and appropriate. We cannot assert that including mean FD alone is sufficient for all situations. Persistence of a small number of residual relationships in our upper vs. lower tercile comparison in the Cambridge dataset (Figures 6 and S8) suggests that including additional covariates may increase protection against false positives, which could also be achieved with more stringent thresholding, although at the cost of reduced sensitivity. At the same time, we note that in situations where a covariate of interest is correlated with motion, group-level covariate approaches to correcting for motion can be conservative, as they remove common variation among regressors. Judgment on the part of the researcher is required to best balance the various risks and benefits for any given study.

As previously discussed, we underscore that two approaches not explicitly intended for motion correction appeared to be superior in removing relationships between motion and R-fMRI metrics across participants – GSR and Z-standardization. Significant concerns have been raised about GSR due to its potential for introducing confounds (Murphy et al., 2009; Saad et al., 2012; Weissenbacher et al., 2009) leading many investigators to dismiss the approach, without considering the specific nuisance signals it may be able to uniquely address. Our findings necessitate further consideration of the nuisance signals removed by GSR, and the development of more statistically valid approaches to account for them. At present, usage of Z-standardization is relatively limited in the literature, primarily to measures such as ALFF, fALFF, ReHo and occasionally to DC (more variably). The present work suggests the potential utility of Z-standardization approaches more broadly. Future work examining their utility and potential impact on the interpretation of R-fMRI metrics more broadly appears merited.

We have included Table 3 to summarize our current recommendations based upon the points discussed above in this section and prior.

Table 3.

Summary recommendations

Summary Recommendation: Individual-level correction with the Friston-24 model is recommended. Additionally, group-level correction for mean FD is recommended, and removes the need for scrubbing. If group-level correction for mean FD is contraindicated or not practical, then individual-level correction with scrubbing is recommended for PCC-FC, VMHC and ReHo (not ALFF*, fALFF, DC**).

Additional Considerations: Inclusion of global signal regression at the individual-level produces robust reductions in the relationships between motion and R-fMRI measures across participants – particularly for measures without Z-standardization. The benefits of GSR need to be balanced against potential risks for introduction of artifact in the specific analyses employed. For studies limited to low motion datasets, the utility of higher-order Friston 24 model decreases. In this case, we recommend consideration of lower-order (i.e., 6 or 12-parameter) models to minimize the potential for over-fitting, as noted in Satterthwaite et al. (2013). fALFF appeared to be relatively insensitive to motion correction strategies in the present work. Prior work (Satterthwaite et al. 2012) has suggested greater sensitivity in higher motion populations; as such we recommend continued application of correction procedures at the present time.

^*Recommendations against scrubbing for ALFF and fALFF apply to commonly employed FFT-based implementations (see section 4.7 for alternatives).

^**Recommendations against scrubbing for DC were based on concerns regarding its ability to compromise graph construction (see section 3.3 for demonstration).

4.6. Are Micromovements Only a Concern for R-fMRI?

While the effects of micromovements have become a central concern in the R-fMRI literature, the community would be remiss to act as if this literature was the only one affected by motion – particularly in studies focusing on inter-individual or group differences. As noted by Friston et al. in 1996, those interested in the effects of a particular task-related manipulation can overlook the presence of spurious activations, assuming that their effect is detectable despite the presence of motion-related noise and motion is unrelated to the task. Although still true, this does not imply that studies of inter-individual variation or group differences in task activation can overlook the presence of motion-related artifact – as they are a source of nonrandom noise. Any systematic sources of noise can create artifactual differences between individuals or groups, regardless of whether task-activation or task-independent fMRI approaches are being conducted – especially if the effects are non-linear. By the same token, researchers should be encouraged to account for other sources of noise, including respiratory or cardiovascular parameters and unintended variation in study design characteristics. Motion is not unique in its ability to confound data; though, given its relationship with age, it is likely to have a disproportionately large impact on developmental studies. As investigators focus on younger ages (e.g., neonates, infants and toddlers), physiological parameters may become of greater importance given well-documented development-related changes in cardiac and respiratory characteristics (Kliegman et al., 2007; Wallis et al., 2005).

4.7. Limitations and Future Directions

Several limitations in the present work merit consideration. First, while the voxel-metric does not make any of the a priori assumptions that cause inflation or underestimation of motion by other measures (e.g., uniform effects of motion, brain morphology, relative contributions of angular rotation), it still cannot be considered a “gold standard”. Attainment of a true gold standard would require objective external measurement of motion. Second, our metrics of motion only take into account between-volume motion; future work should consider estimation and/or correction of within-volume motion (Bhagalia and Kim, 2008). Third, the ALFF and fALFF calculation in the current study is based on FFT, which cannot be applied to scrubbed data due to alteration of its temporal structure by removal of frames. Future work may consider more sophisticated approaches (Babu and Stoica, 2010) such as a regression-based approach to frequency analysis that includes sine and cosine waves to estimate the amplitude for each frequency, while taking the scrubbing regressors into account. Fourth, we set a p threshold for degree centrality calculation to maintain a constant probability of false positives across datasets, despite differing number of time points (Zuo et al., 2012). However, this threshold did not correct for the degrees of freedom eliminated with motion and nuisance regressors, scrubbing and bandpass filtering. The loss of degrees of freedom will change the correlation and the connectivity graph; one could adjust for the degrees of freedom lost, but this may cause more conservative thresholds in one subject as opposed to another. Future work is needed to determine the best approach to account for censored volumes in centrality metrics. Fifth, there are emerging head motion correction strategies (e.g., minimize head motion effects through independent component analysis (Liao et al., 2005; Liao et al., 2006), estimate head motion in k-space (Costagli et al., 2009) and adaptive correction (Yancey et al., 2011)) as well as nuisance regression models (e.g. RETROICOR (Glover et al., 2000; Hu et al., 1995), CompCorr (Behzadi et al., 2007), ANATICOR (Jo et al., 2010) and median angle correction (He and Liu, 2011)), that were not included in the current study. Future work will need to rigorously evaluate the growing range of strategies in accounting for head motion and build upon the findings of the current study. Sixth, we examined regional variation in the linear motion-BOLD relationship in the current study, while more profound non-linear relationships may exist between FD_vox and BOLD. These non-linear relationships could even be region-specific, an issue that needs to be further investigated in the future. Finally, in evaluating head motion effects on TRT reliability, we note that the NYU TRT dataset contains a moderate amount of motion. Consistent with Van Dijk et al. (2012), we were able to demonstrate that this motion was not the primary determinant of the moderately high reliability for R-fMRI metrics (in fact, high motion generally lowered reliability). Nevertheless, it did preclude extensive analysis of the impact of scrubbing on test-retest reliability. A larger sample size TRT dataset is needed to evaluate head motion effects on TRT reliability.

5. CONCLUSIONS

Examination of regional variation in the impact of motion on the BOLD signal provided novel insights into the nature of motion-BOLD relationships, with some appearing to reflect motion-induced artifacts while others seemed to be driven by motion-related changes in neural activity. None of the explicit motion-correction approaches examined in the present work effectively removed motion-related differences in R-fMRI metrics among participants. GSR and Z-standardization did emerge from our work as potentially more effective means of mitigating relationships between motion and R-fMRI metrics, though they do not do so completely. Nonetheless, group-level analysis correction for motion remains crucial. Finally, the present work demonstrated that motion appears to compromise the reliability of most R-fMRI metrics, thus motivating continued efforts to devise novel approaches to prevent and/or correct motion as the field moves forward to discern connectome-phenotype associations.