Significance
X-ray nanocrystallography is a powerful imaging technique which is able to determine the atomic structure of a macromolecule from a large ensemble of nanocrystals. Determining structure from this ensemble is challenging because the images are noisy, and individual crystal sizes, orientations, and incident photon flux densities are unknown. Additionally, lattice symmetries may lead to orientation ambiguities. Here, we show how to determine crystal size, incident photon flux density, and crystal orientation from noisy data. We also demonstrate that these data can be used to perform reconstruction without extra experimental requirements, atomicity assumptions, or knowledge of similar structures.
Abstract
X-ray nanocrystallography allows the structure of a macromolecule to be determined from a large ensemble of nanocrystals. However, several parameters, including crystal sizes, orientations, and incident photon flux densities, are initially unknown and images are highly corrupted with noise. Autoindexing techniques, commonly used in conventional crystallography, can determine orientations using Bragg peak patterns, but only up to crystal lattice symmetry. This limitation results in an ambiguity in the orientations, known as the indexing ambiguity, when the diffraction pattern displays less symmetry than the lattice and leads to data that appear twinned if left unresolved. Furthermore, missing phase information must be recovered to determine the imaged object’s structure. We present an algorithmic framework to determine crystal size, incident photon flux density, and orientation in the presence of the indexing ambiguity. We show that phase information can be computed from nanocrystallographic diffraction using an iterative phasing algorithm, without extra experimental requirements, atomicity assumptions, or knowledge of similar structures required by current phasing methods. The feasibility of this approach is tested on simulated data with parameters and noise levels common in current experiments.
Although conventional X-ray crystallography has been used extensively to determine atomic structure, it is limited to objects that can be formed into large crystal samples  . An appealing alternative, made possible by recent advances in light source technology, is X-ray nanocrystallography, which is able to image structures resistant to large crystallization, such as membrane proteins, by substituting a large ensemble of easier to build nanocrystals, typically
. An appealing alternative, made possible by recent advances in light source technology, is X-ray nanocrystallography, which is able to image structures resistant to large crystallization, such as membrane proteins, by substituting a large ensemble of easier to build nanocrystals, typically 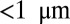 , often delivered to the beam via a liquid jet (1–6) (Fig. 1). However, the beam power required to retrieve sufficient information destroys the crystal, hence ultrafast pulses (≤70 fs) are required to collect data before damage effects alter the signal. Using nanocrystals introduces several challenges. Due to the small crystal size, Bragg peaks are smeared out, and there is noticeable signal between peaks. Typically, only partial peak reflections are measured, resulting in reduced intensities. Variations in crystal size and incident photon flux density, unknown orientations, shot noise, and background signal from the liquid and detector add additional uncertainty to the data.
, often delivered to the beam via a liquid jet (1–6) (Fig. 1). However, the beam power required to retrieve sufficient information destroys the crystal, hence ultrafast pulses (≤70 fs) are required to collect data before damage effects alter the signal. Using nanocrystals introduces several challenges. Due to the small crystal size, Bragg peaks are smeared out, and there is noticeable signal between peaks. Typically, only partial peak reflections are measured, resulting in reduced intensities. Variations in crystal size and incident photon flux density, unknown orientations, shot noise, and background signal from the liquid and detector add additional uncertainty to the data.
Fig. 1.
Liquid jet (blue) delivers nanocrystal samples to the X-ray beam (red). Wide- and small-angle diffraction data are collected using front and rear detectors.
If crystal orientations were known, noise and variation in the peak measurements could be averaged out, and the data could be inverted to retrieve the object’s electron density. Although autoindexing techniques can be used to determine crystal orientation up to lattice symmetry from the location of a sufficient number of Bragg peaks, they typically face difficulties in the presence of partial and non-Bragg reflections common in nanocrystal diffraction images. Furthermore, these techniques only narrow down orientation to a list of possibilities when the diffraction pattern has less symmetry than the lattice, leading to an ambiguity in the image orientation, known as the indexing ambiguity. Current methods of processing the diffraction data are largely based on averaging out the data variance over several images (1–8). However, if the data are processed without resolving the indexing ambiguity then they will appear to be perfectly twinned, i.e., averaged over multiple orientations. Although there has been some success in determining structure from perfectly twinned data, reconstruction is often infeasible without a good initial atomic model of the structure.
We present an algorithmic framework for X-ray nanocrystallographic reconstruction which is based on directly reducing data variance and resolving the indexing ambiguity. First, we design an autoindexing technique that uses both Bragg and non-Bragg data to compute precise orientations, up to lattice symmetry. Crystal sizes are then determined by performing a Fourier analysis around Bragg peak neighborhoods from a finely sampled low-angle image, such as from a rear detector (Fig. 1). Next, we model structure factor magnitudes for each reciprocal lattice point with a multimodal Gaussian distribution, using a multistage expectation maximization algorithm which simultaneously scales and models the data. These multimodal models are used to build a weighted graph which models the structure factor magnitude concurrency. We formulate the solution to the indexing ambiguity problem as finding the maximum edge weight clique in this graph, which can be solved efficiently via a greedy approach. Finally, we demonstrate the feasibility of solving the phase problem using iterative phase retrieval. Whereas several of the presented methods rely on the use of nanocrystals, we note that the scaling–multimodal analysis and indexing ambiguity resolution steps can also be applied to larger crystals  .
.
Formulation
In X-ray crystallography, diffraction patterns are collected from a periodic crystal made up of the target object. The 3D crystal lattice structure may be described by its Bravais lattice characteristic  , and its associated infinite lattice
, and its associated infinite lattice 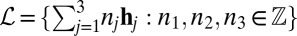 . We define the lattice rotational symmetry group
. We define the lattice rotational symmetry group  to be the set of rotation operators which preserve the lattice structure
to be the set of rotation operators which preserve the lattice structure  .
.
Each lattice has both a Dirac comb  , which is a sum of Dirac delta functions supported on the lattice points, and a dual
, which is a sum of Dirac delta functions supported on the lattice points, and a dual  , known as the reciprocal lattice, given by the support of the Dirac comb’s Fourier transform*
, known as the reciprocal lattice, given by the support of the Dirac comb’s Fourier transform*
 . The Bravais vectors of the reciprocal lattice are given by†
. The Bravais vectors of the reciprocal lattice are given by†
 .
.
In practice, a crystal lattice 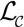 consists of only a finite part of its associated infinite lattice. In this case, the associated Dirac comb’s Fourier transform
consists of only a finite part of its associated infinite lattice. In this case, the associated Dirac comb’s Fourier transform  , known as the shape transform
, known as the shape transform 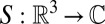 , is no longer a sum of delta functions, but is instead a smeared-out version of
, is no longer a sum of delta functions, but is instead a smeared-out version of  . To simplify the discussion, we will be assuming that the finite crystal lattice can be described as a box with Nj unit cells in the direction of hj, i.e.,
. To simplify the discussion, we will be assuming that the finite crystal lattice can be described as a box with Nj unit cells in the direction of hj, i.e.,  . Here, the squared norm of its associated shape transform is given by
. Here, the squared norm of its associated shape transform is given by
 |
We note that the methods presented in the following sections can be extended to more general crystal shapes, but possibly at the cost of losing a simple closed-form expression for the shape transform.
The electron density 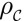 of a crystal with periodic units on the lattice points of
of a crystal with periodic units on the lattice points of  can be expressed in terms of the electron density ρ of one of its periodic unit cells by
can be expressed in terms of the electron density ρ of one of its periodic unit cells by  The space group of a crystal
The space group of a crystal  introduces another form of symmetry on its diffraction pattern, described by the Laue rotational symmetry group
introduces another form of symmetry on its diffraction pattern, described by the Laue rotational symmetry group  .
.
The image of diffraction intensities  due to elastic scattering from a crystal with unit cell electron density
due to elastic scattering from a crystal with unit cell electron density  and orientation
and orientation 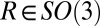 , using a fully coherent X-ray beam with wavelength λ and incident photon flux density J, at a detector with pixel size dx at distance D from the interaction point and normal to the beam, is described by
, using a fully coherent X-ray beam with wavelength λ and incident photon flux density J, at a detector with pixel size dx at distance D from the interaction point and normal to the beam, is described by
where  is the electron cross-section,
is the electron cross-section,  is a polarization factor,
is a polarization factor,  ,
,  is the solid angle subtended by a pixel, and
is the solid angle subtended by a pixel, and  . For elastic scattering, the values of
. For elastic scattering, the values of  are often called the structure factors.
are often called the structure factors.
For large crystals, the shape transform approaches the Dirac comb of the reciprocal lattice, up to a constant factor, and the diffraction images consist of a series of bright spots, known as Bragg peaks, concentrated at reciprocal lattice points. However, for nanocrystallography, small crystal sizes spread the shape transform, and measurements close to, but not directly at, a Bragg peak, known as partial reflections, have a decreased measured intensity. Additionally, the signal at pixels corresponding to lines in between adjacent reciprocal lattice points is often noticeable in nanocrystal diffraction images.
The goal of X-ray nanocrystallography is to determine the unit cell electron density ρ from a large ensemble of diffraction images, which vary in orientation, incident photon flux density, and crystal size and are corrupted with noise. Here we will focus on the case when  , which leads to the indexing ambiguity.‡
, which leads to the indexing ambiguity.‡
Autoindexing
Commonly used autoindexing methods, e.g., refs. 9, 10, can accurately determine a lattice’s unit cell, given by the Bravais vectors in some reference configuration, using a large ensemble of images. However, the orientation information that these methods compute might not be accurate enough to be used in the evaluation of the shape transform, especially in the presence of non-Bragg spots and low Bragg peak counts. Starting from this unit cell information, we devise an algorithm which uses both Bragg and non-Bragg data to generate precise orientations, up to lattice symmetry.
Bravais Characteristic Vector Calculation.
In nanocrystallography images, the strongest signal will occur at reciprocal lattice points ξ, which satisfy 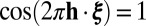 if h is a Bravais vector. However, signal along lattice edges, i.e., lines connecting adjacent reciprocal lattice points, is also commonly noticeable. If ξ is a reciprocal lattice edge point then
if h is a Bravais vector. However, signal along lattice edges, i.e., lines connecting adjacent reciprocal lattice points, is also commonly noticeable. If ξ is a reciprocal lattice edge point then  for two of the Bravais vectors and can be anything in
for two of the Bravais vectors and can be anything in 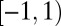 for the remaining vector. The set B of both types of points appear as bright spots in the images, and can be located through thresholding. For a given image, a direction h is then likely to be a Bravais vector for the rotated lattice if
for the remaining vector. The set B of both types of points appear as bright spots in the images, and can be located through thresholding. For a given image, a direction h is then likely to be a Bravais vector for the rotated lattice if  is close to 1 for most
is close to 1 for most  . In particular, when searching for the jth Bravais vector
. In particular, when searching for the jth Bravais vector 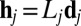 , where
, where  , we attempt to filter out the non-Bragg spots which disagree with dj by looking for a direction d which solves
, we attempt to filter out the non-Bragg spots which disagree with dj by looking for a direction d which solves
 |
where 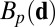 is the set of
is the set of 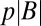 points in B with the largest value of
points in B with the largest value of  . If multiple Bravais vectors have the same length, we search for multiple solutions approximately separated by the known relative angles between these vectors. We generate search directions with an approximately uniform sampling of the half unit sphere (11). After locating the initial directions, we repeat the process on a finer set of sample directions in a restricted angular range around the previously computed directions. If a direction is not found, we use the known relative angles between the other two directions to narrow the search for, or directly deduce, the missing direction.
. If multiple Bravais vectors have the same length, we search for multiple solutions approximately separated by the known relative angles between these vectors. We generate search directions with an approximately uniform sampling of the half unit sphere (11). After locating the initial directions, we repeat the process on a finer set of sample directions in a restricted angular range around the previously computed directions. If a direction is not found, we use the known relative angles between the other two directions to narrow the search for, or directly deduce, the missing direction.
Lattice Orientation Calculation.
Once Bravais directions  for the rotated lattice associated with an image are located, with the sign convention that yields the correct angles between vectors and
for the rotated lattice associated with an image are located, with the sign convention that yields the correct angles between vectors and  , we use the known reference configuration
, we use the known reference configuration  to compute an approximation
to compute an approximation  to the orientation matrix. If
to the orientation matrix. If 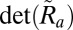 is far from unity then the autoindexing procedure failed to compute an accurate orientation and we thus reject
is far from unity then the autoindexing procedure failed to compute an accurate orientation and we thus reject 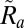 . We then find the closest rotation matrix by computing the singular value decomposition
. We then find the closest rotation matrix by computing the singular value decomposition 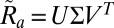 and setting
and setting 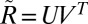 , which is used as the approximation to the image orientation up to lattice symmetry, i.e.,
, which is used as the approximation to the image orientation up to lattice symmetry, i.e., 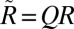 where R is the full orientation and
where R is the full orientation and  .
.
Crystal Size Determination
To compute accurate structure factor magnitudes from measured intensities, the squared magnitude of the shape transform must be divided out of the intensity measurements in Eq. 2. Near a Bragg peak, the shape transform grows quadratically with the crystal size, which often varies up to an order of magnitude in each dimension over the nanocrystal ensemble. We determine these crystal sizes by analyzing intensities around Bragg peaks in low-angle images (Fig. 2) sampled at least twice the Nyquist rate for the crystal, i.e., the pixel spacing is at most 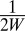 , where W is the width of the crystal. A Fourier analysis of these intensities reveals the crystal sizes.
, where W is the width of the crystal. A Fourier analysis of these intensities reveals the crystal sizes.
Fig. 2.

Example of a low-angle image. The profile of the shape transform around the Bragg peaks (circled) can be used to determine the crystal sizes.
Fourier Analysis of the Shape Transform.
For an image I with orientation§
R, consider its restriction Ir to a small neighborhood  centered at a low-angle Bragg peak with detector coordinates
centered at a low-angle Bragg peak with detector coordinates 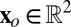 corresponding to the reciprocal lattice point
corresponding to the reciprocal lattice point  , where
, where  is small. In
is small. In  , by taking a linear approximation of q and using the translation invariance of S on
, by taking a linear approximation of q and using the translation invariance of S on 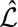 , the intensities are approximated, up to a constant C, by
, the intensities are approximated, up to a constant C, by
 |
where  and
and 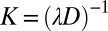 . If we denote
. If we denote 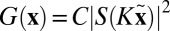 , then Eq. 4 becomes the restriction of G to the rotated plane
, then Eq. 4 becomes the restriction of G to the rotated plane 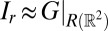 , whose Fourier transform,¶ from the Fourier projection slice theorem and the Wiener–Khinchin theorem, is approximately the X-ray projected autocorrelation of
, whose Fourier transform,¶ from the Fourier projection slice theorem and the Wiener–Khinchin theorem, is approximately the X-ray projected autocorrelation of  :‖
:‖
Note that the support of this projected autocorrelation is given by the Minkowski sum of the rotated projected crystal, i.e., supp  .
.
If we approximate** the crystal lattice as  , where
, where 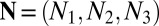 are the crystal sizes for each Bravais direction, then the convex hull of the projected autocorrelation
are the crystal sizes for each Bravais direction, then the convex hull of the projected autocorrelation  , where Conv(X) is the convex hull of the set X, can be expressed as
, where Conv(X) is the convex hull of the set X, can be expressed as
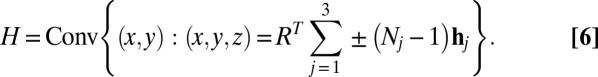 |
By computing 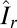 , we can deduce the crystal sizes by analyzing H as long as none of the rotated Bravais vectors
, we can deduce the crystal sizes by analyzing H as long as none of the rotated Bravais vectors 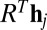 is orthogonal to the detector. In general, the boundary of H consists of a series of line segments, with three normals
is orthogonal to the detector. In general, the boundary of H consists of a series of line segments, with three normals 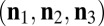 along with their three antiparallel directions, which can be found by computing the convex hull of the rotated projected autocorrelated unit cell, i.e., the right-hand side of Eq. 6 with
along with their three antiparallel directions, which can be found by computing the convex hull of the rotated projected autocorrelated unit cell, i.e., the right-hand side of Eq. 6 with 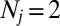 for each j. In the direction ni, the extent of the convex hull
for each j. In the direction ni, the extent of the convex hull 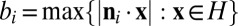 must be equal to that of the unprojected crystal, i.e.,
must be equal to that of the unprojected crystal, i.e., 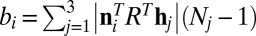 . Therefore, by defining the matrix
. Therefore, by defining the matrix  , the crystal sizes N can be retrieved by solving
, the crystal sizes N can be retrieved by solving  , where
, where 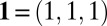 . If the image does not directly pass through a reciprocal lattice point, this analysis is still valid; however, the Fourier-transformed images may contain oscillations, which grow with distance to the lattice point.
. If the image does not directly pass through a reciprocal lattice point, this analysis is still valid; however, the Fourier-transformed images may contain oscillations, which grow with distance to the lattice point.
Image Segmentation.
To retrieve the crystal sizes via the methods of the previous section, we require an estimate for the support of the projected autocorrelated crystal from the Fourier transformed images, i.e., we need to segment the support from the noisy background (Fig. 3). We begin the segmentation by initializing a set H of pixels whose  value is greater than a fixed percentage of the largest†† value. Then, we traverse a sorted list of the remaining values, adding pixels to H until one reaches a point more than some threshold, typically a few pixels, away from all of the pixels currently in H, suggesting that one has reached the end of the support and has begun to see the oscillations from the background.‡‡
value is greater than a fixed percentage of the largest†† value. Then, we traverse a sorted list of the remaining values, adding pixels to H until one reaches a point more than some threshold, typically a few pixels, away from all of the pixels currently in H, suggesting that one has reached the end of the support and has begun to see the oscillations from the background.‡‡
Fig. 3.

The shape transform (Left) around a low-angle peak is Fourier transformed to reveal the projected autocorrelated crystal (middle), which is then segmented (Right).
Structure Factor Magnitude Modeling
Once the lattice orientations  and crystal sizes Nm are known, we can use Eq. 2 to compute an approximation
and crystal sizes Nm are known, we can use Eq. 2 to compute an approximation 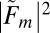 to the structure factor square magnitudes from the image Im, but only up to a constant factor because they are scaled by the unknown incident photon flux density Jm, which varies between images. Furthermore, due to the indexing ambiguity, one only knows the corresponding reciprocal space coordinates associated with the values of
to the structure factor square magnitudes from the image Im, but only up to a constant factor because they are scaled by the unknown incident photon flux density Jm, which varies between images. Furthermore, due to the indexing ambiguity, one only knows the corresponding reciprocal space coordinates associated with the values of  up to the crystal lattice symmetry, i.e., the possible structure factor magnitudes for each point take the form of a multimodal distribution. Moreover, these two problems are strongly coupled together: We cannot perform the scaling correction unless we know what modes to scale to and the modes are indistinguishable in the unscaled data set. Hence, we must simultaneously determine both the scaling and the multimodal parameters.
up to the crystal lattice symmetry, i.e., the possible structure factor magnitudes for each point take the form of a multimodal distribution. Moreover, these two problems are strongly coupled together: We cannot perform the scaling correction unless we know what modes to scale to and the modes are indistinguishable in the unscaled data set. Hence, we must simultaneously determine both the scaling and the multimodal parameters.
Processing the Data.
We approximate the structure factor squared magnitudes at the ith reciprocal lattice point§§
ξi from the mth image by computing an average over the neighboring ball  with radius r:
with radius r:
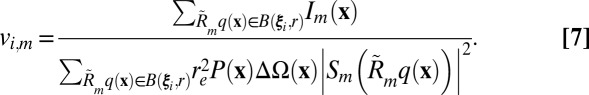 |
We discard any intensities below some fixed threshold from the above sum to prevent large errors from the division. Note that because we only know the orientation up to lattice symmetry, we also set¶¶
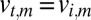 for every
for every 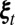 such that for some
such that for some  ,
, 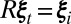 . To simplify notation, we will assume that unmeasured values and corresponding indices are removed from the remaining sets and summations. To reduce the dependence of the standard deviation on the size of the intensities, we use two applications of variance stabilization (12), and instead work with
. To simplify notation, we will assume that unmeasured values and corresponding indices are removed from the remaining sets and summations. To reduce the dependence of the standard deviation on the size of the intensities, we use two applications of variance stabilization (12), and instead work with  .
.
Multimodal Analysis.
Assume for now that the structure factor magnitudes are already properly scaled. Due to the indexing ambiguity, at this point in the procedure we only know the orientations up to the lattice symmetry. Thus, for each reciprocal lattice point  , values of
, values of 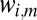 could correspond to K different structure factor magnitudes, e.g., for elastic scattering
could correspond to K different structure factor magnitudes, e.g., for elastic scattering  . A histogram of
. A histogram of 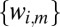 for
for  reveals K different peaks, smeared out as noise and parameter uncertainty are increased. Our goal is to detect these peaks and model the associated multimodal distribution.
reveals K different peaks, smeared out as noise and parameter uncertainty are increased. Our goal is to detect these peaks and model the associated multimodal distribution.
To retrieve the set of possible structure factor magnitudes, we will model the computed values  from each reciprocal lattice point
from each reciprocal lattice point 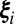 with a multimodal Gaussian distribution. Specifically, the associated probability density functions can be expressed in terms of multiple Gaussian distributions with means
with a multimodal Gaussian distribution. Specifically, the associated probability density functions can be expressed in terms of multiple Gaussian distributions with means 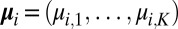 , in monotonically increasing order, and standard deviations
, in monotonically increasing order, and standard deviations  by
by 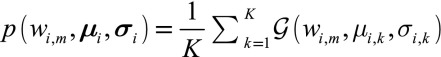 , where
, where  .
.
Given  , we determine its multimodal model through an expectation maximization algorithm. In particular, given an initial guess for model parameters
, we determine its multimodal model through an expectation maximization algorithm. In particular, given an initial guess for model parameters 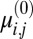 and
and  , we perform several iterations of the following:
, we perform several iterations of the following:
 |
Here, 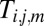 represents the probability that
represents the probability that  is drawn from the jth Gaussian mode. To initialize, we separate the data into K equal bins, define
is drawn from the jth Gaussian mode. To initialize, we separate the data into K equal bins, define 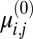 as the location in the jth bin with the greatest density, and set
as the location in the jth bin with the greatest density, and set 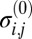 to be less than a typical bin size. Also, we perform outlier rejection by removing any
to be less than a typical bin size. Also, we perform outlier rejection by removing any  in which
in which  is below a given threshold.
is below a given threshold.
Scaling Correction.
In practice, variance in incident photon flux density, noise, and errors in autoindexing and crystal size determination smear out the peaks in the histogram, making them difficult to locate via expectation maximization (Fig. 4): Data must be scaled to properly model the structure factor magnitudes. To do so, we seek scaling factors which minimize the variance in the histograms and alternate this procedure with the expectation maximization step in Eq. 8.
Fig. 4.
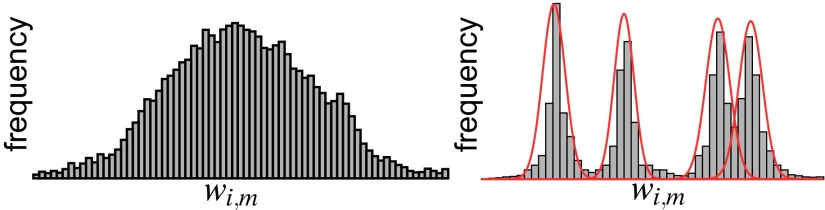
(Left) Histogram of the possible unscaled variance stabilized structure factor magnitudes for a reciprocal lattice point corresponding to a fourfold indexing ambiguity. (Right) Histogram of the scaled data with multimodal Gaussian model (red).
We seek the scaling factor  for the mth image by solving
for the mth image by solving
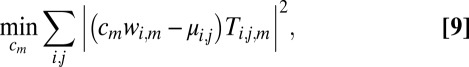 |
whose solution is given by
 |
Once the 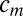 are computed, they are normalized so that
are computed, they are normalized so that  and then used to scale the images by replacing every
and then used to scale the images by replacing every 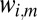 with
with  . Scaling is alternated with expectation maximization until convergence.
. Scaling is alternated with expectation maximization until convergence.
Resolving the Indexing Ambiguity
After the structure factor magnitude modeling, we know up to K possible structure factor magnitudes at each reciprocal lattice point. Resolving the indexing ambiguity amounts to correctly assigning one of these K values to each point. There are K equally valid solutions, related to each other by globally applying a rotation from  . We first use the set of multimodal model parameters to construct a graph theoretic model of the structure factor magnitude concurrency, i.e., the probability that two given structure factor magnitudes occur within the same image. Then, we resolve the indexing ambiguity by finding the maximum edge weight clique of this graph with a greedy approach.
. We first use the set of multimodal model parameters to construct a graph theoretic model of the structure factor magnitude concurrency, i.e., the probability that two given structure factor magnitudes occur within the same image. Then, we resolve the indexing ambiguity by finding the maximum edge weight clique of this graph with a greedy approach.
Graph Theoretic Modeling of Structure Factor Magnitude Concurrency.
Given the scaled variance stabilized structure factor magnitudes 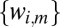 , means
, means  , and standard deviations
, and standard deviations 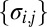 for the mth image and jth mode at the ith reciprocal lattice point, we construct‖‖ a graph
for the mth image and jth mode at the ith reciprocal lattice point, we construct‖‖ a graph  with vertices
with vertices 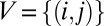 and edges E, where
and edges E, where  if and only if
if and only if  and
and  , i.e., only one j can be selected at each reciprocal lattice point
, i.e., only one j can be selected at each reciprocal lattice point  and each j can only be selected once among its twin-related coordinates
and each j can only be selected once among its twin-related coordinates 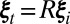 , where
, where  . Consequently, choosing a consistent set of structure factor magnitudes, where each possible value appears exactly once, is equivalent to finding a maximal clique*** in this graph.†††
. Consequently, choosing a consistent set of structure factor magnitudes, where each possible value appears exactly once, is equivalent to finding a maximal clique*** in this graph.†††
We define a directed weight 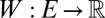 on G as the ratio of the sum of concurrence probabilities over the sum of the occurrence probabilities, where we sum over the sets
on G as the ratio of the sum of concurrence probabilities over the sum of the occurrence probabilities, where we sum over the sets  , consisting of all of the images which potentially measure intensities simultaneously at
, consisting of all of the images which potentially measure intensities simultaneously at  and
and  :
:
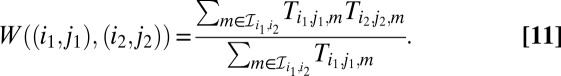 |
W gives a measure of how likely the values of 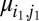 and
and  are to occur together in one of the solutions. With no noise or error, if
are to occur together in one of the solutions. With no noise or error, if  are distinct then W is exactly 1 when
are distinct then W is exactly 1 when  and
and 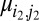 are simultaneously part of one of the solutions and is 0 otherwise. However, if there are B values of k such that
are simultaneously part of one of the solutions and is 0 otherwise. However, if there are B values of k such that  then W is
then W is 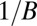 . With noise present, the asymmetry of the weight function favors structure factor magnitudes with strong signal and whose histograms are highly multimodal, providing the most orientation information.
. With noise present, the asymmetry of the weight function favors structure factor magnitudes with strong signal and whose histograms are highly multimodal, providing the most orientation information.
We now formulate the solution to the indexing ambiguity problem. We seek the maximal clique in G with maximum edge weight:
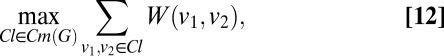 |
where  is the set of all maximal cliques in G. If a sufficient number of images are used, then, in the absence of noise and error, the maximizer of Eq. 12 retrieves one of the exact solutions to the indexing ambiguity problem, i.e., the maximum edge weight clique
is the set of all maximal cliques in G. If a sufficient number of images are used, then, in the absence of noise and error, the maximizer of Eq. 12 retrieves one of the exact solutions to the indexing ambiguity problem, i.e., the maximum edge weight clique  assigns the correct structure factor magnitudes, up to a global rotation. For imperfect data, this maximizer will choose a solution which is most consistent with the observed structure factor magnitude concurrency.
assigns the correct structure factor magnitudes, up to a global rotation. For imperfect data, this maximizer will choose a solution which is most consistent with the observed structure factor magnitude concurrency.
Greedy Approach to the Maximum Edge Weight Clique Problem.
Even though the maximum edge weight clique problem is, in general, nondeterministic polynomial-time hard (13), when constructed from the indexing ambiguity problem via Eq. 12, we can solve it in quadratic time with a greedy approach. We initialize the clique  with some starting vertex‡‡‡
with some starting vertex‡‡‡
 and progressively add vertices that maximize the weight sum of the current clique. In practice, we remove any points whose associated multimodal distributions contain less than the maximum number of modes. For convenience, we use a single index for the vertices
and progressively add vertices that maximize the weight sum of the current clique. In practice, we remove any points whose associated multimodal distributions contain less than the maximum number of modes. For convenience, we use a single index for the vertices  and we set
and we set 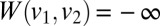 if
if  .§§§
.§§§
Algorithm 1.
 |
The elements of the set 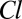 returned by Algorithm 1 are pairs of the form
returned by Algorithm 1 are pairs of the form  , corresponding to choosing the jth modeled variance stabilized structure factor magnitude
, corresponding to choosing the jth modeled variance stabilized structure factor magnitude 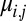 at the reciprocal lattice point
at the reciprocal lattice point  . This induces the map
. This induces the map 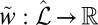 where
where  . With a sufficient number of images and no noise or error, Algorithm 1 retrieves an exact solution to the indexing ambiguity problem, always preferring a vertex
. With a sufficient number of images and no noise or error, Algorithm 1 retrieves an exact solution to the indexing ambiguity problem, always preferring a vertex  with nonzero weighted edges connecting to all elements of the current clique, i.e.,
with nonzero weighted edges connecting to all elements of the current clique, i.e., 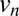 is only chosen if it corresponds to the same solution as the rest of clique. This approach remains robust with imperfect data, as it considers several pairs of measured intensities over all images to choose the structure factor magnitudes at any single point.
is only chosen if it corresponds to the same solution as the rest of clique. This approach remains robust with imperfect data, as it considers several pairs of measured intensities over all images to choose the structure factor magnitudes at any single point.
Orientation Calculation.
Although we can achieve a robust approximation of the complete structure factor magnitudes, accuracy can be improved by using this information to directly orient each image, and then averaging structure factor magnitudes for each corresponding reciprocal lattice point. For every image 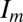 , we compute its full orientation
, we compute its full orientation  , where
, where 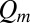 solves
solves
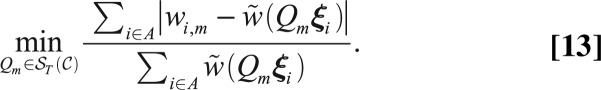 |
Here, A is the set of indices i where 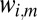 is measured by the image at the orientation
is measured by the image at the orientation  and
and  is a set of class representatives of the quotient group
is a set of class representatives of the quotient group  , i.e.,
, i.e., 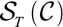 consists of the identity and twinning operators. If there are at least two orientations close to the minimum value, then we reject the computed orientation. Once the orientations are known, we obtain the structure factor magnitudes by averaging the corresponding magnitudes computed from each scaled oriented image.
consists of the identity and twinning operators. If there are at least two orientations close to the minimum value, then we reject the computed orientation. Once the orientations are known, we obtain the structure factor magnitudes by averaging the corresponding magnitudes computed from each scaled oriented image.
Phase Recovery
Once complete structure factor magnitudes are computed, one can determine missing phases and, thus, determine the electron density of a periodic unit with any applicable phasing method, e.g., refs. 14–17. Although these methods have been used extensively to determine structure in X-ray crystallography, each has limitations or introduces extra difficulties into the experimental setup. An appealing alternative is to directly deduce phases from Fourier magnitude data using an iterative phase retrieval technique, which only requires that Fourier magnitudes be sampled at a sufficient rate. Although infeasible in conventional crystallography, the signal from nanocrystals contains significant information between Bragg peaks, which may allow sampling at the required rates.
In general, such iterative phasing is possible if one samples the Fourier magnitudes at points of the form  where
where  (18, 19). In ref. 20 the feasibility of such an approach was demonstrated assuming that adequate signal was collected at each of the required points. However, the square magnitude of the shape transform at
(18, 19). In ref. 20 the feasibility of such an approach was demonstrated assuming that adequate signal was collected at each of the required points. However, the square magnitude of the shape transform at  grows quadratically in the crystal size for each dimension in which
grows quadratically in the crystal size for each dimension in which  . For nanocrystallography, this typically only results in noticeable signal at reciprocal lattice vertices and edges.¶¶¶,‖‖‖ While theory is lacking, this sampling density is sufficient in certain 3D cases (21). Alternatively, a recent approach uses Fourier magnitude information along with its gradient, assuming it can be accurately calculated, only at reciprocal lattice points (22). Here, we test the feasibility of iterative phasing using the Fourier magnitudes computed from our framework at reciprocal lattice vertices and edges.
. For nanocrystallography, this typically only results in noticeable signal at reciprocal lattice vertices and edges.¶¶¶,‖‖‖ While theory is lacking, this sampling density is sufficient in certain 3D cases (21). Alternatively, a recent approach uses Fourier magnitude information along with its gradient, assuming it can be accurately calculated, only at reciprocal lattice points (22). Here, we test the feasibility of iterative phasing using the Fourier magnitudes computed from our framework at reciprocal lattice vertices and edges.
Iterative Phase Retrieval.
Given a domain****
 , Fourier magnitude values
, Fourier magnitude values  , and some support
, and some support  , iterative phase retrieval algorithms seek a function
, iterative phase retrieval algorithms seek a function 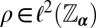 such that
such that 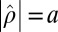 and
and 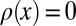 for all
for all  . Given a set Ω of points where a has a recorded value, such algorithms typically make use of the projection operators
. Given a set Ω of points where a has a recorded value, such algorithms typically make use of the projection operators  , where
, where  if
if  and
and 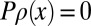 otherwise, and
otherwise, and  , where
, where
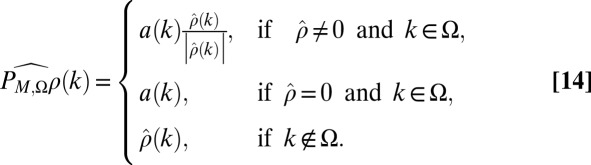 |
We alternate between several iterations of the error reducing algorithm (23):  , and the hybrid input-output algorithm (24):
, and the hybrid input-output algorithm (24): 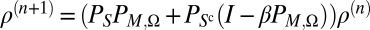 ,
,  , to seek out the solution ρ. Furthermore, we couple these iterations with the Shrinkwrap method (25), which, starting with an initial guess such as the unit cell, updates an estimate of the true support T by convolving the current iterate with a Gaussian and then thresholding.
, to seek out the solution ρ. Furthermore, we couple these iterations with the Shrinkwrap method (25), which, starting with an initial guess such as the unit cell, updates an estimate of the true support T by convolving the current iterate with a Gaussian and then thresholding.
Results
We demonstrate our methodology by determining the structure of PuuE Allantoinase from simulated diffraction data using the atomic coordinates and crystal symmetry recorded in refs. 26, 27 with several different peak incident photon flux densities. Each data set consists of 33,856 diffraction images. We assume knowledge of the Bravais vector lengths and the space group, which, in practice, may be deduced from autoindexing information and reflection conditions.
The crystal displays P4 space-group symmetry, thus diffraction data are symmetric with respect to 90° rotation about the z axis and inversion, and has a twinning operator given by 180° rotation about the x axis, or, equivalently, the y axis.
Image orientations are generated by randomly sampling from a normal distribution of quaternions. Sizes were randomly generated with an average crystal width of μC = 2,948.97 Å and standard deviation σC = 982.99 Å. For each image, we generate random incident photon flux densities J, measured in photons per square Angstrom per pulse, from a peak density  , via
, via  . We use experimental parameters†††† similar to ref. 3. Intensity values are computed via Eq. 2 along with shot and background noise, modeled with a Poisson distribution and a normal distribution, with a standard deviation of 1.3 photons per pixel (Figs. S1–S5).
. We use experimental parameters†††† similar to ref. 3. Intensity values are computed via Eq. 2 along with shot and background noise, modeled with a Poisson distribution and a normal distribution, with a standard deviation of 1.3 photons per pixel (Figs. S1–S5).
Here we present statistics‡‡‡‡ for our framework (Tables 1–3) along with a reconstruction from the processed simulated data (Fig. 5). For further details, see ref. 28.
Table 1.
Autoindexing performance
| Error* |
|||||
| Jo | Accepted | <0.001 | 0.001–0.004 | 0.004–0.016 | >0.016 |
| 21,800 | 32,678 | 7,912 | 21,485 | 3,196 | 85 |
| 2,180 | 28,251 | 6,583 | 17,993 | 3,496 | 179 |
| 218 | 22,701 | 4,733 | 13,588 | 3,947 | 433 |
| 21.8 | 12,859 | 1,786 | 6,224 | 4,180 | 669 |
| 2.18 | 3,926 | 39 | 798 | 2,290 | 799 |
Error in the Frobenius norm modulo  .
.
Table 3.
Orientation determination performance
| Jo | 21,800 | 2,180 | 218 | 21.8 | 2.18 |
| Accepted | 22,645 | 17,844 | 11,663 | 3,775 | 17 |
| Correct, %* | 99.9 | 99.9 | 99.8 | 99.3 | 58.8 |
Given the possible solution sets  and
and  , the number of correct orientations is
, the number of correct orientations is 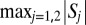 , where Sj consists of all computed orientations Ri closer to the Rj,i solution in the Frobenius norm modulo
, where Sj consists of all computed orientations Ri closer to the Rj,i solution in the Frobenius norm modulo  .
.
Fig. 5.

Electron density contours of the exact solution (Left) and the computed solution with 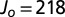 (Center) and overlay with the atomic model (Right).
(Center) and overlay with the atomic model (Right).
Table 2.
Crystal size determination performance
| Error* | ||||||
| Jo | Accepted | <0.1 | 0.1–0.2 | 0.2–0.3 | 0.3–0.4 | >0.4 |
| 21,800 | 30,506 | 19,652 | 9,667 | 903 | 98 | 186 |
| 2,180 | 26,260 | 16,080 | 8,996 | 992 | 71 | 121 |
| 218 | 20,195 | 10,941 | 7,681 | 1,166 | 126 | 281 |
| 21.8 | 10,639 | 4,071 | 4,626 | 1,388 | 184 | 370 |
| 2.18 | 1,851 | 458 | 458 | 387 | 112 | 436 |
Relative error in the geometric average of the crystal sizes.
Supplementary Material
Acknowledgments
We thank Stefano Marchesini for many valuable conversations. This research was supported in part by the Applied Mathematical Sciences subprogram of the Office of Energy Research, US Department of Energy (DOE) under Contract DE-AC02-05CH11231 and by the Division of Mathematical Sciences of the National Science Foundation, and used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the US DOE under Contract DE-AC02-05CH11231. J.A.S. was also supported by an Einstein Visiting Fellowship of the Einstein Foundation, Berlin. J.J.D. was also supported by a DOE Computational Science Graduate Fellowship.
Footnotes
The authors declare no conflict of interest.
*We will use  to denote either the continuous or discrete Fourier transform of f, depending on context.
to denote either the continuous or discrete Fourier transform of f, depending on context.
† refers to the transpose of the inverse of A.
refers to the transpose of the inverse of A.
‡ designates the number of elements in A.
designates the number of elements in A.
§Because the shape transform is symmetric with respect to rotation by elements of  , the use of orientations from autoindexing is sufficient here.
, the use of orientations from autoindexing is sufficient here.
¶ may be slightly smeared out due to grid alignment effects.
may be slightly smeared out due to grid alignment effects.
‖ is the X-ray projection operator through the detector plane normal and A is the autocorrelation operator.
is the X-ray projection operator through the detector plane normal and A is the autocorrelation operator.
**We note that alternative models of the finite lattice may be used here instead.
††We exclude the origin which picks up all of the noise within the image.
‡‡H gives unitless coordinates which should be scaled by  for a restricted image with
for a restricted image with  pixels of size
pixels of size  . Crystal sizes are rejected if they are outside of a set range.
. Crystal sizes are rejected if they are outside of a set range.
§§To keep our notation compact, we are representing the reciprocal lattice points with a single index in place of the traditional Miller indices.
¶¶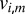 is multivalued for an image which measures intensities at both
is multivalued for an image which measures intensities at both 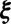 and
and 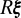 ,
, 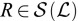 .
.
‖‖For known symmetry in the structure factor magnitudes (e.g., Friedel or Laue symmetry), we simplify G’s structure by merging corresponding symmetric vertices.
*** is a maximal clique if for all
is a maximal clique if for all  with no proper superset
with no proper superset  satisfying the same property.
satisfying the same property.
††† is the set difference of A and B.
is the set difference of A and B.
‡‡‡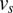 is typically chosen from a point with a highly multimodal distribution and strong signal.
is typically chosen from a point with a highly multimodal distribution and strong signal.
§§§In Algorithm 1,  denotes the assignment operator.
denotes the assignment operator.
¶¶¶The lattice edge structure factor magnitudes may be computed via Eq. 7.
‖‖‖One may also need to resolve the indexing ambiguity on the used non-Bragg data if it has less symmetry than the Laue group.
****This is obtained by linearly mapping the reciprocal lattice onto a uniform grid.
††††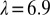 Å,
Å, 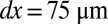 , D = 68/141 mm for the front/rear detectors with 1,024 × 1,024 pixels, horizontal polarization, and
, D = 68/141 mm for the front/rear detectors with 1,024 × 1,024 pixels, horizontal polarization, and  between 0.01 and 100 times current experimental levels.
between 0.01 and 100 times current experimental levels.
‡‡‡‡Here we use the distance in Frobenius norm modulo  .
.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1321790111/-/DCSupplemental.
References
- 1.Aquila A, et al. Time-resolved protein nanocrystallography using an X-ray free-electron laser. Opt Express. 2012;20(3):2706–2716. doi: 10.1364/OE.20.002706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Boutet S, et al. High-resolution protein structure determination by serial femtosecond crystallography. Science. 2012;337(6092):362–364. doi: 10.1126/science.1217737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chapman HN, et al. Femtosecond X-ray protein nanocrystallography. Nature. 2011;470(7332):73–77. doi: 10.1038/nature09750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Johansson LC, et al. Lipidic phase membrane protein serial femtosecond crystallography. Nat Methods. 2012;9(3):263–265. doi: 10.1038/nmeth.1867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kern J, et al. Simultaneous femtosecond X-ray spectroscopy and diffraction of photosystem II at room temperature. Science. 2013;340(6131):491–495. doi: 10.1126/science.1234273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Koopmann R, et al. In vivo protein crystallization opens new routes in structural biology. Nat Methods. 2012;9(3):259–262. doi: 10.1038/nmeth.1859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Spence JCH, Weierstall U, Chapman HN. X-ray lasers for structural and dynamic biology. Rep Prog Phys. 2012;75(10):102601. doi: 10.1088/0034-4885/75/10/102601. [DOI] [PubMed] [Google Scholar]
- 8.White TA, et al. Crystfel: A software suite for snapshot serial crystallography. J Appl Cryst. 2012;45(2):335–341. [Google Scholar]
- 9.Duisenberg AJM. Indexing in single-crystal diffractometry with an obstinate list of reflections. J Appl Cryst. 1992;25:92–96. [Google Scholar]
- 10.Steller I, Bolotovsky R, Rossmann MG. An algorithm for automatic indexing of oscillation images using Fourier analysis. J Appl Cryst. 1997;30:1036–1040. [Google Scholar]
- 11.Lovisolo L, da Silva EAB. Uniform distribution of points on a hyper-sphere with applications to vector bit-plane encoding. IEEE Proc Vision Image Signal Process. 2001;148(3):187–193. [Google Scholar]
- 12.Guan Y. Variance stabilizing transformations of Poisson, binomial and negative binomial distributions. Stat Probab Lett. 2009;14:1621–1629. [Google Scholar]
- 13.Alidaee B, Glover F, Kochenberger G, Wang H. Solving the maximum edge weight clique problem via unconstrained quadratic programming. Eur J Oper Res. 2007;181(2):592–597. [Google Scholar]
- 14.Green DW, Ingram VM, Perutz MF. The structure of haemoglobin. IV. Sign determination by the isomorphous replacement method. Proc. Roy. Soc. A. 1954;225(1162):287–307. [Google Scholar]
- 15.Hauptman H, Karle J. Solution of the Phase Problem I. The Centrosymmetric Crystal, No. 3. New York: American Crystallographic Association; 1953. [Google Scholar]
- 16.Karle J. Some developments in anomalous dispersion for the structural investigation of macromolecular systems in biology. Int J Quantum Chem Quantum Biol Symp. 1980;18(S7):357–367. [Google Scholar]
- 17.Rossmann MG, Blow DM. The detection of sub-units within the crystallographic asymmetric unit. Acta Crystallogr. 1962;15(1):24–31. [Google Scholar]
- 18.Hayes MH. The reconstruction of a multidimensional sequence from the phase or magnitude of its Fourier transform. IEEE Trans Acoust Speech Signal Process. 1982;30(2):140–154. [Google Scholar]
- 19.Rosenblatt J. Phase retrieval. Commun Math Phys. 1984;95:317–343. [Google Scholar]
- 20.Spence JCH, et al. Phasing of coherent femtosecond X-ray diffraction from size-varying nanocrystals. Opt Express. 2011;19(4):2866–2873. doi: 10.1364/OE.19.002866. [DOI] [PubMed] [Google Scholar]
- 21.Millane RP. Multidimensional phase problems. J Opt Soc Am A Opt Image Sci Vis. 1996;13(4):725–734. [Google Scholar]
- 22.Elser V. Direct phasing of nanocrystal diffraction. Acta Crystallogr A. 2013;69:559–569. doi: 10.1107/S0108767313023362. [DOI] [PubMed] [Google Scholar]
- 23.Gerchberg RW, Saxton WO. A practical algorithm for the determination of the phase from image and diffraction plane pictures. Optik (Stuttg) 1972;35:237–246. [Google Scholar]
- 24.Fienup JR. Reconstruction of an object from the modulus of its Fourier transform. Opt Lett. 1978;3(1):27–29. doi: 10.1364/ol.3.000027. [DOI] [PubMed] [Google Scholar]
- 25.Marchesini S, et al. X-ray image reconstruction from a diffraction pattern alone. Phys Rev B. 2003;68(4):140101. [Google Scholar]
- 26.Bernstein FC, et al. The Protein Data Bank: A computer-based archival file for macromolecular structures. J Mol Biol. 1977;112(3):535–542. doi: 10.1016/s0022-2836(77)80200-3. [DOI] [PubMed] [Google Scholar]
- 27.Ramazzina I, et al. Logical identification of an allantoinase analog (puuE) recruited from polysaccharide deacetylases. J Biol Chem. 2008;283(34):23295–23304. doi: 10.1074/jbc.M801195200. [DOI] [PubMed] [Google Scholar]
- 28.Donatelli JJ. 2013. Reconstruction algorithms for x-ray nanocrystallography via solution of the twinning problem, PhD Thesis (University of California, Berkeley)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



