Evidence of Lévy walk foraging patterns in human hunter–gatherers

Significance

Lévy walks are a random walk search strategy used by a wide variety of organisms when searching for heterogeneously distributed food. This type of search involves mostly short move steps (defined as the distance traveled before pausing or changing direction) combined with rarer longer move steps. Here, we show that the Hadza, hunter–gatherers from northern Tanzania, perform Lévy walks when foraging for a wide variety of food items, suggesting that Lévy walks are an important movement pattern for the most cognitively complex foragers on Earth. Our results suggest that scale-invariant, superdiffusive movement profiles are a fundamental feature of human landscape use, regardless of the physical or cultural environment, and may have played an important role in the evolution of human mobility.

Abstract

When searching for food, many organisms adopt a superdiffusive, scale-free movement pattern called a Lévy walk, which is considered optimal when foraging for heterogeneously located resources with little prior knowledge of distribution patterns [Viswanathan GM, da Luz MGE, Raposo EP, Stanley HE (2011) The Physics of Foraging: An Introduction to Random Searches and Biological Encounters]. Although memory of food locations and higher cognition may limit the benefits of random walk strategies, no studies to date have fully explored search patterns in human foraging. Here, we show that human hunter–gatherers, the Hadza of northern Tanzania, perform Lévy walks in nearly one-half of all foraging bouts. Lévy walks occur when searching for a wide variety of foods from animal prey to underground tubers, suggesting that, even in the most cognitively complex forager on Earth, such patterns are essential to understanding elementary foraging mechanisms. This movement pattern may be fundamental to how humans experience and interact with the world across a wide range of ecological contexts, and it may be adaptive to food distribution patterns on the landscape, which previous studies suggested for organisms with more limited cognition. Additionally, Lévy walks may have become common early in our genus when hunting and gathering arose as a major foraging strategy, playing an important role in the evolution of human mobility.

Over the last decade, researchers have applied sophisticated analytical techniques to explore the movement patterns of a wide variety of organisms from insects to mammals (1–8). Many of these taxa seem to use a similar movement pattern during foraging, where the length of move steps (distance traveled between two points marked by either a pause or a change in direction) is distributed according to a power law function with a heavy tail:, where l is move step length and μ is the power law exponent with 1 < μ ≤ 3 (1). In this distribution, termed a Lévy walk, groups of short step lengths are interspersed with longer movements between them, and this pattern is repeated across all scales (i.e., the distribution is scale-free) (9). Modeling studies have shown that this step length distribution is advantageous when searching for resources that are patchily distributed and can be profitably revisited (i.e., resources are not depleted after a given visit) (1, 10, 11). In these cases, the optimal Lévy strategy has μ ∼ 2, because the rare long steps minimize oversampling a given patch and take organisms to new food patches without requiring memory or high levels of cognition (1, 10, 11).

When similar analytical techniques are applied to human movements, researchers have found some support for Lévy walks in our own species (12–15). In most cases, patterns found in urban-dwelling humans are attributed to the requirements of life (work, shopping, etc.) in a human-designed landscape (15) rather than an evolved search strategy as suggested for other organisms (1, 16). One previous study found evidence of Lévy walks in Ju/’hoansi hunter–gatherers of Botswana and Namibia, suggesting that random walk searches may be advantageous to humans living more traditional lifestyles (13, 17). However, this study examined the distribution of distances between residential camp locations [which are largely tied to the locations of permanent waterholes (18)] rather than the steps taken during actual foraging bouts (13). Thus, we are left with the question of whether Lévy walk patterns occur in cognitively complex foragers.

In this study, we examined individual movement patterns among Hadza hunter–gatherers of northern Tanzania to determine whether the most cognitively complex foragers on Earth perform Lévy walks while foraging. The Hadza hunter–gatherers who we worked with adhered to a traditional hunting and gathering lifestyle—foraging for wild plant foods and game on foot with simple tools (bow and arrow, digging sticks, and axes) and without any modern technologies or agriculture (19). We recruited 44 Hadza subjects from two camps to wear global positioning system (GPS) units during foraging bouts (Table S1). Individuals wore GPS units on multiple days, and we collected data from camps during different seasons (SI Methods). We define a foraging bout as a round trip taken by a subject from and back to his or her residential camp. In addition to full foraging bouts, we examined the outbound leg of foraging bouts separately (from camp to the farthest point from camp in a given bout). We analyzed individual subject’s movement data from the longest foraging bout for each day separately (n = 342 total bouts) (analyses of all bouts for all individuals are in SI Methods). Step lengths are defined as the distance traveled between two points followed by either a pause or a change in direction (defined by a turning angle). The definition for a change in direction is generally arbitrary among various studies (15). Here, we ran our full dataset (Dataset S1) through multiple analyses, where the definition of directional change was altered in 10° increments from 0° to 180° (SI Methods).

For each foraging bout and all step length definitions, we used maximum likelihood methods to fit six models (power law, truncated power law, exponential function, and three composite exponential models) to our data, and we used the Akaike Information Criterion (AIC) for model selection (20). Because humans and other animals are limited by physiology and time of day to some maximum step length, the truncated power law is generally thought to better represent movement patterns in nature (3) given by the following probability density function: f(l) = (μ − 1)(a^{1 − μ} − b^{1 − μ})⁻¹l^−μ, where a and b are the minimum and maximum values of l, respectively, for which a distribution is valid (21). In practice, these values are the minimum and maximum step lengths observed in a dataset. We also tested an exponential model to represent Brownian motion, a classic alternative movement strategy to Lévy walks (20): f(l) = 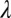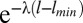. Finally, we tested three composite exponential models (composite Brownian walks) using information in the work by Jansen et al. (22): 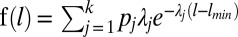, where k is the number of exponential models mixed and p_j is the proportional contribution of the jth model to the overall distribution of steps. We tested models that included two, three, and four exponential functions. We performed Kolmogorov–Smirnov tests to determine the significance of model fits chosen by AIC (23). This method, which directly compares fits of power law models with the alternative exponential models, is considered the most statistically robust for determining the presence of a power law in movement data (20, 23).

Results

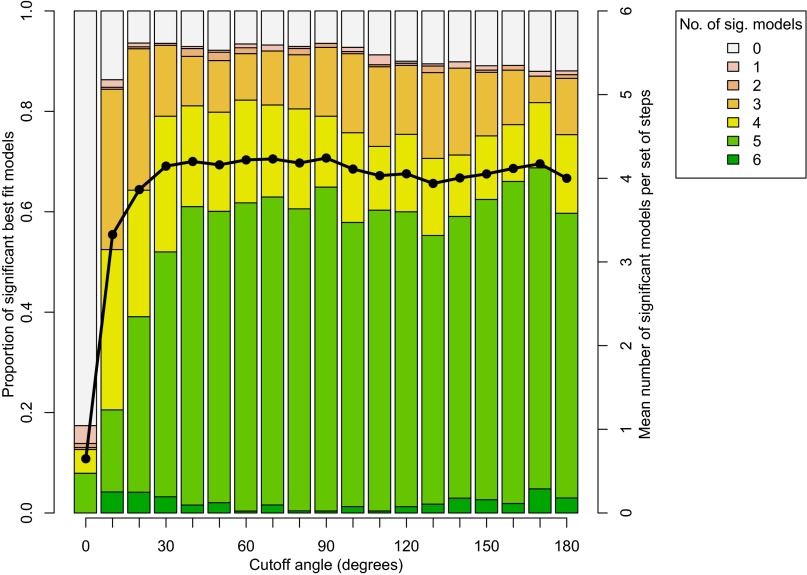
We first sought to determine the turning angle where the number of distributions significantly classified by multiple models approached asymptotic limits (Fig. 1). At these limits, we suggest that analyses have the strongest ability to identify the best fits through model selection statistical comparisons. These limits were reached at turning angles of 40° for full bouts, where step distributions had, on average, four significant model fits from which to choose, and over 60% of bouts had five or six significant model fits from which to choose (Fig. 1).

Fig. 1.

Proportion of significant best fit models. For each turning angle, from 0° to 180° in 10° increments, bars represent the proportion of step distributions significantly fit by a given number of models (from zero to six). Line is the mean number of significant models per set of steps.

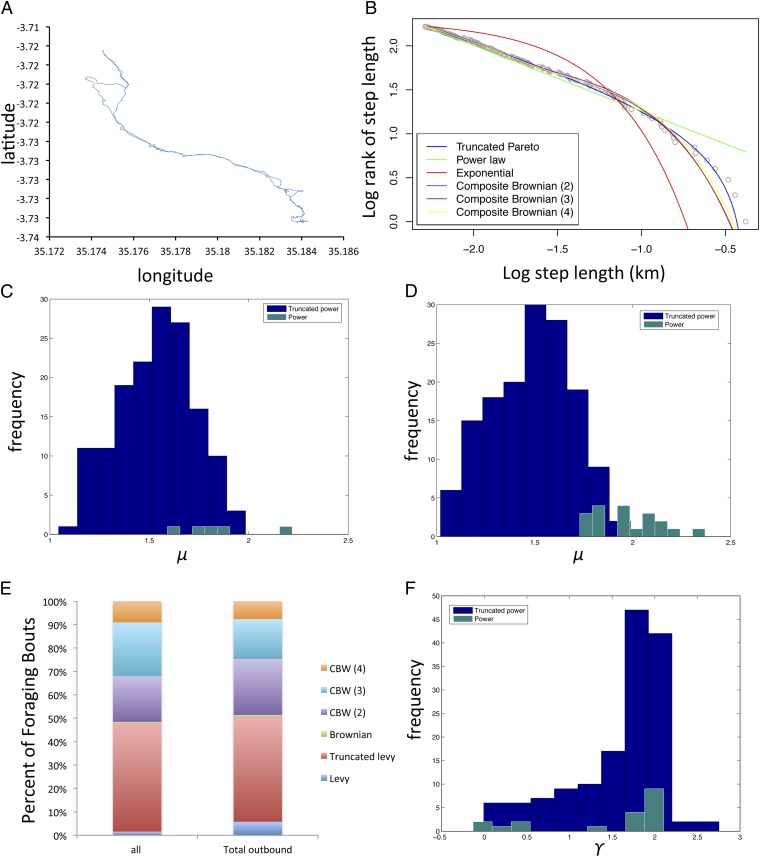
Using 40° as a definition of a change of direction, a plurality of step length distributions is significantly classified as Lévy walks (46.27% truncated power law and 1.55% power law) (Fig. 2). The remainder of foraging bouts were classified as Brownian walks (0.62%) or composite Brownian walks (CBWs), with either two (19.57%), three (22.98%), or four (9.01%) exponential models (Fig. 2). Estimates of μ for power law (1.85 ± 0.23) or truncated power law (1.54 ± 0.19) models in the Hadza dataset fall mostly between one and two (Fig. 2 and Fig. S1). The frequency of Lévy walks performed in outbound portions of foraging bouts did not differ significantly from full foraging bouts [χ² P = 0.5 for comparison of Lévy (power law and truncated power law) vs. non-Lévy (Brownian and all CBWs)], with subjects using step length distributions classified by power laws 5.78% of the time and truncated power laws 44.68% of the time (Fig. 2). Means and ranges of power law and truncated power law exponents in outbound legs were similar to means and ranges calculated for full bouts (μ_power = 1.96 ± 0.17; μ_trunc = 1.49 ± 0.21) (Fig. 2).

Fig. 2.

Model fitting for move step lengths. (A) Example of GPS data from foraging bout for a Hadza male. (B) Rank frequency plot of step length distributions showing model fits (truncated power law is the best fit model in this instance using AIC model selection criteria). (C) Histogram of μ from all foraging bouts best fit by truncated power laws and power laws. (D) Histogram of μ from the outbound portions of all foraging bouts best fit by truncated power laws and power laws. (E) Percentage of foraging bouts significantly fit by a given model. (F) Histogram of γ for the relationship between time and squared displacements of outbound portion of foraging bouts.

We also calculated squared displacements of the outbound leg of foraging bouts [from camp to the farthest distance away from camp using information in the work by Ramos-Fernandez et al. (4)] to determine diffusive characteristics of Hadza foraging (Fig. 2). In normal diffusion, squared displacement should be proportional to time. However, if movements are superdiffusive, as in Lévy walks, squared displacement is proportional to time^γ, where γ > 1 [if γ < 1, movements are described as subdiffusive (15)]. As found in previous studies (15, 24), truncated Levy walks have dichotomous diffusion patterns, with superdiffusion (mean γ = 1.57 ± 0.05) followed by subdiffusion (mean γ = 0.69 ± 0.05) (Fig. S2).

Men, who generally spend their days hunting for animal game and searching for wild honey (19), used truncated power law or power law step length distributions significantly less often than women, who spend their days foraging for tubers, berries, and other plant foods (36.62% of movement bouts for males compared with 56.67% of movement bouts for females; χ² P = 0.001) (Fig. 3). Differences between men and women are greatly reduced when outbound legs of foraging bouts are analyzed separately (48.61% of movement bouts are Lévy walks for males compared with 52.15% of movement bouts are Lévy walks for females; χ² P = 0.02) (Fig. 3). The lower proportion of Lévy walk full foraging bouts in men may be caused by a truncation of long step lengths after successful capture of animal prey or honey, which would explain the similarity in Lévy walk patterns during the outbound portions of foraging bouts (25). Although more detailed data are required to test this hypothesis, it is clear that Lévy walks represent the plurality of foraging bouts for both males and females.

Fig. 3.

Lévy walks by camp and sex and food returns by camp. (A) Percentage of foraging bouts best fit by a given model separated by sex (fit determined by AIC methods and significance tests). (B) Percentage of the outbound portion of foraging bouts best fit by a given model separated by sex. (C) Percentage of foraging bouts best fit by a given model separated by camp. (D) Percentage of outbound foraging bouts best fit by a given model separated by camp. (E) Food returns by camp for three of four camps by mass; food returns were not available for Setako in 2009.

There is little evidence that local environment drives the presence of the Lévy walk patterns. Significant differences in the foods that Hadza subjects brought back to each camp (χ² P < 0.0001) (Fig. 3) do not lead to large intercamp differences in use of Lévy walks (Fig. 3) (χ² P = 0.08 for all steps and P = 0.01 for the outbound leg of foraging bouts). Despite some small intercamp differences, Lévy walks are performed in a plurality of foraging bouts in all camps, and for outbound legs, the percentage of bouts classified as Lévy walks is similar (Fig. 3) [χ² P = 0.55 for intercamp comparisons of Lévy (power law and truncated power law) vs. non- Lévy (Brownian and all CBWs)]. Finally, there are no intrasex differences in search strategy proportions across camps (χ² P_{females,all steps} = 0.23; P_{females,outbound} = 0.24; P_{males,all steps} = 0.69; P_{males,outbound} = 0.62). Thus, it is clear that Lévy walk patterns emerge when foraging for a wide variety of foods, with little evidence that specific food targets drive higher levels of Lévy search patterns.

Discussion

Our results show that Hadza travel patterns, which represent searching for, acquiring, processing, and transporting foods back to camp, display Lévy walk patterns similar to movements observed in a wide array of less cognitively complex taxa (1). Although previous work provides conflicting evidence of the use of Lévy walks in nonhuman primates (2, 4, 26–29), our study presents the largest and most comprehensive dataset analyzed to date showing Lévy walk strategies in human foragers. While we have used model selection statistics to rule out alternative models for step length distributions in foraging bouts conforming to power laws and truncated power laws, it is possible that environmental features may drive these distributions. More detailed data on local ecology are required to fully falsify this hypothesis, but the discovery of a plurality of Lévy step length distributions across camps (different local environments and different search targets) and across sexes (different search targets) suggests that these step distributions are not simply a function of environmental features.

Exponents of best fit power law and truncated power law models suggest that foraging strategies may reflect the complexity of the local habitats and diversity of search targets for human hunter–gatherers (30). When using power law step distributions, Hadza subjects have exponents that approximate values for optimal searching for heterogeneously distributed targets that are not depleted (1.85 for full bouts and 1.96 for outbound legs) (1, 11). Exponents for truncated power law step distributions in the Hadza range between one and two (mean μ ∼ 1.5) and may represent a response to a diverse set of targets. More ballistic searches occur when the exponent nears one, and they are advantageous for more homogeneously distributed resources located far from the subject (31). Values of exponents closer to 1.5 are advantageous when target items vary in distance from the starting point of a search and when landscapes are dynamic, with a high scarcity of resources (30). Values of truncated power law exponents in the Hadza are similar to exponents found for other foragers searching in dynamic and heterogeneous landscapes, such as jellyfish (μ = 1.18) (32) and marine predators (μ = 1.63) (7). Thus, Hadza foraging strategies may reflect the highly dynamic and complex East African savannah landscape, where males and females use Lévy walk patterns when foraging for a wide variety of food resources with different patterns of distribution, variable distances from camp, and different ecological attributes [i.e., mobile animal prey, arboreal resources (baobab fruit), terrestrial resources (berries), and subterranean resources (tubers)] (19, 33, 34).

The fact that an exceedingly small percentage (0.62%) of the full foraging bouts were classified as simple Brownian walks suggests that, unlike other predators (3), the Hadza do not generally use movement patterns that show Brownian properties during foraging. Instead, when human foragers do not use Lévy walk searches, their step length distributions are best fit by composite Brownian walks. Recent work suggests that composite Brownian walks share many similarities with Lévy walks, because they can incorporate distributions with mainly short steps and distributions with mainly long steps in the same foraging bout (35). In some circumstances, organisms may use composite Brownian searches as a way of approximating a Lévy walk, switching between different step length distributions because of intrinsic triggers (35). In other situations, external cues, such a depletion of local search targets, may trigger changes between exponential distributions (35).

Our results show that human hunter–gatherers perform Lévy walks or other random walk searches that can approximate Lévy walks while foraging for a wide variety of food targets. In these cases, cognitive complexity does not shift movement patterns away from Lévy walks, and human foragers take advantage of similar step distributions as other foragers ranging from insects to marine predators to other terrestrial mammals (1). These results have implications for understanding human movement patterns in both the present and the past. Recent work strongly suggests that humans use scale-invariant superdiffusive movement patterns in urban areas (12, 14, 15). These patterns are useful in understanding the spread of disease and planning urban landscapes and telecommunications (12, 14, 15). Our results suggest that scale-invariant, superdiffusive movement profiles are a fundamental feature of human landscape use, regardless of the physical or cultural environment, and may have played an important role in the evolution of human mobility. Given the adoption of a hunting and gathering lifestyle nearly 2 Mya in human ancestors (36), Lévy walk foraging is likely a key element of human prehistory. Superdiffusive foraging may have allowed hominins, such as Homo erectus, to explore the larger home ranges reconstructed for these early hunter–gatherers (36). Lévy walk step distributions may also explain why patterns of raw material transport in the archaeological record often follow power law distributions (37, 38).

Thus, scale-invariant movements play a key role in human mobility, occurring in the vastly different contexts of hunter–gatherer populations in East Africa and more sedentary populations in urban landscapes. Because studies have not identified these types of search strategies in nonhuman primates using sophisticated statistical techniques (26), Lévy walks may have arisen with the evolution of a hunting and gathering lifestyle in human ancestors. The widespread use of this movement pattern among species with great cognitive variation suggests an important link between foraging patterns across different organisms, including humans. Future reconstructions of group movements and the evolution of human mobility patterns must take into account the likely scale invariance of human move steps.

Methods

Subjects.

We recruited 44 subjects (n_male = 20; n_female = 24) from two Hadza camps in northern Tanzania (Setako and Sengeli). Data collection took place over four 2-wk periods in September of 2009, August of 2010, and January of 2011 and covered rainy and dry seasons at the two camp locations (39). Subjects wore Garmin Forerunner 205 GPS units from dawn until dusk (SI Methods).

GPS Analysis.

For each individual, on each day with GPS data, we first determined the longest foraging bout for a given day. We removed all foraging bouts less than 500 m from camp and less than 500 m in distance traveled (total n using these methods = 342). Step lengths were determined from GPS traces [converted into distances using the distVincentyEllipsoid function in the package geosphere of R version 3.0.1 (40,41)] as the distance between two points, where the second point is determined by a change in direction or a pause. We changed the angular definition of direction change in 10° increments from 0° to 180°.

Model Selection.

We calculated exponents and coefficients for best fit models for power laws, truncated power laws, and exponential models using maximum likelihood methods for step length distributions of the Hadza using information in the work by Edwards et al. (20). We used the AIC for model selection and performed an iterative goodness-of-fit procedure, including Kolmogorov–Smirnov tests, to determine significance for models (23). A more detailed explanation of the methods is in SI Methods.