Functional traits explain variation in plant life history strategies

Significance

Plants have evolved diverse life history strategies to succeed in Earth’s varied environments. Some species grow quickly, produce copious seeds, and die within a few weeks. Other species grow slowly and rarely produce seeds but live thousands of years. We show that simple morphological measurements can predict where a species falls within the global range of life history strategies: species with large seeds, long-lived leaves, or dense wood have population growth rates influenced primarily by survival, whereas individual growth and fecundity have a stronger influence on the dynamics of species with small seeds, short-lived leaves, or soft wood. This finding increases the ability of scientists to represent complex population processes with a few easily measured character traits.

Abstract

Ecologists seek general explanations for the dramatic variation in species abundances in space and time. An increasingly popular solution is to predict species distributions, dynamics, and responses to environmental change based on easily measured anatomical and morphological traits. Trait-based approaches assume that simple functional traits influence fitness and life history evolution, but rigorous tests of this assumption are lacking, because they require quantitative information about the full lifecycles of many species representing different life histories. Here, we link a global traits database with empirical matrix population models for 222 species and report strong relationships between functional traits and plant life histories. Species with large seeds, long-lived leaves, or dense wood have slow life histories, with mean fitness (i.e., population growth rates) more strongly influenced by survival than by growth or fecundity, compared with fast life history species with small seeds, short-lived leaves, or soft wood. In contrast to measures of demographic contributions to fitness based on whole lifecycles, analyses focused on raw demographic rates may underestimate the strength of association between traits and mean fitness. Our results help establish the physiological basis for plant life history evolution and show the potential for trait-based approaches in population dynamics.

Recent evidence for global patterns of functional variation in plants, such as the leaf economics spectrum (1, 2), the wood economics spectrum (3), and the seed size–seed number tradeoff (4, 5), has convinced many ecologists that functional traits offer the best available approach for achieving a general predictive understanding of communities and ecosystems (6, 7). Trait-based approaches are now being used to predict the outcome of community assembly (8–10), global vegetation dynamics (11), and the rate of ecosystem processes (6, 12–14). A central assumption of trait-based ecology is that morphological traits determine physiological performance, which influences vital rates and determines individual fitness and life history evolution (15, 16). However, because of the challenge of quantifying the contribution of traits to fitness, the assumed links between functional traits and life history have not been fully tested.

Research in tropical and Mediterranean forests has revealed cross-species relationships between functional traits and the survival and growth rates of individuals (3, 17–24). Although these relationships provide evidence that functional traits influence vital rates, they offer only limited insight into associations between those traits and individual fitness and life history. Vital rates (e.g., survival and fecundity) represent fitness components, but their influence on mean fitness, defined as the population growth rate (λ), is best understood in the context of the full lifecycle of a species (25, 26). A significant negative correlation between wood density and individual growth (18) might not translate into a significant effect on mean fitness if individual growth has little influence on λ. Conversely, a weak relationship between a functional trait and another vital rate could have a significant effect on mean fitness if that vital rate has a strong influence on λ. Perturbation analyses, such as the sensitivities and elasticities frequently applied to matrix projection models (27), address this problem by quantifying the contribution of vital rates to λ (28), making it possible to characterize a species' overall life history in terms of the relative importance of survival, individual growth, and fecundity to mean fitness. Species with slow life histories have population growth rates with high elasticities to survival, whereas species with fast life histories have relatively higher elasticities to individual growth or fecundity (29, 30).

Armed with vital rate elasticities, we can test quantitative hypotheses about whether functional tradeoffs scale up to generate life history tradeoffs. For example, plants can allocate their reproductive effort to provision a few large seeds, which tolerate low light and resource availability and have a high survival probability, or they can spread their reproductive effort among many small seeds, maximizing fitness under high resource availability (31, 32). If this functional tradeoff at the seedling stage translates into a life history tradeoff, seed mass should be positively related to the elasticity of the population growth rate to survival and negatively related to elasticities to individual growth and fecundity. The leaf economics spectrum represents another allocation tradeoff. Species can construct long-lived, well-defended leaves that are often favored in low resource environments or build leaves that assimilate carbon quickly under conditions of high resource availability but are prone to rapid tissue loss (1, 33). Species with slow leaf economics traits, such as long leaf lifespans, low specific leaf area (SLA), and low leaf N, might also lead slow lives, characterized by high elasticities to survival and low elasticities to individual growth and recruitment. A wood economics spectrum also exists: species with dense wood tend to have higher survival but lower relative growth rates than species with soft wood (3, 34). Elasticities to survival should increase with wood density, whereas elasticities to individual growth and fecundity should decrease.

The main obstacle in testing these hypotheses is availability of the detailed demographic data necessary to describe a species’ full lifecycle and estimate vital rate elasticities. We overcame this limitation by crossing the TRY Global Plant Traits Database (35) with the COMPADRE Plant Matrix Database (www.compadre-db.org/), a collection of published matrix population models. This approach produced a dataset of 222 plant species spanning a global range of biomes and perennial growth forms (Table S1), for which we have at least one functional trait measurement as well as a matrix population model that we used to calculate the elasticity of the population growth rate to each of the three vital rates: survival, growth, and fecundity (30).

Our primary objective was to evaluate the ability of functional traits to explain variation across species in life history, which we quantified with vital rate elasticities. Our secondary objective was to evaluate whether inferences about life history can be drawn directly from the raw vital rates, which would save researchers the considerable time and effort required to parameterize population models and calculate elasticities. We used two statistical approaches to quantify relationships between vital rate elasticities and seed mass, wood density, and leaf economics traits (leaf lifespan, SLA, and leaf N). Dirichlet regression is a multivariate approach that accounts for the fact that the survival, growth, and fecundity elasticities for each species sum to one but does not account for phylogenetic relationships. Phylogenetic generalized least squares (PGLS) regression ignores the nonindependence of the elasticities but accounts for phylogenetic relationships. We repeated both types of regressions with plant growth form and then biome included as covariates to confirm that trait effects did not simply represent differences between trees and herbaceous species or plants adapted to different environments.

Results

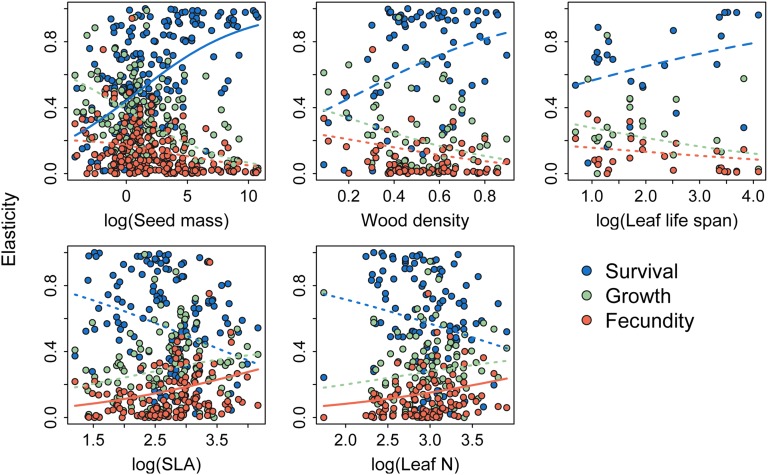
We found strong support for the hypothesis that species with slow anatomical and morphological traits also have slow life history, which is measured by the elasticity of the population growth rate to each of the three vital rates (Fig. 1, Table 1, Fig. S1, and Tables S2–S5). As predicted, species with greater seed mass had higher elasticities to survival in both Dirichlet and PGLS regressions, even with growth form and biome included as covariates. In the Dirichlet regressions, elasticities to individual growth and fecundity did not respond to seed mass. Survival elasticities increased with wood density; the relationship was sensitive to the inclusion of growth form in the Dirichlet regression but not in the PGLS regression. Dirichlet regressions did not show significant relationships between wood density and individual growth or fecundity elasticities. Species with longer-lived leaves were also characterized by higher elasticities to survival. The Dirichlet regression indicated that this effect reflected differences in growth form. However, when we removed one apparent outlier (Pinus nigra, a species with a long leaf lifespan but very low survival elasticity reported from a rapidly expanding invasive population) (36), leaf lifespan was positively associated with the elasticity to survival, even in the presence of growth form (Z = 2.8, P = 0.006) (Fig. S2). Adding biome as a covariate had no qualitative effect on these relationships. Although seed mass, wood density, and leaf lifespan were all significantly correlated with survival elasticities, the traits explained only a modest portion of variation. In simple linear regressions of logit-transformed survival elasticities, the R² was 0.24, 0.08, and 0.29 for seed mass, wood density, and leaf lifespan, respectively.

Fig. 1.

Functional traits are related to vital rate elasticities. Relationships were estimated with Dirichlet regression. Dotted lines show nonsignificant functional trait effects, solid lines show significant functional trait effects, and dashed lines show functional trait effects that were not significant after growth form was added to the model.

Table 1.

Statistical tests of functional trait effects on vital rate elasticities

	Dirichlet regressions						PGLS regressions
	Functional traits only		Traits and growth form		Traits and biome		Functional traits only		Traits and growth form		Traits and biome
Elasticity	Z	P	Z	P	Z	P	t	P	t	P	t	P
Seed mass (n = 193)
Survival	7.112	*	3.882	*	4.912	*	5.007	*	3.231	†	3.94	*
Growth	−1.441	ns	1.202	ns	−2.031	‡	−3.935	*	−2.243	‡	−2.823	†
Fecundity	0.774	ns	1.389	ns	−0.175	ns	0.439	ns	0.348	ns	0.633	ns
Wood density (n = 72)
Survival	3.646	*	0.246	ns	2.059	‡	3.785	*	2.223	‡	3.108	†
Growth	−0.227	ns	−0.164	ns	−0.989	ns	−3.43	†	−2.315	‡	−2.748	†
Fecundity	0.045	ns	−0.373	ns	−0.434	ns	−2.835	†	−2.287	‡	−2.381	‡
Leaf lifespan (n = 27)
Survival	2.456	‡	0.124	ns	3.375	†	3.634	†	3.52	†	2.564	‡
Growth	0.727	ns	−1.393	ns	1.931	§	−1.188	ns	−1.226	ns	−0.595	ns
Fecundity	1.122	ns	−1.026	ns	0.597	ns	0.358	ns	−0.136	ns	−0.859	ns
SLA (n = 135)
Survival	−1.912	§	0.234	ns	−1.453	ns	−1.676	§	−1.03	ns	−2.434	‡
Growth	1.374	ns	0.454	ns	2.069	‡	1.039	ns	0.684	ns	1.535	ns
Fecundity	2.709	†	3.267	†	2.753	†	0.108	ns	0.167	ns	0.093	ns
Leaf N (n = 106)
Survival	−0.427	ns	0.405	ns	2.09	‡	0.807	ns	1.592	ns	1.615	ns
Growth	1.595	ns	0.127	ns	2.652	†	−1.388	ns	−1.999	‡	−2.19	‡
Fecundity	2.697	†	2.724	†	3.749	*	2.296	‡	2.274	‡	2.94	†

The Z and t values correspond to the standardized effect of traits on elasticities in the Dirichlet and PGLS regressions, respectively. Additional models were fit with growth form or biome included as a covariate. ns, not significant.

^*P ≤ 0.001.

^†P ≤ 0.01.

^‡P < 0.05.

^§P ≤ 0.1.

SLA and leaf N, two traits that represent fast leaf economics, were also associated with fast life histories. In Dirichlet regressions, both of these traits were positively related to the elasticity to fecundity. When we accounted for phylogenetic relationships with PGLS regression, the relationship with fecundity elasticities remained significant for leaf N but not SLA. These traits were only associated with elasticities to individual growth when we added growth form or biome covariates. We found a marginally significant negative relationship between SLA (but not leaf N) and elasticity to survival (P = 0.056), but this relationship was not significant when we added growth form and biome covariates.

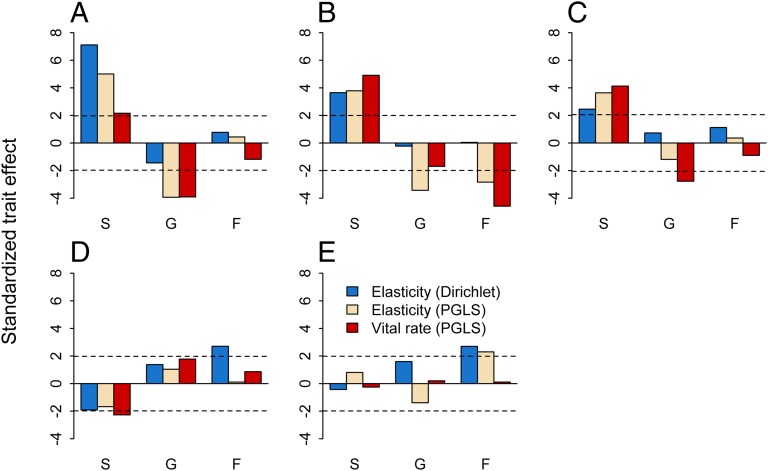
Relationships between functional traits and raw vital rates were often, but not always, consistent with relationships between traits and the elasticities of the vital rates. PGLS regressions of raw vital rates on functional traits showed that, in some cases, the trait–vital rate relationships were consistent with the trait–elasticity relationships (Fig. 2, Table 2, Fig. S3, and Tables S6 and S7). For example, increases in seed mass, wood density, and leaf lifespan led to significant increases in survival rates and elasticities to survival. However, in other cases, the trait–vital rate relationships were inconsistent with the trait–elasticity relationships: SLA and leaf N were unrelated to fecundity rates but significantly associated with elasticities to fecundity. Overall, when functional trait–vital rate relationships were significant, the corresponding trait–elasticity relationships were significant as well, but strong functional trait–elasticity relationships occurred when the corresponding functional trait–vital rate relationships were weak.

Fig. 2.

Comparison of functional trait effects on vitals rate and vital rate elasticities. The standardized effect size is the Z (Dirichlet regression) or t value (PGLS regressions) for the following functional traits: (A) seed mass, (B) wood density, (C) leaf lifespan, (D) SLA, and (E) leaf N. Vital rates are survival (S), growth (G), and fecundity (F). Trait–elasticity relationships were fit using both Dirichlet and PGLS regressions, whereas trait–vital rate relationships were fit using only PGLS regression. The dashed lines show statistically significant effects at α=0.05.

Table 2.

Statistical tests of functional trait effects on vital rates

	Functional traits only		Trait and growth form		Trait and biome
Vital rate	t	P	t	P	t	P
Seed mass (n = 193)
Survival	2.158	‡	2.078	‡	1.506	ns
Growth	−3.912	*	−2.094	‡	−2.874	†
Fecundity	−1.181	ns	−1.498	ns	−0.801	ns
Wood density (n = 72)
Survival	4.912	*	3.974	*	4.215	*
Growth	−1.695	§	−0.121	ns	−1.12	ns
Fecundity	−4.579	*	−4.458	*	−4.153	*
Leaf lifespan (n = 27)
Survival	4.127	*	3.217	†	2.945	†
Growth	−2.773	‡	−1.944	§	−1.28	ns
Fecundity	−0.896	ns	−2.044	§	−2.453	‡
SLA (n = 135)
Survival	−2.27	‡	−1.848	§	−1.322	ns
Growth	1.774	§	0.883	ns	1.878	§
Fecundity	0.866	ns	1.233	ns	1.499	ns
Leaf N (n = 106)
Survival	−0.25	ns	0.52	ns	0.404	ns
Growth	0.202	ns	−0.492	ns	−0.442	ns
Fecundity	0.108	ns	0.097	ns	0.366	ns

Standardized coefficients and significance tests for PGLS regression; t values correspond to the effect of functional traits on vital rates in single-factor and alternative models, in which growth form or biome was included as a covariate. ns, not significant.

^*P < 0.001.

^†P ≤ 0.01.

^‡P ≤ 0.05.

^§P ≤ 0.1.

Discussion

Our results show that global tradeoffs in plant functional traits translate into life history tradeoffs in predictable ways. Species that invest in a few large seeds have life history strategies that feature a higher influence of survival and a lower influence of individual growth and fecundity on population growth rates compared with species that produce small seeds. Species with faster leaf and wood economics also tend to live faster lives, with lower elasticities of the population growth rate to survival and higher elasticities to individual growth and fecundity. Although functional traits explained only a modest portion of the observed variability in vital rates and elasticities, our ability to detect any significant relationships is remarkable given the sources of variation inherent in our comparative approach. By using mean trait values for each species, typically measured in locations far from the site of the demographic observations, we ignored between-population variation in both functional traits (37, 38) and demography (39, 40). The fact that our crude approach successfully revealed links between functional traits and life history strategies indicates the strength of the underlying causal mechanisms.

An important question about these mechanisms remains unanswered. How can functional traits directly affecting only a limited set of physiological processes and demographic rates explain variation in overall life history? One possible explanation is that the affected processes (e.g., seed production and seedling performance in the case of seed mass) (32) are particularly important for fitness. However, the empirical evidence points in the opposite direction. Elasticity analyses typically show that, for long-lived perennial species, the survival rates of mature individuals have a much larger influence on fitness than the fecundity or survival of immature individuals (41). A more likely explanation is that the functional traits we examined and the processes that they influence coevolve with many other traits and processes that collectively determine life history. Seed mass may explain more variation in life history than SLA (Fig. 2) not because the processes that it influences are more important than the processes that SLA influences, but simply because seed mass is a better phenomenological indicator of a strategy coordinated across functions and life stages.

SLA may be a relatively poor indicator of life history strategy because of its plasticity. The dependence of SLA–elasticity relationships on phylogenetic correlations or growth form and biome covariates is consistent with previous studies showing that SLA explained less variation in demographic rates than wood density or seed size (18, 23) and that SLA values are variable and context-dependent (42, 43). We also found that SLA and leaf N had stronger relationships with elasticities to fecundity than growth, an unexpected result given the strong positive correlation between these traits and relative growth rates (1). The responsiveness of fecundity elasticities to these traits may indicate that increased relative growth rates, which reduce the time to reproductive maturity, have important consequences for reproduction, and it illustrates our hypothesis that functional traits influence life history through a complex set of coordinated processes.

Considerable gains in the predictive power of functional trait–elasticity relationships might be achieved simply by measuring functional traits and vital rates at the same times and locations. Another way to reduce unexplained variation would be to focus on species within particular growth forms or in different biomes. We included these covariates in our models to show that they were not driving the functional trait–demography relationships, but in many cases, they had significant independent effects (Tables S2–S7) and often improved our ability to detect functional trait effects. For example, adding biome as a covariate to the Dirichlet regressions changed relationships between growth elasticities and seed mass, SLA, and leaf N from insignificant to significant. Finally, future studies might explain more variation in vital rates and elasticities by basing predictions on multiple functional traits. Although we did not design our study with a multiple regression approach in mind, we had enough species with observations of both seed mass and SLA to permit an initial exploration. A simple linear regression of (logit-transformed) survival elasticities on seed mass had an R² of 0.19, whereas a multiple regression of the survival elasticities on seed mass and SLA increased the R² to 0.25.

Our second objective was to evaluate the use of raw vital rates for drawing inferences about the influence of traits on life history. Population ecologists have argued that, because fitness represents the net outcome of all vital rates, inferences about life history strategies cannot be based on field observations of any individual vital rate (44). We found partial support for this view. On one hand, the significance of relationships between functional traits and raw survival rates was always consistent with relationships between traits and survival elasticities. On the other hand, relationships between raw fecundity rates and SLA and leaf N were not significant, whereas relationships between these traits and fecundity elasticities were significant. For these fast leaf economic traits, reliance on raw vital rate data alone would have underestimated the influence of functional traits on life history.

By combining functional traits and population models, we were able to address long-standing questions about the influence of functional traits on fitness and life histories using quantitative methods developed in comparative demography. We found that previously documented trait–vital rate relationships extend to vital rate elasticities, linking traits directly with a comprehensive measure of individual fitness and validating a central assumption of trait-based ecology. Empirical evidence of strong associations between simple anatomical and morphological traits and life history strategies places trait-based approaches on a firm foundation and should promote applications of functional traits in population ecology. Ultimately, the functional trait approach may help us identify the anatomical and physiological bases of life history evolution, an important unsolved problem at the interface of ecophysiology, population ecology, and evolutionary biology.

Materials and Methods

Plant Functional Traits.

We obtained data on five commonly measured functional traits from TRY, a global repository of plant trait data (35): seed mass (milligrams), wood density (milligrams per millimeter³), leaf lifespan (months), SLA (millimeters² per milligram), and leaf N (milligrams per gram). We extracted functional trait data for any perennial plant species in TRY for which we had demographic data (see below). After removing duplicate functional trait observations and outliers (values greater than 3 SDs from the trait mean for each species), we calculated means for each functional trait observed for each species.

Vital Rates and Elasticities.

We obtained demographic information from the COMPADRE Plant Matrix Database (45) (www.compadre-db.org/), which contains projection matrices for over 500 plant species along with taxonomic and ecological covariates. These projection matrices summarize the underlying demographic processes (i.e., vital rates) that determine the population growth rate (λ), such as survival, changes in stage/size, seedbank and vegetative dormancy, clonal propagation, and sexual reproduction (27).

For each of 222 species that overlapped with the TRY database, we estimated the element-by-element mean matrix for all years and populations that were observed under control conditions (we excluded experimental treatments). If more than one matrix model was available for a given species, we chose the model with the greatest spatial and temporal replication. In the event that two models for the same species had equal spatial and temporal replication, we chose the one with the highest matrix dimension, because higher matrix dimension models offer a higher-resolution description of population dynamics (46). We ignored published studies where the matrix model did not include measures of fecundity, because the calculation of elasticities requires information on the whole lifecycle (27).

We decomposed the vital rates for each species into survival, fecundity, and growth, and we calculated the elasticities of λ with respect to these vital rates using equations 7–11 in ref. 30. This decomposition recognizes that the transition probabilities contained in individual matrix elements often represent more than one vital rate. For example, off-diagonal entries typically represent the probability of survival and progression or retrogression. Vital rates offer an insight on the actual population dynamics (i.e., rates of survival, growth, and reproduction), whereas elasticities provide the relative effect of those demographic processes on the population growth rate (47).

At first glance, measuring growth using matrix population models appears qualitatively different from measures of relative growth rate traditionally used in functional trait research, such as biomass (grams grams⁻¹ year⁻¹) or stem diameter (centimeters centimeters⁻¹ year⁻¹). Our measure of growth represents the average probability that an individual will transition from one size or stage class to another class over a unit time interval, which equaled 1 y in every case. In our dataset, these size and stage classes are defined in a wide variety of ways, such as the number of leaves, stem diameter, rosette diameter, height by age, and/or developmental stage. Regardless of how these sizes and stages are defined, the units of growth are identical and represent relative growth rate (individuals individuals⁻¹ year⁻¹). In fact, regardless of whether relative growth rates are defined in terms of biomass, stem diameter, or transition probabilities, the units are simply year⁻¹. An important advantage of quantifying growth with matrix models is that this approach accounts for size- or stage-dependent variation in relative growth rates. Although decisions about the number of size/stage classes to include may influence the raw growth rates (fewer classes means higher transition probabilities), the total elasticity to growth is not affected by matrix dimension and provides a dimensionless index of the effect of growth on fitness.

Because our demographic unit for comparisons was the genet (genetically identical individual), we lumped clonal propagation with individual progression/growth, retrogression/shrinkage, and vegetative dormancy. Changes in size affect sensitivities and elasticities in relation to the reproductive value of the size classes involved (e.g., growing from class x to x + 1 or retrogressing to x − 1). Positive and negative growth have the same net effect on the reproductive value of an individual of size x (27), but the sign of the effect depends on the direction of change (symmetry of equations 8 and 9 in ref. 30). We chose to quantify the effect of changes in size on population growth regardless of their sign rather than allow one direction to discount the other direction, which could create the unreasonable possibility of change in size having no influence on the population growth rate. Germination of seeds to seedlings within the annual period of seed production and contributions by the seed bank were included in fecundity.

Although vital rate sensitivities are useful for evaluating the contribution to population growth rate of both observed (i.e., positive) and hypothetically positive matrix coefficients (i.e., nonobserved transitions equal to zero) (48, 49), we do not present results for vital rate sensitivities, because their nonadditivity prevents clear comparisons among different vital rates. In addition, the biological relevance of hypothetical transitions is difficult to evaluate when dealing with numerous transitions for hundreds of species.

We did not include matrix dimension as a covariate, because although it is known to influence the summed elasticities of matrix elements (46, 50), it has a minimal effect on the summed elasticities of vital rates (51), giving us confidence that our estimates are robust. In addition, differences among species in matrix dimension often reflect real differences in life history. For example, matrices used to model trees are often larger than matrices used for shrubs or herbs.

Phylogeny.

We attempted to obtain the phylogeny for 222 species in our dataset using two methods: the tree generator based on National Center for Biotechnology Information taxonomy at iTOL (http://itol.embl.de/index.shtml) and phyloGenerator (52). However, GenBank does not contain information for most of the species in our dataset, and even if closely related species could be found in GenBank and used as temporary surrogates, the resulting tree proved difficult to resolve using the suggestions of phyloGenerator. Consequently, we resorted to running the species list with their recognized families in PHYLOMATIC v2 (53) (discontinued January 10, 2013; Phylomatic v3 is now at http://phylodiversity.net/phylomatic/). The resultant tree was then resolved manually in MESQUITE (http://mesquiteproject.org) using information from the Angiosperm Phylogeny Website (www.mobot.org/MOBOT/research/APweb/) and specific detailed studies of phylogenetic relationships within families referred to on the Angiosperm Phylogeny Website or found independently by us. Because not all genera in our dataset have been included in phylogenetic studies (many species lack DNA sequence information in GenBank), we also relied on recognized taxonomic differences based on morphological and phenotypic traits. Although this use of traditional taxonomy may seem arbitrary, the phylogenetic distance differences are small and do not alter the relationships observed, which we confirmed by conducting the analyses at different stages of construction of the final phylogenetic tree. Phylogenetic distances of the maximally resolved phylogenetic tree were interpolated using the bladj function of PHYLOCOM (54) with estimated node ages given in ref. 55.

Analysis.

We used Dirichlet regressions (56, 57) to accommodate the compositional nature of the vital rate elasticities (for each species, the elasticities to survival, growth, and fecundity sum to one), and we used PGLS regression to control for the lack of independence of species with shared ancestry. We found that PGLS regression, which ignores the compositional nature of elasticities, often showed significant trait–elasticity relationships when Dirichlet regression did not. For example, a strong relationship between wood density and survival elasticities inevitably leads to relationships with individual growth or fecundity elasticities that seem significant when considered independently. Therefore, we interpreted the results of the Dirichlet and PGLS regressions in a sequential manner. If the Dirichlet regression indicated a significant trait–elasticity relationship, we examined the PGLS to make sure that this effect was not simply the result of phylogenetic correlations. We fit second and third sets of models, in which we added growth form or biome as categorical independent variables. For wood density, the Dirichlet regression that included biome was overparameterized (the desert biome was represented by only one species). Therefore, we fit the wood density plus biome model after removing the desert singleton. To regress vital rates on functional traits, we used PGLS, as described above, after logit-transforming survival rates and log-transforming growth and fecundity rates.

We implemented Dirichlet Regression in R v.2.15.1 (58) using the package DirichletReg. We implemented PGLS regressions in R with the package ape (59). We used a Brownian motion model of evolution rather than the Ornstein–Uhlenbeck model, because in the very few cases where the results differed, the Brownian model was more conservative with respect to trait effects. For the PGLS regressions, we treated elasticities to survival, growth, and fecundity independently and logit-transformed them.