The Age Pattern of Increases in Mortality Affected by HIV: Bayesian Fit of the Heligman-Pollard Model to Data from the Agincourt HDSS Field Site in Rural Northeast South Africa

Abstract

Background

We investigate the sex-age-specific changes in the mortality of a prospectively monitored rural population in South Africa. We quantify changes in the age pattern of mortality in a parsimonious way by estimating the eight parameters of the Heligman-Pollard (HP) model of age-specific mortality. In its traditional form this model is difficult to fit and does not account for uncertainty.

Objective

1. To quantify changes in the sex-age pattern of mortality experienced by a population with endemic HIV. 2. To develop and demonstrate a robust Bayesian estimation method for the HP model that accounts for uncertainty.

Methods

Bayesian estimation methods are adapted to work with the HP model. Temporal changes in parameter values are related to changes in HIV prevalence.

Results

Over the period when the HIV epidemic in South Africa was growing, mortality in the population described by our data increased profoundly with losses of life expectancy of ~15 years for both males and females. The temporal changes in the HP parameters reflect in a parsimonious way the changes in the age pattern of mortality. We develop a robust Bayesian method to estimate the eight parameters of the HP model and thoroughly demonstrate it.

Conclusions

Changes in mortality in South Africa over the past fifteen years have been profound. The HP model can be fit well using Bayesian methods, and the results can be useful in developing a parsimonious description of changes in the age pattern of mortality.

Comments

The motivating aim of this work is to develop new methods that can be useful in applying the HP eight-parameter model of age-specific mortality. We have done this and chosen an interesting application to demonstrate the new methods.

1 Introduction

This work makes two contributions. The first is a detailed description of the likely impact of HIV on period-sex-age-specific, all-cause mortality as the HIV epidemic grows in a population living in rural northeast South Africa. This task is accomplished by reinterpreting the parameters of the eight-parameter Heligman-Pollard mortality model (Heligman and Pollard, 1980; Rogers and Gard, 1991; Gage and Mode, 1993; Congdon, 1993) and fitting it to age-specific probabilities of dying. The second is a Bayesian fitting procedure developed to produce robust fits of the Heligman-Pollard mortality model that yield probability distributions for the parameters, the age-specific probabilities of dying, and the other columns of the corresponding life tables.

Populations with high HIV prevalence in east and southern Africa have experienced dramatic increases in mortality (Dorrington et al., 2001; UNAIDS and WHO, 2009) and corresponding declines in life expectancy (UNAIDS, 2008). Because the primary modes of transmission of HIV in those populations are heterosexual sex and mother-to-child transmission at birth or through breastfeeding, the majority of HIV positive people are either very young children or sexually-active adults. Consequently there is a characteristic age pattern of deaths resulting from AIDS: very young children who progress through the disease quickly and middle-aged adults who are HIV positive for roughly ten years before dying of AIDS. Adult women living with HIV are typically several years younger than HIV positive men because women tend to have sex with slightly older men.

Using prospectively collected data from people of all ages in a population of roughly 69,000 living in rural northeast South Africa (Kahn et al., 2007, 2012), we look for these signature effects of HIV on sex-age-specific mortality through time. Because we expect to see important changes in child mortality and a well-defined ‘hump’ in the age pattern of mortality for adults, we summarize the age pattern of mortality using the eight-parameter Heligman-Pollard mortality model (Heligman and Pollard, 1980). This model decomposes the age pattern of mortality into three pieces, each with a small number of parameters to control it. There are three parameters to describe child mortality (A, B & C), three to describe a very flexible accident hump typically occurring in young adulthood (D, E & F) and finally two parameters to describe mortality at older ages (G & H). Recognizing that the ‘accident’ hump could just as easily represent the much larger bulge in the age pattern of mortality for adults dying of AIDS, we reinterpret this as the ‘AIDS’ hump and apply the model with this interpretation in the South African setting.

The Heligman-Pollard model is fit to age-specific mortality schedules describing different periods of the HIV epidemic to yield a time series of values for the parameters A-H. Because each parameter controls a specific component of the shape of the age pattern of mortality, the parameters have specific interpretations. As a result, the time series of parameter values describes changes in the age pattern of mortality in a succinct and informative way. For example, different values of D, E & F describe changes in the location, level and spread of the adult mortality hump as HIV becomes more prevalent.

The Heligman-Pollard model is a natural choice in this application, and consequently it is surprising that it has not already been used to describe HIV-related mortality.¹ The likely explanation is that it is hard to fit the Heligman-Pollard model using standard procedures such as minimization of squared errors (Rogers, 1986; Dellaportas, 2001). Our solution is to apply the Bayesian melding method (Poole and Raftery, 2000) that has the added advantage of properly quantifying uncertainty in the estimated parameters and the mortality age patterns output by the model. The resulting probability distributions of the parameters and mortality age patterns are used to argue that significant changes have occurred to the age pattern of mortality in ways that are consistent with the effects of HIV.

This paper is organized in the following way. We begin with the background and significance of the work and a review of the age-specific impact of HIV on mortality, followed by a detailed description of the data, model and Bayesian estimation procedure. We next describe the findings as well as make recommendations and detail future work in this area. Last, the Appendices contain the raw data and additional results.

2 Background & Significance

Our results contribute to a growing literature on the link between HIV prevalence and mortality. We identify age-specific increases in all-cause mortality that follow increases in HIV prevalence with a predictable lag. These results confirm our general understanding of how HIV epidemics work and corroborate and add to the specific findings of other researchers, briefly reviewed below.

2.1 Age-specific Effect of HIV on Mortality

The HIV virus attacks a person’s immune system, gradually wearing it down until it cannot control infections, or even itself. The result is a long period of infection and gradually worsening illness ending in death. Because of the long lag time between infection and death, the effect of HIV on mortality is observed several years after infection. In the absence of antiretroviral treatment, the time between infection and death for children is between five and ten years (Marston et al., 2005) and for adults about ten years (Jaffar et al., 2004; Morgan et al., 2002). The age pattern of the effect of HIV on mortality is determined by the age pattern of transmission and whether or not there is widespread use of antiretroviral drug therapy (Highly Active Anti-Retroviral Therapy, HAART) in the population. The common modes of transmission in high prevalence populations are heterosexual sexual intercourse and mother-to-child transmission at birth or during breastfeeding. Consequently, infections occur at or shortly after birth and at ages when people are most sexually active. Those ages vary from population to population but generally span the late teens through older adulthood, with peaks sometime in the twenties or thirties. Moreover, individual variation in sexual activity effectively protects a fraction of the population and creates a gradient of risk in the remaining fraction. The net result in a mature HIV epidemic in a population without widespread treatment is that the bulk of the at-risk portion of the population is infected soon after becoming sexually active, and as a consequence the effect of HIV on mortality is relatively concentrated at the youngest possible ages, about ten years after the average age at infection. Finally, because women typically pair with slightly older men, the average age at infection for women is usually several years younger than for men, and hence the mortality effect of HIV is slightly younger for women compared to men. In general this leads to an age-profile of HIV-related mortality that affects infants and young children, women roughly aged 25–50, and men roughly aged 30–60. Although there is a lot of variation in this general pattern, depending on the specifics of HIV transmission and whether or not HAART is available, this general sex-age-pattern of HIV mortality is commonly observed in populations with high prevalence (Porter and Żaba, 2004).

2.2 HIV & Mortality in sub-Saharan Africa

In sub-Saharan Africa the HIV epidemic affects all parts of the population stretching beyond high-risk groups and into the most rural communities (Poit et al., 2001). Rising HIV prevalence over the past 15 to 20 years has led to increases in child and adult mortality and dramatic decreases in life expectancy (Tollman et al., 1999; Hosegood et al., 2004). Our understanding of the role of HIV in shaping mortality in sub-Saharan Africa is supported by information from a wide variety of data, including both direct and indirect estimates of mortality. Indirect evidence on adult mortality from national and regional statistics, including censuses and sample surveys, provide an understanding of trends in mortality at national or regional levels (Blacker, 2004), while community-based and cohort studies offer more direct evidence on the role of HIV/AIDS by comparing the mortality experience of infected and non-infected individuals (Żaba et al., 2004, 2007).

Most of Africa does not have a functioning vital registration system that covers enough of the population to produce indicators that are either representative or accurate.² Instead, population censuses and sample surveys have become the main source of representative information on demographic trends. These data reveal consistent large increases in adult mortality, ₄₅q₁₅, since the early 1990s for many countries in sub-Saharan Africa (Blacker, 2004). Based on an analysis of sibling histories in Demographic and Health Surveys, Timæus and Jasseh (2004) report that by the year 2000 an average 15 year old person living in sub-Saharan Africa faced a probability of dying before age 60 of between 0.3 and 0.6, up from 0.1 to 0.3 during the 1980s.

An important limitation of these data is that they do not describe the causes of death. Nonetheless, they still provide strong evidence that HIV is largely responsible for the recent upswing in mortality rates. The sibling history study reported by Timæus and Jasseh (2004) reveals a sharp increase in adult mortality after countries develop a generalized (at least 1% of the population infected³) epidemic. Likewise, the United Nations (2004) report that in countries where adult mortality was either declining or stabilizing, HIV prevalence was 5% or lower, while countries with increasing mortality had prevalence between 7 and 33%. National-level data also suggest a strong effect of HIV on age-specific mortality. Blacker (2004) notes that an examination of the age pattern of mortality increases is useful in assessing the impact of HIV on adult mortality; specifically rapidly rising adult mortality that peaks at younger ages for women compared to men. Timæus and Jasseh (2004) note that the excess mortality they observe in the DHS data is concentrated at ages 25–39 for women and 30–44 for men.

Complementing the ability of census and survey data to describe macro-level trends in mortality, community-based studies that collect data on the HIV serostatus of participants can compare the mortality of infected and uninfected individuals. The age profile of the effect of HIV on mortality is determined by the stage of the epidemic, the age profile of incidence in the past and the average time between infection and death. Because community studies have the ability to track the survival times of infected individuals, they are one of the only sources of data able to provide average times between infection and death. Studies like this that have prospectively monitored cohorts of HIV positive people estimate survival times in the range 9–11 years for individuals infected in their 20s and shorter survival times for people infected at older ages (Porter and Żaba, 2004; Todd et al., 2007). Direct evidence from community-based studies provides the best understanding of the effect of HIV on the level and age pattern of adult mortality (see for example: Porter and Żaba, 2004; Groenewald et al., 2005; Adjuik et al., 2006; Nyirenda et al., 2007; Smith et al., 2007; Żaba et al., 2007; Marston et al., 2007). Data from health and demographic surveillance system (HDSS) field sites in Africa and Asia – all prospective community-level sites – identify seven age patterns of mortality, two of which likely reflect a substantial effect of HIV. Those two patterns have significant humps in the age pattern of mortality between ages 20 to 55 for males and 20 to 45 for females (Clark, 2002).

South Africa is experiencing one of the most rapidly progressing HIV epidemics in the world (Hosegood et al., 2004; Karim and Karim, 1999; Department of Health, Republic of South Africa, 2003). While there was virtually no HIV mortality at the beginning of the 1990s, by 2000 Dorrington et al. (2001) identify significant HIV-related mortality. Hosegood et al. (2004) report that AIDS was the most important single cause of death driving the steep increase in mortality rates in South Africa. As in other parts of sub-Saharan Africa, HIV prevalence among South African women is younger than among men, and the risk of dying from AIDS peaks at younger ages for women (25–39) compared to men (30–44) (Tollman et al., 1999; Hosegood et al., 2004; Groenewald et al., 2005).

HIV is also affecting child mortality in sub-Saharan Africa, and again there are few data to describe this effect. The data that do exist come largely from small hospital-based studies and population-based projects that estimate HIV-related child mortality rates (Żaba et al., 2004) using a variety of methods. Although the effect of HIV on under-five mortality varies broadly by region, the impact appears to be substantial in southern Africa where the worst affected countries are; in these populations HIV may be causing up to half of all child deaths (Newell et al., 2004). Some 90% of pediatric HIV infections occur in sub-Saharan Africa and because many HIV-infected children die before their fifth birthday, childhood mortality overall can be greatly elevated by HIV (Dabis and Ekpini, 2002; Foster and Williamson, 2000; De Cock et al., 2000). Given the high rates of transmission from mother to child, we expect that increases in HIV prevalence of adult women will increase child mortality. HIV may also indirectly affect child mortality through maternal HIV status because children of HIV infected mothers are more likely to die than those of uninfected mothers (Newell et al., 2004; Żaba et al., 2004).

Pertinent to the discussion of HIV related mortality in sub-Saharan Africa is the aggressive scale up by many countries of programs to make highly active antiretroviral therapy available to adults living with HIV around the turn of the century (UNAIDS, 2012). The figures described above refer mostly to the pre-HAART era. Since wide dissemination of treatment began, many populations have regained some lost years of life expectancy as the cause of death for some seropositive individuals shifts to non-HIV-related causes (Crum et al., 2006; Palella et al., 2006; UNAIDS, 2012), which contribute to mortality at higher ages. Complementing treatment programs, concerted efforts to reduce mother to child transmission and new infections among children have also contributed to a decline in overall HIV-related mortality (UNAIDS, 2012).

3 Methods & Data

3.1 The Heligman-Pollard Mortality Model

We use the Heligman-Pollard mortality model (Heligman and Pollard, 1980) to assess mortality at all ages over a 14-year period, below in equation 1. This model expresses the probability of dying as a function of age using a three-term expression that covers the entire age range.

$$q_x=A^{{(x+B)}^C}+D\times e^{-E{(ln(x)-ln(F))}^2}+\frac{{GH}^x}{1+{GH}^x},$$ (1)

where x indexes age⁴, q_x is the probability of death at age x, and A, B, C, …, H (see Table 1) are eight variable parameters that govern the shape of the mortality curve⁵

Table 1.

Heligman-Pollard Parameters

Parameter	Description
A	Level of child mortality, approximately the probability of dying between ages 1 and 2, 1q1
B	Difference between age 0 and 1 mortality probabilities
C	Decline in mortality during childhood
D	Level (or height) of mortality hump
E	Inversely related to the width of the mortality hump
F	Location of the mortality hump on the age axis
G	Late life mortality, intercept of Gompertz curve at age 0
H	Late life mortality, slope of of Gompertz curve

Compared to non-parametric alternatives, the advantages of parametric models like the Heligman-Pollard are: 1) the ability to produce smooth curves, 2) the ability to interpolate and to extrapolate, 3) the possibility of formal manipulation, 4) parsimony, 5) interpretable parameters whose values can be compared easily and 6) the ability to easily capture and reflect trends and mediate comparisons (Dellaportas, 2001; Debón et al., 2005). These last two advantages, along with the ability of parametric models to succinctly summarize large amounts of data, are especially useful to us. The representation of mortality trends via parametric methods facilitates a time-series approach whereby the shape and intensity of age-specific mortality curves can be summarized and compared over time (Debón et al., 2005; Congdon, 1993; Rogers and Gard, 1991; Hartmann, 1987).

The Heligman-Pollard model has been used to document changes in mortality in a variety of contexts (see for example: Heligman and Pollard (1980); Dellaportas (2001); Debón et al. (2005); Congdon (1993); Forfar and Smith (1987); Hartmann (1987); Rogers (1986)). In their original paper Heligman and Pollard (1980) describe Australian mortality over the 20th century, and Rogers and Gard (1991) document declining infant and young adult mortality over the 20th century in the U.S. There are few examples of this type of use for the Heligman-Pollard mortality model in the developing world, and we cannot find a previously published example of the Heligman-Pollard mortality model being used to characterize mortality schedules affected by HIV over time.

Although originally conceived to capture the slight rise in mortality from accidents occurring in the late teens and early adult years, the so-called ‘accident’ hump contained in the Heligman-Pollard mortality model is flexible enough to represent the much larger bulges in adult mortality brought about by AIDS deaths. The ability of the Heligman-Pollard to reflect levels of mortality at all ages and in particular to characterize the level and shape of adult mortality make it well suited to assess the increasing intensity of adult mortality over the 1990s and 2000s in sub-Saharan Africa. Moreover, because the model parameters have straightforward demographic interpretations (e.g. describe not only the level but also the shape and location of adult mortality) we can easily link the parameter changes to lagged HIV prevalence to begin understanding of specific effects of HIV on mortality.

The eight parameters of the Heligman-Pollard model control three separate additive components corresponding to three age ranges of the mortality schedule (child mortality, young adult mortality and late life mortality), and each parameter has a demographic interpretation (Heligman and Pollard, 1980; McNown and Rogers, 1989; Rogers and Gard, 1991). Figure 1 displays each of the components and the sum of all three, i.e. the final curve.⁶Table 1 provides interpretations for the parameters, and the eight panels of Figure 2 illustrate the effect of each of the parameters individually. Each panel plots the modeled mortality schedule with variation in a single parameter while holding the others constant.

Figure 1.

Decomposition of the Heligman-Pollard Model.

Figure 2. Variation Plots for the Heligman-Pollard Mortality Model.

_nq_x refers to the probability of death in the interval x to x + n. Each panel plots the age-specific probabilities of death when varying a single parameter value in the HP model while holding all others constant. For the plots of parameter E and F, D is set to .04 to give sufficient intensity to the hump.

The first three A, B & C control the first component and describe early child mortality. A roughly approximates mortality at age one and can be taken as a measure of the intensity or level of child mortality (McNown and Rogers, 1989; Rogers and Gard, 1991; Hartmann, 1987). B is the age displacement variable (Rogers and Gard, 1991) and reflects the difference between mortality at ages 1 and 0. As the value of B increases, ₁q₀ decreases below 0.5 and begins to approach ₁q₁ (Rogers and Gard, 1991). Finally, C indicates how quickly mortality decreases during childhood and into the young adult years. Parameters A, B & C all have domain (0, 1). Declines in A are consistent with decreasing child mortality (Hartmann, 1987). Because the potential direct impact of pediatric AIDS deaths and the indirect impact of adult AIDS mortality on child mortality, we expect the level of child mortality to increase from period to period leading to increases in A for both sexes as time goes on and the HIV epidemic grows.

The second component of the model is designed to reproduce the ‘accident’ hump in many male mortality schedules, and possibly maternal mortality in female mortality schedules (Heligman and Pollard, 1980; Hartmann, 1987; McNown and Rogers, 1989; Rogers and Gard, 1991). When it reflects accidents, the hump peaks in the (early) twenties. We reinterpret the hump to reflect AIDS mortality at young and slightly older adult ages, so in our use the peak is older and taller. Parameter D controls the level or intensity of young adult mortality, E is inversely related to the spread of the hump and F locates its position along the age axis (Heligman and Pollard, 1980; McNown and Rogers, 1989; Rogers and Gard, 1991). Parameters D and E have domains (0, 1) and (0, ∞) respectively, while the domain of F is less clear. We restrict F to the domain (15, 55) because we do not expect a large number of AIDS deaths at ages older than 55. With the hump reflecting AIDS mortality, we expect increasing levels of adult mortality for both sexes as time progresses, i.e. increases in D. As the epidemic matures we also expect a broadening and aging of the adult mortality hump, i.e. decreases in E and increases in F. Note that if D is sufficiently small the other two parameters controlling this component of the curve have no influence. Inspecting Equation 1 and the panel for parameter D in Figure 2, one can see that the second component of the model is composed of the product of D and the effects of E and F, so a small D essentially negates the effect of the spread and location parameters.

The last two parameters control the late life mortality section of the curve and describe the steep increase in mortality at those ages.⁷ Parameter G measures the base level of mortality at these ages (x = 0) and H defines the rate of increase (Rogers and Gard, 1991). Parameters G and H are the intercept and slope of the Gompertz curve respectively and take domains (0, 1) and (0, ∞) respectively.

The aim is to identify values for the eight parameters that produce a curve that matches a set of mortality measures at various ages. The set of eight parameter values is then the compact, interpretable description of mortality that we want, and the curve they represent is a smoothed version of the empirical data.

3.2 Data

We use data describing mortality and HIV prevalence. Mortality data come from the Agin-court health and demographic surveillance system (HDSS) site in South Africa (Kahn et al., 2007). The site is located in a rural area of Mpumalanga Province in the northeast of South Africa where HIV prevalence is a little less than 30% (Department of Health, Republic of South Africa, 2006). Using time-sex-age-specific counts of deaths and person years for the period 1994–2007, we compute time-sex-age-specific probabilities of dying (_nq_x) using standard life table methods. Our estimation procedure requires the denominator in the probability of dying (l_x) to have approximately the same scale as the empirical data.⁸ This requires us to rescale the l_x column of the life table, and we do this using MS Excel’s ‘solver’ utility to find a value for l₀ that yields the same total number of person years T₀ in the life table as there are in the observed data.

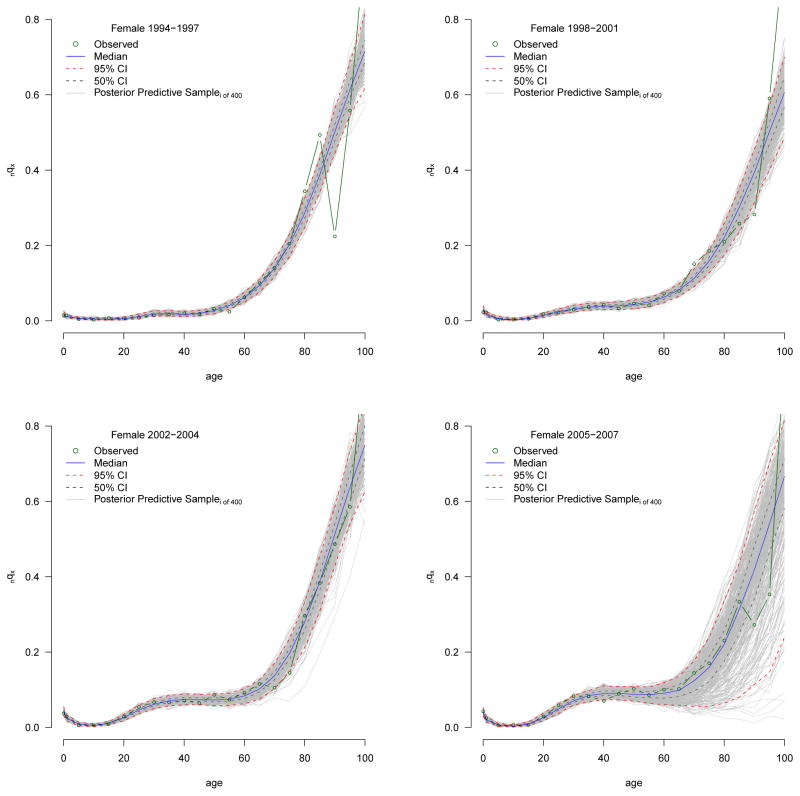
Because the annual data contain few deaths and are rather ‘noisy,’ we aggregate across time. Periods are chosen to contain years with similar mortality rates and to capture as much variability in the age pattern of mortality as possible. The four periods we use are: 1994–1997 ( $l_0^{\mathit{male}}=1,917,l_0^{\mathit{female}}=1,873$), 1998–2001 ( $l_0^{\mathit{male}}=2,100,l_0^{\mathit{female}}=2,049$), 2002–2004 ( $l_0^{\mathit{male}}=1,896,l_0^{\mathit{female}}=1,822$) and 2005–2007 ( $l_0^{\mathit{male}}=1,974,l_0^{\mathit{female}}=1,893$). Figure 3 displays the aggregated and rescaled mortality schedules for males and females. Appendix A lists the data as used in our analysis and Appendix F details the process for aggregating into these periods.

Figure 3. Age Pattern of the Probability of Dying, Agincourt 1994–2007.

_nq_x refers to the probability of death in the interval x to x + n

Data describing the trend in HIV prevalence in Mpumalanga Province are taken from reports published by the South African Department of Health (1995; 1996; 1997; 1998; 2003; 2006). For the most part these estimates are made using anonymous HIV test results from pregnant women who attend antenatal clinics. See section 3.4 for further description on this data source. Antiretroviral therapy become available in this population starting in 2007, and as of this writing coverage is still not complete (Gómez-Olivé et al., 2013).

3.3 Bayesian Melding Estimation

We now turn to the Bayesian method used for parameter estimation. Bayesian melding searches the joint parameter space for sets of parameter values that are most likely given the data and what we know beforehand about the typical values for the parameters and the age patterns of mortality that we are modeling. Instead of identifying just the one most likely set of parameter values, it finds the most likely region of the parameter space and returns the sets of parameter values in that region. Each set of parameter values is associated with a probability corresponding to how well it reflects the data. These probabilities are used to construct joint distributions of the parameter values, which allow us to draw inferences about and characterize uncertainty around the parameter estimates themselves and the mortality patterns they represent.

The following discussion of Bayesian melding is adapted from Clark et al. (2012). For a detailed discussion of Bayesian Melding see Poole and Raftery (2000). In the Bayesian framework parameters are treated as random variables. Prior beliefs about the parameters are quantified in the form of a joint probability density p(θ), where θ is a vector of parameters for which we will make inference. The data y are brought in by specifying a likelihood (y|θ), which is the probability of the observed data for a given value of the parameter vector. Our data are counts of deaths and persons at risk of dying in each time-sex-age cell. We use the binomial likelihood because the observed _nq_x are probabilities describing a binary outcome (see appendix G for a full specification of the likelihood). Bayesian melding (Poole and Raftery, 2000) is designed for problems in which a deterministic model – such as the Heligman-Pollard mortality model – is used in the likelihood function. Let M represent the model which transforms a set of parameter inputs θ into a set of model outputs φ = M(θ). The prior density for the model inputs p(θ) and a likelihood for the outputs and the data (M(θ)) are combined to produce the posterior distribution for the model inputs. Using Bayes’ Theorem and the marginal density of the data p(y), we can update our prior beliefs to obtain the posterior distribution⁹

$$p(\theta \mid \mathbf{y})\propto \mathcal{L}(\mathbf{y}\mid M(\theta ))p(\theta )$$ (2)

which is used to make inference for θ.

In our analysis of the Heligman-Pollald mortality model, we specify independent uniform priors that are intended to be fairly uninformative, placing most of the influence with the observed data. With these priors, our aim is to exert as little influence as possible on the parameter outputs while keeping the parameter output values in plausible ranges. The prior distributions are

$$\begin{array}{lll}A~U[0,0.25]\hfill & D~U[0,0.25]\hfill & G~U[0,0.01]\hfill \\ B~U[0,1]\hfill & E~U[0,20]\hfill & H~U[1,1.5]\hfill \\ C~U[0,1]\hfill & F~U[15,55].\hfill & \hfill \end{array}$$

Inference is performed by sampling from p(θ|y) and summarizing the resulting posterior sample. We can evaluate the model for each set of inputs in the posterior sample to obtain a posterior sample of the model outputs p(φ|y). Note that the posterior sample reflects the distribution of model outputs, and thus the quantiles of the posterior sample can be used to make probabilistic statements about the values of the model outputs (q_x).

In this analysis, we use the Incremental Importance Sampling Algorithm (see appendix H for a discussion of IMIS) to sample 400 sets of parameter values in the final resample from the posterior distribution, which can then be used to calculate 400 separate _nq_x schedules, each covering the whole age range. The result is an approximation of the posterior distribution of _nq_x values, i.e. a distribution of the probabilities of dying, not the number of deaths, which is what we used in the likelihood, and therefore what we want. To produce a predicted distribution of the number of deaths that we can compare to the data, we simulate death counts from the posterior distribution of _nq_x values. This is accomplished using the binomial distribution with the observed number of people at risk of dying and an _nq_x value sampled at random from the posterior distribution of _nq_x. The number of deaths is then divided by the number of people at risk of dying to produce a predicted _nq_x value. This procedure is repeated many times to yield a distribution of predicted _nq_x values. Figure 4 plots the _nq_x values simulated from the posterior output distribution for the first (flat hump) and the last (more intense and concentrated hump) periods for males. The gray clouds are the simulated _nq_x values. This figure shows how the simulated, predicted _nq_x values cluster around the observed age-specific death probabilities and that this model can closely fit _nq_x schedules at the beginning and peak of the HIV epidemic. Appendix D presents the prior and posterior densities for each parameter by sex and year.

Figure 4. Predictive Distributions of Male Age-Specific Probabilities of Dying for Flat Hump (‘94–97) and Intense Hump (‘05–07) Periods.

_nq_x refers to the probability of death in the interval x to x + n

In our application, the Bayesian melding approach has important advantages compared to common alternative estimation procedures. The Heligman-Pollard model is usually fit using least squares methods, but because the number of parameters (eight) is large in comparison to the number of data values in a typical age pattern of mortality (20), the model is on the verge of being over-parameterized (Bebbington et al., 2007; Dellaportas, 2001; Congdon, 1993). Dellaportas (2001) use a different Bayesian approach and reports that the over-parameterization issue is usually resolved by using informative priors (Congdon, 1993). Even with our relatively uninformative priors, the Bayesian approach solves this problem. One way to assess over-parameterization is to examine the correlation between parameters. We present pairs plots for each sex/year combination in Appendix C. The parameters are essentially uncorrelated except G and H, and the correlation of G and H is expected since they act together as a product.

Another difficulty in estimating the Heligman-Pollard model occurs when adult mortality is somewhat flat and the estimated hump parameters can take values beyond a plausible range (Rogers and Gard, 1991; Hartmann, 1987; Heligman and Pollard, 1980). In this case, the level parameter D may be large and the location parameter F on order 100, essentially creating a very broad, flat hump whose upswing merges into the natural rise in mortality at older ages. Fixing one or more parameters and estimating the others tends to resolve this problem (Congdon, 1993; Rogers and Gard, 1991; Hartmann, 1987). Instead, we let all the parameters vary simultaneously while restricting the range on parameter F to between 15 and 55, which keeps the hump parameters in plausible ranges and prevents the hump from merging into old-age mortality.

3.4 Relationship between Parameters and HIV Prevalence over Time

We investigate the temporal relationship between trends in the values of the Heligman-Pollard parameters and HIV prevalence. For each sex we plot the median value of the parameter distributions for parameters A, D, E and F by the mean HIV prevalence in Mpumalanga Province with a five-year lag, Figure 11. We expect increases in HIV prevalence to be followed by increases in both child and adult mortality, so there should be a positive relationship between both child and adult mortality and the level parameters A and D. Additionally we expect the spread and location parameters E and F to reveal changes in the general age structure of adult mortality affected by HIV. Table 4 presents the mean HIV prevalence levels for the relevant five-year lagged periods.

Figure 11. Selected Parameter Values by 5-year Lagged HIV Prevalence.

(OLS regression line in dashed grey).

Table 4.

Life Expectancy for Agincourt and HIV Prevalence for Mpumalanga Province

Period	Male e0a	ΔMaleb	Female e0a	ΔFemaleb	Prev.c	ΔPd	Prev. Period
1994–1997	67.3 (65.2 – 72.0)	—	73.5 (72.0 – 74.9)		1.3	—	1990–1992
1998–2001	63.0 (61.3 – 65.4)	−4.3	69.7 (67.8 – 71.8)	−3.8	11.6	10.4	1993–1996
2002–2004	53.5 (51.6 – 55.4)	−9.5	59.7 (58.1 – 61.9)	−10.0	26.6	15.0	1997–1999
2005–2007	52.2 (50.6 – 54.4)	−1.4	59.4 (56.4 – 64.8)	−0.4	29.2	2.5	2000–2002
Total Change:		−15.2		−14.2		27.9

^ae₀ in years. 95% credible intervals for e₀ in parentheses.

^bΔ(Male, Female) is change in median e₀ from previous period.

^cHIV prevalence is for the surrounding province (Mpumalanga) for all ages in period roughly five years before period in which e₀ is estimated. Source for prevalence estimates: Department of Health, Republic of South Africa 1995; 1996; 1997; 1998; 2003; 2006.

^dΔP is change in HIV prevalence from previous period.

3.5 Calculating Uncertainty around Life Table Columns

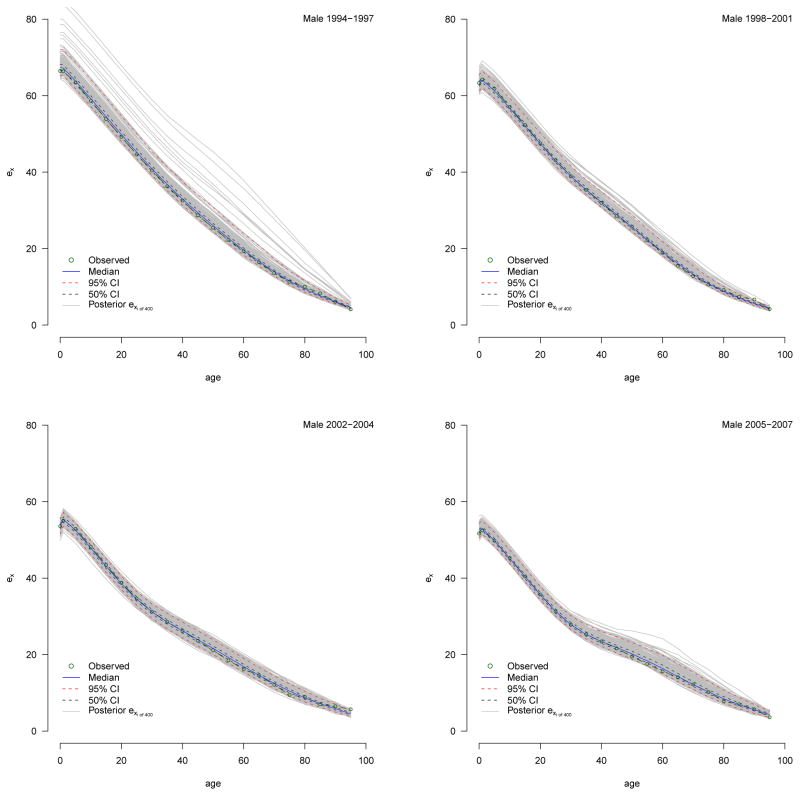
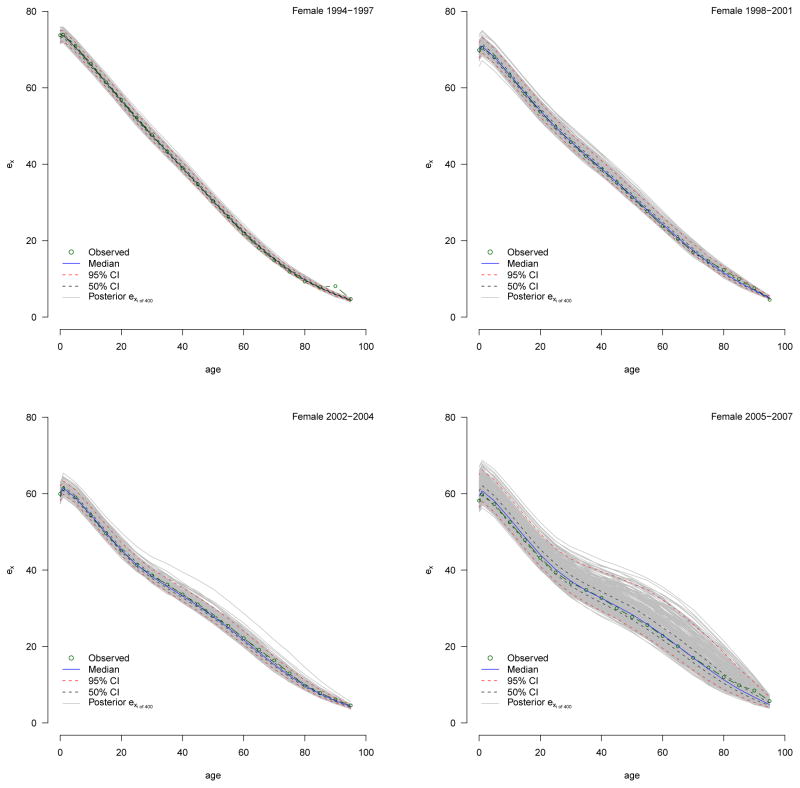
An advantage of the Bayesian approach is the ability to estimate uncertainty bounds around both the model parameters and the outputs. Following a similar method advanced by Lynch and Brown (2005), we exploit this to generate uncertainty bounds around the other columns of a standard life table, in particular around the life expectancy, e_x, schedules.

For each period and sex the predictive _nq_x distributions, shown in Appendix B, contain 400 individual _nq_x schedules from which we calculate a ‘distribution’ of 400 individual life tables. We present the median e_x distributions in Figures 12 and Appendix C and the median e₀ and e₁₀ with measures of uncertainty summarized from their distributions in Tables 4 and 6. We use these to make statistically valid statements about changes in the expectation of life.

Figure 12.

e_x Schedule Predictive Distribution with Median and 95% CI.

Observed data are represented as lightly colored dots.

Table 6.

Life Expectancy at Birth and Age 10

Period	e0a	Δe0b	e10a	Δe10b
MALE
1994–1997	67.3 (65.2 – 72.0)	—	59.2 (57.2 – 64.2)	—
1998–2001	63.0 (61.3 – 65.4)	−4.3	56.8 (55.0 – 59.4)	−2.5
2002–2004	53.5 (51.6 – 55.4)	−9.5	47.9 (46.1 – 49.8)	−8.9
2005–2007	52.2 (50.6 – 54.4)	−1.4	45.1 (43.8 – 47.4)	−2.7
Total Change:		−15.2		−13.1
FEMALE
1994–1997	73.5 (72.0 – 74.9)	—	66.0 (64.7 – 67.3)	—
1998–2001	69.7 (67.8 – 71.8)	−3.8	63.4 (61.8 – 65.6)	−2.6
2002–2004	59.7 (58.1 – 61.9)	−10.0	54.5 (53.1 – 56.5)	−9.0
2005–2007	59.4 (56.4 – 64.8)	−0.4	53.4 (50.4 – 59.0)	−1.0
Total Change:		−14.2		−12.6

^ae_x in years. 95% credible intervals for e_x in parentheses.

^bΔe_x is change in median e_x from previous period.

4 Results

Figure 7 displays the period-specific fits, each period in a different color. For each period the light-colored dots in the background are the observed data, the solid lines are the median fitted curves and the dashed lines define the 95% credible interval around the median, which are not required to be symmetric. The radical increases in age-specific mortality are obvious: massive increases for infants and very young children and for adults aged roughly 15–65. The increases are not uniform with age and peak for men in the early 40s and for women slightly younger. The corresponding decreases in life expectancy are listed in Table 4: men lost fifteen years of life expectancy, and women lost fourteen. The substantive objective of this work is to decompose these changes into their constituent parts and relate those parts to changes in HIV prevalence¹⁰.

Figure 7. Age-specific Probability of Dying by Period for Agincourt.

Median fitted curves (solid lines) with 95% credible intervals (dashed lines). Observed _nq_x values in light-colored dots. _nq_x refers to the probability of death in the interval x to x + n.

Table 5 presents the median parameter estimates and 95% credible intervals. Figure 8 plots the estimated values of parameters A, D, E and F over the four periods in our study. The vertical dashed lines in this figure are the credible intervals around each point estimate.

Table 5.

Heligman-Pollard Parameter Estimates (95% CI)

	1994–1997	1998–2001	2002–2004	2005–2007
MALE
A	0.0106 (0.0059 – 0.0148)	0.0297 (0.0228 – 0.0365)	0.0460 (0.0390 – 0.0529)	0.0262 (0.0194 – 0.0321)
B	0.7829 (0.6673 – 0.8979)	0.9724 (0.9248 – 0.9980)	0.9652 (0.8928 – 0.9981)	0.7754 (0.6930 – 0.8609)
C	0.0855 (0.0320 – 0.1501)	0.1791 (0.1149 – 0.2336)	0.3526 (0.2801 – 0.4191)	0.2083 (0.1573 – 0.2589)
D	0.0243 (0.0160 – 0.0327)	0.0388 (0.0324 – 0.0445)	0.0726 (0.0618 – 0.0836)	0.1199 (0.1062 – 0.1338)
E	5.2779 (3.4764 – 7.1116)	4.5021 (3.0783 – 5.6768)	3.1653 (1.5618 – 4.6151)	3.7761 (2.9309 – 4.6871)
F	45.2412 (41.4002 – 49.0394)	38.5225 (36.3215 – 40.5921)	39.5636 (35.6854 – 43.7599)	42.2610 (39.0647 – 44.7113)
G	0.0010 (0.0003 – 0.0017)	0.0006 (0.0003 – 0.0009)	0.0021 (0.0010 – 0.0034)	0.0009 (0.0004 – 0.0015)
H	1.0798 (1.0725 – 1.0872)	1.0877 (1.0822 – 1.0939)	1.0717 (1.0630 – 1.0805)	1.0827 (1.0772 – 1.0887)
FEMALE
A	0.0148 (0.0118 – 0.0181)	0.0275 (0.0227 – 0.0334)	0.0422 (0.0382 – 0.0473)	0.0356 (0.0305 – 0.0417)
B	0.7852 (0.7047 – 0.8732)	0.9305 (0.8589 – 0.9942)	0.9792 (0.9520 – 0.9985)	0.8563 (0.8085 – 0.9027)
C	0.1048 (0.0697 – 0.1409)	0.2120 (0.1621 – 0.2568)	0.2245 (0.2065 – 0.2447)	0.2373 (0.2064 – 0.2669)
D	0.0126 (0.0083 – 0.0167)	0.0303 (0.0266 – 0.0348)	0.0688 (0.0642 – 0.0733)	0.0867 (0.0808 – 0.0930)
E	14.5269 (13.0611 – 15.8447)	2.6527 (1.9731 – 3.3408)	2.5174 (2.1914 – 2.8271)	2.5266 (2.0314 – 3.1009)
F	31.1959 (28.1650 – 34.0361)	36.5381 (34.0823 – 39.2770)	38.1891 (37.0759 – 39.2378)	40.6617 (38.9361 – 42.2265)
G	0.0003 (0.0002 – 0.0004)	0.0003 (0.0002 – 0.0004)	0.0001 (0.0000 – 0.0001)	0.0001 (0.0000 – 0.0002)
H	1.0958 (1.0904 – 1.1019)	1.0900 (1.0824 – 1.0972)	1.1110 (1.1049 – 1.1170)	1.1092 (1.0976 – 1.1174)

Figure 8.

Estimated Values for Parameters A, D, E, F by Sex and Time.

4.1 Goodness of Fit

Before discussing the parameters themselves, we assess goodness of fit by calculating the percentage of data points contained within posterior credible intervals of varying lengths. Tables 2 and 3 contain the percentage of data points contained in the 50, 80, 90, 95, and 99 percent posterior credible intervals in three age ranges 15–60 (adult mortality), 0–60, and 0–95 for males and females respectively. For each CI we should expect about the same percentage of data points to be contained within the interval. For virtually all years and both sexes, all of the data points in the adult ages are contained within the 99% CI with roughly 90 percent of data points in this age range in the 90 and 95% CIs. Adding in the childhood ages (rows labeled ‘0–60’) and oldest ages (rows labeled ‘0–95’) we see the model again does a good job of fitting these data for both sexes and all periods.

Table 2.

Percentage of data points covered in 50, 80, 90, 95 and 99% posterior credible intervals, Male

Ages	50% CI	80% CI	90% CI	95% CI	99% CI
Male (94–97)
15–60	50	80	90	90	100
0–60	50	71	79	86	100
0–95	48	67	71	86	100
Male (98-01)
15–60	50	90	90	90	100
0–60	50	86	86	86	100
0–95	43	76	81	81	90
Male (02–04)
15–60	60	90	90	90	100
0–60	57	86	86	86	93
0–95	48	71	81	81	86
Male (05–07)
15–60	50	80	90	90	100
0–60	50	79	86	86	100
0–95	43	76	86	90	100

Table 3.

Percentage of data points covered in 50, 80, 90, 95 and 99% posterior credible intervals. Female

Ages	50% CI	80% CI	90% CI	95% CI	99% CI
Female (94–97)
15–60	40	90	90	90	90
0–60	36	93	93	93	93
0–95	33	76	81	81	81
Female (98-01)
15–60	50	70	100	100	100
0–60	43	57	93	100	100
0–95	38	48	76	81	90
Female (02–04)
15–60	60	90	90	90	100
0–60	50	86	93	93	100
0–95	48	81	86	90	100
Female (05–07)
15–60	50	60	80	90	100
0–60	50	64	86	93	100
0–95	52	76	90	95	100

Numerous other parametric forms for the shape of human mortality have been proposed (Gage and Mode, 1993; Wood et al., 2001), so in addition to showing how well the Heligman-Pollard model fits these data, we might also wish to know how well the HP model fits compared to other well-known parametric forms. We fit the four periods for both sexes with two other parametric models (using maximum likelihood), Gompertz-Makeham (Gompertz, 1825; Makeham, 1860) and Siler (Siler, 1979, 1983), and show those fits with the median HP fit. Figures 5 and 6 plot these fits for all four periods. These plots make clear that the HP is able to best replicate all-age mortality in the presence of high HIV prevalence. During the first two periods when mortality is relatively flat in the adult years, all models do relatively well, but when the AIDS hump begins to grow, the other models do not have have the flexibility of the HP model with its three parameters governing the adult hump, and consequently they miss the hump altogether.

Figure 5.

Median HP fit and maximum likelihood fit for Gompertz-Makeham and Siler models to Agincourt data: Female

Figure 6.

Median HP fit and maximum likelihood fit for Gompertz-Makeham and Siler models to Agincourt data: Male

4.2 Child Mortality

The increase in child mortality during the period when the HIV epidemic grows is reflected by increases in parameter A which is roughly the probability of dying between ages one and two, ₁q₁. The upper-left panel of Figure 8 displays a clearly upward trend in the value of parameter A for both male and female children. A quick visual comparison of the credible ranges (dashed vertical line in figure 8) reveals unambiguous increases in parameter A during the first two intervals and a possible decrease during the last interval.

4.3 Adult Mortality

Parameters D, E, F, G and H control adult mortality. We focus on D, E and F because they control the hump while G and H define underlying adult mortality. The plots in Figure 8 reveal striking changes in the hump parameters (upper right and lower two panels). The level parameter D increases significantly over all three intervals for both sexes except during the first interval for males with little to no overlap in the credible intervals from one period to the next. Figures 9 and 10 plot the period-sex-specific hump component of the model in isolation without the other components of the mortality schedule. Figure 9 plots the hump for each sex by period and clearly reveals the growth in the hump from period to period. Figure 10 displays the hump curves with the male and female humps in a single plot for each period, so that the sexes can be compared easily. This figure confirms that although men appear to have slightly higher humps in all periods, the differences between the sexes are small and insignificant except for the last period when women have a substantially lower hump. These movements in parameter D relate directly to the growth of the mortality bulge observed for adults, and the highly regular and significant changes (i.e. non-overlapping credible intervals) demonstrate how large and important the increases in adult mortality have been.

Figure 9.

Hump Component for All Periods and Both Sexes.

Figure 10.

Hump Component for Each Sex for Each Period.

Trends in the width parameter E (inversely related to the width of the hump) indicate that over time the hump has become significantly wider for women and somewhat wider for men, with both converging to a fairly wide configuration and staying that way. The exceptionally high value of the width parameter for women in the first period is picking up a slight but concentrated increase in mortality in the late 20s to early 30s, possibly reflecting the earliest and youngest HIV incidence for women. Although the credible intervals overlap for all periods after the initial period, both sexes experience a slight broadening of the hump as time progresses.

Changes in the location parameter F (location of the hump on the age axis) reveal that the hump has steadily become older for women and became younger and then older again for men. Figures 8 and 10 suggest that the hump is typically slightly older for males; i.e. the male humps usually peak at slightly older ages regardless of the height or spread of the hump. This is especially pronounced during the first period when the mortality effects of HIV are first being observed. Recall that women tend to be infected with HIV at younger ages compared to men and so have high mortality at younger ages. The location parameter accurately reflects this previously observed pattern with the male median estimate of F consistently outpacing the female estimate. Women experience increasing mortality during their 30s (reflecting a female incidence profile that starts infecting a significant number of women in their early 20s) while for men the hump grows from the late 30s to the mid 40s. The unusually large value of the location parameter in the first period for men probably results from a small increase in mortality around the late 40s to early 50s. Because this is the first period, it is unlikely that this small hump is a result of HIV-related deaths. Rather, HIV probably begins to affect the male mortality schedule between the first and second periods, at which time the location and level parameters begin to pick up increasing male mortality in the late 30s, consistent with previously observed HIV mortality patterns. Changes in the hump for men are seen best in figure 9; clearly between the first and second periods the male hump increases slightly in intensity and shifts back to the expected age range.

Comparing humps from the last two periods with those from the first two, two things are clear: 1) the hump becomes taller reflecting the increases in the level parameter, D, and 2) the humps broaden as the width parameter, E, decreases. The widening of the humps is asymmetric with the bulk of the changes happening at older ages (35+) where the hump appears to flatten out. These changes reflect the spreading of increased adult mortality into the older middle adult ages, 35–45, likely reflecting a widening of the age profile of incidence resulting in deaths associated with HIV at increasingly older ages.

4.4 HIV Prevalence

Figure 11 displays the median parameter values for A, D, E and F along with the corresponding HIV prevalence five years earlier from Table 4. The period labels near each point on the plots correspond the the mortality estimation periods associated with the parameter values. The HIV prevalence values come from periods five years before the label on each point. The gray dashed line in each panel is a simple OLS regression line to help the eye assess the linearity of the relationship between the parameter values and HIV prevalence.

For all periods and both sexes, the level parameters A and D increase with HIV prevalence, except for A during the final period. During the final interval the overall level of child mortality is reduced, perhaps reflecting the success of programs to limit mother-to-child transmission (for a brief review see Doherty et al., 2005). The largest increase in level is in the second interval (between the second and third periods) for women, coming just after the largest increase in prevalence; the largest increase for men occurs in the last interval after ten years at high prevalence.

For parameters E (spread or width of hump) and F (location of hump) the relationship with earlier prevalence is less neat but still regular and in-line with expectations. For both sexes there is a downward slope to the relationship between E (width of the hump) and earlier prevalence indicating that as prevalence increases the hump becomes gradually wider; this is especially the case for women whose hump starts off much narrower than men’s.

For men the location of the hump moves from ~ 45 to ~ 38 and then back up to ~ 42. In contrast, women have experienced a consistent ‘aging’ of the hump moving from ~ 31 to ~ 40. This indicates the age locus of the mortality impact of HIV for men has hovered at a little below age 40 while for women it has moved steadily to older ages and is now at about the same age as men.

4.5 Life Expectancy

Table 6 reports expectation of life at birth and age ten for the four periods for both sexes, and Figure 12 plots the median expectation of life schedule with 95% credible intervals. There was a precipitous decline in life expectancy over the entire period with the largest drops occurring between the second and third periods for both sexes. At the beginning of observation during 1994–1997 a male infant could expect to live 67.3 years, and a female infant 73.5. By the end of the final period, a male infant expected only 52.2 years and a female 59.4. Men lost 15.2 years of life expectancy, and women lost 14.2. Judging from the credible intervals, change over the whole period is very significant, with the bulk of the significant drop between periods two and three.

The expectation of life at age ten is not affected by child mortality and consequently describes adult mortality more clearly. Table 6 shows clearly that the majority of the changes in the expectation of life at birth result from changes in adult mortality; the changes in e₁₀ closely track, and in the most recent period, exceed the changes in e₀. The timing of this trend in the expectation of life is consistent with the rise in HIV prevalence. Given a mean survival time of 9–11 years between infection with HIV and death in the absence of access to antiretroviral therapy, we expect and indeed observe rapid increases in mortality at about the turn of century, reflecting increases in HIV prevalence during the 1990s, see Table 4.

5 Discussion

5.1 Summary

In this article we use the parametric Heligman-Pollard mortality model to characterize what we believe is the age-specific impact of HIV on mortality in the Agincourt study population living in rural northeast South Africa over the period 1994–2007. The eight parameters of the Heligman-Pollard model describe the shape of the age-specific _nq_x schedule in three age ranges. We estimate the model using the Bayesian melding method with IMIS to produce robust estimates of the parameter values, the _nq_x schedules output by the model and the corresponding life tables in four periods during which the HIV epidemic grew rapidly in this population. The Bayesian framework yields probabilistic measures of uncertainty around all of these estimates, and we use these to compare both parameter estimates and _nq_x values over time and between the sexes.

The evidence from Agincourt demonstrates the profound effects of HIV on mortality. With a lag of several years after increases in HIV prevalence of 10–15%, the mortality of young children and adults increased dramatically. The corresponding drops in the expectation of life at birth removed about 15 years of life from the average person living in the Agincourt area. All of these changes are highly unlikely to have occurred by chance. Although this is not a new finding, we contribute an unusual nuance – the sex-specific age pattern of increases in mortality following increases in HIV prevalence succinctly summarized with an elegant parametric model.

The eight-parameter Heligman-Pollard model fits HIV-related mortality at Agincourt very well and allows us to summarize the complex age-specific increases in mortality with a small number of estimated parameter values. The parameters that should respond to HIV-related mortality do indeed reflect the increases in mortality associated with HIV in a temporal sequence consistent with changes in HIV prevalence. The increases in young child mortality are captured with parameter A, and the appearance and growth of the hump in adult mortality are reflected by changes in the ‘hump parameters’ – D, E and F. The hump level parameter progressively increases, and the hump spread parameter decreases, corresponding to a gradual widening of the hump. Sex differences in these dynamics suggest that the epidemic started and stays slightly older for men, and for women the epidemic started in a very narrow, young age range and gradually expanded to include older ages. The estimated parameters succeed as a parsimonious and informative description of the age-specific changes in mortality as the HIV epidemic grew.

The Bayesian melding estimation procedure allows us to make robust fits of the eight-parameter Heligman-Pollard model of age-specific mortality to period-sex-age-specific mortality rates covering four phases of the growing HIV epidemic in the Agincourt study population. This Bayesian technique also allows us to characterize uncertainty in both the parameters and outputs of the model (the estimated mortality age schedule) without assuming any special properties for or relationships among the parameters. Bayesian melding results in a joint posterior distribution of the parameters. Running this posterior through the model yields a posterior distribution of _nq_x schedules from which counts of deaths can be simulated and transformed into predicted _nq_x schedules, from which predicted life tables can be constructed. This results in a distribution of life tables, or equivalently, a predictive distribution for each column in the life table from which we calculate measures of uncertainty. The resulting estimates and credible intervals allow us to make strong probability-based statements about differences between mortality schedules and components of mortality schedules.

5.2 R package

We have released an R package, HPbayes (Sharrow, 2011) that implements all of the methods described in this paper, and we will continue to develop and improve that package. The package is available as a standard R package from CRAN that can be run using the R statistical software. The user supplies age-specific counts of deaths and person years, and the package estimates the Heligman-Pollard model for those data and produces a variety of outputs similar to those presented here.

Appendices

A Observed Person Years & Deaths

Table 7.

Female Person Years & Deaths

Age	1994–1997		1998–2001		2002–2004		2005–2007
	PY	Deaths	PY	Deaths	PY	Deaths	PY	Deaths
0	3,771.5	59	3,581.8	83	2,382.8	91	2,567.8	114
1–4	16,100.3	60	14,373.1	82	10,216.0	75	9,555.2	60
5–9	20,370.5	17	19,605.3	12	13,282.0	13	12,666.4	11
10–14	17,551.3	9	18,797.4	12	14,319.4	17	13,365.6	18
15–19	14,853.5	21	15,989.0	17	12,842.0	27	13,536.5	17
20–24	13,002.8	17	13,739.6	50	10,774.3	62	11,542.8	67
25–29	10,749.3	18	11,466.2	51	9,056.7	101	9,354.3	113
30–34	9,163.4	27	9,439.5	56	7,358.1	103	7,436.0	129
35–39	7,026.6	25	8,027.5	61	6,220.5	86	6,172.2	107
40–44	5,831.2	23	6,200.4	54	4,953.4	73	5,418.5	79
45–49	3,973.7	14	5,034.3	34	4,130.0	56	4,153.5	78
50–54	3,248.9	21	3,496.2	33	3,174.8	57	3,526.6	76
55–59	3,140.5	15	3,114.2	26	2,298.6	35	2,577.5	47
60–64	3,042.2	38	2,860.8	44	2,139.9	41	2,039.0	43
65–69	2,834.0	60	2,930.6	48	1,903.7	47	1,894.7	41
70–74	1,742.7	53	2,260.2	73	2,091.9	46	1,725.9	53
75–79	1,200.9	55	1,389.5	56	1,091.5	33	1,682.0	63
80–84	441.0	37	720.9	37	731.4	51	710.4	37
85–89	209.1	28	258.2	16	225.7	22	447.0	38
90–94	99.1	6	99.0	9	109.8	14	110.9	7
95–99	37.3	8	40.1	9	35.0	6	55.6	5
100+	46.0	9	21.4	4	9.2	2	14.9	1

Table 8.

Male Person-Years & Deaths

Age	1994–1997		1998–2001		2002–2004		2005–2007
	PY	Deaths	PY	Deaths	PY	Deaths	PY	Deaths
0	3,795.5	55	3,485.6	103	2,332.6	104	2,587.7	91
1–4	16,183.6	66	14,306.2	91	10,041.9	86	9,321.9	58
5–9	20,452.0	12	19,640.2	12	13,139.5	15	12,326.2	21
10–14	17,469.8	15	18,880.2	17	14,463.3	15	13,113.1	13
15–19	15,055.9	18	16,318.0	13	12,885.9	23	13,803.1	18
20–24	11,798.2	22	13,571.6	36	11,080.0	53	11,514.0	37
25–29	9,543.1	37	10,626.8	41	8,730.0	82	9,418.5	100
30–34	7,803.9	34	8,508.8	65	6,696.8	107	7,005.0	131
35–39	5,863.0	44	6,727.7	63	5,439.4	104	5,505.2	142
40–44	4,833.8	37	5,074.3	56	4,082.4	81	4,488.1	127
45–49	3,810.7	48	4,317.5	67	3,233.4	73	3,244.9	92
50–54	2,698.6	41	3,138.9	41	2,762.8	65	2,759.4	91
55–59	2,461.2	49	2,414.3	38	1,823.0	58	2,102.4	78
60–64	1,617.2	38	2,090.5	38	1,637.4	71	1,389.4	65
65–69	1,529.5	47	1,410.4	45	1,101.4	43	1,350.3	65
70–74	1,190.9	54	1,202.1	57	898.0	39	722.2	39
75–79	848.9	58	888.6	66	556.7	55	674.8	40
80–84	328.6	25	503.9	39	455.1	35	356.1	44
85–89	126.1	12	194.3	25	175.9	23	265.2	31
90–94	45.5	7	51.6	4	60.0	10	69.9	9
95–99	13.5	2	16.8	4	12.4	3	22.2	8
100+	32.7	2	11.0	1	.1	0	3.0	0

B Predictive _nq_x Schedule Distributions

Figure 13. Predictive Distributions of Male Age-Specific Probabilities of Dying.

1994–1997 (upper left), 1998–2001 (upper right), 2002–2004 (bottom left), 2005–2007 (bottom right).

Figure 14. Predictive Distributions of Female Age-Specific Probabilities of Dying.

1994–1997 (upper left), 1998–2001 (upper right), 2002–2004 (bottom left), 2005–2007 (bottom right).

C Predictive e_x Schedule Distributions

Figure 15. Predictive Distributions of Male Age-Specific Expectations of Life.

(e_x): 1994–1997 (upper left), 1998–2001 (upper right), 2002–2004 (bottom left), 2005–2007 (bottom right).

Figure 16. Predictive Distributions of Female Age-Specific Expectations of Life.

(e_x): 1994–1997 (upper left), 1998–2001 (upper right), 2002–2004 (bottom left), 2005–2007 (bottom right).

D Pairs Plots of Estimated Heligman-Pollard Model Parameters

E Prior/Posterior Densities for Estimated Heligman-Pollard Model Parameters

Key: prior - grey, dashed; posterior - black, smooth

F Period Aggregation

We had two motivations for creating these time intervals. First, we have 14 years of data which we would like to aggregate into intervals that would reduce noise to the greatest extent but also maintain the level and shape of mortality in the individual years and be roughly similar in interval length, for the sake of comparison. We first plotted the age-specific deviations between each year’s set of age-specific probabilities of death, _nq_x, and the mean _nq_x among all years (figure 17). Because we aim to assess changes resulting from a growing HIV epidemic, we focus on differences in the adult years where HIV is most influential. Panel (a) of figure 17 shows a clear delineation between 2001 and 2002 for males when HIV prevalence increases substantially. While this break is not as clear for females most of the 2002 deviations remain positive with many 2001 deviations during the adult years falling below the dashed line. For the sake of having time intervals with similar widths, we next divide the two halves (pre-2002 and 2002+) in half yielding the periods under study. These intervals also contain a similar number of persons at risk of death in the first age-group of the life table, l_x (see section 3.2).

Figure 17.

Deviations from mean _nq_x for Agincourt HDSS 1994–2007

G Likelihood specification for HP model

Our data are counts of deaths and persons at risk of dying in each time-sex-age cell. Thus we use the binomial likelihood which is a natural choice given that the observed _nq_x are probabilities of a binary outcome. The likelihoods for each age are treated as independent and combined to produce a total likelihood. The likelihood is the probability of witnessing the observed age distribution of deaths given the age-specific probabilities of dying produced by the Heligman-Pollard model with a given set of parameter values. The likelihood is

$$\mathcal{L}(\mathbf{y}=(\mathbf{d},\mathbf{1})\mid M(\theta )=\mathbf{q})=\prod _{\text{age}i=0}^{100+}\left(\begin{array}{c}{l}_i\\ d_i\end{array}\right)q_i^{d_i}{(1-q_i)}^{l_i-d_i}.$$ (3)

where y = (d, l) are the data consisting of counts of deaths and persons at risk of dying by age and M(θ) = q are the age-specific probabilities of dying output by the Heligman-Pollard model with a given set of values for the parameter vector θ. For a given age group i, l_i is the number of people at risk of dying from the data and d_i is the number of deaths from the data. q_i is the probability of dying in age group i from the model with a specific set of parameter values.

H IMIS algorithm

Bayesian melding has been used to analyze other deterministic models (e.g. Alkema et al., 2007; Ševčíková et al., 2007) using the Sampling Importance Resampling (SIR) algorithm (Rubin, 1987; Poole and Raftery, 2000) to sample from the posterior distribution. Instead we use incremental mixture importance sampling (IMIS) to obtain samples from the posterior distribution. Incremental mixture importance sampling was originally introduced by Steele et al. (2003, 2006) and was later developed for posterior distributions of continuous parameters, in particular for deterministic demographic-epidemiological models, by Raftery and Bao (2010). The SIR algorithm draws a large number of samples from the prior distribution of the model parameters, weights each sample by its likelihood and then resamples with replacement using the computed weights (Rubin, 1988). Sometimes SIR performs poorly and few distinct values are present in the final sample because a small number of large importance weights dominate the resampling step. The IMIS algorithm addresses this problem. After calculating the likelihoods and weights as in the SIR algorithm, at each iteration a multivariate normal distribution centered at the parameter vector value with the highest importance weight and with a variance-covariance matrix estimated from the weighted covariance of the inputs with the smallest Mahalanobis distances to the center is added to the current importance sampling distribution, thus forming a mixture and successfully representing parts of the parameter space that might otherwise be missed.

If the initial sample from the prior misses a high probability region, IMIS may also fail to cover that region. To address this problem Raftery and Bao (2010) suggest inserting an optimization step after the initial stage (i.e. drawing the samples from the prior distribution and calculating their weights) to yield a mixture of d multivariate normal distributions centered around a local maximum of the target distributions. New inputs drawn from the multivariate normal distributions from the optimization step are combined with the initial inputs and new likelihoods and weights are calculated. In the final resampling stage, IMIS resamples x number of inputs with replacement from the mixture distribution with the calculated weights, and it is this final sample that approximates the posterior parameter distribution. Compared to SIR, IMIS is much more efficient.