Abstract
Source memory zROC slopes change from below 1 to above 1 depending on which source gets the strongest learning. This effect has been attributed to memory processes, either in terms of a threshold source recollection process or changes in the variability of continuous source evidence. We propose two decision mechanisms that can produce the slope effect, and we test them in three experiments. The evidence mixing account assumes that people change how they weight item versus source evidence based on which source is stronger, and the converging criteria account assumes that participants become more willing to make high confidence source responses for test probes that have higher item strength. Results failed to support the evidence mixing account, in that the slope effect emerged even when item evidence was not informative for the source judgment (that is, in tests that included strong and weak items from both sources). In contrast, results showed strong support for the converging criteria account. This account not only accommodated the unequal-strength slope effect, but also made a prediction for unstudied (new) items that was empirically confirmed: participants made more high confidence source responses for new items when they were more confident that the item was studied. The converging criteria account has an advantage over accounts based on source recollection or evidence variability, as the latter accounts do not predict the relationship between recognition and source confidence for new items.
Over the past few decades, one type of data has played a particularly important role in attempts to explore the processes underlying recognition and source memory: receiver operating characteristic (ROC) functions (Hilford, Glanzer, Kim, & DeCarlo, 2002; Ratcliff, Sheu, & Gronlund, 1992; Wixted, 2007a; Yonelinas, 1994; Yonelinas & Parks, 2007). ROC functions are plots of the proportion of correct judgments on the proportion of incorrect judgments across conditions in which bias changes but memory evidence remains the same. For example, in a source task the correct judgments could be “male” responses to items heard in a male voice at encoding, whereas incorrect judgments could be “male” responses to items heard in a female voice. For recognition tasks, the correct and incorrect responses are “old” responses to studied (old) or non-studied (new) items, respectively.
Bias is sometimes varied with experimental manipulations (Broder & Schutz, 2009; Ratcliff et al., 1992; Dube & Rotello, 2012; Dube, Starns, Rotello, & Ratcliff, 2012), but here we follow the more common practice of using a confidence scale to define separate ROC points. For example, if participants make source decisions on a scale from 1 (Certain Female) to 6 (Certain Male), the ROC point representing the most conservative responding assumes that participants will only say “male” if they are very confident that the item was studied in a male voice (ratings of 6), and the point representing the most liberal responding assumes that participants say “male” on every trial unless they are very confident that the item was studied in a female voice (all ratings 2-6). Each intermediate level of the confidence scale contributes another point to the ROC function. The proportion of correct and incorrect responses at each bias level are commonly converted to z-scores to produce a zROC function.
Wixted (2007a) and Yonelinas and Parks (2007) recently published reviews of the extensive literature testing memory models with ROC data. Interestingly, the two reviews disagree as to the model best supported, even though they summarize the same empirical results. Wixted argues that the data clearly favor a continuous model in which all evidence for a memory decision is combined into a single strength value. Yonelinas and Parks argue that the data clearly favor a dual process model in which a subset of decisions are based on a continuous familiarity process and others are based on a threshold recollection process. Adding to the irony, both reviews focus on source memory ROCs as some of the strongest evidence discriminating the continuous and dual process models.
Our goal is to investigate the effect of memory strength on the slope of source memory zROC functions, a phenomenon that Yonelinas and Parks (2007) highlighted as support for the dual process model over the continuous model. In the following sections, we describe both models in detail and explain why source memory zROC slopes seem to provide evidence against the continuous model. We then discuss potential mechanisms for accommodating slope effects in the continuous approach that were not considered by Yonelinas and Parks. Finally, we describe the experiments that will be used to test these proposed mechanisms.
The Continuous Model
The continuous model assumes that a single continuous evidence variable informs memory decisions (Egan, 1958; Wixted, 2007a). For recognition, this variable is the total strength of evidence that the item was studied, whereas for source tasks it is the relative strength of evidence that the item was seen in Source 1 versus Source 2. Panel A in Figure 1 shows example distributions for a Male/Female source task in which some items were studied once (weak) and some were studied multiple times (strong). Evidence values on the left end of the continuum represent strong evidence that the item was studied in the female source, and evidence values to the right of the continuum represent strong evidence for the male source. Items studied in a male voice tend to have evidence values that are farther to the right than items studied in a female voice, but there is considerable variability from one item to the next represented by the Gaussian distributions. Criteria are established on the evidence dimension to map strength values onto confidence responses, with the highest confidence “female” responses mapped to the region below the leftmost criterion and the highest confidence “male” responses mapped to the region above the rightmost criterion.
Figure 1.
The continuous model of source memory. Each Gaussian distribution represents source evidence for a particular item type, and the vertical lines show source confidence criteria to divide the evidence space into regions for each confidence level from high-confidence female (furthest to the left) through high-confidence male (furthest to the right). Panel A displays a model in which strong items have both more extreme means and higher standard deviations, and criteria do not vary based on strength. Panel B displays a model in which strong and weak items have the same standard deviation, but the criteria are more tightly grouped for strong items (grey lines) than weak items (black lines). Panels A and B actually display alternative parameterizations of the same model, and they produce exactly the same predicted zROC functions.
The model in Figure 1 predicts linear zROC functions with slopes determined by the relative variability of the evidence distributions. Recognition memory zROCs consistently have a slope below 1, which the continuous model fits by assuming that evidence is more variable for studied than for non-studied items (Egan, 1958; Glanzer, Kim, Hilford, & Adams, 1999; Ratcliff et al., 1992, Ratcliff, Mckoon, & Tindall, 1994; Yonelinas, 1994). Source zROCs within a strength condition typically have a slope close to 1, which the model fits by assuming equal variances in the Source 1 and Source 2 evidence distributions (Hilford et al., 2002; Slotnick, Klein, Dodson, & Shimamura, 2000; Slotnick & Dodson, 2005). Panel A in Figure 1 shows equal variances for male and female items within a strength class and more variable evidence for items with strong compared to weak learning. We will discuss the significance of this pattern when we compare the predictions of the continuous and dual process models.
The Dual Process Model
The dual process model assumes that decisions are based on two distinct processes: familiarity and recollection (Yonelinas, 1994). The familiarity process produces relatively vague information that varies continuously from one item to the next. Initial results suggested that familiarity plays no role in source judgments unless the sources have different levels of memory strength (Yonelinas, 1999), but dual-process theorists have more recently claimed that familiarity can contribute to source discrimination even with equal-strength sources (Elfman, Parks, & Yonelinas, 2008; Parks & Yonelinas, 2007). The recollection process recovers specific qualitative details in a threshold fashion; that is, recollection completely fails for some studied items but succeeds for others. Source judgments should rely more heavily on recollection than familiarity (Yonelinas & Parks, 2007), but both processes play a large role in item recognition. All recollected items produce a correct response with the highest level of confidence.1 When recollection fails, responses are based on the familiarity process. Familiarity is modeled with the exact assumptions of the continuous model above, except that the variance of the evidence distributions is necessarily equal across all item classes. As a result, zROC functions from the familiarity process alone are linear with a slope equal to 1. Adding recollection produces a slight u-shape in the zROC functions and also changes the slope; for example, recollecting targets produces a slope less than 1 for recognition tasks (Yonelinas, 1994).
Comparing the Models with Source zROC Functions
The shape of source memory zROC functions does not clearly support either the continuous or dual process models. Many source memory experiments yield zROCs with a u-shape, as predicted by the dual process model (Hilford et al., 2002; Slotnick et al., 2000; Slotnick & Dodson, 2005; Yonelinas, 1999). However, more recent work reveals that source zROCs approach the linear form predicted by the continuous model as overall memory strength is increased (Slotnick & Dodson, 2005; Wixted, 2007a). For example, Slotnick and Dodson reported u-shaped zROCs when all items were included in the analysis and linear zROCs when the analysis included only items that participants called “studied” with high confidence. Given that shape yields equivocal results and the shape predictions of the two models are often extremely difficult to distinguish empirically, we focus our efforts on a zROC slope effect that has a much clearer signature in the data. We will return to the shape issue in the General Discussion.
Yonelinas and Parks (2007) noted an effect on source memory zROC slopes that appears to support the dual process model over the continuous model: the zROC slope differs from 1 when sources are unequal in strength, and the direction of the deviation is determined by which source is stronger (e.g., Yonelinas, 1999). For example, the slope might be .8 when male items are stronger than female items versus 1.25 when female items are stronger. This effect is naturally predicted by the dual process account, because the zROC slope is determined by the degree of recollection for each source (and recollection should be more likely for items that received stronger encoding). The continuous model can accommodate the slope change by assuming that the source evidence distribution is more variable for strong than for weak items, as depicted in Panel A of Figure 1. However, Yonelinas and Parks note that there is a problem with this account: In recognition tasks, the zROC slope does not differ between strong and weak targets, and fits of the continuous model consistently indicate that evidence variability does not increase with additional learning (e.g., Ratcliff et al., 1992, 1994). To explain both recognition and source data, proponents of the continuous model are required to make the awkward contention that additional learning increases the variance of source evidence but has no effect on the variance of recognition evidence.
We acknowledge that the strength effect on source memory slopes is problematic for the continuous model if evidence variability is the only mechanism influencing zROC slope. In the next section we propose candidate mechanisms that might create the slope difference even if additional learning does not increase evidence variability for either recognition or source tasks. Our experiments test these potential mechanisms.
Alternative Mechanisms for the Slope Effect
Evidence Mixing
The strength effect on zROC slope might arise because people consider different types of evidence for equal- and unequal-strength sources. Only source-specific information can inform decisions with equal-strength sources. With unequal strength, participants can also consider item strength in the absence of specific-source details. That is, even if participants have no memory for the source of an item, they might attribute it to the weak source if they are not sure that the item was studied or attribute it to the strong source if they are certain that the item was studied. We call this the evidence mixing hypothesis because it assumes that people consider a mixture of source and item evidence. Yonelinas (1999) appealed to this sort of mechanism to explain his finding that source ROC functions are linear for equal-strength sources and curved for unequal-strength sources, with the latter reflecting item familiarity in addition to source recollection. However, the account can also be implemented in a purely continuous framework, and this implementation actually produces the slope effect that Yonelinas and Parks (2007) attributed to source recollection.
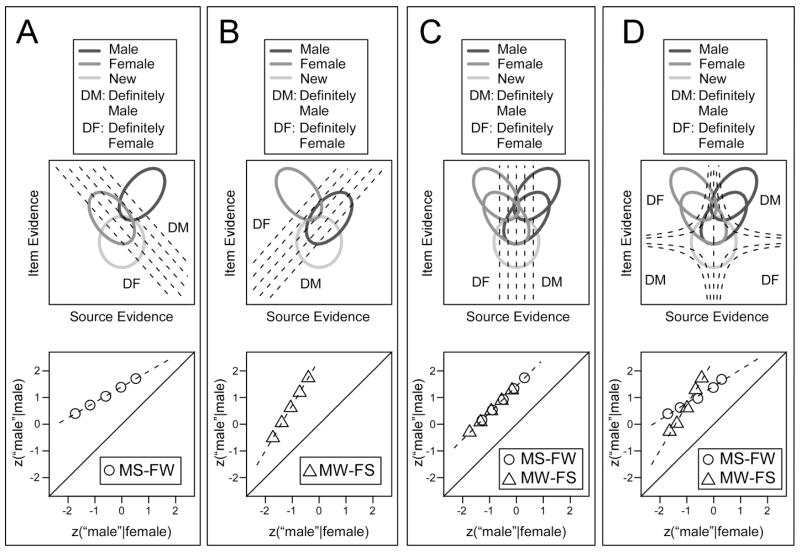
If a continuous model is assumed for the evidence informing both recognition and source decisions, then joint performance on these tasks can be defined with a bivariate signal-detection model (Banks, 2000; DeCarlo, 2003; Glanzer, Hilford, & Kim, 2004; Hautus, Macmillan, & Rotello, 2008). Figure 2 displays several versions of a model with bivariate Gaussian distributions for male, female, and new items. Source evidence is on the x axis and recognition (item) evidence is on the y axis. The ovals on the plot show equal-density contours for each distribution (the probability density of each distribution would be on a 3rd dimension rising out from the page). On the recognition dimension, both male and female items have higher average evidence values than new items. On the source dimension, female items are on the left of the continuum and male items on the right, with new items in the middle (i.e., they are not associated with either source). Panel A shows a test in which male items are exclusively strong and female items are exclusively weak, so the female distribution is closer to the new distribution on both the recognition and source dimensions. Panel B shows the reverse strength relationship, and Panels C and D show balanced conditions that have strong and weak versions of both sources on the test. For the studied items, recognition and source evidence are positively correlated, which is represented by the slant of the male and female distributions.
Figure 2.
Bivariate models for recognition and source responding displaying the alternative decision mechanisms that might produce slope differences with unequal-strength sources. The top plot in each panel shows the model representation, where each oval is an equal-density contour of the bivariate distribution for a given item type and the dashed lines show the source confidence criteria. The “DM” and “DF” symbols demonstrate how the evidence regions are mapped to the “definitely male” and “definitely female” confidence levels, respectively. The bottom plot in each panel shows the source zROC predicted by the displayed model. The predictions were based on 10,000 simulated trials for each item type. MS-FW indicates a function with strong male and weak female items, and MW-FS indicates the reverse. z(“male”|male) indicates the z score for the proportion of male items called “male,” and z(“male”|female) indicates the z score for the proportion of female items called “male.”
The source confidence criteria are shown as dotted lines, and the angle of the criteria represents the relative weighting of source and item evidence (Banks, 2000; also see Ashby & Townsend, 1986). Vertical criteria mean that decisions are based on source evidence alone, horizontal criteria mean that decisions are based on item evidence alone, and other angles represent different mixtures of the two types of information. Panels A-C show criteria that implement the assumptions of the evidence mixing approach. When male items are strong (Panel A), the criteria are oriented such that stronger item memories are more likely to be attributed to the male source, and this relationship flips when female items are strong (Panel B). With balanced lists in which the male and female items are equally strong, item evidence does not help discriminate sources, and only source-specific information is considered (Panel C).
The bottom plot in each panel shows zROC functions produced by taking 10,000 random samples from each evidence distribution and determining the response for each sample using the displayed criteria. In the unbalanced conditions, the slope is below one when male items are strong and female items are weak (MS-FW) and above one when male items are weak and female items are strong (MW-FS). Critically, the male and female distributions have exactly the same variability in both the recognition and source dimensions. In other words, the predictions assume that additional learning does not increase evidence variability. The change in slope is driven by the change in the orientation of the decision criteria. When the sources are balanced in strength and only source evidence is considered (Panel C), there is no slope difference between the MS-FW and FW-MS functions. (We will discuss Panel D in the following section).
Experiment 1 was designed to test the evidence mixing hypothesis. One condition involved tests in which every item from one source was weak and every item from the alternative source was strong (the unbalanced condition). Another condition involved tests with both strong and weak male and female items (the balanced condition). We wanted to ensure that the available memory evidence was the same in both conditions, so we always used the same encoding phase with strong and weak versions of both sources, and only the tests were different. The test instructions informed participants of the test content; for example, for a MS-FW list participants would be told that all male items on the test were studied four times and all female items on the test were studied once. To verify that participants attended to these instructions, we required them to report the strength of each source before they could begin the test. Very similar procedures have been used in strength-based mirror effect research, and these studies demonstrate that participants base their response criteria on the reported content of the test and not the content of the study list (Starns, White, & Ratcliff, 2010, 2012; Starns, Ratcliff, & White, 2012). As displayed in Figure 2, the evidence mixing hypothesis with linear decision bounds predicts different slopes for the MS-FW and MW-FS functions in the unbalanced condition but not the balanced condition.
Converging Criteria Hypothesis
As a second alternative mechanism, we considered the possibility that item strength affects how people set their confidence criteria for the source judgment. Several models that simultaneously account for recognition and source performance include the assumption that source criteria change across different levels of item strength (Hautus et al., 2008; Onyper, Zhang, & Howard, 2010). Onyper et al. fit free parameters for the source criteria at every level of recognition confidence. In fits to data, the criteria for higher item confidence levels were more tightly grouped than the criteria for lower confidence levels. In a discrete-state model, Klauer and Kellen (2010) implemented a “compression function” such that source confidence responses were more concentrated at the center of the rating scale when item confidence was low. Hautus et al. assumed that the criteria for source confidence ratings followed constant likelihood ratios, as displayed in Panel D of Figure 2. As a result of the correlation between item and source evidence, the likelihood bounds for source decisions converge for higher levels of item strength. To be clear, the criteria converge only in terms of the “pure” strength of the source evidence. In terms of likelihood ratios, the criteria have constant values regardless of the level of item strength. Technically, the likelihood bounds reverse for extremely low values of item strength, but this has a negligible effect on predictions given that almost no evidence values ever fall in this region.
In psychological terms, the converging criteria account means that participants are more willing to make high confidence source responses when they are more confident that the item was on the study list. We used likelihood decision bounds as a convenient way to mathematically define the converging criteria mechanism, but the convergence could also reflect a general heuristic whereby participants are unwilling to confidently specify how they studied an item when they are not certain that they studied it (Klauer & Kellen, 2010, call this the principle of consistency). As seen in the zROC plot for Panel D, the converging criteria produce a slope difference between the MS-FW and MW-FS functions even in the balanced design.
To reinforce the concept that apparent changes in evidence variability – that is, differences in zROC slope – might actually be produced by converging criteria, Panel B of Figure 1 shows a model with no strength effect on evidence variability but with the source confidence criteria more tightly grouped for the strong versus the weak items. Panels A and B in Figure 1 actually display alternative parameterizations of the exact same model. That is, one can take any parameter set within the variability version (Panel A) and produce a converging criteria version with the same predicted zROC function (Panel B). Below, we follow tradition by reporting parameters in terms of the variability version, but readers should keep in mind that the continuous fits actually implement both the variability and the converging criteria accounts. Converging criteria would also introduce variability in the source criteria, as different items within a stimulus class will have different item strengths and thus different confidence criteria (Benjamin, Diaz, & Wee, 2009; Mueller & Weidemann, 2008; Treisman & Williams, 1984). In the fits of the continuous model below, any criterion variability would have the same effect as inflating the memory evidence variability for both item types.
Critically, the evidence variability and converging criteria versions of the model make distinct psychological assumptions despite their mathematical equivalence, and thus they can be discriminated. One distinct prediction of the two accounts concerns source responses for non-studied (new) items. New items are not associated with any one source on average, of course, but some of the new items will be confidently attributed to one source or the other as a result of the variability in evidence values. In the converging criteria account, the chances of a new item’s source evidence falling in a high-confidence region should vary based on where the item falls on the item-evidence dimension. Specifically, participants should be more likely to provide high-confidence source responses for new items when they are (erroneously) more confident that the item was on the study list. On the other hand, if source criteria are constant across item strength, as in the variability version of the model, then the distribution of source confidence for new items should be the same regardless of the level of recognition confidence.
Summary of Accounts and Predictions
Our primary goal is to contrast three potential explanations for the effect of unequal strength sources on the zROC slope: 1) a recollection account in the dual process framework, 2) an evidence mixing account whereby slopes change because participants consider item information in addition to source evidence for unequal strength sources, and 3) a converging criteria account in which participants are more willing to make high confidence source responses when they are more confident that the test item was studied. Experiment 1 contrasted unbalanced tests with balanced tests. The evidence mixing account predicts that the MS-FW and MW-FS zROC functions should have different slopes in the unbalanced condition but not the balanced condition. The recollection and converging criteria accounts predict different slopes in both the unbalanced and balanced conditions.
Experiments 2a and 2b (along with a dozen datasets from other studies) were used to explore the pattern of source confidence for new items that participants falsely recognized with either low, medium, or high confidence. The converging criteria account predicts that participants will make more high confidence source responses for new items that are falsely recognized with higher levels of confidence. The other two accounts do not share this prediction. The recollection account assumes that the slope effect is based on a process that only affects studied items (source recollection), so it does not predict that source confidence and recognition confidence will be related for new items. Both Experiments 2a and 2b used the balanced design, so the evidence mixing account predicts no slope difference between the MS-FW and MW-FS functions, and also predicts no relation between item strength and source confidence for new items.
Experiment 1
Method
Participants
Forty undergraduate students from the University of Massachusetts Amherst participated to earn course credit in their psychology courses. Five participants yielded data that were not useful for addressing our research questions and were excluded from analyses. One of these participants used only two levels of the confidence scale for almost all responses (making it impossible to evaluate ROC data) and four had chance-level performance (proportion correct at or below .5 for one or more study/test cycles).
Materials
The words for each session were randomly selected from a pool of 303 items and were randomly assigned to study/test cycles and conditions. Participants studied lists of words spoken by male and female speakers, with ‘weak’ words studied once and ‘strong’ words studied four times. Each study list contained 10 male-strong, 10 female-strong, 10 male-weak, and 10 female-weak words in a random order for a total of 100 item presentations.
There were 3 different types of test list: balanced, male-strong, and female-strong. The balanced test contained all 40 studied items, the male-strong test contained the 10 male-strong items and 10 female-weak items, and the female-strong test contained the 10 female-strong items and 10 male-weak items. No new items were tested in any of the conditions. Each participant completed two study/test cycles in each condition for a total of 20 observations for each item type within each condition.
Procedure
Study/test cycles were randomly assigned to conditions for each participant. Participants pressed the space bar to initiate each study list. A sound file of each study word spoken in a male or female voice was heard through headphones, and a visual display of the word simultaneously appeared in the center of the computer screen. The words remained on the screen for 1100 ms with 100 ms of blank screen between presentations. After each study list, participants completed 15 trials of a digit monitoring task to serve as a filled retention interval. The digits 1 through 9 were presented on the screen in a random order for 1 s each. Participants were instructed to press the “/” key when the number on the screen was the same as the number 2 places back in the sequence. At the end of the 15 trials, participants received feedback on the number of targets in the sequence as well as the number of targets they detected. This feedback remained on the screen for 4 s.
Immediately following the digit monitoring task, participants completed a source memory test. At the beginning of each test, participants were informed how many times the male and female items on the test had been studied (either only once, only four times, or a combination of both). Participants were required to confirm how many times they studied the male items and how many times they studied the female items before the test began. For each study/test cycle, participants rated their confidence that a male or a female voice spoke each word using a 6 point scale from “very sure female” to “very sure male.” Participants were told the proportion of correct source responses at the end of each cycle, and the feedback remained on the screen for 4 s.
Prior to beginning the first study/test cycle, participants practiced using the confidence keys. Symbols corresponding to each level of the confidence scale were presented on the screen (FFF = very sure female, FF = sure female, F = guess female, M = guess male, MM = sure male, and MMM = very sure male), and participants had to hit the corresponding response key as quickly as possible (‘z’, ‘x’, ‘c’, ‘,’, ‘.’, ‘/’ for sure female through sure male, respectively). Participants saw 60 symbols (10 of each), and each symbol remained on the screen until the participant pressed the correct key. Before each test cycle, the same symbols appeared on the screen one time each in a random order to confirm that the participant’s fingers were on the appropriate response keys. After the response key practice, participants completed one practice version of the memory task by completing a full cycle of the balanced condition, including the study list, digit monitoring task, and source memory test. The data from the practice trials were excluded from analysis.
Modeling Procedures
We performed fits by minimizing the G2 statistic, and we compared models using G2, AIC, and BIC (Akaiki, 1973; Schwartz, 1978). The latter two indices include a penalty for the number of free parameters in a model, and lower values indicate a better fit for all of the fit statistics. We performed fits at the group level, because the data for individual participants did not have enough observations for stable parameter estimation. Experiments 2a and 2b have more observations per participant, and fits were performed at both the group and individual levels.
Results and Discussion
Unbalanced Condition
Figure 3 shows the group zROC functions from the unbalanced condition. The lines show the best-fitting functions from the unequal-variance continuous model for each strength condition. The functions were very close to linear, and the slope was much lower for the male-strong/female-weak (MS-FW) function than the male-weak/female-strong (MW-FS) function. We jointly fit the group data from the MS-FW and MW-FS lists; thus, there were four item types overall (strong and weak male and female items). We fit the response frequencies at each of the six confidence levels, producing five degrees of freedom in the data for each item type (the frequencies are constrained to sum to the total number of trials for the item type, eliminating one degree of freedom).
Figure 3.
Source memory zROC functions from the Unbalanced condition in Experiment 1. MS-FW indicates a function with strong male and weak female items, and MW-FS indicates the reverse. Plusses mark the fit of the continuous model with unequal varainces (UV), and x’s mark the fit of the dual process (DP) model. z(“male”|male) indicates the z score for the proportion of male items called “male,” and z(“male”|female) indicates the z score for the proportion of female items called “male.”
The dual process model had 16 free parameters, eight each for the MS-FW and the MW-FS lists. Within each list type, the familiarity process requires five response criteria for the six levels of the confidence scale and two means for the male and female familiarity distributions (the standard deviations of the distributions are fixed at 1). One of these 7 parameters can be fixed at zero without loss of generality, and we chose to fix the center response criterion. There were also two free recollection parameters for male and female items within each list type.
The continuous source model had 13 free parameters, including four free criterion parameters each for MS-FW and MW-FS lists (with the center criterion fixed at zero for both), two means for the male and female source evidence distributions within each list type, and one parameter for the standard deviation of the evidence distributions in the strong condition (the standard deviation was fixed at 1 for weak items and assumed to be equal for male and female items). We compared this unequal-variance version of the model to an equal-variance version in which evidence variability was constrained to be equal for strong and weak items, which eliminates one free parameter.
The plusses show the fit of the unequal-variance model to each zROC point, and the x’s show the dual process fit. Table 1 reports the fit statistics, and Table 2 gives the best fitting memory parameters for each model. Both models fit the data well, with a slight advantage for the continuous model because the dual process model predicts a slight u-shape that is not reflected in the data. In the continuous model, the slope difference is captured by increasing the variability of source evidence in the strong versus the weak condition, which – as noted in the Introduction – could represent either actual changes in evidence variability or source criteria that converge as item strength increases. In the dual process model, the slope effect is accommodated in terms of increased source recollection for strong items compared to weak items. The means of the male and female source familiarity distributions were closer together in the strong than in the weak condition (Table 2), suggesting that strengthening items decreased source familiarity. However, this decrease did not replicate in Experiments 2a and 2b, so we make no attempt to interpret it.
Table 1.
Fit statistics for the source memory data
| Fit Statistic |
|||
|---|---|---|---|
| Model | G2 (df) | AIC | BIC |
| Experiment 1 – Unbalanced | |||
| Dual Process | 34.90 (4) | 184.87 | 279.87 |
| Continuous UV | 10.92 (7) | 154.89 | 232.08 |
| Continuous EV | 115.22 (8) | 257.19 | 328.44 |
| Experiment 1 – Balanced | |||
| Dual Process | 48.91 (8) | 192.35 | 263.60 |
| Continuous UV | 30.35 (11) | 167.79 | 221.23 |
| Continuous EV | 146.67 (12) | 282.11 | 329.61 |
| Experiment 2a (Balanced) | |||
| Dual Process | 49.40 (8) | 208.32 | 288.23 |
| Continuous UV | 32.91 (11) | 185.83 | 245.76 |
| Continuous EV | 170.56 (12) | 321.48 | 374.75 |
| Experiment 2b (Balanced) | |||
| Dual Process | 71.59 (8) | 232.35 | 313.82 |
| Continuous UV | 45.49 (11) | 200.25 | 261.35 |
| Continuous EV | 224.63 (12) | 377.39 | 431.70 |
Note: UV – unequal variance; EV – equal variance
Table 2.
Parameter values from the source memory fits to group data
| Dual Process Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| Dataset | Rwf | Rwm | Rsf | Rsm | μ wf | μ wm | μ sf | μ sm |
|
|
||||||||
| E1 Unbal. | .00 | .00 | .50 | .40 | −0.41 | 0.57 | −0.31 | 0.45 |
| E1 Bal. | .07 | .06 | .42 | .41 | −0.36 | 0.30 | −0.18 | 0.31 |
| E2a | .04 | .00 | .38 | .31 | −0.24 | 0.39 | −0.25 | 0.40 |
| E2b | .04 | .07 | .38 | .40 | −0.49 | 0.12 | −0.43 | 0.12 |
| Continuous Unequal Variance Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| μ wf | μ wm | μ sf | μ sm | σ w | σ s | |||
|
|
||||||||
| E1 Unbal. | −0.42 | 0.60 | −1.52 | 1.42 | 1* | 1.62 | ||
| E1 Bal. | −0.46 | 0.40 | −1.16 | 1.25 | 1* | 1.56 | ||
| E2a | −0.29 | 0.40 | −1.02 | 1.05 | 1* | 1.41 | ||
| E2b | −0.55 | 0.21 | −1.24 | 0.97 | 1* | 1.46 | ||
Note: WF – weak female; WM – weak male; SF – strong female; SM – strong male. For the dual process model, R is the probability of source recollection and μ is the mean of the source familiarity distribution. For the continuous model, μ is the mean and σ is the variance of the source evidence distribution. Parameters marked with an asterisk were fixed in fits. Unbal. – Unbalanced; Bal. – Balanced.
To statistically evaluate the slope effect, we compared the fit of the unequal-variance version of the continuous model discussed above to the fit of an equal-variance version (which forces equal zROC slopes for the MS-FW and MW-FS functions). A G2 test indicated that allowing different zROC slopes produced a significantly better fit [G2 (1) = 104.30, p < .001]. Table 1 shows that the unequal variance model was also preferred by both AIC and BIC.
Balanced Condition
Figure 4 shows group zROC functions and fits for the balanced condition. The left-hand panel shows strong items from one source plotted against weak items from the other source to make it easy to evaluate the predicted slope effect. Critically, the slope effect observed in the unbalanced condition also appeared in the balanced condition, and the zROC functions look remarkably similar between the two. The right panel arranges the data in the more traditional way, with data from the strong and the weak conditions grouped. This panel clearly shows the effectiveness of the strength manipulation on overall source accuracy. As in previous reports, the zROC function in the weak condition had a slight u-shape, whereas the strong function was essentially linear (e.g., Slotnick & Dodson, 2005). Although curvature in the zROC has previously been taken as evidence for the use of a high-threshold recollection process (e,g., Yonelinas, 1994), Hautus et al. (2008) showed that the use of likelihood decision bounds – like those in the converging criteria account – also result in curved zROCs (see Figure 2, Panel D).
Figure 4.
Source memory zROC functions from the Balanced condition in Experiment 1. The first plot shows the unequal-strength zROCs, and the second shows equal-strength zROCs (the same data are displayed in each plot). Plusses mark the fit of the continuous model with unequal variances (UV), and x’s mark the fit of the dual process (DP) model. z(“male”|male) indicates the z score for the proportion of male items called “male,” and z(“male”|female) indicates the z score for the proportion of female items called “male.” MS – male strong; MW – male weak; FS – female strong; FW – female weak.
The models for the balanced condition have fewer free parameters than the unbalanced models, because all four item types (strong and weak male and female items) were on the same test list and only one set of criteria was needed. This eliminated four free parameters for all of the models (four instead of five because the center criterion was fixed at zero in the unbalanced fits). Thus, the balanced fits involved 12 free parameters for the dual process model, 9 free parameters for the unequal-variance version of the continuous model, and 8 free parameters for the equal-variance version. The data have 20 degrees of freedom, as in the unbalanced fits.
Again, both models fit well, with a slight advantage for the continuous model (see Table 1). Allowing different zROC slopes for MS-FW and MW-FS produced a significantly better fit [G2 (1) = 116.32, p< .001], and the different-slope model was also preferred by both AIC and BIC (Table 1).
Summary
The results of Experiment 1 fail to support the evidence mixing hypothesis. Even on the balanced tests in which item strength was independent of source membership, a clear slope effect emerged. In fact, the results were extremely similar in the balanced and unbalanced conditions. The consistency in results might suggest that participants did not respond to the instructions regarding whether the test would be balanced or unbalanced. Given that the study list was always balanced, they might have treated every test as if it were balanced as well. If so, the evidence mixing hypothesis would predict no slope difference between MS-FW and MW-FS functions in either the balanced or unbalanced conditions. Thus, the results refute the evidence mixing account even if participants did not respond to the information about what types of items would be on the test.
The recollection and converging criteria accounts remain viable mechanisms for the slope effect, as they predict the effect even for balanced lists. Our next analyses test these accounts by evaluating their predictions regarding source judgments for unstudied items. The converging criteria account strongly predicts that source confidence will increase for new items that are higher in item strength, whereas the recollection account does not predict this pattern.
Datasets from Other Studies
We first evaluated the converging criteria account with 12 datasets from other studies, some published and some unpublished (the Appendix describes the source of each dataset in detail). Every experiment we considered used a task in which participants made recognition and source confidence ratings in immediate succession for each item on the test. The converging criteria account predicts that participants will be more likely to make high confidence source attributions when they are more confident that the item was studied, even for new items that were never seen in any source. Figure 5 plots the proportion of source responses made at each confidence level for new items, with the lightest colors representing the lowest levels of source confidence and darker colors representing higher confidence (responses are collapsed across source, so the lightest bars represent both low-confidence Source 1 and low-confidence Source 2 responses, and so on). Each bar includes only items that were called “studied” with low, medium, or high confidence. Although there is evidence that people can discriminate sources for targets they claim were not studied if their recognition criterion is conservative (Starns, Hicks, Brown, & Martin, 2008), we did not plot source decisions for items that participants did not think were studied (predictably, participants in each dataset almost always used the lowest source confidence for these items).
Figure 5.
Source confidence for new (unstudied) items in recognition/source datasets from other studies (see the Appendix for a description of the studies). Each plot shows results from a single dataset (DS) with a bar for each level of confidence that the item was studied (“not studied” responses are not shown). The proportion of source responses at each confidence level are displayed in different colors, with the lightest shade representing the lowest confidence level and the darkest representing the highest. Responses were collapsed across source; for example, the black bar represents high confidence claims for either Source 1 or Source 2.
In every dataset, the proportion of high confidence source responses is greatest for the highest level of recognition confidence. In fact, the increase in source confidence with increasing recognition confidence is often quite dramatic: In several datasets participants made almost no high confidence source responses for items recognized with low confidence but made high confidence source responses for the majority of items recognized with high confidence. The fact that they made so many high confidence source responses is surprising, considering that these items were never studied in any source. Clearly, these datasets provide strong support for the converging criteria account.
One potential criticism of our analysis is that the link between recognition and source confidence in these datasets could be an artifact of sequential response biases. Specifically, participants consistently show a tendency to repeat the response made on the last trial across many different types of decision tasks (Malmberg & Annis, 2012; Mueller & Weidemann, 2008; Ratcliff & Starns, 2009; Treisman & Williams, 1984; Ward & Wolff, 1973). In recognition memory, Mueller and Weidemann demonstrated that participants were not only biased to repeat responses, but they also had a tendency to repeat confidence levels even when they switched to a different response. For example, for an item that is judged “new,” a participant would be more likely to select a high confidence level if the previous test item received a high confidence “old” response than if the previous item received a low or medium confidence “old” response. Given that the twelve datasets in Figure 5 used a paradigm in which source judgments immediately followed recognition judgments for each test item, the relationship between recognition and source confidence might reflect sequential biases rather than an effect of item strength on how source confidence criteria are set. We addressed this concern with Experiments 2a and 2b.
Experiments 2a & 2b
To eliminate the influence of simple sequential biases, these experiments used a paradigm in which the recognition and source memory tests were broken into separate phases. After each study list, participants first completed a recognition test, and then they completed a source test that included all of the old items as well as any new items that the participant claimed to have studied. If participants are more willing to make high confidence source judgments for items with stronger item strength, then new items that created a stronger illusion of being studied in the recognition phase should get more high-confidence responses in the source phase.
We did not attempt to jointly model the recognition and source data, because both memory evidence and response criteria could change from the first test list to the second. Our primary interest was performance on the source test, and we used the recognition test to select lure items that were falsely recognized with low, medium, or high confidence. Although evidence can change between test lists, the lures that produced stronger item evidence in the first test should tend to produce stronger item evidence on the second. Thus, we can evaluate whether stronger item evidence makes people more willing to provide high-confidence source responses.
Method
Participants
Experiment 2a included 50 and Experiment 2b included 55 undergraduate students from the University of Massachusetts Amherst. Participants earned extra credit in their psychology courses. We excluded 3 participants in Experiment 2a and 10 in Experiment 2b for failing to use multiple levels of the confidence scale. We also excluded 11 participants in Experiment 2a and 4 in Experiment 2b for chance performance (proportion correct at or below .5 in one or more study/test cycles).
Materials and Procedure
Experiment 2a and 2b were identical to Experiment 1 except for the following details. Participants completed 4 study/test cycles instead of 6, and only the balanced condition was used. This yielded 40 source judgments for each item type within each strength condition, twice as many as Experiment 1. Since all of the study items were included on the test, participants were not informed about the number of presentations for male and female items before the test and were not asked to respond to the questions about how many times each class of items had been studied. After each study list and digit monitoring task, participants first completed a recognition test containing 20 strong targets (half male and half female), 20 weak targets (half male and half female), and 20 lures in a random order. They rated their confidence that each of the test items was old or new on a 6-point scale from “very sure new” to “very sure old.” Following the recognition test, participants completed a source test composed of all the studied items plus any lures that were called “old” on the recognition test. As in Experiment 1, participants rated their confidence that each word was spoken in a male or female voice on a 6-point scale from “very sure female” to “very sure male.” Participants were told their proportion of correct responses at the end of each test, and the feedback remained on the screen for 4 s.
Experiment 2b was identical to Experiment 2a except for the following change. After any “old” response (rating 4-6) on the recognition test and after each response on the source test, participants were asked to make a type of remember-know judgment. These responses are not analyzed below and will not be discussed further.
Results and Discussion
Recognition Memory
As is commonly observed, the recognition memory zROC functions were essentially linear with slopes less than 1. For the recognition fits, there were three item types (new items and strong and weak targets) with 5 degrees of freedom each. Both the dual process and continuous models used nine free parameters to fit these data. For the dual process model, there were two recollection parameters for strong and weak items, five response criteria, and two familiarity means for strong and weak items (with the lure familiarity mean fixed at zero and all standard deviations fixed at 1). For the continuous model, there were five response criteria and two evidence distribution means and standard deviations for strong and weak targets (with the lure distribution fixed at a mean of zero and standard deviation of one). We also fit a continuous model with a single standard deviation parameter for both strong and weak targets to test for variability differences, eliminating one free parameter.
The fit statistics for the recognition data are shown in Table 3. The continuous model appears to provide a better fit than the dual process model, but both models provided a satisfactory account of the data. The standard deviation in memory evidence was very similar for the strong and weak targets (1.39 vs. 1.43 in Experiment 2a, 1.38 vs. 1.49 in Experiment 2b), which reflects the fact that strength had very little effect on the zROC slopes. In Experiment 2a, both AIC and BIC preferred a continuous model with equal variability parameters (i.e., equal slopes) for strong and weak targets rather than a model with different slopes. In Experiment 2b, the AIC values were nearly identical for both versions of the continuous model, but BIC favored the equal-slope model. Analyses on parameters from individual-participant fits also supported this conclusion, with no significant difference between the strong and weak function variability parameters [Experiment 2a: 1.40 vs. 1.51, t(35) = 1.35, ns; Experiment 2b: 1.44 vs. 1.59, t(40) = 1.79, ns]. Recollection in the dual process model was higher in the strong condition than the weak condition [Experiment 2a: .55 vs. .33, t(35) = 4.07, p < .001; Experiment 2b: .49 vs. .35, t(40) = 3.07, p < .005]. The discriminability of the familiarity process (d’) was also higher in the strong than the weak condition in both experiments [Experiment 2a: 1.46 vs. 0.65, t(35) = 6.43, p < .001; Experiment 2b: 1.84 vs. 0.90, t(40) = 6.15, p < .001]. Overall, the recognition results were highly consistent with previous experiments using a strength manipulation (e.g., Heathcote, 2003; Ratcliff et al., 1992, 1994).
Table 3.
Fit statistics for the recognition memory data
| Fit Statistic |
|||
|---|---|---|---|
| Model | G2 (df) | AIC | BIC |
| Experiment 2a | |||
| Dual Process | 78.31 (6) | 202.34 | 265.91 |
| Continuous (2 target SDs) | 40.02 (6) | 164.04 | 227.62 |
| Continuous (1 target SD) | 40.38 (7) | 162.41 | 218.92 |
| Experiment 2b | |||
| Dual Process | 130.88 (6) | 257.18 | 321.92 |
| Continuous (2 target SDs) | 70.25 (6) | 196.55 | 261.33 |
| Continuous (1 target SD) | 73.63 (7) | 197.93 | 255.49 |
Note: The “2 target SDs” model had separate variability parameters for strong and weak targets, and the “1 target SD” model had a single variability parameter for both weak and strong. The target variability could differ from the lure variability in both models.
Source Memory
Figure 6 shows the source zROC functions from Experiments 2a and 2b. The functions look very similar to those from Experiment 1. The left panels show a clear slope difference between the MS-FW and MW-FS functions. In the right panels, the weak functions have a very slight u-shape, and the strong functions are basically linear.
Figure 6.
Source memory zROC functions from Experiments 2a and 2b. The first plot for each experiment shows the unequal-strength zROCs, and the second shows equal strength zROCs (the same data are displayed in each plot). Plusses mark the fit of the continuous model with unequal variances (UV), and x’s mark the fit of the dual process (DP) model. z(“male”|male) indicates the z score for the proportion of male items called “male,” and z(“male”|female) indicates the z score for the proportion of female items called “male.” MS – male strong; MW – male weak; FS – female strong; FW – female weak.
We applied the same source models that were used to fit the balanced condition in Experiment 1. Both models fit the data closely, but the fit statistics in Table 1 show an advantage for the unequal-variance version of the continuous model. As in Experiment 1, the continuous model accommodated the slope effect by increasing the evidence variability for the strong versus weak items, which is equivalent to compressing the source confidence criteria. The dual process model matched the slopes by proposing better source recollection for strong items (Table 2). The source familiarity parameters showed no hint of a strength effect in the dual process model.
Analyses on both the group and individual-participant fits confirmed that the strength effect on slope was reliable for both Experiments 2a and 2b. The AIC and BIC statistics clearly favored the unequal-variance version of the continuous model (which allows different slopes for MS-FW and MW-FS) over the equal-variance version (which does not; Table 1). G2 tests also showed that allowing free variances significantly improved the fits [Experiment 2a: G2(1) = 137.65, p < .001; Experiment 2b: G2(1) = 179.13, p < .001]. For the individual fits, we performed single-sample t-tests on the variability parameter in the strong condition to determine if it significantly differed from the weak variability parameter, which was fixed at 1. The strong variability parameters were significantly higher than 1 in both experiments [Experiment 2a: M = 1.53, t(35) = 8.53, p < .001; Experiment 2b: M = 1.50, t(40) = 9.06, p < .001]. We also analyzed the individual recollection parameters from the dual process model in a 2 (source) × 2 (strength) ANOVA. Source recollection was higher for strong than weak items for both Experiments [Exp. 2a: .38 vs. .11, F (1, 35) = 93.46, p < .001, MSE = .027; Exp. 2b: .42 vs .14, F (1,40) = 118.70, p < .001, MSE = .027]. Neither the source effect nor the interaction of source with strength approached significance for either experiment (lowest p = .26). Familiarity d’ in the dual process model did not significantly differ for strong and weak items in either experiment [Exp. 2a: 0.54 vs. 0.38, t(35) = 1.44, ns; Exp. 2b: 0.63 vs. 0.41, t(40) = 1.92, ns].
The source zROC functions showed clear slope differences for the unequal-strength functions, replicating the balanced condition from Experiment 1. Again, this violates the predictions of the evidence mixing account, but is consistent with both the converging criteria and recollection accounts. The critical test that distinguishes the latter two accounts centers on the source confidence ratings for new items that participants falsely claimed to remember, and we turn to those data next.
New Items
Figure 7 shows the proportion of low, medium, and high confidence source responses for new items that were falsely called “old” at the low, medium, or high confidence levels. Consistent with the data in Figure 5, participants were more likely to make high confidence source responses for unstudied items that were high in item strength. Chi-square tests confirmed the dependence between the recognition and source confidence levels [Exp. 2a: χ2 (4) = 111.97, p < .001; Exp. 2b: χ2 (4) = 24.36, p < .001]. Thus, the relationship observed in Figure 5 was not an artifact of making the recognition and source responses in immediate succession: the same pattern emerges when the two decisions are broken into separate tests.
Figure 7.
Source confidence for new (unstudied) items in Experiments 2a and 2b. Each plot has a bar for each level of confidence that the item was studied (new items that were called “unstudied” did not appear on the source test). The proportion of source responses at each confidence level are displayed in different colors, with the lightest shade representing the lowest confidence level and the darkest representing the highest. Responses were collapsed across source; for example, the black bar represents high confidence claims for either Male or Female.
Summary
The results of Experiments 2a and 2b nicely illustrate the problem for the continuous model that was identified by Yonelinas and Parks (2007): Strengthening items through repetition had no effect on recognition memory zROC slopes but had a large effect on unequal-strength source memory zROC slopes, even when the same participants performed both tasks following the same encoding lists. However, our data also reveal a solution to this conundrum: The source slope effect is produced not by actual changes in the variability of source evidence, but by converging source criteria like those assumed by Hautus et al. (2008). The converging criteria account made a specific prediction for responses to new items that was strongly confirmed in both experiments. Even for words not studied in either source, participants became more willing to make high confidence source responses for items that were judged to have higher item strength.
General Discussion
Yonelinas and Parks (2007) argued that the effect of unequal strength sources on zROC slope was inconsistent with a continuous model of source memory. They assumed that, to account for both recognition and source memory data, the continuous model required the unsupported assertion that additional learning increases the variability of source evidence but has no effect on the variability of item evidence. In contrast, we proposed two decision-based mechanisms that could produce the unequal strength slope effect even if additional learning had no influence on source evidence variability: evidence mixing and converging criteria. We tested these mechanisms in three experiments and with a reconsideration of 12 datasets from other studies. The evidence mixing account was strongly refuted by the results of our experiments. The unequal-strength source effect on zROC slope was observed in the balanced conditions of all 3 experiments, whereas the evidence mixing account predicted no slope difference with balanced tests (Figure 2, Panel C). In contrast, the converging criteria account was strongly supported. This account predicted that the slope effect would emerge even in the balanced conditions, as was observed empirically. More importantly, the converging criteria account made a novel prediction for the pattern of responses to new items that was confirmed in Experiments 2a and 2b as well as 12 other datasets: Participants made more high-confidence source responses for new items that were high in (illusory) item strength.
The dual process model was able to accommodate the unequal-strength source zROC slopes from each experiment. The numeric fit of the dual process model was worse than the continuous model even though the former had more free parameters, but we do not argue that this is strong evidence against the dual process account. A far more important failure of the dual process model is highlighted by the source judgments for new items in Experiments 2a and 2b. The dual process model explains the slope effect in terms of source recollection, a process that is not relevant for items that were never studied in either source (i.e., new items). Therefore, this model does not predict the relationship between source confidence and recognition confidence observed for unstudied items. As such, our data provide stronger support for the converging criteria account than the dual process account, as the dual process model would have to be elaborated to accommodate the new item data.
One way to extend the dual-process account would be to incorporate the converging criteria mechanism by assuming that participants are more willing to make high confidence source responses for test probes that are higher in item familiarity. Even if this possible extension is considered, the success of the converging criteria account shows that unequal-strength source zROC functions would not provide unique support for the dual process model. We have confirmation from 14 datasets that participants are indeed more willing to use high confidence source responses when item memory is strong, and this decision strategy produces the strength effect on zROC slope by itself, without the need for additional memory processes.
Combining recollection and converging criteria would also produce a model with two redundant mechanisms for explaining source zROC slopes, which would mean that researchers could not accurately estimate source recollection by fitting ROC functions. To illustrate this point, we fit the dual-process model to the simulated data from the model in Figure 1D, which has converging criteria and no threshold recollection process (the same simulated data that generated the zROC functions shown in the Figure). The source recollection (R) estimates were .16 for weak items and .56 for strong items. Of course, the data were actually generated with R = 0 for all conditions. This demonstrates that converging criteria produce data patterns that mimic the effects of source recollection, and zROC functions cannot discriminate the two. If the dual process model were extended to jointly accommodate recognition and source confidence ratings, then the data for new items could make it possible to separately estimate converging criteria and source recollection. In such a model, the question would be whether the data show any evidence of source recollection that cannot be accommodated by converging criteria.
ROC Functions and Memory Processes
Our results reinforce a more general conclusion highlighted in recent modeling efforts: zROC slopes and shapes do not provide direct measures of memory evidence characteristics (Benjamin et al., 2009; Mueller & Weidemann, 2008; Ratcliff & Starns, 2009; Rouder, Pratte, & Morey, 2010; Starns, Ratcliff, & McKoon, 2012; Van Zandt, 2000; see also Schulman & Greenberg, 1970; Treisman & Faulkner, 1984, for related results in perception). This problem can be shown in a number of ways. Estimated values of recollection and familiarity in the dual process model – as well as the relative variability of distributions in the continuous model – are critically dependent on distributional assumptions (Rouder et al., 2010; but see Wixted & Mickes, 2010, for a defense of common distributional assumptions). Moreover, when more complete models are developed that accommodate response time (RT) data in addition to response proportions, changes in decision criteria can influence zROC slope and shape in a variety of ways (Ratcliff & Starns, 2009; Van Zandt, 2000). The continuous and dual process signal detection models both assume that slope and shape map directly onto memory processes; thus, they are prone to returning invalid interpretations.
Our results also demonstrate that changes in response criteria can masquerade as changes in memory processes. Converging source criteria produce a slope effect that the dual process approach interprets as a change in source recollection and a standard continuous approach interprets as a change in the variability of source evidence. Coincidentally, it is interesting to note that the source zROCs predicted with a likelihood ratio decision rule in Figure 2 (Panel D) are slightly u-shaped (Hautus et al., 2008), when the exact same memory evidence distributions would predict linear functions with linear criteria – yet another way that decision assumptions can influence zROC characteristics. Given all of these factors, conclusions that rely on the specific values of memory evidence parameters should be considered with caution. In the future, theorists should make concerted efforts to explore whether their conclusions are robust to changing assumptions about distributional form and decision processes.
Source zROC Shape and RT Modeling
As mentioned in the introduction, researchers have attempted to discriminate the dual process and continuous models by evaluating whether source memory zROCs are u-shaped (dual process) or linear (continuous). Our findings replicate previous demonstrations that zROCs are slightly u-shaped when memory is weak and basically linear when memory is strong (Slotnick & Dodson, 2005; Wixted, 2007a). This result fails to strongly support either model, and theorists from both camps have offered potential explanations for the variation in shape based on memory strength. Proponents of the continuous model have suggested that low-performance conditions are contaminated with trials that are pure guesses, which can artifactually produce u-shaped functions (Kelley & Wixted, 2001; Slotnick & Dodson, 2005; Wixted, 2007a). Dual process theorists have proposed that source-specific familiarity increases with strong learning, producing more linear source memory zROCs. One difficulty with the dual-process account is that strong learning should also increase source recollection (see Wixted, 2007b, for a detailed critique). Indeed, fits of the dual process model to our data indicate that additional learning had a large influence on source recollection with no discernible effect on source-specific familiarity. Nevertheless, our source zROCs were essentially linear in the strong conditions.
The recent development of sequential sampling models for both zROC and RT data might shed new light on the interpretation of source zROC shapes (Ratcliff & Starns, 2009; Starns, Ratcliff, & McKoon, 2012; Dube et al., 2012). The RTCON model includes decision criteria representing how much evidence must accumulate for a particular confidence level before a participant will make the corresponding response. Unlike signal detection models, changing the position of these decision criteria can affect both zROC slope and zROC shape (Ratcliff & Starns, 2009). Critically, the shape of the zROC function follows the contour of the decision criteria, with u-shaped functions when participants are biased to use the middle confidence responses and are reluctant to use the high-confidence responses at the end of the scale. Our source data for new items suggest that people are generally reluctant to use the high-confidence levels in their source judgments when item evidence is weak, but become more willing to make high confidence source judgments for strong item memories. When this pattern is translated into the decision criteria of the RTCON model, the model predicts that zROCs should be more u-shaped when item evidence is weak versus when it is strong. This, of course, is precisely the pattern observed in source experiments. Therefore, considering RT data in addition to zROC data might be critical for understanding source zROC shape.
As noted, a likelihood ratio decision rule can also produce u-shaped source zROCs even without a threshold recollection process. However, it is unclear whether this mechanism can produce both u-shaped functions for a weak class of items and linear functions for a strong class of items, as observed in our experiments. Likelihood bounds do predict that strong conditions should have zROC points that are more tightly grouped (because the criteria converge), which would at least make it harder to detect a u-shape in the strong function.
Parameter Plausibility and Process Models
Our results show that continuous theorists can make the same assumptions about evidence variability for recognition and source tasks; that is, variability is higher for studied than non-studied items but does not increase with additional learning. In source tasks, additional learning only appears to increase variability because source confidence criteria converge as item evidence increases. However, some challenge the assumption that additional learning does not affect variability as implausible in itself: If being presented on the list increases variability for targets relative to lures (as assumed by continuous theorists, e.g., Wixted, 2007), then being on the list multiple times (or for a longer period of time) should increase the variability even more (Koen & Yonelinas, 2010; Yonelinas & Parks, 2007). Koen and Yonelinas recently published a demonstration that varying encoding time over two levels does not reduce zROC slope compared to one constant encoding time, which they suggest is inconsistent with the idea that zROC slopes reflect evidence variability. However, Jang, Mickes, and Wixted (2012) and Starns, Rotello, and Ratcliff (2012) demonstrate that their manipulation would not be predicted to affect zROC slope even under a variability-based account. More generally, whether or not the variability levels needed to accommodate zROC slopes are psychologically plausible is a question that can only be addressed in terms of process models that specify how memory evidence is generated. We briefly discuss some prominent process models and their implications for this debate.
The idea that learning increases the variability for targets compared to lures is supported by a wide range of process models of memory, including both the older class of global matching models (see Clark & Gronlund, 1996, for a review) and the newer Bayesian matching models (Dennis & Humphreys, 2001; McClelland & Chappell, 1998; Shiffrin & Steyvers, 1997). All of these models align with the continuous approach, as they assume that decisions are based on a single, continuously varying match strength between a memory probe and the contents of memory. Many of these models do predict that variability should continue to increase with additional learning, which is inconsistent with empirical results (Ratcliff et al., 1992). However, some process models can predict constant zROC slopes with additional learning. For example, Shiffrin and Steyvers (1997) report a simulation of the Retrieving Effectively from Memory (REM) model with two levels of target strength. The zROC slopes were less than one for both functions and roughly equal for strong and weak targets. This demonstrates that it is possible to develop a continuous model that accommodates zROC slopes without predicting that slopes decrease with additional learning (also see McClelland & Chappell, 1998).
Theorists should also acknowledge that the parameter plausibility issue cuts both ways. That is, we should also consider whether or not there is a process model underlying the dual process account that explains how variables influence the recollection and familiarity processes. To take an example from our own results, why should it be the case that additional learning has a large effect on familiarity in the recognition task but no discernible effect on familiarity in the source task? This is a central question, given that dual process theorists have explicitly claimed that zROCs for stronger items should reflect higher levels of source-specific familiarity (Parks & Yonelinas, 2007). Clearly, psychologically validating the constellation of parameters needed to accommodate empirical results is a substantial challenge for both continuous and dual process theorists.
Likelihood Ratio Decision Bounds
The converging criteria account might simply reflect some general heuristic whereby participants are unwilling to confidently specify the source of an item when they are not even confident that it was studied, a tendency that Klauer and Kellen (2010) call the principle of consistency. Another possibility is that people use something approximating a likelihood ratio decision rule, as depicted in Panel D of Figure 2 (Hautus et al., 2008). This is an attractive alternative, because likelihood ratio bounds produce optimal decision making. A common criticism leveled against likelihood-based accounts is that participants could not possibly have sufficient knowledge of the evidence distributions to define the likelihoods (Hintzman, 1994). However, participants might base likelihood judgments of rough estimates of the underlying distributions even if they are incapable of computing true likelihood ratios. In fact, Turner, Van Zandt, and Brown (2011) recently developed a model in which likelihood estimates begin with relatively impoverished estimates that are refined based on experience with the test stimuli. This could provide a psychologically plausible mechanism by which people implement a likelihood-based decision rule.
Before we conclude the discussion of likelihood-ratio decision bounds, we must qualify that our results only refute the evidence mixing account with linear response boundaries. Likelihood-ratio bounds actually implement evidence mixing when there are unequal-strength sources; that is, the bounds change their orientation based on whether Source 1 or Source 2 is stronger, similar to Panels A and B in Figure 2 (except that the likelihood bounds do not follow straight lines). Therefore, a likelihood-based decision rule can potentially encompass both an evidence mixing mechanism with unbalanced lists and a converging criteria mechanism with balanced lists. As noted, evidence mixing alone cannot explain the full pattern of slope effects, but a likelihood-ratio approach that has evidence mixing as a special case could be quite successful.
Conclusion
Theorists have made many attempts to explain the shape and slope of source memory zROC functions in terms of memory processes (e.g., Wixted, 2007a; Yonelinas & Parks, 2007). Our results demonstrate that decision processes can have a substantial impact on these characteristics, joining a number of previous demonstrations in which decision variables affect zROC slope and/or shape (Hautus et al., 2008; Mueller & Weidemann, 2008; Ratcliff & Starns, 2009; Van Zandt, 2000). Responding for new items demonstrates that participants change the way that they map source evidence onto levels of the confidence scale depending on item strength, and researchers must acknowledge the effects of this decision strategy when attempting to interpret source memory zROCs.
Acknowledgments
Collection of some of the datatsets in Figure 5 was supported by grant MH 60274 from the National Institute of Mental Health to C.M.R.
Appendix
This appendix describes the datasets that contributed data to Figure 5.
Published Studies
Datasets 1-5 in Figure 5 are from published studies in which participants were required to make confidence ratings for both their old/new and source decisions for each test item. Specific methodological details can be found in the Method sections of the published reports.
Dataset 1
Experiment 2 from Slotnick, Klein, Dodson, and Shimamura (2000).
Dataset 2
Experiment 3 from Slotnick et al. (2000).
Dataset 3
Experiment 1 from Slotnick and Dodson (2005).
Dataset 4
Experiment 2 from Slotnick and Dodson (2005).
Dataset 5
Experiment 2 from Yonelinas (1999).
Unpublished Data
Datasets 6-12 were taken from unpublished data collected at the University of Massachusetts Amherst. We provide a rough outline of the methods for each experiment.
Dataset 6
Datasets 6, 7, and 8 are three between-subject conditions from the same experiment. For dataset 6, 18 subjects studied 80 words presented in a female voice and 80 words presented in a male voice. At test, subjects were presented with the 160 studied items along with 80 new items. For each test item, subjects first rated their confidence that the word had been studied on a 6-point scale from “sure old” to “sure new.” Then, regardless of their old-new confidence response, subjects rated their confidence that the word had been presented in a male voice or a female voice, on a 6-point scale from “sure male” to “sure female.” Before completing the recognition test, subjects were told that about half of the test items had appeared on the study list.
Dataset 7
Eighteen subjects completed this condition, in which subjects studied 106 words presented in a male voice and 54 words presented in a female voice. At test, subjects were presented with the 106 studied male items, the 54 studied female items, and 80 new items. Subjects rated their old-new and source confidence as described in dataset 6. Prior to the start of the test, subjects were instructed that about two-thirds of the studied test items had been presented in a male voice.
Dataset 8
Eighteen subjects completed this condition. The procedure for this condition was the same as described in dataset 6, except that the test was composed of the 80 words studied in a male voice, a randomly-chosen half of the words studied in a female voice, and 120 lures. Because of a programming error, about half the subjects in this condition were tested on a few (range 2-11; median=2) lures twice. Additionally, all subjects were tested on at least one “lure” that was actually a studied item (range 1-11, median=7). These trials were removed prior to data analysis, resulting in a loss of 9% of lure trials, on average. No subjects’ lure data loss exceeded 11%. Subjects were told that about two-thirds of the studied test items had been presented in a male voice.
Dataset 9
Datasets 9 and 10 are two between-subject conditions from the same experiment. The procedure for these datasets was identical to the procedure described in dataset 6 except that response bias was manipulated with a payoff scheme that differed across conditions. Dataset 9 included 24 subjects, and immediately prior to testing, subjects were told that they would earn 2 points for every correct response and lose 3 points for every error (the points earned were converted to ticket entries in a lottery for a $50 prize). All other details were the same as described for dataset 6.
Dataset 10
Twenty-two subjects completed this condition. All procedures were the same as above, except that subjects were told that they would earn 2 points for every correct response, they would lose 5 points for responding “male” when the word had actually been presented in a female voice, and they would lose 1 point for responding “female” when the word had been presented in a male voice. Thus, the payoff matrix was intended to yield a preference to respond “female.”
Dataset 11
Datasets 11 and 12 are two between-subject conditions from the same experiment. The procedure for these datasets was identical to the procedure described in dataset 6 except that the memory strength of one source relative to the other was manipulated across conditions. Dataset 11 included 24 subjects, and at test, half of the 80 items studied in a male voice and half of the 80 items studied in a female voice were randomly selected and presented as targets along with 40 new words.
Dataset 12
Twenty-three subjects completed this condition. All procedures were the same as described above except that at study, 80 words were presented once each in the female voice and 40 words were presented twice each in the male voice. The test was composed of all 40 words presented in the male voice, a randomly-selected half of the 80 words presented in the female voice, and 40 new words.
Footnotes
Some researchers have developed dual-process models that accommodate false recollection (e.g., Stahl & Klauer, 2009) or recollection that is graded across confidence levels (e.g., Rotello, Macmillan, Hicks, & Hautus, 2006), but the standard dual-process model generates predictions under the assumption that recollection always produces correct, high-confidence responses.
Publisher's Disclaimer: The following manuscript is the final accepted manuscript. It has not been subjected to the final copyediting, fact-checking, and proofreading required for formal publication. It is not the definitive, publisher-authenticated version. The American Psychological Association and its Council of Editors disclaim any responsibility or liabilities for errors or omissions of this manuscript version, any version derived from this manuscript by NIH, or other third parties. The published version is available at www.apa.org/pubs/journals/xlm
References
- Akaiki H. Information theory as an extension of the maximum likelihood principle. In: Petrov BN, Csaki F, editors. Second International Symposium on Information Theory. Akademiai Kiado; Budapest: 1973. pp. 267–281. [Google Scholar]
- Ashby FG, Townsend JT. Varieties of perceptual independence. Psychological Review. 1986;93:154–179. [PubMed] [Google Scholar]
- Banks WP. Recognition and source memory as multivariate decision processes. Psychological Science. 2000;11:267–273. doi: 10.1111/1467-9280.00254. [DOI] [PubMed] [Google Scholar]
- Benjamin AS, Diaz M, Wee S. Signal detection with criterion noise: Applications to recognition memory. Psychological Review. 2009;116:84–115. doi: 10.1037/a0014351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bröder A, Schütz J. Recognition ROCs are curvilinear – or are they? On premature arguments against the two-high-threshold model of recognition. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2009;35:587–606. doi: 10.1037/a0015279. [DOI] [PubMed] [Google Scholar]
- Clark SE, Gronlund SD. Global matching models of recognition memory: How the models match the data. Psychonomic Bulletin & Review. 1996;3:37–60. doi: 10.3758/BF03210740. [DOI] [PubMed] [Google Scholar]
- DeCarlo LT. Source monitoring and multivariate signal detection theory, with a model for selection. Journal of Mathematical Psychology. 2003;47:292–303. [Google Scholar]
- Dennis S, Humphreys MS. A context noise model of episodic word recognition. Psychological Review. 2001;108:452–478. doi: 10.1037/0033-295x.108.2.452. [DOI] [PubMed] [Google Scholar]
- Dube C, Rotello CM. Binary ROCs in perception and recognition memory are curved. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2012;38:130–151. doi: 10.1037/a0024957. [DOI] [PubMed] [Google Scholar]
- Dube C, Starns JJ, Rotello CM, Ratcliff R. Beyond ROC curvature: Strength effects and response time data support continuous-evidence models of recognition memory. Journal of Memory and Language. 2012;67:389–406. doi: 10.1016/j.jml.2012.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egan JP. Recognition memory and the operating characteristic (Tech. Note AFCRC-TN-58-51) Hearing and Communication Laboratory, Indiana University; 1958. [Google Scholar]
- Elfman KW, Parks CM, Yonelinas AP. Testing a neurocomputational model of recollection, familiarity, and source recognition. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2008;34:752–768. doi: 10.1037/0278-7393.34.4.752. [DOI] [PubMed] [Google Scholar]
- Glanzer M, Hilford A, Kim K. Six regularities of source recognition. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2004;30:1176–1195. doi: 10.1037/0278-7393.30.6.1176. [DOI] [PubMed] [Google Scholar]
- Glanzer M, Kim K, Hilford A, Adams JK. Slope of the receiver-operating characteristic in recognition memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1999;25:500–513. [Google Scholar]
- Hautus MJ, Macmillan NA, Rotello CM. Toward a complete decision model of item and source recognition. Psychonomic Bulletin & Review. 2008;15:889–905. doi: 10.3758/PBR.15.5.889. [DOI] [PubMed] [Google Scholar]
- Heathcote A. Item Recognition Memory and the Receiver Operating Characteristic. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2003;29:1210–1230. doi: 10.1037/0278-7393.29.6.1210. [DOI] [PubMed] [Google Scholar]
- Hilford A, Glanzer M, Kim K, DeCarlo LT. Regularities of source recognition: ROC analysis. Journal of Experimental Psychology: General. 2002;131:494–510. doi: 10.1037//0096-3445.131.4.494. [DOI] [PubMed] [Google Scholar]
- Hintzman DL. On explaining the mirror effect. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1994;20:201–205. [Google Scholar]
- Jang Y, Mickes L, Wixted JT. Three tests and three corrections: Comment on Koen and Yonelinas (2010) Journal of Experimental Psychology: Learning, Memory, and Cognition. 2012;38:513–523. doi: 10.1037/a0025880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelley R, Wixted JT. On the nature of associative information in recognition memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2001;27:701–722. [PubMed] [Google Scholar]
- Klauer KC, Kellen D. Toward a complete decision model of item and source recognition: A discrete-state approach. Psychonomic Bulletin & Review. 2010;17:465–478. doi: 10.3758/PBR.17.4.465. [DOI] [PubMed] [Google Scholar]
- Koen JD, Yonelinas AP. Memory variability is due to the contribution of recollection and familiarity, not encoding variability. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2010;36:1536–1542. doi: 10.1037/a0020448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malmberg KJ, Annis J. On the relationship between memory and perception: Sequential dependencies in recognition memory testing. Journal of Experimental Psychology: General. 2012;141:233–259. doi: 10.1037/a0025277. [DOI] [PubMed] [Google Scholar]
- McClelland JL, Chappell M. Familiarity breeds differentiation: A subjective-likelihood approach to the effects of experience in recognition memory. Psychological Review. 1998;105:724–760. doi: 10.1037/0033-295x.105.4.734-760. [DOI] [PubMed] [Google Scholar]
- Mueller ST, Weidemann CT. Decision noise: An explanation for observed violations of signal detection theory. Psychonomic Bulletin & Review. 2008;15:465–494. doi: 10.3758/pbr.15.3.465. [DOI] [PubMed] [Google Scholar]
- Onyper SV, Zhang YX, Howard MW. Some-or-none recollection: Evidence from item and source memory. Journal of Experimental Psychology: General. 2010;139:341–364. doi: 10.1037/a0018926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parks CM, Yonelinas AP. Moving beyond pure signal-detection models: Comment on Wixted (2007) Psychological Review. 2007;114:188–201. doi: 10.1037/0033-295X.114.1.188. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, McKoon G, Tindall MH. Empirical generality of data from recognition memory receiver-operating characteristic functions and implications for the global memory models. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1994;20:763–785. doi: 10.1037//0278-7393.20.4.763. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Sheu C-F, Gronlund S. Testing global memory models using ROC curves. Psychological Review. 1992;99:518–535. doi: 10.1037/0033-295x.99.3.518. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Starns JJ. Modeling confidence and response time in recognition memory. Psychological Review. 2009;116:59–83. doi: 10.1037/a0014086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rotello CM, Macmillan NA, Hicks JL, Hautus M. Interpreting the effects of response bias on remember-know judgments using signal-detection and threshold models. Memory & Cognition. 2006;34:1598–1614. doi: 10.3758/bf03195923. [DOI] [PubMed] [Google Scholar]
- Rouder JN, Pratte MS, Morey RD. Latent mnemonic strengths are latent: A comment on Mickes, Wixted, and Wais (2007) Psychonomic Bulletin & Review. 2010;17:427–435. doi: 10.3758/PBR.17.3.427. [DOI] [PubMed] [Google Scholar]
- Schulman AI, Greenberg GZ. Operating characteristics and a priori probability of the signal. Perception & Psychophysics. 1970;8:317–320. [Google Scholar]
- Schwartz G. Estimating the dimension of a model. The Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Shiffrin RM, Steyvers M. A model for recognition memory: REM – retrieving effectively from memory. Psychonomic Bulletin and Review. 1997;4:145–166. doi: 10.3758/BF03209391. [DOI] [PubMed] [Google Scholar]
- Slotnick SD, Dodson CS. Support for a continuous (single-process) model of recognition memory and source memory. Memory & Cognition. 2005;33:151–170. doi: 10.3758/bf03195305. [DOI] [PubMed] [Google Scholar]
- Slotnick SD, Klein SA, Dodson CS, Shimamura AP. An analysis of signal detection and threshold models of source memory. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2000;26:1499–1517. doi: 10.1037//0278-7393.26.6.1499. [DOI] [PubMed] [Google Scholar]
- Stahl C, Klauer KC. Measuring phantom recollection in the simplified conjoint recognition paradigm. Journal of Memory and Language. 2009;60:180–193. [Google Scholar]
- Starns JJ, Hicks JL, Brown NL, Martin BA. Source memory for unrecognized items: Predictions from multivariate signal detection theory. Memory & Cognition. 2008;36:1–8. doi: 10.3758/mc.36.1.1. [DOI] [PubMed] [Google Scholar]
- Starns JJ, Ratcliff R, McKoon G. Evaluating the unequal-variance and dual-process explanations of zROC slopes with response time data and the diffusion model. Cognitive Psychology. 2012;64:1–34. doi: 10.1016/j.cogpsych.2011.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starns JJ, Ratcliff R, White CN. Diffusion model drift rates can be influenced by decision processes: An analysis of the strength-based mirror effect. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2012;38:1137–1151. doi: 10.1037/a0028151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starns JJ, Rotello CM, Ratcliff R. Mixing strong and weak targets provides no evidence against the unequal-variance explanation of ʐROC slope: A comment on Koen and Yonelinas (2010) Journal of Experimental Psychology: Learning, Memory, and Cognition. 2012;38:793–801. doi: 10.1037/a0027040. [DOI] [PubMed] [Google Scholar]
- Starns JJ, White CN, Ratcliff R. A direct test of the differentiation mechanism: REM, BCDMEM, and the strength-based mirror effect in recognition memory. Journal of Memory and Language. 2010;63:18–34. doi: 10.1016/j.jml.2010.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starns JJ, White CN, Ratcliff R. The strength-based mirror effect in subjective strength ratings: The evidence for differentiation can be produced without differentiation. Memory and Cognition. 2012;40:1189–1199. doi: 10.3758/s13421-012-0225-1. [DOI] [PubMed] [Google Scholar]
- Treisman M, Faulkner A. The effect of signal probability on the slope of the receiver operating characteristic given by the rating procedure. British Journal of Mathematical and Statistical Psychology. 1984;37:199–215. [Google Scholar]
- Treisman M, Williams TC. A theory of criterion setting with an application to sequential dependencies. Psychological Review. 1984;91:68–111. [Google Scholar]
- Turner BM, Van Zandt T, Brown S. A dynamic stimulus-driven model of signal detection. Psychological Review. 2011;118:583–613. doi: 10.1037/a0025191. [DOI] [PubMed] [Google Scholar]
- Van Zandt T. ROC curves and confidence judgments in recognition memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2000;26:582–600. doi: 10.1037//0278-7393.26.3.582. [DOI] [PubMed] [Google Scholar]
- Ward LM, Wolff G. Repeated magnitude estimations with a variable standard: Sequential effects and other properties. Perception & Psychophysics. 1973;13:193–200. [Google Scholar]
- Wixted JT. Dual-Process Theory and Signal-Detection Theory of Recognition Memory. Psychological Review. 2007a;114:152–176. doi: 10.1037/0033-295X.114.1.152. [DOI] [PubMed] [Google Scholar]
- Wixted JT. Spotlighting the probative findings: Reply to Parks and Yonelinas (2007) Psychological Review. 2007b;114:203–209. [Google Scholar]
- Wixted JT, Mickes L. Useful scientific theories are useful: A reply to Rouder, Pratte, and Morey (2010) Psychonomic Bulletin & Review. 2010;17:436–442. [Google Scholar]
- Yonelinas AP. Receiver-operating characteristics in recognition memory: Evidence for a dual-process model. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1994;20:1341–1354. doi: 10.1037//0278-7393.20.6.1341. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP. The contribution of recollection and familiarity to recognition and source-memory judgments: A formal dual-process model and an analysis of receiver operating characterstics. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1999;25:1415–1434. doi: 10.1037//0278-7393.25.6.1415. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP, Parks CM. Receiver operating characteristics (ROCs) in recognition memory: A review. Psychological Bulletin. 2007;133:800–832. doi: 10.1037/0033-2909.133.5.800. [DOI] [PubMed] [Google Scholar]