Validating the unequal-variance assumption in recognition memory using response time distributions instead of ROC functions: A diffusion model analysis

Abstract

Recognition memory z-transformed Receiver Operating Characteristic (zROC) functions have a slope less than 1. One way to accommodate this finding is to assume that memory evidence is more variable for studied (old) items than non-studied (new) items. This assumption has been implemented in signal detection models, but this approach cannot accommodate the time course of decision making. We tested the unequal-variance assumption by fitting the diffusion model to accuracy and response time (RT) distributions from nine old/new recognition data sets comprising previously-published data from 376 participants. The η parameter in the diffusion model measures between-trial variability in evidence based on accuracy and the RT distributions for correct and error responses. In fits to nine data sets, η estimates were higher for targets than lures in all cases, and fitting results rejected an equal-variance version of the model in favor of an unequal-variance version. Parameter recovery simulations showed that the variability differences were not produced by biased estimation of the η parameter. Estimates of the other model parameters were largely consistent between the equal- and unequal-variance versions of the model. Our results provide independent support for the unequal-variance assumption without using zROC data.

Recognition memory involves deciding whether or not a given item was previously encountered in a particular context, such as whether a particular word was in a study list. In a standard recognition experiment, participants are asked to respond “old” for words that they studied (targets) and “new” for words that they did not (lures). Theorists agree that recognition judgments can be influenced by various types of information (e.g., Johnson, Hashtroudi, & Lindsay, 1993), and a popular assumption is that recognition decisions are based on a single overall strength value derived by combining all of these types of evidence (Ratcliff, 1978; Wixted, 2007). This univariate approach has been implemented in signal detection models that are used to fit receiver-operating characteristic (ROC) functions, which are plots that show the relative change in correct versus incorrect responding over a number of levels of response bias (Egan, 1958). The points on an ROC function are often converted to z-scores, yielding a zROC function.

Recognition memory zROC functions have a slope less than one, and this result has been replicated in dozens of experiments (for reviews see Wixted, 2007; Yonelinas & Parks, 2007). Researchers have accommodated this pattern by assuming that evidence strength is more variable for targets than for lures (Egan, 1958). Some have suggested that this is an unjustified and ad hoc assumption (DeCarlo, 2002; Koen & Yonelinas, 2010), although many process models of recognition memory do produce unequal-variance distributions (Gillund & Shiffrin, 1984; Hintzman, 1986; McClelland & Chappell, 1998; Ratcliff, Sheu, & Gronlund, 1992; Shiffrin & Steyvers, 1997). Moreover, the unequal-variance assumption has been justified by noting that some targets will be learned more effectively than others, introducing an extra source of variability for these items (e.g., Wixted, 2007). Although this seems like a compelling argument for unequal variance, the learning-variability account remains controversial (e.g., Koen & Yonelinas, 2010).

Our goal was to test the unequal-variance assumption using response time (RT) data. We achieved this by fitting the diffusion model to accuracy and RT distributions from recognition memory experiments (Ratcliff, 1978). This model is capable of estimating between-trial variability in memory evidence (as explained in detail shortly), and we will take advantage of this property to test for unequal variances without relying on ROC data. If the unequal-variance assumption is valid, then diffusion model estimates should indicate that memory evidence is more variable for targets than for lures.

The Diffusion Model

The diffusion model has been successfully applied to accuracy and RT data across a wide variety of two-choice decision tasks (for reviews, see Ratcliff & McKoon, 2008; Wagenmakers, 2009). The model assumes that evidence is sampled from a stimulus over time, and the decision maker accumulates evidence from these samples until one of the two response alternatives is sufficiently supported. As shown in Figure 1, this process is modeled by establishing two response boundaries for each alternative response, such as “old” versus “new” in a recognition task. The distance between the boundaries (a) represents response caution, with wide boundaries indicating that a great deal of evidence must accumulate before a decision is made. The evidence accumulation process begins at a starting point z between these two boundaries and approaches one boundary or the other with an average drift rate v. The starting point represents response biases (for example, moving it closer to the top boundary would produce a bias toward “old” responses) and the drift rate represents the strength of evidence from the stimulus. Drift rate varies from moment to moment within a trial to reflect variability in evidence samples, and the standard deviation (SD) of this variation is treated as scaling parameter, s. Following convention, we set s to .1 in all experimental conditions (although it is actually only necessary to fix s in a single condition; Donkin, Brown, and Heathcote, 2009). The accumulation process continues until it reaches one of the boundaries, at which point the corresponding response is made. An additional non-decision time (T_er) is added to the duration of the accumulation process to produce the total time for the trial. T_er absorbs the time for processes like constructing a memory probe for the test word and pressing the response key after a decision has been made.

Figure 1.

The diffusion model for two-choice responding (this Figure was first presented by Starns, Ratcliff, & McKoon, 2012). The top panel shows distributions of drift rates across test trials for both targets (mean = ν_T) and lures (mean =ν_L). The vertical line is the drift criterion (dc), and the drift rate on each trial is determined by the distance from the drift criterion to a value sampled from the drift distribution, as shown with the dashed line. The bottom panel shows three examples of accumulation paths for a trial with the displayed drift rate. The starting point of accumulation follows a uniform distribution with mean z and range s_Z. Paths terminating on the top and bottom boundaries produce “old” and “new” responses, respectively.

The model includes across-trial variability in all of the major parameters, and this variability is critical for matching empirical data (Ratcliff & McKoon, 2008; Ratcliff, Van Zandt, & McKoon, 1999). Starting point and non-decision time have uniform distributions across trials with ranges s_Z and s_T, respectively. Most importantly for our purposes, drift rates also vary across trials; for example, some old items are particularly well-learned and produce high positive drift rates, whereas other old items are poorly learned and produce lower positive drift rates or even negative drift rates. The Gaussian distributions in Figure 1 show the between-trial variation in drift, and the SD of these drift distributions is estimated with the parameter η. The drift criterion is a subject-controlled parameter representing how strong memory evidence needs to be for the accumulation process to move toward the top boundary. The drift rate for each trial is determined by the distance between the drift criterion and a value sampled from the drift distribution, with negative drifts for values below the criterion and positive drifts for values above it.

Nearly all previous applications of the diffusion model have used a fixed η parameter across all stimulus types, even for recognition memory experiments (Criss, 2010; Ratcliff, Thapar, & McKoon, 2004, 2010; Starns, Ratcliff, & White, 2012). In other words, previous RT modeling efforts assume that memory evidence is equally variable for targets and lures. Fixing the η parameter is partially motivated by the fact that this parameter has high estimation variability (Ratcliff & Tuerlinckx, 2002). Starns, Ratcliff, and McKoon (2012) fit the diffusion model to zROC data from a two-choice task with a bias manipulation, and a model with higher η values for targets than for lures out-performed an equal-variance version of the model. However, the main failure of the equal-variance version was that it could not accommodate the zROC slopes. Our goal here is to determine if the unequal-variance assumption is supported independently of zROC data. Accordingly, we focused on two-choice experiments without bias manipulations, meaning that η estimates were based solely on accuracy and the RT distributions for correct and error responses.

Evidence Variability and RT Distributions

Figure 2 demonstrates the impact of evidence variability on accuracy and RT predictions. The first panel shows that increasing drift variability (η) decreases accuracy if all of the other parameters are held constant. This effect is intuitive: adding noise to memory evidence should degrade performance. However, the effect of η on accuracy does not actually help to estimate unique values of the parameter in fits, because the other parameter values are not held constant (i.e., they are simultaneously being optimized to fit the data). Specifically, any condition with a free η value in fits of the model will also have a free parameter for the average drift rate (ν), and this parameter can be adjusted to match the accuracy level regardless of the η value. For example, if η is increased, ν can also be increased to cancel out the drop in accuracy. Fortunately, different combinations of η and ν produce different RT distributions even when they produce the same accuracy value, and this is why unique values of η can potentially be recovered from fits.

Figure 2.

Effects of the η parameter on accuracy and RT distributions. Panel 1 shows how increasing η affects accuracy when other parameters are held constant. Panel 2 shows predicted response time (RT) distributions for correct responses (top) and errors (bottom) with either a low (.1) or high (.2) value of the η parameter. The .1, .5, and .9 RT quantiles are labeled on each plot. Accuracy was manipulated by varying the drift rate over a range from 0 to .4. Values of the other parameters were a = .12, z = .06, s_Z = .02, T_er = 400 ms, s_T = 150 ms, p_O = .001.

The second panel of Figure 2 shows how different values of η affect RT distributions at a given accuracy level. The solid lines show predictions with a low value of η (.10) and the dashed lines show a higher value of η (.20).¹ Predictions are shown over a range of average drift rates (ν) from 0 to .4, which represents evidence for target items ranging from no memory to very strong memory. RT predictions are shown for both correct responses (processes that terminate on the “studied” boundary) and errors (processes that terminate on the “not studied” boundary). The three groups of lines on each plot are the .1, .5, and .9 quantiles of the predicted RT distributions; that is, the points in time at which 10%, 50%, or 90% of the responses have already been made. The .1 quantile shows the leading edge of the distribution; that is, the point at which the fastest responses are beginning to be made. The .5 quantile shows the central tendency of the RT distribution, and the .9 quantile shows the tail of the distribution. For correct responses, increasing evidence variability decreases RTs. The variability effect is small for the leading edge of the distribution, slightly larger for the median, and larger still for the tail. For error responses, the effect of evidence variability depends on the overall accuracy level: higher η values produce faster error responses when accuracy is low and slower error responses when accuracy is high. In general, higher η values produce faster correct responses relative to errors, but this pattern can only be clearly seen for high accuracy values (Ratcliff & McKoon, 2008).

Figure 2 illustrates several important points. First, the figure illustrates that the model should be able to correctly recover η values from RT distributions, but estimation of this parameter could be quite noisy given its subtle effects on the data and the inherent variability in empirical RT distributions (especially for low-probability responses such as errors in high-accuracy conditions). Thus, many observations are needed to validly assess the unequal-variance assumption. Second, one might be tempted to conclude that RT distributions support an equal-variance model, given that many data sets have been successfully fit with a single η parameter for targets and lures. However, Figure 2 reveals that the misses resulting from imposing an equal-variance model on unequal-variance data would be subtle and could easily go unnoticed. The largest differences are for the tails of the distributions (.9 quantiles), but these are usually highly variable in empirical data (Ratcliff & McKoon, 2008). Moreover, the figure shows an exaggerated difference in η values, with η doubling from the low-variance to the high-variance predictions. When an equal-variance model is fit to data with a higher η for targets than lures, the single η value estimated by the model can compromise between the two item types. For example, if the target η was .2 and the lure η was .1, then the equal-variance model could estimate η to be .15. Moreover, the other model parameters could partially compensate for the misses produced by misspecifying η. So the actual misses might be considerably smaller than those shown in Figure 2.

To explore differences in η values, we considered 15 separate experiments that have been previously published with the equal-variance version of the diffusion model. We re-fit the data from each participant using free η parameters for targets and lures. If the unequal-variance assumption is valid, then the fits should show higher η values for targets than for lures. We also assessed the consistency in parameter estimates between the equal- and unequal-variance versions of the model. If recognition memory truly reflects an unequal-variance process, then we must ensure that the general conclusions of past studies using an equal-variance model are valid.

Recovery Simulations

Given that the η parameter is estimated based on subtle aspects of the data, we performed parameter recovery simulations to ensure that our data sets were appropriate for estimating evidence variability (Ratcliff & Tuerlinckx, 2002). These simulations are reported after the fits to empirical data. For each participant in each data set, we repeatedly generated new data by simulating the diffusion process with the participant’s best fitting equal-variance parameters. We fit all of the simulated data sets using a model that had free η parameters for targets and lures, and we evaluated the deviation between the fitted η values and the η values used to generate the data. Critically, this analysis can reveal any potential estimation biases that produce apparent differences in η values between targets and lures even for data that were actually generated from an equal-variance model.

We also performed model recovery simulations to determine whether the data provided stronger support for an equal- or unequal-variance model (Wagenmakers, Ratcliff, Gomez, & Iverson, 2004). In these simulations, data sets were generated from both models, and we evaluated the proportion of data sets that supported the unequal-variance model according to both the Akaike Information Criterion (AIC; Akaike, 1973) and the Bayesian Information Criterion (BIC; Schwarz, 1978). The results should show that the unequal-variance model is preferred more often for the data sets generated from the unequal-variance model than for the data sets generated from the equal-variance model. If target evidence is truly more variable than lure evidence, then the AIC and BIC results for the empirical data should be similar to the data sets simulated from the unequal-variance model.

Method

Data Sets

Table 1 provides information about all of the data sets that we consider. When a study had multiple experiments with the same design, we combined participants from all of the experiments into a single data set. The data sets are quite disparate, ranging from experiments with only two conditions and a little over 100 observations for each participant to experiments with 18 conditions and over 1000 observations from each participant.

Table 1.

Data sets used in the fits

Data Set	Source	N	Obs.	Con.	Variables
1	Criss (2010) Ex. 1	14	983.7	4	Item type (target, lure); Target proportion (30%, 70%)
2	Criss (2010) Ex. 2	16	1520.3	8	Item type (target, lure); List strength (strong, weak); Word frequency (high, low)
3	SRW (2012) Mixed and Pure-Within	98	208.9	4	Item type (target, lure); List strength (strong, weak)
4	SRW (2012) Weak Pure-Between	41	118.9	2	Item type (target, lure)
5	SRW (2012) Strong Pure-Between	43	118.1		Item type (target, lure)
6	RTM (2004) Young	39	1357.3	18	Item type (weak target, strong target, lure); Word frequency (high, low, very low); Speed vs. accuracy emphasis
7	RTM (2004) Older	41	1766.8	18	(same as above)
8	RTM (2010) Young	43	794.6	6	Item type (weak target, strong target, lure); Word frequency (high, low)
9	RTM (2010) Older	41	795.0	6	(same as above)

Notes: N = number of subjects; Obs. = average number of observations for each subject; Con. = number of conditions; SRW = Starns, Ratcliff, & White; RTM = Ratcliff, Thapar, & McKoon. Some subjects reported in the original papers were removed due to chance performance, including five subjects in Data Set 1, two from Data Set 8, and one from Data Set 9. An additional participant was removed from Data Set 9 because they had no errors for lure items in any condition (making it impossible to define the RT distributions).

Fitting Methods

Fits to Empirical Data

We used the χ² fitting method described by Ratcliff & Tuerlinckx (2002) because it produces accurate parameter recovery and is robust to outliers in the data. Parameters were optimized using the SIMPLEX routine (Nelder & Mead, 1965). The Appendix lists the free parameters for each fit. Here, we simply describe the principles that we followed in assigning parameters to conditions. For all of the fits, a separate drift rate (ν) parameter was fit for each level of any variable that could impact memory evidence, including item type, strength, and word frequency (see Table 1). When strong and weak targets appeared on separate tests, we allowed the drift rate for lures to vary between the two strength conditions (Criss, 2010; Starns, Ratcliff, & White, 2012). This includes all experiments in Table 1 for which “list strength” is listed as a variable. When strong and weak targets were mixed into the same test list, the model included only a single lure drift rate. This includes all of the experiments for which the “item type” variable has the levels “strong target,” “weak target,” and “lure.” We fit separate boundary (a) and starting point (z) parameters for any conditions that varied across test lists (e.g., speed-emphasis versus accuracy-emphasis tests), but we fit a single boundary and starting point for any conditions that were mixed into a single test list (e.g., high and low frequency words). The range of starting point variability (s_Z) was fixed across all conditions for every data set. The non-decision time mean (T_er) and range (s_T) were also fixed across conditions, except for the speed-versus accuracy-emphasis blocks in Data Sets 6 and 7.

We placed upper and lower limits on some of the parameter values in the SIMPLEX fitting routines. η values were constrained to be between .02 and .4 to avoid failures in the numerical integration routines used by the fitting program. The proportion of estimates truncated as these boundaries ranged from 0% to around 30% across data sets, and we discuss this further in the results section. We set an upper limit of .32 for the boundary width parameter (a), and this affected .3% of the boundary estimates. The code that implements the prediction equations also fails when the range of starting point variability (s_Z) is zero, so we set a lower limit that was near zero for this parameter (.001). Starting point variability was generally low (M = .022), and 11% of the estimates were truncated at the lower boundary. Finally, the proportion of trials with RT contaminants could not go below zero, and a large number of the estimates were at this lower limit (53%). This reflects the fact that the contaminant parameter was consistently very low (mean = .0008 across all data sets). The contaminant parameter measures the proportion of trials with RT delays resulting from distraction (see Ratcliff & Tuerlinkx, 2002), and the extremely low values indicate that this kind of contamination had almost no influence on the data.

For our initial analyses, we fit each data set with two model versions: an equal-variance version in which there was a single η parameter across all conditions, and an unequal-variance version in which there was one η parameter for all target conditions and a separate η parameter for all lure conditions. We did not attempt to estimate different η values for different types of targets and lures (e.g., high and low frequency). We also report secondary analyses that addressed how variability is affected by various independent variables. Given that η estimates rely on very subtle aspects of the data (Figure 2), the secondary analyses were restricted to data sets with a high number of observations per condition (Data Sets 1–2 and 6–9).

Data Set 1 included a bias manipulation with two levels (tests were either 30% or 70% targets), so results from this study could be used to form a 2-point ROC function. Our goal was to estimate evidence variability from RT distributions independent of ROC data, so we performed separate fits to the 30% and 70% conditions. In each fit, only the RT distributions constrained the estimation of different η values. To get each participant’s overall η estimate for targets and lures, we averaged the estimates from the two fits. When we compared fit statistics between the equal- and unequal-variance models for this data set, we only considered fits to the 70% condition. This was the conservative choice in terms of detecting variability differences, because the 70% fits showed a smaller difference between the target and lure η values than the 30% fits.

Parameter Recovery Simulations

For the parameter recovery simulations, we simulated data from an equal-variance diffusion model and then fit this data with an unequal-variance diffusion model. We generated data from each participant’s best-fitting equal-variance parameter values, and the number of simulated trials was adjusted to match the actual number of observations from each participant. Doing this for every participant in a data set produced one simulated experiment. We generated 20 simulated experiments for each data set except for Data Sets 1 and 2. For these, we generated 50 simulated experiments because these data sets included a relatively low number of participants. All told, the recovery simulations involved 8420 fits. In addition to the parameter-recovery simulations, we performed model-recovery simulations to define how often AIC and BIC selected the unequal-variance model when data were generated from an equal- versus an unequal-variance process. For data simulated with unequal variance, we first fit each participant’s data with a model in which the lure η was constrained to be .6 of the target η. We chose .6 because this was the approximate lure/target ratio needed to fit the diffusion model to joint RT and ROC data in Starns, Ratcliff, and McKoon (2012). We generated one simulated data set using each participant’s unequal-variance parameters and another using the equal-variance parameters, and we fit both simulated data sets with both equal- and unequal-variance versions of the diffusion model.

Results

Variability Results

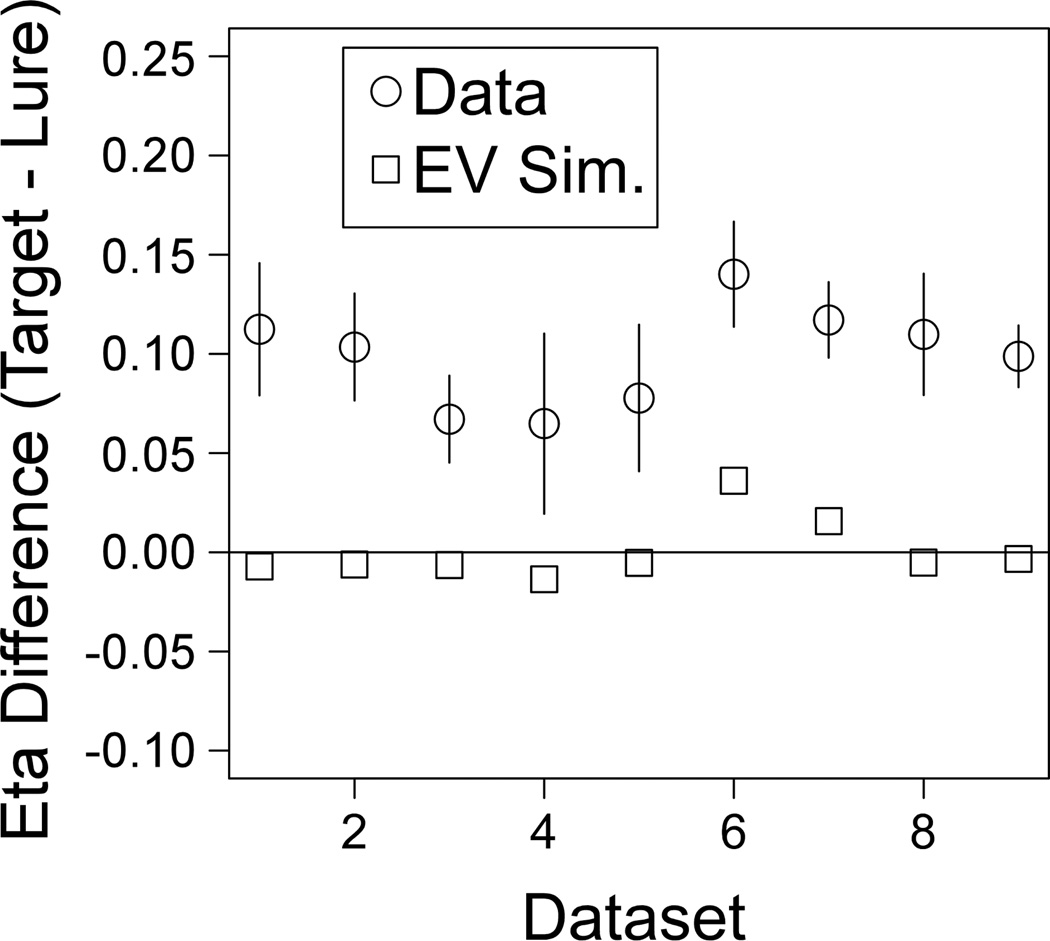
Figure 3 shows the difference between the target and lure η values for each data set along with 95% confidence intervals. The squares show the results from the equal-variance parameter recovery simulations. For every data set, η values were higher for targets than lures, and the difference was significant by a paired-samples t-test (i.e., none the confidence intervals include zero). Moreover, none of the confidence intervals overlap the simulation results, so the empirical η values are not consistent with estimates produced by fitting equal-variance data.

Figure 3.

Results from fits to empirical data (Data) and data sets simulated from an equal-variance model (EV Sim.). Error bars shows 95% confidence intervals on the difference between target and lure η values.

For the equal-variance simulations, the difference between the target and lure η estimates was very close to zero in all but two of the data sets. Data Sets 6 and 7 showed substantial bias to estimate higher target than lure η values. Interestingly, these are the only two data sets that had both speed-emphasis and accuracy-emphasis conditions, suggesting that this might be a factor in the estimation bias. Notably, the actual difference between the target and lure η values for these two data sets was clearly larger than what one would expect based on the estimation bias alone.

In ROC studies, target and lure variability estimates are usually compared in terms of a ratio as opposed to a difference.² The ratios (lure η / target η) from each data set ranged from about .4 to .7 with a mean of .54 across studies. These values are farther below zero than the typical ratios seen when fitting a signal-detection model to ROC data (Glanzer, Kim, Hilford, & Adams, 1999; Ratcliff et al., 1992; Wixted, 2007). However, the ratio is consistently more extreme in RT models, because these models separately estimate other sources of variability (variability in accumulation and variability in decision criteria) that affect ROC estimates of variability in memory evidence (Ratcliff & Starns, 2009). Starns, Ratcliff, and McKoon (2012) found that ratios of around .6 were needed to fit ROC data with the diffusion model. Therefore, the variability results based on RT distributions alone are similar to the variability assumptions needed to fit ROC data.

Fitting Results

We also compared the equal- and unequal-variance versions of the model in terms of fit. Table 3 shows the mean χ² values for each data set along with the associated degrees of freedom (df) for the fit (i.e., the df in the data minus the number of free parameters in the model). If the model had no systematic deviations from the data, then the mean χ² values would be approximately equal to the degrees of freedom. The actual χ² values were higher than this standard, sometimes substantially so. This is very common for RT models, because subtle systematic deviations between predictions and data can dramatically inflate the χ² value, especially for data sets with a high number of observations and many experimental conditions (this is demonstrated in Ratcliff, Thapar, Gomez, & McKoon, 2004, p. 285 and in Ratcliff & Starns, 2009, p. 74–75). The original papers for each data set include plots to visually display the model fit, and they all reported a close match between theory and data (Criss, 2010; Ratcliff, Thapar, & McKoon, 2004, 2010; Starns, Ratcliff, & White, 2012). Other decision tasks also show a pattern in which χ² values are substantially higher than expectations for an “ideal” model but visual fits are good, including lexical decision (e.g., Ratcliff, Thapar, Gomez, & McKoon, 2004), numerousity discrimination (e.g., Starns & Ratcliff, 2012), and brightness discrimination (e.g., Ratcliff, Thapar, & McKoon, 2003). Moreover, because the boundary RTs used to bin response frequencies are based on the empirical quantiles instead of being fixed before the data were observed, the resulting χ² values do not necessarily conform to standard distributional assumptions (Speckman & Rouder, 2004).³ Therefore, we conclude that both versions of the model fit well by RT-model standards. Of course, the fit is better for the more flexible unequal-variance version of the model. The critical issue is whether this difference is large enough to reject the equal-variance model.

Table 3.

Eta (η) estimates across the different list conditions in Data Set 2

	Item Type
List Condition	Target	Lure
High-Frequency Weak	.24	.15
Low-Frequency Weak	.29	.15
High-Frequency Strong	.27	.18
Low-Frequency Strong	.26	.16

Note: Standard errors ranged from .021 to .032

To compare the equal- and unequal-variance models, we assessed which model was selected by AIC and BIC for each participant. These measures include a fit component and a complexity penalty based on the number of free parameters used by the model. The difference in fit between two models is equal to the difference in their G² values, which we approximated using the difference in χ² (the two metrics are nearly identical for large data sets). The complexity penalty for AIC is the number of free parameters multiplied by 2, and the penalty for BIC is the the number of parameters multiplied by the natural logarithm of the sample size, ln(N). The equal- and unequal-variance models differ by a single parameter, so the unequal-variance model is preferred by AIC if allowing different η parameters for targets and lures lowers the χ² value by more than 2, and by BIC if the fit improves by more than ln(N).

Figure 4 shows the proportion of participants whose data support the unequal-variance version of the model based on AIC and BIC. Results are shown for simulated equal-variance data, simulated unequal-variance data, and the empirical data. Results are segregated into high-constraint data sets (with many observations per participant) and low-constraint data sets (with fewer observations). Not surprisingly, there were more results favoring the unequal-variance model in the unequal-variance simulations than in the equal-variance simulations. This difference is greater for the high-constraint data sets than the low constraint data sets; that is, the data better differentiate the alternative models when there are more observations. Notably, the proportion of simulated unequal-variance data sets that correctly supported the unequal-variance model was sometimes quite low, especially for the low-constraint data sets and for the BIC metric with its more severe complexity penalty. Critically, these results demonstrate that fit metrics like AIC and BIC cannot be assumed to always produce the correct conclusion: sometimes the vast majority of fits support the equal-variance model even when every data set was generated with unequal variance (for another case in which BIC consistently selects the wrong model, see Dube, Starns, Rotello, & Ratcliff, 2012). Wagenmakers et al. (2004) used recovery simulations to build distributions of fit differences for data generated by each of two alternative models, and these distributions show that the optimal criterion for selecting a winning model can deviate substantially from the criterion corresponding to the complexity penalty used by either AIC or BIC. For our data, the especially poor recovery performance for the low-constraint data sets again highlights that unequal variance has a relatively subtle signature in the RT distributions, so a large number of observations are required to achieve enough power to consistently support the unequal-variance model.

Figure 4.

Proportion of participants for which AIC and BIC selected the unequal-variance model over the equal-variance model. Results are shown for fits to simulated equal-variance data (“EV Sim.”), simulated unequal-variance data (“UV Sim.”), and empirical data. The high-constraint data sets had a large number of observations per participants (Data Sets 1–2 and 6–9) and the low-constraint data sets had fewer observations (Data Sets 3–5). The error bars are 95% high-density intervals on the posterior distribution for the proportion parameter assuming an uninformative prior distribution (i.e., a uniform distribution between 0 and 1). AIC = Akaike Information Criterion; BIC = Bayesian Information Criterion.

Most importantly, the empirical results are much more consistent with the unequal-variance simulations than the equal-variance simulations. Certainly, the unequal-variance version of the model was preferred for a much higher proportion of participants than one would expect if the data truly reflected an equal-variance process. Therefore, the fit statistics agree with the traditional analyses on η estimates in supporting the unequal-variance model.

Recovery of η Values

Figure 5 shows histograms of the difference between the η value used to generate a simulated data set and the η values produced in fits to these data. Of course, a difference of zero indicates accurate recovery; thus, distributions that are centered on zero indicate no estimation bias. As expected, most data sets supported accurate recovery, but with considerable variation in estimates. The high variability is expected given the subtle impact that changes in η have on the model predictions (Figure 2). The variability is particularly pronounced in data sets with low numbers of observations from each participant.

Figure 5.

Deviation between the η values used to generate simulated data and the η values recovered in fits. Results for targets and lures from each data set (DS) are displayed. The vertical lines mark the average deviation across the simulated data sets, so a vertical line at zero indicates no estimation bias. See the text for an explanation of the spike just below zero for Data Sets 3–5.

Data Sets 3, 4, and 5 all have a high number of deviations just below zero. This occurred because these data sets had relatively few observations, resulting in a large number of η estimates at the maximum value (which we set at .4). Specifically, the proportion of η estimates truncated at the maximum for Data Sets 3, 4 and 5 was .12, .33, and .29, respectively. In the recovery simulations, the simulated data were generated with the maximum possible η value, and any miss in the recovered value was necessarily on the negative side. The bump right below zero indicates that the model usually got close to the correct η value, but it could only miss low. This artifact led to a slight under-estimation of both the target and lure η values, most noticeably in Data Set 5. As such, the results from Data Sets 3–5 should be viewed with caution. However, these low-constraint data sets supported the same conclusion about evidence variability as the data sets with more observations per participant, and the high-constraint data sets had a much lower proportion of eta estimates truncated at the maximum value. Specifically, the proportion of truncated estimates for Data Sets 1, 2, 6, 7, 8, and 9 was 0, .03, 0, .01, .08, and .06, respectively. The histograms for these data sets did not show a spike just below zero. Notably, the need to impose a maximum η value makes it more difficult to support the unequal-variance model; that is, if the lure η estimate is near the maximum value, then the target estimate cannot be much higher. Nevertheless, the low-constraint data sets still supported the unequal-variance model just like the high-constraint data sets.⁴

Data Sets 6 and 7 are the ones with a bias to estimate higher target than lure η values, and the target histograms for these data sets are clearly shifted to the right. The lure values either show no bias toward over estimation (Data Set 6), or a much smaller bias (Data Set 7). Again, this bias was not large enough to account for the difference in target and lure η observed in the fits to the empirical data.

Parameter Comparisons

Figure 6 shows scatterplots relating parameter estimates in the equal- and unequal-variance versions of the model (each point is a participant) as well as histograms of the difference between the two. The scatterplots show that parameter values are largely consistent in the two versions of the model, with slight systematic deviations for a few of the parameters. The boundary width and non-decision time estimates were extremely consistent in the two model versions. Compared to the equal-variance results, target drift rates tended to be farther above zero in the unequal-variance version of the model, and lure drift rates were closer to zero. This is a natural consequence of the effect of adding variability on predicted performance levels. Increasing η produces lower levels of performance, which can be canceled out by moving the average drift rate farther from zero (and vice versa). The unequal-variance version of the model has higher η values for targets and lower η values for lures compared to the equal-variance version, which explains the slight shift in average drift rates.

Figure 6.

Comparison between parameter values from the equal-variance (EV) and unequal-variance (UV) fits of the diffusion model. The scatterplots show data from each of the 376 participants. Below each scatterplot is a histogram of the differences between the two model versions with a reference line at zero.

The starting point parameter also shows a small systemic deviation between the two model versions, such that the starting point is slightly closer to the “new” boundary in the unequal-variance fits. This difference is expected given the changes in average drift rates. That is, both the target and lure drift rates are slightly biased away from the bottom boundary and towards the top boundary in the unequal-variance model. With no change in starting point, this shift would produce more “old” responses for the unequal-variance model. The slight shift in starting point towards the bottom boundary cancels out this bias, bringing predictions back in line with the data.

Figure 6 demonstrates that general conclusions made based on equal-variance fits of the diffusion model are unlikely to change when unequal variances are allowed. Diffusion model research almost always concerns whether a particular independent variable or individual-difference factor affects drift rate, boundary separation, non-decision time, or some combination of these parameters (Ratcliff & McKoon, 2008; Wagenmakers, 2009). Such conclusions will not change based on variability assumptions; for example, a manipulation that affects boundaries in the unequal-variance model won’t appear to affect drift rate in the equal variance version. However, conclusions that depend on the level of bias in drift rates and/or starting point could be affected by model choice; that is, if data that truly reflect unequal-variances are fit with an equal-variance model, then the drift rates will appear to be slightly biased toward the bottom boundary (across all item types) and the starting point will appear to be slightly biased toward the top boundary.

Effects of Variables

We chose five data sets (2 and 6–9) to evaluate the effects of dependent variables on η estimates. These were the data sets that had many observations per participant and manipulated an independent variable other than item type. We re-ran fits for these data sets with free η parameters for every condition. The mean η values from each condition are reported in Table 3 and Table 4.

Table 4.

Eta (η) estimates by word frequency and strength from Data Sets 6–9

	Item Type
Frequency	Strong Target		Weak Target	Lure
		Data Set 6
High	.19		.20	.11
Low	.17		.21	.11
Very Low	.37		.20	.11
		Data Set 7		.11
High	.24		.22	.16
Low	.25		.22	.14
Very Low	.35		.24	.12
		Data Set 8
High	.30		.29	.18
Low	.25		.27	.16
		Data Set 9
High	.31		.30	.21
Low			.29	.19

Note: Standard errors range from .010 to .017.

Data Set 2 allowed us to evaluate the effects of high and low taxonomic word frequency and repeated learning trials for target items, with targets studied once on weak lists and targets studied five times on strong lists. The design had separate study/test cycles for each frequency × strength combination, so in the re-analysis of this data set we fit each condition separately. Therefore, there were only two conditions in each individual fit (targets and lures), and the fit for each condition used the same parameters reported for Data Sets 4 and 5 in the Appendix. Table 3 reports the average η values for targets and lures for each type of list, and we submitted these data to a 2 (frequency) × 2 (strength) × 2 (item type) ANOVA. Consistent with our initial analyses, η values were higher for targets (.26) than for lures (.16), F(1, 15) = 67.00, p < .001, MSE = .005. None of the other effects reached significance (lowest p vale = .22).

Data Sets 8 and 9 also varied word frequency and strength, with weak targets studied once and strong targets studied twice. Unlike Data Set 2, weak and strong targets were mixed into the same test list with a single pool of lure items, so we used a single item-type variable with the levels strong target, weak target, and lure (instead of entering strength and item type as separate factors). For Data Set 8, there was a significant effect of item type, F(2, 84) = 40.86, p < .001, MSE = .008. As shown in Table 4, this effect emerged because lure η estimates (.17) were lower than those for targets, with almost no difference between weak (.27) and strong (.28) targets. The effect of word frequency also reached significance, F(1, 42) = 8.25, p = .006, MSE = .007, although the actual difference between high-frequency (.25) and low-frequency (.23) words was extremely small. There was no interaction between item type and word frequency, F(2, 84) = 1.69, ns, MSE = .003.

Data Set 9 also showed an effect of item type, F(2, 80) = 52.54, p < .001, MSE = .004, with lower η values for lures (.20) than either strong targets (.28) or weak targets (.29). There was a very small difference between high-frequency (.26) and low-frequency (.25) words, but it did reach statistical significance, F(1, 40) = 5.33, p < .05, MSE = .003. There was no interaction between frequency and item type, F(2, 80) = 0.76, ns, MSE = .002.

Data Sets 6 and 7 also had target strength and word frequency manipulations, but these experiments added a class of very-low frequency words. Weak targets were studied once, and strong targets were studied three times. Both strength classes appeared on the same test with a common set of lures, so we again used an item-type variable with the levels strong target, weak target, and lure. As can be seen in Table 4, the results for high and low frequency words were quite similar to Data Sets 8 and 9: η values were higher for targets than for lures, but very similar for strong and weak targets and for high and low frequency. For the very-low frequency words, the η values for lures and weak targets were near those for the other frequency classes, but the strong targets had much higher η values than the other conditions. This one stand-out condition produced a significant interaction between item type and frequency in both data sets, F(4, 152) = 53.31, p < .001, MSE = .003 for Data Set 8, and F(4, 160) = 20.05, p < .001, MSE = .003 for Data Set 9. The effects of item type and frequency were significant for both datasets, but the means suggest that both effects were driven by the one extreme cell for very-low frequency targets studied multiple times. To explore this, we analyzed these datasets with the very-low frequency condition excluded. For Data Set 8, these analyses showed an effect of item type, F(2, 76) = 32.58, p < .001, MSE = .005, with lures (.11) substantially less variable than targets studied once (.18) or three times (.20). Again, evidence variability was consistent across the different target strengths. Neither the frequency effect nor the interaction approached significance (lowest p = .174). Data Set 9 showed the same pattern, with lures (.15) less variable than weak (.24) or strong (.22) targets, F(2, 80) = 52.68, p < .001, MSE = .004. There was no effect of frequency and no interaction (lowest p = .367).

In summary, the effect analyses suggest that repeated presentation on the study list had little or no effect on evidence variability, and high versus low word frequency had a modest effect at best (although evidence variability increased dramatically for very-low-frequency words with strong learning). The study-repetition results are consistent with prior ROC research, which shows that slopes are generally unaffected by the repetition of studied items (e.g., Glanzer et al., 1999; Ratcliff et al., 1992), although Heathcote (2003) did report slightly higher slopes for repeated than non-repeated targets. In contrast, the word frequency results do not match the ROC literature. The ROC results suggest the following pattern: low-frequency targets have higher variance than high-frequency targets, low-frequency lures have higher variance than high-frequency lures, and the difference in variability is larger for targets than for lures (e.g., Glanzer et al., 1999). The RT-based estimates show no hint of this pattern.

The word frequency results suggest that RT and ROC results might not always agree on the specific effects of independent variables, although they are consistent in showing that evidence is more variable for targets than lures. One possibility is that the RT-based estimates are less sensitive to changes in variability than the ROC estimates, making it harder to detect differences across conditions. Another possibility is that the ROC estimates are influenced by artifacts that are specific to the confidence-rating procedures used to define different points on the function. We return to this issue in the General Discussion.

Free Drift Rates for Speed- and Accuracy-Emphasis

Starns, Ratcliff, & McKoon (2012) and Rae, Heathcote, Donkin, and Brown (submitted) reported evidence that drift rates were farther from zero when subjects were asked to emphasize accuracy than when they were asked to emphasize speed. Data Sets 6 and 7 included a speed-accuracy manipulation, and the fits reported above held drift rate constant across those conditions. To ensure that this parameter constraint did not influence our conclusions about evidence variability, we refit those data with separate drift rate parameters for speed and accuracy emphasis. Critically, the η estimates from these fits showed the same pattern as the original fits; that is, η estimates were higher for targets than for lures. For Data Set 6, the average η values were .26 for targets and .12 for lures, t (38) = 12.54, p < .001. For Data Set 7, the average η values were .25 for targets and .13 for lures, t (40) = 12.15, p < .001. Thus, both the free-drift and fixed-drift models strongly supported the unequal-variance assumption.

To evaluate differences in drift rate across the speed-accuracy conditions, we submitted the combined data from Data Sets 6 and 7 to a 2 (strength) × 3 (word frequency) × 2 (age) × 2 (speed vs. accuracy instructions) ANOVA on drift rate (ν) estimates for target items. Results showed no main effect of speed (.22) versus accuracy (.22) instructions, F (1, 78) = 0.80, ns, MSE = .019. Drift rates were higher for strong targets (.33) than for weak targets (. 11), F (1, 78) = 297.89, p < .001, MSE = .041. Drift rates also increased from high (.10) to low (.24) to very-low (.31) word frequency, F (2, 156) = 196.11, p < .001, MSE = .018. Drift rates were quite similar for young (.23) and older (.21) participants, F (1, 78) = 1.11, ns. The three-way interaction of instructions, strength, and frequency was significant, F (2, 156) = 6.51, p < .01, MSE = .013. This emerged because the effect of instruction was very small (less than .01) for all of the conditions except strong targets with very-low word frequency. The latter condition had a drift rate of .49 with speed instructions and .41 with accuracy instructions, opposite the pattern seen in earlier experiments (Rae et al., submitted; Starns, Ratcliff, & McKoon, 2012).

We similarly analyzed the drift rates for lures with a 3 (word frequency) × 2 (age) × 2 (speed vs. accuracy instructions) ANOVA. Negative numbers that are farther below zero represent better performance (i.e., stronger evidence for a “new” response). Like the target drift rates, the lure drift rates were quite similar with speed instructions (−.20) and accuracy instructions (−.21), F(1, 78) = 2.14, ns, MSE = .07. Performance increased from high (−.17) to low (−.21) to very low (−.23) frequency words, F(2, 156) = 70.49, p < .001, MSE = .002. Performance was very similar for young participants (−.21) and older participants (−.20), F(1, 78) = 0.26, ns. There was a significant interaction between age and instruction, which arose because drift rates for older participants were slightly worse with accuracy (−.19) versus speed (−.20) instructions, whereas drift rates for young participants were slightly better for accuracy (−.23) versus speed (−.19), F(1, 78) = 7.96, p < .01, MSE = .007. However, the instruction effect was small even for the young participants, and the young participants did not show an instruction effect on target drift rates. Therefore, the results provided little evidence that drift rates were different for speed and accuracy.

AIC and BIC statistics also did not provide strong support for a model with free drift rates for speed versus accuracy instructions versus a model with fixed drift rates. AIC preferred the free-drift model over the fixed-drift model for 77% of the young participants (Data Set 6) but only 51% of the older participants (Data Set 7). With BIC’s more severe complexity penalty, the free drift model was preferred for only 5% of the young participants and none of the older participants. Thus, the current results are not consistent with the recognition results in Starns, Ratcliff, & McKoon (2012), where drift rates were substantially higher with accuracy-emphasis than with speed-emphasis and the free-drift model was clearly preferred. However, the participants in Starns et al. were put under intense time pressure in the speed-emphasis blocks, and this might be the basis of the different results. Again, the key point for our purposes is that the fits strongly support the unequal-variance assumption in both the free-drift and fixed-drift models.

Discussion

We tested whether the unequal-variance account of zROC slopes could successfully predict the pattern of variability estimates returned by the diffusion model. By estimating variability solely on the basis of accuracy and RT data, we found clear evidence that memory strength is more variable for targets than for lures. This result was consistent across nine data sets using a variety of experimental designs. Parameter recovery simulations demonstrated that η parameters were usually recovered accurately, but there was considerable variability in the estimates and a few data sets showed estimation biases. Most importantly, the fits to simulated equal-variance data did not resemble the empirical results. For each data set the observed difference between the target and lure η estimates was much larger than expected if the data truly came from an equal-variance process. Moreover, the proportion of participants for which AIC and BIC favored the unequal-variance model was very similar in the empirical data and in the model-recovery simulations with unequal-variance data, whereas the equal-variance recovery simulations were far out of range of the empirical results. Therefore, the unequal-variance assumption is now supported by fits to ROC data (e.g., Ratcliff et al., 1992), combined ROC and RT data (Ratcliff & Starns, 2009, in press; Starns, Ratcliff, & McKoon, 2012), and RT data in the absence of ROC data.

Although the RT data support the general notion that targets are more variable than lures, RT and zROC data might not always lead to the same conclusions regarding the effects of specific independent variables. We found that the RT-based estimates showed the same pattern as zROC estimates for a strength manipulation (number of learning trials), but the RT-based estimates showed little or no hint of the word frequency effects that are observed for zROC functions (e.g., Glanzer et al., 1999). As mentioned, the RT-based estimates might simply be less sensitive to changes in variability. However, another possibility is that the effect of word frequency on zROC slopes does not actually reflect changes in the underlying memory evidence distributions. Many non-mnemonic factors can influence zROC slope, such as the position of decision boundaries in an RT model (Ratcliff & Starns, 2009; Van Zandt, 2000), variability in decision criteria (Benjamin, Diaz, & Wee, 2009; Mueller & Weidemann, 2008), and changes in the position of the confidence criteria across the different levels of a variable (Starns, Pazzaglia, Rotello, Hautus, & Macmillan, 2013, Figure 1). Admittedly, mixing high- and low-frequency words into the same test makes it less likely that decision processes will differ across conditions, and a number of results show that participants are generally reluctant to make trial-by-trial changes in decision processes (e.g., Stretch & Wixted, 1998). However, trial-by-trial shifts have been observed under some conditions (e.g., Singer & Wixted, 2006, Experiments 3 & 4), and word frequency might be a relatively “natural” signal for a change in decision standards (i.e., when a rare word comes up on the test, participants naturally expect that they should have a strong memory of seeing the word if it was studied). Therefore, researchers should remain open to the possibility that decision processes play some role in the word-frequency effect on zROC slope.

Other Tests of the Unequal Variance Assumption

Researchers have also attempted to test the unequal-variance assumption by directly calculating the variability of memory-strength ratings on scales that have many levels (e.g., 20 or 100 different rating options; Mickes, Wixted, & Wais, 2007; also see Criss, 2009, and Starns, White, & Ratcliff, 2012). As expected, studies of this sort show that ratings are more variable for targets than for lures. Although the conclusion that higher variability in the ratings is produced by higher variability in the underlying evidence is only valid under certain processing assumptions (Rouder, Pratte, & Morey, 2010), the results at least match the most straightforward prediction of the unequal-variance account (Wixted & Mickes, 2010).

Recent modeling developments permit the separate estimation of “nuisance” variability (such as participant and item effects) and other sources of variation that might be more central to the memory system (such as fluctuations in attention; Pratte, Rouder, & Morey, 2010). These advancements employ hierarchical Bayesian modeling to directly estimate participant- and item-based variation. Model fits suggest that both participants and items contribute substantial variability to performance, but the results still favor an unequal-variance version of the continuous model when these sources of variation are removed (Pratte et al., 2010).

Koen and Yonelinas (2010) recently attempted a direct test of the idea that variability in learning produces an unequal-variance model. They compared a pure condition in which all words were studied for 2.5 s to a mixed condition in which half of the words were studied for 1 s and the other half for 4 s. Results showed no evidence of a difference in zROC slope between the two groups, making it appear that slopes are not influenced by learning variability. Jang, Mickes, and Wixted (2012) and Starns, Rotello, and Ratcliff (2012) both challenged this conclusion. These commentaries demonstrated that mixing the performance levels from Koen and Yonelinas’ 1 s and 4 s conditions produces slope effects so small that they could never be detected in a psychology experiment. Thus, the results have no bearing on the role of variability in explaining zROC slopes.

In general, we agree with Koen and Yonelinas (2010) that researchers should try to find direct ways to manipulate evidence variability, but high levels of baseline variability are a substantial barrier to achieving this goal. That is, even within a single strength condition, different target items can span a range from so weak that they are practically indistinguishable from a non-presented item to so strong that participants can attribute them to the list with complete certainty. Increasing this level of variability with a manipulation of learning effectiveness is not trivial. Researchers must also be aware that performance actually reflects variability from a number of sources. For example, within-trial variability in evidence accumulation and variability in decision criteria influence recognition decisions regardless of the level of learning strength (Ratcliff & Starns, 2009).

Distributional Assumptions

Ratcliff (in press) demonstrated that accuracy and RT predictions from the diffusion model remain largely consistent over a wide range of distributional assumptions. The same is true for ROC data, as recently demonstrated by Rouder et al. (2010) and less-recently demonstrated by Banks (1970) and Lockhart and Murdock (1970). This is an important point for our purposes, because variance estimates critically depend on distributional assumptions. For example, the low-density tail in a highly skewed distribution could have a huge impact on variance but might have little discernible signature in the data (only a small proportion of trials will be influenced by the tail). Our variability estimates assume Gaussian evidence distributions, and they could vary widely if other distributional forms were substituted (although not all potential distribution shapes will be consistent with the data, of course). Given that distributional assumptions are so critical, what general conclusions can be drawn from the current results (and indeed from the entire ROC literature)?

First, and most critically, our results show that the distributional assumptions that work for ROC data also work for RT distributions. Both forms of data are well accommodated by unequal-variance Gaussian distributions, and the unequal-variance model is clearly superior to the equal-variance model for both. This convergence lends more credibility to these distributional assumptions than could be gleaned from either form of data in isolation. Second, our results – along with the ROC literature – show that the difference between the target and lure evidence distributions is not just a matter of location. That is, the target distribution is not just the lure distribution shifted up to a higher average evidence value – something else about the distribution also changes. As mentioned, one successful way to model this additional factor is to assume that both the mean and variability of memory evidence differs between targets and lures. It is possible that a successful model could be developed in which the location and shape of the evidence distribution differs between targets and lures, but the variability remains the same (see Rouder et al., 2010). Of course, it might also be the case that the location, shape, and variability all change. Regardless, a change only in terms of location is ruled out by the data, and this is the case for both ROC functions and RT data (and again, the same distributional assumptions are successful for both).

Some theorists have proposed that target evidence is more variable than lure evidence because target trials come from a mixture of separate latent categories with different average strength values, such as attended versus unattended items (e.g., DeCarlo, 2002). Mixing distinct classes of target items and increasing the variability of single target distribution have very similar effects on RT distributions. Thus, our results do not specify exactly how variance increases for targets, and a mixing mechanism remains a viable alternative.

Dual Process

One alternative to the unequal-variance approach assumes that a subset of decisions are based on a threshold recollection process that either succeeds or fails in recovering contextual information, whereas other decisions are based on a continuous feeling of familiarity that is higher on average for more recently encountered items (Yonelinas, 1994; Yonelinas & Parks, 2007). This dual-process approach assumes that a given decision is made based on either recollection or familiarity, as opposed to all types of information being combined for every decision as proposed by the univariate view (Ratcliff, 1978, pp. 62–63; Wixted, 2007). Mixing the different processes across test trials produces a zROC slope below one without assuming unequal variance in evidence values.

The unequal-variance and dual-process signal detection models can produce very similar ROC functions (Wixted, 2007; Yonelinas & Parks, 2007). Thus, it is important to consider whether the RT patterns that support the unequal-variance model could also be explained in terms of a threshold recollection process. Currently, we have no way to definitely answer this question, because the dual process account has not been extended to RT distributions. This development is an important future goal for dual process theorists.

However, based on the general theoretical assumptions of the dual process approach, we can speculate that a threshold recollection process might have a different RT signature than unequal variance. A central assumption in the dual process approach holds that recollection is a slower process than familiarity (Yonelinas, 2002; McElree, Dolan, & Jacoby, 1999). As shown in Figure 2, increasing η produces faster correct responses, which seems inconsistent with an increased role for the slower recollection process. Moreover, increasing the variability of memory evidence affects both correct and error responses, with higher variability producing faster errors in low-performance conditions and producing slower errors in high-performance conditions (see Figure 2). Threshold recollection is assumed to always lead to a correct response, so this process might not make the same predictions for error RTs as unequal variance. Thus, the two processes might be more discriminable in terms of RT distributions than in terms of ROC functions. More rigorous investigation of these issues must await an explicit model for the time course of recollection and familiarity.

Some previous reports have used RT data to test the dual process framework, although the RT data were not directly modeled. For example, RT data have been used to evaluate the dual process explanation for the Remember/Know task, in which “remember” responses are assumed to be based on the threshold recollection process and “know” responses are assumed to be based on familiarity. Results show that “remember” responses are made more quickly than “know” responses, which seems more consistent with the idea that “remember” responses reflect the high end of a strength continuum than the idea that “remember” responses are driven by the slower recollection process (Dewhurst & Conway, 1994; Dewhurst, Holmes, Brandt, & Dean, 2006). An alternative interpretation is that “know” responses are slower because participants wait to see if recollection will succeed before they make a response based on familiarity alone, although Dewhurst et al. (2006) showed that the RT pattern held even when remember/know judgments were deferred until after old/new decisions were made for all of the test items. More compellingly, “remember” false alarms are made more quickly than “know” hits (Wixted & Stretch, 2004). This result cannot be explained in terms of recollection succeeding while participants are deliberately delaying a familiarity-based response, because recollection should not occur for lures. Finally, the RT difference between “remember” and “know” responses is dramatically attenuated when responses are matched for the overall level of confidence that an item was studied (Rotello & Zeng, 2008), which is consistent with the idea that the RT difference is driven by differences in continuous strength values.

While we are considering whether or not a threshold recollection model could explain RT distributions, we should also note that some results challenge the claim that threshold recollection is the process that produces zROC slopes less than one (e.g., Glanzer et al., 1999; Starns & Ratcliff, 2008; Wixted, 2007). To highlight just a couple, results demonstrate that zROC slopes remain well below 1 even when participants make the majority of their responses in less than 600 ms (Starns, Ratcliff, & McKoon, 2012). This finding is inconsistent with the claim that slopes are driven by a slow recollection process. Also, neural data show that the retrieval of context-specific details occurs even for items that participants do not claim to recollect, which suggests that recollection is a graded process (Johnson, McDuff, Rugg, & Norman, 2009; White & Poldrack, 2013).

RT-based ROCs

A few researchers have used RT as a proxy for confidence to construct ROC functions (e.g., Norman & Wickelgren, 1969; Thomas & Myers, 1972). This analysis is based on the proposal that decision time is a function of the distance between the response criterion and the evidence value for the test item, with fast “old” responses for strength values far above the criterion, slow “old” responses for strength values just above the criterion, slow “new” responses for strength values just below the criterion, and fast “new” responses for strength values far below the criterion. For example, Norman and Wickelgren plotted functions from a short-term memory task in which participants had to recognize digit pairs from lists of four pairs with a 3 s retention interval. The RT-based zROC functions had a pronounced inverted-u shape, whereas the confidence-based functions were more linear. This suggests that RT might not be a good substitute for confidence, which is understandable given that RTs are influenced by many factors other than between-trial differences in memory strength, including within-trial variation in evidence accumulation and variation in decision boundaries (e.g., Ratcliff & Starns, 2009). To our knowledge, no one has addressed whether RT-based zROC functions for long-term recognition have a slope less than 1.

Conclusion

Our results demonstrate that the unequal-variance account is not just an ad hoc way to fit ROC data (DeCarlo, 2002). Instead, the account successfully predicted the pattern of variability estimates produced by fitting the diffusion model to accuracy and RT data. Thus, our results validate the unequal-variance assumption with data that are completely independent of ROC functions.

Table 2.

Mean χ² values across all data sets.

	Model Version
	Equal Variance		Unequal Variance
Data Set	df	χ2	df	χ2
1	13	27.1	12	23.4
2	67	120.8	66	110.8
3	31	40.4	30	37.4
4	13	20.9	12	18.8
5	13	17.3	12	16.3
6	179	386.8	178	368.2
7	179	335.3	178	317.8
8	53	94.8	52	85.1
9	53	87.1	52	79.4

Note: The degrees of freedom (df) for each fit are the degrees of freedom in the data minus the number of free parameters in the model.

Response time (RT) distributions validate the unequal-variance assumption in memory

An unequal-variance diffusion model fits better than an equal-variance version

Parameters are largely consistent for equal- and unequal-variance fits

Appendix

This appendix lists all of the free parameter values in fits of the unequal-variance diffusion model. The equal-variance fits were identical, except that the η parameters for targets and lures were constrained to be equal. For each parameter within each data set, the conditions over which the parameter value could vary are listed below the parameter label. If no conditions are listed, then the parameter had the same value across all conditions.

Parameter Labels and Descriptions

a – boundary width

z – starting point

s_Z – range in starting point variation

ν – average drift rate

η – across-trial standard deviation in drift rate

T_er – average non-decision time

s_T – range in non-decision time variation

p_O – proportion of trials with RT contaminants (see Ratcliff & Tuerlinckx, 2002)

Data Set 1

Parameters listed here were used to fit the 30%-targets and 70%-targets conditions separately.

a	z	sZ	ν	η	Ter	sT	pO
			Target	Target
			Lure	Lure

Data Set 2

Word frequency and strength (number of study presentations) were manipulated between lists, and item type (target, lure) was manipulated within lists. HF = high frequency; LF = low frequency.

a	z	sZ	ν	η	Ter	sT	PO
HF Weak	HF Weak		HF Weak Target	Target
HF Strong	HF Strong		HF Strong Target	Lure
LF Weak	LF Weak		LF Weak Target
LF Strong	LF Strong		LF Strong Target
			HF Weak Lure
			HF Strong Lure
			LF Weak Lure
			LF Strong Lure

Data Set 3

Strength (number of study presentations) was manipulated between lists, and item type (target, lure) was manipulated within lists.

a	z	sZ	ν	η	Ter	sT	pO
Weak Test	Weak Test		Weak Target	Target
Strong Test	Strong Test		Strong Target	Lure
			Weak Lure
			Strong Lure

Data Sets 4 and 5

a	z	sZ	ν	η	Ter	sT	pO
			Target	Target
			Lure	Lure

Data Sets 6 and 7

Speed versus accuracy emphasis was manipulated between lists, and all other variables were manipulated within lists. HF = high frequency; LF = low frequency; VF = very low frequency.

a	z	sZ	ν	η	Ter	sT	pO
Speed	Speed		HF Weak Target	Target	Speed
Accuracy	Accuracy		HF Strong Target	Lure	Accuracy
			HF Lure
			LF Weak Target
			LF Strong Target
			LF Lure
			VF Weak Target
			VF Strong Target
			VF Lure

Data Sets 8 and 9

All variables were manipulated within lists. HF = high frequency; LF = low frequency.

a	z	sZ	ν	η	Ter	sT	pO
			HF Weak Target	Target
			HF Strong Target	Lure
			HF Lure
			LF Weak Target
			LF Strong Target
			LF Lure