Abstract
Cartilage material properties provide important insights into joint health, and cartilage material models are used in whole-joint finite element models. Although the biphasic model representing experimental creep indentation tests is commonly used to characterize cartilage, cartilage short-term response to loading is generally not characterized using the biphasic model. The purpose of this study was to determine the short-term and equilibrium material properties of human patella cartilage using a viscoelastic model representation of creep indentation tests. We performed 24 experimental creep indentation tests from 14 human patellar specimens ranging in age from 20 to 90 years (median age 61 years). We used a finite element model to reproduce the experimental tests and determined cartilage material properties from viscoelastic and biphasic representations of cartilage. The viscoelastic model consistently provided excellent representation of the short-term and equilibrium creep displacements. We determined initial elastic modulus, equilibrium elastic modulus, and equilibrium Poisson’s ratio using the viscoelastic model. The viscoelastic model can represent the short-term and equilibrium response of cartilage and may easily be implemented in whole-joint finite element models.
Keywords: biphasic, finite element model, poroelastic, cartilage, modeling
Cartilage material properties provide important insights into joint health, and cartilage material models are used in whole-joint finite element models.1–5 Altered cartilage material properties are often associated with musculoskeletal disorders.6–9 For example, osteoarthritis, the most common musculoskeletal disorder, is marked by degeneration of the articular cartilage.
Cartilage material properties are determined using constitutive models of varying complexity. Constitutive models range from linear spring models described by a single constant;10 isotropic, linear elastic models having two material constants;11 a biphasic model with three material constants;12 to highly complex models with seven,13,14 eight,15 or ten material constants.16 The biphasic model of cartilage has been used extensively, in part, because the material constants of this model have physical interpretation. In the biphasic model, one parameter (permeability) models the flow of fluid through the porous solid matrix, and two parameters (aggregate modulus, Poisson’s ratio) represent the elastic solid matrix.12 The biphasic model has been widely used to analyze experimental data, including in situ creep indentation tests.17–19
Although the biphasic model is commonly used to characterize creep indentation tests, this model is generally applied only to the final 30% of the creep displacement curve.18–21 The first 70% of the displacement curve is discarded based on the assertion that initial contact between the indenter and cartilage surface is difficult to model accurately due to imperfect application of the initial step load and the assumption of frictionless indenter-cartilage contact.18–21 As a result, the biphasic model is generally not used to characterize the short-term creep response. However, characterizing the short-term response to loading is important when evaluating cartilage behavior during high-frequency activities such as walking and running.
Whole-joint finite element models are used to study tissue and joint response during simulated activities of daily living. These finite element models could benefit from a material model that characterizes the short-term response, in addition to the equilibrium response of cartilage. In whole-joint models, cartilage is commonly represented as a linear elastic material; linear elastic material models can represent the short-term response but not the time-dependent properties. The biphasic model and cartilage models with multiple material constants13–16 can represent time-dependent properties, but these models can be difficult to implement due to the complexity of some of these constitutive models and due to the evolving fluid flow boundary conditions with joint contact in models that explicitly include a fluid phase.
A viscoelastic representation of cartilage can characterize both the short-term and equilibrium creep response of cartilage and may be easily implemented in whole-joint finite element models. A viscoelastic model is based on the intrinsic viscoelastic nature of cartilage15,22,23 and is able to predict the time-dependent properties, including the short-term response.8 Viscoelastic approximations have been used to estimate cartilage material properties only from portions of indentation creep tests.24–27 It is currently unknown whether a purely viscoelastic model can represent the entire indentation creep test. The purpose of this study was to determine the short-term and equilibrium material properties of human patella cartilage using a viscoelastic model representation of creep indentation tests. We hypothesized that a viscoelastic model of cartilage will be able to represent the entire creep displacement curve. The specific aims of the study were (1) to determine the cartilage material properties using a viscoelastic model representation of the entire creep displacement curve and (2) to compare the viscoelastic material properties to the commonly used biphasic material properties.
Methods
Specimen Characteristics
This study included 24 experimental creep tests from 14 (eight males, six females) human patellae specimens ranging in age from 22 to 90 years (median age 61 years). The patellae were acquired as part of fresh-frozen cadaveric knee joints (midfemur to midtibia) from the National Disease Research Interchange (Philadelphia, PA), Anatomy Gifts Registry (Glen Burnie, MD), and the University of California San Francisco Willed Body Program (San Francisco, CA). Healthy patellae and those with varied degrees of degeneration were included in this study; any patella regions with full-thickness defects were excluded.
Specimen Preparation
To prepare a cartilage specimen for the creep indentation test, the patella was dissected from the knee joint. The anterior patella bone was excised with a band saw, and the subchondral bone with the intact cartilage was bonded to an acrylic plate using ethyl-2-cyanoacrylate adhesive (Krazy Glue, New York, NY).
Experimental Setup and Data Acquisition
A computer-controlled indentation testing system17 was used to characterize the creep response of cartilage (Figure 1). The experimental setup consisted of a five degree-of-freedom positioning platform, a linear actuator (M-230.25, Physik Instrument, Karlsruhe, Germany), a load cell (1000 g, Model 31/1426-02, Sensotec, Columbus, OH, USA), an indenter, and a specimen container. The experimental setup also consisted of a Windows-based computer with custom Lab View software (Lab View 8.6, National Instruments, Austin, TX), a motion controller/ data acquisition card (NIPCI-7352, National Instruments, Austin, TX), a motion I/O interface (C-809.40, Physik Instrument, Karlsruhe, Germany), and a gain amplifier (2120B, Vishay, Raleigh, NC, USA). We used a custom porous flat-ended indenter to apply a load to the surface of the cartilage. The indenter was made of 316-sintered stainless steel (50% porosity) with a cylindrical radius of 1 mm and a fillet radius of 127 µm. The five degree-of-freedom positioning platform, load cell, linear actuator, and specimen container were housed in an environmental chamber (Caron Products and Services, Marietta, OH) that maintained the air temperature in a range of 22–25°C.
Figure 1.
The indentation creep test experimental setup.
We positioned a cartilage specimen under the indenter and applied an initial tare load to bring the indenter in contact with the cartilage. The acrylic plate with a specimen attached was affixed to the specimen container on the positioning platform. To determine a perpendicular orientation of the indenter with respect to the cartilage surface, a small steel alignment cylinder (1 mm radius, 4 mm height) was placed on the surface at the test site. The positioning platform was adjusted until the top of the alignment cylinder was visually parallel and concentric to the flat end of the indenter tip. The positioning platform was secured, the alignment cylinder was removed, and the specimen container was filled with phosphate-buffered saline with protease inhibitors. The indenter was brought into contact with the cartilage surface, and a tare load (0.015 N) was allowed to equilibrate to ensure contact between the cartilage surface and the indenter. Tare equilibrium was defined as a displacement-time slope of less than 10−5 mm·s−1 and ranged from 318 to 3911 seconds (average = 684 seconds; SD = 709 seconds). The tare step is a low-load creep test, and the time to equilibrium was dependent on stiffness at the test site.
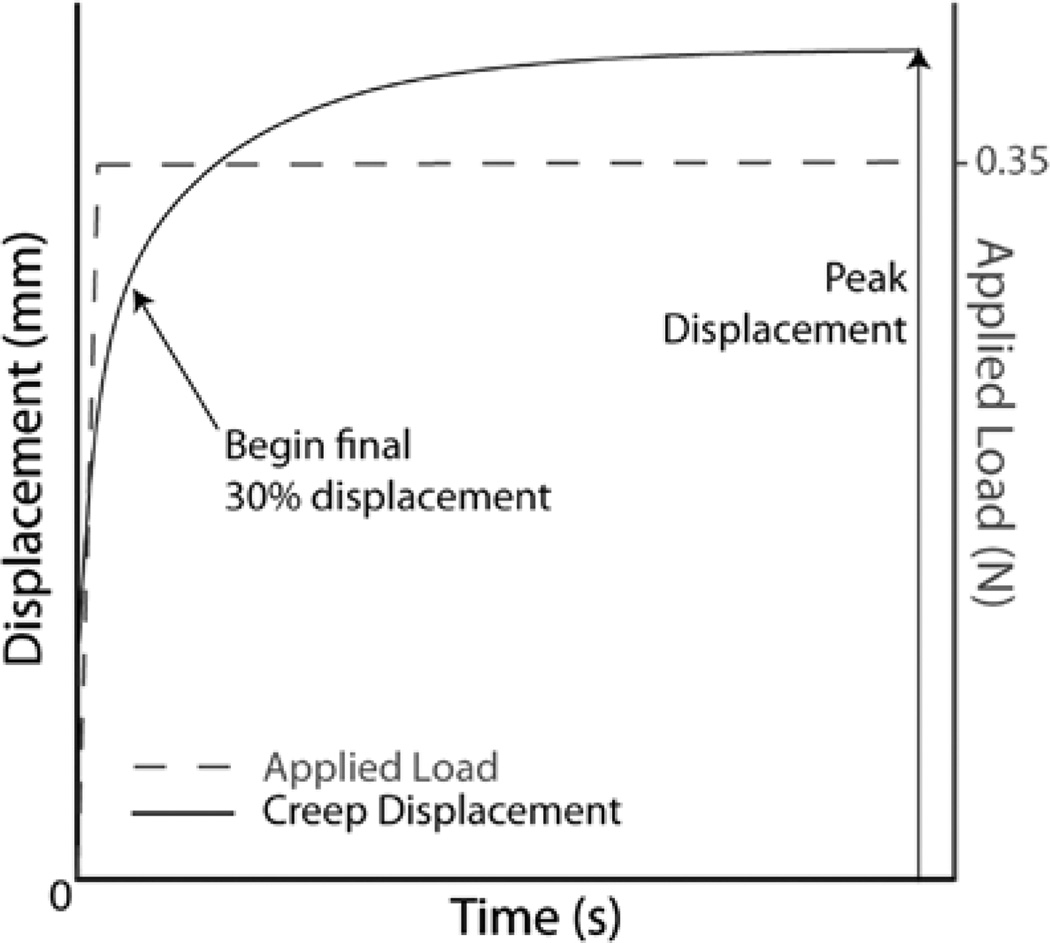
Following tare load equilibrium, the controller ramped up the applied load to a target creep load of 0.35 N,17 which was maintained for the duration of the creep test (Figure 2). The target creep load was applied using a load feedback control. The ramp time to reach the target creep load depended on specimen stiffness and varied from 0.16 to 1.07 seconds. The target creep load was applied to the cartilage surface until the tissue reached creep equilibrium, defined as less than 10−6 mm change in displacement per second.28 Test duration for all specimens ranged from 950 to 7500 seconds (average = 3089 seconds; SD = 1460 seconds). Experimental load and displacement data were recorded every 2.5 µm or every 100 seconds of test time, depending on whichever condition was reached first. Following the creep indentation test, the cartilage thickness was measured at the test site with a needle-probe system.17–19 The indenter was replaced by a needle, and we determined cartilage thickness from displacement data corresponding to the changes in force at cartilage surface penetration and contact with the subchondral bone.
Figure 2.
The applied target load and an idealized creep response from an indentation test.
Determination of Viscoelastic Material Properties
We determined viscoelastic material properties of cartilage using a finite element model (Figure 3) to reproduce our experimental creep displacement curves. The model was constructed in Abaqus (Simulia, Providence, RI) using axisymmetric, quadrilateral continuum elements with biquadratic displacement shape functions (CAX8). The cartilage nodes were biased linearly in both the radial and axial directions to create a finer mesh under the corner of the indenter. In the model, cartilage specimen diameter (10.0 mm) was five times the indenter diameter (2.0 mm) to minimize the effects of boundary interactions on the modeled test site. Cartilage thickness in the finite element models was input from experimental measurements at each test site. The indenter was modeled as a porous, rigid surface with a fillet radius of 127 µm to match the experimental conditions. Contact between the indenter and the cartilage surface was modeled with a coefficient of friction, µs = 0.26, determined from indenter-specific experimental testing.29
Figure 3.
Finite element model of an experimental indentation creep test illustrating mesh deformation at equilibrium for a representative specimen.
In the finite element model, the load was ramped up to the target creep load of 0.35 N using experiment-specific ramp force and time data. The model applied a constant load of 0.35 N for the remainder of the creep test (Figure 2).
We adopted a time domain Prony series representation of viscoelasticity31–32 implemented in Abaqus. In this implementation, the response is assumed to be isotropic, and the shear modulus (G) and bulk modulus (K) are time dependent. The shear and bulk moduli as a function of time, t, are represented as follows:
| (1) |
| (2) |
where G0 and K0 are the instantaneous shear and bulk moduli, respectively; the three Prony series parameters are the shear response (g), volumetric response (k), and time constant (τ); and NP is the number of sets of Prony series terms. The initial elastic modulus (E0) and initial Poisson’s ratio (v0) are related to G0 and K0 using the relations from isotropic elasticity. We assumed that the experimental data could be represented by one set of Prony series terms (NP = 1). After substituting for G0 and K0 in terms of E0 and v0 in Eqs. 1 and 2, the Prony series equations were rewritten as
| (3) |
| (4) |
In this form of the Prony series, the viscoelastic response was characterized by five parameters: E0, v0, g, k, and τ.
We reduced the five independent parameters of the Prony series to three based on two assumptions. First, we assumed near incompressibility of cartilage33 and assigned an initial Poisson’s ratio26,34 of v0 = 0.47. Second, for each cartilage test an initial elastic modulus (E0) was estimated from the experimental data at an initial time of 0.15 second using the following elastic solution for the initial modulus given by Hayes et al:35
| (5) |
where P0 and d0 were the applied load and resulting displacement, respectively, at initial time (0.15 second), r was the indenter radius (1 mm). The term κ was a dimensionless number determined for each experimental creep test dependent on the indenter radius, indentation displacement, cartilage thickness, and Poisson’s ratio.35 The initial time, t0 = 0.15 second, was chosen such that this time was before every test reaching the target creep load and was after the entire indenter surface was in complete contact with the cartilage surface. This viscoelastic model then required the specification of the three independent Prony series parameters, g, k, and τ, to characterize the entire experimental creep displacement. We calculated the equilibrium shear and bulk moduli (Geq and Keq) using Eqs. 1 and 2 evaluated at t = teq:
| (6) |
| (7) |
The equilibrium Poisson’s ratio (veq) and equilibrium elastic modulus (Eeq) were calculated from Geq, Keq using the isotropic elasticity relationships.
The three independent Prony series parameters (g, k, τ) were optimized in the finite element model to best fit each experimental creep curve. A least-squares gradient-based optimization algorithm implemented in Matlab (MathWorks, Natick, MA) was used to determine the best fit to the experimental creep curve. To fit each experimental creep curve, the optimization algorithm was run 20 times with randomly selected initial parameters to ensure that the final solution was independent of the initial parameters. The optimization bounds on the Prony series parameters g and k were 0.001 to 0.99, predetermined by Abaqus; the optimization bounds on τ were 1 to 100 seconds, determined from preliminary studies. The optimization function minimized the difference between an experimental creep curve and its model prediction over the entire creep displacement, given by the sum of squared error:
| (8) |
where N represents the total number of sample points, n represents each individual sampled point, and Model Predicted (tn) and Experimental (tn) represent the displacements at time tn for the model-predicted and the experimental creep curves, respectively.
Determination of Biphasic Material Properties
We determined the biphasic material properties using an interpolant response surface.29 This method performs a least-squares residual search of a previously compiled four-parameter surface to determine the best-fit curve to the final 30% of an experimental creep displacement. The biphasic material properties for an experimental test were those that yielded the lowest root mean square error. Details of this method were reported in Keenan et al.29
Evaluation of Viscoelastic and Biphasic Models
We evaluated the root mean square error (RMSE) between the entire experimental and viscoelastic model creep displacements:
| (9) |
We also evaluated the RMSE between the final 30% of experimental and predicted creep curves from the viscoelastic and biphasic models. We compared the relationships between the viscoelastic and biphasic model material parameters using ordinary least squares regression. Statistical analyses were performed using Stata Release 9.2 (StataCorp LP, College Station, TX).
Results
The viscoelastic model provided excellent representation of the entire experimental creep displacement for all indentation tests (Figure 4). Root mean square error between the experimental and viscoelastic model-predicted creep displacements ranged from 0.75 µm to 4.72 µm. The viscoelastic model-predicted material properties of cartilage were on average (SD): 3.60 (1.78) MPa for initial elastic modulus, 0.729 (0.094) for g, 0.978 (0.008) for k, 17.3 (13.7) seconds for τ, 0.67 (0.31) MPa for equilibrium elastic modulus, and 0.20 (0.06) for equilibrium Poisson’s ratio (Table 1).
Figure 4.
Viscoelastic and biphasic model-predicted creep displacements for specimens corresponding to the best-fit and worst-fit cases determined by the RMSE. The viscoelastic model-prediction RMSE was measured over the entire experimental data, and the biphasic model-prediction RMSE was measured over the final 30% of the experimental data.
Table 1.
Test site characteristics (specimen age, cartilage thickness) and model-predicted viscoelastic and biphasic material properties of cartilage. The viscoelastic model initial Poisson’s ratio was assumed to be a constant (0.47). The biphasic model-predicted Poisson’s ratio was 0.0 for all tests.
| Test | Age | Thickness (mm) |
Viscoelastic Model Parameters |
Biphasic Parameters |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Initial Elastic Modulus (MPa) |
Prony series |
Equil. Elastic Modulus (MPa) |
Equil. Poisson’s Ratio |
Aggregate Modulus (MPa) |
Permeability (E-15 mm4N−1s−1) |
|||||
| g | k | τ (s) | ||||||||
| 1 | 86 | 2.14 | 1.08 | 0.572 | 0.959 | 72.7 | 0.39 | 0.24 | 0.38 | 1.4 |
| 2 | 90 | 2.91 | 5.09 | 0.805 | 0.987 | 16.3 | 0.78 | 0.14 | 0.73 | 1.2 |
| 3 | 90 | 2.77 | 5.74 | 0.798 | 0.984 | 10.1 | 0.94 | 0.19 | 0.90 | 1.6 |
| 4 | 71 | 4.63 | 4.36 | 0.784 | 0.979 | 9.6 | 0.79 | 0.24 | 0.73 | 1.8 |
| 5 | 71 | 2.04 | 8.07 | 0.839 | 0.985 | 6.3 | 1.09 | 0.23 | 1.13 | 2.3 |
| 6 | 71 | 3.78 | 2.17 | 0.622 | 0.984 | 17.0 | 0.57 | 0.11 | 0.53 | 1.6 |
| 7 | 22 | 3.01 | 4.38 | 0.814 | 0.982 | 24.1 | 0.67 | 0.24 | 0.65 | 1.2 |
| 8 | 26 | 2.27 | 1.94 | 0.684 | 0.965 | 24.8 | 0.53 | 0.27 | 0.55 | 2.9 |
| 9 | 26 | 3.98 | 5.16 | 0.890 | 0.984 | 15.6 | 0.51 | 0.32 | 0.55 | 2.9 |
| 10 | 26 | 2.56 | 7.18 | 0.837 | 0.982 | 5.3 | 1.01 | 0.26 | 1.05 | 4.0 |
| 11 | 27 | 3.12 | 4.41 | 0.713 | 0.978 | 6.9 | 1.03 | 0.19 | 1.00 | 3.1 |
| 12 | 27 | 3.22 | 2.43 | 0.701 | 0.978 | 11.5 | 0.58 | 0.18 | 0.55 | 3.5 |
| 13 | 27 | 3.98 | 2.35 | 0.734 | 0.980 | 12.2 | 0.50 | 0.19 | 0.48 | 3.2 |
| 14 | 27 | 1.74 | 3.60 | 0.591 | 0.958 | 4.5 | 1.25 | 0.25 | 1.33 | 6.4 |
| 15 | 27 | 4.07 | 4.17 | 0.801 | 0.990 | 8.7 | 0.60 | 0.07 | 0.55 | 1.9 |
| 16 | 27 | 2.32 | 3.74 | 0.688 | 0.972 | 10.1 | 0.97 | 0.23 | 1.00 | 3.2 |
| 17 | 69 | 2.74 | 1.88 | 0.629 | 0.975 | 28.7 | 0.55 | 0.16 | 0.50 | 1.5 |
| 18 | 66 | 2.47 | 3.79 | 0.820 | 0.979 | 13.2 | 0.59 | 0.28 | 0.60 | 2.4 |
| 19 | 20 | 4.71 | 3.00 | 0.765 | 0.988 | 23.7 | 0.51 | 0.07 | 0.45 | 8.0 |
| 20 | 20 | 2.94 | 3.86 | 0.611 | 0.973 | 10.3 | 1.18 | 0.16 | 1.13 | 2.0 |
| 21 | 56 | 2.41 | 2.07 | 0.697 | 0.975 | 20.6 | 0.28 | 0.20 | 0.50 | 2.4 |
| 22 | 90 | 1.84 | 1.53 | 0.599 | 0.971 | 24.8 | 0.25 | 0.17 | 0.43 | 1.2 |
| 23 | 71 | 1.99 | 1.48 | 0.633 | 0.972 | 18.3 | 0.23 | 0.18 | 0.45 | 2.2 |
| 24 | 26 | 2.03 | 2.96 | 0.839 | 0.986 | 15.6 | 0.22 | 0.21 | 0.38 | 1.8 |
We found significant relationships between the viscoelastic and biphasic material properties. The two equilibrium parameters—the viscoelastic model equilibrium elastic modulus and the biphasic model aggregate modulus—were highly correlated (Figure 5a). We found correlations between initial elastic modulus and aggregate modulus (Figure 5c), τ and aggregate modulus (Figure 5e), and τ and permeability (Figure 5f). There were no correlations between equilibrium elastic modulus and permeability (Figure 5b), between initial elastic modulus and permeability (Figure 5d), or between the remaining viscoelastic (g, k, equilibrium Poisson’s ratio), and biphasic parameters. Using a multifactorial regression analysis to relate initial elastic modulus with aggregate modulus and permeability, permeability did not contribute to the prediction of initial elastic modulus (P = .500), whereas aggregate modulus did (P < .001).
Figure 5.
Relationships between the viscoelastic and biphasic model parameters. The regression lines are shown for the significant relationships.
The viscoelastic model consistently characterized the experimental data with lower RMSE than the biphasic model over the final 30% of creep displacement (Table 2). Over the final 30% of creep displacement, the RMSE ranged from 0.33 µm to 2.25 µm for the viscoelastic model, and 0.68 µm to 8.67 µm for the biphasic model (Table 2).
Table 2.
Root-mean-square-error (µm) measured over the entire creep displacement for the viscoelastic model and over the final 30% displacement for the biphasic and viscoelastic models
| Test | Viscoelastic RMSE (µm), measured over the entire displacement |
Biphasic RMSE (µm), measured over the final 30% displacement |
Viscoelastic RMSE (µm), measured over the final 30% displacement |
|---|---|---|---|
| 1 | 2.61 | 5.20 | 2.25 |
| 2 | 1.96 | 5.32 | 1.30 |
| 3 | 1.48 | 2.63 | 0.96 |
| 4 | 2.05 | 3.64 | 1.18 |
| 5 | 0.75 | 1.38 | 0.46 |
| 6 | 2.10 | 6.17 | 0.79 |
| 7 | 2.97 | 5.30 | 1.81 |
| 8 | 1.24 | 2.58 | 0.90 |
| 9 | 4.72 | 6.13 | 1.22 |
| 10 | 1.21 | 1.68 | 0.33 |
| 11 | 1.36 | 2.06 | 0.59 |
| 12 | 1.84 | 3.83 | 0.77 |
| 13 | 3.57 | 4.66 | 1.68 |
| 14 | 1.07 | 0.68 | 0.60 |
| 15 | 2.29 | 5.69 | 0.88 |
| 16 | 1.48 | 1.21 | 0.55 |
| 17 | 1.57 | 4.02 | 0.86 |
| 18 | 2.29 | 3.16 | 0.64 |
| 19 | 3.18 | 8.67 | 1.59 |
| 20 | 1.22 | 1.45 | 0.60 |
| 21 | 2.23 | 3.35 | 0.69 |
| 22 | 1.47 | 2.68 | 0.75 |
| 23 | 3.49 | 2.25 | 2.17 |
| 24 | 2.83 | 3.90 | 1.55 |
Discussion
The purpose of this study was to determine the short-term and equilibrium material properties of patella cartilage using a viscoelastic model representation of creep indentation tests. Our results suggest that a viscoelastic model can provide excellent representation of the entire cartilage creep indentation test (Figure 4). We determined the short-term and equilibrium material properties of patella cartilage using the viscoelastic model (Table 1). A second aim of this study was to correlate the viscoelastic material properties to the commonly used biphasic material properties. We found novel relationships between the viscoelastic and biphasic material properties (Figure 5). Specifically, the viscoelastic equilibrium elastic modulus was highly correlated with the biphasic aggregate modulus. This result suggests that the biphasic aggregate modulus and viscoelastic equilibrium elastic modulus are comparable material properties; this finding is corroborated by sensitivity analyses on the biphasic29 and viscoelastic models (not shown) demonstrating similar effects of aggregate modulus and equilibrium elastic modulus on final creep displacement.
This study complements previous work determining cartilage material properties with the commonly used biphasic model.12,17–19 The biphasic model provides cartilage material properties based on characterizing only the final 30% of the experimental creep displacement. The first 70% of the experimental creep displacement is discarded based on the assumption that initial contact between the indenter and cartilage surface is difficult to model.18–21 This study demonstrates the feasibility of acquiring short-term and equilibrium material properties of patella cartilage based on characterization of the entire experimental creep displacement. The ability of the viscoelastic model to characterize the entire experimental creep displacement is likely due to the initial elastic modulus. The initial elastic modulus influenced the slope of the viscoelastic model in the short-term regimen to accurately characterize the initial experimental displacement. The biphasic model has no comparable parameter to the viscoelastic model’s initial elastic modulus; this may explain the inability of the biphasic model to characterize the first 70% of the experimental creep displacement. A combination of viscoelastic and biphasic modeling has been shown to fit the entire creep displacement.36 Complex models (with seven or more material constants) were able to characterize a broad range of mechanical tests, such as tension-compression, nonlinearity, anisotropy, and permeability of cartilage;13,15,16,37 the ability of the viscoelastic model to characterize those mechanical tests is unknown.
The viscoelastic model may be an improvement over current material representations of cartilage for evaluation of joint health using subject-specific finite element modeling.1–5 Cartilage is typically represented as a linear elastic material in finite element models simulating activities of daily living.1–5 A linear elastic material model assumption is considered valid due to the short-term elastic response of the cartilage during activities involving loading frequencies greater than 0.1 Hz, such as walking.38 However, a linear elastic model cannot account for the time-dependent cartilage properties to represent activities such as prolonged kneeling or squatting. For example, in previous whole-joint finite element models of the knee using linear elastic cartilage models, the predicted joint contact area following a static squat held for two minutes did not exactly match experimentally measured contact area.4 The viscoelastic model can represent short- and long-term deformations and would better represent the cartilage creep that would be expected during a static squat. A biphasic representation is challenging to implement in whole-joint modeling due to the difficulties in incorporating evolving fluid-flow conditions at interfaces that come into and out of contact with joint movement. The viscoelastic model implemented via a Prony series representation, avoids these difficulties since the time-dependency is not explicitly associated with fluid flow. As a result, fluid flow boundary conditions are not needed when implementing the viscoelastic model in a whole-joint model. In addition, the short-term loading response of the viscoelastic model is comparable to a linear elastic model35 when representing activities involving loading frequencies greater than 0.1 Hz.38 The viscoelastic model can be used in whole-joint models to also obtain a realistic time-dependent cartilage response, and a viscoelastic material model is substantially easier to implement than a material model that requires evolving fluid flow boundary conditions.
An important advantage of the viscoelastic model presented here is the ease of implementation in commercial finite element programs. Implementation of more complex constitutive models of cartilage13,15,16 can require substantial theoretical and mathematical expertise and custom software. The viscoelastic model as presented requires four material properties, and the Prony series representation is available as a standard material model in most general-purpose finite element programs, such as Abaqus, ANSYS, and Marc. The values for the means and standard deviations obtained from our dataset for donors under the age of 30 years were E0 = 3.78 (1.38) MPa, g = 0.744 (0.090), k = 0.978 (0.009), τ = 13.3 (7.1) seconds, with an assumed initial Poisson’s ratio of 0.47. The mean value of the initial elastic modulus of 3.78 MPa is close to the value of 4.0 MPa, used by Elias et al.39 In addition, for donors under the age of 30 years, the range of values of E0 of 1.94–7.18 MPa is relatively close to the range of 3.5–10 MPa examined by Li et al40 in whole-joint finite element models. In keeping with the use of round numbers, we suggest a value of E0 = 5.0 MPa for healthy cartilage in whole-joint finite element models when using a viscoelastic model.
To understand the physical interpretation of the viscoelastic model, we correlated the viscoelastic material properties to biphasic material properties. We found significant relationships between equilibrium elastic modulus and aggregate modulus, and between initial elastic modulus and aggregate modulus (Figures 5a, 5c). This result is plausible because equilibrium elastic modulus, initial elastic modulus, and aggregate modulus all depend on collagen stiffness and the amount of bound water in the cartilage.
A limitation of this study is that we chose a fixed value of 0.47 for the initial Poisson’s ratio. This assumption was based on near-incompressible behavior of cartilage at initial load.33,34 There is likely inherent variability in initial Poisson’s ratio in cartilage, and initial Poisson’s ratio is difficult to measure experimentally. Another potential limitation, the choice of t0 affected the value of initial elastic modulus, and we found initial elastic modulus nonlinearly increased with a shorter t0. Given our experimental test, we selected the best t0: if t0 < 0.15 second, the indenter may not be in complete contact with the cartilage, and if t0 > 0.15 second, some tests may have reached the test load and begun to creep. A third potential limitation is that this study did not account for the dependence of κ (Eq. 5) on indenter-cartilage friction and indentation depth.41 We calculated a change in initial elastic modulus of less than 5% from our reported values using the relationships described in Zhang et al,41 minimally affecting our reported results.
This study demonstrates the feasibility of determining cartilage material properties using a viscoelastic model representation of the entire displacement curve of creep indentation tests. The viscoelastic model is a computationally efficient method to represent the mechanical response of cartilage and is available in commercial software packages. The viscoelastic model has the potential for widespread application in whole-joint finite element modeling studies.
Acknowledgments
The Department of Veterans Affairs, Rehabilitation Research & Development Service grant #A2592R; National Institutes of Health EB002524; National Institutes of Health EB005790; and a Stanford Bio-X Fellowship.
References
- 1.Baldwin MA, Clary C, Maletsky LP, Rullkoetter PJ. Verification of predicted specimen-specific natural and implanted patellofemoral kinematics during simulated deep knee bend. J Biomech. 2009;42(14):2341–2348. doi: 10.1016/j.jbiomech.2009.06.028. [DOI] [PubMed] [Google Scholar]
- 2.Farrokhi S, Keyak JH, Powers CM. Individuals with patellofemoral pain exhibit greater patellofemoral joint stress: a finite element analysis study. Osteoarthritis Cartilage. 2011;19(3):287–294. doi: 10.1016/j.joca.2010.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Besier TF, Gold GE, Beaupre GS, Delp SL. A modeling framework to estimate patellofemoral joint cartilage stress in vivo. Med Sci Sports Exerc. 2005;37(11):1924–1930. doi: 10.1249/01.mss.0000176686.18683.64. [DOI] [PubMed] [Google Scholar]
- 4.Besier TF, Gold GE, Delp SL, Fredericson M, Beaupre GS. The influence of femoral internal and external rotation on cartilage stresses within the patellofemoral joint. J Orthop Res. 2008;26(12):1627–1635. doi: 10.1002/jor.20663. [DOI] [PubMed] [Google Scholar]
- 5.Mesfar W, Shirazi-Adl A. Biomechanics of changes in ACL and PCL material properties or prestrains in flexion under muscle force-implications in ligament reconstruction. Comput Methods Biomech Biomed Engin. 2006;9(4):201–209. doi: 10.1080/10255840600795959. [DOI] [PubMed] [Google Scholar]
- 6.DiSilvestro MR, Suh JKF. Biphasic poroviscoelastic characteristics of proteoglycan-depleted articular cartilage: Simulation of degeneration. Ann Biomed Eng. 2002;30(6):792–800. doi: 10.1114/1.1496088. [DOI] [PubMed] [Google Scholar]
- 7.Swann AC, Seedhom BB. The stiffness of normal articular cartilage and the predominant acting stress levels: implications for the aetiology of osteoarthrosis. Br J Rheumatol. 1993;32(1):16–25. doi: 10.1093/rheumatology/32.1.16. [DOI] [PubMed] [Google Scholar]
- 8.Hayes WC, Mockros LF. Viscoelastic Properties of Human Articular Cartilage. J Appl Phys. 1971;31:562–568. doi: 10.1152/jappl.1971.31.4.562. PubMed. [DOI] [PubMed] [Google Scholar]
- 9.Eckstein F, Putz R, Muller-Gerbl M, Steinlechner M, Benedetto KP. Cartilage degeneration in the human patellae and its relationship to the mineralisation of the underlying bone: a key to the understanding of chondromalacia patellae and femoropatellar arthrosis. Surg Radiol Anat. 1993;15(4):279–286. doi: 10.1007/BF01627879. [DOI] [PubMed] [Google Scholar]
- 10.Loch DA, Luo ZP, Lewis JL, Stewart NJ. A Theoretical Model of the Knee and ACL: Theory and Experimental Verification. J Biomech. 1992;25(1):81–90. doi: 10.1016/0021-9290(92)90247-x. [DOI] [PubMed] [Google Scholar]
- 11.Blankevoort L, Kuiper JH, Huiskes R, Grootenboer HJ. Articular Contact in a 3-Dimensional Model of the Knee. J Biomech. 1991;24(11):1019–1031. doi: 10.1016/0021-9290(91)90019-j. [DOI] [PubMed] [Google Scholar]
- 12.Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic Creep and Stress-Relaxation of Articular-Cartilage in Compression - Theory and Experiments. J Biomech Eng. 1980;102(1):73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- 13.Garcia JJ, Cortes DH. A nonlinear biphasic viscohyperelastic model for articular cartilage. J Biomech. 2006;39:2991–2998. doi: 10.1016/j.jbiomech.2005.10.017. [DOI] [PubMed] [Google Scholar]
- 14.Pierce DM, Trobin W, Trattnig S, Bischof H, Holzapfel GA. A phenomenological approach toward patient-specific computational modeling of articular cartilage including collagen fiber tracking. J Biomech Eng. 2009;131(9):091006. doi: 10.1115/1.3148471. [DOI] [PubMed] [Google Scholar]
- 15.Huang CY, Mow VC, Ateshian GA. The role of flow-independent viscoelasticity in the biphasic tensile and compressive responses of articular cartilage. J Biomech Eng. 2001;123(5):410–117. doi: 10.1115/1.1392316. [DOI] [PubMed] [Google Scholar]
- 16.Wilson W, van Donkelaar CC, van Rietbergen B, Huiskes R. A fibril-reinforced poroviscoelastic swelling model for articular cartilage. J Biomech. 2005;38(6):1195–1204. doi: 10.1016/j.jbiomech.2004.07.003. [DOI] [PubMed] [Google Scholar]
- 17.Athanasiou KA, Rosenwasser MP, Buckwalter JA, Malinin TI, Mow VC. Interspecies Comparisons of In situ Intrinsic Mechanical-Properties of Distal Femoral Cartilage. J Orthop Res. 1991;9(3):330–340. doi: 10.1002/jor.1100090304. [DOI] [PubMed] [Google Scholar]
- 18.Roemhildt ML, Coughlin KM, Peura GD, Fleming BC, Beynnon BD. Material properties of articular cartilage in the rabbit tibial plateau. J Biomech. 2006;39(12):2331–2337. doi: 10.1016/j.jbiomech.2005.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Setton LA, Mow VC, Muller FJ, Pita JC, Howell DS. Mechanical-Properties of Canine Articular-Cartilage Are Significantly Altered Following Transection of the Anterior Cruciate Ligament. J Orthop Res. 1994;12(4):451–163. doi: 10.1002/jor.1100120402. [DOI] [PubMed] [Google Scholar]
- 20.Miller GJ, Morgan EF. Use of microindentation to characterize the mechanical properties of articular cartilage: comparison of biphasic material properties across length scales. Osteoarthritis Cartilage. 2010;18(8):1051–1057. doi: 10.1016/j.joca.2010.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mow VC, Gibbs MC, Lai WM, Zhu WB, Athanasiou KA. Biphasic Indentation of Articular-Cartilage. 2. A Numerical Algorithm and an Experimental-Study. J Biomech. 1989;22(8–9):853–861. doi: 10.1016/0021-9290(89)90069-9. [DOI] [PubMed] [Google Scholar]
- 22.Huang CY, Soltz MA, Kopacz M, Mow VC, Ateshian GA. Experimental verification of the roles of intrinsic matrix viscoelasticity and tension-compression nonlinearsity in the biphasic response of cartilage. J Biomech Eng. 2003;125(1):84–93. doi: 10.1115/1.1531656. [DOI] [PubMed] [Google Scholar]
- 23.Mak AF. The apparent viscoelastic behavior of articular cartilage–the contributions from the intrinsic matrix viscoelasticity and interstitial fluid flows. J Biomech Eng. 1986;108(2):123–130. doi: 10.1115/1.3138591. [DOI] [PubMed] [Google Scholar]
- 24.Jin H, Lewis JL. Determination of Poisson’s ratio of articular cartilage by indentation using different-sized indenters. J Biomech Eng. 2004;126(2):138–145. doi: 10.1115/1.1688772. [DOI] [PubMed] [Google Scholar]
- 25.Kempson GE, Freeman MA, Swanson SA. The determination of a creep modulus for articular cartilage from indentation tests of the human femoral head. J Biomech. 1971;4(4):239–250. doi: 10.1016/0021-9290(71)90030-3. [DOI] [PubMed] [Google Scholar]
- 26.Hori RY, Mockros LF. Indentation tests of human articular cartilage. J Biomech. 1976;9(4):259–268. doi: 10.1016/0021-9290(76)90012-9. [DOI] [PubMed] [Google Scholar]
- 27.Korhonen RK, Laasanen MS, Toyras J, et al. Comparison of the equilibrium response of articular cartilage in uncon-fined compression, confined compression and indentation. J Biomech. 2002;35(7):903–909. doi: 10.1016/s0021-9290(02)00052-0. [DOI] [PubMed] [Google Scholar]
- 28.Athanasiou KA, Agarwal A, Dzida FJ. Comparative study of the intrinsic mechanical properties of the human acetabular and femoral head cartilage. J Orthop Res. 1994;12(3):340–349. doi: 10.1002/jor.1100120306. [DOI] [PubMed] [Google Scholar]
- 29.Keenan KE, Kourtis LC, Besier TF, et al. New resource for the computation of cartilage biphasic material properties with the interpolant response surface method. Comput Methods Biomech Biomed Engin. 2009;1(4):415–22. doi: 10.1080/10255840802654319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cao Y, Ma D, Raabe D. The use of flat punch indentation to determine the viscoelastic properties in the time and frequency domains of a soft layer bonded to a rigid substrate. Acta Biomater. 2009;5(1):240–248. doi: 10.1016/j.actbio.2008.07.020. [DOI] [PubMed] [Google Scholar]
- 31.Kalyanam S, Yapp RD. Insana MF Poro-viscoelastic behavior of gelatin hydrogels under compression-implications for bioelasticity imaging. J Biomech Eng. 2009;131(8):081005. doi: 10.1115/1.3127250. [DOI] [PubMed] [Google Scholar]
- 32.Raghunathan S, Evans D, Sparks JL. Poroviscoelastic modeling of liver biomechanical response in unconfined compression. Ann Biomed Eng. 2010;38(5):1789–1800. doi: 10.1007/s10439-010-9957-x. [DOI] [PubMed] [Google Scholar]
- 33.Mak AF, Lai WM, Mow VC. Biphasic Indentation of Articular-Cartilage. 1. Theoretical-Analysis. J Biomech. 1987;20(7):703–714. doi: 10.1016/0021-9290(87)90036-4. [DOI] [PubMed] [Google Scholar]
- 34.Carter DR, Orr TE, Fyhrie DP, Schurman DJ. Influences of Mechanical-Stress on Prenatal and Postnatal Skeletal Development. Clin Orthop Relat Res. 1987;(219):237–250. PubMed. [PubMed] [Google Scholar]
- 35.Hayes W, Keer L, Herrmann G, Mockros L. Mathematical Analysis for Indentation Tests of Articular Cartilage. J Biomech. 1972;5:541–551. doi: 10.1016/0021-9290(72)90010-3. [DOI] [PubMed] [Google Scholar]
- 36.DiSilvestro MR, Suh JKF. A cross-validation of the biphasic poroviscoelastic model of articular cartilage in unconfined compression, indentation, and confined compression. J Biomech. 2001;34(4):519–525. doi: 10.1016/s0021-9290(00)00224-4. [DOI] [PubMed] [Google Scholar]
- 37.Julkunen P, Jurvelin JS, Isaksson H. Contribution of tissue composition and structure to mechanical response of articular cartilage under different loading geometries and strain rates. Biomech Model Mechanobiol. 2009;9(2):237–245. doi: 10.1007/s10237-009-0169-y. [DOI] [PubMed] [Google Scholar]
- 38.Higginson GR, Snaith JE. The mechanical stiffness of articular cartilage in confined oscillating compression. Eng Med. 1979;8:11–14. [Google Scholar]
- 39.Elias JJ, Bratton DR, Weinstein DM, Cosgarea AJ. Comparing two estimations of the quadriceps force distribution for use during patellofemoral simulation. J Biomech. 2006;39(5):865–872. doi: 10.1016/j.jbiomech.2005.01.030. [DOI] [PubMed] [Google Scholar]
- 40.Li G, Lopez O, Rubash H. Variability of a three-dimensional finite element model constructed using magnetic resonance images of a knee for joint contact stress analysis. J Biomech Eng. 2001;123(4):341–346. doi: 10.1115/1.1385841. [DOI] [PubMed] [Google Scholar]
- 41.Zhang M, Zheng YP, Mak AFT. Estimating the effective Young’s modulus of soft tissues from indentation tests -nonlinear finite element analysis of effects of friction and large deformation. Med Eng Phys. 1997;19(6):512–517. doi: 10.1016/s1350-4533(97)00017-9. [DOI] [PubMed] [Google Scholar]