High-order interactions observed in multi-task intrinsic networks are dominant indicators of aberrant brain function in schizophrenia

Abstract

Identifying the complex activity relationships present in rich, modern neuroimaging data sets remains a key challenge for neuroscience. The problem is hard because (a) the underlying spatial and temporal networks may be nonlinear and multivariate and (b) the observed data may be driven by numerous latent factors. Further, modern experiments often produce data sets containing multiple stimulus contexts or tasks processed by the same subjects. Fusing such multi-session data sets may reveal additional structure, but raises further statistical challenges. We present a novel analysis method for extracting complex activity networks from such multifaceted imaging data sets. Compared to previous methods, we choose a new point in the trade-off space, sacrificing detailed generative probability models and explicit latent variable inference in order to achieve robust estimation of multivariate, nonlinear group factors (“network clusters”). We apply our method to identify relationships of task-specific intrinsic networks in schizophrenia patients and control subjects from a large fMRI study. After identifying network-clusters characterized by within- and between-task interactions, we find significant differences between patient and control groups in interaction strength among networks. Our results are consistent with known findings of brain regions exhibiting deviations in schizophrenic patients. However, we also find high-order, nonlinear interactions that discriminate groups but that are not detected by linear, pair-wise methods. We additionally identify high-order relationships that provide new insights into schizophrenia but that have not been found by traditional univariate or second-order methods. Overall, our approach can identify key relationships that are missed by existing analysis methods, without losing the ability to find relationships that are known to be important.

1. Introduction

Despite enormous strides made in our understanding of neural physiology, the manner in which cellular and subcellular functional variability leads to variations in human behavior is poorly understood. Accumulating evidence suggests that complex behavior arises from a rich mix of dynamic interactions among neurons, neural groups, and larger functional areas. These interactions arise due to feedback loops, recursive processes, multiple conditioning, and other properties. Mechanisms of neural interactions are evident in the brain at all levels of its hierarchical organization (Amari et al., 2003; Ganmor et al., 2011; Ince et al., 2009; Montani et al., 2009; Yu et al., 2011). Understanding neural interactions is crucial to understanding brain function. Dynamic interactions of the brain are difficult to measure directly¹ and models insufficiently describe their properties. For example, algorithms that are capable of representing arbitrary relations, such as graphical models (GM) (Jordan, 1998; Spirtes et al., 2001), often sacrifice the power to model high-order interactions and instead use pairwise criteria (Friedman et al., 1999). This almost becomes a requirement in the more difficult case where latent variables are involved (Elidan and Friedman, 2005).

It is rarely possible to measure every component of a complex system. Often, one only observes a subset of components for which relations amongst components and with unobserved components are unknown. In a typical neuroimaging study it is nearly impossible to identify and document all confounding factors (e.g. sensory input, mood states) that exert concurrent influence on multiple brain regions simultaneously. Failing to measure key components of a system further complicates resolving the interaction of components. It was shown by Macke et al. (Macke et al., 2011) that including common input into a model of neural populations can eliminate some, otherwise apparent (Amari et al., 2003; Montani et al., 2009), high-order interactions. Thus, failure to include common causes in the model can increase interaction order among observed entities, such as neural populations. The situation is more difficult when one considers interaction of high-level brain features. Because we lack a complete understanding of the physiological basis of intrinsic networks that are revealed in analyses of data collected from different tasks and/or different imaging modalities some common sources go unspecified. As a result, we are unable to consider important confounding factors in imaging studies.

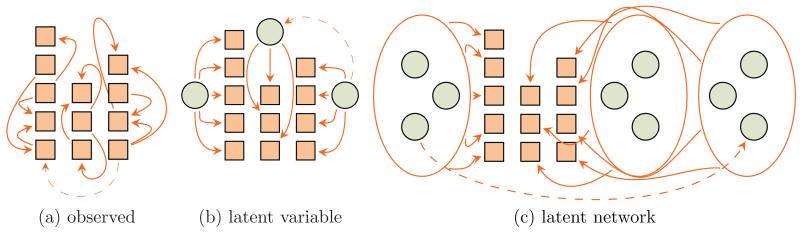
Variants of possible interdependence between observed components (e.g. brain intrinsic networks, modality-specific spatial maps) and latent factors are unbounded making modeling of all confounding factors practically infeasible (Settimi and Smith, 1998). Examples of a limited subset of possible interactions in the complete system leading to interactions among observed random variables are shown in Figure 1.

Figure 1.

Some of the possible scenarios of interdependence among random variables, which can be brain intrinsic networks, data of various modalities etc. A directed graphical model is shown as an example only and it may as well be an undirected or a mixed type relationship. Solid and dashed arrows denote strong and weak statistical interactions respectively. Squares are the observed random variables and circles are the latent variables.

The fully observed case is illustrated in Figure 1a, where random variables can be split into 3 groups shown as columns of squares on the figure (further referred to as factors) with high intra-factor connectivity and weak inter-factor relations. Figure 1b shows a scenario where each factor is regulated by a single latent variable. Figure 1c shows the most general case, where interactions among variables within each factor are governed by a complex unknown network of latent variables. In all cases, variables in a single factor are commonly regulated (coregulated), either by direct interactions among each other or by a latent isolated variable/network. Failure to either measure confounding factors or to model them as latent variables can lead to high-order interactions likely undetectable via a pairwise approach.

From the point of view of data fusion (Goodman et al., 1997; Horwitz and Poeppel, 2002), the difficulty of identifying interactions can be approached via a combined analysis of various data sources, such as imaging modalities. Data fusion combines multiple data sources to allow extraction of information that is richer than a direct sum of univariate data sources. Put differently, data fusion identifies otherwise undetected information about high-order interactions among data sources. To date, there has been no method to analyze all available data sources at the same time in a single model. While in some instances of network modeling we can have latent variables with a clear interpretation (e.g. coherently activating spatial areas in independent component analysis (ICA) models of the brain (Calhoun et al., 2001; McKeown et al., 1998)), assigning meaning to latent variables that govern relations among data sources is difficult despite the relative ease of the mathematical operation to introduce a latent variable. Instead, current fusion methods are mostly focused on simultaneous pairwise analyses of modalities (Calhoun and Adali, 2009; Groves et al., 2011; Michael et al., 2009), although three-way methods of analysis are already under development (Boutte et al., 2012; Sui et al., 2012). Hence, the field is moving towards methods that examine the relationships among interacting variables in an unsupervised fashion (Takane et al., 2008). For computational and statistical reasons it does not seem plausible to simultaneously analyze all available data sources simultaneously. Hence, contemporary methods will strongly benefit from a procedure for automatic and efficient selection of subsets of most informative data sources.

Here we present a novel and effective approach to the problem of identifying functional units exhibiting higher-order interactions. We capture complexity of interactions via an indirect measure: Shannon’s entropy (Mackay, 2002), nonparametrically estimated from the data (Faivishevsky and Goldberger, 2010). Then, we search for a partition of random variables in which factors exhibit more complex interactions according to our measure. Such an approach allows us to group components that are interacting without an explicit model of all possible interactions and confounding factors. Specifically, we define an objective function over partitions of random variables (multi-task intrinsic networks in our application) and optimize it directly within the partition space. To tackle the combinatorial difficulty of searching for such interactions, we present a practical method that relies on a trade-off (i. e. sacrifice the fine-grained graphical structure of interactions for an ability to capture multiway interplay) different from those taken by GM (i. e. sacrifice multi-way interactions for the fine-grained structure), clustering (i. e. sacrifice interaction complexity altogether for speed of processing large scale datasets), and model-based multiple clustering (i. e. sacrifice complexity of interactions by modeling factors via a parametric model for the ability to optimize the model). Our method helps to highlight relevant groups of random variables (neuroimaging data sources in our application below) that express interesting interactions (according to the amount of complexity and surprise expressed by our objective function).

To demonstrate the advantages of our method, we perform a rigorous examination of its accuracy and computational run-time on a range of synthetic but realistic datasets that provide controlled conditions while emulating complexity of real brain data. Next, we apply the method to data that comes from a large multi-task functional magnetic resonance imaging (fMRI) dataset of schizophrenia patients and controls consisting of task-specific intrinsic networks. This dataset was previously analyzed in a pairwise fashion (Kim et al., 2010) and our study lays the ground for multi-way analyses by partitioning intrinsic networks into groups that are related across and within the tasks. Although, the resulting factors can also be used as an input to further analysis, the partitions already provide interesting and novel insights into the differences between patients with schizophrenia and matched healthy control subjects. To capture these differences, we use a metric of interaction strength and compare patients and controls. We further compare these two groups with respect to the stability of the identified factors.

2. Materials and Methods

2.1. Coregulation Analysis

We approach the task of finding interacting groups in the data via random variable modeling. Given a set of n random variables X = {X₁, X₂, … X_n} the task is to partition them into k factors {F₁, F₂, … F_k} containing non-overlapping subsets of X. The assignment of random variables to factors should satisfy the following conditions:

1. The assignment forms a partition of X.

2. Variables in a factor are maximally dependent.

3. Factors are maximally independent.

We formulate an objective function that, when minimized, satisfies the above requirements (see Appendix A). It is based on maximizing intra-factor and minimizing interfactor mutual information. We settle on using multi-information (Slonim, 2002) as a multi-dimensional mutual information criterion for continuous real-valued data and use a non-parametric approach to estimating its quantity (Kraskov et al., 2004). When all of the conditions for satisfactory partitioning are accounted for, multiinformation reduces to the entropy of individual factors and our objective takes the following form:

$$\min {\mathcal{J}}_{\mathcal{I}}=\sum _{j=1}^{m}H\left({\mathit{F}}_j\right),$$ (1)

where F_j denotes a group of random variables. Objective ${\mathcal{J}}_{\mathcal{I}}$ provides a clear intuition of our goals: partition random variables (to be more concrete – multi-task intrinsic networks) into groups, such that their interactions are most structured (have lower randomness). After expanding expression (1) using the employed entropy estimator (Kraskov et al., 2004) and eliminating terms not affected by the way the data is partitioned (see Appendix B for details) we obtain:

$$\min {\mathcal{J}}_{\wr }=\sum _{\mathit{F}}\left(\log \left(c_{d_{\mathit{F}}}\right)+\frac{d_{\mathit{F}}}{z(z-1)}\sum _{i\ne j}log\mid \mid x_i-x_j\mid \mid \right),$$ (2)

where d_F is the dimension (number of elements) of factor F, z is the total number of samples, x_i is the i^th sample of the d_F-dimensional subset of X, and c_dF is the volume of the d_F-dimensional unit ball.

To capture multiway interactions, objective (2) is formulated directly in the space of factors F: interactions of all variables within a factor are considered simultaneously when computing multidimensional entropy in (1). This is in contrast to clustering methods where entropy measures are also used but predominantly in a pairwise fashion. The entropy in expression (1) and its estimator in (2) measure the group property. which is exponential in the number of elements². We tame this complexity by taking advantage of the problem structure that allows us to smooth the objective function in a spline interpolation framework of Yackley et al. (2008). This further reduces complexity through interpolation of objective values at given partitions based on computing the actual values only on a small subset of the partitions. The details of the construction process and of a greedy optimization algorithm are described in Appendix C.

With this approach we are enabling the coregulation analysis via the spectrum of the hypercube (CASH). By “coregulation” we denote direct interactions as well as interactions due to common confounding factors. These can still be expressed in the data but tend to be multi-way and high-order (Macke et al., 2011). Hypercube spectrum approximation is at the core of metagraph analysis of Yackley et al. (2008) and plays an important role for the efficiency of CASH.

2.2. Synthetic datasets

When one is facing the problem of partitioning the data, clustering methods have the highest likelihood to be tried first. Among those are the widespread simple pairwise k-means clustering with the common L₂ and cross-correlation (CC) metrics. Next to try are more sophisticated methods that target nonlinear aspects of the data. The nonparametric information clustering (NIC) (Faivishevsky and Goldberger, 2010) can represent this class.

For the task we target, a better approach would be to use methods that pursue the goal of partitioning the attribute space. Such approaches are available in the field of multi-view clustering (Galimberti and Soffritti, 2007). They explicitly model marginal distributions of each factor via a universal function approximator: the partitioned Gaussian mixture model (PGMM) (Galimberti and Soffritti, 2007). Even further, these approaches explicitly model interactions between the factors: the pouch latent tree model (PLTM) (Poon et al., 2010).

Listed approaches (L₂, CC, NIC, PGMM, and PLTM) are representative of the approaches that can compete with CASH and we use them for performance comparison on synthetic data. In experiments, we sample from the models described below and use co-occurring values of the observed variables as the input. Our comparison metrics are accuracy of assigning random variables to factors and the running time. We measure accuracy as an error fraction of the minimum number of variables mis-assigned relative to the true assignment across all label permutation normalized by the maximum possible number of mis-assignments. We measure the running time by the internal computer clock.

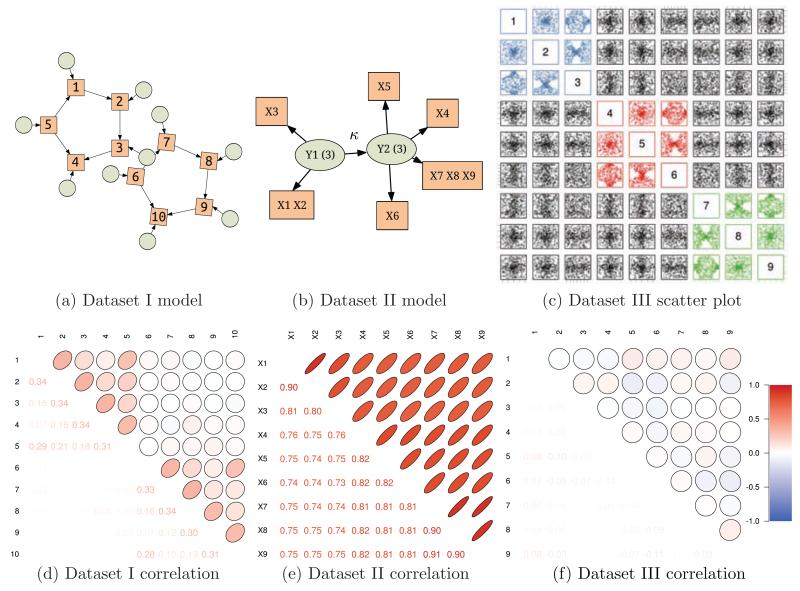
Dataset I comes from a model used by Smith et al. (2010) to generate physiologically relevant simulations of interacting brain regions as observed via fMRI. It involves a model of neural interactions, as well as a hemodynamic model of blood flow that describes ensuing blood oxygenation level dependent (BOLD) signals. The structure of the underlying model, two noninteracting groups each containing five observed nodes (rectangles, Figure 2a), makes these synthetic data particularly interesting for our purpose.

Figure 2.

The three synthetic datasets: Realistic simulations by Smith et al. (2010): a two factor dataset (Figure 2a: rectangles are the observed nodes and circles are the latents), with groups clearly visible in the block structure of the correlation matrix of Figure 2d (diagonal of 1 is not shown). A two factor pouch model of Poon et al. (2010). Two latent variables defining the factors are tightly linked (Figure 2b) resulting in an almost uniformly high correlation values across the correlation matrix (Figure 2e). A scatter plot of a 3 triplet dataset can reveal some structure, but correlation matrix (Figure E.7c) remains completely insensitive.

Dataset II is generated by the PLTM model used for comparisons in the original PLTM paper (Poon et al., 2010). The structure of the underlying graphical model is shown in Figure 2b, where latent rectangular nodes signify the two partitions that are present in the data. Note the link κ between these partitions. The strength of κ determines how closely related the factors are. In the simulation it is κ = 0.91. The correlation matrix in Figure 2e is not as informative as the one of Figure 2d: everything appears correlated.

Dataset III is designed to be harder still. Specifically, we construct a dataset such that the random variables are related via a nonlinear manifold. This is to represent a case of multiway interactions which are frequent in biological datasets, in particular those from neural populations (Amari et al., 2003; Ganmor et al., 2011; Ince et al., 2009; Montani et al., 2009; Yu et al., 2011). For clarity of interpretation, we represent pure tri-way interactions not contaminated by pairwise interactions which are addressed above (see further details in Appendix E). A pairwise scatter plot matrix for a dataset containing three groups is shown in Figure E.7b. The scatter plot is helpful in showing how the correlation matrix in Figure E.7c turns out diagonal for this dataset, i.e. pairwise methods have only minimum information in the data to rely on.

2.3. Multi-task Data Collection

A variety of neuroimaging studies have now used multiple tasks to probe potential biomarkers in schizophrenia patients and our analysis took advantage of this. Our goal is maximizing information content of subsequent meta-analysis by exploring correspondence between intrinsic networks extracted from various tasks using different approaches. For example, the same intrinsic networks activate across tasks with varying degree of variability and task relatedness, but is their spatial distribution really similar across the tasks? If some intrinsic networks are invariant to the task, CASH shall place them in the same factor. If these networks are more coherent with some other networks rather than their counterparts CASH factoring should provide that information. Moreover, for patients and controls factoring results may be different and the difference may be informative and provide class discriminative markers. As we are interested in inter-task relations of intrinsic networks un-confounded by the differences in intrinsic network composition of each task we have selected the same networks in all of the tasks.

To meet these goals, we extracted features from three well-known paradigms: an auditory sensorimotor task (Mattay et al., 1997), a Sternberg working memory task (Manoach et al., 1999) and a auditory oddball task (Kiehl et al., 2005a) using GLM from 68 patients with schizophrenia and 86 controls as part of the Mind Clinical Imaging Consortium (MCIC) study.

Participants

Schizophrenia patients along with their matched healthy controls provided written informed consent for the Mind Clinical Imaging Consortium. Healthy controls were free from any Axis 1 disorder, as assessed with the Structured Clinical Interview for DSM-IV-TR (SCID) screening device. Patients met criteria for schizophrenia in the DSM-IV based on the SCID and a review of the case file by experienced raters located within each site. All patients were stabilized on medication prior to the fMRI scan session. Between patients and controls, significant differences were seen in the participant level of education, but no meaningful differences in the level of parental or maternal education. WRAT scores showed significant IQ differences between the two groups, which might be attributed to the debilitating cognitive effects of schizophrenia. Patients and controls were age matched, thus there were no significant differences between the two groups regarding this criteria. This information including handedness and gender can be found in (Table 1).

Table 1.

Participants

Demographics
	Age in Years (n=154)	Gender (n=154)	Handedness (n=152)
C (μ/σ)	30.70/11.30	54M/32F	78R/3L/4B
P (μ/σ)	31.85/11.35	55M/13F	60R/4L/2B
T (t/p)	0.6289/0.5304	Male/Female	Right/Left/Both

Education & Intelligence
	Education (n=152)	Paternal edu (n=142)	Maternal edu (n=142)	WRAT (n=149)
C (μ/σ)	15.24/2.06	14.87/3.36	13.98/2.60	51.19/3.73
P (μ/σ)	13.72/2.44	14.46/3.86	13.83/3.73	48.13/5.51
T (t/p)	4.1521/ < 10−4	0.6738/0.5015	0.2886/0.7733	4.0397/ < 10−4

FMRI Tasks:

1. Auditory oddball task (Target and Novel) (AOD): The auditory oddball task stimulated the subject with three kinds of sounds: target (1200Hz with probability, p = 0.09), novel (computer generated complex tones, p = 0.09), and standard (1000Hz, p = 0.82) presented through a computer system via sound insulated, MR-compatible earphones. Stimuli were presented sequentially in pseudorandom order for 200ms each with inter-stimulus interval (ISI) varying randomly from 500 to 2050ms. A subject was asked to make a quick button-press response with their right index finger upon each presentation of the target stimulus and no response was required for the other two stimuli. There were 4 runs, each comprising of 90 stimuli (3.2min) (Kiehl and Liddle, 2001; Kiehl et al., 2005b).

2. Sternberg working memory task (Encode and Probe) (SIRP): The Sternberg working memory task (Manoach et al., 2001, 1999) requires subjects to memorize a list of digits (displayed simultaneously) and later to identify if a probe digit was in the list. Three working memory loads: high (5 digits), medium (3 digits) and low (1 digit) were used in this paradigm. Each run contained two blocks of each of the three loads in a pseudorandom order. Half of the probe digits were targets (digits previously displayed) and half were foils. Subjects were asked to respond with their right thumb if the probe digit was a target and with their left thumb for a foil.

3. Sensorimotor Task (SM): The sensorimotor task (Haslinger et al., 2005; Mattay et al., 1997) consisted of an on/o block design, each with a duration of 16s. During the on-block cycles of 8 ascending-pitched and 8 descending-pitched, 200ms tones were presented. There were three runs each with duration of 4 minutes. The participant was instructed to press the right thumb of the input device after each tone was presented.

Imaging Parameters

Scanning was performed across four sites: the University of New Mexico (UNM), University of Iowa (IOWA), University of Minnesota (MINN), and Massachusetts General Hospital (MGH). All sites, except for UNM, utilized a Siemens 3 Tesla Trio Scanner, while UNM utilized a Siemens 1.5 Tesla Sonata. The scanners were equipped with a 40 mT/m gradient and a standard quadrature head coil. The fMRI pulse sequence parameters were identical for all three tasks (AOD, SIRP, SM) and were the following: single-shot echo planar imaging (EPI); scan plane = oblique axial (AC-PC); time to repeat (TR) = 2 s; echo time (TE) = 30 ms; field of view (FOV) = 22 cm, matrix = 64 × 64; flip angle = 90 degrees; voxel size = 3.4 × 3.4 × 4 mm³; slice thickness = 4 mm; slice-gap = 1 mm; number of slices = 27; slice acquisition = ascending.

FMRI Preprocessing

Datasets were preprocessed using SPM5. Realignment of fMRI images were performed using INRIalign, a motion correction algorithm unbiased by local signal changes (Freire et al., 2002). Datasets were then spatially normalized into the standard Montreal Neurological Institute (MNI) space (Friston et al., 1995) using an echo planar imaging template found in SPM5 and slightly subsampled to 3 × 3 × 3 mm³, resulting in 53 × 63 × 46 voxels. Finally, spatial smoothing was performed with a 9 × 9 × 9 mm³ full width half maximum Gaussian kernel.

Feature Extraction: General Linear Model

For feature extraction in this study we have used the approach of Kim et al. (2010) described in details thereof. For each individual task (AOD, SIRP, SM), a GLM approach was used to find task-associated brain regions, labeled as contrast maps. A univariate regression of each voxel’s time-course with an experimental design matrix was generated by the convolution of the task onset times with a hemodynamic response function. This resulted in a set of beta-weight maps associated with each parametric regressor for each task. The subtraction of one beta-weight map with another is often referred to as a contrast map, which represents the effect of a task in relation to an experimental baseline. For our purposes, we were interested in the relative effect of target or novel stimuli versus standard stimuli in the AOD task, the average probe effect or the average encode effect for the SIRP task, and the SM tapping effect for the SM task.

Feature Extraction: Independent Component Analysis

A group spatial ICA was performed³ using the infomax algorithm (Bell and Sejnowski, 1995) within the GIFT toolbox v1.3d (http://icatb.sourcefourge.net). We found the optimal number of components for ICA by using a modified minimum description length algorithm (Li et al., 2007), which was found to be 19 for the AOD task, 23 for the SIRP task, and 22 for the SM task. Since ICA with infomax is a stochastic process, the end results are not always identical. To remedy this, we applied ICASSO (Himberg et al., 2004) to our initial ICA analysis which allowed us to reiterate our ICA analysis for 20 iterations and to take the centroid of the resulting spatial maps. The spatial maps and their respective timecourses were calibrated using z-scores. The features selected for our CASH analysis comprised of 8 components that were highly similar across our three tasks, containing activation patterns seen from previous ICA studies of fMRI. A full listing of the features selected for both ICA and GLM, along with their respective descriptions can be found in (Table 2).

Table 2.

Features selected for ICA and GLM

Description	Label	Type	Tasks
Left dorsal lateral prefrontal cortex	LDLPFC	ICA	AOD,SIRP,SM
Right dorsal lateral prefrontal cortex	RDLPFC	ICA	AOD,SIRP,SM
Primary Visual	V1	ICA	AOD,SIRP,SM
Bilateral Temporal	Temporal	ICA	AOD,SIRP,SM
Default Mode Network Posterior	DMN1	ICA	AOD,SIRP,SM
Default Mode Network Anterior	DNM2	ICA	AOD,SIRP,SM
Bilateral Frontal Pole	FPOLE	ICA	AOD,SIRP,SM
Pre/Post Central Gyrus	Central	ICA	AOD,SIRP,SM
Targets vs Standards	Targets	SPM	AOD
Novels vs. Standards	Novels	SPM	AOD
Encode Block Average	Encode	SPM	SIRP
Probe Block Average	Probe	SPM	SIRP
Motor Tapping Block Average	Motor	SPM	SM

Large Sample Size

Using a common mask for subjects within each group and stacking the masked data in the subjects dimension, we have obtained an n × z dataset matrix D with n = 29 denoting number of random variables representing the features and z = 3832684 (4699126) – number of samples for patients (controls). To cope with the large sample size we use a heuristic down-sampling approach described in Appendix D.

3. Results

3.1. Synthetic Datasets

In this section we demonstrate on synthetic data that CASH performs well on the whole spectrum of problem difficulties, whereas competing methods are only good when their model conditions are met.

Dataset I Although accepted as a fairly realistic, the model turned out to be not challenging for a partitioning algorithm, as seen from the clear block structure of the correlation matrix of the data (Figure 2d). Notably, the model is also quite easy for the structure search since the edges stand out in the correlation matrix having a higher strength. It is not surprising that all competing models perform well and are statistically indistinguishable (not shown).

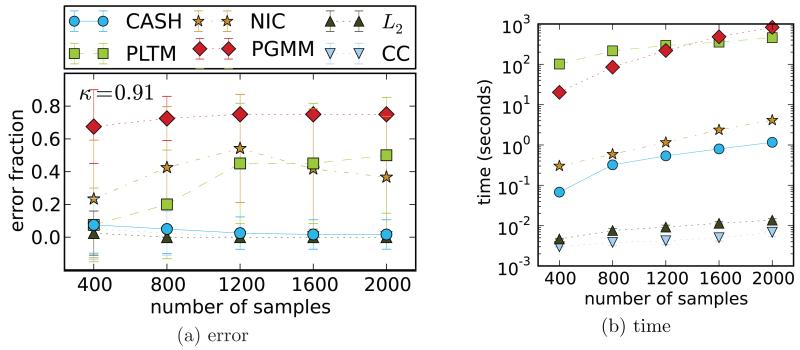
Dataset II When κ is low, all 6 methods perform well with a close to zero error (not shown). However, this pattern changes when factors become related (κ ≥ 0.9). Figure 3 shows performance of the competing approaches on a dataset just like that (κ = 0.91). The most accurate models are CASH, L₂, and CC k-mean. The PGMM model fails at all sample sizes. Interestingly, NIC and PLTM perform better with smaller as compared to larger sample sizes. In case of NIC it is most likely due to the “curse of dimensionality” (Mackay, 2002) since for clustering algorithms the sample size is the dimensionality of the space containing data. PLTM and PGMM models behave surprisingly poor, which we attribute to their low robustness to correlated datasets. The good performance of k-means approaches is also interesting and worth noting. Another major difference is in the wall-clock time comparison shown in Figure 3b, where k-means algorithms are the fastest, with CASH holding the third place, and model based methods being slowest (up to 3 orders of magnitude slower than CASH).

Figure 3.

Dataset II: accuracy and run time comparison on the data simulated from the two factor PLTM of Figure 2b. CASH and k-means demonstrate good performance whereas the other algorithms fail. Each point on the plots is the average of 50 runs on 50 randomly generated datasets. The most accurate methods are also the fastest.

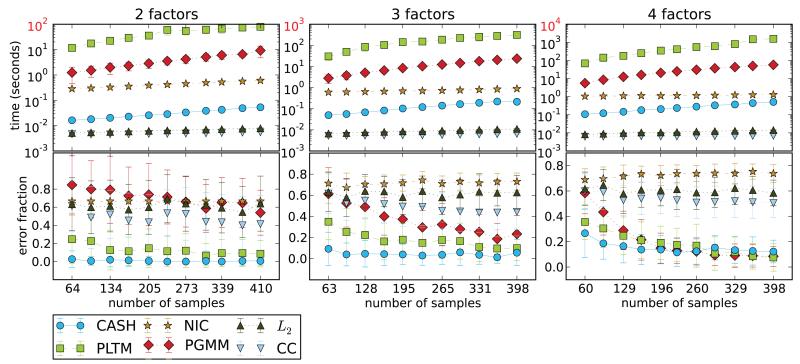
Dataset III Figure 4 shows error and wall-clock time comparison of all competing algorithms on a 2, 3 and 4 factor manifold datasets. All three clustering algorithms (L₂, CC, NIC) perform quite poorly on this dataset. This is expected for k-means, since there is no pairwise information that can be used. NIC, however, is based on mutual information, and, in fact, estimates entropy like CASH using the mean nearest neighbor estimator (Faivishevsky and Goldberger, 2010). The mode of operation, however, imposes a strong “curse of dimensionality” condition on NIC (Mackay, 2002). Its failure on these data provides further support for the need for novel methods of attribute partitioning, like CASH. PLTM performs quite well and almost identical to CASH only requiring a larger samples size. PGMM has comparable performance too, only failing on the 2 factor dataset and needing even larger sample size than PLTM for comparable accuracy. The failures of PGMM are mostly due to its consistent overestimation of the number of factors, which can be expected since the method directly optimizes the BIC (Bayesian information criterion) score (Schwarz, 1978). As before, k-means is the fastest algorithm among all. However, it is not able to recover the structure underlying the data. Among the 3 most accurate algorithms CASH is the fastest and dramatically so: it is 2 (vs PGMM) to 3 (vs PLTM) orders of magnitude faster.

Figure 4.

Dataset III: accuracy and run time comparison on data with 2, 3, and 4 factors. CASH performs well in all cases and generally needs fewer samples to achieve low error rate. Each point on the plots is the average of 50 runs on 50 randomly generated datasets.

3.2. Factoring Multi-Task Data

Comparisons on synthetic data demonstrate competitive features of CASH and provides confidence in its preparedness for large scale applications. Now we apply CASH to our multi-task fMRI data. Our random variables are now data sources and instantiations of these variables are voxel values determined by data collection and processing methods. A chief purpose of multitask fMRI data fusion is to access the joint information provided by multiple tasks, which in turn can be useful for identifying dysfunctional regions implicated in brain disorders. Our goal is to partition data sources into functionally relevant and meaningful groups.

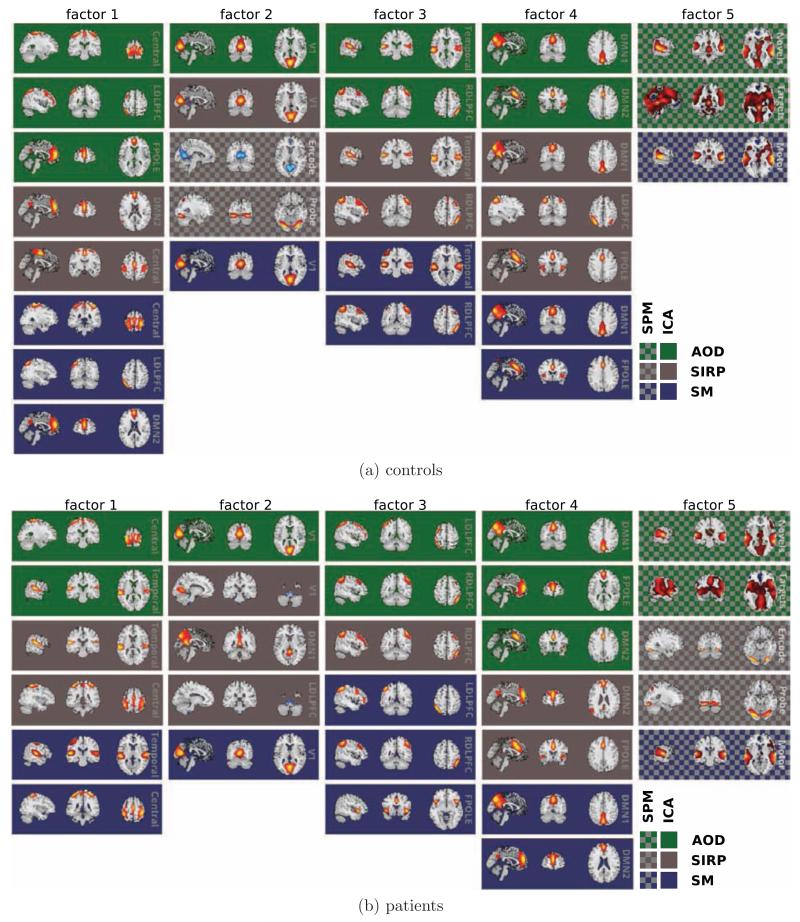
We use data of all subjects in both groups (patients and controls).⁴ We apply CASH with the upper bound on the number of factors set to 5 (see below). We run CASH 50 times with a random starting partition. The partition that has the lowest objective (2) value is used as our best solution. Note, we are not solving the problem of setting the model order optimally in this paper and it is a hyper-parameter in CASH as in many other related methods (k-means, ICA and others (Mackay, 2002)). Furthermore, since CASH uses the input number of factors as an upper bound, the exact value of this parameter is not very restrictive. Nevertheless, we have CASH run for various values of this hyper-parameter m and found denser groups with smaller m. The selected value of m = 5 is at the factor content level that is easier to interpret: factors are not overwhelmingly dense while including several classes of intrinsic networks. The rest of the findings are consistent across choices of m we have tried. The factoring of features corresponding to the best objective value is shown in Figure 5a for controls and in Figure 5b for patients.

Figure 5.

Multitask brain intrinsic networks partitioned by CASH into 5 factors for patients and controls. Color denotes one of the three tasks, checkerboard background denotes statistical parametric map, solid background is for ICA. CASH was run separately on these datasets and resulted in a group specific partition of brain intrinsic networks.

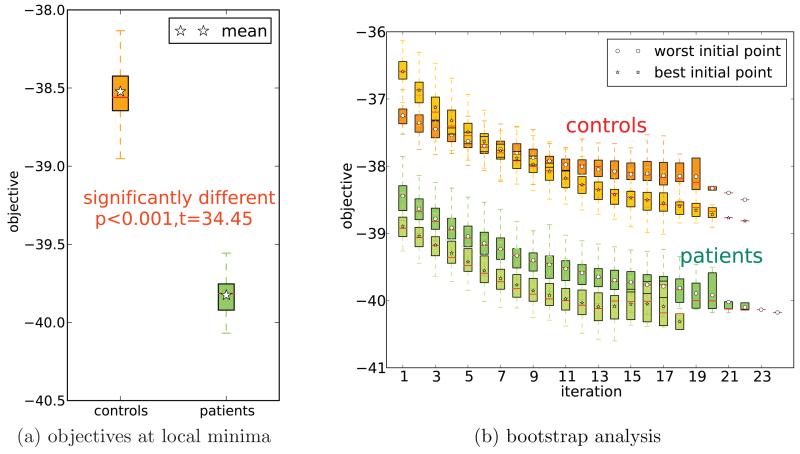
Each of the 50 runs of CASH returned a solution after converging at a local minimum. The values of the objective at these minima are summarized in the box and whisker plot of Figure 6a. As the figure shows, solutions for patients and controls have significantly different distributions of the objectives at these local minima (p < 0.001). This difference means that the spatial variability of intrinsic networks that comprise a factor is significantly lower in patients than in controls. Regardless of the task the co-regulated groups of intrinsic networks consist of networks that are more related in patients than controls. Evidently, in patients intrinsic networks have statistical properties that are similar across tasks, networks and extraction methods (ICA and GLM) more than for controls.

Figure 6.

Distribution of the CASH objective values (lower is better) on the multi-task feature dataset - box and whisker (1.5IQR) plots. Figure 6a shows distributions of objectives at 50 local minima found by running the algorithm with 50 random starting points using complete datasets. Figure 6b summarizes results of the bootstrap analysis of the same dataset re-sampling subjects with replacement 50 times. Trajectories for only two starting points are shown for each group: one that converged to the best solution in the experiment of Figure 6a, and one that converged to the worst (the highest objective value).

The dataset sizes for patients and controls provide some confidence that the results are not due to a random chance of subject selection. However, to be sure that the differences in the groups and factoring results are not due to outliers we also performed a bootstrap analysis re-sampling the subjects with replacement and generating 50 new separate datasets. For each of these datasets we ran CASH using 2 starting points: one that gave the best (best initial partition (BIP)) and the other the worst solution (worst initial partition (WIP)) in the run using the complete dataset (Figure 6a). Figure 6b summarizes these runs in a box and whisker plot. Since the number of iterations is different for each dataset – the averages have fewer points at high iteration numbers (see Figure 6b iterations 21 through 24). The bootstrap experiment shows that the difference between the local minima objective values in patient and control groups is not due to outlier subjects. Another conclusion: CASH solutions are quite stable with respect to subject resampling. In majority of the cases for each group the BIP solution has better objective value than the WIP solution. This may be an evidence of the objective function landscape not experiencing drastic changes with resampling.

Despite its relative stability (worst and best initial points lead to solutions of corresponding quality), CASH returns different solutions for each of the datasets. To estimate the effect of factoring stability we have selected the best solution and computed the partition distance with every other solution in the 50 runs for each of the groups. To estimate whether the so computed distribution of mismatches for patients and controls are different, we have applied the nonparametric Mann-Whitney U-test. The test showed that the distributions are significantly different with p = 0.003.

To obtain further detail on this difference we have looked at 10 features that have changed their factor assignment the least in the 50 runs with respect to the partition obtained using the complete dataset (Figure 5). These are the most stable features for each group. Since they do not change their factor assignment as frequently as other features, we consider them group discriminative. Table 3 lists these top 10 stable features for patients and controls along with their distance coefficient (k): number of times out of the 50 runs a feature was assigned to a factor different from the one in the best partition of the complete dataset.

Table 3.

Labels of 10 most stable features (sorted by the distance coefficient k). Features unique to each group are highlighted. k denotes the number of times out of the 50 runs a given feature was in a cluster different from the cluster it was assigned to in the best solution obtained using the complete dataset.

#	k	Controls			k	Patients
1	0	Central	SIRP	ICA	0	DMN2	SM	ICA
2	0	Central	SM	ICA	0	FPOLE	AOD	ICA
3	1	Targets	AOD	SPM	1	V1	SIRP	ICA
4	1	Central	AOD	ICA	3	Central	AOD	ICA
5	1	DMN2	AOD	ICA	3	RDLPFC	AOD	ICA
6	10	V1	SIRP	ICA	4	RDLPFC	SM	ICA
7	13	V1	SM	ICA	4	Encode	SIRP	SPM
8	13	V1	AOD	ICA	4	Targets	AOD	SPM
9	14	Novels	AOD	SPM	4	RDLPFC	SIRP	ICA
10	14	Motor	SM	SPM	4	DMN2	AOD	ICA

As our synthetic experiments show, CASH is rarely less accurate than the other methods. However, if our multi-task data only contain linear pairwise relations (the kind of Dataset I and II) then k-means methods may be a better choice. In this case, they are as accurate as CASH but work faster. We ran L₂ and CC k-means on these data with k = 5 and the same 50 starting locations used in CASH runs. L₂ k-means resulted in uneven clusters placing 19 out of 29 networks in a single cluster and we do not consider it further. CC k-means resulted in a reasonable four six-network clusters and a single five-network cluster (see Appendix F). However, they were very similar for patients and controls and even the objective values were close to each other (11.67 and 11.28 respectively). This is in contrast to CASH which has, as was shown, identified considerable group differences in the extracted networks.

4. Discussion

CASH can be related to clustering methods (less so) and to the multi-view clustering approaches (Galimberti and Soffritti, 2007; Poon et al., 2010). The latter could be direct alternatives to CASH were they not orders of magnitude slower when applied to proper neuroimaging datasets.

We have shown that CASH can capture a wide range of possible interactions with comparable speed and accuracy, whereas other algorithms fail in some of the settings. Note, high order interactions can also be captured by graphical model structure search algorithms such as PC (see Spirtes et al., 2001, §5.4.2, pp. 84-88). We did not compare to these, as their output is not a partition but a graph which complicates direct comparison. We conclude that CASH is safe to use when the latent structure of the data is unknown a priori – it will not fail on an “easy” dataset while providing meaningful factors in the hard cases. CASH is also robust to the change in co-regulation structure among random variables as well as to the connection strength between the factors contained in the data.

Factoring Multitask Data

When using datasets comprised of complete subject sets for patients as well as for controls, we obtained a factoring of features displayed in Figure 5. A notable feature is that in the patient group the temporal lobe is grouped with motor areas (factor 1 in Figure 5b), whereas in controls it is grouped with higher cognitive areas (factor 3 in Figure 5a). We found that similar intrinsic networks grouped together irrespective of the task data from which they were derived, arguing for consistency of neural systems across tasks.

A notable difference between the groups (see Figure 5) is the placement of all of the SPM features in a single factor for patients, while splitting them between two factors in the control group. This observation supports previous findings of “more similar” activations in schizophrenia patient than controls (Calhoun et al., 2006; Michael et al., 2009). Furthermore, our objective function (2) provides a quantitative measure of similarity that extends beyond second order interactions. This allows us to judge similarities between patients and controls. Figure 6a shows a quantitative measure of how patients are “more similar” than controls and amounts to a statistically significant difference: p < 0.001.

In Table 3 for patients the distance from the complete dataset partition (k) is lower than for controls: group discriminative features are more stable for patients whereas the variability is higher in controls. The features that are different between the groups are shown in color. For controls notable discriminative features include pre/post central gyrus (Central) in all of the tasks as well as the primary visual cortex (V1) in all tasks. For patients, right dorsal lateral prefrontal cortex (RDLPFC) for all tasks is group discriminative, although the most stable are default mode network anterior (DMN2) and bilateral frontal pole (FPOLE) features.

Our analysis does not specifically aim at identifying intrinsic networks most discriminative between patients and controls. The most stable networks can be thought of as rather the most characteristic for each group. However, prior work on identification of discriminative features has shown results consistent with ours (Sui et al., 2009, 2011). For example, schizophrenia is associated with altered temporal frequency and spatial location of the default mode network (the most characteristic component for the patients group) (Bluhm et al., 2007; Garrity et al., 2007; Sui et al., 2009). RDLPFC is among the most stable networks for all 3 tasks in patients and it is known to play an important role in sensory integration, cognitive control and regulation of cognitive function. Dysfunction and lack of functional connectivity of this region is frequently reported in patients with schizophrenia (Badcock et al., 2005; Hamilton et al., 2009; Sui et al., 2011). A prior study using pairwise similarity criteria has shown default mode network anterior in a sensory-motor task and frontal pole in an AOD task as well as V1 in a SIRP task to be one of the most discriminative for patients and controls (Kim et al., 2010). It is important to note that nearly all patients were taking psychotropic medications for their mental disorder while such medications were essentially absent in the control participants. Patients were generally stable in their prescribed dosages of medications prior to the fMRI scan session. A detailed medical history was not available for all subjects and thus the examination of medication effect was omitted.

In the absence of the ground truth, it is hard to prefer one factoring of the multitask dataset over another without additional information. Based on synthetic data, when comparing k-means with CASH we expect either both of the methods to provide similar partitions or k-means be incorrect. Although, there may still be a chance that k-means resulted in a better factorization – it is unlikely in our case. We have prior information that patients and controls groups are different. The fact that CC k-means returns very close clusters for these groups (in composition as well as in the objective value) raises a question of cluster’s validity. Furthermore, uniform cluster sizes serve as an evidence that CC k-means sees the space of intrinsic networks as flat so the best Voronoi tesselation is a grid. Previous work has suggested the prevalence of nonlinear over linear effects in discriminating patients from controls in unimodal imaging data (Burge et al., 2009; Kim et al., 2008) but these effects have not been directly investigated and contrasted with linear effects nor have they been studied in the context of multi-task data.

5. Conclusions

We have described the coregulation analysis framework for capturing arbitrarily complex, multi-way interactions among random variables based on information theory: CASH. Claims about performance of CASH in detecting multi-way interactions were carefully evaluated in a comparison using synthetic data. We conclude that CASH, in contrast to competing methods, performs well in all tested contexts while providing competitive computational running time. As running time is proportional to the dataset size, the results of evaluation tests position CASH as a practical tool for neuroimaging data analysis when multi-way interactions can be present. We apply CASH to a large multi-task fMRI dataset of schizophrenia patients and controls consisting of task-specific intrinsic networks. In addition to finding meaningful groups of intrinsic networks we observed statistically significant differences in inta-group relations according to our entropy criterion: intrinsic networks of patient are more interrelated than those of controls. This finding holds after bootstrapping of subjects. In addition, CC k-means results provide evidence that nonlinear high-order interactions can provide group discriminative information for schizophrenia patients and controls that is not visible otherwise. Our results are consistent with and extend known findings from univariate and second order-based methods, thus arguing for approaches such as CASH that can capture true higher-order dependencies in datasets from complex domains such as neuroscience.

Highlights.

• –New approach to identify high order links among multiple imaging modalities
• –Evidence of important relationships not detected by existing analysis methods
• –Multimodal relationships highlight important changes in schizophrenia

Appendix A. Partitioning Objective

Given a set of n random variables X = {X₁, X₂, … X_n} the task is to partition their joint probability density into k ≤ m factors {F₁, F₂, … F_k}. The assignment of random variables to factors should satisfy the following conditions:

1. The assignment forms a partition of X.

2. Variables in a factor are maximally dependent.

3. Factors are maximally independent.

Unlike factor analysis and related methods we do not aim at reducing the dimensionality of the data by discovering a smaller set of latents expressed as a linear combination of the observed variables. Rather, we aim at factoring the joint distribution to enable more detailed analyses on the subsets.

A solution algorithm needs to estimate the number of factors k while the upper bound m is an input parameter. In practice, m can be estimated with penalized search (Duda et al., 2000) or Chinese Restaurant Process-based Bayesian estimates (Xing et al., 2004).

Let us denote by $X_i^F$ the i^th random variable assigned to factor F, and by $\mathcal{D}$ the criterion used to evaluate statistical dependence ($\mathcal{D}$, for example, can be mutual information or multiinformation). Now we express condition 2 as:

$$\max {\mathcal{J}}_2=\sum _{i=1}^k\mathcal{D}\left({\mathit{F}}_i\right)=\sum _{i=1}^k\mathcal{D}(X_1^{{\mathit{F}}_i},\dots X_{\mid {\mathit{F}}_i\mid }^{{\mathit{F}}_i}),$$ (A.1)

and condition 3 as:

$$\min {\mathcal{J}}_1=\mathcal{D}({\mathit{F}}_1,{\mathit{F}}_2,\dots {\mathit{F}}_k).$$ (A.2)

The cumulative objective function for the proposed factoring of the joint distribution of the random variables is then

$$\min \mathcal{J}=\frac{{\mathcal{J}}_1^{\alpha }}{{\mathcal{J}}_2^{1-\alpha }},$$ (A.3)

where α ∈ [0, 1] controls relative importance of intra-cluster dependence over inter-cluster independence. Condition 1 is enforced by limiting the space of possible solutions while minimizing $\mathcal{J}$.

Appendix B. Estimating Dependence

A number of options for the dependence criterion, $\mathcal{D}$, are available, including multiinformation (MI) (Studený and Vejnarová, 1998), Kullback-Leibler (KL) divergence (Kullback and Leibler, 1951), α-divergence and the Hilbert Schmidt Information Criterion (HSIC) (Gretton et al., 2006); a full evaluation of their relative merits is beyond the scope of this paper.

If we use definition of multiinformation ${\mathcal{D}}_{\mathcal{I}}(X_1,\dots ,X_n)$ presented in (Slonim, 2002, eq. 1.12) for discrete variables, and extended to continuous random variables as:

$${\int }_{x_1,\dots ,x_n}p(x_1,\dots ,x_n)\log \frac{p(x_1,\dots ,x_n)}{p\left(x_1\right)\dots p\left(x_n\right)}d{x}_1\dots d{x}_n,$$ (B.1)

then we can compute it as KL divergence ${\mathcal{D}}_{\mathcal{KL}}\left[p\right(x_1,\dots ,x_n)\mid p(x_1\left)\dots p\right(x_n\left)\right]$.

However, in the case when mutual information is used as a dependence criterion we can rewrite the objective (A.3) using the following identity I(X, Y) = H(X)+H(Y)−H(X, Y), where H denotes the Shannon’s entropy, as

$$\frac{\sum _{i=1}^{m}H\left({\mathit{F}}_i\right)-H({\mathit{F}}_1,{\mathit{F}}_2,\dots ,{\mathit{F}}_m)}{\sum _{j=1}^m\left(\sum _{X\in {\mathit{F}}_j}H\right(X)-H({\mathit{F}}_j\left)\right)}.$$ (B.2)

Since F_js partition the space of X, the first sum in the denominator (after removing brackets) runs over all random variables and we end up with

$$\frac{\sum _{i=1}^{m}H\left({\mathit{F}}_i\right)-H({\mathit{F}}_1,{\mathit{F}}_2,\dots ,{\mathit{F}}_m)}{\sum _{i}H\left(X_i\right)-\sum _{j=1}^{m}H\left({\mathit{F}}_j\right)}.$$ (B.3)

Note that neither sum of the entropies of the individual variables (the first term in the denominator) nor the entropy of all of the random variables (the second term in the numerator) depend on the way we factor the joint. Thus objective (A.3) with MI criterion can be minimized by minimizing a single quantity ${\sum }_{j=1}^{m}H\left({\mathit{F}}_j\right)$, which simultaneously maximizes the numerator and minimizes the denominator of (B.3)⁵. And our objective becomes:

$$\min {\mathcal{J}}_{\mathcal{I}}=\sum _{j=1}^{m}H\left({\mathit{F}}_j\right)$$ (B.4)

Information theoretic criteria are difficult to estimate and require complicated bias correction terms in higher dimensions (Nemenman et al., 2001). Fortunately, for our purpose, we are more interested in the discrepancy among random variables (their clusters) than in the exact MI value. A paper by Pérez-Cruz (2008) demonstrates suitability of the k-nearest neighbor mutual information (MI) estimator (Kraskov et al., 2004) to measuring discrepancy in random variables, together with proving almost sure convergence for k-nn type estimators of MI, KL divergence and differential entropy.

Nearest neighbor search in the k-nn estimators is an expensive operation, which can be, fortunately, avoided by averaging over all possible values of k, as it has been shown by Faivishevsky and Goldberger (2009, 2010). The estimator of H(F_l), for some 0 < l < m, is expressed as

$$\widehat{H}\left({\mathit{F}}_l\right)=\psi \left(n\right)+\log \left(c_d\right)-\frac{1}{n-1}\sum _k^{n-1}\psi \left(k\right)+\frac{d}{n(n-1)}\sum _{i\ne j}log\mid \mid x_i-x_j\mid \mid ,$$ (B.5)

where x_i and x_j are vectors of values of all random variables at instances i and j respectively, ψ(·) is the digamma function, n is the number of data instances, d is the number of random variables in the current factor F_l and c_d = π^d/2/Γ(1 + d/2) is the volume of the unit ball in ${\mathcal{R}}^d$. Importantly, the accuracy of an entropy estimator is irrelevant for our optimization problem as long as relative values of the objective ${\mathcal{J}}_{\wr }$ provide correct ordering of partitions with respect to their optimality. This property indeed holds as Pérez-Cruz (2008) previously observed and our simulations and applications provide empirical support.

Dropping the terms that are not affected by a change in partition (those that include (ψ(·)), we arrive at the final form of our objective employed in the rest of the paper:

$$\min {\mathcal{J}}_{\wr }=\sum _{\mathit{F}}\left(\log \left(c_d\right)+\frac{d}{n(n-1)}\sum _{i\ne j}log\mid \mid x_i-x_j\mid \mid \right).$$ (B.6)

Although the estimator in (B.6) is polynomial in number of instances (O(dn²)), it is still expensive to compute at each iteration of a search procedure even for datasets of moderate sizes. However, among its advantages is a smoother⁶ resulting estimate, a property we will need in Section Appendix C and demonstrate its use in 3.1.

Appendix C. Approximating the Objective

Estimation of the objective, ${\mathcal{J}}_{\wr }$, is computationally expensive due to the complexity dependent on the number of variables, number of factors and the sample size. In this section we show a way to overcome this problem by (pre)computing only a small number of values y_i of the objective and approximating the rest.

We start with describing a framework for approximating Bayesian network score using a meta-graph kernel introduced by Yackley et al. (2008). Following the original exposition, we present the framework from the point of view of a structure-search score approximation. However, the approach allows approximation of arbitrary smooth functions on a hypercube by representing them in the basis of eigenvectors of its Laplacian and we adapt it to our factoring problem in the next section.

Yackley et al. has shown how to efficiently compute any specific elements of desired eigenvectors of the Hamming cube graph Laplacian and we give an intuition of how it is done. First note that for n nodes there are n² possible edges in a directed graph. In a given graph each of these edges can be either present or absent giving the total number of possible graphs 2ⁿ². Representing adjacency matrix with a bit string and connecting by an edge those bit-strings that differ only in a single bit state, we define a meta-graph over all possible directed⁷ graphs on n nodes. This graph is the Hamming cube.

Laplacian of an n-node graph G is defined as L_G = D_G − A_G, where D_G is an n × n diagonal matrix with node degrees as the diagonal elements, and A_G is the n × n adjacency matrix of the graph.

Yackley et al. observed that the eigenvectors of L_G form the Hadamard matrix, and the eigenvectors of the hypercube Laplacian are columns of the Hadamard matrix, for which the entries can be computed in closed form (see their paper for details). This leads to an efficient solution of the following minimization problem (expressed in terms of our task):

$${\widehat{\mathcal{J}}}_{\wr }=\arg \underset{f}{\min }\frac{1}{N}\sum _{i=1}^N{\mid \mid f\left({\rho }_i\right)-{\mathcal{J}}_{\wr }\left({\rho }_i\right)\mid \mid }^2+c{f}^T{L}^{l}f,$$ (C.1)

where ρ_i denotes a partition for which we have pre-computed the data using ${\mathcal{J}}_{\wr }$, c and l are regularization parameters, N is the number of pre-computed values, and L is the Laplacian of the graph describing the domain on which ${\mathcal{J}}_{\wr }$ is defined. The goal is to find a smooth f that approximates values of ${\mathcal{J}}_{\wr }$ at partitions where it has not been computed.

The problem is formulated and solved within the Reproducing Kernel Hilbert Space (RKHS) framework (Wahba, 1990; Yackley et al., 2008). The authors show that one needs to compute values of the kernel matrix only for those columns where the pre-computed $\mathcal{J}\left({\rho }_i\right)$ is available and only for those rows where we need to approximate its value.

Appendix C.1. Hypercube Representation

Although the framework of Yackley et al. (2008) is formulated for Bayesian network structure scoring, it is more general and applies to any problem of approximating smooth functions over a hypercube. We represent the problem of factoring random variables defined in Section Appendix A as a hypercube graph and use their approximation framework.

First we show that the factoring problem of Section Appendix A represents a subset of vertices on a hypercube. This will allow us to define smooth functions approximating our objective ${\mathcal{J}}_{\wr }$ (B.6) on the vertices of the hypercube but use the approximation only on the subset that represents valid partitions.

At the risk of being pedantic, we prove the following simple lemma. It serves the purpose making our further development clearer.

Lemma 1. In the case when m is the upper bound on the number of factors, and overlapping factors as well as empty ones (including all empty simultaneously) are allowed ⁸, the space of possible assignments forms the Hamming cube.

Proof. Let us represent a single assignment of a variable to a cluster by a single bit in a binary vector of length n representing that cluster. Thus for k ≤ m clusters and n variables all possible assignments can be represented by a binary number of mn bits, for which there are 2^mn possible assignments. These assignments form the vertex set of a hypercube in ${\mathcal{R}}^{mn}$. Two vertices from this set are connected by an edge if their binary representations differ by a single bit. This results in a Hamming cube.

Let b ∈ {0, 1}^m×n be a binary vector of length mn, where b_ij = 1 indicates that variable X_j is assigned to cluster i. According to Lemma 1, together with the Hamming metric, the set of such vectors forms the mn-dimensional Hamming hypercube, ${\mathcal{H}}^{mn}$. Note that this is an overcomplete representation of a clustering because it relaxes the partition condition 1 (see Section Appendix A).

The set of all vertices of ${\mathcal{H}}^{mn}$ is substantially larger than the set of vertices denoting partitions. If we attempt to minimize ${\mathcal{J}}_{\wr }$ over the entire Hamming cube, then we will hit many vertices before reaching one that is a valid partition. However, constraining the space of the considered vertices to partitions turns out to be easy.

First, we reshape b into an m × n binary matrix representation:

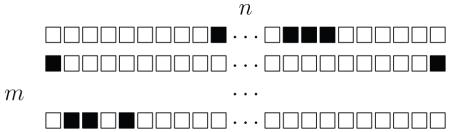(C.2)

where there is a column of length m per random variable. In order for b to be a valid partition, all but one bits of each column are set to 0 (denoted by a □) and exactly one bit is set to 1 (denoted by a ■).

The matrix representation provides an easy check if a length mn binary vector b is a partition (all column sums must be equal to 1). Switching from a valid partition to a valid neighboring partition is also easy. It is done by swapping the active bit in a column with another bit in the same column. However, the mⁿ-element set of such partition representations contains m! equivalent partitions due to the reordering of rows of (C.2). All equivalent partitions have the same objective value (B.6) complicating optimization.

We adopt a canonical form of partition representations of the kind shown in (C.2) in order to consider a partition only once and instead of mⁿ of them work with only ${\sum }_{i=1}^m\left\{\begin{array}{c}\hfill n\hfill \\ \hfill i\hfill \end{array}\right\}$ unique partitions, where $\left\{\begin{array}{c}\hfill °\hfill \\ \hfill °\hfill \end{array}\right\}$ denotes the Stirling number of the second kind. We call a representation canonical if the row-sum m-element vector is sorted in the descending order (i.e. each higher row in (C.2) have more bits set than any of the lower rows). This representation is similar up to a transposition to the one used by Griffiths and Ghahramani (2005). The set of canonical representations contains only unique partitions which form a graph $\mathcal{G}$ by connecting partitions that can be obtain one from another via a single swap of the active and an inactive bit in any of the columns of (C.2).

In this section we have constructed a hypercube graph $\mathcal{H}$, and the graph of canonical partitions $\mathcal{G}$, whose nodes are formed by a subset of vertices of $\mathcal{H}$. When we minimize ${\mathcal{J}}_{\wr }$ later in the paper, we perform searches with respect to $\mathcal{G}$, while approximating the values of ${\mathcal{J}}_{\wr }$ on the nodes of $\mathcal{G}$ using $\mathcal{H}$.

Appendix C.2. A Greedy Algorithm

We have established an objective to measure our success, a topology $\mathcal{H}$ to approximate this objective, a fast way to perform this approximation, and a topology $\mathcal{G}$ to search over. Since now we are enabling the coregulation analysis via the spectra of the hypercube approximation, we further call it CASH⁹. The only missing part before we can formulate a greedy search algorithm is a strategy for choosing partitions to precompute values of ${\mathcal{J}}_{\wr }\left({\rho }_i\right)$ needed for approximation to work.

Since the interpolation framework of Yackley et al. (2008) is by nature local, we only consider immediate neighbors of the current best partition. We (pre)compute the objective at a subset of these neighbors, and then approximate the objective values at the rest of the neighbors. Note that the precomputed subset used for approximation does not grow in size. We pick the neighboring partition with the smallest objective, or finish the search at a local minimum, as detailed in Algorithm 1.

Algorithm 1 greedy search
Require: The data matrix, percentage of neighboring partitions to pre-compute the objec-   tive for (ρ), an upper bound on clusters m
1: Randomly select initial best node bc on $\mathcal{G}$
2: repeat
3: Select all neighbors of bc in $\mathcal{G}$
4: Pre-compute ${\mathcal{J}}_{\wr }$ at the subset of ρ neighbors.
5: Approximate on the rest (Section Appendix C).
6: Select the partition with the minimal ${\mathcal{J}}_{\wr }:{\mathit{b}}_c=\arg \min ({\left\{\mathcal{J}\right(b_i\left)\right\}}_{i=0}^N,\mathcal{J}({\mathit{b}}_c\left)\right)$
7: until convergence

Different pre-computation strategies may be devised depending on user needs. For instance, there might be a need to precompute $\mathcal{J}$ only at factorizations with few random variables per factor. This can be beneficial in the cases of sparse data, when the values of the estimate of $\mathcal{J}$ can not be computed reliably for factors of large sizes. Then it is better to precompute only the reliable parts (i.e. small factors) and fallback to the smoothing approximation on the rest.

Appendix D. Entropy Computation Heuristic

As noted earlier, complexity of computing our objective function (B.6) is O(dz²) and we can further improve the running time by pre-computing the distances between all samples for each random variable. This pre-computation is based on the following observation:

$${\mid \mid x_i-x_j\mid \mid }^2=\sum _{k=1}^d{\left(x_i^{\left(k\right)}-x_j^{\left(k\right)}\right)}^2,$$ (D.1)

where the left hand side distance is the key component of expression (B.6) and the superscript k denotes the k^th element¹⁰ of vector x. All of the differences between samples j and i on the right hand side can be pre-computed for each k eliminating the need to do so at each computation of (B.6). When computing the objective function at pivot points in Algorithm 1 only these elements which correspond to a given factor are summed together. This summation can be efficiently computed on modern multi-core machines by framing it as a matrix multiplication and taking advantages of highly optimized and parallelized linear algebra packages.

All experiments up until this section have been optimized using this procedure. However, dimensionality of the feature matrix D creates problems for storing the pre-computed cache in RAM. To cope with this problem while taking advantage of pre-caching and parallel computation we use the following heuristic:

1. Subsample the original dataset D into c matrices of reduced size (c = 10 in this work).

2. Precompute the cache matrix for each of the subsampled matrices.

3. Compute the objective (B.6) using each of the cache matrices independently subsequently averaging the result.

This is a heuristic and we can foresee situations where the procedure will fail (for example when rare samples in the dataset produce a large effect on the value of the objective). However, our tests (not shown) on comparing the values of the objective produced using the complete datasets for both groups and using this heuristic produced consistent results. Our application results also show that this heuristic performs well on the data we are using.

Appendix E. Synthetic Dataset III

Details of the data generation process are schematically shown in Figure E.7.

Figure E.7.

Description of the manifold data generation process. Figure E.7a shows how each triplet is constructed in a manner to provide an interaction that simultaneously involves 3 variables and does not decompose into their pairwise interactions. A scatter plot of a 3 triplet dataset can reveal some structure, but correlation matrix (Figure E.7c) remains completely insensitive.

Appendix F. CC k-means on Multi-Task Data

The CC k-means clusters are shown in Figure F.8. They are uniform in size and closely similar across patients and controls groups. This failure of k-means to discriminate the groups can be interpreted as an evidence of high-order nature of the group differences in the data.

Figure F.8.

CC k-means factoring of the multi-task data.