Modeling Disease Progression with Longitudinal Markers

Abstract

In this paper we propose a Bayesian natural history model for disease progression based on the joint modeling of longitudinal biomarker levels, age at clinical detection of disease and disease status at diagnosis. We establish a link between the longitudinal responses and the natural history of the disease by using an underlying latent disease process which describes the onset of the disease and models the transition to an advanced stage of the disease as dependent on the biomarker levels. We apply our model to the data from the Baltimore Longitudinal Study of Aging on prostate specific antigen (PSA) to investigate the natural history of prostate cancer.

1 Introduction

Natural history models chart the progression of disease. There are many different ways to describe how a disease progresses. For example, studies of colorectal and lung cancer have described natural history as a series of transformations from normal to mutated epithelium, to malignant clone, to adenoma (Moolgavkar and Knudson, 1981; Luebeck and Moolgavkar, 2002). Studies of lung and breast cancer have described natural history in terms of tumor size and metastatic status, with the risk of metastasis increasing as tumor size increases (Kimmel and Flehinger,1991; Plevritis et al, 2004). Other models in cancer and HIV have taken the concept of natural history to a higher level of abstraction, specifying only that disease progresses from a preclinical or latent state to a clinically apparent or symptomatic state (Louis, Albert and Heghinian, 1978; Walter and Day, 1983; De Gruttola and Lagakos, 1989). In both AIDS and cancer, these models have been extended to describe progression through several clinical stages of disease (Longini et al, 1989; Pinsky, 2001).

Why are natural history models of interest? In the case of cancer, they provide critical information about the early stages of disease during which cure is more likely. In particular, knowledge of the transition rate from preclinical to clinical disease provides an assessment of the window of opportunity for early detection. Knowledge of natural history has been used to develop recommendations for breast and colorectal cancer screening schedules (Parmigiani, Skates and Zelen, 2002; Loeve et al, 2000), and has been used to predict the likely benefits of preventive interventions such as the administration of non-steroidal, anti-inflammatory drugs to prevent colorectal cancer (Luebeck and Moolgavkar, 2002). In case of HIV, natural history models have been of critical importance in projecting the size of the infected population and their likely health resource needs (Taylor, 1989; Brookmeyer, 1991).

Estimating the parameters of natural history models can be challenging because many of the events comprising disease progression are unobservable. Serial monitoring, or screening, of asymptomatic individuals can narrow down the interval or intervals during which progression events may have occurred. Indeed, some of the most well-known studies of the natural history of breast cancer have been based on data from a single screening trial that took place in the late 1960’s (Walter and Day, 1983; Day and Walter, 1984). Similarly, many of the early studies of HIV latency were based on large studies in which asymptomatic individuals were serially tested to determine their HIV seropositivity status (Brookmeyer and Goedert, 1989; De Gruttola and Lagakos, 1989).

In both cancer and HIV, the availability of biomarkers indicating the presence or progression of disease can greatly enhance our estimation and understanding of disease natural history. In prostate cancer, for example, serial studies of PSA levels taken prior to disease diagnosis have provided rough estimates of the sojourn time, which is the time from when the disease first becomes PSA-detectable, to clinical diagnosis in the absence of PSA screening (Morrell et al, 1995; Whittemore et al, 1995). Similarly, in HIV, serial modeling of longitudinal CD4 counts has provided information on the interval from seroconversion to diagnosis of AIDS. (DeGruttola, Lange and Dafni, 1991; Lange, Carlin and Gelfand, 1992; Pawitan and Self, 1993).

As more studies have begun to routinely measure marker levels, markers have become a part of the natural history description. New classes of models have been developed that simultaneously model marker growth and disease progression. At the one extreme, disease states may be defined by marker levels (see, for example, Longini et al., 1989; Jackson and Sharples, 2002; Jackson et al. 2003). More generally, marker levels are assumed to be associated with disease progression, and to evolve concurrently with transitions between disease states. An early example, by Pawitan and Self (1993), modeled the longitudinal CD4 trajectory using a random-effects model, but allowed the marker growth to depend on the times of seroconversion and AIDS. Pawitan and Self (1993) used standard survival analysis techniques to deal with censoring and truncation in their data. There now exists a large literature on the joint estimation of longitudinal and failure-time data which, although related to our approach, is not directly relevant to our goal in this paper.

In cancer, most studies of longitudinal and failure time data pertain to disease progression and marker growth after a cancer diagnosis (e.g., Klein, Kotz and Grever, 1984; Kay, 1986; Law, Taylor and Sandler, 2002). In contrast, this paper addresses the estimation of marker growth and disease progression prior to diagnosis. Our natural history model consists of three disease states: healthy, localized and metastatic. Our goal is to estimate transition rates between these states as well as the rate of transition from preclinical (latent) disease to clinical diagnosis, which may depend on the disease state. Our data consist of longitudinal measurements of a marker that is associated with disease presence and progression. The marker levels are measured for disease cases prior to clinical diagnosis and for a set of controls without the disease, using stored serum. At diagnosis, information is available on the stage of the disease, i.e., whether it is localized or metastatic. However, this information is not known at any time prior to diagnosis. Thus, models which require longitudinal data on both marker measurements and disease status (e.g., Craig et al, 1999), are not applicable. We assume that the observed stage of disease is correct; in this, our models differ from hidden Markov models, in which the observed disease state is subject to misclassification, and the underlying disease state is a hidden process that continuously evolves over time (Jackson et al. 2003; Foulkes and DeGruttola, 2003).

Our model shares some similarities with models in which the risk of disease progression is assumed to be dependent on tumor size (Kimmel and Flehinger, 1991; Bartoszynski et al, 2001). We replace the tumor size variable in these models by an individual-specific marker trajectory, which we estimate concurrently with the transition rates between disease states. Our approach is advantageous over tumor-size-based models in that it allows for the utilization of serial marker data measured prior to diagnosis, whereas tumor size is generally only available at the time of diagnosis. Moreover, our approach is applicable to cancers for which tumor size is not easily quantified. An example of such a cancer is prostate cancer, which tends to be multifocal, and is not always surgically removed.

In our application we use the PSA data from the Baltimore Longitudinal Study of Aging to study the natural history of prostate cancer. While PSA growth in cancer cases has been well documented, little is known about the connection between PSA growth trajectory and disease progression. Carter et al (1997) hinted at this gap in knowledge when they suggested, without formal justification, that a PSA level of 5.0 ng/ml or more represented a level at which “cure is less likely”. Our model allows us to answer questions like: what is the distribution of PSA level at the onset of disease and at the transition to an advanced metastatic stage? And, for an individual, what is the probability of a transition to metastatic disease given prior PSA growth and a current PSA level?

This paper is organized as follows. In Section 2 we present our generic natural history model for disease progression. In Section 3 we specify our model to estimate the connection between PSA growth and progression of prostate cancer. In Section 4 we present our model fit results. We conclude with a discussion in Section 5.

2 A Natural History Model

Let y_ij denote the response observed at age t_ij, where i = 1,…, N indexes subjects and j = 1, 2,…, n_i indexes longitudinal observations within subject i. We denote by y_i the vector of longitudinal responses measured at the vector of ages t_i in patient i, that is, y_i = (y_i1, y_i2,…, y_ini)′, and t_i = (t_i1, t_i2,…, t_ini)′. Let x_i denote clinical stage of the disease in patient i. Without loss of generality, we assume that there are three possible stages of the disease: x_i = 0 denotes a normal patient, while x_i = 1 denotes a patient with initial stage of the disease and x_i = 2 denotes advanced disease. We note that the definition of advanced disease is specific to the disease being studied. For example, in our application to prostate cancer we define advanced disease as metastatic disease. Let t_ic denote the age of disease clinical diagnosis. The models we formulate are for symptomatically detected disease. Moreover, we assume that the disease is progressive in that after onset the disease is in an early stage and, left untreated, it progresses to a more advanced stage.

Let θ denote the parameter vector describing the joint distribution of the responses. The likelihood function is given by

$$L(\mathit{\theta }\mid \mathit{t},\mathit{y},{\mathit{t}}_c,\mathit{x})\propto \prod _{i=1}^N\mathcal{L}(\mathit{\theta }\mid {\mathit{t}}_i,{\mathit{y}}_i,t_{ic},x_i),$$ (1)

where $\mathit{t}={({\mathit{t}}_1^{\prime },\dots ,{\mathit{t}}_N^{\prime })}^{\prime },\mathit{y}={({\mathit{y}}_1^{\prime },{\mathit{y}}_2^{\prime },\dots ,{\mathit{y}}_N^{\prime })}^{\prime }$, t_c = (t_1c,…, t_Nc)′ and x = x₁, x₂,…, x_N)′. We note that for a normal patient t_ic is censored at t_ini.

Let us examine the contribution to the likelihood function given by the observed data (y_i, t_ic, x_i) in subject i. We first discuss the likelihood function for patients with disease. Age at clinical diagnosis depends on the age of disease onset and it may also depend on whether the disease transitioned to an advanced stage. Let t_i0 and t_iA denote, respectively, age of disease onset and age of transition to an advanced stage of the disease in patient i. Both, t_i0 and t_iA, are non–observed latent variables that apply to diagnosed cases. We assume that clinical stage of the disease is informative about these ages of transitions. A patient in the initial stage of the disease experienced t_i0, but not t_iA by age t_ic, that is, the event {x_i = 1} corresponds to {t_i0 < t_ic < t_iA}. Analogously, a patient with an advanced stage of the disease experienced both t_i0 and t_iA, that is,{x_i = 2} corresponds to the event {t_i0 < t_iA < t_ic}. In other words, for a patient with disease, stage is an event of the (latent and observed) ages (t_i0, t_iA, t_iC). Under these assumptions, for patients in the initial stage of the disease the corresponding factor in the likelihood function (1) is as follows. We use f (·) to generically denote a probability density or mass function and I_A to denote the indicator function for event A.

$$\begin{array}{l}\mathcal{L}(\mathit{\theta }\mid {\mathit{t}}_i,{\mathit{y}}_i,t_{ic},x_i=1)=f({\mathit{y}}_i,t_{ic},x_i=1\mid {\mathit{t}}_i,\mathit{\theta })\\ =f({\mathit{y}}_i,t_{ic}\mid {\mathit{t}}_i,\mathit{\theta },x_i=1)f(x_i=1\mid {\mathit{t}}_i,\mathit{\theta })\\ ={\int }_0^{\infty }{\int }_0^{\infty }f({\mathit{y}}_i,t_{ic},t_{i0},t_{iA}\mid {\mathit{t}}_i,\mathit{\theta },x_i=1)f(x_i=1\mid {\mathit{t}}_i,\mathit{\theta }){dt}_{iA}{dt}_{i0}\\ ={\int }_0^{\infty }{\int }_0^{\infty }f({\mathit{y}}_i,t_{ic},t_{i0},t_{iA}\mid {\mathit{t}}_i,\mathit{\theta })I_{\{t_{i0}<t_{ic}<t_{iA}\}}{dt}_{iA}{dt}_{i0}\\ ={\int }_0^{t_{ic}}{\int }_{t_{ic}}^{\infty }f({\mathit{y}}_i\mid {\mathit{t}}_i,\mathit{\theta },t_{ic},t_{iA},t_{i0})f(t_{ic}\mid {\mathit{t}}_i,\mathit{\theta },t_{iA},t_{i0})f(t_{iA}\mid {\mathit{t}}_i,\mathit{\theta },t_{i0})f(t_{i0}\mid \mathit{t},\mathit{\theta }){dt}_{iA}{dt}_{i0}.\end{array}$$ (2)

Similarly, for patients with advanced disease:

$$\begin{array}{l}\mathcal{L}(\mathit{\theta }\mid {\mathit{t}}_i,{\mathit{y}}_i,t_{ic},x_i=2)=f({\mathit{y}}_i,t_{ic},x_i=2\mid {\mathit{t}}_i,\mathit{\theta })\\ ={\int }_0^{\infty }{\int }_0^{\infty }f(\mathit{y},t_{ic},t_{i0},t_{iA}\mid {\mathit{t}}_i,\mathit{\theta },x_i=2)f(x_i=2\mid {\mathit{t}}_i,\mathit{\theta }){dt}_{iA}{dt}_{i0}\\ ={\int }_0^{\infty }{\int }_0^{\infty }f({\mathit{y}}_i,t_{ic},t_{i0},t_{iA}\mid {\mathit{t}}_i,\mathit{\theta })I_{\{t_{i0}<t_{iA}<t_{ic}\}}{dt}_{iA}{dt}_{i0}\\ ={\int }_0^{t_{ic}}{\int }_{t_{i0}}^{t_{ic}}f({\mathit{y}}_i\mid {\mathit{t}}_i,\mathit{\theta },t_{ic},t_{iA},t_{i0})f(t_{ic}\mid {\mathit{t}}_i,\mathit{\theta },t_{iA},t_{i0})f(t_{iA}\mid {\mathit{t}}_i,\mathit{\theta },t_{i0})f(t_{i0}\mid {\mathit{t}}_i,\mathit{\theta }){dt}_{iA}{dt}_{i0}.\end{array}$$ (3)

Finally, we assume that the likelihood contribution for normal patients is as follows. For normal patients we define t_iC to be the last observation time, i.e. t_iC is the censoring time for the unobserved clinical detection.

$$\begin{array}{l}\mathcal{L}(\mathit{\theta }\mid {\mathit{t}}_i,{\mathit{y}}_i,t_{ic},x_i=0)={\int }_0^{t_{ic}}f({\mathit{y}}_i,t_{ic},x_i=0,t_{i0}\mid {\mathit{t}}_i,\mathit{\theta }){dt}_{i0}+{\int }_{t_{ic}}^{\infty }f({\mathit{y}}_i,t_{ic},x_i=0,t_{i0}\mid {\mathit{t}}_i,\mathit{\theta }){dt}_{i0}\\ ={\int }_0^{t_{ic}}f({\mathit{y}}_i\mid {\mathit{t}}_i,\mathit{\theta },t_{i0})S_c(t_{ic}\mid \mathit{\theta },t_{i0})f(t_{i0}\mid \mathit{\theta }){dt}_{i0}+{\int }_{t_{ic}}^{\infty }f(\mathit{y}\mid {\mathit{t}}_i,\mathit{\theta },t_{i0})f(t_{i0}\mid \mathit{\theta }){dt}_{i0}.\end{array}$$ (4)

where S_c is the survival function for age at disease clinical detection. For a normal patient, the first term in (4) corresponds to disease onset t_i0 before t_iC. In this case, the likelihood contribution comes from the longitudinal responses and the censored information that the patient survived detection of the disease to age t_iC. The second term corresponds to onset after t_iC and thus the likelihood contribution is only through the longitudinal response.

We estimate the proposed natural history model under the Bayesian approach. Let π(θ) denote the prior distribution on the model parameters θ. The posterior distribution of the model parameters given the data (y, t_c, x) is given by

$$\pi (\mathit{\theta }\mid \mathit{y},{\mathit{t}}_c,\mathit{x})\propto \pi (\mathit{\theta })L(\mathit{\theta }\mid \mathit{t},\mathit{y},{\mathit{t}}_c,\mathit{x}).$$ (5)

Note that our model has two subject–specific latent variables t_i0 and t_iA. The likelihood factors for patients with disease formally requires double integration over t_i0 and t_iA. In general, this integral will not be available in closed analytical form. This also implies that the posterior distribution of the model parameters is not in closed form. To overcome the above difficulties we implement posterior inference using Markov Chain Monte Carlo simulation with chained data augmentation (Tanner, 1996). Let M denote the total number of patients with the disease and t₀ = (t₁₀, t₂₀,…, t_M0)′, t_A = (t_1A, t_2A,…, t_MA)′, where t_i0, t_iA denote, respectively, age of disease onset and age of transition to an advanced stage in subject i. Introducing the latent event times t_A and t₀ we find:

$$\pi (\mathit{\theta }\mid \mathit{y},{\mathit{t}}_c,\mathit{x})=\int \pi (\mathit{\theta }\mid \mathit{y},{\mathit{t}}_c,\mathit{x},{\mathit{t}}_0,{\mathit{t}}_A)\pi ({\mathit{t}}_0,{\mathit{t}}_A\mid \mathit{y},{\mathit{t}}_c,\mathit{x})d{\mathit{t}}_0{\mathit{t}}_A.$$ (6)

Moreover,

$$\pi ({\mathit{t}}_0,{\mathit{t}}_A\mid \mathit{y},{\mathit{t}}_c,\mathit{x})=\int \pi ({\mathit{t}}_0,{\mathit{t}}_A\mid \mathit{\theta },\mathit{y},{\mathit{t}}_c,\mathit{x})\pi (\mathit{\theta }\mid \mathit{y},{\mathit{t}}_c,\mathit{x})d\mathit{\theta }.$$ (7)

A convenient feature is that by augmenting the data with t₀ and t_A we eliminate the double integrals in equations (2) and (3). The interval censored information on the onset age and transition to an advanced disease is still accounted for by including the event x in π(t₀, t_A|θ, y, t_c, x). The chained data augmentation algorithm for posterior simulation consists of three steps:

1. Given ( ${\mathit{t}}_0^{(k-1)},{\mathit{t}}_A^{(k-1)}$), generate θ^(k) from π(θ|y, t_c, x, $\pi (\mathit{\theta }\mid \mathit{y},{\mathit{t}}_c,\mathit{x},{\mathit{t}}_0^{(k-1)},{\mathit{t}}_A^{(k-1)})$

2. Given θ^(k), generate ( ${\mathit{t}}_0^{(k)},{\mathit{t}}_A^{(k)}$) from π(t₀, t_A|θ^(k)t_c, y, t_c, x)

3. Repeat (i)–(ii) iteratively for k = 1,…, K iterations.

Note that (i) and (ii) are usual steps in the Gibbs sampler algorithm. Values of (t₀, t_A) “augment” the data. Their role is to facilitate estimation of the model parameters θ. However, they are not known – they are also “parameters” and as such they must be estimated using the observed data. This is accomplished with the iterative simulation procedure described above.

In the next section, we discuss model estimation in the context of a study of the natural history of prostate cancer.

3 PSA and Prostate Cancer

3.1 The Data

We apply our natural history model to the PSA data from the Baltimore Longitudinal Study of Aging (BLSA). The BLSA is an ongoing multi–disciplinary study that began in 1958. Besides describing human physiological changes that occur with age, the study has also been beneficial in helping examine differences between normal aging and disease processes (Shock et al., 1984). Study participants are volunteers who return to the study center every two years for three days of free biomedical and psychological examinations. In our analyses we use serum PSA levels measured in male BLSA participants using a frozen serum bank for available retrospective samples donated during participant visits. Moreover, we utilize data from men who had at least two PSA measurements. One man had a PSA measurement recorded as zero. In our analyses we replace the zero with the minimally detectable PSA level (equal to 0.03 ng/ml).

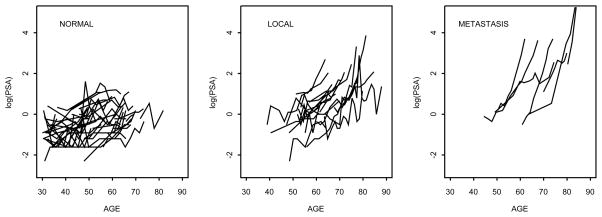
Table 1 provides some additional information on this study. Figure 1 shows the longitudinal (log) PSA trajectories in normal and prostate cancer patients. Though PSA levels increase in both groups of men, those who develop prostate cancer show higher growth rates in PSA.

Table 1.

Summary statistics. Means and standard deviations (std) are provided for the age at last follow up (FU) and length of follow up (in years).

GROUP	Individuals	Age at last FU		Length of FU		Measurements
		mean	(std)	mean	(std)	mean	(std)
Normal	193	54.81	(10.12)	13.87	(6.28)	4.64	(1.37)
Local	18	74.18	(7.28)	19.69	(4.44)	9.83	(3.43)
Metastasis	8	77.20	(8.11)	18.16	(8.27)	8.13	(3.04)

Figure 1.

PSA trajectories. The panel shows the log–transformed PSA levels by age at follow–up. In the group with normal patients we show the trajectories for a randomly selected subset of men.

Using the general model structure introduced in Section 2 we now define for each component of the likelihood function models that are suitable for the described prostate cancer study. We start with a basic model in Section 3.2. In Section 3.3 we introduce alternative model elaborations that we will use to validate the proposed model.

3.2 Basic Model

3.2.1 Longitudinal PSA

For patient i we consider the following model to describe his PSA level y_it at age t:

$$\begin{array}{lll}\hfill log(y_{it})& =\hfill & {\phi }_i(t)+{\epsilon }_{it},\hfill \\ \hfill {\phi }_i(t)& =\hfill & b_{i0}+b_{i1}t+b_{i2}{(t-t_{i0})}^{+}.\hfill \end{array}$$ (8)

We assume that the residuals are independent and identically distributed, that is, ε_it ~ Normal(0, σ²), and x⁺ = max(x, 0).

In (8), the function φ(.) describes the true growth of the log–transformed PSA. The growth of log–PSA is constant until disease onset at age t_i0 which in turn induces a change in the log–PSA trajectory. Change–point models such as this have been extensively used to describe PSA growth in prostate cancer patients (see, for example, Inoue, et al., 2004 and the references therein).

3.2.2 Time to transition and to clinical detection

Let λ₀, λ_A, λ_c denote the hazard functions for t_i0, t_iA and t_ic, respectively. We assume that the hazard rate for the onset of disease increases linearly with age, that is:

$${\lambda }_0(t)={\gamma }_{0}t,t>0.$$ (9)

We assume that the hazard functions of t_iA, t_ic are proportional to the true PSA level, ỹ(t) = exp(φ(t)), that is,

$${\lambda }_A(t)=\{\begin{array}{ll}0,\hfill & 0<t\le t_{i0}\hfill \\ {\gamma }_A\stackrel{\sim }{y}(t),\hfill & t>t_{i0}\hfill \end{array}\text{and}{\lambda }_C(t)=\{\begin{array}{ll}0,\hfill & 0<t\le t_{i0}\hfill \\ {\gamma }_C\stackrel{\sim }{y}(t),\hfill & t>t_{i0}\hfill \end{array}$$ (10)

The above formulation implies that the cumulative hazard function for t_iA is H_A(t) = γ_A(ỹ(t) − ỹ(t_i0))/(b_i1 + b_i2)I_{{t>t_i0}}, that is, it depends only on the ratio of true PSA increment and annual log–PSA velocity (b_i1 + b_i2). A similar statement applies to the cumulative hazard function for t_ic.

3.2.3 Hierarchical model

We complete the model formulation with the specification of priors on the model parameters. We assume a hierarchical model for the growth rate parameters with:

$$b_{ij}~\mathit{Normal}({\beta }_j,{\sigma }_j^2)\text{and}{\beta }_j~\mathit{Normal}(m_j,v_j^2),$$

for i = 1,…, N, j = 0, 1, 2. We impose monotonicity in PSA growth by assuming that b_i1 + b_i2 > 0. Moreover, we assume that

$$1/{\sigma }_j^2~\mathit{Gamma}(a_{{\sigma }_j},b_{{\sigma }_j}),j=0,1,2\text{and}1/{\sigma }^2~\mathit{Gamma}(a_{\sigma },b_{\sigma }).$$

For parameters associated with transition times we assume that

$${\gamma }_0~\mathit{Gamma}(a_0,b_0),{\gamma }_A~\mathit{Gamma}(a_A,b_A),\text{and}{\gamma }_C~\mathit{Gamma}(a_C,b_C).$$

The model described in Sections 3.2.1 through 3.2.3 has 5 subject–specific parameters b_i0, b_i1, b_i2, t_i0, t_iA)′ and 10 population level parameters ${({\beta }_0,{\beta }_1,{\beta }_2,{\sigma }_0^2,{\sigma }_1^2,{\sigma }_2^2,{\sigma }^2,{\gamma }_0,{\gamma }_A,{\gamma }_C)}^{\prime }$ which define the generic vector θ introduced in Section 2. In this application, the components of the likelihood factors described in equations (2)–(3) are further simplified as f(y_i|t_i, θ, t_ic, t_iA, t_i0) = f(y_i|t_i, b_i0, b_i1, b_i2, t_i0), f (t_ic|t_i, θ, t_iA, t_i0) = f (t_ic|b_i0, b_i1, b_i2, γ_C, t_i0), f(t_iA|t_i, θ, t_i0) = f(t_iA|b_i0, b_i1, b_i2, γ_A, t_i0) and f(t_i0|t_i, θ) = f(t_i0|γ₀).

3.3 Alternative models

Denote with M₀ the model described in Sections 3.2.1 through 3.2.3. In this section we introduce several alternative specifications for the hazard functions for t_i0, t_iA and t_iC. Table 2 summarizes the alternative model specifications.

Table 2.

Hazard functions for different model specifications.

Model	Hazard	Priors
M0	h0(t) = γ0t	γ0 ~ Gamma(a0, b0)
	hA(t) = γAỹ(t)	γA ~ Gamma(aA, bA)
	hC(t) = γCỹ(t)	γC ~ Gamma(aC, bC)
M1	h0(t) = γ0tα	γ0 ~ Gamma(a0, b0), $\alpha ~\mathit{Normal}(m_{\alpha },v_{\alpha }^2)I_{\{\alpha >-1\}}$
	hA(t) = γAỹ(t)	γA ~ Gamma(aA, bA)
	hC(t) = γCỹ(t)	γC ~ Gamma(aC, bC)
M2	h0(t) = (1 − π)γ00t + πγ01t	γ0j ~ Gamma(a0, b0), j = 0, 1, π ~ Beta(aπ, bπ)
	hA(t) = γAỹ(t)	γA ~ Gamma(aA, bA)
	hC(t) = γCỹ(t)	γC ~ Gamma(aC, bC)
M3	h0(t) = γ0t	γ0 ~ Gamma(a0, b0)
	hA(t) = γA(t − t 0)	γA ~ Gamma(aA, bA)
	hC(t) = γCỹ(t)	γC ~ Gamma(aC, bC)
M4	h0(t) = γ0t	γ0 ~ Gamma(a0, b0)
	hA(t) = exp(γA0 + γA1(t − t0) + γA2 φ(t))	${\gamma }_{A0}~\mathit{Normal}(m_A,v_A^2),{\gamma }_{Aj}~\mathit{Normal}(m_A,v_A^2)I_{\{{\gamma }_{Aj}>0\}}$, j = 0, 1
	hC(t) = γC ỹ(t)	γC ~ Gamma(aC, bC)
M4,1	h0(t) = γ0t	γ0 ~ Gamma(a0, b0)
	hA(t) = exp(γA0 + γA1(t − t0))	${\gamma }_{A0}~\mathit{Normal}(m_A,v_A^2),{\gamma }_{A1}~\mathit{Normal}(m_A,v_A^2)I_{\{{\gamma }_{A1}>0\}}$
	hC (t) = γCỹ(t)	γC ~ Gamma(aC, bC)
M4,2	h0(t) = γ0t	γ0 ~ Gamma(a0, b0)
	hA(t) = exp(γA0 + γA1φ(t))	${\gamma }_{A0}~\mathit{Normal}(m_A,v_A^2),{\gamma }_{A1}~\mathit{Normal}(m_A,v_A^2)I_{\{{\gamma }_{A1}>0\}}$
	hC(t) = γCỹ(t)	γC ~ Gamma(aC, bC)
M5	h0(t) = γ0t	γ0 ~ Gamma(a0, b0)
	hA(t) = γAỹ(t)	γA ~ Gamma(aA, bA)
	hC(t) = γC0ỹ(t), t < tA, γC1ỹ(t), t ≥ tA	γCj ~ Gamma(aC, bC), j = 0, 1 γC0 < γC1
M6	h0(t) = γ0t	γ0 ~ Gamma(a0, b0)
	hA(t) = γAỹ(t)	γA ~ Gamma(aA, bA)
	hC(t) = γC (t − t0)	γC ~ Gamma(aC, bC)
M7	h0(t) = γ0t	γ0 ~ Gamma(a0, b0)
	hA(t) = γAỹ(t)	γA ~ Gamma(aA, bA)
	hC(t) = exp(γC0 + γC1(t − t0) + γC2φ(t))	${\gamma }_{C0}~\mathit{Normal}(m_C,v_C^2),{\gamma }_{Cj}~\mathit{Normal}(m_C,v_C^2)I_{\{{\gamma }_{Cj}>0\}}$, j = 0, 1
M7,1	h0(t) = γ0t	γ0 ~ Gamma(a0, b0)
	hA(t) = γAỹ(t)	γA ~ Gamma(aA, bA)
	hC(t) = exp(γC0 + γC1(t − t0))	${\gamma }_{C0}~\mathit{Normal}(m_C,v_C^2),{\gamma }_{C1}~\mathit{Normal}(m_C,v_C^2)I_{\{{\gamma }_{C1}>0\}}$
M7,2	h0(t) = γ0t	γ0 ~ Gamma(a0, b0)
	hA(t) = γAỹ(t)	γA ~ Gamma(aA, bA)
	hC(t) = exp(γC0 + γC1φ(t))	${\gamma }_{C0}~\mathit{Normal}(m_C,v_C^2),{\gamma }_{C1}~\mathit{Normal}(m_C,v_C^2)I_{\{{\gamma }_{C1}>0\}}$

Specifically, models M₁ and M₂ investigate the appropriateness of the assumption that the hazard of disease onset increases linearly with age. In model M₁ we address this question using a nonlinear function of age. In model M₂ we assume that disease onset t_i0 arises from the mixture πf₁(t_i0) + (1 − π)f₀(t_i0), where f_j is the density characterized by the hazard function λ_0j (t) = λ_0j t, j = 0, 1. The mixture allows for representing a heterogeneous population of men, including subpopulations with early and late disease onset.

Models M₃, M₄, M_4,1 and M_4,2 allow us to investigate another critical assumption under model M₀. We consider modifications of the assumed linear hazard function for transition to metastatic disease. Specifically, in model M₃ the hazard for transition is linearly dependent on years from disease onset. In model M₄ we investigate whether transition is dependent on nonlinear functions of both, years from disease onset and true PSA levels. Models M_4,1 and M_4,2, nested within M₄, are used to assess whether both covariates in M₄ should be included and, if not, which covariate provides a better fit to the data.

Finally, models M₅ through M_7,2 are alternative models investigating the assumption, under model M₀, that detection is linearly dependent on true PSA levels. In words, model M₅ specifies that metastatic patients have higher likelihood to be detected sooner than patients with localized disease. Model M₆ specifies that clinical detection is linearly dependent on years from disease onset. In model M₇ we investigate whether clinical detection is dependent on nonlinear functions of both years from disease onset and true PSA levels. The nested models M_7,1 and M_7,2 are used to assess whether both covariates in model M₇ should be added.

Other alternative choices for h_A and h_c were considered, such as those in which the hazard functions were dependent on different functions of the true PSA growth. We considered the functions $h_A^{(1)}(t)={\gamma }_A(b_{i1}+b_{i2})I_{\{t>t_{i0}\}}$ as well as $h_A^{(2)}(t)={\gamma }_A(b_{i1}+b_{i2})(t-t_{i0})I_{\{t>t_{i0}\}}$ as alternative descriptions of the hazard functions for metastatic transition. Both alternative formulations imply that the hazard for metastatic transition is dependent on PSA velocity. However, $h_A^{(1)}$ implies an exponential distribution for metastatic transition, while $h_A^{(2)}$ implies a distribution with a linearly increasing hazard function for transition. Similar formulations were considered for the hazard of clinical detection. Models fit with these alternative formulations for the hazard function, however, showed to have poor fit and have been omitted from the table.

3.4 Model Assessment and Comparison

To assess the competing models we calculate the posterior predictive density of observation (y_i, t_ic, x_i) for subject i conditional on all observed data except that from subject i, that is, we compute

$$f({\mathit{y}}_i,t_{ic},x_i\mid {\mathit{y}}_{-i},{\mathit{t}}_{c,-i},{\mathit{x}}_{-i}),$$

where −i indicates the exclusion of data from subject i. This value is known as the conditional predictive ordinate (CPO) (Gelfand, Dey and Chang, 2002) and may be used as an outlier diagnostic tool. Observations having a low CPO indicate poor (predictive) fit of the model. The CPO is also often used for model selection. Models with, on average, higher CPOs are favored over those with lower CPOs.

We note that

$$\begin{array}{l}f({\mathit{y}}_i,t_{ic},x_i\mid {\mathit{y}}_{-i},{\mathit{t}}_{c,-i},{\mathit{x}}_{-i})=E[f({\mathit{y}}_i,t_{ic},x_i\mid \mathit{\theta },{\mathit{y}}_{-i},{\mathit{t}}_{c,-i},{\mathit{x}}_{-i})]\\ =\int f({\mathit{y}}_i,t_{ic},x_i\mid \mathit{\theta })f(\mathit{\theta }\mid {\mathit{y}}_{-i},{\mathit{t}}_{c,-i},{\mathit{x}}_{-i})d\mathit{\theta }.\end{array}$$

Thus, the calculation of the CPOs entails the re–estimation of the model by excluding data from each subject i at a time. That is, one evaluates f (θ|y_−i, t_c,−i, x_−i), i = 1,…, N the posterior distribution of parameters θ conditional on all the data except that from a particular subject i. This would make the computational task challenging in multiparametric models involving a moderate to large number of observations. However, a simplification of the computational efforts is achieved by observing that

$$f(\mathit{\theta }\mid {\mathit{y}}_{-i},{\mathit{t}}_{c,-i},{\mathit{x}}_{i-})\propto \frac{f(\mathit{\theta }\mid \mathit{y},\mathit{t},\mathit{x})}{f({\mathit{y}}_i,t_{ic},x_i\mid \mathit{\theta })}.$$

Thus we can use importance sampling to evaluate CPOs, using the posterior distribution f (θ|y, t, x) as the importance sampling density and w(θ) = [f(y_i, t_ic, x_i|θ)]⁻¹ as the weight function. For subject i we compute the weighted average

$$\begin{array}{l}f({\mathit{y}}_i,t_{ic},x_i\mid {\mathit{y}}_{-i},{\mathit{t}}_{c,-i},{\mathit{x}}_{-i})\approx \frac{{\sum }_{k}f({\mathit{y}}_i,t_{ic},x_i\mid {\mathit{\theta }}^{(k)})w({\mathit{\theta }}^{(k)})}{{\sum }_{k}w({\mathit{\theta }}^{(k)})}\\ ={\left[\frac{1}{K}\sum _{k=1}^K\frac{1}{f({\mathit{y}}_i,t_{ic},x_i\mid {\mathit{\theta }}^{(k)})}\right]}^{-1},\end{array}$$

where θ^(k), k = 1,…, K are samples from f (θ|y, t, x). We need to obtain samples from the posterior distribution of θ only once, conditioning on all observations. This makes the calculation of CPOs feasible.

In addition to the CPOs, we calculate Bayes factors (Kass and Raftery, 1995) to summarize the evidence provided by the data in favor of one model over an alternative. The Bayes factor for comparing models M_i and M_j is the ratio BF_ij = f(y, t, x|M_i)/f (y, t, x|M_j). We use the interpretation guidelines provided by Kass and Raftery(1995) in which there is positive evidence against model M_i when 1 ≤ log(BF_ij) < 3 and strong evidence when log(BF_ij) ≥ 3.

3.5 Bayesian Estimation

Our priors for the PSA growth rate parameters at the population level were centered at the mean value zero. Priors for the hazard rate parameters were centered at the mean value 0.1 and the remaining parameters were centered at 1. Prior variances for growth rate and hazard rate parameters were set equal to 0.1. For the remaining parameters, prior variances were set equal to 1. We note that prior variances for the population level growth rate parameters were based on published analysis of PSA growth using other data sets (see Inoue et al., 2004). In the next section we report the results from our analysis using the above prior, and also comment on a sensitivity analysis in which we inflated the prior variances.

We estimate the natural history model using Markov Chain Monte Carlo simulation with data augmentation as discussed in Section 2. In particular, we use a hybrid algorithm with Gibbs steps to update population level parameters and Metropolis steps to update the remaining parameters (Metropolis et al, 1953; Geman and Geman, 1984, Gelfand and Smith, 1990).

To obtain samples from the posterior distribution of all parameters, we ran our Markov Chain for a burn–in period of 10, 000, 000 iterations, followed by additional 500, 000 iterations from which we stored sampled values at every 20^th iteration. Convergence diagnostics were performed with BOA (Bayesian Output Analysis) package developed by B.J. Smith (Smith, 2005) using Geweke’s (Geweke, 1992) and Raftery and Lewis’ diagnostic tests (Raftery and Lewis, 1992). Under Geweke’s diagnostic test, none of the p–values was less than 0.01. Moreover, Raftery and Lewis convergence diagnostic test gives dependence factors, which measures the increase in the number of iterations needed to reach convergence, less than 5. These results do not provide evidence against convergence of our chains.

4 Results

We calculated the values of log(BF_0j) for comparing model M₀ with an alternative model M_j. The results, shown in Table 3, indicate that model M₀ is superior to most of the alternative models. The comparisons with model M_4,1 is less conclusive, but slightly pointing towards the simpler model M₀. Models M₇ and M_7,1 are both superior to model M₀. In particular, model M_7,1 is slightly superior to model M₇.

Table 3.

Model Comparison using Bayes factors.

Comparison	log(BF)
M0 vs M1	3.83
M0 vs M2	16.48
M0 vs M3	5.58
M0 vs M4	14.07
M0 vs M4,1	1.09
M0 vs M4,2	13.84
M0 vs M5	16.39
M0 vs M6	16.01
M0 vs M7	−9.69
M0 vs M7,1	−10.66
M0 vs M7,2	10.00

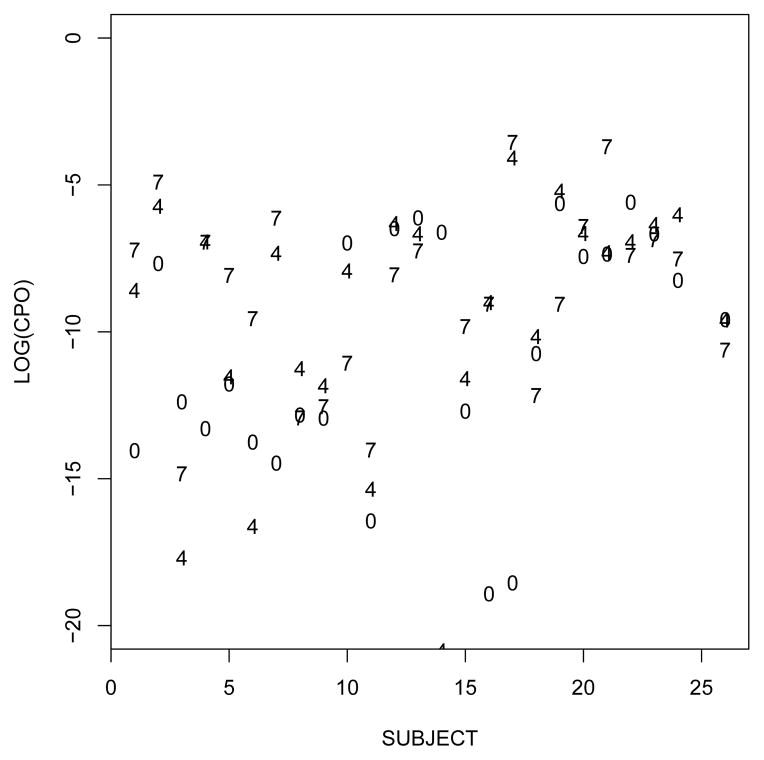
To further compare models and assess the predictive fit in each subject we computed CPOs. Figure 2 shows the log–transformed CPOs for prostate cancer patients computed under models M₀ (which dominated most of the alternative models), M_4,1 (for which no conclusive evidence in favor of model M₀ could be drawn) and M_7,1 (which dominated model M₀). The CPOs also favor model M_7,1. When comparing models M₇ and M_7,1, the CPOs also favored model M_7,1 (not shown). Comparisons are based on the frequency of subjects i with higher CPO under one versus the other model.

Figure 2.

Log–transformed conditional predictive ordinate (CPO) for prostate–cancer patients calculated under models M₀, M_4,1, and M_7,1 (denoted in the Figure by labels 0, 4, and 7 respectively).

Based on the above comparisons, there is no strong evidence against the assumption that the hazard of disease onset is linearly increasing with age. Moreover, there is no strong evidence against the assumption that transition to metastatic disease is linearly dependent on the true PSA growth. There is some evidence that the hazard of clinical detection only depends (non–linearly) on time since disease onset.

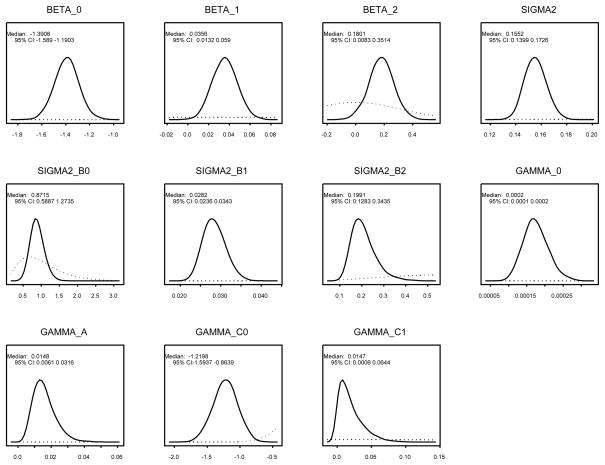
In what follows we present additional results for model M_7,1 only. Figure 3 shows the marginal posterior distributions of the population level parameters superimposed with the respective priors. The figure shows substantial learning from the data. The marginal posterior distributions show changes in both, location and spread, when compared with the prior distributions. We estimate a 3.62% annual percent change of PSA growth pre–onset with a 95% posterior credible interval (CI) [1.33%, 6.08%], and a post–onset growth of 24.21% with a 95% CI=[4.22%, 47.83%].

Figure 3.

Marginal posterior distributions for the population level parameters. In each panel we represent the posterior density (in full line) superimposed with the prior density (in dotted line and shown within the range of the estimated marginal posterior distribution).

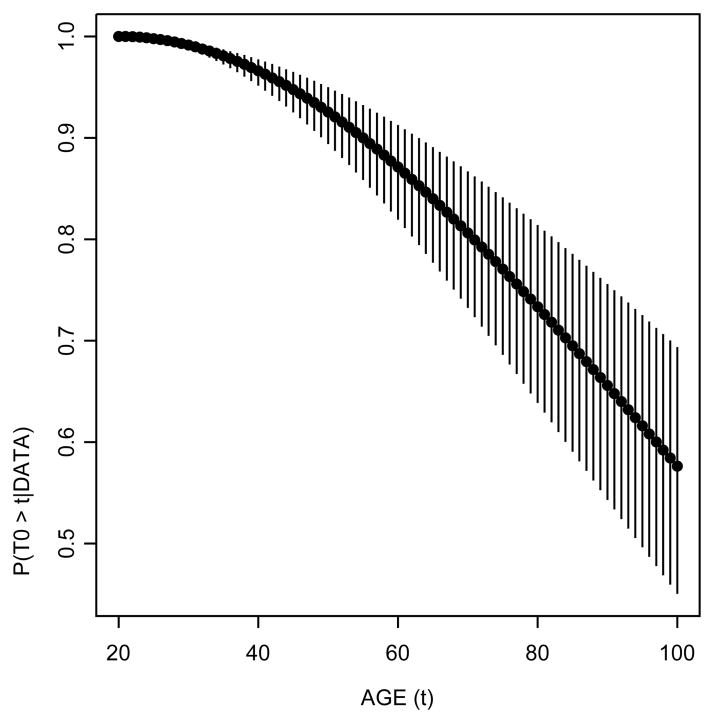
In Figure 4 we show the posterior probability of disease onset beyond a given age, that is, P (t₀ > t|data). We find, for example, that the posterior probability that a transition occurs after age 70 is 80.63% (95% credible interval=[73.24%, 86.69%]). Thus, we estimate that roughly one out of five men has developed latent disease by age 70.

Figure 4.

Posterior survival probability of disease onset. Circles represent the median posterior probability while the vertical lines denote the limits of the 95% posterior credible intervals. The posterior probability that the onset occurs after age 70 is approximately 81% with the 95% credible interval ranging from 73% to 87%.

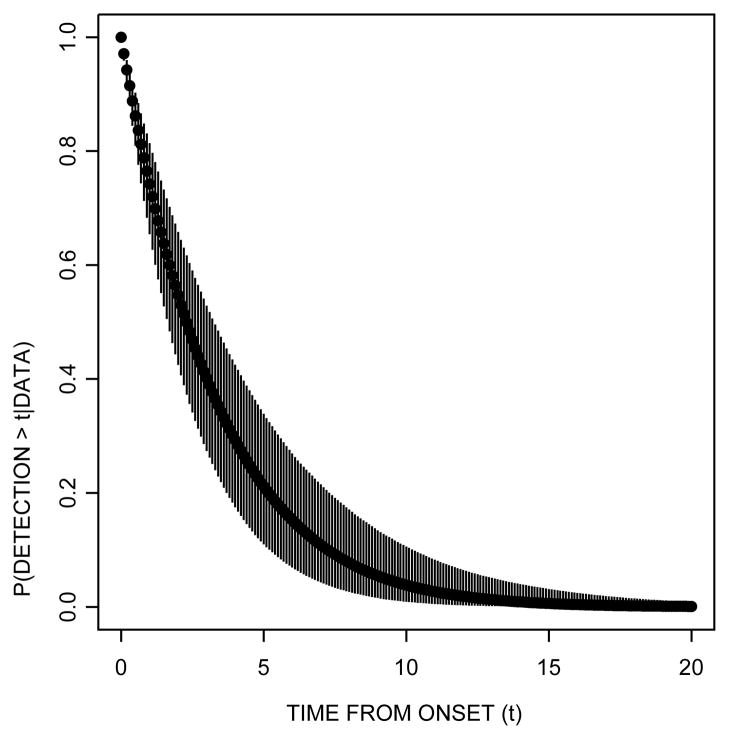
Similarly, Figure 5 shows the posterior probability of clinical detection beyond a given time from disease onset. The figure shows that the posterior probability of clinical detection after one year post–disease onset is 74.23% (95% CI = [65.42%, 81.40%]). The probability of detection after two years from disease onset decreases to 54.72% (95% CI=[42.46%, 65.83%]).

Figure 5.

Posterior survival probability of clinical detection from disease onset time. Circles represent the median posterior probability while the vertical lines denote the limits of the 95% posterior credible intervals. The posterior probability that clinical detection occurs after one year post–disease onset is 71% (95% CI=[65%, 81%]). The probability of detection after two years from disease onset decreases to 54% (95% CI= [42%, 66%]).

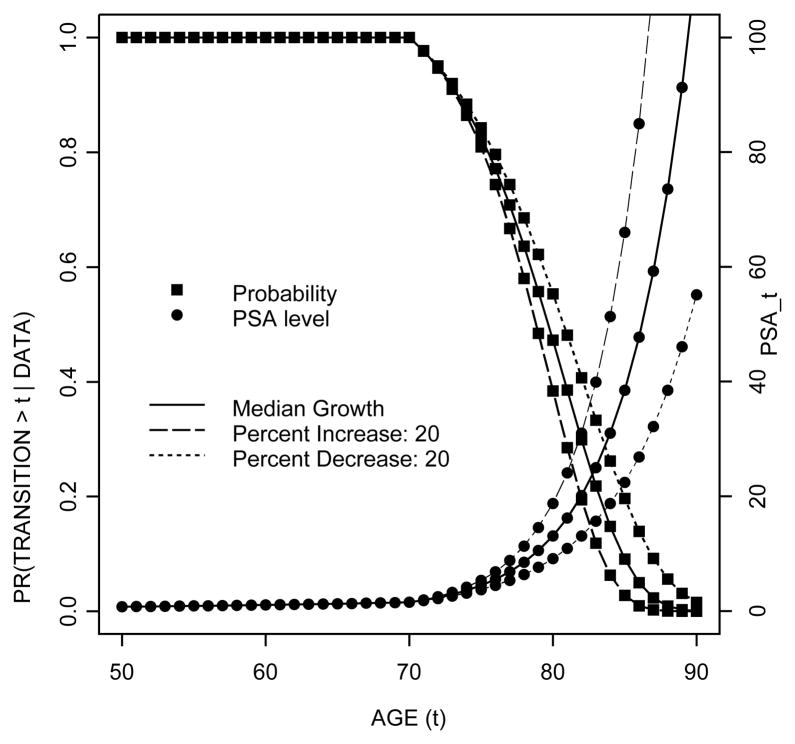
Figure 6 shows the posterior probability of metastatic transition beyond a given age along with the predictive PSA trajectory for subjects with different PSA growth patterns after disease onset at age 70. We assume that, with the exception of b_i2, the subject–specific parameters are at the population median levels (that is, b_i0 = −1.39, b_i1 = 0.04). We then consider three different values for b_i2. The solid line represents a case with median post change-point PSA growth (that is, b_i2 = 0.18). The dotted line represents a case with slower growth, while the dashed line represents a case with faster growth, where slower and faster growths are defined in terms of percent decrease/increase relative to the median growth. The figure shows that for a case with the median PSA growth, there is approximately a 17.30% chance of metastasis within 5 years from disease onset and a 52.73% chance of metastasis within 10 years from disease onset. The figure also shows that transitions to metastatic disease happen at an earlier age for patients with faster PSA growth than those with slower growth. Moreover, for patients with faster PSA growth, transitions happen at a higher level of PSA. For a case with median PSA growth the chance of metastasis by the time PSA reaches a level of 10 ng/ml is 44.27%, and this increases to 70.08% by the time PSA level reaches 20 ng/ml.

Figure 6.

Posterior survival probability of metastatic transition and posterior predictive level of PSA by age (t). The figure shows, for example, that in a case with the median PSA growth with disease onset at age 70, there is approximately a 83% chance of metastatic spread after age 75, with a predictive PSA level of 4.44 ng/ml. The probability drops to 47% at age 80 with PSA level of 13.07 ng/ml.

Figure 7 shows 95% posterior credible intervals for subject–specific parameters by stage of the disease at clinical detection. To facilitate visualization of the results, we only show credible intervals for prostate cancer patients. The figure indicates that patients with metastatic disease have similar PSA slopes before disease onset, but slightly higher PSA post–onset slopes than patients with localized disease, as shown in panels (b) and (c). For localized patients, as specified by the model, metastatic transition happens after diagnosis, while for metastatic patients, the transition happens before. It is noteworthy that in this data set metastatic patients are predicted to have had the transition about 2.84 years before diagnosis on average, while localized patients are predicted to transition within 5.88 years from the time of disease diagnosis. We also calculated the 95% posterior credible intervals for subject–specific parameters in normal patients. For normal patients, disease onsets are predicted to occur, on average, 61.49 years after the last follow–up, which implies that they basically only experienced the linear growth of PSA. Moreover, on average, the subject–specific pre–change point slopes are lower than those observed in prostate cancer patients.

Figure 7.

95% Posterior credible intervals for subject–specific parameters by stage of the disease at detection. Circles denote posterior medians. For panels (d) and (e) time is denoted from years prior to disease diagnosis.

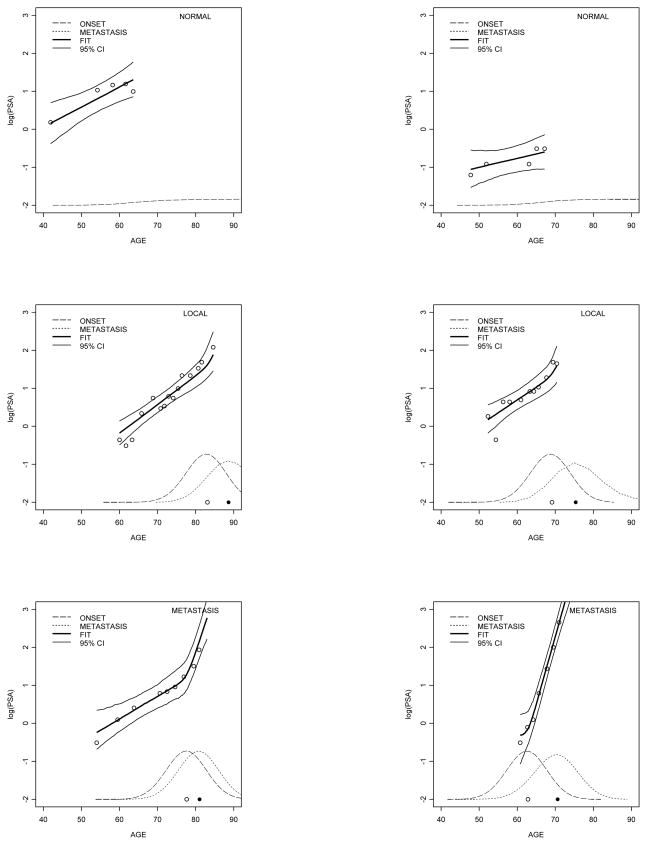
Figure 8 shows the fit of six randomly selected patients along with the estimated predictive distributions of disease onset and transition to metastatic disease. The figure shows that our model captures the non–linear growth in log–PSA after disease onset in prostate cancer patients.

Figure 8.

Fit of the longitudinal PSA trajectory for randomly selected patients in the data set. Data for each patient are represented by circles. The fitted response in heavy full line is the median. Light full lines represent the boundaries of the 95% posterior credible intervals. The predictive density of time to disease onset is in dashed line and time to metastatic transition in dotted line. Posterior medians of disease onset and metastatic transition are represented by circles in the x-axis.

Finally, we note that we performed sensitivity analysis by inflating (doubling) the prior variances. The implied estimates, however, did not change substantially. For example, the posterior median pre–onset growth rate is 3.71% (95% CI=[1.41%, 6.17%]) while the posterior median post–onset growth rate is 24.87% (95% CI = [4.86%, 48.17%]).

To explore clinical implications of our model results, we simulated a cohort of 500,000 men, setting the population level parameters at the posterior median values estimated under model M_7,1, but now also accounting for death. We note that survival information is not available in our data set. Thus, we simulate time to death from other causes using external information from life tables (http://www.demog.berkeley.edu/wilmoth/mortality/states.html). The simulation generates subject–specific PSA trajectories and events in each man’s lifetime by generating disease onset, transition to metastatic disease and death from other causes. This enables us to compute the likelihood of overdiagnosis, which we define as the probability of prostate cancer detection through PSA testing that would have otherwise not been diagnosed during patient’s lifetime. The following Table 4 shows the overdiagnosis by age at the screen and PSA thresholds defining a positive test along with test sensitivity and specificity. As expected, test sensitivity decreases with higher thresholds and increases when the screen occurs at older ages. The specificity, on the other hand, increases with higher thresholds and decreases at older ages. The values are within the range of those reported in the medical literature. Crawford et al. (1999), for example, using the 4.0 ng/ml cut-off, report sensitivity of 33.9% and specificity of 70.4% among 50–59 year old men. Table 4 also shows that among cases detected by a positive PSA at age 50, about 5% would never become clinical cases in their lifetime across our different choices of PSA thresholds. The overdiagnosis probabilities increase at older ages. At age 80, we estimate that about 55% of cases are overdiagnosed. Our estimates for older men are compatible with those reported by Etzioni et al. (2002) who estimated that, among 60–84 year–old men, the overdiagnosis rates were approximately 30%.

Table 4.

Test sensitivity, specificity and probability of overdiagnosis by age at screen and thresholds of positive PSA test (in ng/ml).

Age at Screen	PSA Thresholds (ng/ml)
	2.0	2.5	3.0	3.5	4.0	4.5	5.0
	Sensitivity
50	0.27	0.23	0.21	0.19	0.17	0.16	0.15
60	0.49	0.47	0.45	0.43	0.41	0.40	0.39
70	0.60	0.58	0.57	0.55	0.54	0.54	0.53
80	0.65	0.64	0.63	0.63	0.62	0.61	0.61
	Specificity
50	0.76	0.80	0.82	0.84	0.86	0.87	0.88
60	0.58	0.60	0.62	0.64	0.65	0.67	0.68
70	0.50	0.52	0.53	0.54	0.55	0.56	0.57
80	0.47	0.48	0.49	0.50	0.51	0.51	0.52
	Overdiagnosis
50	0.05	0.05	0.04	0.04	0.03	0.03	0.03
60	0.15	0.15	0.14	0.14	0.14	0.14	0.14
70	0.28	0.27	0.27	0.28	0.28	0.28	0.28
80	0.56	0.56	0.55	0.55	0.55	0.55	0.55

5 Discussion

In this paper we have proposed a natural history model for disease progression and biomarker growth prior to diagnosis. In the context of our application, the basic premise of our model is that PSA increases with time from disease onset and that disease progresses as PSA grows. The implication is that there is a single population of PSA growth curves with disease status changing over time as the PSA level changes. Our model explicitly links PSA and disease progression; it is, to our knowledge, the first formal specification of this connection. The model specifies that transitions to metastasis and to clinical detection depend on the level of PSA, which is assumed to follow a piecewise exponential form, after other investigators (Morrell et al, 1995; Whittemore et al, 1995). Our results suggest that for a case with median PSA growth after diagnosis and disease onset at age 70 (see Figure 6), the likelihood of transition to metastasis by the time PSA reaches the level 5 ng/ml is, on average 19.97%, and the likelihood of transition to metastasis by the time PSA reaches a level of 10 ng/ml is, on average, 44.27%. Assuming that localized disease is curable, our results thus indicate that at a PSA level of 5, cure is rather more likely than not.

In our model we estimate an average annual PSA increase of 3.62% before disease onset, and of 24.21% afterwards. The post–onset rate is within the range of values found in a meta–analysis (Inoue et al., 2004) which estimated annual growth rates of 15% for localized disease and 63% for metastatic disease. We note, however, that our sample of cases may represent a relatively agressive subgroup. Several results support this notion. Average PSA levels at last followup were 8.13 ng/ml for local cases and 69.75 ng/ml for metastatic cases. These levels are extremely high, particularly for metastatic cases. Also, on average, the predictive median time from onset to diagnosis (sojourn time) is less than five years (mean= 3.27, 95% predictive credible interval = [0.09, 11.58]). Other studies (e.g. Gann et al, 1995) have estimated the lead time (time from positive PSA to clinical diagnosis) to be roughly 5 years on average (Gann et al, 1995), which exceeds our average sojourn time. While this again indicates that our cohort may be weighted towards more aggressive cancers, it also suggests that the changepoint in PSA growth which we have used as a proxy for disease onset may be occurring some time after the true biological onset time which cannot be estimated from this dataset.

Our model is fully parametric, which raises the question of adequacy of our model assumptions. We evaluated many parametric choices for describing the hazard functions of onset, transition to metastatic disease and clinical detection. Our comparisons with alternative models did not indicate strong evidence against the assumption that the hazard of disease onset increases linearly with age. We also did not find strong evidence against the assumption that the hazard of metastatic transition is dependent on a linear function of PSA. There was evidence that the hazard of disease detection is dependent on a non–linear function of time from disease onset. Finally, we note that instead of considering parametric models, one could, alternatively, use semi– or non–parametric methods for modeling the hazard functions (see, for example, Müller and Quintana, 2004). We did not pursue this approach in our application due to the limited number of metastatic patients in our data set.