Abstract
Noninvasive imaging is widely used in speech research as a means to investigate the shaping and dynamics of the vocal tract during speech production. 3D dynamic MRI would be a major advance, as it would provide 3D dynamic visualization of the entire vocal tract. We present a novel method for the creation of 3D dynamic movies of vocal tract shaping based on the acquisition of 2D dynamic data from parallel slices and temporal alignment of the image sequences using audio information. Multiple sagittal 2D real-time movies with synchronized audio recordings are acquired for English vowel-consonant-vowel stimuli /ala/, /aɹa/, /asa/ and /aʃa/. Audio data are aligned using mel-frequency cepstral coefficients (MFCC) extracted from windowed intervals of the speech signal. Sagittal image sequences acquired from all slices are then aligned using dynamic time warping (DTW). The aligned image sequences enable dynamic 3D visualization by creating synthesized movies of the moving airway in the coronal planes, visualizing desired tissue surfaces and tube-shaped vocal tract airway after manual segmentation of targeted articulators and smoothing. The resulting volumes allow for dynamic 3D visualization of salient aspects of lingual articulation, including the formation of tongue grooves and sublingual cavities, with a temporal resolution of 78 ms.
Index Terms: Articulation, dynamic time warping, real-time MRI, retrospective gating, speech production, vocal tract shaping
I. INTRODUCTION
The vocal tract is the universal human instrument, played with great dexterity and skill in the production of spoken language. Speech researchers are interested in characterizing the relationship between articulation and acoustics, and understanding critically-controlled aspects of vocal tract shaping during speech. Visualization of the movements of the lips, tongue and velum can provide important information about the spatiotemporal properties of speech gestures.
Several techniques have been utilized to visualize tongue shaping during speech, including computed tomography (CT) [1], electromagnetic articulography (EMA) [2], x-ray [3][4], x-ray microbeam [5][6], ultrasound [7], and magnetic resonance imaging (MRI) [8]-[19]. However, each of these approaches has important limitations. Both CT and x-ray expose subjects to radiation. In addition, x-ray averages the entire vocal tract volume into a two-dimensional (2D) image from one projection. EMA provides three-dimensional (3D) data with high temporal resolution, but the EMA sensors are spatially sparse and difficult to attach to pharyngeal structures. Ultrasound is safe and noninvasive, but it detects only the first air-tissue boundary, and typically does not image either the tongue tip or lower pharyngeal articulation. Furthermore, the ultrasound transducer probe is typically in contact with the jaw and may affect the speech production. Although MRI has provided relatively lower spatial and temporal resolution, it has the unique advantage that it can produce complete views, and quantitative measurements, of the entire vocal tract including the velum, posterior oral cavity, and pharyngeal portions. Phonetic data from these regions are not easily acquired using other modalities, but can be safely and non-invasively imaged with MRI, making it a promising tool for speech research. A critical discussion of various techniques can be found in [20].
MRI of the upper airway for speech research has been limited by slow acquisition speed. A number of the early MRI acquisition techniques for speech have been based on imaging of multiple 2D slices [8]-[12] with long scan times in the order of minutes, typically requiring multiple sustained repetitions of the utterance under investigation. The recent introduction of 3D-encoded MRI techniques combined with either compressed sensing or parallel imaging has accelerated the acquisition speed within the duration (typically 6 to 10 s) of a single sustained sound production [13][14]. Compared with 2D multi-slice MRI, 3D-encoded MRI can provide higher acceleration with pseudo-random undersampling available in 2D k-space, and also has the potential for thinner slices and higher signal-to-noise ratio (SNR).
More recently, dynamic MRI methods have been used to provide information about changes in vocal tract shaping during speech. Cine-MRI enables obtaining a set of images by repeatedly scanning the vocal tract while subjects produce (hopefully) identical repetitions of the same utterance. During each repetition, part of the k-space (e.g. one row) is acquired sequentially [15]-[17]. In order to construct images from these data, cine-MRI usually requires synchronization in data acquisition and image reconstruction. Moreover, cine-MRI fills the k-space in a predetermined pattern, which assumes that different repetitions of production have the same pace and duration. Real-time MRI, on the other hand, does not involve the synchronization of k-space acquisition and motions of the soft tissue (e.g., tongue motion, ventricular motion of the beating heart), and captures the motion using fast image acquisition techniques. Demolin et al. demonstrated real-time MRI of speech using turbo spin echo sequence (TSE) with 4 fps on a single slice [18]. Narayanan et al. proposed real-time MRI of vocal tract dynamics with 20–24 fps using a spiral gradient echo sequence and sliding window reconstruction, which is sufficient to capture the underlying motion and physiology of interest during the production of speech [19].
Dynamic imaging of the full 3D vocal tract with high spatial and temporal resolution is, however, more desirable than just a single plane view for a proper understanding of articulation during fluent speech. Current MRI systems do not meet the requirements for capturing 3D vocal tract dynamics in real-time. Interesting engineering, but compromised, solutions have included model-fitting methods and multi-planar imaging in separate operations. Several approaches (including non-MRI ones) have been proposed. Engwall established a 3D parametric tongue model using static MRI and electropalatography (EPG), and estimated parameters for tongue movements using EMA [21]. Video data acquired from pellets marked on the human face were combined with 3D static MRI data to linearly model the articulators [22]. Yang and Stone reconstructed 3D tongue surface motions by temporal registration of ultrasound images from multiple scan locations [23]. Takemoto et al. demonstrated a 3D cine-MRI technique that measures the shaping of the vocal tract using multi-planar 2D cine-MRI [24]. The success of cine-MRI depends crucially on synchronization between speech production and MRI acquisition. This can be challenging to speakers who are not trained to repeat the utterances at the same speech rate. Inspired by multi-planar 2D imaging techniques, in this paper, we propose a novel approach to reconstruct 3D dynamics from multi-planar real-time MRI.
The proposed method constructs 3D movies of the tongue shape and vocal tract dynamics by temporal alignment of parallel 2D MRI data of overlapping sagittal slices covering the entire vocal tract. We briefly introduced the approach and demonstrated the preliminary results first in [25]. The remainder of this paper is organized as follows. We first briefly review real-time MRI of speech, acoustic features mel-frequency cepstral coefficients (MFCC), and a well-known algorithm to measure sequence similarity, called dynamic time warping (DTW). We then describe a systematic approach of parameter selection for extracting MFCCs and evaluation of the performance of different methods of parameterization. Following which, we demonstrate the in-vivo results of audio alignment, synthesized coronal images, and 3D dynamic visualization of tongue and vocal tract shaping during fluent speech. Finally, we critically discuss the current approach, and propose potential future directions for this work.
II. BACKGROUND
A. 2D Real-time MRI of Speech
2D Real-time MRI specifically refers to directly acquiring, reconstructing and displaying MR images in real-time. Spiral readout is one of the most time-efficient schemes commonly used in real-time MRI. The design of spiral trajectories balances trade-offs among temporal resolution, spatial resolution and SNR [19]. This technique has been used to study the vocal tract shaping aspects such as of English speech production [26] and emotional speech production [27]. The implementation of 2D real-time MRI continuously acquires the k-space data in an interleaved spiral scheme, normally with 10 to 20 spiral arms to form a single image [19]. A sliding window reconstruction is applied to reconstruct images after a subset of interleaves are acquired. Synchronized and noise-robust audio recordings (sample rate 20 kHz) are acquired simultaneously with the MR data acquisition to record speech and other vocalizations. Adaptive noise cancellation can effectively remove the MRI acoustic noise [28].
B. Mel-Frequency Cepstral Coefficients
MFCCs are one type of short-term spectral features extracted from the acoustic speech signal. This signal representation is motivated by the signal processing in the human auditory system (cochlea) [29]. MFCCs attempt to encapsulate characteristics of the signal which are salient in human speech perception. In this study, we use MFCCs to represent continuous overlapping speech segments (frames), forming a time series of MFCC feature vectors for each audio recording. MFCCs can be computed as follows:
-
Apply a discrete Fourier transform (DFT) to each Hamming-windowed audio frame and generate the short-term power spectrum:
(1) where s represents a frame of the audio recording, and S(k) is the power spectrum on frequency k.
-
Pass the power spectrum through a triangular band-pass filter bank with M filters (m = 1, 2, …, M), M usually ranges from 24 to 40 [29]:
(2) and obtain a weighted average power spectrum around the filter bank frequencies f[m] that are uniformly spaced in the mel cepstrum. This step smooths the frequency responses and eliminates harmonics.
Compute the log of power spectrum filtered by (2), and perform a discrete cosine transform (DCT) to obtain the MFCCs. Typically the first 13 MFCCs are sufficient to characterize the segmental phonetic information in a speech audio frame [29].
C. Dynamic Time Warping
DTW is a dynamic programming technique that measures the similarity and finds the minimum-distance warping path between two time series [30]. Given two time series A and B, of length m and n, respectively,
| (3) |
| (4) |
the distance (typically Euclidean) of ai and bj is denoted
| (5) |
A 2D cost matrix D of size m by n is constructed, where D(i, j) represents the minimum distance between two partial series A′ = [a1, a2, a3…ai] and B′ = [b1, b2, b3…bj]. Boundaries of D are initialized as
| (6) |
and then D is filled from D(1, 1) to D(m, n) with the pattern
| (7) |
The monotonicity criterion imposed on D constrains the minimum-distance warping path D(i, j) to go through one of the previous-state cells. The algorithm increments i and j until the cost matrix is filled such that D(m, n) is the minimum distance between series A and B. The minimum-distance warping path can be determined by back-tracking from D(m, n) to D(1, 1) by locating the minimum-distance previous states. Since a single member in one series can map to multiple successive members in the other series, the two series can be of different lengths. In the presented work we apply DTW to align pairs of audio feature series, and obtain the warping relationships for the subsequent alignment of the videos.
III. METHOD
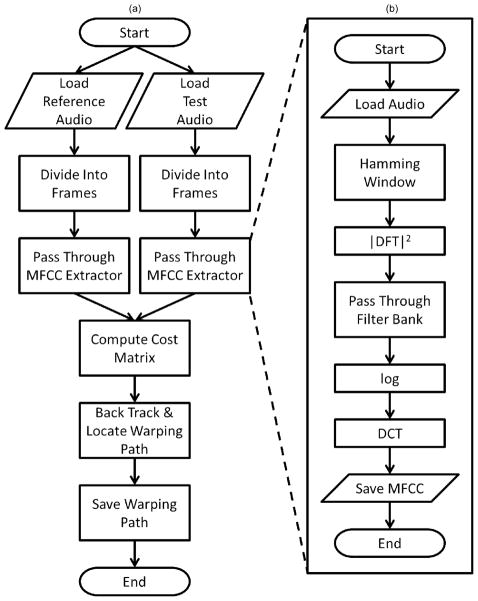
Dynamic 3D MRI reconstruction makes use of two companion data sets: real-time MR data, and synchronized noise-cancelled audio recordings. We acquired MR data from a set of parasagittal scan planes, covering the entire upper airway. The same speech corpus was elicited from the subject at each scan plane acquisition. As a preprocessing step, we extracted the MR data/audio tracks that correspond to a token of interest (e.g., utterance /ala/) from a long video/audio acquisition. Since the speech rate tended to vary even during repeated utterances of the same stimuli, we employed audio-based alignment by applying DTW on the audio MFCC time series (MFCC-DTW alignment) to synchronize pairwise repetitions of the stimuli, as illustrated by the flow charts in Fig. 1. The applied 13 MFCC filter bank frequencies in Hz were:
| (8) |
Fig. 1.
(a) MFCC-DTW alignment takes a pair of noise-cancelled audio recordings as input, segments them into overlapping speech frames, and then passes each frame through the (b) MFCC extractor. The MFCC extractor follows the standard MFCC extraction procedures, including generation of short-term power spectrum, passing through a triangular band-pass filter bank, computing the log and the discrete cosine transform (DCT). MFCC-DTW alignment constructs a cost matrix for each pair of MFCCs series, and then back tracks and locates the minimum-distance warping path.
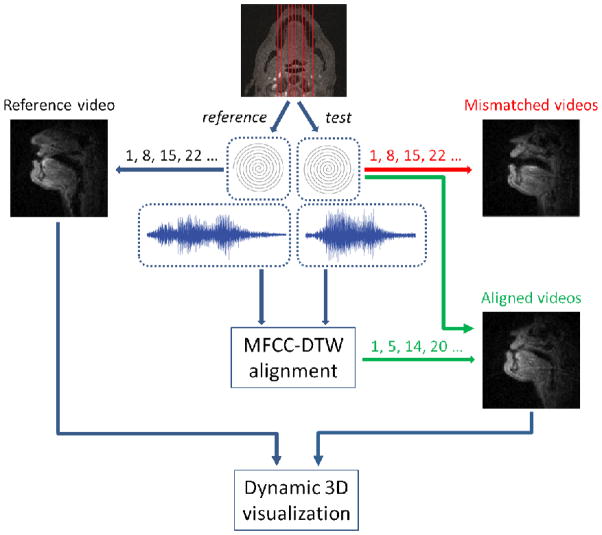
We subsequently generated aligned videos from the MR data by controlling the placement of the sliding window according to the acoustic alignment. As a result, the temporal resolution of the aligned movies is identical to that obtained from real-time 2D imaging. Finally, we constructed the dynamic 3D visualizations in three ways: synthesized movies along 3 coronal planes, 3D tissue surfaces, and 3D vocal tract dynamics using manually segmented features from aligned frames. Fig. 2 shows the flow of pairwise data processing. Here we use the terms reference and test to refer to a pair of data sets as input of the process, in which test is aligned to reference. Notice that the pairwise data processing is audio-based, therefore applicable to align data acquired from different scan planes. In addition, the audio of a reference is synchronized with all aligned test videos, and is the only audio being used with visualization after alignment.
Fig. 2.
The flow of pairwise data processing. A set of parasagittal scan planes covers the entire upper airway. Acquired data include real-time MR data, and synchronized companion noise-cancelled audio recordings. Since the speech rate and duration tend to vary, reconstruction using the same sliding window would lead to mismatched videos. Audio-based MFCC-DTW alignment synchronizes pairwise audio recordings, and the resulting warping paths guide the placement of the sliding window in reconstructing aligned videos. One reference video and aligned videos from other sagittal planes enable the dynamic 3D visualization, such as the synthesized coronal movies, the 3D tissue surfaces and vocal tract dynamics.
A. Parameter Selection
MFCC-DTW alignment employs the DTW algorithm to align pairs of MFCC vector time series extracted from multiple utterances of comparable speech recordings. It is common to use a frame width from 5 ms to 100 ms, and shift subsequent windows by 1/3 of the frame width in MFCC computation [30]. Euclidean distances of two MFCC vectors series from two audio recordings form the cost matrix D in (7), from which the MFCC-DTW algorithm derives the minimum-distance warping path. It is then feasible to match each audio frame with each imaging time of repetition (TR) using a nearest neighbor method. This avoids any restriction on the frame width and shift size when synchronizing the MFCC series with the MR data.
We performed a two-stage test to exhaustively find a suitable frame width and shift size, using pilot data from midsagittal plane scans. The data included two sets of acquisitions: one with deliberately varied speech rates, and the other with a normal speech rate. In the first experiment, we applied MFCC-DTW alignment with all possible combinations of frame width and shift size, using values 1, 2, 3 … 500 ms for both. We aligned four utterances in the pilot data for three cases: long audio to short audio (long-to-short) alignment, short audio to long audio (short-to-long) alignment, and normal audio to normal audio (normal-length) alignment. In total, 500×500×3×4 aligned videos were generated to examine residual alignment errors.
In the second experiment, we measured error-to-noise ratio (ENR) of all the aligned videos. In computing ENR, it is assumed that: a) additive noise in the image is independent and identically distributed with mean 0 and variance σ2; b) the true image is uncorrelated with noise. Therefore,
| (9) |
where E(ΔΔ*), E(ee*) and E(nn*) are the mean squared errors between pixel intensities within the reference and test frames, the pure signal differences (i.e., alignment errors) and the pure noise differences, respectively. E(ΔΔ*) and E(ee*) are computed thus:
| (10) |
| (11) |
where Nx and Ny are dimensions of the frame, and Nt is the total number of frames. VR(x, y, t) and VT(x, y, t) denote image pixel intensity in spatial coordinates (x, y) in the t-th frame of the reference video and test video, respectively. SR(x, y, t) and ST(x, y, t) denote pure signal pixel intensity from the reference video and test video, respectively. Here, E(ee*) = 0 means that the two videos are perfectly aligned. MFCC-DTW alignment parameter selection aims to discover the parameters that minimize E(ee*). Apparently E(ee*) is not directly assessable because the noise is always embedded in the acquired videos. However, the noise variance σ2 can be estimated from the background regions with no signal. In this work, we define ENR to be:
| (12) |
The minimum possible value of ENR is 0; ENR = 1means that the error energy due to signal misalignment is identical to the noise energy.
B. In Vivo Experiments
Experiments were performed on a 1.5 T Signa Excite HD MRI scanner system (GE Healthcare, Waukesha, WI) with gradients supporting maximum amplitude of 40 mT/m and maximum slew rate of 150 T/m/s. The sampling period was set to 4 μs (receiver bandwidth ±125 kHz). We used a body coil for radio frequency (RF) transmission and a custom 4-channel upper airway coil (two anterior elements, two posterior elements) for signal reception. Data from the two anterior elements only were used for image reconstruction as the two posterior elements provided low coil sensitivity in the upper airway regions. Parallel imaging was not utilized in this study. MR imaging was performed with a custom real-time imaging framework [31], providing interactive control of scan parameters, image reconstruction, and frame display in real-time. Subject utterances were monitored in real-time using an FOMRI-III in-scanner noise reducing optical microphone system (Optoacoustics, Moshav Mazor, Israel) during MRI scans. In-scanner audio recordings were made simultaneously with MRI acquisitions [28].
The MRI pulse sequence consisted of 1.5 ms excitation, 2.5 ms spiral readout, and 2 ms for gradient rewinder and spoiler. TR was 6.0 ms. 13 spiral interleaves were used to form each image, resulting in temporal resolution of 78 ms. We used gridding reconstruction to reconstruct every single frame and obtained an effective video frame rate of 23.8 fps using a sliding window reconstruction, updating frames every 7-TR (i.e., 42 ms). Each frame had 20 cm × 20 cm field of view (FOV) and 2.4 mm × 2.4 mm spatial resolution.
Three male native speakers of English (two American English, one Australian English) were used as subjects. Subjects’ ages ranged from 25 to 30 years; none had undergone any major dental work, major oral or maxillofacial surgery, and had no prior linguistic training. Each subject was screened and provided informed consent in accordance with institutional policy. Each subject was scanned in the supine position with the head immobilized from left-right tilting using foam pads between the head and the receiver coil. Stimuli were projected onto a screen in the scanner room, which could be seen by the subjects through a mirror attached to the receiver coil. All subjects made their best efforts to keep their heads stationary during the experiments. Stimuli consisted of English vowel-consonant-vowel (VCV) sequences /ala/, /aɹa/, /asa/, and /aʃa/. Details of each token and the associated regions of interest in the vocal tract are given in Table i.
Table I.
List of targeted articulatory characteristics associated with observed 3D features from English vowel-consonant-vowel (VCV) sequences /ala/, /aɹa/, /asa/, and /aʃa/.
| Study | Articulation under examination | Stimuli | 3D features observed |
|---|---|---|---|
| Liquids |
|
/ala/ |
|
| /aɹa/ |
|
||
| Sibilants |
|
/asa/ |
|
| /aʃa/ |
|
First, pilot data from the midsagittal scan plane with varied and normal speech rates were obtained for the purpose of choosing parameters for MFCC-DTW alignment (see Section III-A). In acquisition of varied-rate speeches, one subject was instructed to read the stimuli at slow speech rates (typically slower than 2.0 s/utterance), and to repeat the productions at fast speech rates (typically faster than 1.0 s/utterance), by artificial elongation and contraction, respectively. We monitored and verified the speech rates on-the-fly.
Twenty-one parallel sagittal slices together covered the entire vocal tract volume. Each slice was 6 mm thick, located with 3 mm overlap with neighboring slices. Subjects uttered 21 repetitions of each token at a normal speech rate, which amounted to a mean value of 1.1 s/utterance and a variance of ±0.2 s/utterance during each real-time scan. Pulse sequences were programmed to execute automatic and continuous sweeping of the entire 21 slices without a scanner pause during real-time imaging of the vocal tract. The slice acquisition scheme commenced at the midsagittal slice, and then proceeded to parasagittal slices in an interleaved center-out pattern (see the supplementary video). In addition, the spiral readout gradients between successive slice acquisitions were turned off as a means to provide an auditory trigger for the subjects to prepare for the next repetition. We used the data from 21 sagittal slices to synthesize movies on the other orthogonal planes (e.g., coronal), and used the data from 13 central sagittal slices to construct the dynamic 3D tongue and vocal tract visualization.
Finally, we acquired data from 3 uniformly spaced coronal scan planes on the tongue individually, while the subjects were asked to repeat the same speech corpus. The directly acquired coronal movies were utilized for method validation.
C. Data Visualization and Analysis
An orthogonal slice cut in the data volume formed by aligned sagittal frames constitutes the orthogonal 2D view (e.g., coronal, axial). As a result, the number of pixel columns in the synthesized views equal to the number of acquired sagittal slices. The cross-plane (right-left, or R-L direction) resolution is the shift size of the sequential slices (3 mm), but the true spatial resolution is the slice thickness (6 mm), which is lower than in-plane resolution (2.4 mm). The FOV of synthesized view was 200 mm × 63 mm, therefore we resized frames, using bicubic interpolation, to the isotropic resolution 1 mm × 1 mm that is the greatest common divisor of FOV on two directions, in order to obtain reasonable visualization. Bicubic interpolation is widely used in image processing to resize image by estimating interpolated pixels using a number of closest surrounding pixels. We iterated the process to generate the synthesized coronal videos frame-by-frame. Directly acquired coronal data sets were also aligned to sagittal reference data set using the same MFCC-DTW alignment approach.
We evaluated the aligned 3D data using synthesized coronal planes, in comparison with directly imaged coronal movies on the same anterior-posterior (A-P) positions. If the 3D data are correctly aligned, we would visualize tongue features that are evident in directly imaged coronal views, such as the tongue groove [8]. The smoothness of the tongue surface in coronal slices serves as another criterion for method evaluation, because alignment errors will manifest as apparent tissue irregularities in a coronal section of the tongue. We quantitatively assessed the smoothness using a curve fitting method. We first manually segmented the tongues using a locally thresholding tool from sliceOmatic (TomoVision, Magog, Quebec, Canada) software, and then extracted the upper tongue surfaces, and fitted the surfaces to polynomial curves,
| (13) |
where c(x) is a fitted curve with polynomial coefficients c1, c2, … cn+1 of degree n, in a least squares sense. We used the root-mean-square (RMS) error of the fitted curve,
| (14) |
to quantitatively assess tongue surface irregularity, where denotes number of points on the upper tongue surface, T(x) and C(x) are vertical positions of tongue and fitted curve in horizontal position x. The degree of polynomial curve on each coronal plane was selected as the minimum degree of curve fitting on directly imaged coronal view that results in sub-millimeter RMS error.
Manually segmented tongue and lower jaw contours from aligned sagittal videos establish the cross-section of the 3D surfaces. The volumetric vocal tract data is ready for visualization after 3D nearest neighbor interpolation along the R-L direction. The Matlab (The MathWorks, Natick, MA) 3D visualization toolbox was used to smooth the data volume with a box convolution kernel size of 5, and to extract an isosurface – a 3D surface of identical value (isovalue) – from the volumetric static data. We empirically determined the isovalue to provide sufficient smoothing of the reconstructed lingual volume, preserving the major anatomical features of the tongue (and surrounding parts of the vocal tract). Since one contour depicts the vocal tract boundary on each parallel plane, the synthesized 3D surfaces look like ribbons enclosing the vocal tract with openings at the right and the left ends of the imaged volume (see Fig. 7). Similarly, manually segmented vocal tracts from aligned sagittal videos build the tube-shaped vocal tract airway [9]. We performed 3D cubic interpolation on the data in Matlab and smoothed the volume with a box convolution kernel size of 3. Instead of using an isosurface, we color-coded the segmented areas on different sagittal planes in the visualization. Sequences of 3D static models portray 3D tongue motion and vocal tract articulatory dynamics, which provide efficient visualizations of vocal tract shaping, observable from any viewing angle.
Fig. 7.
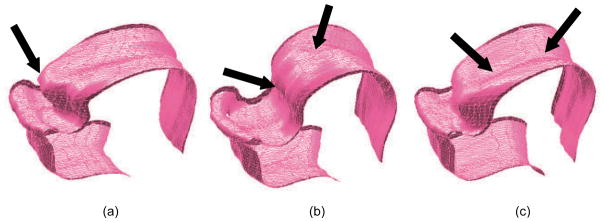
Selected individual frames from dynamic 3D visualizations of the tongue and the jaw surfaces for the consonants /l/, /ɹ/ and /s/ in the utterances of /ala/, /aɹa/ and /asa/ (linguistically salient aspects of vocal tract shaping indicated with arrows). (a) apical coronal articulation (approximation of the tongue tip to the alveolar ridge) during lateral production in the utterance /l/, (b) bunched coronal articulation during production of rhotic approximant in the utterance /ɹ/, and (c) tongue groove formation during sibilant production in the utterance /s/. The 3D models appear qualitatively less accurate at the far right and far left ends of the volume, potentially due to rapid changes in tongue geometry, leading to blurry sagittal images and difficulty with manual segmentation. The dynamic 3D visualization of the four utterances is provided as supplemental materials.
IV. RESULTS
A. Parameter Selection
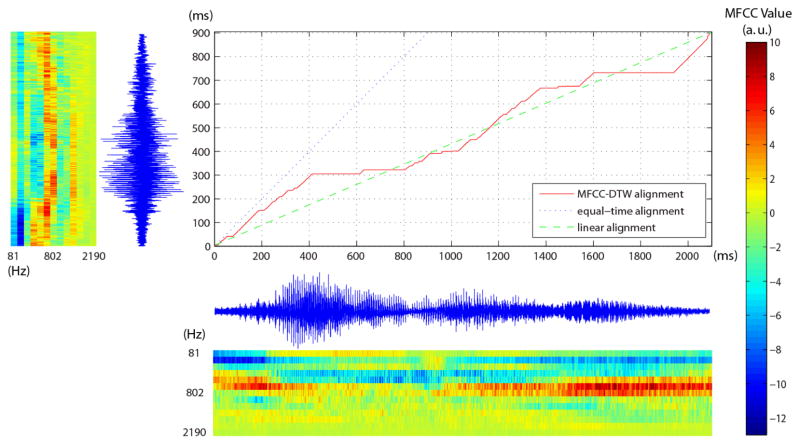
Fig. 3 displays the minimum-distance warping path for two audio recordings of the utterance /ala/ from the pilot data. The red line represents the preliminary non-linear warping using MFCC-DTW alignment with conventional MFCC settings extracted over 10 ms timeframes (within the region suggested by [30]), using a 1 ms shift size, demonstrating high resolution alignment pairs. Each point on the red line (e.g. (x, y)) stands for the mapping of a frame centered at position x in the longer duration audio signal to a frame centered at position y in the shorter duration audio signal. In contrast, the dotted blue line indicates the naive equal-time alignment (i.e., unaligned case), and the green dashed line shows a uniform end-to-end linear alignment. Amplitude waveforms of the two audio signals and their corresponding MFCC series are shown along the horizontal and vertical axes. Notice that despite the fact that the MFCC frame width and shift size were not yet optimized at this stage, conventional settings already offered reasonable alignment results.
Fig. 3.
Minimum-distance warping path for aligning pilot data /ala/ long recording to short recording using preliminary MFCC-DTW alignment (red line) with conventional MFCC settings extracted over 10 ms timeframes, using a 1 ms shift size. Each point on the red line (e.g. (x, y)) stands for the mapping of a frame centered at position x in the longer duration audio signal to a frame centered at position y in the shorter duration audio signal. In contrast, the dotted blue line indicates the naive equal-time alignment (i.e., unaligned case), and the green dashed line shows a uniform end-to-end linear alignment. Amplitude waveforms of the two audio signals and their corresponding MFCC series are shown along the horizontal and vertical axes.
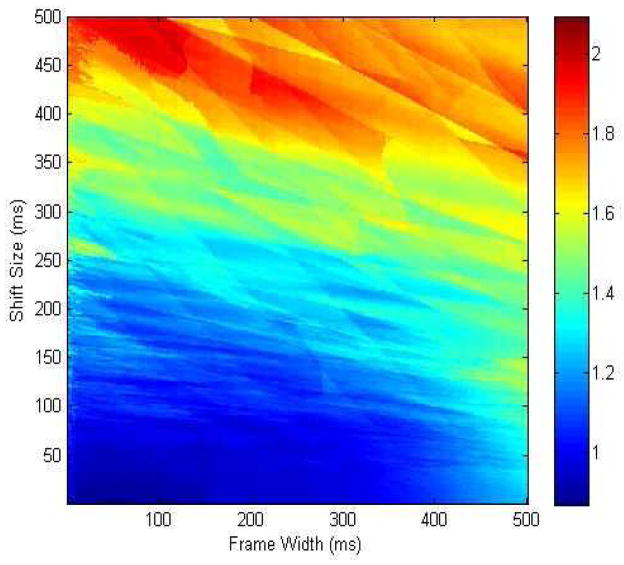
We used the pilot data to experiment with parameter selection. Each test involved long-to-short alignment, short-to-long alignment and normal-length alignment. We noted that the results of long-to-short alignment were highly consistent with the results of normal-length alignment, but different from the results of short-to-long alignment. Our findings suggest that it is necessary to avoid aligning an extra-short utterance to an extra-long repetition of the same utterance. We therefore excluded the usage of short-to-long alignment results for the following parameter selection. Fig. 4 illustrates the average map of ENR (see Equation 12) on the aligned videos of the utterances /ala/, /aɹa/, /asa/ and /aʃa/. Both frame width and shift size range from 1 ms to 500 ms with 1 ms spacing, which guarantee wide and dense coverage of all possible parameter combinations. Although there is no universal minimum-error setting, the data reveal a general trend that smaller frame widths and shift sizes result in smaller errors. We obtained an estimate of the optimal parameter setting – 36 ms frame width and 8 ms shift size – by averaging 100 minimum-error settings.
Fig. 4.
Error-to-noise ratio (ENR) map of average results of MFCC-DTW long-to-short and normal-length alignments from four utterances /ala/, /aɹa/, /asa/ and /aʃa/ with frame widths and shift sizes ranging from 1 ms to 500 ms with 1 ms spacing. Frame width and shift size are critical to MFCC extraction, but there is no widely accepted values among different applications. Here the tested parameter combinations guarantee wide and dense coverage of possible choices. There is a general trend that smaller frame widths and shift sizes result in smaller errors.36 ms frame width and 8 ms shift size are estimated optimal parameter setting from averaging 100 minimum-error settings.
B. Evaluation and Data Visualization
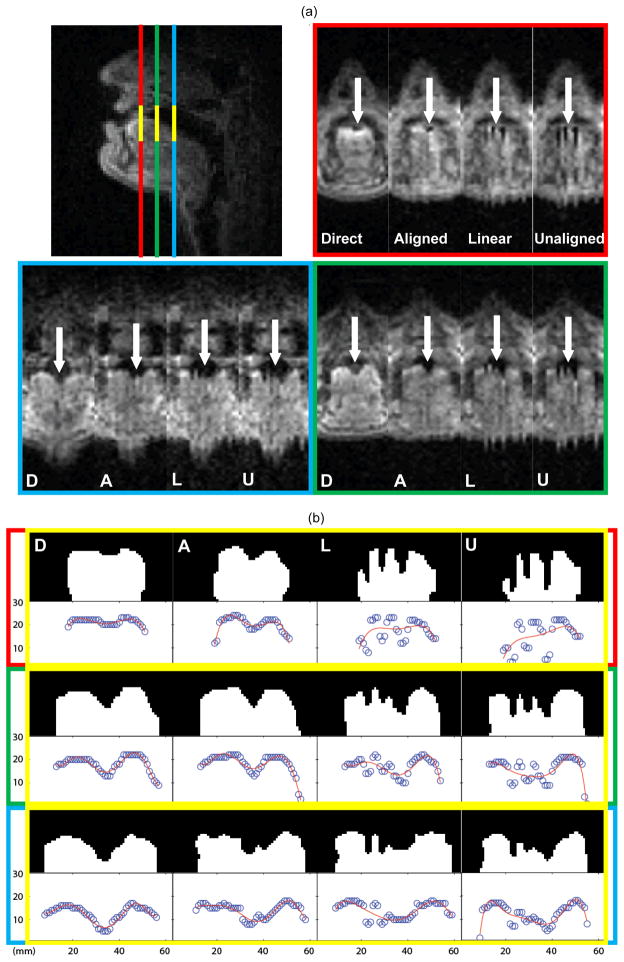
We qualitatively and quantitatively assessed the plausibility of the results by comparing directly acquired coronal movies (ground truth) and synthesized coronal movies. Fig. 5(a) illustrates such comparison among directly acquired (D), reformatted MFCC-DTW aligned (A), linearly aligned (L) and unaligned (U) coronal images on 3 color-coded parallel coronal planes: tongue tip (alveolar, in red), tongue blade (post-alveolar, in green) and tongue front (hard palate, in blue). Images were selected from the production of /s/ in the utterance /asa/ from one subject when his fricative constriction degree was maximal. The directly acquired images were manually trimmed to display the same FOV (200 mm × 63 mm) as the synthesized images. The arrows in the coronal images indicate tongue groove sibilant formation in the three tongue regions. The MFCC-DTW alignment results clearly indicate the tongue groove pattern similar to the directly acquired one, whereas data are poorly synchronized by linear and equal-time alignments. Other salient vocal tract features involving tongue shaping were observed in synthesized images of /ala/, /aɹa/ and /aʃa/ utterances respectively (not shown, see supplemental video). Fig. 5(b) presents segmented tongues from coronal views, and the fitted tongue surfaces from sparse upper tongue surfaces. The bright areas standing out of black background are the results from zoomed-in areas highlighted by yellow columns in the sagittal image in Fig. 5(a). Upper tongue surface points were extracted as circles, and fitted to polynomial curves. The degrees of polynomial fitting were 4, 6 and 7 for red, green and blue slices (from anterior to posterior), respectively.
Fig. 5.
(a) Comparison among directly acquired (D), reformatted MFCC-DTW aligned (A), linearly aligned (L), and equal-time aligned (U) coronal images on 3 color-coded parallel coronal planes: tongue tip (alveolar, in red), tongue blade (post-alveolar, in green) and tongue front (hard palate, in blue). Images were selected from the production of /s/ in the utterance /asa/ from one subject when coronal constriction degree was maximal. Tongue groove formation may be clearly seen in the directly acquired images and reformatted MFCC-DTW aligned images (see arrows), but not in results of linear and equal-time alignments. Comparison of other salient vocal tract features involving tongue shaping is provided in a supplemental video. (b) Manually segmented tongues from coronal views, and the fitted tongue surfaces from sparse upper tongue surfaces. The bright areas are the segmentation results from zoomed-in areas highlighted by yellow columns in the sagittal image in Fig. 5(a). Upper lingual points were extracted as circles, and fitted to polynomial curves. Each coronal plane (each row of fitted curves) has an individual degree of polynomial fitting, which is set to the minimum degree that results in sub-millimeter RMS error of the directly acquired tongue (4, 6 and 7 for red, green and blue slices, respectively).
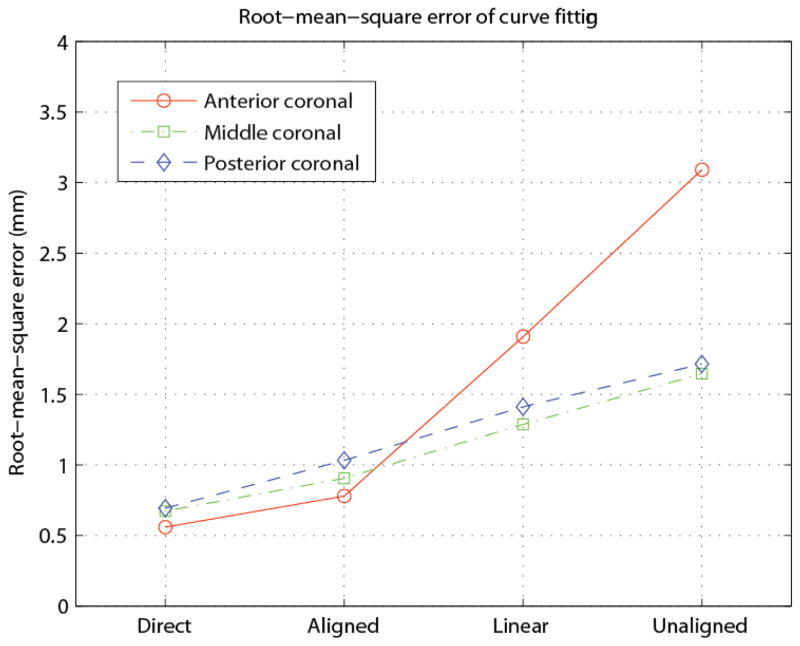
Fig. 6 displays the average RMS errors of tongue surfaces curve fitting from maximum constrictions of all subjects eliciting the consonants from /ala/, /aɹa/, /asa/ and /aʃa/, excluding /aɹa/ and /aʃa/ on the anterior plane because the retracted tongues did not appear in the coronal images. The fitting degrees were individually chosen, for anterior, middle and posterior coronal slices, as the minimum degrees of curve fitting on directly imaged coronal views that result in sub-millimeter RMS errors. The figure indicates that MFCC-DTW alignment (A) RMS errors are comparable to the RMS errors of directly acquired (D) data, and much lower than the RMS errors of linear alignment (L) and equal-time alignment (U) in all coronal slices, especially in the anterior coronal slice.
Fig. 6.
Average root-mean-square (RMS) errors of tongue surface fitting: maximum constrictions of all subjects during consonant production in /ala/, /aɹa/, /asa/ and /aʃa/ sequences, excluding /aɹa/ and /aʃa/ on the anterior plane. The fitting degrees are individually chosen, for anterior, middle and posterior coronal slices, as the minimum degrees of curve fitting on directly imaged coronal views that result in sub-millimeter RMS errors. MFCC-DTW alignment (A) results are comparable to directly acquired (D) results, and are much lower than results of linear alignment (L) and equal-time alignment (U) in all coronal slices, especially in the anterior coronal slice.
Fig. 7 illustrates 3D visualization of the tongue and the jaw surfaces for the consonants /l/, /ɹ/ and /s/ in the utterances of /ala/, /aɹa/ and /asa/. Many details of lingual articulation are evident in the reconstructed tongue surfaces (see arrows), including apical approximation of coronals (/l/), bunched production of rhotic approximants (/ɹ/), and groove formation during sibilant productions (/s/). The 3D models appear qualitatively less accurate at the far right and far left ends of the volume, potentially due to rapid changes in tongue geometry, leading to blurry sagittal images and difficulty with manual segmentation. Images shown in Fig. 7 were extracted from the reconstructed dynamic 3D movie (78 ms temporal resolution) that is provided as supplemental material. Supplemental materials also include dynamic 3D movies of the tube-shaped vocal tract, in which the segmented airway from each sagittal slice is color-coded.
V. DISCUSSION
To our knowledge, the proposed method is the first demonstration of dynamic 3D visualization of the vocal tract shaping using real-time MRI and synchronized audio recordings. Since the proposed method relies on 2D real-time MRI data, it inherits the image quality problems of 2D real-time MRI. Significantly low SNR due to poor coil sensitivities of our current receiver coil array was observed in the middle to lower neck. This made it difficult to observe the dynamics of the vocal cord, which is another region of interest for the application of the proposed approach. In addition, the proposed technique requires finer slice resolution than 6 mm to improve visualization of coronal-slice tongue shape, but the image SNR is unacceptable with the slice thickness thinner than 6 mm in our current 2D real-time MRI of speech. Together 6 mm thickness and 3 mm overlap result in a volume covering the entire vocal tract with reasonable pixel resolution and data fidelity in the cross-plane direction, since a 2D image is a projection of tissue slice. We made trade-offs among image quality, data fidelity and scan time. Midsagittal plane is most commonly used in speech research to get a full view of the vocal tract from the lip opening to the glottic region, and acquisition of contiguous parallel sagittal planes is more time-efficient in covering the entire vocal tract than acquisition of stack of axial or coronal planes, because vocal tract has much smaller dimension alone R-L direction than A-P or superior-inferior (S-I) direction. If we prescribe axial or coronal plane, more slices are required for covering the entire vocal tract, leading to more repetitions of the speech corpus for subjects.
We have performed our experiment on three subjects using different stimuli including VCV utterances, long English words, and English sentences. Experiments involving English sentences require multiple separate scans to acquire data for all the sagittal slices covering the entire vocal tract, because of scan time limitations. Nevertheless, the MFCC-DTW technique successfully aligned separately-acquired data to a similar level in all cases (more than ten). We demonstrate manually-segmented results of four short, representative VCV utterances in Fig. 7 and the supplemental dynamic 3D movies, which demonstrate 3D features of interest.
The number of triangular filters used in MFCC extraction, 24 to 40, is widely accepted in audio signal processing community [29], and for speech processing applications, the first 13 out of 24 MFCCs are commonly used [29]. We tried different values within the range, and observed little differences in the alignment results. Fig. 3 shows that the minimum-distance warping path is a non-decreasing, discontinuous curve constrained by the monotonicity criterion. The curve verifies the abilities of MFCC-DTW alignment to align two productions where the speech rates are unstable, and to align two MFCC sequences of different lengths because one-to-many and many-to-one mappings are both allowed. The drawbacks of DTW include quadratic time complexity and memory requirement. DTW is a dynamic programming algorithm using a cost matrix whose size is proportional to the product of the lengths of two time series [32]. This puts practical limits on the usage of DTW for aligning extremely long acquisitions or using extremely small shift sizes. Other groups have accelerated traditional DTW and improved memory occupancy efficiency by sacrificing minor accuracy. Following Salvador and Chan’s classification [32], established approaches fall into three categories: 1) Constraints which limit the number of cells in the cost matrix to be evaluated, such as Sakoe-Chiba Band [33] and Itakura Parallelogram [34]; 2) Data Abstraction which reduces the sizes of time series as DTW input [35]; and 3) Indexing which prunes out the number of times DTW runs using lower-bounding functions [36].
Our results indicate that the performance of long-to-short alignment is superior to that of short-to-long alignment. We believe this is because when a subject intentionally produces short utterances, most acoustic features are shortened, and some may be discarded. When a subject intentionally prolongs utterances, he appears to preserve all the acoustic features, or even adds some abnormal acoustic features. The MFCC-DTW algorithm simply discards additional features by mapping multiple entries to a single entry in the test audio in long-to-short alignment, such as period 1.6 s to 1.9 s in Fig. 3. But when the algorithm aligns a short utterance to a long utterance, misalignments may occur when the algorithm aligns normal acoustic features to abnormal ones due to artificial elongation of the utterance. Since experimental audio recordings for utterances collected to date have a mean of 1.1 s/utterance and a variance of ±0.2 s/utterance, this suggests that short-to-long alignment is not a concern in real audio alignment.
There is no universal optimal value of frame width or shift size for short-time audio processing, such as MFCC extraction. We observed that 100 minimum-error parameter settings cluster in a small area, and thus we averaged them for our estimate. The resulting 36 ms frame width falls into the typical range conventionally used in speech processing (5 ms to 100 ms, [30]), and is very close to that of 40 ms used in [29], but the shift size is only 2/9 of the frame width, smaller than the suggested 1/3 of the frame width [30].
Coronal views derived from the reconstructed data using this technique are a good example of the type of arbitrary reformatting that can only be done with 3D data, and provide a clear method by which to examine the synthesized 3D vocal tract data. Poor alignment leads to asymmetry of reconstructed tongue and jagged surfaces (i.e., stair-step artifact), which are evident in linear and equal-time alignment results, but are greatly mitigated in MFCC-DTW alignment results. The results from the RMS error plots show that DTW-MFCC alignment invariably outperforms the other two alignment methods, and confirm the observations of qualitative evaluations. The RMS errors of linear and equal-time alignments from anterior slice are significantly higher than from middle and posterior slices (see Fig. 6), because the vocal tract constriction of /l/ and /s/ is located between the tongue tip and alveolar ridge, and lasts for a very short period (about 100 ms to 200 ms), so that any misalignment would be manifest as stair-step artifact. In addition, linear and equal-time alignments tend to be very sensitive to the duration, the start and end of segmented data, to which MFCC-DTW alignment exhibits the robustness. Therefore the careful data/audio segmentation of single short utterances by mutual inspection of video/audio in the preprocessing improves accuracy of the linear and equal-time alignments.
From a temporal perspective, MFCC-DTW alignment has poorer results at the start and the end of each utterance, compared with the medial data portions. The likely reason is that MFCC-DTW alignment relies on audio information, but there are no clearly identifiable acoustic landmarks to support proper alignment at the start and end of the utterance, corresponding to points in time when the articulators just leave from or move back to rest positions (without producing sound). In spite of these limitations, the intervals of most interest for linguistic research are focused on periods of more active articulation, when acoustic-articulatory alignment is more easily achieved, and slight mismatches at the start and the end of each utterance are therefore less problematic.
The 3D movies generated using this technique successfully allowed for the dynamic visualization of many of the salient articulatory features anticipated in these stimuli. However, one important limitation of the method at this stage of development is the presence of minor surface irregularities in the reconstructed object. Several possible reasons are: 1) Image quality issues: off-resonance and motion artifacts could blur the air-tissue boundaries, resulting in contour tracking errors. 2) Slice thickness: the shape of the tongue changes along the R-L direction, especially at both ends of the tongue, where steep changes exist. 3) Gross head motion: some head movement is inevitable during multiple repetitions, despite the limiting effect of having subjects’ heads immobilized using foam paddings. 4) Varying degrees of jaw opening: subjects could not precisely repeat the same degree of jaw opening in different repetitions. 5) Manual segmentation errors: manual segmentation currently outperforms any automatic segmentation methods, but can be weakened by shortcomings including reproducibility errors, operator fatigue and bias.
Finally, it is worth noting that high temporal resolution 3D vocal tract data is valuable not only to linguistic studies, but could also be useful for clinical research, including the investigation of articulatory differences between the pre- and post-operative vocal tracts in glossectomy patients [37].
VI. CONCLUSION
We presented a novel method for 3D dynamic imaging of human vocal tract airway shaping (and of the associated articulators, notably, the tongue) based on 2D real-time MRI of parallel sagittal slices that are independently acquired from repetitions of the same speech corpus. The technique applies DTW to comparable series of audio MFCC feature vectors to compensate for the temporal mismatches of the videos resulting from varied speech rates. With this technique, we were able to reconstruct 3D vocal tract movies with 2.4 mm × 2.4 mm × 3 mm spatial resolution and 78 ms temporal resolution, from which we successfully visualized lingual features of several tested utterances. The proposed method can give improved insights into the goals of speech production, since it can provide high temporal resolution information about the changing geometry of the entire vocal tract – data which are not available from conventional 2D/3D MRI techniques.
Acknowledgments
This work is supported by NIH Grant R01 DC007124. The authors acknowledge the support and collaboration of the SPAN (Speech Production and Articulation kNowledge) group at the University of Southern California.
References
- 1.Perrier P, Boë L, Sock R. Vocal tract area function estimation from midsagittal dimensions with CT scans and a vocal tract cast modeling the transition with two sets of coefficients. J Speech Hearing Res. 1992 Feb;35:53–67. doi: 10.1044/jshr.3501.53. [DOI] [PubMed] [Google Scholar]
- 2.Perkell JS, Cohen MH, Svirsky MA, Matthies ML, Garabieta I, Jackson MTT. Electromagnetic midsagittal articulometer systems for transducing speech articulatory movements. J Acoust Soc Am. 1992 Dec;92:3078–3096. doi: 10.1121/1.404204. [DOI] [PubMed] [Google Scholar]
- 3.Delattre P, Freeman DC. A dialect study of American r’s by x-ray motion picture. Linguistics. 1968;44:29–68. [Google Scholar]
- 4.Wood S. Working Papers in Linguistics. Vol. 23. Lund University; 1982. X-ray and model studies of vowel articulation. [Google Scholar]
- 5.Nadler RD, Abbs JH, Fujimura O. Speech movement research using the new X-ray microbeam system. Proc 11th Inter Congress of Phon Sci. 1987;1:221–224. [Google Scholar]
- 6.Westbury JR, Turner G, Dembowski J. X-ray microbeam speech production database user’s handbook. Waisman Center on Mental Retardation and Human Development, University of Wisconsin; 1994. [Google Scholar]
- 7.Stone M, Shawker TH, Talbot TL, Rich AH. Cross-sectional tongue shape during the production of vowels. J Acoust Soc Am. 1988 Apr;83:1586–1596. doi: 10.1121/1.395913. [DOI] [PubMed] [Google Scholar]
- 8.Baer T, Gore JC, Gracco LC, Nye PW. Analysis of vocal tract shape and dimensions using magnetic resonance imaging: Vowels. J Acoust Soc Am. 1991 Aug;90:799–828. doi: 10.1121/1.401949. [DOI] [PubMed] [Google Scholar]
- 9.Story BH, Titze IR, Hoffman EA. Vocal tract area functions from magnetic resonance imaging. J Acoust Soc Am. 1996 Jul;100:537–554. doi: 10.1121/1.415960. [DOI] [PubMed] [Google Scholar]
- 10.Narayanan SS, Alwan AA, Haker K. An articulatory study of fricative consonants using magnetic resonance imaging. J Acoust Soc Am. 1995 Sep;98:1325–1347. [Google Scholar]
- 11.Narayanan SS, Alwan AA, Haker K. Toward articulatory-acoustic models for liquid approximants based on MRI and EPG data. Part I. The laterals. J Acoust Soc Am. 1997 Feb;101:1064–1077. doi: 10.1121/1.418030. [DOI] [PubMed] [Google Scholar]
- 12.Proctor MI, Shadle CH, Iskarous K. Pharyngeal articulation in the production of voiced and voiceless fricatives. J Acoust Soc Am. 2010 Mar;127:1507–1518. doi: 10.1121/1.3299199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kim Y, Narayanan SS, Nayak KS. Accelerated three-dimensional upper airway MRI using compressed sensing. Magn Reson Med. 2009 Jun;61:1434–1440. doi: 10.1002/mrm.21953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kim Y, Narayanan SS, Nayak KS. Accelerated 3D MRI of vocal tract shaping using compressed sensing and parallel imaging. Proc. ICASSP; Apr. 2009. [Google Scholar]
- 15.Foldvik AK, Kristiansen U, Kvaerness J. A time-evolving three-dimensional vocal tract model by means of magnetic resonance imaging (MRI). EUROSPEECH 1993; Sep. 1993. [Google Scholar]
- 16.Masaki S, Tiede MK, Honda K, Shimada Y, Fujimoto I, Nakamura Y, Ninomiya N. MRI-based speech production study using a synchronized sampling method. J Acoust Soc Jpn E. 1999;20(5):375–379. [Google Scholar]
- 17.Stone M, Davis EP, Douglas AS, Nessaiver M, Gullapalli R, Levine WS, Lundberg A. Modeling the motion of the internal tongue from tagged cine-MRI images. J Acoust Soc Am. 2001 Jun;109:2974–2982. doi: 10.1121/1.1344163. [DOI] [PubMed] [Google Scholar]
- 18.Demolin D, Metens T, Soquet A. Real time MRI and articulatory coordinates in vowels speech production. Proc. Speech Production Seminar; 2000. pp. 86–93. [Google Scholar]
- 19.Narayanan SS, Nayak KS, Lee S, Sethy A, Byrd D. An approach to real-time magnetic resonance imaging for speech production. J Acoust Soc Am. 2004 Apr;115:1771–1776. doi: 10.1121/1.1652588. [DOI] [PubMed] [Google Scholar]
- 20.Bresch E, Kim Y, Nayak KS, Byrd D, Narayanan SS. Seeing speech: capturing vocal tract shaping using real-time magnetic resonance imaging. IEEE Sig Proc Mag. 2008 May;25:123–132. [Google Scholar]
- 21.Engwall O. Combining MRI, EMA and EPG measurements in a three-dimensional tongue model. Speech Communication. 2003 Oct;41:303–329. [Google Scholar]
- 22.Badin P, Bailly G, Revéret L, Baciu M, Segebarth C, Savariaux C. Three-dimensional linear articulatory modeling of tongue, lips and face, based on MRI and video images. J Phon. 2002 Jul;30:533–553. [Google Scholar]
- 23.Yang C, Stone M. Dynamic programming method for temporal registration of three-dimensional tongue surface motion from multiple utterances. Speech Communication. 2002 Sep;38:201–209. [Google Scholar]
- 24.Takemoto H, Honda K, Masaki S, Shimada Y, Fujimoto I. Measurement of temporal changes in vocal tract area function from 3D cine-MRI data. J Acoust Soc Am. 2006 Feb;119:1037–1049. doi: 10.1121/1.2151823. [DOI] [PubMed] [Google Scholar]
- 25.Zhu Y, Kim Y-C, Proctor MI, Narayanan SS, Nayak KS. Dynamic 3D visualization of vocal tract shaping during speech. Proc. ISMRM; 2011. p. 4355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bresch E, Riggs D, Goldstein L, Byrd D, Lee S, Narayanan SS. An analysis of vocal tract shaping in English sibilant fricatives using real-time magnetic resonance imaging. INTERSPEECH 2008; 2008. pp. 2823–2826. [Google Scholar]
- 27.Lee S, Bresch E, Adams J, Kazemzadeh A, Narayanan SS. A study of emotional speech articulation using a fast magnetic resonance imaging technique. INTERSPEECH 2006; 2006. pp. 1792–1795. [Google Scholar]
- 28.Bresch E, Nielsen J, Nayak KS, Narayanan SS. Synchronized and noise-robust audio recordings during realtime magnetic resonance imaging scans. J Acoust Soc Am. 2006 Oct;120:1791–1794. doi: 10.1121/1.2335423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Huang X, Acero A, Hon H. Spoken language processing: A guide to theory, algorithm, and system development. Prentice-Hall; 2001. [Google Scholar]
- 30.Rabiner L, Juang BH. Fundamentals of speech recognition. Prentice-Hall; 1993. [Google Scholar]
- 31.Santos JM, Wright G, Yang P, Pauly JM. Adaptive architecture for real-time imaging systems. Proc. ISMRM; 2002. p. 468. [Google Scholar]
- 32.Salvador S, Chan P. Toward accurate dynamic time warping in linear time and space. KDD Workshop; 2004. pp. 70–80. [Google Scholar]
- 33.Sakoe H, Chiba S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans Acoust Speech and Sig Proc. 1978;ASSP-26:43–49. [Google Scholar]
- 34.Itakura F. Minimum prediction residual principle applied to speech recognition. IEEE Trans Acoust Speech and Sig Proc. 1975;ASSP-23:52–72. [Google Scholar]
- 35.Chu S, Keogh E, Hart D, Pazzani M. Iterative deepening dynamic time warping for time series. In Proc. 2nd SIAM Inter. Conf. Data Mining; 2002. [Google Scholar]
- 36.Keogh E. Exact indexing of dynamic time warping. In VLDB. 2002:406–417. [Google Scholar]
- 37.Mady K, Sader R, Zimmermann A, Hoole P, Beer A, Zeilhofer HF, Hannig C. Use of real-time MRI in assessment of consonant articulation before and after tongue surgery and tongue reconstruction. In: Maassen B, Hulstijn W, Kent R, Peters H, van Lieshout P, editors. Speech Motor Control in Normal and Disordered Speech; 4th Inter. Speech Motor Conf.; 2001. pp. 142–145. [Google Scholar]