Abstract
Microenvironmental mechanics play an important role in determining the morphology, traction, migration, proliferation, and differentiation of cells. A stochastic motor-clutch model has been proposed to describe this stiffness sensitivity. In this work, we present a master equation-based ordinary differential equation (ODE) description of the motor-clutch model, from which we derive an analytical expression to for a cell’s optimum stiffness (i.e. the stiffness at which the traction force is maximal). This analytical expression provides insight into the requirements for stiffness sensing by establishing fundamental relationships between the key controlling cell-specific parameters. We find that the fundamental controlling parameters are the numbers of motors and clutches (constrained to be nearly equal), and the time scale of the on-off kinetics of the clutches (constrained to favor clutch binding over clutch unbinding). Both the ODE solution and the analytical expression show good agreement with Monte Carlo motor-clutch output, and reduce computation time by several orders of magnitude, which potentially enables long time scale behaviors (hours-days) to be studied computationally in an efficient manner. The ODE solution and the analytical expression may be incorporated into larger scale models of cellular behavior to bridge the gap from molecular time scales to cellular and tissue time scales.
Introduction
Many models of cell migration and force transmission implement stochastic simulation methods because they deal with small numbers of molecules1,2 or treat single cells as black box particles3. However, stochastic simulations are more computationally intensive than deterministic ones because the stochastic simulations must be run many times to produce the mean system behavior. If we desire to cross scales from molecular scale models to molecularly detailed whole-cell models, we must find a way to bridge between the molecular scale and the cellular scale. In addition, a mean-field treatment naturally lends itself to dimensional analysis and identification of key parameter groupings that dictate system behavior and regimes.
One stochastic model of cell force transmission based on the motor-clutch hypothesis4 was presented by Chan and Odde5 (Fig. 1). Briefly, this model includes molecular motors which transport F-actin retrogradely from the leading edge via a force-velocity relationship. Molecular clutches bind the F-actin to the microenvironment outside the cell. These clutches stochastically bind at a constant rate and unbind according to a force-dependent Bell model6. Importantly, this implementation of the motor-clutch hypothesis shows tunable sensitivity to the microenvironmental mechanics around the cell5,7, complementing experimental results showing stiffness-sensitive cell morphology8,9, migration10,11,12,13, and traction10,14.
Figure 1. Motor-clutch model.
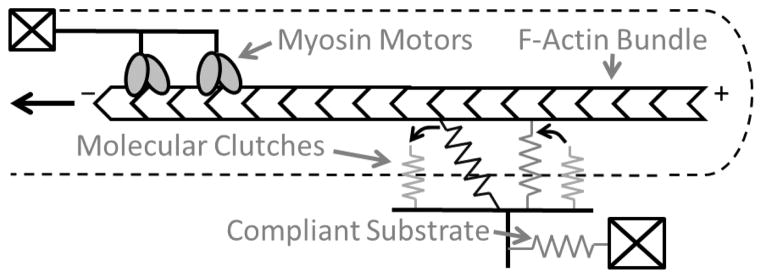
The motor-clutch model describes the transmission of force from myosin motors through F-actin and molecular clutches to a compliant substrate. The myosin motors retract F-actin retrogradely while the molecular clutches and compliant substrate, each modeled as springs, resist this motion. Clutches bind at a constant rate and unbind at a rate increasing with tension. The F-actin bundle/network is treated as inextensible, so that the spatial positions of clutches along the F-actin do not affect the model force balance. Note that although clutch failure is shown as occurring intracellularly, the model does not specifically require this to be the case and applies equally to failure on the extracellular interface between clutches and the substrate.
When modeling many cellular adhesions over an F-actin network or an entire migrating cell, it may be unnecessary to model the dynamics of every individual molecular clutch. Instead, the average dynamics of a motor-clutch module may be sufficient when describing larger-scale events like whole-cell migration. It may also be helpful to utilize an analytical expression for cell optimum stiffness as it relates to molecular-level quantities. In this study, we present a mean-field treatment of an ordinary differential equation (ODE) description of the stochastic motor-clutch model, which may in turn be used to bridge the gap between molecular time scales and cellular time scales. While not as accurate as the stochastic output, this new model solution may possibly be incorporated into a multi-scale model to describe F-actin networks or whole-cell migration, while reducing computational intensity. From our master equation approach, we have now derived an explicit analytical expression for the optimum stiffness (i.e. the substrate stiffness at which traction force is maximal) as a function of the motor-clutch parameters and have also derived a dimensionless number that defines the optimum.
Model Description
Single clutch equations
In the stochastic motor-clutch simulation, clutch binding and unbinding events are calculated using a Gillespie Stochastic Simulation Algorithm15,7 also known as Kinetic Monte Carlo. In the following master equation approach, calculation of individual binding and unbinding events is discarded in favor of calculating the probability that a clutch is bound or unbound at any given time. The change over time in the probability that the ith clutch is bound (pb,i) is given by the master equation in Equation 1.
| (1) |
The clutch can exist in two states, bound or unbound, with respective probabilities pb,i and 1-pb,i. An unbound clutch transitions into the bound state at rate kon, and a bound clutch transitions into the unbound state at rate . The value of at any time depends on the current force on the clutch, and is calculated from the following algebraic Equations 2,4–6.
Equation 2 is a Hooke’s Law relating the force on the ith clutch (Fc,i) to the extension of the clutch through the clutch spring constant (κc).
| (2) |
The position of the substrate (xs) defines one end of the clutch, while the position of the clutch bond to actin (xc,i) defines the other end. Note that the model is formulated in one spatial dimension for simplicity, although in principle it can be generalized to two and three dimensions.
The substrate position is calculated through an elastic force balance between the clutch ensemble force and the substrate spring force which sum to zero, given by Equation 3 where κs is the substrate spring constant and nc is the number of clutches.
| (3) |
In the case of the Monte Carlo simulation, the summation in Equation 3 may equivalently include only the bound clutches because the unbound clutches have zero extension and do not contribute to the force sum. However, in the current mean-field treatment, no individual clutch is either bound or unbound. Each clutch merely has a probability of being bound or unbound. Therefore, we maintain the summation over all clutches, because all clutches have some probabilistic mean extension. Equation 3 may be solved for the substrate position to give Equation 4.
| (4) |
The clutch off-rate ( ) is calculated through the Bell model6 in Equation 5 where koff is the clutch unloaded off-rate and Fb is the characteristic bond rupture force.
| (5) |
Finally, the actin retrograde flow velocity (vf) is calculated through the linear force-velocity relationship in Equation 6 where vu is the unloaded velocity, nm is the number of motors, and Fm is the force per motor.
| (6) |
Unfortunately, this set of equations is insufficient to solve the system because there are six unknowns (pb,i; ; Fc,i; xc,i; xs; and vf) and only five equations. In order to solve the system, we define an equation for the velocity of the end of the ith clutch (Eqn. 7).
| (7) |
If the clutch is unbound, its end is moving at the velocity of the substrate because it has zero extension. If the clutch is bound, its end moves at the actin retrograde flow rate. The total velocity of the clutch is the sum of these two velocities weighted by the respective probabilities that the clutch is either bound or unbound.
Equations 1,2,4–7 can be used to solve for the time course behavior of a single clutch, and validation of these equations is given in the Supplementary Information. In these and all following solutions, the base parameter set from Chan and Odde5 was used unless otherwise specified (see Supplementary Table S1).
Clutch ensemble equations
To solve for the behavior of an ensemble of clutches, we can take the ensemble average of Equations 1,2,4–7. All equations except Equation 5 involve only linear operations, and we can therefore take the average by simply substituting average values for the individual clutch values of bound probability, force, position, and off-rate. This gives Equations 8–12. We also assume that the mean probability that a clutch is bound (〈pb,i〉) equals the mean proportion of clutches bound in the ensemble (Pb), similar to the ergodic hypothesis16.
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
The Bell model for the clutch off-rate (Eqn. 5) involves a non-linear exponential operation, so the mean off-rate must be calculated using the definition of the mean, i.e. integrating the product of the Bell model function and the probability density function of clutch forces f(Fc,i) over all clutch forces as shown in Equation 13.
| (13) |
The probability density function was defined to have two components, one for the unbound distribution and one for the bound distribution. Both components must be included because each clutch has some probability of being bound and another probability of being unbound. The distributions of the bound and unbound states are weighted by the respective probability of each state. An unbound clutch has zero force, so the probability density function for the unbound distribution is a delta function at force zero which appears as the first term in Equation 14. A gamma distribution was chosen to represent the bound force distribution because the shape can be made to approximate a variety of force distribution shapes by changing the gamma shape parameter. Additionally, no clutch should ever have a negative force, and the gamma distribution does not allow for negative values. This gamma distribution is the second term in Equation 14, where r is the gamma distribution shape parameter and θ is the scale parameter, both of which we estimate below.
| (14) |
We can substitute Equation 14 into Equation 13, to obtain Equation 15. Also, the limits of integration have been changed to 0 and nmFm because those are the respective minimum and maximum possible forces on a clutch.
| (15) |
Integrating Equation 15 gives Equation 16.
| (16) |
In order to avoid the physically impossible case where , we must maintain that 1/θ > 1/Fb or θ < Fb. With this constraint and assuming that nmFm ≫ Fb, Equation 16 simplifies to Equation 17.
| (17) |
In the gamma distribution, the mean of the distribution equals the product of the shape and scale parameters. In this case, the gamma distribution only applies to bound clutches. We define 〈Fc,b〉 as the mean force on the bound clutches, so 〈Fc,b〉 = θr. We can also define the mean force over all clutches as the sum of the mean force of the unbound clutches (which is zero) and the mean force of the bound clutches, each scaled by their respective proportions, so 〈Fc〉 = Pb〈Fc,b〉. With this information we can solve for the gamma distribution scale parameter in terms of 〈Fc〉 to obtain Equation 18.
| (18) |
The constraint involving θ can also now be written as 〈Fc〉 < rPbFb. This constraint is evaluated in the Supplementary Information. Substituting Equation 18 into Equation 17 gives Equation 19, the force sensitive mean off-rate, which can be solved along with the ensemble of Equations 8–12.
| (19) |
The value of the shape parameter r can be varied according to the particular situation being simulated. Equations 8–12,19 were solved simultaneously using the MATLAB ODE solver ode15s for stiff systems because the characteristic time of unbinding changes by orders of magnitude over the time evolution of the system.
Derivation of an analytical expression for optimum stiffness
As previously shown7, the optimum stiffness for cell traction occurs when the cycle time equals the amount of time needed for all clutches to bind. Because the clutches bind as a Poisson process, the expected amount of time for all nc clutches to bind is equal to the sum of the time for the first clutch to bind plus the time for the second clutch to bind, etc. This time (tbind) can be written as the summation shown in Equation 20.
| (20) |
The summation in Equation 20 is a general harmonic series which obeys the property given in Equation 21 relating to Euler’s constant (γ ≈ 0.577).
| (21) |
Therefore, for high nc, we can approximate this limit as an equality, solve for the summation and substitute it into Equation 20 to obtain Equation 22.
| (22) |
Also for high nc, ln(nc) ≫ γ so we can make a final simplification by dropping γ to obtain Equation 23.
| (23) |
In order to derive an equation for the cycle time (tcycle), we start by decomposing the actin filament velocity (vf) into two components, one related to the ensemble clutch deformation (xc), and the other related to the substrate deformation (xs). The result is shown in Equation 24.
| (24) |
As previously shown7, at the optimum substrate stiffness, the ensemble clutch stiffness is larger than the substrate stiffness. Additionally, the substrate and the clutch ensemble bear the same force, and that force is distributed over many clutches. Using these two facts, we can expect the change in the ensemble clutch deformation to be much less than the change in the substrate deformation. Applying this assumption and substituting the force-velocity relationship for vf (Eqn. 6) gives Equation 25.
| (25) |
Integrating Equation 25 with the initial condition xs(0) = 0 gives Equation 26.
| (26) |
Equation 26 asymptotically approaches its maximum value of xs,max = Fmnm/κs as time progresses. We may assume that the cycle ends when xs reaches some fraction of its maximum value, defined as (1−ε)xs,max where 0 < ε < 1. We may then substitute the cycle end condition of xs(tcycle) = (1−ε)Fmnm/κs into Equation 26 and simplify to obtain Equation 27.
| (27) |
Solving for tcycle gives Equation 28.
| (28) |
Setting Equation 28 equal to Equation 23 to obtain the optimum stiffness gives Equation 29.
| (29) |
Finally, solving for κs,opt gives Equation 30, which is an analytical expression for the optimum stiffness for cell traction.
| (30) |
The value of ε is somewhat arbitrary, but it is some small number less than one. In reality, the value of ε is probably dependent on the other parameters in the model. For our case we chose ε = 0.01. The application of Equation 30 requires that the motor-clutch system is in a stiffness sensitive regime possessing an optimum stiffness. To ensure this, parameters must be maintained within a certain range as previously shown7 and as discussed below.
Results
Clutch ensemble ODE solution matches multiple clutch Monte Carlo simulation output
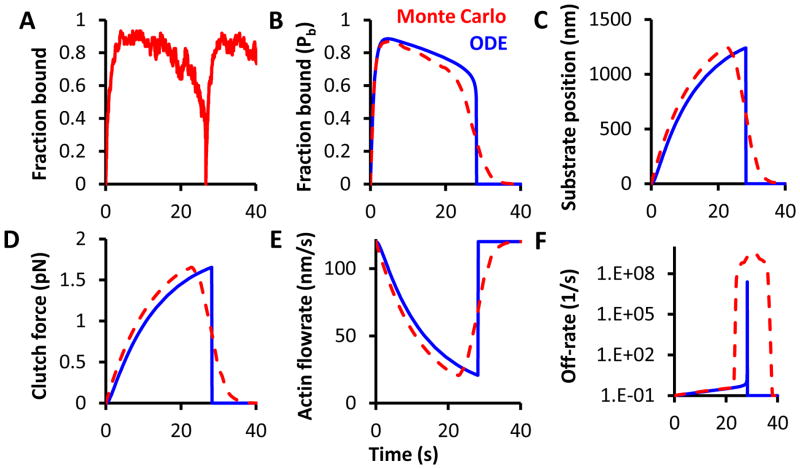
The ensemble clutch equations show good agreement with the Monte Carlo simulations for many clutches5(cite BJ). In the Monte Carlo simulation of multiple clutches, more clutches become bound as the cycle progresses until they reach a cascading failure (Fig. 2A). Figures 2B–F depict both Monte Carlo outputs and ODE solutions for the mean cycle behavior. As the bound clutches (Fig. 2B) transmit the motor force displacing the substrate (Fig. 2C), the tension builds on these clutches (Fig. 2D). Since the resisting force on the motors increases, the actin velocity slows according to the force-velocity relationship (Fig. 2E). The increasing force on the clutches also causes a sharp rise in the clutch off-rate (Fig 2F). This spike in the off-rate causes system failure, and all quantities return to their initial values (Figs. 2B–F).
Figure 2. ODE and Monte Carlo behavior of a motor-clutch load-and-fail cycle.
A) During a Monte Carlo cycle, clutches initially bind, and the fraction of clutches bound fluctuates over time. Once a sufficiently high load builds, the clutch bonds successively break resulting in failure of the system which happens near 25 s in this example. B–F) Motor-clutch model outputs are presented for both the clutch ensemble ODEs and the mean Monte Carlo simulation output. The Monte Carlo output is shown as red dashed lines while the ODE solution is shown as solid blue lines. Monte Carlo output was averaged over 1000 simulations of motor-clutch cycles. All data presented is for the base parameter values on κsub = 0.1 pN/nm.
The Monte Carlo results were averaged over 1000 simulated cycles, and r = 2 was used for the ODE force distribution shape parameter. The ODE results vary slightly from the Monte Carlo results, mainly due to the abrupt failure in the ODE solution and the gradual failure obtained from averaging over many Monte Carlo simulations. To be clear, the failure in any one Monte Carlo simulation is abrupt (Fig. 2A), but the average failure over many simulations is gradual. The abrupt failure in the ODE solution is due to a spike in the mean clutch off-rate (Fig. 2F). This spike causes a fast transition of clutches into the unbound state. The average off-rate for the Monte Carlo simulation possesses a broader peak, again because of averaging over many abrupt failure events occurring at different times.
ODE force distribution resembles Monte Carlo force distribution
We have chosen a gamma distribution to represent the distribution of forces among bound clutches at any time. Figure 3 presents the evolution of this distribution over time along with the bound clutch force distribution from the Monte Carlo output. This data was obtained on substrate stiffness κs = 0.1 pN/nm and r = 2 was used for the ODE force distribution shape parameter. At short times in both the Monte Carlo and ODE cases, few clutches are bound, and those that are have low forces. As time progresses, more clutches bind, the force on the clutches increases, and the distribution of forces becomes wider. These trends hold for both the Monte Carlo distribution of forces and the assumed gamma distribution of forces. However, the gamma distribution remains tighter than the Monte Carlo output, indicating there is a larger variance in clutch forces than predicted by the gamma distribution. The variance in the gamma distribution of forces equals rθ2, so the distribution may be broadened by increasing the shape parameter, r. However, increasing r also increases the cycle time (see Supplemental Information), which may lead to less accurate results. Overall, the gamma distribution provides a reasonable first approximation to the force distribution.
Figure 3. Force distribution on molecular clutches.
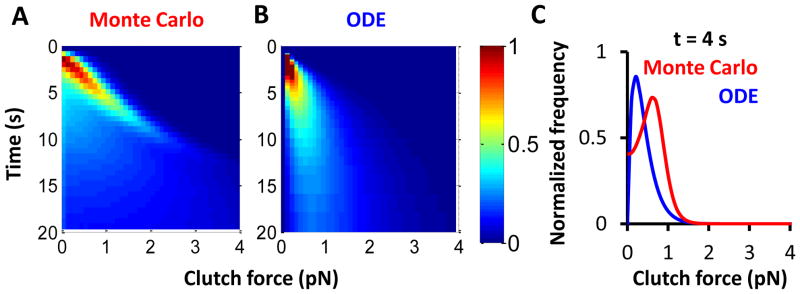
A) and B) each present two-dimensional histograms of clutch forces over time for both Monte Carlo and ODE motor-clutch cycles. The color coding indicates the frequency of observation. At short times, low clutch forces are frequent, but this distribution broadens over time. The mode also shifts to higher forces as time progresses. The gamma distribution used for the ODE solution maintains a tighter distribution than the output of the Monte Carlo simulations. Monte Carlo simulations were run for 10,000 cycles to obtain the distribution, and the ODE solution is for r = 2. C) Cross-sections of both force distributions at t = 4 s show good qualitative agreement, but again the ODE solution distribution is tighter than the Monte Carlo output.
Clutch ensemble equations show shift in stiffness optimum
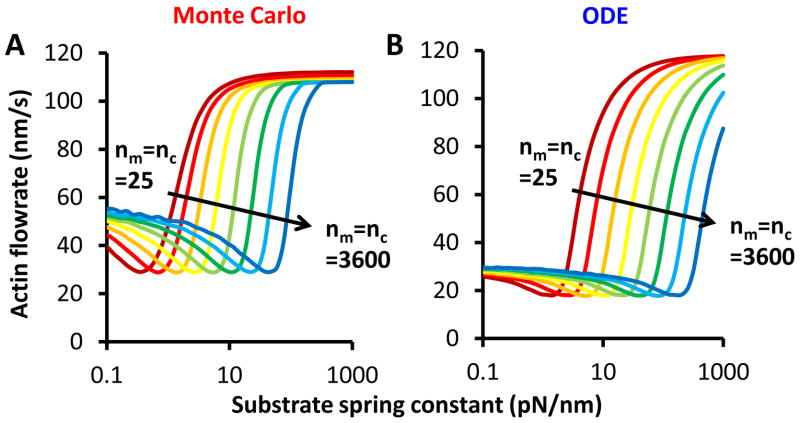
Tunability of the optimum stiffness was a key finding of the Monte Carlo simulated motor-clutch model7. As shown in Figure 4, the ODE solution captures this behavior of the Monte Carlo output. When coordinately increasing the numbers of motors and clutches, optimum stiffness shifts to higher values7. The ODE solution maintains this prediction. However, the optimum is not as pronounced for the ODE solution as it is for the Monte Carlo output, and the ODE solution optimum is shifted slightly higher. This is likely due to the complexity of the force distribution of clutches. The Monte Carlo output of frictional slippage due to rebinding on soft substrates may account for a change in the distribution that is not captured in the ODE solution. Overall, the ODE model provides a reasonable approximation of the qualitative response of the motor-clutch system to varying substrate stiffness, and in particular reproduces the biphasic response to substrate stiffness.
Figure 4. Shifting the optimum stiffness.
A) The Monte Carlo simulations produce a tunable optimum (cite BJ) which should be reproduced by the ODE solution. Increasing the numbers of motors and clutches from 25 to 3600 shifts the optimum stiffness (characterized by the minimum actin flow rate) from 0.4 pN/nm to 50 pN/nm. Monte Carlo actin flow was averaged over 106 events on each stiffness. B) The ODE solutions also produce an optimum stiffness, but the actin flow curves are shaped slightly differently than for the Monte Carlo output. Over the same change in motors and clutches, the optimum shifts from 1 pN/nm to 200 pN/nm, meaning that the use of the ODE solution may slightly over-predict the optimum stiffness. ODE solutions were obtained using r = 3.
Analytical expression predicts optimum stiffness
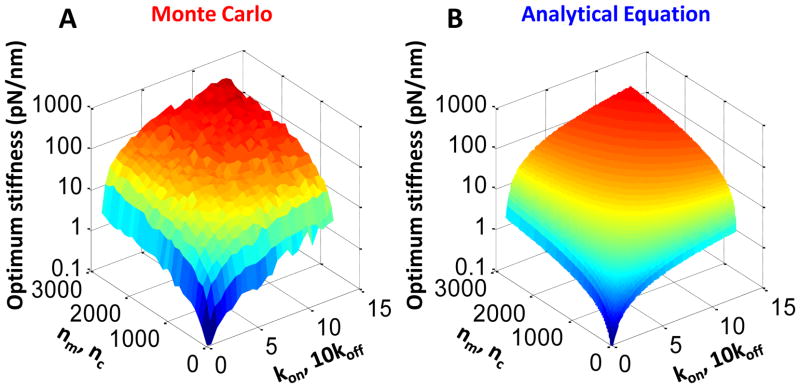
As previously shown7, parameters within the motor-clutch model must remain within a constrained parameter range in order for the system to maintain stiffness sensitivity, a requirement for possessing an optimum stiffness. Most importantly, motor parameters must be approximately balanced against clutch parameters, e.g. nm ≈ nc, Fm ≈ Fb, and kon ≈ 10koff. If the motors are too strong, the retrograde flow is nearly the unloaded motor velocity at all substrate stiffnesses, and the system lacks sensitivity to the substrate stiffness. Conversely, if the clutches are too strong, the retrograde flow is nearly zero at all substrate stiffnesses, and again the system loses stiffness sensitivity. By combining these constraints with Equation 30, a complete description of the motor-clutch optimum stiffness relating to all of the parameters can be given. Figure 5A shows optimum stiffness output from the Monte Carlo simulations while varying the numbers of motor-clutch molecules and the kinetic constants subject to the constraints that nm = nc and kon = 10koff. The analytical results obtained from Equation 30 show very good agreement with the Monte Carlo output for the same situation (Fig. 5B). Equation 30 may be used to quickly determine the optimum stiffness for a given parameter set and can quickly predict the effect of altering motor-clutch parameters on the optimum stiffness. Interestingly, only four of the motor-clutch parameters are involved in setting the optimum stiffness (Fm, nm, kon, and vu), while three of the remaining parameters (nc, Fb, and koff) must be balanced against those four in order to maintain stiffness sensitivity (see discussion for further analysis). The final parameter, κc, does not appear in the analytical expression for optimum stiffness, consistent with Monte Carlo simulations that show that clutch stiffness has little effect on the optimum stiffness7.
Figure 5. Analytical optimum stiffness.
A) Maintaining the balance of nm = nc and kon = 10koff, the parameters were altered to change the optimum stiffness of the Monte Carlo output (as defined by the stiffness at which traction force is maximum). The presented changes in these parameters result in nearly a four order of magnitude shift in the optimum stiffness. B) Again maintaining the parameter relationships of nm = nc and kon = 10koff, the analytical solution for optimum stiffness (Eqn. 30) behaves very similarly to the Monte Carlo output.
ODE calculation reduces motor-clutch computation time
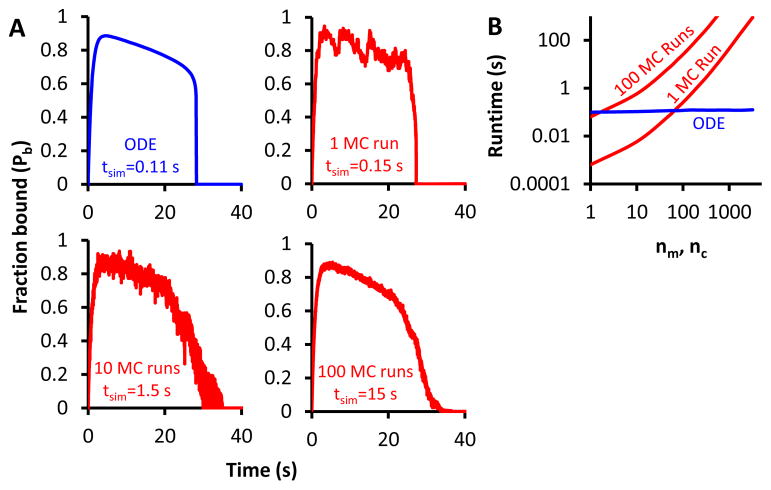
In order to determine mean behavior in the Monte Carlo simulations, they must be run many times and averaged together to smooth out fluctuations. The ODE equations must be solved only once to obtain mean behavior, potentially saving on computation time. Figure 6A compares the ODE solution and computation time to the cases of simulating 1, 10, and 100 Monte Carlo runs of a motor-clutch cycle. The time for one Monte Carlo run is similar to the time for the ODE solution, but the Monte Carlo accuracy increases with the number of runs as does the computation time.
Figure 6. Computation time for ODE and Monte Carlo simulations.
A) A single motor-clutch cycle may take vastly different times to simulate depending on the method used and accuracy desired. The ODE solution for one average cycle using the base parameters on κsub = 0.1 pN/nm takes 0.11s, while the Monte Carlo (MC) simulation time for one average cycle increases from 0.15 s to 15 s as desired accuracy increases. B) Run times for 1 and 100 Monte Carlo runs are compared to ODE solution times over varying motor and clutch parameters (maintaining the balance of nm = nc). At low motor and clutch numbers, the single-run Monte Carlo time is shorter (but may be inaccurate due to lack of averaging), and increases as motors and clutches increase. The ODE solution time remains constant regardless of the parameters used and was faster than the single-run Monte Carlo simulation time at approximately 70 clutches (balanced by 70 motors). When averaging over 100 Monte Carlo run, the ODE solution becomes faster at only 2 clutches. ODE solutions were calculated using r = 2.
It is possible that in large scale applications of the motor-clutch model, stochastic events unassociated with the motor-clutch model may be highly variable and require more significant averaging than the motor-clutch model to obtain mean behavior. In this case, averaging over motor-clutch behavior may be unnecessary, and a single Monte Carlo simulation run would be sufficient. Since a single run of the Monte Carlo simulation takes a comparable time to solving the ODEs, little is gained by abandoning the Monte Carlo method. However, if we alter the parameter sets, ODE solution again becomes faster than Monte Carlo simulation. Figure 6B shows the computation time for 1 and 100 runs of the Monte Carlo simulation and the ODE solution as we increase the number of motors and clutches. At low motor and clutch numbers, a single run of the Monte Carlo simulation is faster than the ODE solution, but the Monte Carlo run time increases as the parameters do because it must simulate every individual clutch. The ODE time remains constant because the number of clutches is simply a value input into the equations. At higher clutch numbers, the ODE solution is orders of magnitude more computationally efficient than the Monte Carlo simulation.
Discussion
This study has presented an ODE-based articulation of the motor-clutch model, as well as the derivation of an analytical expression for the optimum stiffness for cell traction mediated by a motor-clutch mechanism. The ODE solution qualitatively and approximately quantitatively captures the motor-clutch behavior observed in Monte Carlo simulations. These ODEs may be helpful in larger scale simulations (e.g. for a whole cell or an ensemble of cells) because their solution is less computationally intensive than the Monte Carlo simulation. As mentioned previously7, individual motor-clutch modules may be linked together to form larger actin networks or to simulate whole-cell migration. Since these simulations would encompass phenomena on larger spatial and temporal scales than motor-clutch dynamics, the individual clutch events are less important. These ODEs capture the average behavior of a motor-clutch module and may be sufficient to bridge the scales of molecular level clutch dynamics to larger scale actin networks and whole-cell adhesion and migration.
Insight into the clutch kinetic parameters can be gained through an order of magnitude examination of Equation 30, which may be rearranged as shown in Equation 31 for easier analysis where the number of motors and the number of clutches are both represented by n because nm ≈ nc to avoid situations where either the motors or the clutches dominate (see above).
| (31) |
The first quantity, Fm/vu, pertains to the motors, and is constrained to a relatively narrow range of values based on experimental observations of myosin molecular motors. Specifically, Fm has been found to be on the order of 1 pN17 and is constrained by the energy from ATP hydrolysis expended over nanometers-scale step sizes18, while vu is on the order of 0.1 μm/s5,19,20,21, so Fm/vu ≈ 10 pN-s/μm. Similar values are obtained for the force-velocity relationship of F-actin self-assembly, which may drive retrograde flow in some cases22,23. To achieve traction force on the order of 1000 pN24,25, the number of motors must be of order 1000 if each one has Fm ≈ 1 pN. In this case the second quantity, n/ln(n), is of order 100, and in any case scales approximately linearly in n due to the relatively weak log dependence of the denominator. Assuming ε = 0.01, the quantity ln(1/ε) = 4.6 which is of order 1, and has a weak log dependence (i.e. changing ε by 10-fold changes this quantity by ~2-fold). Substituting these estimates leaves us with . Therefore, to obtain an optimum substrate stiffness in the range of 1–1000 kPa11,26,27 (κs ≈ 1–1000 pN/nm)5, kon must range from 1–1000 s−1. Since koff must be about an order of magnitude less than kon7, it would range from 0.1–100 s−1.
This analysis shows that the strongest determinants of the optimum stiffness are the numbers of motors/clutches and the kinetics of the clutch binding/unbinding. By changing these parameters together, as depicted in Figure 5B, the system remains out of the stalled and free-flowing regimes, and maintains sensitivity to the stiffness of the environment. We should note that the molecular clutch is likely composed of many different molecules in an adhesion complex28, and the clutch parameters in this study represent the limiting quantities of these complexes. The on-rate refers to the limiting rate of bond formation along the adhesion, and the off-rate refers to the off-rate of the weakest bond along the adhesion, whether inside or outside of the cell. Finally, the clutch stiffness also refers to the stiffness of the weakest part of the adhesion.
Equation 31 also lends itself to a new dimensionless number (Ncr) by dividing the substrate stiffness, κs, by the optimum stiffness, i.e. Ncr = κs/κs,opt. The resulting dimensionless quantity is given in Equation 32 where k = kon = 10koff, and ln(1/ε) is assumed to be order 1.
| (32) |
When Ncr = 1, the motor-clutch system is on its optimum substrate stiffness. If Ncr > 1, the substrate stiffness is above the optimum, but the system is still stiffness sensitive until Ncr ≫ 1, at which point the system is in the high stiffness frictional slippage regime. If Ncr < 1, the system is in the low stiffness frictional slippage regime7. The dimensionless number Ncr describes the motor-clutch behavior on a given substrate stiffness, and may be used to quickly define the motor-clutch regime of a system.
It is suspected that the deviations of the ODE solution from the Monte Carlo output are due to the imposed clutch force distribution, in particular the choice of the shape parameter r. A constant value of r is used for all ODE solutions, regardless of other parameters, substrate stiffness, or time. In reality, the value of r may be dependent on the parameter set used and on the substrate stiffness. Moreover, the value of r may be changing in time as a cycle progresses. Future work on this model may determine the dependence of r on the model parameters and its evolution in time.
This motor-clutch model is advantageous because it is stiffness sensitive, allows load and fail dynamics, and employs a force velocity relationship for actin flow. Another model of adhesion allows load and fail dynamics, but imposes an empirical stiffness sensitivity29. A whole cell actomyosin and adhesion model has also been presented, but does not include stiffness sensitivity, load and fail dynamics, or the force-velocity relationship30. Aspects of these and other models such as actin dynamics30,31, membrane tension32,33, and adhesion formation and maturation2,34,35 could be incorporated to provide further insight into actomyosin, adhesion complex, and membrane behavior. For example, the individual clutch molecules could be included, each with its own kinetic rates and spring constant to better describe adhesion formation and maturation. Actin polymerization against an additional membrane force could be added to the actin velocity calculation. Finally, individual motor-clutch modules described by the presented ODEs could be coupled together to describe larger actin network behavior36. These actin, adhesion, and membrane properties could be important if the ODEs are to be integrated into larger-scale cell migration simulations. Inclusion of these properties could also be important in the analytical Equation 30 because they likely affect the motor-clutch cycle time. However, the added complexity would slow the computation and may be unnecessary to capture average cellular scale behavior.
The ODEs presented in this paper, which are based on a master equation approach, may be used to bridge scales from molecular level adhesion dynamics to larger-scale actin network behavior and whole-cell migration simulations. These simulations could become computationally intensive as multiple motor-clutch modules would be involved and averaging of many simulations would be required. The ODEs bypass this computational hurdle and may be integrated into these complex models to provide quick, accurate results relating to cell adhesion, morphology, and migration.
Supplementary Material
References
- 1.Gao H, Qian J, Chen B. Probing mechanical principles of focal contacts in cell-matrix adhesion with a coupled stochastic-elastic modelling framework. Journal of the Royal Society, Interface. 2011;8:1217–32. doi: 10.1098/rsif.2011.0157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Paszek MJ, Boettiger D, Weaver VM, Hammer Da. Integrin clustering is driven by mechanical resistance from the glycocalyx and the substrate. PLoS Computational Biology. 2009;5:e1000604. doi: 10.1371/journal.pcbi.1000604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dickinson RB, Tranquillo RT. A stochastic model for adhesion-mediated cell random motility and haptotaxis. Journal of Mathematical Biology. 1993;31:563–600. doi: 10.1007/BF00161199. [DOI] [PubMed] [Google Scholar]
- 4.Mitchison T, Kirschner M. Cytoskeletal dynamics and nerve growth. Neuron. 1988;1:761. doi: 10.1016/0896-6273(88)90124-9. [DOI] [PubMed] [Google Scholar]
- 5.Chan CE, Odde DJ. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–91. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- 6.Bell GI. Models for the specific adhesion of cells to cells. Science. 1978;200:618–27. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 7.Bangasser BL, Rosenfeld SS, Odde DJ. Determinants of Maximal Force Transmission in a Motor-Clutch Model of Cell Traction in a Compliant Microenvironment. Biophysical Journal. 2013;105:581–92. doi: 10.1016/j.bpj.2013.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ulrich TA, de Juan Pardo EM, Kumar S. The mechanical rigidity of the extracellular matrix regulates the structure, motility, and proliferation of glioma cells. Cancer Research. 2009;69:4167–74. doi: 10.1158/0008-5472.CAN-08-4859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Thomas TW, DiMilla PA. Spreading and motility of human glioblastoma cells on sheets of silicone rubber depend on substratum compliance. Medical & Biological Engineering & Computing. 2000;38:360–70. doi: 10.1007/BF02347059. [DOI] [PubMed] [Google Scholar]
- 10.Lo CM, Wang HB, Dembo M, Wang YL. Cell movement is guided by the rigidity of the substrate. Biophysical Journal. 2000;79:144–52. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Peyton SR, Putnam AJ. Extracellular matrix rigidity governs smooth muscle cell motility in a biphasic fashion. Journal of Cellular Physiology. 2005;204:198–209. doi: 10.1002/jcp.20274. [DOI] [PubMed] [Google Scholar]
- 12.Isenberg BC, DiMilla PA, Walker M, Kim S, Wong JY. Vascular smooth muscle cell durotaxis depends on substrate stiffness gradient strength. Biophysical Journal. 2009;97:1313–22. doi: 10.1016/j.bpj.2009.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ng MR, Besser A, Danuser G, Brugge JS. Substrate stiffness regulates cadherin-dependent collective migration through myosin-II contractility. The Journal of Cell Biology. 2012;199:545–63. doi: 10.1083/jcb.201207148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Califano JP, Reinhart-King CA. Substrate stiffness and cell area predict cellular traction stresses in single cells and cells in contact. Cellular and Molecular Bioengineering. 2010;3:68–75. doi: 10.1007/s12195-010-0102-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gillespie DT. Exact Stochastic Simulation of Coupled Chemical Reactions. The Journal of Physical Chemistry. 1977;81:2340–61. [Google Scholar]
- 16.Kaznessis YN. Statistical Thermodynamics and Stochastic Kinetics: An Introduction for Engineers. Cambridge University Press; 2012. [Google Scholar]
- 17.Molloy JE, Burns JE, Kendrick-Jones J, Tregear RT, White DCS. Movement and force produced by a single myosin head. Nature. 1995;378:209–12. doi: 10.1038/378209a0. [DOI] [PubMed] [Google Scholar]
- 18.Kolomeisky AB, Fisher ME. Molecular motors: a theorist’s perspective. Annual Review of Physical Chemistry. 2007;58:675–95. doi: 10.1146/annurev.physchem.58.032806.104532. [DOI] [PubMed] [Google Scholar]
- 19.Cuda G, Pate E, Cooke R, Sellers JR. In vitro actin filament sliding velocities produced by mixtures of different types of myosin. Biophysical Journal. 1997;72:1767–79. doi: 10.1016/S0006-3495(97)78823-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gardel ML, Sabass B, Ji L, Danuser G, Schwarz US, Waterman CM. Traction stress in focal adhesions correlates biphasically with actin retrograde flow speed. The Journal of Cell Biology. 2008;183:999–1005. doi: 10.1083/jcb.200810060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vallotton P, Danuser G, Bohnet S, Meister JJ, Verkhovsky AB. Tracking retrograde flow in keratocytes: news from the front. Molecular Biology of the Cell. 2005;16:1223–31. doi: 10.1091/mbc.E04-07-0615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Dickinson RB, Caro L, Purich DL. Force generation by cytoskeletal filament end-tracking proteins. Biophysical Journal. 2004;87:2838–54. doi: 10.1529/biophysj.104.045211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Craig EM, Van Goor D, Forscher P, Mogilner A. Membrane Tension, Myosin Force, and Actin Turnover Maintain Actin Treadmill in the Nerve Growth Cone. Biophysical Journal. 2012;102:1503–13. doi: 10.1016/j.bpj.2012.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bridgman PC, Dave S, Asnes CF, Tullio AN, Adelstein RS. Myosin IIB is Required for Growth Cone Motility. The Journal of Neuroscience. 2001;21:6159–69. doi: 10.1523/JNEUROSCI.21-16-06159.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ricart BG, Yang MT, Hunter CA, Chen CS, Hammer DA. Measuring Traction Forces of Motile Dendritic Cells on Micropost Arrays. Biophysical Journal. 2011;101:2620–8. doi: 10.1016/j.bpj.2011.09.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Stroka KM, Aranda-Espinoza H. Neutrophils display biphasic relationship between migration and substrate stiffness. Cell Motility and the Cytoskeleton. 2009;66:328–41. doi: 10.1002/cm.20363. [DOI] [PubMed] [Google Scholar]
- 27.Pathak A, Kumar S. Biophysical regulation of tumor cell invasion: moving beyond matrix stiffness. Integrative Biology: Quantitative Biosciences from Nano to Macro. 2011:267–78. doi: 10.1039/c0ib00095g. [DOI] [PubMed] [Google Scholar]
- 28.Kanchanawong P, Shtengel G, Pasapera AM, Ramko EB, Davidson MW, Hess HF, Waterman CM. Nanoscale architecture of integrin-based cell adhesions. Nature. 2010;468:580–4. doi: 10.1038/nature09621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Shemesh T, Bershadsky AD, Kozlov MM. Physical Model for Self-Organization of Actin Cytoskeleton and Adhesion Complexes at the Cell Front. Biophysical Journal. 2012;102:1746–56. doi: 10.1016/j.bpj.2012.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Barnhart EL, Lee KC, Keren K, Mogilner A, Theriot JA. An Adhesion-Dependent Switch between Mechanisms That Determine Motile Cell Shape. PLoS Biology. 2011;9:e1001059. doi: 10.1371/journal.pbio.1001059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shao D, Levine H, Rappel W-J. Coupling actin flow, adhesion, and morphology in a computational cell motility model. Proceedings of the National Academy of Sciences of the United States of America; 2012; 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Enculescu M, Sabouri-Ghomi M, Danuser G, Falcke M. Modeling of protrusion phenotypes driven by the actin-membrane interaction. Biophysical Journal. 2010;98:1571–81. doi: 10.1016/j.bpj.2009.12.4311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mogilner A, Oster G. Cell motility driven by actin polymerization. Biophysical Journal. 1996;71:3030–45. doi: 10.1016/S0006-3495(96)79496-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Macdonald A, Horwitz AR, Lauffenburger DA. Kinetic model for lamellipodal actin-integrin “clutch” dynamics. Cell Adhesion & Migration. 2008;2:95–105. doi: 10.4161/cam.2.2.6210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Walcott S, Kim DH, Wirtz D, Sun SX. Nucleation and decay initiation are the stiffness-sensitive phases of focal adhesion maturation. Biophysical Journal. 2011;101:2919–28. doi: 10.1016/j.bpj.2011.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Walcott S, Sun SX. A mechanical model of actin stress fiber formation and substrate elasticity sensing in adherent cells. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:7757–62. doi: 10.1073/pnas.0912739107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.