From label fusion to correspondence fusion: a new approach to unbiased groupwise registration

Abstract

Label fusion strategies are used in multi-atlas image segmentation approaches to compute a consensus segmentation of an image, given a set of candidate segmentations produced by registering the image to a set of atlases [19, 11, 8]. Effective label fusion strategies, such as local similarity-weighted voting [1, 13] substantially reduce segmentation errors compared to single-atlas segmentation. This paper extends the label fusion idea to the problem of finding correspondences across a set of images. Instead of computing a consensus segmentation, weighted voting is used to estimate a consensus coordinate map between a target image and a reference space. Two variants of the problem are considered: (1) where correspondences between a set of atlases are known and are propagated to the target image; (2) where correspondences are estimated across a set of images without prior knowledge. Evaluation in synthetic data shows that correspondences recovered by fusion methods are more accurate than those based on registration to a population template. In a 2D example in real MRI data, fusion methods result in more consistent mappings between manual segmentations of the hippocampus.

1. Introduction

Multi-atlas segmentation has emerged as a top performer in a number of difficult segmentation problems. This approach warps expert segmentations from multiple atlas images into the space of a target image using deformable registration, and combines the warped segmentations into a consensus segmentation using a label fusion strategy. This multi-atlas label fusion (MALF) approach has been shown to perform consistently better than single-atlas segmentation. Among MALF methods, those that incorporate image similarity in assigning relative weights to atlases during label fusion (e.g., [7]) tend to outperform methods that do not use similarity (majority voting [11, 8], STAPLE [19]), and methods that allow these weights to vary spatially across the target image (e.g., [1, 13, 17]) tend to outperform methods with global weighting. MALF is effective because it reduces both random and systematic errors in segmentation, the former by averaging data from multiple sources, and the latter because it reduces biases due to atlas-target dissimilarity. MALF is particularly useful for heterogeneous populations, as long as the atlas set is representative of the underlying heterogeneity. However, a limitation of MALF is its inability to estimate a pointwise correspondence map between the structures segmented in the target image and the atlas images, something that is explicitly provided by approaches based on registration to a single atlas.

Such correspondences, are, of course, essential in many applications. For example, a correspondence between segmented structures is needed to analyze functional MRI data in a structure of interest across a population. Correspondence maps can be obtained by applying shape analysis techniques to the segmented structures, but such shape-based correspondences ignore the underlying intensity information. On the other hand, using registration to a single labeled atlas or population-derived template [9, 3] provides correspondences at the cost of reduced accuracy relative to MALF. Thus, there is an acute need for a technique that shares the segmentation performance characteristics of MALF, while also providing pointwise correspondences between subjects in a population.

This paper aims to develop such a technique. It builds on the MALF framework, adapting it from the problem of label fusion to the problem of correspondence fusion: given a set of candidate mappings from the target image to a common coordinate space, weighted voting-based fusion is used to derive a consensus coordinate mapping. Two algorithms are proposed. In fusion-based correspondence propagation (FCP), one is given a set of atlases with known correspondences between all pairs of atlases, and seeks to extend this correspondence onto a new target image. Correspondence is represented by a coordinate vector at every voxel of every image, such that corresponding points on different images share the same coordinates, and such that the mapping between each image and the coordinate domain is diffeomorphic. FCP is a straightforward extension of MALF, with existing label fusion strategies applied to coordinate maps instead of label maps. To ensure that corresponding maps obtained by fusion are diffeomorphic, the fusion problem is formulated as an optimization problem and solved using the greedy approach [9]. The second approach, fusion-based groupwise correspondence (FGC), performs correspondence propagation simultaneously among a set of images, without any prior known correspondences. It serves the same purpose as population template methods [9, 3], i.e., to find pointwise correspondences across a set of images. Solving FGC for n images involves simultaneously solving n FCP problems.

We hypothesize that FCP and FGC generate better correspondences than approaches based on registering images to a population template. This hypothesis is tested on synthetic data with known correspondences, as well as in slices from real MRI data, with pairwise overlap between manual segmentations used to test correspondence quality.

2. Methods

2.1. Overview of Multi-Atlas Label Fusion

We review the MALF problem briefly. Given a set of k “atlases,” each consisting of an intensity image I_i and a manually generated label image L_i, we seek to obtain a segmentation of the target image I_T . For simplicity, we assume that the segmentation problem involves only two labels, and L_i(x) describes the probability of voxel x having the foreground label. Deformable registration is used to warp each atlas to the target image, producing a warped intensity image Î_i and a warped label image L̂_i. The task of label fusion is to derive a consensus label image L_T by combining information from the set of images {I_T, Î₁, . . . , Î_k, L̂₁, . . . , L̂_k}.

Label fusion with local similarity-weighted voting has proven particularly successful in practice. In this framework, the consensus label image is computed as

$$L_T\left(x\right)=\sum _{i=1}^k{w}_i\left(x\right){\widehat{L}}_i\left(x\right)\mathrm{subj}.\text{to}\sum _{i=1}^k{w}_i\left(x\right)=1,$$ (1)

where w_i(x) is a spatially varying weight function, typically derived from the similarity between images Î_i and I_T in the neighborhood of x. Thus, segmentations from atlases that closely resemble I_T near x are assigned a larger weight. Several weighting functions have been proposed in the literature [1, 13, 7]. For example, Artaechevarria et al. [1] proposed the following inverse polynomial weighting scheme:

$$w_i\left(x\right)=\frac{1}{Z\left(x\right)}{\left[\sum _{y\in \mathcal{N}\left(x\right)}{[I_T\left(y\right)-{\widehat{I}}_i\left(y\right)]}^2\right]}^{-\beta },$$ (2)

where Z is a normalizing constant, $\mathcal{N}\left(x\right)$ is a neighborhood of a voxel x, and β > 0 is a parameter controlling the weight distribution.

2.2. Fusion-Based Correspondence Propagation

Let {I₁ . . . I_n} be a set of atlas images with known correspondences, and let I_T be the target image. For simplicity, assume that all images have been rigidly aligned and are defined on a common domain $\Omega \in {\mathbb{R}}^d$. For each atlas i, let the known correspondence be specified by the diffeomorphic map ϕ_i : Ω → Ω, such that a point x in image I_i corresponds to the point y in image I_j if and only if ${\varphi }_i^{-1}\left(x\right)={\varphi }_j^{-1}\left(y\right)$. Conversely, for a point z ∈ Ω, ϕ_i(z) and ϕ_j(z) are corresponding points in images I_i and I_j for all i, j ∈ [1, n]. Suppose that non-linear diffeomorphic registration is performed between I (as a fixed image) and each atlas. Let ψ_i represent the resulting deformation from I_T to I_i. Then the i-th candidate correspondence map for image I_T is given by ψ^–1 ○ ϕ_i. FCP fuses these candidate maps into a single consensus correspondence map ϕ_T.

Let $w_i:\Omega \to \mathbb{R}$ be a weight map for the atlas I_i, subject to ${\sum }_{i=1}^n{w}_i\left(x\right)=1$. The weight map represents our confidence in atlas I_i being well matched to I_T in the neighborhood of a point x in I_T. These weight maps are computed in the same way as in similarity-weighted MALF methods above, i.e., w_i(x) is a function of intensity similarity between I_i ○ ψ_i and I_T, computed in the neighborhood of x. Our formulation is agnostic to exactly how w_i(x) is computed, and a specific choice is discussed later in Sec. 2.5.2.

Following the logic of label fusion, we want the inverse consensus correspondence map ${\varphi }_T^{-1}$ to be as close as possible to the weighted sum of the inverse candidate correspondence maps $\{{\varphi }_i^{-1}\circ {\psi }_i\}$, with weighting provided by {w_i}. To ensure that ϕ_T is diffeomorphic, we solve

$${\varphi }_T^{\ast }=\underset{{\varphi }_T\in \mathrm{Diff}\left(\Omega \right)}{\arg \min }{\Vert {\varphi }_T^{-1}-\sum _{i=1}^n{w}_i\cdot {\varphi }_i^{-1}\circ {\psi }_i\Vert }_{L^2}^2+\rho \left({\varphi }_T\right),$$ (3)

where Diff(Ω) is the group of diffeomorphic maps on Ω, ∥. . .∥_L² is the standard L² norm, and ρ is some spatial regularization term, e.g., favoring smooth deformations.

Minimization (3) can be solved using existing tools for diffeomorphic image registration. Simply denote J_p as the image formed by the p-th component of the map ${\sum }_{i=1}^n{w}_i\cdot {\varphi }_i^{-1}\circ {\psi }_i$, and let ${\mathcal{I}}_p$ denote the p-th component of the identity map, i.e., ${\mathcal{I}}_p(x_1,\dots ,x_d)=x_p$. We must then solve the simple image registration problem

$${\varphi }_T^{\ast }=\underset{{\varphi }_T\in \mathrm{Diff}\left(\Omega \right)}{\arg \min }\sum _d{\Vert {\mathcal{I}}_d\circ {\varphi }_T^{-1}-J_d\Vert }_{L^2}^2+\rho \left({\varphi }_T\right).$$ (4)

This registration problem can be solved by any image registration tool with diffeomorphic constraints that supports the mean square difference metric and can accept multiple pairs of fixed/moving images as input. Specific implementation issues are discussed in Sec. 2.5.1.

2.3. Fusion-Based Groupwise Correspondence

Atlas sets with predefined correspondences are seldom available, and can be expensive to generate. Thus, the main focus of this paper is on leveraging MALF ideas for the computation of groupwise correspondences between a set of unannotated images. Finding such correspondences is at the heart of deformation-based morphometry. We hypothesize that by making locally similar images have locally similar correspondences, we can improve the overall correspondence between a group of images.

The FGC problem involves k images I₁, . . . , I_k defined over a common domain Ω. For each image, only the intensity information is available. We formulate the FGC problem as a set of k concurrent FCP problems (3) in which each image is treated as the target image and the remaining images are treated as atlases. As a preliminary step, image registration is performed between all pairs of images, yielding a set of transformations {ψ_ij}. Specifically, ψ_ij is the transformation that is used to optimally warp image I_j into the space of image I_i, according to the chosen registration method. Next, for each image i, we compute a set of weight maps {w_ij}, satisfying ${\sum }_{j=1}^k{w}_{ij}\left(x\right)=1$. For each i and j, w_ij(x) reflects the local similarity between image I_i and the warped image I_j ○ ψ_ij near x, according to some weighting strategy (the specific choice for this paper is given in Sec. 2.5.2). To simplify the subsequent expressions, let w_ii(x) = 0 and let ψ_ii(x) = x for all i and x.

FGC seeks to find a set of diffeomorphic transformations {ϕ_i : Ω → Ω} between a reference space and each of the k images, which minimizes the overall objective function:

$$\left\{{\varphi }_i^{\ast }\right\}=\underset{\left\{{\varphi }_i\right\}\in \mathrm{Diff}\left(\Omega \right)}{\arg \min }\sum _{i=1}^k{\Vert {\varphi }_i^{-1}-\sum _{j=1}^k{w}_{ij}\cdot {\varphi }_j^{-1}\circ {\psi }_{ij}\Vert }_{L^2}^2+\sum _{i=1}^k\rho \left({\varphi }_i\right).$$ (5)

Despite the similarity between (5) and (3), the FGC objective function in (5) can no longer be optimized using existing registration tools because it cannot be reformulated as a set of pairwise image registrations. Instead, we minimize the objective using a variational approach. Let ψ_ij(x) = x + v_ij(x) and ${\varphi }_i^{-1}=x+{\mathbf{u}}_i\left(x\right)$. Let

$${\Delta }_i={\varphi }_i^{-1}-\sum _{j=1}^k{w}_{ij}\cdot {\varphi }_j^{-1}\circ {\psi }_{ij}={\mathbf{u}}_i-\sum _{j=1}^k{w}_{ij}\cdot [{\mathbf{v}}_{ij}+{\mathbf{u}}_j\circ {\psi }_{ij}]$$ (6)

Then we may write the component of the objective function in (5) not related to regularization as

$$E({\mathbf{u}}_1,\dots ,{\mathbf{u}}_k)=\sum _{i=1}^k{\Vert {\Delta }_i\Vert }_{L^2}^2.$$ (7)

Let h_m be a variation in the displacement field u_m. The Gateaux derivative of E with respect to h_m is

$$\frac{1}{2}{\delta }_{h_m}E=\sum _{i=1}^k<{\Delta }_i,{\delta }_{h_m}{\Delta }_i>=\sum _{i=1}^k<{\Delta }_i,{\delta }_{i,m}\cdot h_m-w_{im}\cdot h_m\circ {\psi }_{im}>=<{\Delta }_m,h_m>-2\sum _{i=1}^k<{\Delta }_i,w_{im}\cdot h_m\circ {\psi }_{im}>=<{\Delta }_m-\sum _{i=1}^k({\Delta }_i\circ {\psi }_{im}^{-1})(w_{im}\circ {\psi }_{im}^{-1})\mid D{\varphi }_{im}^{-1}\mid ,h_m>,$$ (8)

where δ_i,m is the Kronecker delta and D is the Jacobian operator. From this, the gradient of E is given by

$$\frac{1}{2}{D}_{{\mathbf{u}}_m}E={\Delta }_m-\sum _{i=1}^k(w_{im}\cdot {\Delta }_i)\circ {\psi }_{im}^{-1}\cdot \mid D{\varphi }_{ij}^{-1}\mid .$$ (9)

To restrict the space of solutions to diffeomorphic transformations and to provide an implicit regularization prior, we adopt a greedy iterative strategy [9]. At the beginning, the displacement fields $\left\{{\mathbf{u}}_i^0\right\}$ are initialized at zero. At each iteration, the displacement fields are updated as

$$\Delta {\mathbf{u}}_m^t=-∊\cdot G_{\gamma }\ast D_{{\mathbf{u}}_m^t}E,$$ (10)

$${\mathbf{u}}_m^{t+1}={\mathbf{u}}_m^t\circ (\mathbf{x}+\Delta {\mathbf{u}}_m^t)+\Delta {\mathbf{u}}_m^t,$$ (11)

where ε is the step size, and G_γ is a Gaussian convolution kernel with standard deviation γ. Smoothing of the gradient with a Gaussian kernel in (10) provides implicit regularization for the deformation field. Successive composition of small deformations in (11) ensures that $\mathbf{x}+{\mathbf{u}}_m^t$ is diffeomorphic. The above iteration produces the set of transformations $\left\{{\varphi }_i^{-1}\right\}$ that minimize the energy E (plus an implicit regularization term). To obtain transformations ϕ_i, the inverse of these transformations is computed directly, using the fixed point approach in [6].

The minimization (5) is highly parallelizable and, in theory, can be implemented efficiently in a parallel environment with k compute nodes. During each iteration, Δ_i would first be computed at each node i. Then the fields {Δ_i} would be distributed across all the nodes. Next, each node would perform the update step (10,11) in parallel. Lastly, the updated fields $\left\{{\mathbf{u}}_i^{t+1}\right\}$ would be distributed across all the nodes. Overall, the greatest computational expense associated with this method comes from performing the initial set of O(k²) pairwise registrations.

2.4. Comparison Method: Population Templates

In the evaluation presented below, we compare FGC to the leading alternative approach for computing groupwise correspondence between sets of images, which, for brevity, we call the unbiased population template (UPT) approach. UPT, which was originally developed by Joshi et al. [9], constructs an unbiased, population-specific template from a set of images by iterative application of diffeomorphic registration and intensity averaging. By construction, this method provides a set of correspondences between the input images and the template. Our implementation of UPT is based on subsequent work by Avants et al. [3], which includes a shape averaging step and allows the use of the cross-correlation image match metric for similarity computation during diffeomorphic registration.

2.5. Implementation Details

2.5.1 Registration

All pairwise registrations between images are performed using the greedy diffeomorphic Symmetric Normalization (SyN) algorithm [2], implemented as part of the open-source ANTS software package. SyN registrations used the cross-correlation metric with a 9 × 9 window; 3 resolution levels with maximum 50 iterations per level; step size 0.25; Gaussian regularization with standard deviation of 3 pixels. Our UPT implementation uses SyN and the accompanying ANTS scripts for unbiased atlas construction.

2.5.2 Weight Maps

Weight maps, i.e., the term w_i in (3) and the term w_ij in (5), were generated using a rank-based scheme proposed by [20]. As before, let I_T be the target image, and let Î₁ . . . Î_k be a set of k images registered to I_T. Let ν_i(x) denote the similarity map between Î_i and I_T. We use normalized cross-correlation over a 9 × 9 pixel neighborhood as the local similarity measure. Let ρ_i(x) be the local rank of the image Î_i in terms of similarity:

$${\rho }_i\left(x\right)=\mid \{j\in [1,k]:{\nu }_j\left(x\right)>{\nu }_i\left(x\right)\}\mid .$$ (12)

Then the weight function is given as

$$w_i\left(x\right)=\left[\frac{1}{Z}{e}^{-\alpha {\rho }_i\left(x\right)}\right]\ast G_{\sigma }\left(x\right),$$ (13)

where $Z={\sum }_{i=1}^k{e}^{-\alpha k}$ is a normalization constant, G_σ is the Gaussian convolution kernel with standard deviation σ. Parameter α controls bias towards best-matching atlases in the weighting, and σ controls the spatial regularization of the weight map. This paper uses α = 0.5 and σ = 1.2 (in pixel units). The appeal of this rank-based weighting scheme is that the weights are not affected by absolute values of the similarity metric, presumably making the scheme application-independent. However, note that any of the many spatially-varying, similarity-weighted label fusion schemes proposed recently (e.g., [1, 13]) could also be used instead.

3. Experiments

3.1. Simulated Data

Simulated 2D datasets are constructed to evaluate the FCP (Sec. 2.2) and FGC (Sec. 2.3) algorithms using known true correspondences. A high-resolution (512 × 512 pixels) image of a histological slice of the hippocampus (Figure 1) is randomly deformed to generate simulated images. The i-th random deformation is constructed by generating a random time-varying velocity field V_i(x, t), with t ∈ [0, 1], and solving the flow ODE for the diffeomorphism ξ_i:

$$\partial {\xi }_i(x,t)∕\partial t=V_i(\xi (x,t),t);{\xi }_i(x,0)=0.$$ (14)

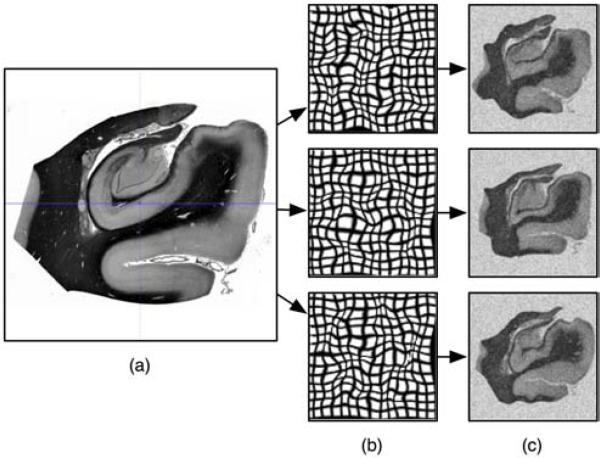
For brevity, let ξ_i(x) = ξ_i(x, 1) denote the end-point diffeomorphism. Random velocity fields are constructed as follows. A set of N_p control points is chosen randomly in the unit cube in x₁ × x₂ × t space. A random displacement is applied to the x₁ and x₂ coordinates of each point, by sampling from a zero mean isotropic normal distribution with standard deviation σ_p. Additional control points are sampled regularly from the faces of the unit cube and assigned a zero displacement. Field V_i(x, t) is computed by applying radial basis function interpolation to the control points. Parameters N_p and σ_p influence the complexity and the magnitude of the random displacement, respectively. The flow ODE (14) is solved using the semi-Lagrangian approach [4] with time step 0.04. The high-resolution image is warped by the transformation ξ^–1, resampled to 96 × 96 resolution, and corrupted by adding uncorrelated Gaussian noise with standard deviation σ_n. Examples of images obtained by this random deformation process are shown in Figure 1.

Figure 1.

Generation of synthetic images for evaluation. A high-resolution image (a) undergoes random diffeomorphic deformations (b), subsampling, and additive noise (c).

We generate 51 random simulation datasets. In order to search the parameter space uniformly and without bias, the simulation parameters, N_p, σ_p, σ_n, as well as the number of simulated images, k, are sampled randomly from uniform distributions: N_p ~ U(100, 1000), σ_p ~ U(10, 100), σ_n ~ U(0, 50), and k × U(2, 48).

3.2. FCP Evaluation in Simulated Data

FCP (3) is evaluated using a leave-one-out strategy. The q-th simulation image is treated as the target image and the other k – 1 images are treated as atlases with known correspondences to a common reference space (provided by the mappings {ξ_i}). To evaluate the accuracy of FCP for image q, the consensus correspondence mapping ϕ_q computed using (3) is compared to the ground truth correspondence mapping ξ_q. Specifically, for each point x in the q-th simulated image, ${\xi }_q^{-1}$ gives the true corresponding location in the undeformed image, and ${\varphi }_q^{-1}\left(x\right)$ gives the FCP estimate of this location. The Euclidean distance between ${\xi }_q^{-1}\left(x\right)$ and ${\varphi }_q^{-1}\left(x\right)$ is a measure of FCP error. This error is integrated over the foreground voxels in the q-th simulation image (as we are not interested in background correspondence), and averaged over all k leave-one-out experiments. This leads to the leave-one-out FCP error metric

$${\mathcal{E}}_{\mathrm{FCP}}=\frac{1}{k}\sum _{q=1}^k\frac{1}{\mid M_q\mid }{\int }_{M_q}\Vert {\varphi }_q^{-1}\left(x\right)-{\xi }_q^{-1}\left(x\right)\Vert \mathrm{d}x,$$ (15)

where M_q is the foreground region in the q-th image, and |M_q| is its area.

For comparison, we compute the average correspondence error from performing direct registration between each simulated image and the undeformed source image (Fig. 1a) resampled to 96×96 resolution. The undeformed image can be viewed as an idealized population-specific template, and correspondence error between the unper-formed image and the simulated images provides the lower bound for correspondence errors that would result from registering simulated images to a population-derived template. The error from direct registration is denoted ${\mathcal{E}}_{\mathrm{DR}}$.

Results

For brevity, we only report the results in terms of the relative improvement of FCP over direct registration:

$${\Delta }_{\mathrm{FCP}}=\frac{{\mathcal{E}}_{\mathrm{DR}}-{\mathcal{E}}_{\mathrm{FCP}}}{{\mathcal{E}}_{\mathrm{DR}}}\cdot 100\%$$ (16)

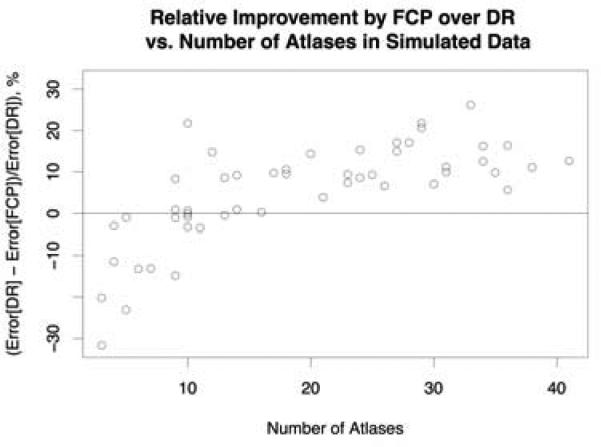
Figure 2 plots Δ_FCP against the number of atlases, k, in all 51 simulation experiments. FCP clearly underperforms DR when fewer than 10 atlases are available, but as the number of atlases increases, FCP reaches a consistent improvement. When k ≥ 16 atlases are used, Δ_FCP > 10% in 54% of experiments and Δ_FCP > 5% in 93% of experiments. Among the experiments with k ≥ 16, Δ_FCP is negatively correlated with the additive noise parameter σ_n (R = –0.64, p < 0.001), but there is no significant correlation with parameters N_p and σ_p. We conclude that, given a relatively small number of atlases, FCP consistently recovers the ground truth correspondence better than direct registration to the template.

Figure 2.

Relative improvement Δ_FCP of fusion-based correspondence propagation (FCP) over direct registration (DT) in simulated data experiments, plotted against the number of simulated atlases in each experiment, k. Positive values mean lower error with FCP.

3.3. FGC Evaluation in Simulated Data

To evaluate the group-wise FGC approach, we perform the optimization (5) among all k simulated images, yielding correspondence maps ϕ₁, . . . , ϕ_k from a common reference space to the simulated images. These recovered correspondences are correct if for each voxel x and each pair of images (i, j), we have

$${\xi }_i^{-1}\left({\varphi }_i\left(x\right)\right)={\xi }_j^{-1}\left({\varphi }_j\left(x\right)\right)$$ (17)

Note that this does not necessarily imply ϕ_i = ξ_i. Thus to define the error associated with the correspondence maps ϕ₁, . . . , ϕ_k, we can measure the degree to which (17) is violated, i.e., how far apart, on average, the points $\{{\xi }_1^{-1}\left({\varphi }_1\left(x\right)\right),\dots ,{\xi }_k^{-1}\left({\varphi }_k\left(x\right)\right)\}$ are from each other. This leads to the groupwise correspondence error metric

$${\mathcal{E}}_{GRP}=\frac{1}{k^2\mid M\mid }\cdot {\int }_M{\left[\sum _{i=1}^k\sum _{j=1}^k{\Vert {\xi }_i^{-1}\left({\varphi }_i\left(x\right)\right)-{\xi }_j^{-1}\left({\varphi }_j\left(x\right)\right)\Vert }^2\right]}^{\frac{1}{2}}\mathrm{d}x.$$ (18)

To evaluate FGC, we compare its groupwise correspondence error to that of UPT (Sec. 2.4), and our analysis focuses on their relative difference:

$${\Delta }_{\mathrm{FGC}}=\frac{{\mathcal{E}}_{\mathrm{GRP}}^{\mathrm{UPT}}-{\mathcal{E}}_{\mathrm{GRP}}^{\mathrm{FGC}}}{{\mathcal{E}}_{\mathrm{GRP}}^{\mathrm{UPT}}}\cdot 100\%.$$ (19)

Results

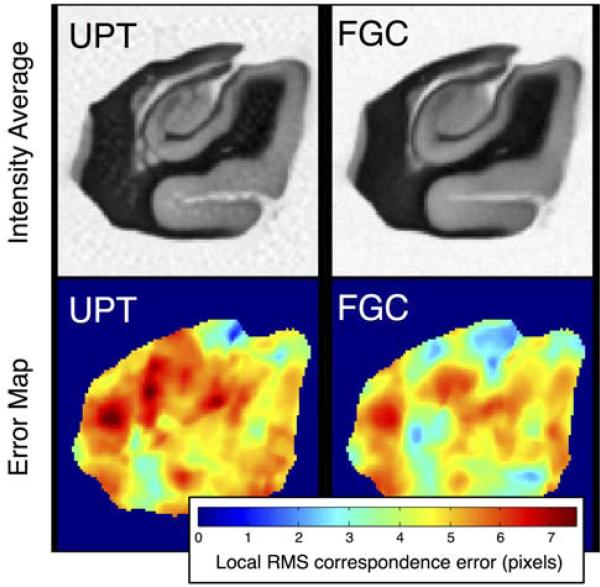
Figure 3 visualizes the correspondences and correspondence errors produced by FGC and UPT in one simulation experiment. The top row shows the mean correspondence difference maps, i.e., the integrand in (18), for the two methods, and the bottom row shows the mean intensity image computed by warping the simulated images into the common reference space and averaging their intensity. FGC produces lower correspondence error in the hippocampus, and its mean image is more crisp, and matches the undeformed image in Fig. 1a more closely.

Figure 3.

Average intensity images and pointwise local correspondence error maps computed in the common reference space after obtaining groupwise correspondences using the unbiased population template (UPT) and fusion-based (FGC) methods in one of the synthetic data experiments. The simulation experiment chosen for this figure has a very large deformation parameter value (σ_p = 90) in order to emphasize the difference between the methods.

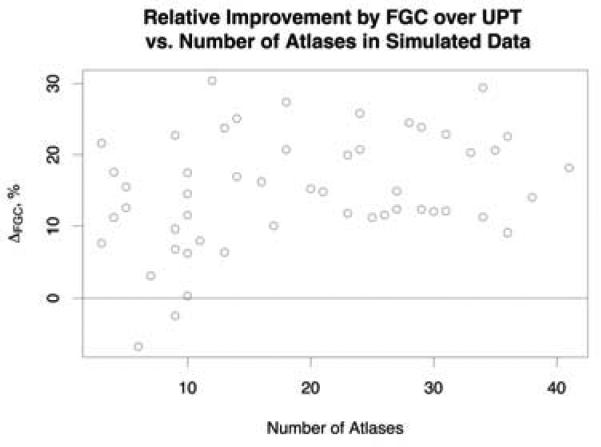
Figure 4 plots Δ_FGC against the size of the simulated image set, k, across all simulation experiments. Unlike FCP, there is little effect of k on Δ_FGC. Among all experiments, Δ_FGC > 5% in 92% of experiments, Δ_FGC > 10% in 78% of experiments, and Δ_FGC > 20% in 31% of experiments. Δ_FGC is significantly negatively correlated with σ_p (R = –0.73, p < 0.001) and positively correlated with σ_n (R = 0.35, p = 0.01). Overall, we conclude that FGC achieves consistently lower errors than UPT across all parameter values.

Figure 4.

Relative improvement of the FGC over UPT across all simulated data experiments.

3.4. FGC Evaluation in MRI Slices

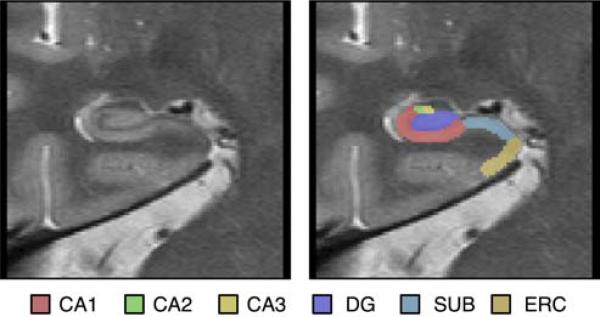
As a preliminary evaluation of FGC in real imaging data, we use it to compute groupwise correspondences between a set of 2D MRI slices from 32 subjects from a study of aging and cognitive impairment [10]. The data consists of T2-weighted MR images of the hippocampal region with highly anisotropic resolution (0.4mm × 0.4mm × 2.0mm), acquired in an oblique coronal plane angled orthogonally to the long axis of the hippocampus. Manual segmentation has been used to divide each hippocampus formation (HF) into head, tail and body regions, with the body region typically extending over 3-5 slices and partitioned into 7 subfields. For this evaluation, we extract for each subject a single slice near the center of the body of the left HF, and crop a 96 × 96 pixel region around the center of the manual segmentation. An example of such an image and its segmentation are shown in Fig. 5. We perform rigid registration to remove differences in pose between the input images. We then proceed to use the FGC and UPT methods to compute groupwise correspondences between the images.

Figure 5.

An example T2-weighted MR image of the hippocampus from the evaluation dataset, and its manual segmentation. Color labels correspond to different subfields of the hippocampus.

Lacking the availability of a “ground truth” correspondence between the images, we evaluate the groupwise correspondence by measuring how well it matches labels assigned by manual segmentation to pairs of corresponding voxels. Specifically, given correspondence maps ϕ₁ . . . ϕ_k from a common reference space to each of the input images, and given segmentation label maps L₁ . . . L_k : Ω → {0, . . . , 7}, we measure the total label agreement error

$${\mathcal{E}}_{\mathrm{LAB}}==\frac{1}{k^2\mid \Omega \mid }{\int }_{\Omega }\sum _i^k\sum _j^k\delta [L_i\left({\varphi }_i\left(x\right)\right),L_j\left({\varphi }_j\left(x\right)\right)]\mathrm{d}x,$$ (20)

where δ[•, •] is the Kronecker delta function. Underlying the use of this metric is the assumption that manual segmentation correctly identifies corresponding anatomical regions in different images.

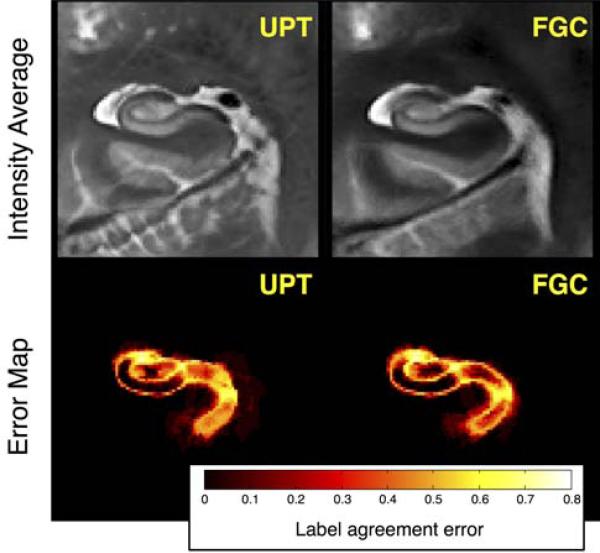
Results

Figure 6 shows the average images constructed by averaging the intensity of the input images warped into a common reference space using FCP and UPT correspondence maps, as well as the map of average pointwise label agreement error, i.e., the integrand in (20). The total label agreement error is 0.0330 for FGC and 0.0358 for UPT, i.e. the FGC error is 7.8% lower. Thus, we can conclude that the results of the real data experiment were generally consistent with the simulated data experiments.

Figure 6.

Average intensity images (top) and label agreement maps (bottom) computed from the UPT and FGC groupwise correspondences in the T2-weighted MRI dataset.

4. Discussion and Conclusions

We have presented a new approach to groupwise image correspondence derivation that uses multi-atlas registration and similarity-weighted voting-based fusion techniques, which, to our knowledge, have only been used for image segmentation until now. We have shown this fusion-based approach (FGC) to perform better than UPT in simulated and real data experiments, although the improvements in simulated data (10-20%) were greater than in the real data experiment (8%). These improvements do come at a considerable additional computational cost, since k² registrations are required as input to FGC. By contrast, UPT only performs O(mk) registrations, where m is the number of iterations, typically < 10. However, this added cost, which is similarly a drawback of MALF segmentation, has not prevented MALF from being widely adopted in the biomedical imaging field. Hence, we expect that if the error reduction demonstrated in this paper can be shown to extend to 3D imaging datasets, the proposed FGC framework would also find numerous applications in this field. Thus, our future work will focus on implementing FGC in the parallel computing environment and evaluating it in 3D image datasets.

Although our evaluation focused on a comparison with the UPT method, there are a number of other groupwise correspondence finding methods that are also available. Among the closest to our work are methods that optimize an information theoretic groupwise objective function, e.g., the congealing work of Zollei et al. [21], the minimum description length work of Twinning et al. [16], or the groupwise approaches of Studholme and Cardenas [15] and Bhatia et al. [5]. Although we cannot speak to the relative performance of FGC and these methods, we can note that the objective function minimized in FGC is substantially simpler (involving essentially quadratic forms) and that FGC has an advantage of allowing any image registration algorithm and metric to be used for pairwise image registration. A number of methods have also derived groupwise correspondences from the results of k² registrations. For instance, Seghers et al. [14] compose deformations from pairwise registrations to construct a population mean. However, this approach does not assign preferences to the pairwise registrations with greater similarity as FGC does, nor does it guarantee diffeomorphic registrations. To simplify the complexity of the O(k²) groupwise registration problem, some authors proposed hierarchical clustering approaches [18, 12]. Similar strategies could prove useful to reduce the complexity of FGC. We also note the actual label fusion strategy (13) that we use has not been extensively optimized, and more advanced label fusion strategies (e.g. [13, 1, 17] may lead to further improvements in FGC performance.

In conclusion, this paper presented a new groupwise image registration approach that uses the spatially-varying similarity-weighted voting strategy that has proven very successful in multi-atlas segmentation, to establish group-wise correspondences. In simulated and read 2D image sets, this new approach consistently improved upon unbiased population template generation, one of the leading approaches to groupwise image registration.