Fully automatic segmentation of the mitral leaflets in 3D transesophageal echocardiographic images using multi-atlas joint label fusion and deformable medial modeling

Abstract

Comprehensive visual and quantitative analysis of in vivo human mitral valve morphology is central to the diagnosis and surgical treatment of mitral valve disease. Real-time 3D transesophageal echocardiography (3D TEE) is a practical, highly informative imaging modality for examining the mitral valve in a clinical setting. To facilitate visual and quantitative 3D TEE image analysis, we describe a fully automated method for segmenting the mitral leaflets in 3D TEE image data. The algorithm integrates complementary probabilistic segmentation and shape modeling techniques (multi-atlas joint label fusion and deformable modeling with continuous medial representation) to automatically generate 3D geometric models of the mitral leaflets from 3D TEE image data. These models are unique in that they establish a shape-based coordinate system on the valves of different subjects and represent the leaflets volumetrically, as structures with locally varying thickness. In this work, expert image analysis is the gold standard for evaluating automatic segmentation. Without any user interaction, we demonstrate that the automatic segmentation method accurately captures patient-specific leaflet geometry at both systole and diastole in 3D TEE data acquired from a mixed population of subjects with normal valve morphology and mitral valve disease.

1. Introduction

In a physiologically normal state, the mitral valve maintains unidirectional blood flow across the left heart, and its geometry and mechanics are essential to proper cardiac function. The valve consists of two leaflets (anterior and posterior), a fibro-elastic ring (the annulus) which anchors the leaflets to the surrounding heart tissue, and a subvalvular apparatus comprised of chordae tendinae and papillary muscles that synchronize mitral leaflet, annular, and left ventricular wall motion.

Three dimensional transesophageal echocardiography (3D TEE) has been effectively used in both research and clinical settings to visualize and quantify mitral valve morphology and motion in vivo (Abraham et al., 1997; Ahmed et al., 2003; Grewal et al., 2009; Sugeng et al., 2008; Vergnat et al., 2011; Veronesi et al., 2006; Wei et al., 2010). Comprehensive evaluation of 3D valve morphology is essential for the diagnosis and surgical treatment of many valvular heart diseases, especially those associated with complex morphological abnormalities. Ischemic mitral regurgitation, in particular, manifests as a variable combination of distortions in valve geometry: annular dilatation and apical leaflet tethering. These distortions are patient-specific and underscore distinct pathophysiologic mechanisms and abnormalities (Kwan et al., 2003; Levine et al., 2002; Watanabe et al., 2005). 3D examination of patient-specific valve anatomy is a pre-requisite for disease characterization and selection of appropriate surgical treatment strategies. 3D TEE has been demonstrated to be a valuable tool in preoperative surgical planning (Garcia-Orta et al., 2007), intraoperative guidance (Eng et al., 2009; Swaans et al., 2009), and immediate and long-term follow-up to determine the need for further surgical intervention (De Castro et al., 2002). However, the limitation of the current commercial 3D TEE imaging platforms is that they provide visually impressive 3DE image volume renderings, but enable only a limited number of quantitative measurements to be made off-line with somewhat cumbersome user interaction. The existing 3D TEE image analysis tools are therefore impractical and inadequate for use in quantitative image-based surgical planning.

To increase the practicality and ease of mitral valve quantification with 3D TEE, several semi-automatic and one fully automatic method for mitral leaflet segmentation have been proposed (Burlina et al., 2010; Ionasec et al., 2010; Pouch et al., 2012b; Schneider et al., 2011a). The goal of these techniques is to derive quantitative measurements and 3D visualizations of annular and leaflet geometry from 3D TEE images. The methods vary in the extent of requisite user interaction and the level of detail with which the mitral leaflets are represented. Fig. 1 illustrates several of the challenges specific to mitral leaflet and annular segmentation in 3D TEE images. For one, there is no intensity-based boundary between the leaflets and adjacent heart tissue, making it difficult to identify the annulus and leaflet boundaries based in image intensity information alone. Secondly, the posterior leaflet often gets pressed against the left ventricular wall during diastole and is characterized by signal dropout, making it difficult for an automated segmentation algorithm to capture posterior leaflet geometry when the valve is open. Thirdly, the anterior and posterior leaflets are difficult to distinguish in the coaptation zone during systole since there is no intensity-based distinction between the two leaflets.

Fig. 1.

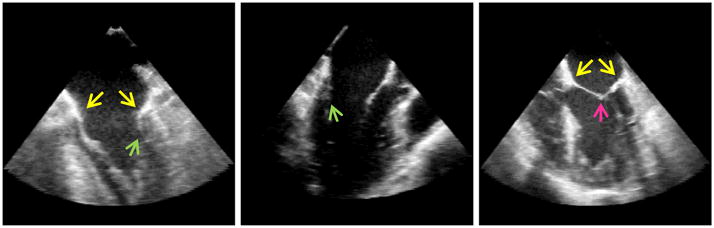
Cross-sectional images of 3D TEE image volumes at diastole (left and center) and systole (right), illustrating the challenges specific to mitral leaflet segmentation. The yellow arrows point toward points on the annulus, showing that there is no image-based boundary between the mitral leaflets and adjacent tissue to which the leaflets are attached. The green arrows point towards the posterior leaflet at diastole, which is often pressed against the ventricular wall and is characterized by signal dropout. The pink arrow points to the coaptation zone of the leaflets at systole, showing there is no intensity-based demarcation between the anterior and posterior leaflets. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

To address these challenges, Schneider et al. (2011b) present a multi-stage method for segmenting the open mitral leaflets in 3D TEE datasets, wherein the leaflets are represented by a discrete mesh. First, the mitral annulus is semi-automatically segmented (Schneider et al., 2010) and an initial leaflet search space is defined in the image volume. The search space is subsequently refined, and the leaflet surfaces are estimated using graph cut and active contour methods. This technique requires some minimal user interaction to generate patient-specific leaflet representations. Ionasec et al. (2010) describe a fully automatic technique for segmenting and tracking the aortic and mitral leaflets in computed tomography and 3D TEE data. Given a large database of manually labeled images, machine learning algorithms are used to globally locate and then track several valve landmarks throughout the cardiac cycle. Leaflet geometry is subsequently represented by a parametric model fitted through these points. While this method is fully automated and establishes correspondences, the use of sparse landmarks potentially limits patient-specific detail of leaflet geometry. The techniques described by Schneider et al. (2011b) and Ionasec et al. (2010) both represent the mitral leaflets as a single surface, rather than structures with thickness. Alternatively, Burlina et al. (2010) use 3D active contours and thin tissue detection to recover mitral leaflet geometry at end-diastole in 3D TEE image data. While this method captures detail of leaflet geometry, it requires user initialization and manual refinement. Several other techniques, largely based on manual leaflet tracing in either custom or commercial software, have also been proposed (Tsukiji et al., 2006; Vergnat et al., 2011; Veronesi et al., 2006). While these techniques provide spatially dense, expert-defined representations of leaflet and annular geometry, they are the most labor intensive methods.

Although automatic 3D quantification tools have significant implications for diagnostics and surgical care, the existing methodologies remain labor and time intensive. Methods that reduce interobserver variability in 3D TEE image analysis would maximize its practicality for use at the bedside and in the operating room (Lang and Adams, 2012). The goal of the present work is to develop an alternative leaflet segmentation method that is fully automated, captures patient-specific detail, represents the leaflets with finite thickness, and establishes correspondences on valves of different subjects. To accomplish these goals, we propose a segmentation technique that integrates probabilistic segmentation and geometric modeling techniques. These complementary methods are multi-atlas joint label fusion and deformable modeling with continuous medial representation (cm-rep).

Cm-rep is a type of shape representation that describes an object in terms of its medial geometry, i.e. a radial thickness field mapped to a skeleton, or medial axis (Pizer et al., 2003; Yushkevich et al., 2006b). The representation has been used to model various anatomical shapes, including the hippocampus (Yushkevich, 2009) and cardiac ventricles (Sun et al., 2010), and is especially useful for modeling thin, sheet-like structures. We have previously shown that cm-rep is an appropriate shape model for describing mitral leaflet and annular geometry (Pouch et al., 2012b). It establishes correspondences on different valve shapes and facilitates measurement of clinically relevant features of annular and leaflet geometry. In our earlier work, the cm-rep of a given valve shape is obtained by deforming a pre-defined template by Bayesian optimization to match a user-initialized segmentation of the leaflets (Pouch et al., 2012a,b). This user-initialized segmentation method, based on 3D active contours with region competition, requires multiple interactive steps to identify valve location in the image volume, establish boundaries between the leaflets and adjacent heart tissue, and estimate a threshold to guide region competition. In the present work, the need for user initialization is completely eliminated with the use of multi-atlas joint label fusion, which generates probabilistic segmentations that guide model fitting.

Given a target image to segment, multi-atlas joint label fusion registers a set of manually labeled atlases of the mitral leaflets to the target image and propagates the segmentation labels to this target image. Joint label fusion assigns weights to the labels of different atlases based on the similarity between the atlas and target image, as well as the similarity between different atlases (Wang et al., 2013). Although label fusion alone can generate segmentations of the mitral leaflets, the technique does not preserve leaflet topology or assign correspondences to different valve shapes. To overcome these challenges, the probabilistic segmentation obtained with joint label fusion is incorporated as the likelihood term of the objective function optimized during deformable modeling with cm-rep. In effect, a model-based Bayesian segmentation of the target image is performed, where joint label fusion specifies the likelihood and the regularization terms imposed by cm-rep act as shape priors that preserve leaflet topology and constrain model fitting. Our objective is to demonstrate that these two complementary techniques generate accurate, patient-specific representations of mitral leaflet geometry without any need for user interaction. Moreover, the segmentation method is applied to different time points in the cardiac cycle, mid-systole and mid-diastole, to test if it can effectively capture different geometric configurations of the mitral leaflets. Manual image segmentation is considered the gold standard for assessing the performance of the fully automated technique.

The paper is organized as follows. In Section 2, the methods of 3D TEE image acquisition and manual and automatic segmentation of the mitral leaflets are described. Background information on multi-atlas joint label fusion and deformable modeling with cm-rep is provided. Section 3 presents a comparison of the manual and automatic leaflet segmentation results. A discussion of the results and a comparison of the automatic segmentation method to existing methods for mitral valve quantification are presented in Section 4. The paper concludes with Section 5.

2. Methods

2.1. Image acquisition

Twenty patients undergoing cardiac surgery at the University of Pennsylvania were imaged pre-operatively using real-time 3D TEE. This cohort included 6 subjects with normal mitral valve anatomy and function, 6 subjects with mild mitral regurgitation undergoing surgery for either coronary artery or aortic valve disease, and 8 subjects with severe ischemic mitral regurgitation undergoing mitral valve repair surgery. The imaging protocol was approved by the University of Pennsylvania School of Medicine Institutional Review Board. All studies were performed after induction of general anesthesia and before initiation of cardiopulmonary bypass. Electrocardiographically gated full-volume images were acquired with the iE33 platform (Philips Medical Systems, Andover, MA) using a 2–7 MHz transesophageal matrix-array transducer over four consecutive cardiac cycles. No restrictions were specified for the orientation or angulation of the transesophageal probe. The frame rate was 17–30 Hz, and the imaging depth was 12–16 cm. From each subject's data series, 3D TEE images of the mitral valve at mid-systole and mid-diastole were selected for analysis. These 3D TEE images were exported in Cartesian format (224 × 208 × 208 voxels), with an approximate isotropic resolution of 0.6–0.8 mm.

2.2. Manual segmentation

The 40 images selected for analysis were traced in ITK-SNAP (Yushkevich et al., 2006a), an open-source software package for medical image segmentation. The 40 images consisted of two per subject, one acquired at diastole and one at systole. An expert observer manually segmented the anterior and posterior leaflets in their entirety, associating the two leaflets with separate labels (label 1 = anterior leaflet, label 2 = posterior leaflet). All unmarked voxels were assigned label 0, corresponding to the image background. The final products of manual segmentation were two separate atlas sets: one consisting of 20 labeled images at diastole and the second consisting of 20 labeled images at systole. Manual segmentation was performed without knowledge of mitral valve pathology.

2.3. Automatic segmentation

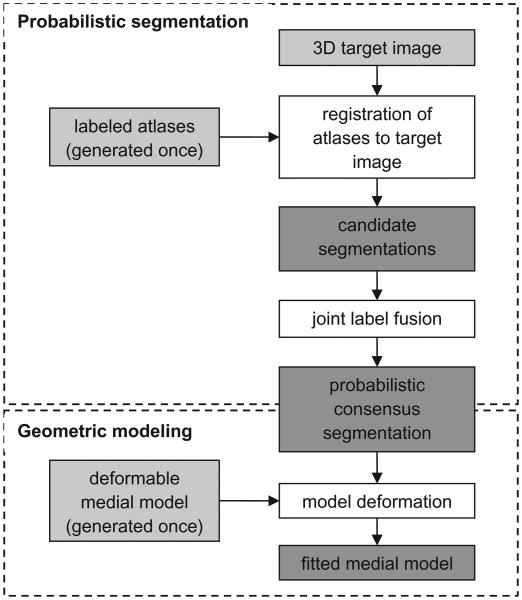
A schematic of the automatic segmentation algorithm is presented in Fig. 2. First, a set of 3D TEE atlases of the mitral valve are generated and a 3D deformable template of the open leaflets is constructed (Fig. 3). These two steps are performed once. Given an unseen 3D TEE target image to segment, the atlases are registered to the target image to obtain a set of candidate segmentations. Subsequently, joint label fusion generates a probabilistic consensus segmentation of the target image, which is used to guide 3D deformable medial modeling. The output is a 3D geometric model of the mitral leaflets in the target image volume. Fig. 4 illustrates the segmentation and geometric modeling of the mitral leaflets for a given subject. Segmentation of the diastolic image volume is performed first. Then, segmentation of the systolic image volume is performed using the same subject's open-valve medial model for initialization of closed-valve model fitting. Background information on these methods is presented in Sections 2.3.1 and 2.3.2.

Fig. 2.

Schematic of the automatic segmentation algorithm. The input is shown in light gray and the intermediate products and output are shown in dark gray. First, a set of 3D TEE atlases of the mitral leaflets is generated and a deformable medial model is constructed. Atlas and template generation is performed once. Given a 3D target image to segment, the atlases are registered to the target image and the atlas labels are propagated to the target image to obtain a set of candidate segmentations. Joint label fusion generates a probabilistic consensus segmentation, which is used to guide 3D deformable modeling. The output of the algorithm is a 3D geometric model of the mitral leaflets in the target image.

Fig. 3.

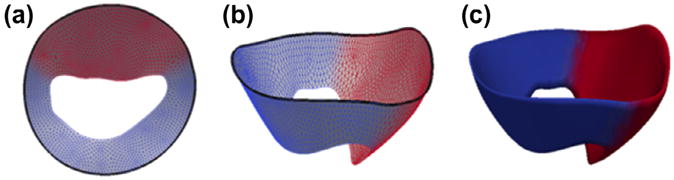
Cm-rep template of the open mitral leaflets used for deformable modeling. (a and b) The medial manifold of the template is a triangulated mesh, with red nodes referring to the anterior leaflet and blue labels referring to the posterior leaflet. The mitral annulus is represented by the bold black curve on the outer medial edge. (c) Leaflet boundaries constructed analytically from the medial manifold, given a constant radial thickness for initialization. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 4.

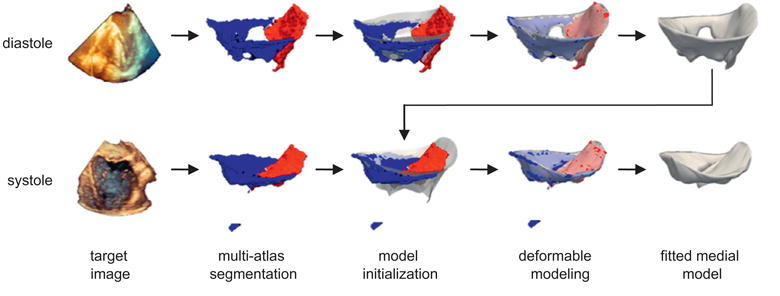
Automatic segmentation of the mitral leaflets at diastole (top row) and systole (bottom row) for a given patient. First, a probabilistic segmentation is generated by multi-atlas label fusion (red = anterior leaflet, blue = posterior leaflet). Then the cm-rep template (translucent) is initialized to the multi-atlas segmentation and the template is deformed to obtain a medial model of the mitral leaflets. The medial template shown in Fig. 3 is used for model initialization at diastole, and the fitted diastolic model is used to initialize model fitting of the same subject's valve at systole. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.3.1. Multi-atlas joint label fusion

Multi-atlas label fusion is a segmentation strategy that has been applied to a number of medical image segmentation problems, most notably magnetic resonance imaging of the brain (Artaechevarria et al., 2009; Heckemann et al., 2006; Lotjonen et al., 2010; Svarer et al., 2005). The method makes use of a set of expert-labeled atlases, where each atlas consists of a sample image and a set of labels for the anatomic structures in that image. When a new target image is presented for segmentation, each atlas image is registered to the target image. The deformation fields obtained by registration are then used to propagate the atlas labels to the target image. Depending on dissimilarities in anatomy and appearance between the atlas and target images, each atlas produces a different segmentation of the target image. Multi-atlas label fusion strategies combine these results, either by majority or weighted voting, to produce a consensus or probabilistic segmentation of the target image.

Majority voting methods count votes for each label from each atlas and select the label receiving the majority of votes to produce the final segmentation (Hansen and Salamon, 1990; Kittler, 1998). Alternatively, in weighted voting methods, each atlas contributes to the final segmentation according to a weight, with atlases more similar to the target image receiving higher weights (Heckemann et al., 2006; Isgum et al., 2009; Sabuncu et al., 2009). In some cases, information from atlases that are globally or locally dissimilar to the target image will be discarded during voting (Artaechevarria et al., 2009; Collins and Pruessner, 2010). It has been demonstrated that voting methods with spatially varying weights derived from local similarities between the atlas and target image are most effective in practice (Artaechevarria et al., 2009; Isgum et al., 2009; Sabuncu et al., 2009). The drawback of many majority and weighted voting methods, however, is that they assign weights to each atlas independently without considering similarities between different atlases. In other words, the methods assume that errors produced by different atlases are uncorrelated. This assumption can lead to labeling inaccuracies caused by replication or redundancy in the atlas set.

Joint label fusion is an extension of multi-atlas label fusion with weighted voting that reduces segmentation errors produced by redundancies in the atlas set (Wang et al., 2013). When computing voting weights, the method accounts for both similarity between each atlas and the target as well as similarity between atlases, under the assumption that the expected label error produced by one atlas is large when the image intensity difference between the warped atlas and target image is large. The expectation that any two atlases both produce a label error is large only when both atlases have large intensity differences from the target image. As described by Wang et al. (2013), weighted voting is formulated in terms of minimizing the total expected labeling error in the final estimated segmentation, which requires knowledge of the expected pairwise joint label differences between the atlas and target images. Since this information is unknown, the joint label differences are explicitly modeled and estimated based on local intensity similarities between the atlases and target image. Spatially-varying voting weights are efficiently solved in closed form. The result of multi-atlas joint label fusion is a probabilistic segmentation, where each voxel in the target image space is assigned a probability of having a given label. A final segmentation is produced by assigning each voxel the label with the greatest probability.

In this work, intensity-based registration is performed between all pairs of reference atlases, as well as between all reference atlases and the target image. Registration consists of two stages. First, the FSL FLIRT tool (Jenkinson and Smith, 2001) is used to perform global registration with six degrees of freedom. Second, the ANTS Symmetric Normalization algorithm (Avants et al., 2008) is used to perform deformable registration. Cross-correlation is the similarity metric used for registration, and a Gaussian regularizer with sigma = 3 is applied. Finally, each atlas is warped into the target image space using the obtained deformation fields, generating a candidate segmentation of the target image. The candidate labels are then fused to create probabilistic consensus segmentation according to the method described in Wang et al. (2013).

2.3.2. Deformable modeling with continuous medial representation

Once probabilistic segmentations are generated with multi-atlas joint label fusion, the mitral leaflets are geometrically modeled using cm-rep, a continuous form of medial representation (Yushkevich, 2009). Briefly, a medial model is a type of shape representation that describes an object's geometry in terms of its skeleton, or medial axis. Blum (1967) has defined the medial axis of an object as a locus of the centers of maximal inscribed balls (MIBs) that lie inside the object and cannot be made any larger without crossing the object boundary. The center of each MIB is associated with a radius R, the distance between that point on the skeleton and the object boundary. While there are a number of methods for defining or extracting an object's medial geometry, cm-rep makes use of deformable modeling and inverse skeletonization (Pizer et al., 2003; Yushkevich et al., 2006b). The technique begins with a deformable medial model, or template, of an object with pre-defined topology. The skeleton of the model is explicitly represented as a set of continuous parametric manifolds m : Ω → ℝ³, Ω ∈ ℝ², and object thickness R : Ω → ℝ+ is modeled parametrically as a scalar field defined over the skeleton. Given a new instance of the object, the template is deformed through Bayesian optimization such that the object's skeleton is defined first, and then the object boundary is derived analytically from the skeleton. The result is a fitted cm-rep of the object that describes its shape in terms of medial geometry, a radial thickness field R mapped to one or more medial manifolds m. An advantage of deformable medial modeling is that it imposes a shape-based coordinate system on the object and thereby establishes correspondences on different instances of that object. Moreover, it ensures that different instances of the object have consistent topology, which is not necessarily guaranteed by other shape recovery methods.

In this work, the deformable cm-rep of the mitral leaflets is represented by a single non-branching medial manifold illustrated in Fig. 3. The manifold is discretely represented as a triangulated mesh using a Loop subdivision surface scheme (Loop, 1987) and is constructed in a manner similar to that described in (Pouch et al., 2012b). In this approach, the template is generated by computing the Voronoi skeleton of a pre-existing open-valve segmentation, pruning the skeleton to obtain the desirable single-sheet branching structure, fitting the single-sheet skeleton with a parametric surface, and triangulating. The segmentation used to create the template is from a single subject (not included as an atlas in this study), but the steps described above cause the shape to undergo considerable smoothing and simplification so that it becomes a rather generic representation of the open mitral leaflets shown in Fig. 3. We have demonstrated in Pouch et al. (2012b) that the performance of cm-rep model fitting to mitral leaflet segmentations is robust to the choice of the data set used to generate the template. Unlike our previous work, the anterior and posterior leaflets are represented in the present work by a single labeled medial manifold, rather than separate manifolds for each leaflet. The medial mesh has 146 control points. Each control point is a tuple of values (m, R, L), where m =(m_x,m_y,m_z) are the point coordinates in ℝ³, R is the radial thickness or distance from that node to the leaflet's atrial and ventricular surfaces, and L is a label corresponding to either the anterior or posterior leaflet. The nodes on the outer medial edge correspond to the mitral annulus, and the nodes on the inner medial edge correspond to the free edges of the leaflets. In Fig. 3, the anterior leaflet nodes are colored red, the posterior leaflet nodes are colored blue, and the mitral annulus is demarcated by a bold black curve. When the model is fitted to image data, the control point mesh is subdivided by applying Loop subdivision surface rules twice, which results in a mesh with 1886 vertices. The boundary mesh is derived from the subdivided medial mesh using inverse skeletonization and has 3504 vertices.

To capture leaflet geometry in a target image, the cm-rep template is deformed such that the negative log of a Bayesian posterior probability is minimized. The Bayesian objective function consists of a likelihood term, regularization prior, and penalties used to ensure that inequality constraints required for inverse skeletonization are met:

$$-log(p(M|I))\sim w_{\text{likelihood}}\cdot T_{\text{likelihood}}+\sum _i{w}_{{\text{regularity}}_i}\cdot T_{{\text{regularity}}_i}+\sum _j{w}_{{\text{validity}}_j}\cdot T_{{\text{validity}}_j}$$ (1)

Here, p(M|I) is the probability of observing the model M given the target image I, and w are the relative weights of terms T. The first term in Eq. (1), T_likelihood, is proportional to the negative log of p(I|M), the probability of observing the target image I given the model M. This term is driven by the probability maps given by multi-atlas joint label fusion. The sum of the weighted terms T_regularity and T_validity is proportional to the negative log of p(M), the prior probability enforced by constraints in the cm-rep deformable modeling framework.

The likelihood of the Bayesian posterior energy is constructed as a probability integral term that utilizes the probabilistic segmentation maps, P^l(x), generated by multi-atlas joint label fusion. Suppose that P^l(x) is the probability of voxel x having the label l, where l has three possible values: 0 (background), 1 (anterior leaflet), and 2 (posterior leaflet). The likelihood is formulated as follows:

$$-log(p(I|M))\sim 1-\frac{\sum _l{P}^l(x){|}_{M_l}}{I_{\text{volume}}}$$ (2)

where l indexes through each label, x indexes through the image voxels, I_volume is the target image volume given in pixels, and M_l represents the part of the model M associated with label l. Here, M₁ and M₂ refer to the anterior and posterior leaflets and M₀ refers to the exterior of the model. Note that this term samples probabilities over the entire target image domain. For segmentation of the open leaflets, P^l(x) ranges from 0 to 1. For segmentation of the closed leaflets, P^l(x) is either 0 or 1, where the value 1 is assigned to the label with the highest probability at x. The use of binary values for P^l(x) at systole strengthens model fitting in the coaptation zone since the closed leaflets are most challenging to distinguish in this region and probability assignments are relatively low.

The second set of terms in Eq. (1) constitutes the regularization prior that controls the smoothness of the outer medial edge and penalizes non-uniform expansion and contraction of the mitral leaflets during model fitting. Given N nodes on the outer edge of the triangulated medial mesh, the first regularization term consists of two components. The first component penalizes the angle between adjacent normal vectors around the medial edge, and the second penalizes the angle between consecutive line segments along the outer medial edge:

$$T_{{\text{regularity}}_1}=\sum _{i=1}^N[(1-cos({\theta }_i))+(1-cos({\varphi }_i))]$$ (3)

where θ_i is the angle between the outward normals at adjacent outer edge nodes m_i and m_i+1, and ϕ_i is the angle between adjacent line segments formed by nodes m_i−1 and m_i and nodes m_i and m_i+1. In effect, this term prevents twisting and rippling of the medial manifold's outer edge during model deformation.

The second regularization term penalizes non-uniform expansion and contraction of the mitral leaflets. This term has a low weight during open leaflet model fitting, when it is used to strengthen correspondences on the valves of different subjects. The term has a higher weight during closed leaflet fitting, when the open leaflet model for a given subject is deformed to estimate the closed valve geometry. In the latter case, the term is primarily used to ensure accurate correspondences on the same subject's valve at different time points. The term has two components: a medial Jacobian distortion penalty and boundary Jacobian distortion penalty, which penalize the Jacobians of the medial manifold and leaflet boundaries, respectively. The term is formulated as follows:

$$T_{{\text{regularity}}_2}={\nabla }_{m}log\left(\frac{A_m}{A_{m,\mathit{\text{ref}}}}\right)+{\nabla }_{b}log\left(\frac{A_b}{A_{b,\mathit{\text{ref}}}}\right)$$ (4)

where A_m and A_b refer to the area of triangles on the medial manifold and model boundary, A_m,ref and A_b,ref refer the area of the triangles prior to model deformation, and ∇_m and ∇_b are the gradients over the medial manifold and model boundary.

The last five terms in the objective function, {T_validityi, i = 1, 2, … , 5}, ensure that the cm-rep is an example of valid medial geometry. The inequality constraints required for valid medial geometry have been previously outlined and presented in detail (Pouch et al., 2012b; Yushkevich, 2009). Briefly, the first penalty prevents singularities on the medial model boundary by ensuring that the Jacobian of the medial-boundary mapping is positive. The second term ensures that the radial thickness field R remains positive during model fitting, i.e. R > 0. The third constrains ∇_mR at non-edge medial nodes to ensure valid derivative computation for inverse skeletonization. The fourth term prevents degenerate tangent vectors at boundary vertices, and the fifth prevents overlaps and self-intersections in the medial model.

To initialize deformable modeling with cm-rep at diastole, an affine transform is obtained by registering images of the deformable template and the multi-atlas segmentation result with the robust point matching algorithm (Papademetris et al., 2003) first and then with the FSL FLIRT tool (Jenkinson and Smith, 2001). To obtain the initialization transform for systole, multi-label images of the open-leaflet template and closed-valve multi-atlas segmentation are registered with the Advanced Normalization Toolkit (Avants et al., 2011). The template used for initialization of open leaflet modeling is the one shown in Fig. 3, and closed leaflet model fitting is initialized with a rigidly transformed open leaflet model from the same subject. Open and closed leaflet segmentation and deformable modeling are performed sequentially, as shown in Fig. 4. Deformable model fitting is performed by minimizing Eq. (1) by conjugate gradient descent. The weights used in the Bayesian objective function are given in Appendix A.

2.3.3. Comparison of manual and automatic segmentation

Automatic segmentation is tested in a leave-one-out framework, using a separate set of atlases for leaflet segmentation at systole and diastole. Both sets consist of 20 manually labeled atlases with separate labels for the anterior and posterior leaflets. For each segmentation test, an atlas is selected as a target image for automatic leaflet segmentation, and the remaining 19 manually labeled atlases are used as references for joint label fusion. The automatic segmentation is compared to its corresponding manual segmentation based on mean boundary displacement (MBD). To ensure a symmetric measurement, MBD is the average of the distances measured from the manual to automated segmentation and from the automated to manual segmentation. Given two meshed shapes P and Q, MBD is defined as follows:

$$\text{MBD}=\frac{1}{2}(d(P,Q)+d(Q,P))$$ (5)

where d(P,Q) is the distance from P to Q and d(Q,P) is the distance from Q to P. The distance between two meshes is given by

$$d(P,Q)\cong \frac{1}{A_P}{\int }_{x\in P}\underset{y\in Q}{inf}\Vert x-y\Vert \mathit{\text{dA}}$$ (6)

where x is a point on mesh P, y is a point on mesh Q, and A_P is the surface area of mesh P.

3. Results

In the cross-validation segmentation tests, the automatic method produced valid segmentations of the open and closed mitral leaflets for 19 of 20 subjects. Image data from the 19 subjects for which segmentation was successful included the entire left ventricle and mitral valve in the field of view. The image data from the subject whose segmentation failed had a smaller field of view excluding most of the left ventricle, which likely contributed to poor registration results and consequently an invalid segmentation. Figs. 5 and 6 illustrate examples of manual and automatic segmentations of open and closed mitral leaflets. These figures qualitatively demonstrate that the automatic method captures patient-specific detail of the mitral leaflets, with both normal and pathologic geometries, at two different time points in the cardiac cycle. Fig. 7 presents an example of an open leaflet segmentation in which multi-atlas label fusion produced leaflet labeling errors and topological inconsistencies due to registration errors. Nonetheless, with the shape constraints imposed by the cm-rep framework, the automatic method generated a valid, accurate geometric model of the leaflets in the image data.

Fig. 5.

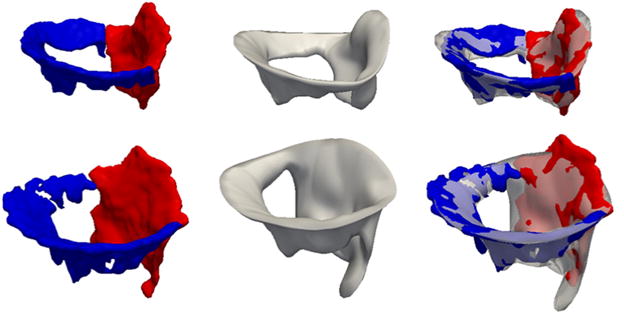
Automatic and manual open-leaflet segmentations for two subjects: one with a normal mitral valve (top row) and one with an incompetent valve (second row). The left column shows the manual segmentation with the anterior leaflet in red and posterior leaflet in blue. The center column shows the automatic segmentation, and the right column shows the automatic segmentation overlaid on the manual segmentation. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 6.

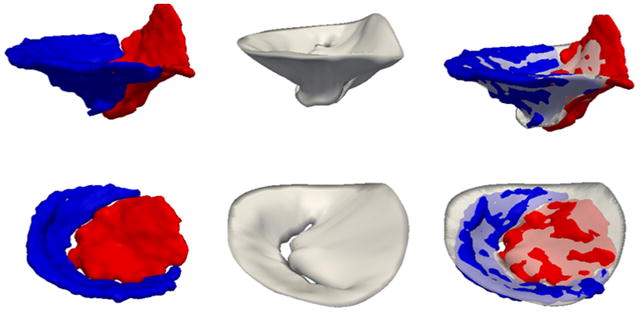
Automatic and manual closed-leaflet segmentations for two subjects: one with a normal mitral valve (top row) and one with an incompetent valve (second row). The left column shows the manual segmentation with the anterior leaflet in red and posterior leaflet in blue. The center column shows the automatic segmentation, and the right column shows the automatic segmentation overlaid on the manual segmentation. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 7.

The multi-atlas segmentation of an open valve, with the anterior leaflet in red and posterior leaflet in blue (left). The fitted cm-rep of the open leaflets (center). The fitted model overlaid on multi-atlas segmentation (right), illustrating that cm-rep corrects for labeling and topological inconsistencies in multi-atlas segmentation. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 8 presents the accuracy of each intermediate step and the output of fully automated image analysis at mid-diastole and mid-systole. The mean boundary displacement between the manual segmentation and each of the following outputs is given: the candidate segmentations generated by individual atlases, the consensus segmentation obtained by joint label fusion of the candidate segmentations, and the model-based segmentation generated by fitting the deformable medial model to the target image. The results are broken down into four categories: all subjects grouped together, subjects with normal mitral valve function, mildly diseased subjects, and subjects with severe mitral valve disease. In all categories, the accuracy of the consensus segmentation was significantly greater than the average accuracy of individual candidate segmentations and in some cases was greater than the best candidate segmentation. The best individual candidate segmentations had mean boundary displacements ranging between 0.6 and 1.2 mm (diastole) and between 0.3 and 1.6 mm (systole). These observations demonstrate that joint label fusion improves segmentation accuracy when low-quality candidate segmentations are created as a result of registration error. The accuracy of model-based segmentation was consistent with that of the consensus segmentation, which is expected since the multi-atlas segmentation results guide model deformation. Note that the goal of cm-rep modeling is not necessarily to improve segmentation accuracy, but to obtain a geometric description that establishes a shape-based coordinate system on the leaflets.

Fig. 8.

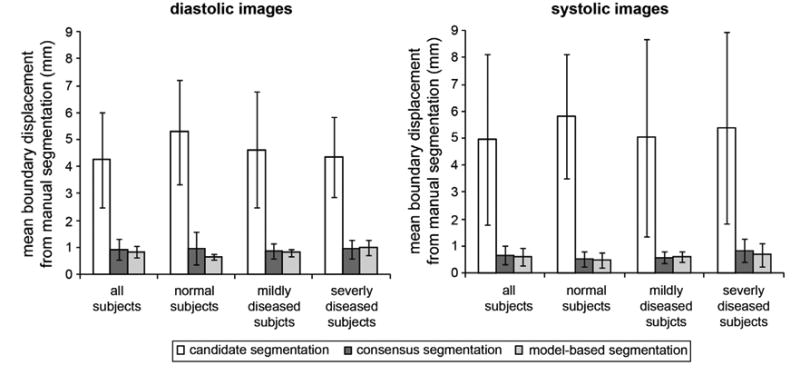
Segmentation results at diastole (left) and systole (right). The bar graphs show the mean boundary displacement between the manual segmentation and each of the following: the candidate segmentations obtained by single-atlas registration, the consensus segmentation generated by joint label fusion, and the model-based segmentation created with the deformable cm-rep. The results are broken down by disease category: all subjects, subjects with normal mitral valve function, mildly diseased subjects, and subjects with severe mitral regurgitation.

Table 1 presents the mean distance between the manual and automatic segmentations, for both the open and closed leaflets. When considering the segmentation as a single binary image, the mean distance between the manual and automatic segmentations was 0.8 ± 0.2 mm (open) and 0.6 ± 0.2 mm (closed). Here, the standard deviation refers to the variation from the mean distance observed in the 19 successful segmentation tests. These distances are on the order of one voxel, as the average isotropic voxel resolution is roughly 0.7 mm. 95% of points on the manual and automatic segmentations were less than 1.8 mm apart for the open leaflets and 1.4 mm for the closed leaflets. Fig. 9 (top row) shows maps of the localized distances between the manual and automatic segmentations for the open and closed leaflets. These maps show that the largest discrepancies occur around the posterior annulus and the free edge of the anterior leaflet, indicating that the manual and automatic segmentations included slightly different amounts of tissue around the posterior annulus and chordal tissue at the anterior leaflet margin.

Table 1.

Mean distances between the automatic and manual segmentations of the mitral leaflets at diastole and systole. 95% of points on the manual and automatic segmentations fall within the 95th percentile distance. The distances are computed for a single-label segmentation (leaflets combined) and for the anterior and posterior leaflet segmentations individually.

	Mean distance (mm)	95th percentile distance (mm)
Diastole (open leaflets)
Both leaflets	0.8 ± 0.2	1.8
Anterior leaflet	0.9 ± 0.3	3.7
Posterior leaflet	1.0 ± 0.3	2.3
Systole (closed leaflets)
Both leaflets	0.6 ± 0.2	1.4
Anterior leaflet	0.8 ± 0.4	4.5
Posterior leaflet	1.0 ± 0.3	2.5

Fig. 9.

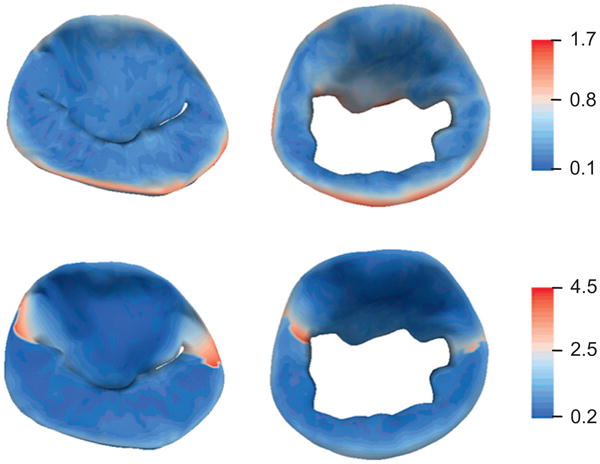
Color maps showing localized mean distance between the automatic and manual segmentations in millimeters. The results are shown for the leaflets at systole (left column) and diastole (right column). Segmentation accuracy is evaluated in terms of a single-label model (top row) and multi-label model (bottom row), in which the anterior and posterior leaflet segmentations are evaluated independently. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

When evaluating the anterior and leaflet segmentations individually (such that the leaflets are assigned different labels), the mean distances between the automatic and manual leaflet models were: 0.9 ± 0.3 and 1.0 ± 0.3 mm for the open anterior and posterior leaflets, and 0.8 ± 0.4 and 1.0 ± 0.3 for the closed anterior and posterior leaflets. 95% of points on the manual and automatic segmentations were within 3.7 and 2.3 mm for the open anterior and posterior leaflets, and within 4.5 and 2.5 mm for the closed anterior and posterior leaflets. Fig. 9 (bottom row) illustrates that the largest discrepancies in anterior and posterior leaflet labeling occur near the leaflet commissures.

To examine the effect of reference atlas set construction on the multi-atlas segmentation results, joint label fusion was repeated using reference atlases from subgroups of the population: (1) subjects with normal mitral valve function or mild mitral regurgitation, and (2) subjects with severe mitral regurgitation. For example, images acquired from normal and mildly diseased subjects were segmented with atlases from the same group and then with atlases constructed from severely diseased subjects only. In these experiments, normal and mildly diseased subjects were combined into a single subset, since more than six atlases were needed to generate valid segmentations for most subjects. Table 2 presents the multi-atlas segmentation results produced when subsets of the original atlas sets are used. The results indicate that consensus segmentation accuracy depends to some extent on both atlas set size and composition of the reference atlas set. For one, there were more invalid segmentations generated when subjects in a given category were segmented with references atlases from another category. For all tests except for normal systolic image segmentation, it is notable that one normal subject's and one severely diseased subject's segmentations were invalid when either one of the reference atlas subsets was used. This observation suggests that segmentation accuracy for those patients dramatically increased when the reference atlas subsets were combined into a single larger reference atlas set.

Table 2.

Mean boundary displacement between the multi-atlas consensus segmentation and manual segmentation when different reference atlas subsets are used in a leave-one-out cross-validation experiment. The number of invalid consensus segmentations is indicated in parentheses. Eight atlases from severely diseased subjects and 11 atlases from normal and mildly diseased subjects were included in the test. Note that the normal atlas whose segmentation failed when all reference atlases were used was excluded from these experiments.

	Normal and mild disease reference atlas set	Severe disease reference atlas set
Diastole (open leaflets)
Target images
Normal and mild disease	0.7 ± 0.2 mm (1 of 11)	0.9 ± 0.1 (3 of 11)
Severe disease	1.1 ± 0.5 mm (4 of 8)	0.9 ± 0.2 (1 of 8)
Systole (closed leaflets)
Target images
Normal and mild disease	0.5 ± 0.3 mm (0 of 11)	0.7 ± 0.4 mm (2 of 11)
Severe disease	0.8 ± 0.4 mm (2 of 8)	0.8 ± 0.6 mm (1 of 8)

To estimate the accuracy of fully automated leaflet thickness measurements, the deformable medial model was fitted directly to each manual segmentation so that corresponding leaflet thickness measurements could be compared. Leaflet thickness was defined as the distance between the atrial and ventricular boundary nodes associated with each medial node. Mean thicknesses of 1.7 ± 0.5 mm (automated) and 1.5 ± 0.4 mm (manual) were computed for the open valve and a mean thickness of 1.5 ± 0.4 mm (both manual and automated) was computed for the closed valve. These thickness measurements are on the order of 2–3 voxels. The mean difference in thickness derived from automated and manual image analysis was 0.2 ± 0.8 mm (open valve) and −0.1 ± 0.6 mm (closed valve), which is on the order of 1 voxel. The largest discrepancies in the manual and automated measurements occurred on the leaflet rough zones, where the automated segmentation revealed more leaflet thickening. There was no statistically significant difference in leaflet thickness in normal, mildly diseased, and severely diseased subjects, which is not surprising since the etiology of valve disease in this population is not generally associated with leaflet thickening. Note that this thickness comparison is influenced by the accuracy of model fitting to the manual segmentation. Mean boundary displacements of 0.4 ± 0.1 mm (open valve) and 0.3 ± 0.03 mm (closed valve) between the fitted model and manual segmentation were computed.

The computational time of the automated segmentation method, which is currently not parallelized or optimized for time efficiency, was on par with the time needed for an expert to manually segment the valve, which is on the order of several hours depending on the quality of the image data and the complexity of valve geometry. The majority of the time needed for automated segmentation is devoted to deformable registration, which requires several hours for the large image volumes processed in this study. Label fusion takes approximates 10 min and deformable model fitting requires roughly 30 min on a single processor, depending on the extent of which the initialized template must deform to match the leaflets in the target image data.

4. Discussion

4.1. Contributions

The described automatic leaflet segmentation method makes significant contributions to both 3D ultrasound image analysis and the study of in vivo mitral valve geometry. The technique is the first of its kind to use both multi-atlas label fusion and deformable modeling with cm-rep to generate patient-specific models of the mitral leaflets from 3D TEE images. The method is effectively applied to different time points in the cardiac cycle (mid-diastole and mid-systole) and accurately captures different geometric configurations of the mitral leaflets (open and closed). First, the superiority of multi-atlas joint label fusion over single-atlas-based segmentation is clearly demonstrated in the experiments (Fig. 8) that evaluate the accuracy of each step in the image analysis algorithm. Secondly, multi-atlas joint label fusion and cm-rep prove to be highly complementary segmentation techniques. Joint label fusion automatically generates probabilistic segmentations of the mitral leaflets, which are incorporated as the likelihood of the Bayesian posterior probability used in cm-rep fitting. These probability maps are the driving force for an accurate model-based segmentation. At the same time, the regularization and validity constraints imposed by the cm-rep framework function as strong priors in the posterior probability. These two components of the Bayesian objective function, the likelihood and regularization prior, work together to ensure an accurate, topologically consistent labeling of the mitral leaflets in the target image data, as shown in the examples in Figs. 5 and 6. Fig. 7 shows that deformable modeling with cm-rep aids in circumstances in which atlas-based segmentation produces topological inconsistencies or labeling errors. While probabilistic segmentations generated by joint label fusion do not identify correspondences, deformable modeling with cm-rep imposes a shape-based coordinate system on the mitral leaflets and establishes correspondences on leaflets of different subjects. Anatomic landmarks identified in the cm-rep coordinate system facilitate measurement of clinically relevant features of leaflet and annular geometry (Pouch et al., 2012b). In addition, the ability to measure localized leaflet thickness is a unique advantage of using a volumetric segmentation method and cm-rep, as leaflet thickness is a relevant parameter in constitutive models of the mitral valve and characterization of myxomatous disease. Although the evaluation of automated leaflet thickness assessment presented in Section 3 is not an ideal validation method, the results suggest that the error in fully automated measurements of localized leaflet thickness are less than the mean boundary displacement between the automated and manual segmentations. Moreover, the leaflet thicknesses presented in this study are on par with previously reported echocardiographic and ex vivo measurements (Louie et al., 1995; Sahasakul et al., 1988).

Unlike most of the existing methods for mitral leaflet segmentation, this technique models mitral leaflet and annular geometry without the need for user interaction, thereby completely eliminating the issue of inter- and intra-observer variability in image analysis. Once a set of manually labeled atlases is obtained, there is no need for an observer to initialize or supervise segmentation. In addition to being fully automated, the segmentation method yields spatially dense, detailed representations of a given patient's valve. Manual segmentation of the mitral valve requires several hours of an expert's time. The automated method presented in this work can be performed without any expert's time or knowledge of the mitral valve and how it appears in ultrasound images. Therefore, the method is more accessible to users who have limited experience in interpreting mitral valve geometry in ultrasound images. Moreover, the automated analysis can be performed immediately after image acquisition without any user interaction. The development of this fully automated technique is a significant step towards creating a practical, informative tool for preoperative assessment of patient-specific mitral valve morphology.

Our approach improves on the only existing fully automatic mitral valve segmentation method in the literature (mean boundary displacement error of ∼0.7 mm versus 1.54 mm in Ionasec et al. (2010)) and is competitive with a semi-automatic method that requires some user input (0.76 ± 0.65 mm in Schneider et al. (2011b)). This error is in line with inter observer variability in manual image analysis, where mean boundary displacements of 0.60 ± 0.17 mm (mitral leaflets) and 2.38 ± 0.76 mm (mitral annulus) have been reported (Jassar et al., 2011). Our results are consistent with this previous study, as Fig. 9 (top row) shows that the greatest variability in manual and automatic segmentation occurs at the boundaries of the model, rather than along the leaflet surfaces. This variability is a consequence of the annulus, or model edge, being located at a somewhat arbitrary (non-intensity-based) boundary between the leaflets and the surrounding tissue to which they are anchored. Discrepancies between the manual and automated segmentations were also observed on the anterior leaflet free edge. These discrepancies are due to the lack of a well-defined criterion for demarcating the leaflet free edge at prominent chordal attachment sites. Therefore, the manual-versus-automated segmentation comparison may be influenced by inclusion of variable amounts of chordal attachment tissue along the free edges and of variable amounts of leaflet attachment tissue around the annulus. Additionally, areas of signal dropout present in a manual segmentation may be filled in by the model-based segmentation. Overall, the leaflet segmentation methods presented in the literature report average differences between manual and automatic segmentations on the order of one to two voxels, which compares favorably to the average error of approximately one voxel measured in this study. The 95th percentile distances reported here (1.6 mm, on average) are in line with those reported in Schneider et al. (2011a), which were 2.1 mm.

To the best of our knowledge, all previous studies have evaluated mitral leaflet segmentation accuracy with respect to a single-label model, where the leaflets were not assigned different labels. This study evaluates segmentation accuracy in terms of both single and multi-label models. As anticipated, somewhat larger discrepancies between the manual and automatic segmentations were observed when the anterior and posterior leaflet delineations were independently evaluated. These discrepancies were localized to the tissue between the commissures and annulus, indicating that the manual and automatic observers consistently identified valve tissue in this area, but may have assigned these voxels different labels. This observation is expected for two reasons. For one, the coapted leaflets are difficult to distinguish, especially in the commissural region, by both expert and automated observers. Secondly, the tissue in the commissural area varies substantially between subjects and may in fact constitute a separate commissural leaflet. The fact that the greatest error is localized to this region indicates that the manual and automatic segmentations are in close agreement in other clinically significant aspects of leaflet geometry, including the leaflet bellies and coaptation zone.

Image-derived, anatomically accurate models of in vivo leaflet geometry have a number of clinically significant applications. The models can assist in the diagnosis of mitral valve disease, guide surgical interventions such as mitral valve repair, and be used as input to biomechanical simulations of valve function. Emphasizing the importance of characterizing in vivo valve morphology, Lang and Adams point out that the surgical treatment of functional mitral regurgitation with downsized complete ring annuloplasty is frequently performed irrespective of patient-specific valve geometry (Lang and Adams, 2012). Not surprisingly, this surgical repair strategy has been associated with unexpectedly high rates of recurrent mitral regurgitation (Crabtree et al., 2008; Flameng et al., 2003; Mihaljevic et al., 2007; Serri et al., 2006). Automatic modeling of in vivo mitral valve geometry can lead to improved clinical outcomes by aiding in the simulation and selection of repair strategies involving different annuloplasty ring characteristics and subvalvular adjustments (Lang and Adams, 2012). Along these lines, we have shown that image-derived leaflet models can be loaded with physiologic pressures using finite element analysis to estimate stress distributions in normal and regurgitant valves (Pouch et al., 2012a). Such information is useful for understanding stress-related phenomena associated with mitral valve repair failures and for identifying patients with high leaflet stresses in the early post-operative period. Several research groups have also explored the integration of mitral valve imaging and biomechanical modeling for simulation of mitral valve dynamics and computation of leaflet mechanics (Burlina et al., 2010; Mansi et al., 2012; Rausch et al., 2012; Sacks et al., 2006; Votta et al., 2008).

4.2. Limitations and future work

Future studies will address the limitations of the proposed segmentation method. First, errors produced by atlas-based segmentation are mainly due to registration errors, which occur when registration associates wrong regions from an atlas to the target image. In this study, invalid registrations occurred with respect to 1 of 20 atlases in which the mitral leaflets were imaged with a different field of view. To prevent these invalid segmentations, multiple atlas sets can be constructed using images acquired in different modes and with varying fields of view. Alternatively, a feature detection method can be developed to identify a specific field of view in the target image data prior to segmentation. Future studies can also explore optimal atlas construction to determine the minimum number of atlases needed to maintain the same degree of accuracy, comparable to interobserver variability in manual segmentation. It has been shown that increasing the atlas set size improves segmentation accuracy, but with diminishing returns (Wang et al., 2011). The incorporation of 4D regularization constraints in the multi-atlas label fusion and deformable modeling steps can potentially prevent leaflet labeling inaccuracies.

While the current algorithm is not optimized for efficiency, there are several ways in which computation time can be significantly reduced to enhance the method's clinical applicability. Both the multi-atlas segmentation and deformable modeling steps are highly parallelizable and well-suited for GPU implementation. In future work, smaller regions of interest can be used for deformable registration, and less computationally expensive image registration algorithms can be explored. A multi-resolution implementation of deformable modeling can be used, which would decrease the time required for computation of the regularization terms. In addition, a scheme for automatically selecting the weights used in the Bayesian objective function may further enhance model fitting accuracy.

5. Conclusion

Physiological models of the mitral valve constructed from 3D TEE provide visual and quantitative information about in vivo mitral valve morphology that can aid in the diagnosis and treatment of mitral valve disease. To expedite image analysis in clinical and research settings, the presented method generates quantitative geometric models of the mitral valve without any need for user interaction. The integration of multi-atlas joint label fusion and 3D deformable modeling techniques provides for a model-based Bayesian segmentation that is accurate relative to expert manual image analysis. This methodology is a step towards developing a fully automatic tool that can be easily used to study mitral valve geometry and dynamics and aid in image-based surgical guidance.

Appendix A.

In this work, deformable medial models are fitted to 3D TEE images of the mitral leaflets with the guidance of probability maps generated by multi-atlas label fusion. The objective function minimized during model fitting takes the form of Eq. (1), where w are the relative weights of terms T. The likelihood term maximizes the agreement between the deformable model and the probability maps produced by label fusion (Eq. (2)). The regularity terms (Eqs. (3) and (4)) prevent non-physiological distortions of the model, and the validity terms enforce inequality constraints that are required for valid medial geometry (outlined in Pouch et al. (2012b)). For both open and closed leaflet model fitting, two deformation stages are used. The table below summarizes the terms and weights used in the objective function during each stage of model fitting. The weights used in closed leaflet model fitting are shown in parentheses where they differ from those used in open leaflet model fitting.

The weights for the validity and regularity terms were manually selected such that the individual contributions of these terms to the Bayesian objective were on the same order of magnitude, at least one order of magnitude smaller than the likelihood term. The regularity terms are weighted differently for closed and open leaflet model fitting to accommodate for differences in the probability values used in the likelihood term, as described in Section 2.3.2. Additionally, the leaflet overlap constraint is weighted more heavily for closed leaflet model fitting, since overlap is more likely to occur in the coaptation zone of the closed valve. For all segmentation experiments, the distortion penalty is removed during the second fitting stage to allow the model to capture finer detail of leaflet geometry.

Term	Description	Fitting phase 1	Fitting phase 2
Tlikelihood	Multi-label probability integral	1	1
Tvalidity1	Boundary Jacobian constraint	10−3	10−3
Tvalidity2	Radial thickness constraint	10−6	10−6
Tvalidity3	Boundary ∇mR constraint	0.5	0.5
Tvalidity4	Loop tangent constraint	10−2	10−2
Tvalidity5	Leaflet overlap constraint	10−4(10)	10−4(0.1)
Tregularity1	Medial edge regularizer	0.1 (1.0)	0.1 (1.0)
Tregularity2	Distortion penalty	0.1 (10.0)	0.0