Physiologically based pharmacokinetic model of lapatinib developed in mice and scaled to humans

Abstract

Lapatinib is an oral 4-anilinoquinazoline derivative that dually inhibits epidermal growth factor receptor and human epidermal growth factor receptor 2 (HER2). This drug is a mere decade old and has only been approved by the FDA for the treatment of breast cancer since 2007. Consequently, the intricacies of the pharmacokinetics are still being elucidated. In the work presented herein, we determined the biodistribution of orally administered lapatinib in mouse plasma, brain, heart, lung, kidney, intestine, liver, muscle and adipose tissue. Using this data, we subsequently developed a physiologically based pharmacokinetic (PBPK) model of lapatinib in mice that accurately predicted the tissue concentrations after doses of 30, 60 and 90 mg/kg. By taking into account interspecies differences in physiology and physiochemistry, we then extrapolated the mouse PBPK model to humans. Our model predictions closely reflected lapatinib plasma pharmacokinetics in healthy subjects. Additionally, we were also able to simulate the pharmacokinetics of this drug in the plasma of patients with solid malignancies by incorporating a decrease in liver metabolism into the model. Finally, our PBPK model also facilitated the estimation of various human tissue exposures to lapatinib, which harmonize with the organ-specific toxicities observed in clinical trials. This first-generation PBPK model of lapatinib can be further improved with a greater understanding of lapatinib absorption, distribution, metabolism and excretion garnered from subsequent in vitro and in vivo studies and expanded to include other pharmacokinetic determinants, including efflux transporters, metabolite generation, combination dosing, etc., to better predict lapatinib disposition in both mouse and man.

Introduction

Lapatinib is an oral 4-anilinoquinazoline derivative that dually inhibits epidermal growth factor receptor (EGFR) and human epidermal growth factor receptor 2 (HER2) (estimated ${\mathrm{K}}_{\mathrm{i}}^{\text{app}}$ values of 3 and 13 nM, respectively) by competing with ATP [1]. Aberrant signaling of these tyrosine kinases is prevalent in various types of solid tumors, thus making them attractive therapeutic targets. Presently, lapatinib is approved by the US Food and Drug Administration (FDA) in combination with capecitabine for the treatment of HER2 positive metastatic breast cancer and in combination with letrozole for the treatment of hormone receptor positive, HER2 positive metastatic breast cancer. In addition, there are approximately 250 current clinical trials in cancer patients involving this drug [2].

Numerous preclinical studies and clinical trials have investigated the plasma pharmacokinetics of lapatinib [3–15]. However, none have elucidated the biodistribution of this compound in tissues other than blood. Based on adverse reactions reported in humans (including cardiac, hepatic, gastrointestinal and lung toxicities), it can be presumed that there are significant levels of drug in these organs.

To empirically determine both plasma and organ exposure to lapatinib, we developed a physiologically based pharmacokinetic (PBPK) model in mice and then scaled this model to humans. This type of pharmacologic modeling is a useful tool that facilitates the prediction of target tissue drug concentrations by incorporating mathematical descriptions of the uptake and disposition of chemicals based on quantitative interrelations among the critical determinants of physiological processes (i.e., absorption, metabolism, excretion and tissue solubility phenomena) [16]. Accordingly, PBPK models are comprised of compartments corresponding to discrete tissues or groupings of tissues with appropriate volumes, blood flows, and pathways for xenobiotic clearance including pertinent biochemical and physiochemical constants [17]. Each compartment in the model is described with a mass-balance differential equation whose terms mathematically represent biological processes; the set of equations is then solved by numerical integration to simulate tissue time-course concentrations of chemicals and their metabolites [17]. The PBPK model of lapatinib presented herein consisted of eight tissue compartments (plasma, brain, heart, lung, kidney, intestine, liver and slowly perfused tissues) and incorporated drug absorption, intestinal and hepatic metabolism and fecal elimination in both mouse and man.

Materials and methods

Chemicals

Lapatinib (GW572016) and GW572016AH were generously provided by GlaxoSmithKline. Hydroxypropyl methylcellulose and Tween^® 80 were purchased from Sigma-Aldrich. All other reagents were of analytical grade.

Lapatinib pharmacokinetic studies in mice

Five to six-week-old female FVB mice were purchased from Taconic. Animals were housed in polycarbonate cages and kept on a 12 h light/dark cycle. Food and water were given ad libitum. All experimental procedures were approved by Colorado State University’s Animal Care and Use Committee and the Department of Defense US Army Medical Research and Material Command (USAMRMC) Animal Care and Use Review Office (ACURO).

Upon arrival, mice acclimated for a minimum of seven days prior to any experimentation. After acclimation, a time course distribution study of lapatinib was conducted at doses of 30, 60 and 90 mg/kg. Lapatinib was formulated as a suspension in 0.5 % hydroxypropyl methylcellulose: 0.1 % Tween^® 80 in Milli-Q water and was administered via oral gavage as a single bolus dose. Subsequently, three mice were sacrificed at 0.25, 0.5, 1, 2, 4, 8, 12 and 16 h by cardiac stick exsanguination under isoflurane anesthesia. Plasma, brain, liver, proximal small intestine, kidney, heart, lung, muscle and adipose tissue were immediately collected, rinsed with phosphate buffered saline, frozen in liquid nitrogen and stored at −80 °C until analysis.

Lapatinib high-pressure liquid chromatography-tandem mass spectrometry analysis

Analysis of lapatinib in plasma and tissue was done using high-pressure liquid chromatography-tandem mass spectrometry (LC/MS/MS) analysis based on the method of Bai et al. [18], modified as follows. Briefly, lapatinib was extracted from plasma by adding 210 μL of acetonitrile and 10 μL of internal standard (17.2 pmol GW572016AH) to 100 μL of unknown sample plasma, vortexing for 10 min and centrifuging at 18,000×g for 10 min at 4 °C. An aliquot of 20 μL of the supernatant was injected into the LC/MS/MS system for analysis. Tissues (brain, liver, proximal small intestine, kidney, heart, lung, muscle and adipose) were homogenized at 100 mg/mL in water and 100 μL of the homogenates were extracted using the method for plasma detailed above. Standards and quality control samples were prepared in the appropriate matrix and analyzed as described above.

The HPLC system consisted of an Agilent 1200 Series binary pump SL, vacuum degasser, thermostatted column compartment SL (Agilent Technologies, Santa Clara, CA, USA) and a CTC Analytics HTC PAL System autosampler (Leap Technologies, Carrboro, NC, USA). The HPLC column was a Waters Sunfire C8 column (4.6 × 50 mm I.D., 2.5 μm bead size) (Waters Corporation, Milford, MA, USA) protected by a SecurityGuard^™ C18 cartridge (4 × 2.0 mm I.D.) (Phenomenex, Torrance, CA, USA) and maintained at room temperature. The mobile phase consisted of an aqueous component (A) of 20 mM ammonium formate in MilliQ water, pH 2.2 (with formic acid) and an organic component (B) of acetonitrile with 1 % formic acid. The 3.5 min run consisted of the following linear gradient elution: 95 % A and 5 % B at 0 min, 95 % A and 5 % B at 0.25 min, 25 % A and 75 % B at 0.35 min, 25 % A and 75 % B at 3.0 min, 95 % A and 5 % B at 3.1 min and 95 % A and 5 % B at 3.5 min. The system operated at a flow-rate of 0.75 mL/min.

Mass spectrometric detection was performed on an API 3200^™ triple quadrupole instrument (Applied Biosystems Inc., Foster City, CA, USA) using multiple reaction monitoring (MRM). Ions were generated in positive ionization mode using an electrospray interface. Lapatinib compound-dependent parameters were as follows: declustering potential (DP): 60 V; entrance potential (EP): 10 V; collision cell entrance potential (CEP): 21 V; collision energy (CE): 51 V and collision cell exit potential (CXP): 5.8 V. GW572016AH (internal standard) compound-dependent parameters were as follows: DP: 67 V; EP: 7.5 V; CEP: 23 V; CE: 49 V and CXP: 5.5 V. Source-dependent parameters were as follows: nebulizer gas (GS1): 50 psi; auxiliary (turbo) gas (GS2): 60 psi; turbo gas temperature (TEM): 500 °C; curtain gas [7]: 10 psi; collision-activated dissociation (CAD) gas (nitrogen): 6 psi; ionspray voltage (IS): 5,000 V and interface heater (IH): 500 °C. Peak areas ratios obtained from MRM of lapatinib (m/z 581 → 365.1) and GW572016AH (m/z 587 → 367) were used for quantification.

The lower limit of quantitation for this assay was 1 ng/mL for plasma and 5 ng/g for tissues. The accuracy for the assay was 95.61 ± 4.60 % in plasma and 95.83 ± 3.47 % in tissues. The precision of the assay was 1.97 % in plasma and 3.75 % in tissues.

PBPK model development

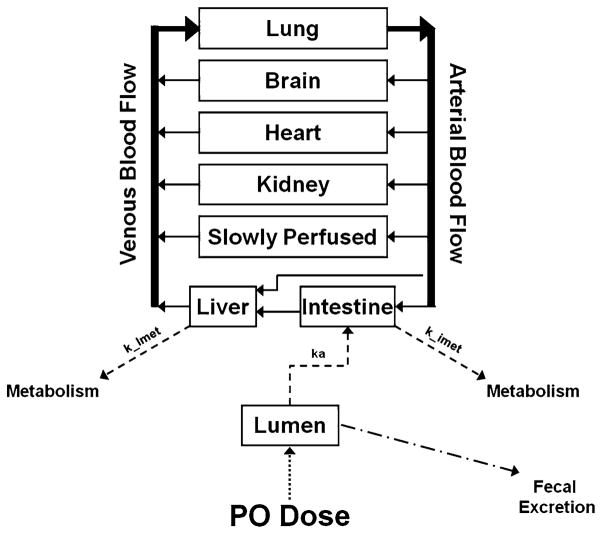
A PBPK model for lapatinib was developed incorporating absorption, intestinal and hepatic metabolism and fecal elimination. This flow-limited model was comprised of eight tissue compartments: plasma, brain, heart, lung, kidney, intestine, liver and slowly perfused tissue (Fig. 1). Physiological parameters (tissue volumes and tissue blood flows) were obtained from Brown et al. [19] and are shown in Table 1.

Fig. 1.

Schematic representation of a physiologically based pharmacokinetic (PBPK) model of lapatinib. Solid arrows represent blood flow. Dashed lines represent first-order rate constants for absorption from intestinal lumen (ka), hepatic metabolism (k_lmet) and intestinal metabolism (k_imet). The dotted line represents lapatinib input into the system via per os (p.o.) dosing. Drug remaining in the lumen is eliminated via fecal excretion

Table 1.

PBPK model parameter values

Parameter	Units	Mouse	Human
Lapatinib properties
Molecular weight		581.06 g/mol
Percent unbound		1 %
Tissue volumea	% of body weight
Blood		4.90	7.9
Brain		1.65	2.0
Heart		0.50	0.5
Lung		0.73	0.8
Kidney		1.67	0.4
Intestine		4.22	1.7
Liver		5.49	2.6
Slowly perfusedb		80.84	84.1
Tissue blood flowa	% of cardiac output
Brain		3.3	11.4
Heart		6.6	4.0
Lung		100	100
Kidney		9.1	17.5
Intestine		14.1	18.1
Liver		2.0	4.6
Slowly perfusedb		64.9	44.4
Partition coefficientsc	Ratio
Brain:plasma		10 (19)	10
Heart:plasma		215 (22)	215
Lung:plasma		1,643 (19)	1,643
Kidney:plasma		1,064 (18)	1,064
Intestine:plasma		531 (31)	531
Liver:plasma		12 (20)	12
Slowly perfused:plasma		65 (20)	65
Absorption rate constantsd	h−1
Lumen → Intestine		0.237 (2)	0.07 (6)
Metabolism rate constants	h−1
Liverd		127 (13)	75 (5)
Intestine		2.5e	0.975f

^aPhysiological parameters obtained from Brown et al. [19]

^bSlowly perfused tissue parameters calculated as the remaining percent

^cDetermined by parameter estimation optimized for observed plasma and tissue concentrations from mouse 60 mg/kg dose cohort. Data is parameter estimate (CV%)

^dFirst-order rate constants determined by parameter estimation optimized for observed plasma and tissue concentrations from mouse 60 mg/kg dose cohort for mouse model and observed plasma concentrations from healthy subject human data for human model. Data is parameter estimate (CV%)

^eCalculated as 2 % of liver metabolism

^fCalculated as 1.3 % of liver metabolism

The unbound fraction of drug in the plasma was set at 0.01 (1 %), as lapatinib is highly bound (>99 %) to albumin and alpha-1 acid glycoprotein [1]. The arterial blood drug concentration available to all tissues except liver was considered to be the unbound lapatinib concentration in the blood. Both unbound and bound lapatinib were available for uptake into the liver.

Tissue:plasma partition coefficients were determined by parameter estimation, optimizing the fit for the observed plasma and tissue concentrations from the mouse 60 mg/kg dose cohort. These fitted values were compared with values calculated as detailed in Chen and Gross [44] using our experimental data (Online Resource 1). For these calculations, we used our concentration–time data from the mouse 60 mg/kg dose study and considered the terminal elimination phase to include the 4, 8, 12 and 16 h time points. The tissue:plasma partition coefficients were calculated as ${\mathrm{C}}_{\mathrm{T}}^0/{\mathrm{C}}_{\mathrm{P}}^0$, where ${\mathrm{C}}_{\mathrm{T}}^0$ and ${\mathrm{C}}_{\mathrm{P}}^0$ are the tissue and plasma intercepts (initial concentrations), respectively, from the concentration–time curves of the terminal elimination phase on a semilogarithmic plot. After the partition coefficients were determined, the values had to be adjusted because when we measured the plasma concentrations via LC/MS/MS, we analyzed both bound and unbound drug in the plasma. Thus, to correct the partition coefficients so they reflected only the unbound drug available for tissue uptake (1 % unbound), we multiplied the calculated value by 100. The Chen and Gross method [44] was applicable for the determination of kidney, lung and slowly perfused tissue (adipose and muscle were used as representative slowly perfused tissues) partition coefficients. However, for brain and heart partition coefficients, we were unable to utilize this method because the criteria for implementation of this equation were not met for these two tissues (K/Q was not ≪ 1, where K is the organ clearance and Q is the blood flow). Additionally, for liver and intestine partition coefficients, Chen and Gross [44] describes unique equations, which we could not use because we did not have the values for all necessary variables. Therefore, because we were only able to determine three of the seven tissue partition coefficients using the Chen and Gross equations [44], we chose to estimate all partition coefficients by fitting these parameters to the model. For kidney, lung and slowly perfused tissue partition coefficients, the fitted values were 37, 7 and 12 % different than the calculated values, respectively. For brain, heart, liver and intestine partition coefficients, the fitted values were 10, 42, 29 and 16 % different than the calculated values, respectively.

The first-order rate constants for absorption from intestinal lumen and hepatic metabolism were determined by parameter estimation. For the mouse model, the fit was optimized for the observed plasma and tissue concentrations from the mouse 60 mg/kg dose cohort. For the human model, the fit was optimized for the observed plasma concentrations from a single 100 mg dose study conducted by GlaxoSmithKline in healthy subjects (n = 21).

The first-order rate constant for intestinal metabolism was estimated as a constant percentage of hepatic metabolism based on the ratio of total liver:intestinal CYP3A, the major cytochrome P450 enzyme sub-family responsible for lapatinib metabolism [1]. In mice, the mean quantity of immunoreactive CYP3A is 2.24 and 0.64 pmol/mg microsomal protein in liver and intestinal microsomes, respectively [45]. The total amount of microsomal protein in a 20 g mouse liver (5.49 % body weight [19] = 1.098 g) and small intestine is 38.9 mg (35.4 mg hepatic microsomal protein/g liver [46] × 1.098 g) and 2.67 mg [47], respectively. Accordingly, the total amount of CYP3A in a 20 g mouse liver and small intestine is 87.136 and 1.709 pmol, respectively. As a result, we concluded that the first-order rate constant for intestinal metabolism in mice is 2 % that of liver metabolism. In humans, total hepatic and small intestine (duodenum, jejunum and ileum) CYP3A was calculated to be 5,490 and 70.5 nmol, respectively [48]. Therefore, we represented the first-order rate constant for human intestinal metabolism as 1.3 % that of liver metabolism. This ratio held true for the microsomal intrinsic clearance of midazolam, a CYP3A-specific substrate, which was 15800 mL/min and 213.7 mL/min (or 1.35 %) in human liver and small intestine, respectively [48].

Table 1 lists all parameter values for both the mouse and human PBPK models.

The rate of change of the amount of drug in a generic storage tissue compartment mass balance equation is as follows:

$$\frac{{dA}_T}{dt}=Q_T\times (C_A-C_{VT})$$

where A_T is the amount of drug in the tissue compartment, t is time, Q_T is the blood flow to the tissue compartment, C_A is the arterial blood drug concentration entering the tissue compartment and C_VT is the venous blood drug concentration exiting the tissue compartment. Assuming venous equilibration, the drug concentration in the venous blood is:

$$C_{VT}=C_T/P_T$$

where C_T is the concentration of drug in the tissue compartment and P_T is the tissue:plasma partition coefficient.

Assuming the volume of the tissue (V_T) is constant, the drug concentration in the tissue is:

$$\frac{{dC}_T}{dt}=Q_T\times (C_A-C_{VT})/V_T$$

For metabolizing tissues (liver and intestine), the rate of change of the amount of drug metabolized (A_M) is as follows:

$$\frac{{dA}_M}{dt}=k\times C_{VT}\times V_T$$

where k is a first-order rate constant.

Computer simulation

For PBPK modeling, acslX Libero version 3.0.2.1 (The AEgis Technologies Group, Inc.) was used.

Pharmacokinetic analysis

Pharmacokinetic parameters were calculated using non-compartmental modeling performed with Microsoft Excel and standard equations for noncompartmental analysis.

Data analysis

The predictive capability of the model was evaluated by calculating the prediction error (PE%) as follows [20, 21]:

$$PE\%=\frac{{\mathit{Value}}_{\mathit{predicted}}-{\mathit{Value}}_{\mathit{measured}}}{{\mathit{Value}}_{\mathit{measured}}}\times 100$$

As a measure of the precision of the prediction, the median absolute prediction error (MAPE%) was calculated as follows:

$$\mathit{MAPE}\%=\mathit{median}(\mid PE\%1\mid ,\mid PE\%2\mid ,\dots \mid PE\%n\mid )$$

As a measure of the bias of the prediction, the median prediction error (MPE%) was calculated as follows:

$$\mathit{MPE}\%=\mathit{median}(PE\%1,PE\%2,\dots PE\%n)$$

Sensitivity analysis

A normalized sensitivity analysis was performed as described in Loccisano et al. [22] to assess the influence of each PBPK model parameter on the simulated plasma area under the concentration–time curve (AUC) for both the mouse and human models. Briefly, sensitivity coefficients were calculated with the original parameters and for those resulting from a 1 % change in each parameter value. The following equation was used to calculate the normalized sensitivity coefficient (SC):

$$SC=\frac{(A-B)/B}{(C-D)/D}$$

where A is the AUC resulting from the 1 % increase in the parameter value, B is the AUC resulting from the original parameter value, C is the parameter value increased by 1 % and D is the original parameter value.

Results

Lapatinib pharmacokinetics and model simulations in mice

A time course tissue distribution study of lapatinib was conducted in female FVB mice. Plasma and tissue concentrations were measured after single oral doses of 30, 60 and 90 mg/kg at 0.25, 0.5, 1, 2, 4, 8, 12 and 16 h post drug administration. These time points were chosen for sacrifice to provide multiple samplings during each pharmacokinetic phase (absorption, distribution and elimination).

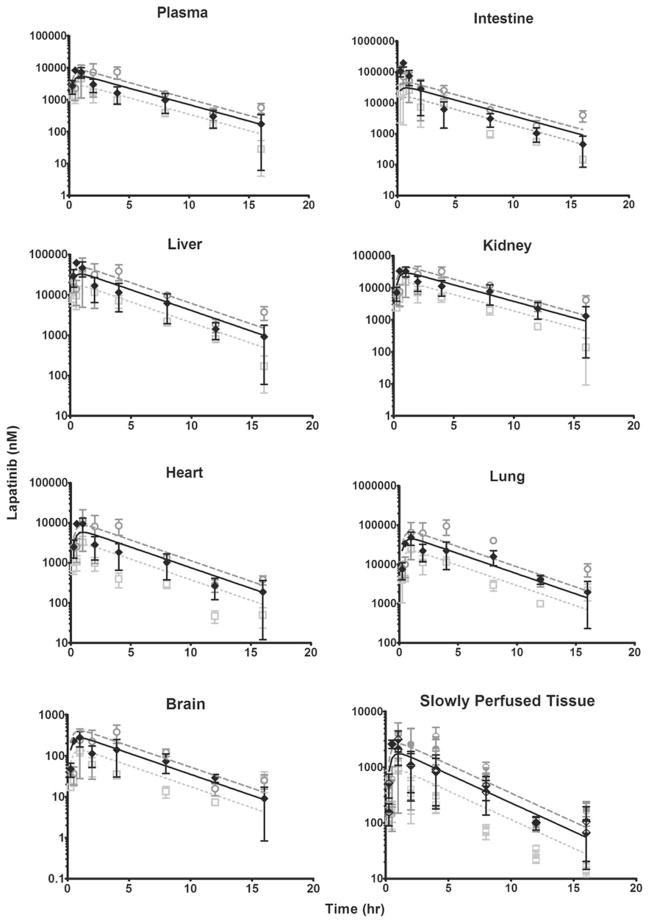
The mouse PBPK model development was based on the concentration–time data from the 60 mg/kg dose cohort; partition coefficients and first-order rate constants were determined by parameter estimation, optimizing the fit for the observed plasma and tissue concentrations from this study. The concentration–time profiles of lapatinib in plasma, intestine, liver, kidney, heart, lung, slowly perfused tissue and brain and the resulting PBPK model simulations are shown in Fig. 2. For all tissues except intestine, the PBPK model simulations closely mirrored the observed data.

Fig. 2.

Observed and model-simulated lapatinib concentrations in mouse plasma, intestine, liver, kidney, heart, lung, brain and slowly perfused tissue after oral gavage dosing of 30, 60 and 90 mg/kg. In all graphs except slowly perfused tissue, open light gray squares, filled diamonds and open dark gray circles represent the observed data from the 30, 60 and 90 mg/kg cohorts, respectively. In the slowly perfused tissue graph, the observed data from the 30 mg/kg dose cohort is represented by the upper half-filled light gray squares (adipose tissue) and lower half-filled light gray squares (muscle tissue); the observed data from the 60 mg/kg dose cohort is represented by upper half-filled black diamonds (adipose tissue) and lower half-filled black diamonds (muscle tissue); and the observed data from the 90 mg/kg dose cohort is represented by upper half-filled dark gray circles (adipose tissue) and lower half-filled dark gray circles (muscle tissue). For all observed data, error bars symbolize the standard error of the mean (SEM). Light gray dottedlines, solid black lines, and dark gray dashed lines represent model simulations for the 30, 60 and 90 mg/kg dose cohorts, respectively

The model-predicted intestine concentrations for the first four time points (0.25, 0.5, 1 and 2 h) are significantly lower than the actual data. We suspect that the observed data is not an accurate measurement of the drug concentration in the intestinal epithelium. Instead, the measured values reflect both the lapatinib in the intestinal epithelium and unabsorbed lapatinib in the proximal intestinal lumen. As an attempt to circumvent this anticipated problem, we flushed the intestinal lumen with saline immediately after tissue collection; however, we still noted yellow aggregates of undissolved lapatinib within the lumen (resulting from administration of the drug as a suspension via oral gavage). Thus, the measured drug concentrations in the intestine are likely inflated due to the lapatinib suspension in the proximal intestinal lumen. After approximately 3 h, the model simulation accurately reflects the observed values. It is probable that the lapatinib suspension has moved through the intestinal lumen by this time, as the intestinal transit time in a mouse is approximately 3 h. Therefore, at these later time points, the measured drug is presumably only lapatinib that has been absorbed into the intestinal epithelium.

After developing the mouse PBPK model with the 60 mg/kg dose cohort as a training set, we employed the other two dose cohorts (30 and 90 mg/kg) as test sets. The concentration–time data and the corresponding model simulations for these dose cohorts are also presented in Fig. 2. Again, the model simulations approximated the observed data with the exception of the early time points in the intestine, likely a result of the same phenomenon as described previously for the 60 mg/kg dose cohort.

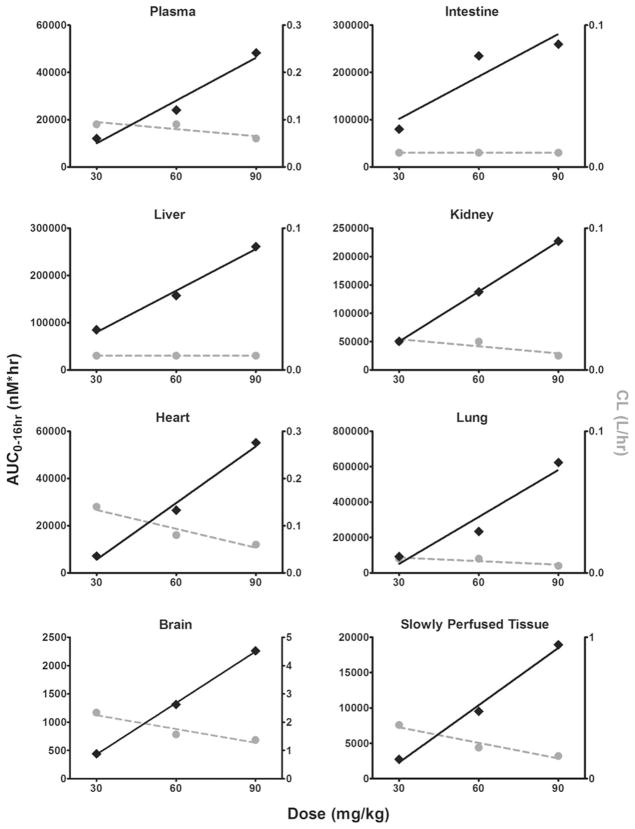
The area under the concentration–time curve from 0 to 16 h (AUC_{0–16 h}), clearance (CL) and elimination half-life (t_1/2) were calculated for both the observed and simulated data using noncompartmental analysis (Table 2). Lapatinib exhibits linear pharmacokinetics in all tissues within the 30–90 mg/kg dose range, as evidenced by a dose-dependent increase in AUC_{0–16 h} and constant CL (Fig. 3). To compare the actual and predicted data, we determined the ratio of the observed to model-predicted values (Table 2). The mean AUC_{0–16 h} ratio for all tissues was 1.00 and the range was 0.48 (heart from the 30 mg/kg dose cohort) to 1.81 (lung from the 90 mg/kg dose cohort), indicating that our model-predicted drug exposures reasonably mimicked the observed exposure for all tissues analyzed. As for CL, the model predictions also emulated the actual data; all ratios were between 0.45 (intestine from the 90 mg/kg dose cohort) and 2.10 (heart from the 30 mg/kg dose cohort), with the average ratio being 1.06. Lastly, all t_1/2 ratios were within the range of 0.52 (slowly perfused tissue from the 90 mg/kg dose cohort) and 1.24 (brain from the 30 mg/kg dose cohort), with an average ratio of 0.90. Overall, the PK parameters derived from the PBPK model simulations accurately mirrored the observed mouse data.

Table 2.

Observed and model-simulated lapatinib pharmacokinetic (PK) parameters in mice^a

PK parameter	Dose		Plasma	Intestine	Liver	Kidney	Heart	Lung	Brain	Slowly perfused
AUC0–16 h (nM × h)b	30	Observed	12,008	79,885	84,946	50,440	7,156	92,409	440.8	2,738
		Simulated	13,972	78,143	83,505	74,392	15,022	114,792	698.6	4,544
		Ratio	0.86	1.02	1.02	0.68	0.48	0.81	0.63	0.60
	60	Observed	24,052	235,114	157,288	137,624	26,545	233,760	1,315	9,519
		Simulated	27,944	156,284	167,010	148,784	30,044	229,583	1,397	9,087
		Ratio	0.86	1.50	0.94	0.92	0.88	1.02	0.94	1.05
	90	Observed	48,230	259,808	261,237	227,184	55,179	623,277	2,261	18,930
		Simulated	41,916	234,426	250,515	223,176	45,066	344,375	2,096	13,631
		Ratio	1.15	1.11	1.04	1.02	1.22	1.81	1.08	1.39
CL (L/h)c	30	Observed	0.09	0.01	0.01	0.02	0.14	0.01	2.34	0.38
		Simulated	0.07	0.01	0.01	0.01	0.07	0.01	1.48	0.23
		Ratio	1.16	0.98	0.98	1.47	2.10	1.24	1.58	1.66
	60	Observed	0.09	0.01	0.01	0.02	0.08	0.01	1.57	0.22
		Simulated	0.07	0.01	0.01	0.01	0.07	0.01	1.48	0.23
		Ratio	1.16	0.66	1.06	1.08	1.13	0.98	1.06	0.95
	90	Observed	0.06	0.01	0.01	0.01	0.06	0.005	1.37	0.16
		Simulated	0.08	0.03	0.01	0.01	0.07	0.01	1.48	0.22
		Ratio	0.78	0.45	0.96	0.98	0.79	0.55	0.93	0.73
t1/2 (h)d	30	Observed	2.73	2.79	2.48	2.53	2.59	2.39	3.70	3.88
		Simulated	2.99	2.96	2.95	3.00	2.99	2.99	2.99	2.99
		Ratio	0.91	0.94	0.84	0.84	0.87	0.80	1.24	1.30
	60	Observed	3.42	3.05	2.75	3.57	3.05	3.04	3.12	2.57
		Simulated	2.99	2.96	2.95	3.00	2.99	2.99	2.99	2.99
		Ratio	1.14	1.03	0.93	1.19	1.02	1.02	1.04	0.86
	90	Observed	2.36	2.55	1.91	2.51	2.32	1.72	1.76	1.55
		Simulated	2.99	2.96	2.95	3.00	2.99	2.99	2.99	2.99
		Ratio	0.79	0.86	0.65	0.83	0.78	0.58	0.59	0.52

^aPK parameters were calculated using noncompartmental modeling

^bAUC_{0–16 h} is the area under the concentration–time curve from 0 to 16 h

^cCL is clearance

^dt_1/2 is the half-life for elimination as calculated from linear regression of the terminal elimination phase

Fig. 3.

Area under the concentration–time curve calculated from 0 to 16 h (AUC_{0–16 h}) and clearance (CL) for the mouse 30, 60 and 90 mg/kg dose cohorts in plasma, intestine, liver, kidney, heart, lung, brain and slowly perfused tissue. AUC_{0–16 h} is presented on the left y axis and is represented by the solid black diamonds, with the corresponding linear regression trendline shown as the solid black line. CL is presented on the right y axis and is represented by the solid gray circles with the corresponding linear regression trendline shown as the dashed gray line. Both AUC_{0–16 h} and CL were determined by noncompartmental analysis

To further assess the predictive performance of the mouse model, we calculated the median prediction error (MPE%) and the median absolute prediction error (MAPE%) for the concentrations, AUCs_{0–16 h} and half-lives as measures of the bias and precision of the simulations, respectively (Table 3). Of these three variables, the concentrations were the most poorly predicted, with a mean MPE% of 28.6 and a mean MAPE% of 57.4. Although these prediction error assessments are not optimal, they are not surprising considering the large degree of variability in the data (mean concentration coefficient of variation of 78.6 %), likely due to the variable absorption of lapatinib when administered to unfasted animals. AUC_{0–16 h} and t_1/2 prediction errors were substantially better than the concentration prediction errors, feasibly because these parameters are derived from the cumulation of the concentration values and thus, the error of the individual points is muted. For AUC_{0–16 h}, the average MPE% was 14.5 and the average MAPE% was 3.2. The MPE% for plasma and all tissue AUCs_{0–16 h} was less than 28.0 and the MAPE% was less than 16.2. Regarding half-life, the average MPE% was 13.2 and the average MAPE% was 17.4, with no individual plasma or tissue MPE% and MAPE% being more than ±25.2 and 25.2 %, respectively.

Table 3.

Predictive performance for mouse PBPK model

	Concentrations		AUC0–16ha		t1/2b
	MPE%c	MAPE%d	MPE%c	MAPE%d	MPE%c	MAPE%d
Plasma	28.53	43.36	16.18	16.18	9.57	12.64
Intestine	−8.40	68.10	9.77	−9.77	6.09	6.09
Liver	23.57	51.03	4.10	−1.70	19.11	19.11
Kidney	45.40	52.90	8.11	8.11	18.57	18.57
Heart	52.81	73.34	18.33	13.18	15.41	15.41
Lung	4.45	59.25	24.22	−1.79	25.14	25.14
Slowly perfused	28.77	47.40	27.99	−4.53	16.24	22.96
Brain	53.30	63.65	7.30	6.24	−4.29	19.16

^aAUC_{0–16 h} is the area under the concentration–time curve from 0 to 16 h

^bt_1/2 is the half-life for elimination as calculated from linear regression of the terminal elimination phase

^cMPE% is the median prediction error, which is a measure of the bias of the prediction

^dMAPE% is the median absolute prediction error, which is a measure of the precision of the prediction

Lapatinib pharmacokinetics and model simulations in humans

The mouse PBPK model developed using the 60 mg/kg dose cohort was scaled to humans by using human parameters for tissue volumes and tissue blood flows and fitting the first-order rate constants for absorption and liver metabolism to the observed plasma concentrations from a single 100 mg dose study conducted by GlaxoSmithKline in healthy subjects (n = 21) (Table 1). The first-order rate constant for intestinal metabolism was set as 1.3 % that of liver metabolism as explained previously.

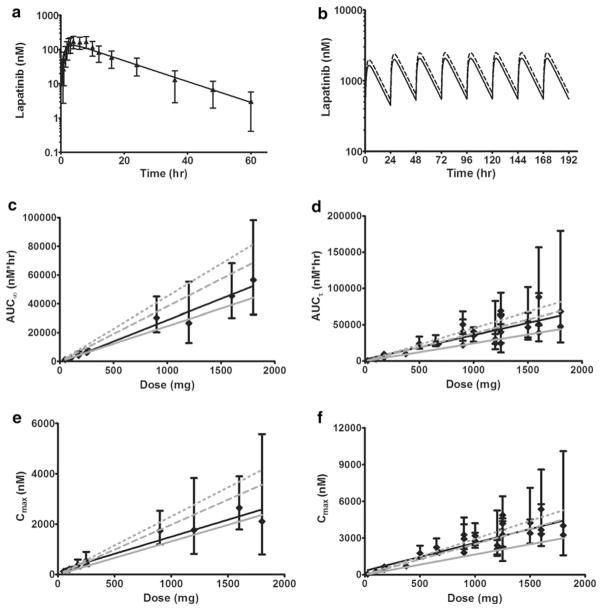
The concentration–time profiles of lapatinib in actual human plasma and the resulting PBPK model simulation are shown in Fig. 4a. The PBPK model prediction closely parallels the observed plasma concentration data. The MPE% and MAPE% for the lapatinib concentrations were − 8.17 and 11.69, respectively. Regarding the actual and simulated plasma pharmacokinetic parameters, AUCs_{0–60 h} were 2,698 and 2,409 nM × h, CLs were 63.8 and 71.4 L/h and half-lives were 9.5 and 10.0 h, respectively. The AUCs_{0–60 h} for plasma and all tissues in the model are shown in Table 4. From largest to smallest, exposure to lapatinib ranked as follows: intestine, lung, liver, kidney, heart, plasma, slowly perfused tissue and brain.

Fig. 4.

Observed and model-simulated lapatinib concentrations, area under the concentration–time curve (AUC) and maximum concentration (C_max) in human plasma. a Single oral dose of 100 mg. Filled black triangles represent the observed data with error bars symbolizing the standard deviation (SD). The solid black line represents the model simulation. b Multiple doses (q24 h) for 8 days. Solid black line represents the model simulation for daily dosing of 1,250 mg. Dashed black line represents the model simulation for daily dosing of 1,500 mg. c After a single dose of lapatinib, solid black diamonds represent observed AUCs_∞ (calculated from time 0 to infinity) with error bars symbolizing the 95 % confidence intervals and the solid black line is the corresponding linear regression trendline. The solid gray line represents the model-predicted AUCs_∞. The dashed gray line represents simulated AUCs_∞ from the model with moderate hepatic impairment. The dotted gray line represents simulated AUCs_∞ from the model with severe hepatic impairment. d After multiple doses (q24 h) of lapatinib, solid black diamonds represent observed steady-state AUCs_τ (calculated within the dosing interval from time 0 to 24 h) with error bars symbolizing the 95 % confidence intervals and the solid black line is the corresponding linear regression trendline. The solid gray line represents the model-predicted AUCs_∞. The dashed gray line represents simulated AUCs_τ from the model with moderate hepatic impairment. The dotted gray line represents simulated AUCs_τ from the model with severe hepatic impairment. e After a single dose of lapatinib, solid black diamonds represent observed C_max with error bars symbolizing the 95 % confidence intervals and the black line is the corresponding linear regression trendline. The solid gray line represents the model-predicted C_max. The dashed gray line represents simulated C_max from the model with moderate hepatic impairment. The dotted gray lines represents simulated C_max from the model with severe hepatic impairment. f After multiple doses (q24 h) of lapatinib, solid black diamonds represent observed C_max with error bars symbolizing the 95 % confidence intervals and the solid black line is the corresponding linear regression trendline. The solid gray line represents the model-predicted C_max. The dashed gray line represents simulated C_max from the model with moderate hepatic impairment. The dotted gray line represents simulated C_max from the model with severe hepatic impairment

Table 4.

Human tissue AUCs for single and multiple (q24 h) lapatinib doses

	100 mg single dose AUC0–60 ha(nM × h)	1,250 mg multiple dose q24 h AUCτb (nM × h)	1,500 mg multiple dose q24 h AUCτb(nM × h)
Plasma	2,409	30,631	36,757
Intestine	21,884	277,286	332,744
Liver	14,470	183,723	220,468
Kidney	12,817	162,959	195,550
Heart	2,590	32,929	39,514
Lung	19,792	251,637	301,964
Brain	121	1,532	1,838
Slowly perfused	783	9,955	11,946

^aAUC_{0–60 h} is the area under the concentration–time curve from 0 to 60 h

^bAUC_τ is the steady-state area under the concentration–time curve within the dosing interval (0–24 h)

Clinically, the recommended dose of lapatinib is 1,250 or 1,500 mg orally once daily continuously with either capecitabine (for advanced or metastatic breast cancer) or letrozole (for hormone receptor positive, HER2 positive metastatic breast cancer), respectively [1]. Thus, we modified our original model to incorporate multiple dosing of lapatinib. The resulting simulations of 1,250 and 1,500 mg doses of lapatinib q24 h for 8 days are shown in Fig. 4b. The steady-state area under the concentration–time curves calculated within the dosing interval from 0 to 24 h (AUC_τ) for plasma and all tissues in the model are shown in Table 4.

To further assess the predictive performance of the human model, we were not able to accrue concentration–time data for any other subjects/patients so we compared our model-predicted AUC, half-life, maximum concentration (C_max) and time of maximum concentration (T_max) values with those found in the literature for both healthy subjects [4, 24] and patients with solid tumors [5–13, 15]. The results along with the subject/patient characteristics (disease state, fasted or not fasted when administered lapatinib, liver function and age) are presented in Table 5 (single dose lapatinib) and Tables 6, 7 (multiple dose lapatinib). Graphically, observed and predicted AUCs are depicted in Fig. 4c, d. For the single dose comparison, all of the prediction errors were less than ±27.2 %, with a MPE% of 0.29 and a MAPE% of 7.7. The single dose prediction errors were smaller for the area under the concentration–time curve calculated from time 0 to infinity (AUCs_∞) of healthy subjects (MPE% of 1.5 and MAPE% of 2.5, n = 6 studies) than for the AUCs_∞ of patients with solid tumors (MPE% of −17.8 and MAPE% of 17.8, n = 4 studies), which was not surprising given that our model was developed with data from healthy subjects who presumably cleared (metabolized) lapatinib more efficiently than the patients with advanced solid malignancies, as they were both younger and had normal liver function. Thus, our model tended to underpredict the AUC_∞ for the patients with solid tumors, as indicated by the negative value of the MPE%. For the multiple dose lapatinib study, the prediction errors were larger, with a MPE% of −29.9 and a MAPE% of 29.9. Again, the negative MPE% was the result of our model simulations underpredicting lapatinib exposure, likely due to impaired hepatic function related to the age and disease state of the test population (n = 24 studies with cancer patients and only three studies with healthy subjects) versus the healthy training population used to develop the PBPK model.

Table 5.

Single dose lapatinib observed and predicted human AUC_∞ and subject characteristics

Dose (mg)	Observed AUC∞ (nM × h)	Predicted AUC∞ (nM × h)	AUC∞ PE%c	Subjects	Food	Bilirubind	ASTd	ALTd	Age (years)e	Reference
50	1,170 (756–1,817)a	1,225	4.7	Healthy	Fasted	Normal	Normal	Normal	22 (18–53)	[4]
100	2,096 (1,492–2,941)a	2,450	16.9	Healthy	Fasted	Normal	Normal	Normal	22 (18–53)	[4]
100	2,459 (2,062–2,933)b	2,450	−0.4	Healthy	Not fasted	Normal	Normal	Normal	28 (20–47)	[14]
175	4,206 (2,588–6,834)a	4,288	1.9	Healthy	Fasted	Normal	Normal	Normal	22 (18–53)	[4]
250	6,313 (4,550–8,758)a	6,126	−3.0	Healthy	Fasted	Normal	Normal	Normal	22 (18–53)	[4]
250	6,068 (4,970–7,411)b	6,126	1.0	Healthy	Not fasted	Normal	Normal	Normal	29 (20–48)	[14]
900	30,250 (20,328–45,011)a	22,054	−27.1	Cancer	Fasted	≤1.5× ULN	≤2.5× ULN	≤2.5× ULN	60 (37–73)	[13]
1,200	26,574 (12,753–55,375)a	29,405	10.7	Cancer	Fasted	≤1.5× ULN	≤2.5× ULN	≤2.5× ULN	60 (37–73)	[13]
1,600	45,367 (30,150–68,263)a	39,207	−13.6	Cancer	Fasted	≤1.5× ULN	≤2.5× ULN	≤2.5× ULN	60 (37–73)	[13]
1,800	56,519 (32,499–98,293)a	44,108	−22.0	Cancer	Fasted	≤1.5× ULN	≤2.5× ULN	≤2.5× ULN	60 (37–73)	[13]

^aAUC_∞ is the geometric mean (95 % confidence interval) of the area under the concentration–time curve calculated from time 0 to infinity

^bAUC_∞ is the geometric mean (range) of the area under the concentration–time curve calculated from time 0 to infinity

^cPE% is the prediction error

^dBilirubin, aspartate transaminase (AST) and alanine transaminase (ALT) are measures of liver function. ULN is upper limit of normal

^eMedian age (range)

Table 6.

Multiple dose lapatinib (25–1,200 mg) observed and predicted human AUC_τ and subject characteristics

Dose (mg)	Observed AUCτ (nM × h)a	Predicted AUCτ (nM × h)	AUCτ PE%b	Subjects	Food	Bilirubinc	ASTc	ALTc	Age (years)d	Reference
25	515 (329–809)	613	19.1	Healthy	Fasted	Normal	Normal	Normal	22 (19–38)	[4]
100	25,68 (1,594–4,137)	2,450	−4.6	Healthy	Fasted	Normal	Normal	Normal	22 (19–38)	[4]
175	4,869 (3,313–7,154)	4,288	−11.9	Healthy	Fasted	Normal	Normal	Normal	22 (19–38)	[4]
175	9,431	4,288	−54.5	Cancer	Fasted	≤2 mg/dL	≤3.0× ULN	≤3.0× ULN	61 (25–80)	[15]
375	9,878	9,189	−7.0	Cancer	Fasted	≤2 mg/dL	≤3.0× ULN	≤3.0× ULN	62 (25–81)	[15]
500	23,922 (17,107–33,731)	12,252	−48.8	Cancer	Not fasted	≤2 mg/dL	≤3.0× ULN	≤3.0× ULN	56 (28–74)	[5]
650	27,020 (20,480–35,797)	15,928	−41.1	Cancer	Not fasted	≤2 mg/dL	≤3.0× ULN	≤3.0× ULN	60 (37–82)	[5]
675	23,578	16,540	−29.8	Cancer	Fasted	≤2 mg/dL	≤3.0× ULN	≤3.0× ULN	63 (25–82)	[15]
900	21,857	22,054	0.9	Cancer	Fasted	≤2 mg/dL	≤3.0× ULN	≤3.0× ULN	64 (25–83)	[15]
900	40,099 (28,052–57,481)	22,054	−45.0	Cancer	Not fasted	≤2 mg/dL	≤3.0× ULN	≤3.0× ULN	57 (34–82)	[5]
900	50,377 (37,204–68,217)	22,054	−56.2	Cancer	Fasted	≤1.5× ULN	≤2.5× ULN	≤2.5× ULN	60 (37–73)	[13]
1,000	40,615 (35,452–46,639)	24,504	−39.7	Cancer	Not fasted	≤2 mg/dL	≤3.0× ULN	≤3.0× ULN	53 (43–59)	[5]
1,000	35,280 (26,847–46,295)	24,504	−30.5	Cancer	Fasted	Adequate	Adequate	Adequate	53 (30–80)	[9]
1,200	24,610 (16,212–37,518)	29,405	19.5	Cancer	Not fasted	≤2 mg/dL	≤3.0× ULN	≤3.0× ULN	54 (37–67)	[5]
1,200	44,195 (23,626–82,673)	29,405	−33.5	Cancer	Fasted	≤1.5× ULN	≤2.5× ULN	≤2.5× ULN	60 (37–73)	[13]
1,200	29,773	29,405	−1.2	Cancer	Fasted	≤2 mg/dL	≤3.0× ULN	≤3.0× ULN	65 (25–84)	[15]

^aAUC_τ is the geometric mean (95 % confidence interval) of the steady-state area under the concentration–time curve calculated within the dosing interval (0–24 h)

^bPE% is the prediction error

^cBilirubin, aspartate transaminase (AST) and alanine transaminase (ALT) are measures of liver function. ULN is upper limit of normal

^dMedian age (range)

Table 7.

Multiple dose lapatinib (1,250–1,800 mg) observed and predicted human AUC_τ and subject characteristics

Dose (mg)	Observed AUCτ (nM × h)	Predicted AUCτ (nM × h)	AUCτ PE%c	Subjects	Food	Bilirubind	ASTd	ALTd	Age (years)e	Reference
1,250	62,300 (40,271–96,376)a	30,631	−50.8	Cancer	Not fasted	≤1.5 mg/dL	≤2.0× ULN	≤2.0× ULN	58.3 (2–79)	[7]
1,250	68,840 (50,425–94,138)b	30,631	−55.5	Cancer	Not fasted	Significant dysfunction excluded			58 (34–78)	[8]
1,250	24,438 (11,789–50,941)b	30,631	25.3	Cancer	Fasted	≤1.5 mg/dL	≤2.0× ULN	≤2.0× ULN	59 (19–74)	[10]
1,250	40,099 (24,954–64,193)b	30,631	−23.6	Cancer	Not fasted	≤2.0× ULN	≤5.0× ULN	≤5.0× ULN	57.5 (33–74)	[12]
1,500	46,639 (32,699–66,430)b	36,757	−21.2	Cancer	Not fasted	≤1.5 mg/dL	≤2.0× ULN	≤2.0× ULN	59.5 (39–73)	[6]
1,500	54,900 (29,601–101,833)b	36,757	−33.0	Cancer	Fasted	≤1.5 mg/dL	≤3.0× ULN	≤3.0× ULN	57 (31–73)	[11]
1,600	50,597 (27,364–93,450)b	39,207	−22.5	Cancer	Not fasted	≤2.0 mg/dL	≤3.0× ULN	≤3.0× ULN	55 (38–70)	[5]
1,600	87,941 (49,348–156,717)b	39,207	−55.4	Cancer	Fasted	≤1.5× ULN	≤2.5 × ULN	≤2.5× ULN	60 (37–73)	[13]
1,600	39,067b	39,207	0.4	Cancer	Fasted	≤2.0 mg/dL	≤3.0× ULN	≤3.0× ULN	66 (25–85)	[15]
1,800	47,671b	44,108	−7.5	Cancer	Fasted	≤2.0 mg/dL	≤3.0× ULN	≤3.0× ULN	67 (25–86)	[15]
1,800	67,895 (25,658–179,656)b	44,108	−35.0	Cancer	Fasted	≤1.5× ULN	≤2.5 × ULN	≤2.5× ULN	60 (37–73)	[13]

^aAUC_τ is the mean (90 % confidence interval) of the steady-state area under the concentration–time curve calculated within the dosing interval (0–24 h)

^bAUC_τ is the geometric mean (95 % confidence interval) of the steady-state area under the concentration–time curve calculated within the dosing interval (0–24 h)

^cPE% is the prediction error

^dBilirubin, aspartate transaminase (AST) and alanine transaminase (ALT) are measures of liver function. ULN is upper limit of normal

^eMedian age (range)

Previously, lapatinib pharmacokinetics were assessed in subjects with moderate or severe hepatic impairment (Child-Pugh scores of 7–9, or greater than 9, respectively) and in 8 healthy control subjects; after a single oral dose of 100 mg, the lapatinib AUC increased approximately 56 and 85 % in subjects with moderate and severe hepatic impairment, respectively [25]. To imitate this liver dysfunction in our model, we decreased the first-order rate constant for liver metabolism by 35 and 45 % and, accordingly, achieved AUC increases of 56 and 85 %, respectively. Decreased liver metabolism of this magnitude has been observed in aged patients; a review of 16 cytochrome P450 (CYP) 3A substrates showed an average 37.2 % reduction in the clearance of these substrates by elderly versus young volunteers or patients [26]. The resulting AUC predictions from our modified model are graphed in Fig. 4c, d. The AUCs_∞ resulting from hepatic impairment in the single dose studies both overpredicted exposure, conceivably because 60 % of the studies were done in healthy subjects. In contrast, the moderately impaired liver function simulation more correctly reflected the observed AUCs_τ from the multiple dose lapatinib clinical trials in which 86 % of the studies were done in cancer patients. Thus, decreasing the liver metabolism in our model improves the lapatinib exposure predictions for cancer patients.

In addition to actual and simulated human lapatinib exposures, we also wanted to evaluate concentration–time curve shape parameters. Accordingly, we compared observed and predicted half-life, C_max and T_max (Tables 8, 9, 10). For single dose lapatinib, the model-predicted and mean observed (n = 10 studies) half-lives were 10.0 and 10.3 h, respectively. For multiple dose lapatinib, the model predicted and mean observed (n = 6 studies) half-lives were 10.2 and 16.6 h, respectively. Overall, half-life MPE% was −8.1 and MAPE% was 28.1. In healthy subjects, the model overpredicted the half-life in 78 % of the studies (MPE% of 14.6) and in cancer patients, the model underpredicted the half-life in all studies (MPE% of −38.0).

Table 8.

Single dose lapatinib observed and predicted human half-life (t_1/2), maximum concentration (C_max) and time of maximum concentration (T_max)

Dose (mg)	Observed t1/2 (h)	Predicted t1/2 (h)	T1/2 PE%c	Observed Cmax (nM)	Predicted Cmax (nM)	Cmax PE%c	Observed Tmax (h)	Predicted Tmax (h)	Tmax PE%c	Reference
50	6.0a (4.8–7.5)	10.0	66.7	124 (88–177)d	66	−46.7	3.0 (2.0–6.0)f	3.75	25.0	[4]
100	6.3a (5.6–7.0)	10.0	58.7	213 (148–308)d	132	−38.1	4.0 (2.5–5.9)f	3.75	−6.3	[4]
100	9.6a (8.5–10.7)	10.0	4.2	198 (174–224)e	132	−33.3	4.0 (2.5–8.0)f	3.75	−6.3	[14]
175	8.2a (6.7–9.9)	10.0	22.0	380 (241–599)d	231	−39.3	3.0 (2.0–4.0)f	3.75	25.0	[4]
250	8.8a (6.6–11.7)	10.0	13.6	546 (330–902)d	329	−39.7	4.0 (3.0–6.0)f	3.75	−6.3	[4]
250	10.2a (9.24–11.3)	10.0	−2.0	449 (360–563)e	329	−26.8	4.0 (2.5–6.0)f	3.75	−6.3	[14]
900	12.9b (10.1–18.3)	10.0	−22.5	1,740 (1,194–2,533)d	1,185	−31.9	4.0 (2.0–6.0)g	3.75	−6.3	[13]
1,200	11.5b (10.1–19.5)	10.0	−13.0	1,767 (816–3,833)d	1,581	−10.5	3.5 (2.1–6.0)g	3.75	7.1	[13]
1,600	13.9b (9.6–18.0)	10.0	−28.1	2,647 (1,793–3,903)d	2,107	−20.4	4.0 (2.0–8.0)g	3.75	−6.3	[13]
1,800	15.7b (11.0–133.1)	10.0	−36.3	2,112 (800–5,579)d	2,371	12.3	3.9 (3.0–8.0)g	3.75	−3.8	[13]

^at_1/2 is the terminal half-life geometric mean (95 % confidence interval)

^bt_1/2 is the terminal half-life median (95 % confidence interval)

^cPE% is the prediction error

^dIs the geometric mean (95 % confidence interval) of C_max

^eIs the geometric mean (range) of C_max

^fIs the median (range) of T_max

^gIs the median (95 % confidence interval) of T_max

Table 9.

Multiple dose lapatinib (25–1,200 mg) observed and predicted human half-life (t_1/2), maximum concentration (C_max) and time of maximum concentration (T_max)

Dose (mg)	Observed t1/2 (h)	Predicted t1/2 (h)	t1/2 PE%c	Observed Cmaxd (nM)	Predicted Cmax (nM)	Cmax PE%c	Observed Tmax (h)	Predicted Tmax (h)	Tmax PE%c	Reference
25	7.9a (6.4–9.8)	10.2	29.1	55 (38–81)	42	−23.7	2.7 (2.5–4.0)e	3.5	29.6	[4]
100	8.9a (6.1–12.9)	10.2	14.6	251 (150–420)	166	−33.9	3.0 (2.0–6.0)e	3.5	16.7	[4]
175	11.1a (7.3–16.8)	10.2	−8.1	429 (270–678)	290	−32.3	4.0 (3.0–6.0)e	3.5	−12.5	[4]
175	ND	10.2	NA	637	290	−54.5	ND	3.5	NA	[15]
375	ND	10.2	NA	706	622	−11.8	ND	3.5	NA	[15]
500	ND	10.2	NA	1,755 (1,308–2,375)	830	−52.7	ND	3.5	NA	[5]
650	ND	10.2	NA	2,237 (1,687–2,960)	1,078	−51.8	ND	3.5	NA	[5]
675	ND	10.2	NA	1,824	1,120	−38.6	ND	3.5	NA	[15]
900	ND	10.2	NA	1,807	1,493	−17.4	ND	3.5	NA	[15]
900	ND	10.2	NA	2,926 (2,082–4,130)	1,493	−49.0	ND	3.5	NA	[5]
900	23.1b (9.8–38.2)	10.2	−55.8	3,261 (2,270–4,683)	1,493	−54.2	4.0 (3.0–6.0)f	3.5	–12.5	[13]
1,000	ND	10.2	NA	3,184 (2,409–4,216)	1,659	−47.9	ND	3.5	NA	[5]
1,000	ND	10.2	NA	2,754 (2,203–3,442)	1,659	–39.8	ND	3.5	NA	[9]
1,200	ND	10.2	NA	2,100 (1,549–2,840)	1,990	−5.2	ND	3.5	NA	[5]
1,200	16.9b (15.1–34.3)	10.2	−39.6	2,952 (1,661–5,246)	1,990	−32.6	3.6 (3.0–7.9)f	3.5	−2.8	[13]
1,200	ND	10.2	NA	2,392	1,990	−16.8	ND	3.5	NA	[15]

ND not determined, NA not applicable

^at_1/2 is the terminal half-life geometric mean (95 % confidence interval)

^bt_1/2 is the terminal half-life median (95 % confidence interval)

^cPE% is the prediction error

^dIs the geometric mean (95 % confidence interval) of C_max

^eIs the median (range) of T_max

^fIs the median (95 % confidence interval) of T_max

Table 10.

Multiple dose lapatinib (1,250–1,800 mg) observed and predicted human half-life (t_1/2), maximum concentration (C_max) and time of maximum concentration (T_max)

Dose (mg)	Observed t1/2 (h)a	Predicted t1/2 (h)	t1/2 PE%b	Observed ${\mathrm{C}}_{max}^{\S }$ (nM)	Predicted Cmax (nM)	Cmax PE%b	Observed Tmax (h)	Predicted Tmax (h)	Tmax PE%b	Reference
1,250	ND	10.2	NA	4,182 (2,702–6,488)c	2,073	−50.4	3.5 (2.0–10)e	3.5	0	[7]
1,250	ND	10.2	NA	4,870 (3,700–6,419)d	2,073	−57.4	ND	3.5	NA	[8]
1,250	ND	10.2	NA	2,220 (1,119–4,389)d	2,073	−6.6	3.0 (1.5–8.0)f	3.5	16.7	[10]
1,250	ND	10.2	NA	3,253 (2,289–4,612)d	2,073	−36.3	3.0 (2.6–8.0)f	3.5	16.7	[12]
1,500	ND	10.2	NA	3,390 (2,547–4,526)d	2,488	−26.6	3.4 (0.0–6.0)f	3.5	3.2	[6]
1,500	ND	10.2	NA	4,251 (2,530–7,108)d	2,488	−41.5	3.0 (0.0–12.2)f	3.5	16.7	[11]
1,600	ND	10.2	NA	3,666 (2,341–5,765)d	2,654	−27.6	ND	3.5	NA	[5]
1,600	26.2 (12.9–48.3)	10.2	−61.1	5,354 (3,334–8,598)d	2,654	−50.4	5.1 (0.9–8.0)g	3.5	−31.4	[13]
1,600	ND	10.2	NA	3,304d	2,654	−19.7	ND	3.5	NA	[15]
1,800	ND	10.2	NA	3,253d	2,986	−8.2	ND	3.5	NA	[15]
1,800	21.8 (18.5–104.5)	10.2	−53.2	4,015 (1,595–10,102)d	2,986	−25.6	3.9 (3.0–7.9)g	3.5	−10.3	[13]

ND not determined, NA not applicable

^at_1/2 is the terminal half-life median (95 % confidence interval)

^bPE% is the prediction error

^cIs the mean (90 % confidence interval) of C_max

^dIs the geometric mean (95 % confidence interval) of C_max

^eIs the median (90 % confidence interval) of T_max

^fIs the median (range) of T_max

^gIs the median (95 % confidence interval) of T_max

For single dose lapatinib, our model-predicted T_max to be at 3.75 h post administration and the average observed T_max was 3.7 h. The MPE% and MAPE% were −6.3 and 9.6, respectively. For multiple dose lapatinib, our model-predicted steady-state T_max was 3.5 h and the mean observed T_max was 3.5 h. The MPE% and MAPE% were 1.6 and 14.6, respectively.

Regarding C_max, the actual values versus our model-simulated values are graphically shown in Fig. 4e, f. The single dose predictions directly paralleled the actual C_max (MPE% and MAPE% of −28.8 and 28.8, respectively). For the multiple dose predictions, our model underestimated steady-state C_max (MPE% and MAPE% of −33.9 and 33.9, respectively). However, when we decreased liver metabolism to mimic hepatic impairment (as we did with AUC), the predicted steady-state C_max for moderate liver dysfunction closely mirrored the observed data.

Overall, our PBPK model properly predicted lapatinib pharmacokinetic parameters from actual populations. As our model was developed with data from healthy subjects, the predictions were better for studies which were conducted in healthy subjects versus patients with solid tumors. To improve our model simulations for cancer patients, we altered our liver metabolism parameter to reflect hepatic impairment resulting from disease and/or age. With this modification, the model more precisely reproduced actual AUCs and C_max from patients with solid tumors.

Sensitivity analysis

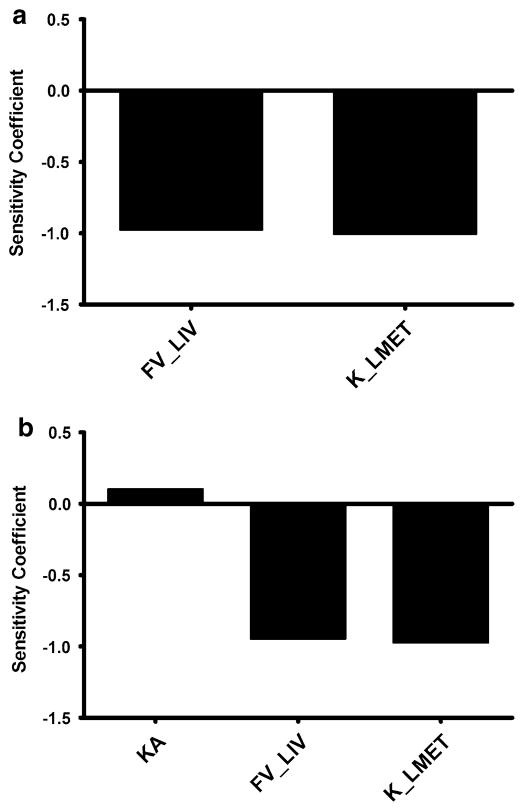
The normalized sensitivity coefficients for the mouse (60 mg/kg dose) and human (100 mg dose) PBPK models with respect to plasma AUC are shown in Fig. 5. Only parameters with sensitivity coefficients greater than 0.1 are shown. In both models, no normalized sensitivity coefficient was greater than ±1, indicating that there are no amplified parameter errors.

Fig. 5.

Calculated sensitivity coefficients for PBPK model parameters with respect to plasma AUC for the (a) mouse model and (b) human single dose model. Only parameters with sensitivity coefficients>0.1 are shown. FV_LIV fractional volume of liver, K_LMET first-order rate constant for liver metabolism; and KA first-order rate constant for absorption from intestinal lumen

Discussion

Physiologically based pharmacokinetic models have been developed for numerous antineoplastic agents including methotrexate [27, 28], cisplatin [29], actinomycin-D [30], 5-fluorouracil [31], capecitabine [32], 1-β-D-arabinofuranosylcytosine [33], adriamycin [34–36], topotecan [37] and docetaxel [38]. The need for these types of pharmacokinetic models for chemotherapeutics is great because of the challenges presented by this class of pharmaceutical compounds, specifically the narrow therapeutic index which is governed by drug distribution in the body. With PBPK modeling, the dynamics of drug distribution can be predicted using basic information on physiochemical properties, transport, biotransformation and excretion, thus leading to a better understanding of target tissue exposure resulting in either a therapeutic or toxic effect.

We have successfully developed a first-generation PBPK model for the dual EGFR/HER2 tyrosine kinase inhibitor lapatinib. This drug is a mere decade old and has only been approved by the FDA for the treatment of breast cancer since 2007. Consequently, the intricacies of the pharmacokinetics are still being elucidated. To our knowledge, the details of mouse tissue distribution of lapatinib have been limited to plasma and brain [39, 40] whereas, in humans, only plasma concentrations have been determined [3–15]. The tissue distribution of [¹⁴C] lapatinib was resolved by whole-body autoradiography in rats with detectable amounts quantified in the blood, brain, cerebrospinal fluid, harderian gland, heart, kidney, liver and muscle [41]. Our mouse data demonstrated tissue:blood concentration ratios that were comparable to those presented by Polli et al. [41], indicating that lapatinib exhibits similar distribution dynamics in these two rodents. Considering the autoradiography data [41] and the work presented herein, we now have a comprehensive assessment of the biodistribution of lapatinib in rats and mice.

By incorporating the mouse tissue distribution data into a PBPK model, we were able to effectively predict lapatinib concentrations in mouse plasma, brain, heart, lung, kidney, intestine, liver and slowly perfused tissue after oral doses of 30, 60 and 90 mg/kg. Subsequently, by taking into account interspecies differences in physiology and physiochemistry, we extrapolated this PBPK model to humans. To validate the human model, we were only able to compare our model simulations with observed plasma lapatinib concentrations and pharmacokinetic parameters, as there is no data in the literature regarding human tissue levels. Our model correctly predicted plasma exposure [23], C_max, T_max and half-life following single doses of lapatinib ranging from 50 to 1,800 mg and following multiple doses of lapatinib ranging from 25 to 1,800 mg. After taking the clinical trial subject/patient characteristics into consideration, it was evident that our model predictions were more accurate for healthy subjects than for patients with solid tumors (whose AUCs and C_max were consistently underpredicted). This was not surprising given that our human PBPK model was developed with data from healthy subjects. In addition to the absence or presence of solid malignancies, the other major biological differences between these two populations were age and liver function. Both most likely contribute to hepatic impairment which results in a decrease in lapatinib clearance via metabolism and a subsequent increase in tissue exposure. When we altered our PBPK model to mimic hepatic impairment by decreasing the first-order rate constant for liver metabolism, the simulations for moderate hepatic impairment (incorporated as a 35 % decrease in liver metabolism) closely reflected the observed AUC and C_max in cancer patients. Thus, our model can not only predict lapatinib plasma pharmacokinetics in healthy subjects but, with a minor metabolic alteration, can also predict the pharmacokinetics of this drug in the plasma of patients with solid malignancies.

The human PBPK model additionally facilitates the estimation of tissue levels of lapatinib. There is incredible utility in this application of the model, as it is not feasible to collect actual tissue concentration data from humans. Based on the adverse reactions to lapatinib observed in clinical trials, we can speculate as to the organ distribution of this drug. It is probable that the heart, liver, intestine and lung are exposed to significant levels of lapatinib as patients administered this compound have experienced decreased left ventricular ejection fraction, QT prolongation, hepatotoxicity, diarrhea and interstitial lung disease/pneumonitis. From largest to smallest, our multiple dose (1,250 mg q24 h) model-predicted ratios of lapatinib tissue:plasma AUCs_τ were intestine (9.1), lung (8.2), liver (6.0), kidney (5.3), heart (1.1), slowly perfused tissue (0.3) and brain (0.05). Thus, for all organs in which adverse reactions to lapatinib have been noted, our model predicted tissue:plasma AUC ratios greater than 1, indicating substantial distribution into these tissues. Regarding brain, our model predicted low levels of lapatinib, which is consistent with the poor central nervous system (CNS) penetration observed in mice, owing to ABCB1- and ABCB2-mediated efflux [39]. Despite low lapatinib exposure in normal brain tissue, this drug has been shown to reduce the burden of metastatic breast cancer cells in the brains of mice [42] and have a modest CNS antitumor activity in human patients with brain metastases from HER2-positive breast cancer [43].

In summary, we have been able to successfully develop a PBPK model of lapatinib in mice, scale this model to humans and accurately predict the pharmacokinetics of this drug in human plasma over a wide range of doses. Additionally, our model also facilitated the estimation of various tissue exposures to lapatinib, which harmonize with the organ-specific toxicities documented in clinical trials. We acknowledge that this is a first-generation PBPK model which can be further improved with a greater understanding of lapatinib absorption, distribution, metabolism and excretion garnered from subsequent in vitro and in vivo studies. Moreover, our base model can be expanded to include other pharmacokinetic determinants, including efflux transporters, metabolite generation, combination dosing, etc., to make this PBPK model even more beneficial for the prediction of lapatinib disposition in both mouse and man.