The Effects of Practice on Coordination

Abstract

We review practice-induced changes in two variance components defined based on the uncontrolled manifold hypothesis: One of them affects task performance while the other one does not. Practice leads to a drop in the former component (higher accuracy), while the latter can drop, stay unchanged, or even increase. The last scenario can be achieved with practice that challenges performance stability.

INTRODUCTION: TRADITIONAL VIEW ON MOTOR LEARNING

Practice may have a number of goals, for example, to become stronger, faster, or more accurate. In this review, we consider only the latter goal of practice when the timing of a task and the level of effort are either prescribed or can be selected freely by the performer. Such tasks are common in both everyday life (e.g., slicing cheese, moving a cup of coffee filled to the brim, and walking along a narrow path) and athletics (e.g., archery, playing pool, putting in golf, and some gymnastic exercises). All these movements, just as all natural human movements, are characterized by problems of motor redundancy (3). This implies that the number of constraints associated with typical tasks is lower than the number of variables produced by elements (elemental variables or degrees-of-freedom, DOFs) at any level of description of the neuromotor system.

In his studies of professional blacksmiths, Bernstein (2) showed that the consistent motor performance (consistent trajectories of the hammer) could result from variable behavior of individual elements involved in the movement (variable joint rotations). Based on these and other studies, Bernstein offered a view on a staged process involved in skill acquisition. This, now classical, view (4, 32) considers three stages of motor learning. At the first stage, redundant DOFs are eliminated by adding constraints to the movement. At the second stage, some DOFs are gradually released which results in added variability at the level of elements. At the third stage, the elements are coordinated to utilize the reactive phenomena induced in movement execution. In this review, we will describe an alternative view that does not involve changes in the number of DOFs but rather changes in their co-variation patterns in the process of motor learning (14, 35).

When one deals with a redundant system, there are different strategies of achieving similar levels of accuracy. For example, variability of the output of each element can decrease with practice. Alternatively, the outputs of individual elements may remain noisy but their co-variation can improve leading to lower variability of a functionally important performance variable, to which all of the elements contribute. In this review, we present evidence for a less obvious strategy: Individual elements become more variable with practice while their combined output becomes less variable. Our studies are based on a recently developed view on the problem of motor redundancy, which considers the apparently redundant design of the neuromotor system as abundant, that is, as contributing to both stability of motor actions and the ability to perform multiple tasks based on the same set of elements. The main hypothesis has been that properly organized practice can lead to an increase in variability within the space of elemental variables accompanied by a drop in the variability in performance variables due to the improved co-variation.

MOTOR ABUNDANCE, SYNERGIES, AND THE UNCONTROLLED MANIFOLD HYPOTHESIS

The alternative view on the apparently redundant design of the human body has been cast as the principle of abundance (11, 18). This principle is based on a general view that the system for movement production is physical (physiological), not computational (17). The word “controller” is used in this framework as a substitute for decision-making processes within the central nervous system with currently unknown physics. According to the principle of abundance, families of solutions are always facilitated for any motor task in the space of elemental variables. Such families reflect different stability of the movement trajectory in different directions within the space of elemental variables: Directions that correspond to changes in important performance variables are relatively more stable compared to directions that do not change those variables. Effectively, relatively large amounts of variability are produced compatible with task-related patterns of important performance variables. Besides being a reflection of high stability of performance, these large amounts of variability allow performing secondary tasks with the same set of elemental variables without negative interference with the primary task (37). For example, a soccer player kicking a ball has to use many muscles of the trunk and extremities that are also involved in providing stability of the vertical posture. A toddler kicking a ball frequently loses balance and falls. When a person learns how to unite the involved muscle groups into functional units (synergies) that provide postural stability while allowing large amounts of variability in the muscle activation space, kicking the ball can be performed without causing postural problems. The variability resulting from such an abundant design has been viewed as a prerequisite for flexibility and adaptability in biological behavior (15, 25).

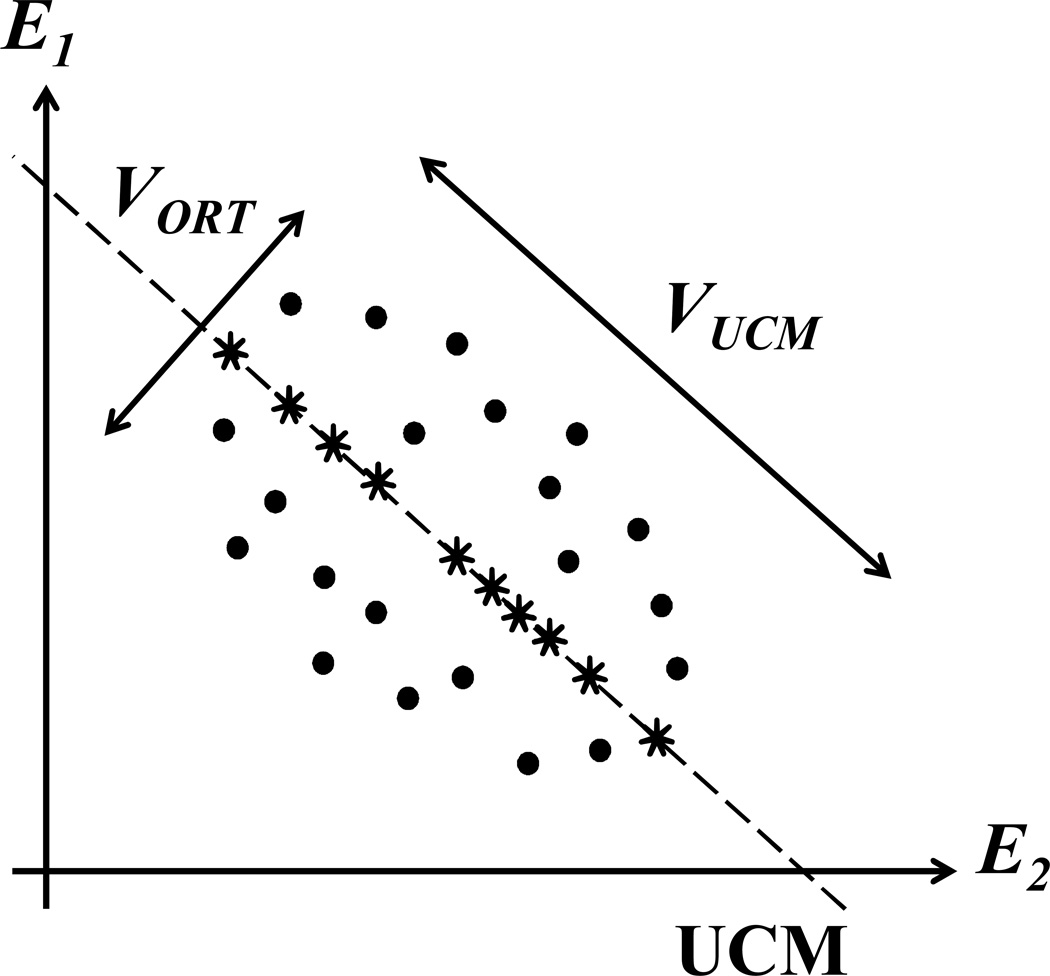
Neural mechanisms that bring about task-specific patterns of variability have been termed synergies (16, 20). Synergies can be characterized by two indices, the average (across trials) sharing of important performance variables among elemental variables and across-trials co-variation in the space of elemental variables. The latter characteristic has been quantified within the framework of the uncontrolled manifold (UCM) hypothesis (30). The UCM hypothesis states that neural mechanisms act to constrain variability in a redundant space of elemental variables to a sub-space (UCM) compatible with a desired value of an important performance variable. In contrast, variability along the UCM is relatively less constrained. The stars in Figure 1 are exact solutions for a task to produce a fixed sum of two elemental variables (E₁ and E₂), while the dots are attempts with errors. The dashed line is the UCM for this task, and variance along the UCM does not affect the performance (V_UCM, sometimes addressed as “good variance”), while variance orthogonal to the UCM (V_ORT) affects task performance and, therefore, it is sometimes addressed as “bad variance”. A synergy index has been used: ΔV = (V_UCM − V_ORT)/V_TOT, where V_TOT is the total variance in the space of elemental variables and each variance index is computed per DOF in the corresponding space. When ΔV > 0, it is concluded that a motor synergy stabilizes the performance variable, for which the index has been computed.

Figure 1.

An illustration of the UCM hypothesis for a task of producing a constant sum of two elemental variables (E₁ and E₂). The stars are exact solutions that belong to the UCM, while the dots are attempts with errors. V_UCM is the variance along the UCM within which deviations have no influence on the performance. V_ORT is the variance in the direction orthogonal to the UCM. The variance of performance is determined by V_ORT.

CHANGES IN MOTOR SYNERGIES WITH PRACTICE

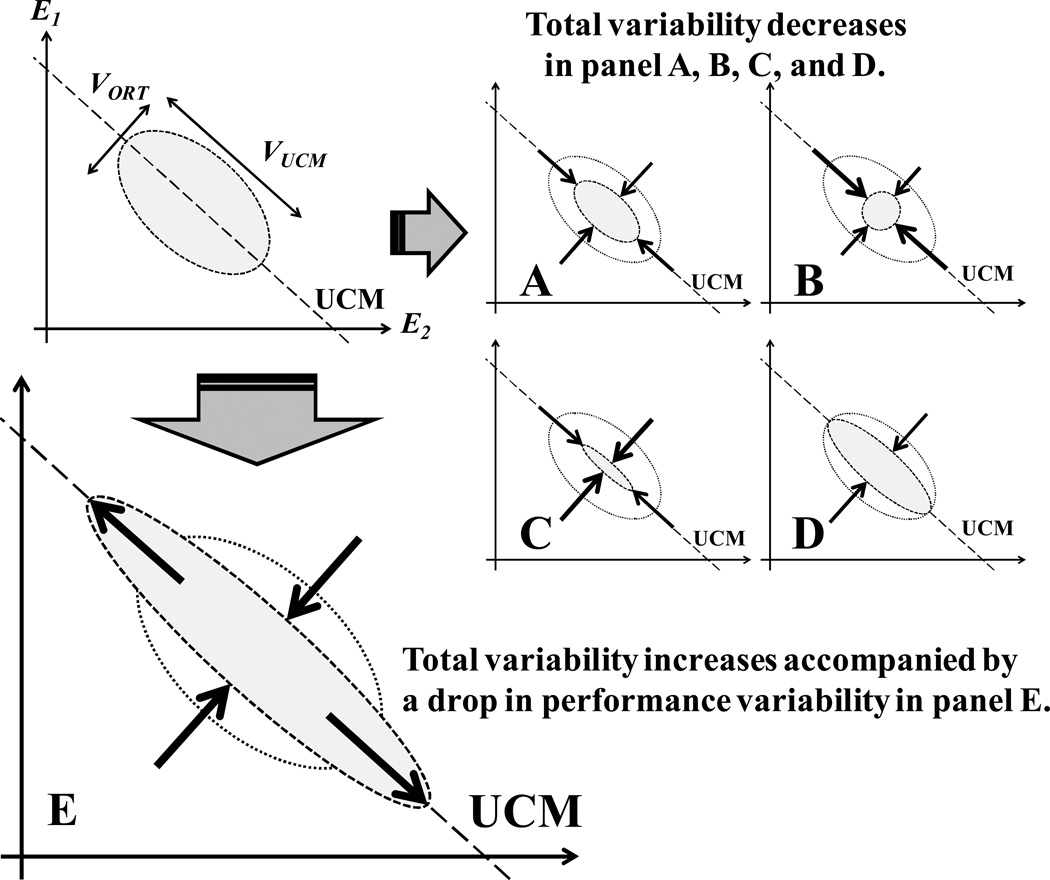
Practice with the purpose to increase accuracy is expected to lead to more consistent performance, which means that a drop in the corresponding V_ORT is expected. Changes in V_UCM are much harder to predict because, by definition, V_UCM has no effect on performance. Figure 2 illustrates five possibilities of changes in V_UCM (and ΔV) with practice. First, all variance components can change proportionally resulting in no changes in ΔV (Figure 2A). Second, ΔV can drop if V_UCM decreases more than V_ORT (Figure 2B). In the other three scenarios (Figure 2C–E), ΔV is increased, which may be associated with a relatively small drop in V_UCM, no changes in V_UCM, or even an increase in V_UCM (cf. (17)). Data compatible with all the scenarios illustrated in Figure 2 have been published: Indeed, a drop in the synergy index (9), no change in this index (8), and an increase in the index (12, 35) have been reported after practice emphasizing accuracy of performance. Our main hypothesis is illustrated conceptually by panel E in Figure 2. This panel shows that an increase in variability within the space of elemental variables (caused by an increase in V_UCM) can be accompanied by a drop in the variability in the performance variable (reflected in low V_ORT) due to the improved co-variation. Until recently, no studies showed changes in the structure of variance corresponding to Fig. 2E.

Figure 2.

Five possible changes in the structure of variance are illustrated in the space of two elemental variables involved in a task similar to the one illustrated in Fig. 1. (A) ΔV remains the same due to proportional changes in V_UCM and V_ORT. (B) ΔV decreases because of V_UCM drops more than V_ORT. (C), (D), and (E) ΔV is increased due to the relative increase of V_UCM compared to V_ORT: (C) V_UCM drops less than V_ORT; (D) V_UCM does not change while V_ORT drops; (E) V_UCM and V_ORT change in opposite directions. Panel E conceptually illustrates our main hypothesis by showing that an increase in variability within the space of elemental variables (caused by an increase in V_UCM) is accompanied by a drop in the variability in the performance variable (reflected in low V_ORT) due to the improved co-variation.

Recent studies (reviewed in (17)) have suggested a two-stage process of how DOFs are coordinated, rather than frozen and released, to stabilize performance. Both stages were observed in a study of accurate three-finger force production with unexpected transcranial magnetic stimuli applied over the contralateral primary motor cortex (21). The first stage was characterized by a significant drop in V_ORT with minimal changes in V_UCM, while during the second phase V_UCM decreased with little change in V_ORT. The first stage was interpreted as developing a synergy with respect to the explicit task requirement. During the second stage, performance was tuned with respect to other factors such as coping with the perturbing effects of the transcranial magnetic stimuli. This resulted in selecting particular combinations of individual finger forces within the UCM leading to a smaller area within the UCM that was used by the subject. During the second stage, the synergy index dropped. It is also possible that, during the second stage, V_ORT drops to such a low level that the reduction in the variability of performance approaches a plateau, while V_UCM continues to drop. During this second stage, practice optimizes features of performance other than those explicitly defined by the task, for example those related to possible perturbations (as in (21)), comfort, avoiding fatigue, etc. As a result, the synergy index computed for the explicitly defined performance variables drops. An interpretation of the two-stage process mediating effects of practice on coordination has been developed (17) based on the equilibrium-point hypothesis (10).

The idea on the two stages of changes in motor synergies suggests that learning a motor task involves developing coordination among elements rather than searching for a unique solution for optimal performance. It follows naturally the classical idea of “repetition without repetition” introduced by Bernstein (3), which implies that the individual repeats a process of achieving the task goal under varying initial conditions and external forces, which results in non-repetitive patterns of elemental variables providing for stability of important features of the action.

IT IS GOOD TO HAVE “GOOD VARIABILITY”

Human movements are always performed in varying external conditions, which are impossible to predict with certainty. In addition, excitability of neural structures involved in movement production varies from trial to trial. These factors make all movements, even well-practiced ones, unlike each other and emphasize the requirements for movement stability. Under this term, we imply an ability to accomplish a task (a final value or a time profile of an important performance variable) under varying initial conditions and possible transient perturbations. This feature is reflected in the structure of across-trials variance in the space of elemental variables quantified with the indices V_UCM, V_ORT, and ΔV. In particular, low V_UCM, which seems irrelevant to movement outcome, is a sign of stereotypy, a control strategy that may be able to accomplish the task but only in a highly sterile environment, when no major changes in the initial conditions and external forces happen. In more natural conditions, we believe that sufficiently high V_UCM values reflect stability of the movement. One more benefit of high amount of V_UCM is that the individual has the flexibility of performing a secondary task while keeping the stability of the first task performance. The larger range of the V_UCM allows the two solution spaces for the two tasks to overlap (37).

Imagine walking down the hallway with a mug filled with coffee held in the hand. This everyday task is performed easily, while it represents a very complex mechanical problem of keeping the vertical axis of the mug parallel to the direction of gravity at all times despite the poorly predictable ground reaction forces acting at each step and other forces that propagate through the mechanically linked body segments. Preserving stability of the important variable (mug orientation) is possible only with the help of a multi-joint synergy that channels all the perturbations into a kinematic sub-space compatible with the required mug orientation (cf. 24). Having large amounts of V_UCM also allows using the same arm to perform another task (e.g., pressing on the door handle with the elbow) without spilling the coffee.

Several of our and other’s studies have documented relatively low amounts of V_UCM in populations characterized by impaired motor coordination such as healthy older persons (13), persons with Down syndrome (5, 31), and patients with Parkinson’s disease and cerebellar disorders (27, 28). The purpose of a series of our recent studies (33, 34) has been to find a way to encourage high amounts of V_UCM while simultaneously making sure that performance variability is low (low V_ORT).

ENCOURAGING MORE “GOOD VARIABILITY”

The idea of challenging stability of action can be traced back to the classical book by Nikolai Bernstein “On Dexterity and Its Development” (4). Bernstein had an insight that achieving top-level performance in athletes, such as gymnasts, and circus performers requires practicing the task under varying initial conditions and external forces. Such manipulations naturally challenge stability of the practiced action.

There are a few important features in the practice schedule we designed to improve performance and simultaneously encourage large amounts of “good variability”. These include using non-repetitive tasks (to discourage development of stereotypical solutions) and manipulating the stability conditions for performance thus making the task more and more challenging in terms of stability without changing any of the other task attributes. While this task can be implemented for various actions, in the first studies we explored the effects of practice on accurate multi-finger force production, a task that has been well developed to address issues associated with the problem of motor redundancy ((22), reviewed in (36)).

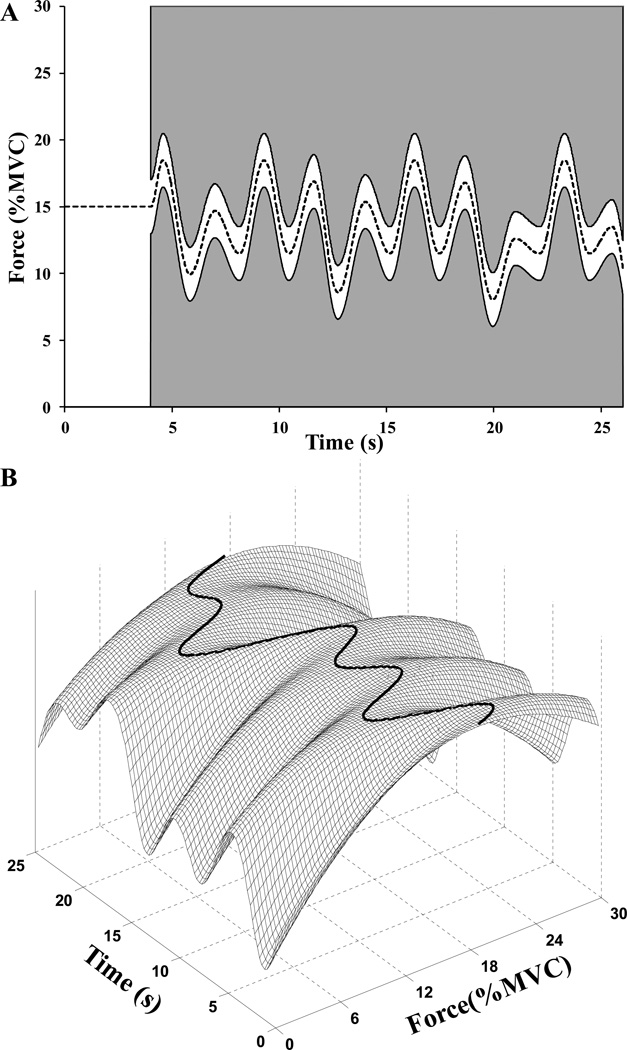
We instructed the subjects to follow a template with the total force produced by two or more fingers (a redundant task, R-task). The template is built with concatenated half-cycles of sine-like patterns selected from a set with normal distributions of the amplitude and duration parameters (as shown in Figure 3A). A new template was presented to subjects for each attempt. We manipulated stability of the task by a gain factor (G), which altered force feedback (F_FB) on the monitor:

$$F_{\mathit{\text{FB}}}=F_{\mathit{\text{ACT}}}+G\times \mathit{\text{sign}}(F_{\mathit{\text{ACT}}}-F_{\mathit{\text{TASK}}})\times {(F_{\mathit{\text{ACT}}}-F_{\mathit{\text{TASK}}})}^2;$$

Figure 3.

(A) The task template is built with randomly selected and concatenated half-cycle sine-like patterns. (B) The adjustable instability factor (G) modifies the visual feedback so that the task becomes similar to walk along a ridge of a mountain.

To trace the target under such feedback is similar to moving along a ridge of a mountain with the slope modifiable with the G factor (Figure 3B). As the subjects improved their performance, the G factor increased thus making the conditions less and less stable.

A single session of practice in such conditions led to rather dramatic changes in the structure of variance in the space of commands to fingers (finger modes, (7, 19)). Our study compared effects of practice by a redundant set of fingers (R-task) with a comparable amount of practice of a similar task by each finger separately (non-redundant, NR-task) (33). Accuracy of performance improved similarly in both groups (V_ORT dropped by similar proportions). In contrast V_UCM increased in the group that practiced the R-task while it dropped parallel to V_ORT in the group that practiced the NR-task. These effects of practice on the two variance components lasted for at least two weeks as the retention test showed.

Note that, even prior to practice, V_UCM >> V_ORT, that is, there were synergies stabilizing the total force time profiles. As a result, the increase in V_UCM after practice was larger than the drop in V_ORT resulting in the counter-intuitive increase in the total amount of variance in the space of commands to fingers. In other words, this task design allowed combining higher variability in the space of elemental variables with lower variability in important performance variables.

In a follow-up study (34), we observed similar effects in both younger and older persons, again after a single practice session that lasted for less than 1.5 h. In both studies, practicing the R-task led to an increase in the total amount of variance in the space of commands to fingers. This was accompanied by a significant improvement in accuracy of performance. A schematic illustration of the main results of these two studies is presented in Figure 2E.

Our second study also led to a somewhat discouraging result: After practice, performance of a different task improved while there was no transfer of the effects on the structure of variance. This could be due to using a simpler task as the transfer task: The subjects were asked to track a perfect sine-wave. The question whether the effects of such practice on the structure of variance and synergy index can be transferred to more ecologically valid, more complex tasks remains open. Note that several recent studies described limited transfer effects of practice in a novel sensory feedback environment (23, 29), while other studies have shown more general transfer effects of training in an unusual force field (1, 6). The controversy of transfer effects in motor learning makes us cautious but optimistic about developing the practice protocol for rehabilitation.

CONCLUDING COMMENTS

Our research shows that practice can lead to changes in coordination as reflected by changed indices of motor synergies. Such effects are not limited to young healthy persons as shown by studies of the beneficial effects of practice on performance and synergy indices in individuals with Down syndrome (31) and in healthy elderly persons (26, 34). The described protocol to encourage flexible involvement of fingers can be readily applied to hand training in populations with significantly decreased relative amounts of “good variability”. We hope that effects of such training will transfer to prehensile tasks and improve stability of the hand action in ecologically valid tasks. The protocol with adjustments in stability can also be used to train a wide range of motor tasks, such as reaching movement, postural tasks, and locomotion. The positive results of improving motor synergies by properly designed tasks make us optimistic about possible future developments of the method for motor rehabilitation.

Summary.

Practice can lead to an increase in total variance within a redundant system combined with more accurate performance and improved stability.