A Bayesian Model for Misclassified Binary Outcomes and Correlated Survival Data with Applications to Breast Cancer

Abstract

Breast cancer patients may experience ipsilateral breast tumor relapse (IBTR) after breast conservation therapy. IBTR is classified as either true local recurrence (TR) or new ipsilateral primary tumor (NP). The correct classification of IBTR status has significant implications in therapeutic decision-making and patient management. However, the diagnostic tests to classify IBTR are imperfect and prone to misclassification. In addition, some observed survival data (e.g., time to relapse, time from relapse to death) are strongly correlated with IBTR status. We present a Bayesian approach to model the potentially misclassified IBTR status and the correlated survival information. The inference is conducted using a Bayesian framework via Markov Chain Monte Carlo simulation implemented in WinBUGS. Extensive simulation shows that the proposed method corrects biases and provides more efficient estimates for the covariate effects on the probability of IBTR and the diagnostic test accuracy. Moreover, our method provides useful subject-specific patient prognostic information. Our method is motivated by, and applied to, a dataset of 397 breast cancer patients.

1. Introduction

Breast conservation therapy (BCT) offers similar overall survival and disease-free survival rates as does mastectomy in breast cancer patients [1]. Approximately 8%-20% of patients experience ipsilateral breast tumor relapse (IBTR), defined as the recurrence of tumor in the previously treated breast, after undergoing BCT [2, 3, 4, 5]. IBTR is often classified as either true local recurrence (TR) or new ipsilateral primary tumor (NP). TR is described as “cases consistent with the regrowth of malignant cells not removed by surgery or not killed by radiotherapy”, whereas NP is described as “de novo cases of malignancies arising from mammary epithelial cells of the residual breast tissue” [6]. The correct classification of IBTR status has significant implications in therapeutic decision-making and patient management; for example, TR patients will benefit from aggressive hormone therapy, chemotherapy, and/or additional radiotherapy, whereas NP patients may need only mild treatment. However, because of the inherent uncertainties of the clinical and pathologic criteria used for classification, the diagnostic tests to classify IBTR are subject to misclassification, and the validity of these tests has not been evaluated because there is no widely recognized classification standard for IBTR.

We thus developed a Bayesian method to (1) estimate the accuracy (i.e., sensitivity and specificity) of each diagnostic test to help clinicians make better decisions on which test to use based on the sensitivity-specificity trade-off; (2) quantify the covariate effects on the probability of IBTR's being NP and on the hazards of IBTR recurrence and death; and (3) provide useful prognostic information to future patients experiencing IBTR, i.e., the prediction of the IBTR status and the median survival time (i.e., from IBTR to death).

1.1. A motivating dataset

Our methodology development has been motivated by the dataset consisting of 397 patients with invasive breast cancer who underwent BCT between 1970 and 2005 at The University of Texas MD Anderson Cancer Center and later developed IBTR as a first recurrence. The variables we collected included patient characteristics (age, race, family history of breast cancer, other cancer history), primary tumor characteristics (contralateral breast cancer, i.e., the occurrence of a second independent primary cancer in the other breast, location, histology, stage, size, estrogen receptor [ER] status), treatment characteristics (surgery, radiation), and patient status at last follow-up. ERs are tissue markers useful in assessing prognosis in breast cancer patients. An ER positive (ER+) score indicates that estrogen is causing the tumor to grow and that the cancer should respond well to hormone-suppression treatments, while ER negative (ER-) score implies that the tumor is not driven by estrogen [7].

IBTR patients in this dataset were classified as having either NP or TR using two diagnostic tests based on readily available clinical and pathologic data. Test 1 is based on tumor location and histologic subtype: IBTR was defined as TR if the tumor was located within 3 cm of the primary tumor bed and its histologic subtype was consistent with that of the primary tumor; otherwise, IBTR was defined as NP [8, 9, 10]. Test 2 is based on tumor location, histologic subtype, and ER status: IBTR was defined as TR if the tumor was located within 3 cm of the primary tumor bed, and its histologic subtype and ER status were consistent with those of the primary tumor, otherwise, IBTR was defined as NP [11, 12].

Because two criteria (tumor location and histology) are used in both test 1 and test 2 and because one additional criterion (ER status) is used in test 2 only, the following inherent relationships are true: NP by test 1 implies NP by test 2; TR by test 1 and NP by test 2 implies no change in tumor location and histology but change in ER status; and NP by test 1 and TR by test 2 is a null event. Therefore, test 2 always classifies more patients' IBTR as NP than does test 1; in our dataset, test 2 classified 213 IBTRs (53.6%) as NP, whereas test 1 classified 196 IBTRs (49.4%) as NP. If NP represents disease and TR represents nondisease in the conventional definitions of sensitivity and specificity, test 2 always has higher sensitivity but lower specificity than test 1. While clinicians may use test 2 if higher sensitivity is preferred or use test 1 if higher specificity is preferred, it is essential to develop a methodological framework that provides accurate estimates of sensitivity and specificity for each diagnostic test to help clinicians select the test that best fits their preference.

1.2. Statistical challenges and solutions

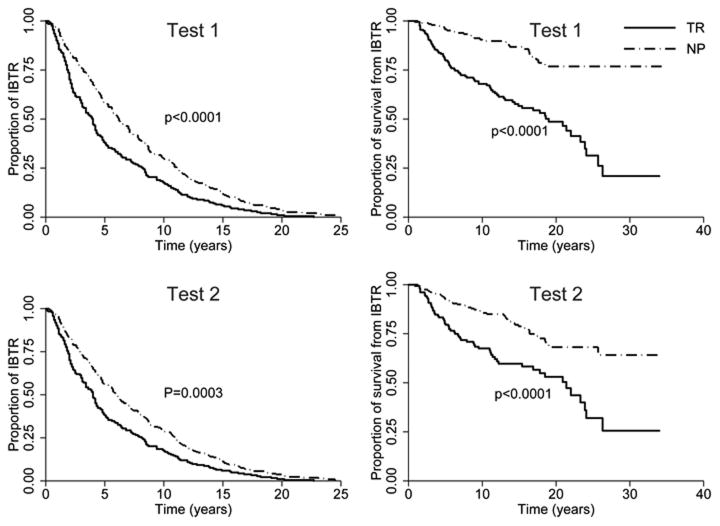
Figure 1 displays the time plot of one patient, where t₁ represents the time from BCT to IBTR (referred to as time to relapse) and t₂ represents time from IBTR to cause-specific death or censoring (referred to as time from IBTR to death). An interesting feature of our patient dataset is the presence of two survival times and their strong correlation with IBTR status. To visualize the correlation, Figure 2 shows the Kaplan-Meier curves displaying differences in time to relapse (left panels) and time from IBTR to death (right panels) for patients classified as NP and TR by test 1 (top panels) and test 2 (bottom panels). Specifically, the left panels show that TR patients had shorter time to relapse than NP patients (mean: TR 5.4 years vs. NP 7.6 years; p< 0.0001 from test 1; mean: TR 5.4 years vs. NP 7.4 years; p= 0.0003 from test 2). The right panels of Figure 2 show that TR patients also had shorter time from IBTR to death than NP patients (mean, TR 5.5 years vs. NP 5.9 years; p< 0.0001 from test 1; mean, TR 5.6 years vs. NP 5.8 years; p< 0.0001 from test 2). If properly included in the model, this survival information can be used to help classify IBTR. Consider an extreme case as an example: If all NP patients lived longer than 15 years from IBTR and all TR patients died before 15 years from IBTR, then the length of survival time from IBTR would perfectly classify the IBTR status. Although our dataset does not reflect this perfect dichotomy, the large gaps between NP and TR patients' Kaplan-Meier curves provide useful information on the IBTR status.

Figure 1.

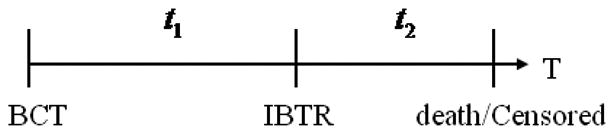
Time plot of one patient. t₁ is the time from BCT to IBTR and t₂ is time from IBTR to cause-specific death or censoring

Figure 2.

Kaplan-Meier curves displaying differences in time to relapse (left panels) and time from IBTR to death (right panels) for patients classified as having new primary tumors (NP) and true recurrences (TR) by test 1 (top panels) and test 2 (bottom panels).

To identify and quantify the risk factors associated with the binary IBTR status, researchers often use binomial regression models, which assume that the variables included in the model are accurately measured. In practice, categorical variables are often subject to misclassification, and continuous variables are subject to measurement error. Misclassification is due to many factors, including inaccuracy of data collection methods, limited sensitivity and specificity of the diagnostic tests, inadequacy of information derived from medical or other records, and recall bias in assessing exposure status [13]. Misclassification in binomial regression yields biased estimators of the association of covariates with response [14, 15].

Misclassification may occur in outcome variables, covariates, or both. In this article, we address misclassification in outcome variables. Magder and Hughes [16] showed that corrected odds ratios can be obtained by incorporating external estimates of test sensitivity and specificity into the likelihood for logistic regression. However, in many practical cases, a gold standard or a validation subsample either does not exist or may be too expensive or invasive to obtain. Therefore, it is impossible to have external estimates of sensitivity and specificity. In addition, Magder and Hughes [16] treated test sensitivity and specificity as fixed values and did not account for their uncertainty. To address this issue and to model the covariate effects in prevalence estimation, researchers have proposed various Bayesian models that use likelihood functions that are based on observed and latent variables [17, 18, 19] or observed variables only [20]. A unique feature of our proposed method is that the likelihood formulation incorporates both the test sensitivity and specificity and the correlated survival information, thus improving the estimation of the covariate effects on the probability of IBTR's being NP and the diagnostic test accuracy.

In the statistical literature of misclassification, a common assumption is conditional independence, i.e., that multiple diagnostic tests are independent conditional on the true disease status. This assumption is relatively strong and unrealistic in many practical situations [21]. Some models have been proposed to relax this assumption, including a model with more than two latent classes [22, 23, 24], a random effects model [25], and a model with two additional parameters [26]. Because the two diagnostic tests used in our dataset have special relationships, we propose a simple two-latent-classes model that naturally incorporates conditional dependence without using any additional parameters.

The purpose of this article is to develop a Bayesian method to model the binomial regression with misclassified binary outcome and the time to relapse and time from IBTR to death. We describe a Bayesian model, a method to relax conditional independence assumption, and model inference in Section 2. The proposed method is evaluated via extensive simulation in Section 3. We apply our method to analyze the breast cancer dataset in Section 4. Section 5 provides the discussion.

2. Statistical methodology

2.1. Model and notation

In this section, we consider two diagnostic tests for IBTR status and formulate the modeling framework. Let the subscript j = 1, 2 denote time to relapse and time from IBTR to death, respectively. Suppose y (1 if NP, 0 if TR) is the unobserved true IBTR status. Let y₁ and y₂ (1 if NP, 0 if TR) be the observed outcomes from two diagnostic tests. Let (p_k, q_k), for k = 1, 2, be the sensitivity and specificity of test k given the true IBTR status y, i.e., p_k = p(y_k = 1|y = 1) and q_k = p(y_k = 0|y = 0). We assume that p_k and q_k do not depend on covariates (non-differential assumption). Given covariate x, we use binomial regression model for the probability that the IBTR being NP with π(x) = P(y = 1|x) = g⁻¹(xβ), where β is a vector of regression coefficients and g⁻¹ is the inverse of a link function (e.g., probit, logit, complementary log-log). Specifically, we use logit link function. The likelihood of observing outcomes y₁ and y₂ for one patient is:

$$\begin{array}{lll}\hfill f(y_1,y_2|\mathit{x})& =\hfill & {[\pi (\mathit{x})p_1{p}_2+\overline{\pi }(\mathit{x}){\overline{q}}_1{\overline{q}}_2]}^{y_1{y}_2}{[\pi (\mathit{x}){\overline{p}}_1{p}_2+\overline{\pi }(\mathit{x})q_1{\overline{q}}_2]}^{{\overline{y}}_1{y}_2}\hfill \\ \hfill & \hfill & \hfill {[\pi (\mathit{x})p_1{\overline{p}}_2+\overline{\pi }(\mathit{x}){\overline{q}}_1{q}_2]}^{y_1{\overline{y}}_2}{[\pi (\mathit{x}){\overline{p}}_1{\overline{p}}_2+\overline{\pi }(\mathit{x})q_1{q}_2]}^{{\overline{y}}_1{\overline{y}}_2},\end{array}$$ (1)

where the overhead bar denotes 1 minus the variable (e.g., π̄(x) = 1 − π(x)). The likelihood derivation (Appendix A) assumes that two diagnostic tests are independent conditional on the true IBTR status (conditional independence assumption). This assumption will be relaxed in Section 2.2. The likelihood formulation involves only the binomial regression with misclassified outcome and is essentially identical to model (2) of Tu et al. [17] or model (2) of McInturff et al. [20].

Next, we extend the above model by including the time to relapse t₁ and the time from IBTR to death t₂ (Figure 1). Following the notation of Cox proportional hazards model, λ_j0 is the baseline hazard function of survival time for t_j, with j = 1, 2. We consider two types of baseline hazard function: Weibull distribution (Appendix B) and piecewise constant function. Lawless and Zhan [27] and Feng et al [28] illustrated that models using a piecewise constant baseline hazard yield good estimators for both fixed effects and frailty. Piecewise constant baseline hazard function has been widely used in the literature [29, 30, 31, 32, 33, 34]. Given a set of fixed time points 0 = τ_j0 < τ_j1 < … < τ_jm < τ_j(m+1), and the baseline hazard vector g = (g₁, g₂) with g_j = (g_j0, g_j1, …, g_jm), we define the piecewise constant hazard function as ${\lambda }_{j0}(t_j)={\sum }_{l=0}^m{g}_{ij}{I}_{ij}(t_j)$, with I_jl(t_j) = 1 if τ_jl ≤ t_ji < τ_j(l+1) and 0 otherwise. Let δ_j (1 if uncensored, 0 otherwise) be the censoring indicator for time t_j. Because the event for t₁ is IBTR and is observed in every patient, δ₁ ≡ 1, whereas δ₂ can be either 1 or 0 due to censoring.

To account for the within-patient correlation between t₁ and t₂, we use the shared frailty b and assume b follows normal distribution with mean 0 and variance σ. We also assume that t₁ and t₂ are independent conditional on the frailty term b. The hazard function of survival time t_j is λ^N(t_j) = λ_j0(t_j) exp(xγ_j + b), where the superscript N denotes NP status. Note that the covariates included in the hazard function can differ or overlap with those in model (1). The corresponding survival function is $S_j^N(t_j)=exp\left[-exp(\mathit{x}{\mathit{\gamma }}_j+b){\int }_0^{t_j}{\sum }_{l=0}^m{g}_{ij}{I}_{ij}(s)\mathit{\text{ds}}\right]$. If τ_ja ≤ t_j < τ_j(a+1), the survival function can be simplified to $S_j^N(t_j)=exp\left\{-exp(\mathit{x}{\mathit{\gamma }}_j+b)\left[{\sum }_{l=0}^{a-1}{g}_{ij}({\tau }_{j(l+1)}-{\tau }_{ij})+g_{ja}(t_j-{\tau }_{ja})\right]\right\}$. To solve for t_j:

$$t_j^N={\tau }_{ja}-\frac{log{S}_j^N(t_j)}{g_{ja}exp(\mathit{x}{\mathit{\gamma }}_j+b)}-\frac{1}{g_{ja}}\sum _{l=0}^{a-1}{g}_{ij}({\tau }_{j(l+1)}-{\tau }_{ij}).$$ (2)

The condition τ_ja ≤ t_j < τ_j(a+1) imposes the following constraint: $-exp(\mathit{x}{\mathit{\gamma }}_j+b){\sum }_{l=0}^a{g}_{ij}({\tau }_{j(l+1)}-{\tau }_{ij})<log{S}_j^N(t_j)\le -exp(\mathit{x}{\mathit{\gamma }}_j+b){\sum }_{l=0}^{a-1}{g}_{ij}({\tau }_{j(l+1)}-{\tau }_{ij})$. The hazard function for TR patients is ${\lambda }_j^T(t_j)={\lambda }_j^N(t_j)e^{{\alpha }_j}={\lambda }_{j0}(t_j)exp(\mathit{x}{\mathit{\gamma }}_j+b+{\alpha }_j)$, where α_j describes the additional hazard of being TR patients compared with NP patients and the superscript T denotes TR status. Following the same procedure, we can derive $S_j^T(t_j)$, $t_j^T$, and the constraint of $S_j^T(t_j)$.

The likelihoods of observing t_j for NP and TR patients are $L_j^N={[{\lambda }_j^N(t_j)]}^{{\delta }_j}{S}_j^N(t_j)$ and $L_j^T=[{\lambda }_j^T{(t_j)]}^{{\delta }_j}{S}_j^T(t_j)$, respectively. By multiplying the survival likelihood functions $L_j^N$ and $L_j^T$ into model (1), the observed likelihood conditional on frailty b for one patient is:

$$\begin{array}{lll}\hfill L(\mathit{\theta }|b)& =\hfill & {[\pi (\mathit{x})p_1{p}_2{L}_1^N{L}_2^N+\overline{\pi }(\mathit{x}){\overline{q}}_1{\overline{q}}_2{L}_1^T{L}_2^T]}^{y_1{y}_2}{[\pi (\mathit{x}){\overline{p}}_1{p}_2{L}_1^N{L}_2^N+\overline{\pi }(\mathit{x})q_1{\overline{q}}_2{L}_1^T{L}_2^T]}^{{\overline{y}}_1{y}_2}\hfill \\ \hfill & \cdot \hfill & {[\pi (\mathit{x})p_1{\overline{p}}_2{L}_1^N{L}_2^N+\overline{\pi }(\mathit{x}){\overline{q}}_1{q}_2{L}_1^T{L}_2^T]}^{y_1{\overline{y}}_2}{[\pi (\mathit{x}){\overline{p}}_1{\overline{p}}_2{L}_1^N{L}_2^N+\overline{\pi }(\mathit{x})q_1{q}_2{L}_1^T{L}_2^T]}^{{\overline{y}}_1{\overline{y}}_2},\hfill \end{array}$$ (3)

where θ = (β, p₁, q₁, p₂, q₂, γ₁, α₁, γ₂, α₂, σ, g) is the unknown parameter vector. The likelihood formulation (3) involves both the binomial regression with the misclassified outcome and the survival times. The marginal likelihood is L(θ) = ∫ L(θ|b)f(b)db. Because this integral cannot be evaluated analytically we use Bayesian inference based on Markov Chain Monte Carlo (MCMC) posterior simulation (Section 2.3).

2.2. Conditional dependence

As discussed in Section 1.1, the two diagnostic tests used to classify IBTR share some criteria (tumor location and histology). These two tests are likely to be highly correlated, even conditional on the true IBTR status. Therefore, the likelihood formulations (1) and (3) in Section 2.1, which are derived under conditional independence assumption, may not be valid. In this section, we discuss how to address this issue of conditional dependence.

Tumor location and histology are clinical and pathologic features, respectively, whereas ER status is measured by standard immunohistochemistry with antigen retrieval prior to antibody incubation. One can assume that these three features are different phenotypes representing the underlying disease trait (i.e., the true IBTR status), which contains all information that the three features share. Thus, we assume that ER status is independent of tumor location and histology (i.e., that ER is independent of the outcome of test 1), conditional on the true IBTR status. This assumption is much weaker than the conditional independence assumption in Section 2.1.

We define the indicator function I_E for ER status change (1 if ER status changes, 0 otherwise). Similar to the definitions of sensitivity and specificity, we define p_E = P(I_E = 1|y = 1) and q_E = P(I_E = 0|y = 0), respectively. Using the relationships between test 1 and test 2 illustrated in Section 1.1, the sensitivity and specificity of test 2 are:

$$p_2=P(y_1=1|y=1)+P(y_1=0,I_E=1|y=1)=p_1+{\overline{p}}_1{p}_E;q_2=P(y_1=0,I_E=0|y=0)=q_1{q}_E.$$ (4)

Test 1 and test 2 are now dependent conditional on the true IBTR status.

The likelihood of observing outcomes y₁ and y₂ for one patient is

$$f(y_1,y_2|\mathit{x})={[\pi (\mathit{x})p_1+\overline{\pi }(\mathit{x}){\overline{q}}_1]}^{y_1{y}_2}{[\pi (\mathit{x}){\overline{p}}_1{p}_E+\overline{\pi }(\mathit{x})q_1{\overline{q}}_E]}^{{\overline{y}}_1{y}_2}{[\pi (\mathit{x}){\overline{p}}_1{\overline{p}}_E+\overline{\pi }(\mathit{x})q_1{q}_E]}^{{\overline{y}}_1{\overline{y}}_2}.$$ (5)

The derivation of the likelihood is detailed in Appendix C. After including the survival information, the observed likelihood conditional on frailty b for one patient becomes

$$\begin{array}{l}\begin{array}{lll}L(\mathit{\theta }|b)\hfill & =\hfill & {[\pi (\mathit{x})p_1{L}_1^N{L}_2^N+\overline{\pi }(\mathit{x}){\overline{q}}_1{L}_1^T{L}_2^T]}^{y_1{y}_2}{[\pi (\mathit{x}){\overline{p}}_1{p}_E{L}_1^N{L}_2^N+\overline{\pi }(\mathit{x})q_1{\overline{q}}_E{L}_1^T{L}_2^T]}^{{\overline{y}}_1{y}_2}\hfill \\ \hfill & \cdot \hfill & {[\pi (\mathit{x}){\overline{p}}_1{\overline{p}}_E{L}_1^N{L}_2^N+\overline{\pi }(\mathit{x})q_1{q}_E{L}_1^T{L}_2^T]}^{{\overline{y}}_1{\overline{y}}_2},\hfill \end{array}\hfill \end{array}$$ (6)

where unknown parameter vector θ = (β, p₁, q₁, p_E, q_E, γ₁, α₁, γ₂, α₂, σ, g). The estimates of p₂ and q₂ can be computed from the estimates of θ using Eq (4). Throughout the article, we refer to models (1) and (5) as the “reduced model” and models (3) and (6) as the “proposed model” due to the fact that the reduced model is a special case of the proposed model when there is no survival information available.

2.3. Bayesian inference

In this section, we describe our Bayesian framework for parameter estimation. To obtain the parameter estimates, we use Bayesian inference based on MCMC posterior simulation. Vague prior distributions are used for all parameters. Specifically, independent normal distribution with mean 0 and variance 10 is taken for each component of the parameter vectors β, γ_j, and α_j, where j = 1, 2. Assuming the diagnostic tests are more accurate than the toss of a fair coin, we use uniform prior distribution p_k, q_k ∼ Unif(0.5, 1), for k = 1, 2, under the conditional independence case or use uniform prior distributions p₁, q₁ ∼ Unif(0.5, 1) and p_E, q_E ∼ Unif(0, 1) under the conditional dependence case. While this accuracy assumption is slightly stronger than the identifiability condition, i.e., p + q > 1, employed by Fujisawa and Izumi [35], we believe that the assumption is reasonable for tests in practical use. For the frailty variance σ and each component in baseline hazard vector g, we assume a noninformative inverse gamma prior distribution, IG(0.01, 0.01) so that the distribution has mean of 1 and variance of 100. If a Weibull distribution is used as the baseline hazard function, the prior distribution for the scale and shape parameters is log-normal, i.e., log(λ_j), log(υ_j) follows a normal distribution with mean 0 and variance 10. The MCMC sampler is implemented using WinBUGS software [36]. We use the trace plots available in WinBUGS and view the absence of apparent trend in the plots as evidence of convergence. In addition, we run multiple chains with disperse initial values and compute Gelman-Rubin scale reduction statistics R̂ to ensure R̂ of all parameters are smaller than 1.1.

To select between Weibull distribution and piecewise constant function as the baseline hazard function and to determine the covariates in the proposed method, we adopt a model selection approach using the deviance information criterion (DIC) proposed by Spiegelhalter et al. [37]. The DIC provides an assessment of model fit and a penalty for model complexity. The deviance statistics is defined as D(θ, b) = −2 log f(y|θ, b) + 2 log h(y), where f(y|θ, b) is the likelihood function for the observed data vector y given the parameter vector θ and frailty b, and h(y) denotes a standardizing function of the data alone that has no impact on model selection [38]. The DIC is defined as DIC = 2D̄ − D(θ̄, b̄) = D̄ + p_D, where D̄ = E_θ,b|y [D] is the posterior mean of the deviance, D(θ̄,b̄) = D(E_θ,b|y [θ, b]) is the deviance evaluated at the posterior means θ̄ and b̄, and p_D = D̄ − D(θ̄, b̄) is the effective number of parameters. Smaller values of DIC indicate a better-fitting model. WinBUGS is used to compute DIC. This DIC definition applies the original definition of DIC to the conditional distribution and it is the conditional DIC (i.e., DIC₇) defined in Celeus et al [39].

3. Simulation studies

We evaluated the performance of our method using extensive simulation studies. We considered four covariates: x = (x₁, x₂, x₃, x₄)′, where x₁ was continuous and generated from N(47, 12²), and centered at its rounded median; and x₂, x₃, and x₄ were binary, were generated from Bernoulli distributions with probabilities of 0.3, 0.1, and 0.3, respectively. The details of these variables are presented in Section 4 and the numbers used to generate them resemble their characteristics. We simulated 100 datasets of 400 subjects each. To determine the burn-in iterations and assess the MCMC convergence and mixing properties, we examined the trace plots and the autocorrelations. We found that the chains converged reasonably fast and all achieved stationarity within 10, 000 iterations with R̄ of all parameters smaller than 1.1. To ensure the convergence, we chose 25,000 iterations for burn-in for each MCMC sample and the inference was based on the subsequent 25,000 iterations. The histories of 8 parameters of interest from one randomly selected chain for one of the simulated datasets indicated reasonable convergence and mixing properties, even though, for clarity, only every 100th simulation was displayed (Web Figure 1). Similar good chain properties were noted in all other examples presented in this article.

In the first set of simulation, we used the Weibull distribution as the baseline hazard function and simulated data structure consisting of an imperfectly classified binary outcome and the correlated survival information. We estimated the parameters of the proposed model using Weibull distribution as the baseline hazard function and examined the advantages of the proposed model over the logistic regression method and the reduced model under either conditional independence or conditional dependence assumption. We simulated the data using the following steps.

1. Simulated y using Bernoulli distribution with π(x) generated from logit[π(x)] = xβ with β = (0.31, 0.006, −1.8, 0.7)′ and x = (x₀, x₁, x₂, x₃).

2. Conditional on y, simulated the observed outcomes y₁ and y₂ with sensitivity and specificity p₁ = 0.8, q₁ = 0.85, p₂ = 0.9, and q₂ = 0.7 for the conditional independence case or p₁ = 0.8, q₁ = 0.85, p_E = 0.15, and q_E = 0.75 to get p₂ = 0.830 and q₂ = 0.638 for the conditional dependence case.

3. Simulated the shared frailty b from normal distribution N(0, 0.1²).

4. Simulated the survival probabilities $S_j^N$ and $S_j^T$ from uniform(0, 1) for j = 1, 2.

5. Conditional on y, generated the time to relapse $t_1^N$ and $t_1^T$ from Eq (2) with γ₁ = (−0.02, 0.2)′, and the covariate vector being (x₁, x₄), α₁ = 1, and the Weibull distribution parameters λ₁ = υ₁ = 1.

6. Conditional on y, generated the uncensored time from IBTR to death ζ^N and ζ^T from Eq (2) with γ₂ = (−0.004, 0.7)′, and the covariate vector being (x₁, x₄), α₂ = 3, and the Weibull distribution parameters λ₂ = υ₂= 1.

7. Simulate the censoring time from IBTR to death c₂ from uniform(0.1, 30). Let the observed time from IBTR to death $t_2^N=min({\zeta }^N,c_2)$ and $t_2^T=min({\zeta }^T,c_2)$ and obtain the censoring indicator δ₂ accordingly.

8. Repeated steps 1 to 7 until all subjects were generated.

The mean, standard error (the square root of the average of the posterior variances, denoted by SE), standard deviation (the standard deviation of the posterior means, denoted by SD), and coverage probabilities (CP) of 95% credible intervals estimated from logistic regression (LR) model (in which the second measurement y₂ was treated as the true y), the reduced model, and the proposed model are shown in Table 1. When conditional independence was assumed, logistic regression gave severely biased parameter estimates, and the coverage probabilities were far away from the nominal level of 95% (Table 1a). The reduced model was valid in this scenario, giving consistent estimates and coverage probabilities close to 95% nominal level. Compared with the reduced model, the proposed model provided estimates with negligible bias and much smaller standard deviation for all parameters while retaining the coverage probabilities at 95%. The asymptotic relative efficiency (i.e., ARE, comparing the estimator based on the proposed model to the reduced model) in Table 1a indicates large efficiency gain in all parameter estimates (ranging from 5.378 to 1.690). These results indicated that the proposed model, which incorporates the additional correlated survival information, markedly improved the parameter estimation in terms of bias and efficiency.

Table 1.

The estimates of the mean, standard error (SE), standard deviation (SD), and coverage probabilities (CP) of 95% credible intervals based on logistic regression (LR), the reduced model, and the proposed model assuming either conditional independence or conditional dependence. ARE is asymptotic relative efficiency of the proposed model with respect to the reduced model.

(a) Conditional independence
	True	β0	β1	β2	β3	p1	q1	p2	q2
	pars	0.310	0.006	−1.800	0.700	0.800	0.850	0.900	0.700
LR	Mean	0.599	0.004	-0.929	0.297
	SD	0.142	0.009	0.245	0.375
	SE	0.131	0.009	0.225	0.368
	CP	0.400	0.930	0.030	0.740
Reduced model	Mean	0.282	0.008	−1.932	0.635	0.812	0.849	0.894	0.690
	SD	0.222	0.012	0.501	0.436	0.064	0.042	0.037	0.052
	SE	0.327	0.013	0.537	0.478	0.072	0.052	0.048	0.066
	CP	0.990	0.950	0.950	0.980	0.980	0.990	0.990	0.980
Proposed model	Mean	0.288	0.007	−1.827	0.652	0.797	0.846	0.898	0.694
	SD	0.149	0.010	0.332	0.352	0.032	0.029	0.022	0.032
	SE	0.141	0.010	0.290	0.386	0.032	0.028	0.024	0.034
	CP	0.940	0.950	0.930	0.950	0.950	0.960	0.980	0.960
	ARE	5.378	1.690	3.429	1.533	5.062	3.449	4.000	3.768

(b) Conditional dependence
	True	β0	β1	β2	β3	p1	q1	p2	q2
	pars	0.310	0.006	−1.800	0.700	0.800	0.850	0.830	0.638
LR	Mean	0.552	0.004	−0.769	0.219
	SD	0.119	0.010	0.222	0.365
	SE	0.130	0.009	0.224	0.363
	CP	0.530	0.910	0.000	0.710
Reduced model	Mean	0.330	0.008	−1.910	0.677	0.798	0.845	0.825	0.631
	SD	0.290	0.018	0.656	0.641	0.076	0.055	0.047	0.065
	SE	0.338	0.019	0.717	0.714	0.091	0.065	0.055	0.068
	CP	0.990	0.920	0.980	0.940	0.980	0.970	0.940	0.980
Proposed model	Mean	0.278	0.008	−1.834	0.661	0.803	0.846	0.838	0.633
	SD	0.175	0.012	0.330	0.389	0.039	0.034	0.035	0.036
	SE	0.196	0.012	0.346	0.439	0.042	0.039	0.038	0.040
	CP	0.960	0.950	0.960	0.990	0.990	0.980	0.970	0.970
	ARE	2.974	2.507	4.294	2.645	4.694	2.778	2.095	2.890

Table 1b displays the estimation results under conditional dependence. Logistic regression had severe bias for all parameters. Because the reduced model correctly accounted for the conditional dependence structure, it was a valid model with consistent estimates and coverage probabilities close to 95%. In contrast, the proposed model's parameter estimates all had small bias and coverage probabilities that were reasonably close to 95%. These findings indicated that the conditional dependence between two diagnostic tests could be successfully addressed using the techniques in Section 2.2. The ARE in Table 1b indicated large efficiency gain in the proposed model due to the inclusion of the correlated survival time information.

Web Table 1 displays the simulation results when no misclassification was present (p_j = q_j = 1 for j = 1, 2) and conditional independence was assumed. All three methods provided comparable results, i.e., the bias was negligible and the credible interval coverage probabilities were reasonably close to the nominal level of 95%. In addition, all estimates of sensitivity and specificity were close to 1. The results indicated that both the reduced and proposed models were robust in parameter estimation when no misclassification existed. The proposed model's estimates of the parameters (γ₁, α₁, γ₂, α₂, g, σ) related to survival information had small bias, and the coverage probabilities of 95% credible intervals were close to 95% nominal levels (results not shown).

In the second set of simulation, we investigated the performance of our method when the piecewise constant function was used as the baseline hazard function. The data simulation followed the steps above with changes in step 5 using the baseline hazard vector g₁ = g₂ = (0.05, 0.07, 0.1, 0.12, 0.16, 0.17, 0.18, 0.2, 0.15, 0.3, 0.1) at the fixed time points τ₁ = (0, 2.5, 5, 7.5, 10, 12.5, 15, 17.5, 20, 22.5, 25, 200) and τ₂ = (0, 2, 4, 6, 8, 10, 12, 14, 20, 30, 40, 200), respectively. We simulated the datasets and estimated the parameters using piecewise constant baseline hazard function while assuming either conditional independence (Table 2a) or conditional dependence (Table 2c). Our model provided unbiased estimates, the SE close to the SD, and coverage probabilities close to 95%. In addition, we simulated the datasets using Weibull distribution as the baseline hazard function, but estimated the parameters using piecewise constant function while assuming either conditional independence (Table 2b) or conditional dependence (Table 2d). Bias was small, SE was close to SD, and coverage probabilities were close to 95% in all parameters except α₁ and α₂, whose estimates were slightly off the true values and whose coverage probabilities were off from the nominal value. These results indicated that our model could account for the misclassification, and could recover the true parameters, and was generally robust to baseline hazard function misspecification.

Table 2.

The estimates of the mean, standard error (SE), standard deviation (SD), and coverage probabilities (CP) of 95% credible intervals under various simulation scenarios.

	regression model								time to recurrence			time to death
True	β0	β1	β2	β3	p1	q1	p2	q2	γ11	γ12	α1	γ21	γ22	α2
pars	0.310	0.006	−1.800	0.700	0.800	0.850	0.900	0.700	−0.020	0.200	1.000	−0.004	0.700	3.000
(a) Simulate and estimate using piecewise constant function assuming conditional independence
Mean	0.337	0.008	−1.849	0.674	0.794	0.850	0.898	0.700	−0.021	0.205	0.992	−0.004	0.692	2.948
SD	0.136	0.011	0.281	0.309	0.035	0.030	0.023	0.036	0.005	0.107	0.134	0.005	0.120	0.243
SE	0.149	0.010	0.294	0.426	0.032	0.029	0.025	0.035	0.005	0.122	0.134	0.005	0.141	0.245
CP	0.990	0.910	0.960	0.990	0.950	0.970	0.960	0.950	0.950	0.990	0.950	0.950	0.990	0.950
(b) Simulate from Weibull and estimate using piecewise constant function assuming conditional independence
Mean	0.336	0.006	−1.808	0.693	0.797	0.856	0.896	0.702	−0.021	0.175	0.936	−0.004	0.680	2.746
SD	0.153	0.011	0.320	0.372	0.033	0.029	0.021	0.033	0.004	0.110	0.130	0.004	0.104	0.206
SE	0.147	0.010	0.293	0.426	0.032	0.028	0.025	0.035	0.005	0.116	0.125	0.005	0.129	0.222
CP	0.960	0.940	0.930	0.960	0.950	0.970	0.990	0.940	0.970	0.940	0.900	0.990	0.990	0.770

True	β0	β1	β2	β3	p1	q1	p2	q2	γ11	γ12	α1	γ21	γ22	α2
pars	0.310	0.006	−1.800	0.700	0.800	0.850	0.830	0.638	−0.020	0.200	1.000	−0.004	0.700	3.000
(c) Simulate and estimate using piecewise constant function assuming conditional dependence
Mean	0.316	0.006	−1.813	0.668	0.803	0.857	0.836	0.642	−0.022	0.177	0.965	−0.005	0.699	2.984
SD	0.172	0.011	0.337	0.398	0.034	0.031	0.033	0.035	0.005	0.106	0.151	0.006	0.112	0.332
SE	0.165	0.011	0.308	0.449	0.034	0.033	0.031	0.037	0.005	0.124	0.141	0.006	0.148	0.278
CP	0.950	0.950	0.950	0.990	0.960	0.950	0.930	0.960	0.930	0.990	0.930	0.970	0.970	0.910
(d) Simulate from Weibull and estimate using piecewise constant function assuming conditional dependence
Mean	0.348	0.008	−1.838	0.721	0.791	0.858	0.825	0.639	−0.019	0.173	0.946	−0.003	0.668	2.665
SD	0.139	0.012	0.297	0.398	0.032	0.033	0.030	0.038	0.004	0.106	0.133	0.004	0.097	0.239
SE	0.164	0.011	0.307	0.454	0.034	0.032	0.032	0.037	0.005	0.117	0.134	0.005	0.135	0.252
CP	0.990	0.920	0.970	0.970	0.960	0.960	0.960	0.920	0.960	0.950	0.910	0.970	0.990	0.740

4. Application to the breast cancer dataset

We applied the proposed method to the breast cancer patient dataset. We used three parallel chains with overdispersed initial values and ran each chain for 50, 000 iterations. The first 25, 000 iterations were discarded as burn-in; the parameter estimates were based on the remaining 25, 000 iterations from each chain. Good mixing properties of the chains for the model parameter were observed in the trace plots.

We considered 4 covariates in our method: x₁ represented age at breast cancer diagnosis (mean: 47.5 years; SD: 11.3 years); x₂ represented whether a distant recurrence developed in organs other than breasts (e.g., bones, lung, brain, liver; prevalence: 26.7%); x₃ represented whether contralateral breast carcinoma developed (prevalence: 12.8%); x₄ represented primary tumor stage (x₄ = 1 if more aggressive stage II or higher and 0 otherwise; prevalence: 28%) [40]. Using the quantiles of each survival time, we obtained the time points τ₁ = (0, 1.3, 2.2, 3.6, 4.8, 7.0, 9.7, 13.5, 24.6) and τ₂ = (0, 1.15, 1.9, 2.5, 3.7, 5.2, 7.7, 12.1, 31.4).

For model selection and comparison, we computed the DIC (illustrated in Section 2.3). Web Table 2 presents estimated DICs for some models using either the piecewise constant function or the Weibull distribution as the baseline hazard function. The piecewise constant model, with x₁, x₂, and x₄ in the binomial regression part and x₁ and x₄ in both survival parts of our model, had the lowest DIC value and was selected as the final model. To check the proportional hazard assumption in modeling the survival times, we plotted the product-limit estimates of log cumulative hazard rates for the covariates (e.g., tumor stage displayed in Web Figure 2). The absence of gross departure from the hypothesis of parallel curves suggested that the proportional hazard assumption was reasonable. In addition, to check the assumption of constant hazard ratio for TR patients compared with NP patients, we plotted in Web Figure 3 the product-limit estimates of log cumulative hazard rates of time to relapse (left panels) and time from IBTR to death (right panels) for patients classified as NP or TR by test 1 (top panels) and test 2 (bottom panels). The pattern of parallel curves indicated that the proportionality assumption for being NP was reasonable.

Table 3 provides the means, SDs, and 95% CIs from our model assuming conditional dependence as illustrated in Section 2.2. The rows labeled “Regression” in Table 3 display the results of modeling the probability of have NP. A negative sign for a parameter β indicated a smaller probability of having NP, or a larger probability of having TR. The odds ratio of the IBTR being NP for the patients who developed distant recurrence in organs other than breasts was 0.0011 (i.e., exp(−6.737); 95% CI: [4.067e – 5, 0.010]) compared with the patients without distant recurrence. The covariates age at diagnosis and tumor stage were not statistically significant. These findings were consistent with the results of previous studies [8, 9, 10]. The sensitivity and specificity estimates of both tests were below 0.8, while test 2 had higher sensitivity but lower specificity than test 1. Because TR patients tend to have shorter survival time from IBTR to death and need more aggressive treatment than NP patients, the misclassification of TR patients into NP are likely to be more costly than vice versa. Thus test 1 may be more preferable because of its higher specificity and the proposed model provided the estimates of the test accuracy.

Table 3. The means, standard deviations (SD), and 95% credible intervals (CI) of the parameters from the proposed model.

		Mean	SD	95% CI
Regression	Intercept	1.929	1.291	−0.636	4.279
	Age at diagnosis	0.016	0.027	−0.032	0.072
	Distant recurrence	−6.737	1.425	−10.110	−4.655
	Tumor stage	−0.348	0.809	−1.736	1.421
	p1	0.618	0.031	0.557	0.677
	q1	0.769	0.042	0.684	0.847
	p2	0.654	0.030	0.594	0.712
	q2	0.700	0.044	0.610	0.784
T1	Age at diagnosis	0.022	0.005	0.011	0.032
	Tumor stage	0.347	0.157	0.051	0.664
	α1	0.682	0.161	0.367	1.004
T2	Age at diagnosis	0.024	0.012	0.001	0.048
	Tumor stage	0.291	0.281	−0.263	0.850
	α2	5.408	1.444	3.481	9.143
	σ	0.483	0.224	0.128	0.998

The rows labeled T₁ in Table 3 show the results of modeling the hazard of IBTR occurrence after BCT. The hazard rate of IBTR occurrence is 1.246 (95% CI: [1.116, 1.377]) for every 10-year increase in the age at breast cancer diagnosis. The relative risk of IBTR in patients with stage II or higher tumors relative to patients with stage I tumors was 1.415 (95% CI: [1.052, 1.943]). The TR status significantly increased the risk of IBTR, with a relative risk of 1.978 (95% CI: [1.443, 2.729]) compared with NP patients. Finally, the rows labeled T₂ in Table 3 show the results of modeling the hazard of death. The hazard rate of death is 1.271 (95% CI: [1.010, 1.616]) for every 10-year increase in age at breast cancer diagnosis. Tumor stage was not associated with the risk of death whereas TR status significantly increased the risk. The large risk differences between TR and NP statues (indicated by the significant estimates of α₁ and α₂) are visually displayed in the large gaps in the Kaplan-Meier curves (Figure 2) and had been reported previously [8, 9, 41].

We further provided some insight into our model's ability to compute the subject-specific estimates and predictions for future patients who develop IBTR. We obtained data from 20 additional breast cancer patients who were treated at MD Anderson Cancer Center, had experienced IBTR, and were not included in the above analysis. We applied our model-fitting results to this new dataset. We first calculated the probability of the IBTR being NP and obtained a minimum probability being 0.01, mean probability of 0.40, and maximum probability of 0.98. Using 0.90 as cut point, eight patients' IBTR were classified as NP. Based on the IBTR status, each patient's median survival time could be computed. For example, one patient had breast cancer at age 50 years, IBTR at age 52 years, no distant recurrence, and a stage II or higher tumor. The estimated probability of her IBTR being NP was 0.02 and was therefore classified as TR. The estimated median survival time from IBTR to death was 1.4 years. In contrast, another patient had breast cancer at age 45 years, IBTR at age 54 years, had distant recurrence, and a stage I tumor. The estimated probability of her IBTR being NP was 0.95 and was therefore classified as NP. The estimated median survival time from IBTR was 14.3 years.

5. Discussion

In this article, we developed a Bayesian method to model binomial regression with the misclassified binary outcome and two correlated survival times (time to relapse and time from IBTR to death). We described a simple two-latent-classes model to relax the assumption of conditional independence between diagnostic tests conditional on the true IBTR status. Using extensive simulation, we found that our modeling framework corrects biases and provides more efficient estimates for the covariate effects on the probability of IBTR and the diagnostic test sensitivity and specificity, compared with the method that does not use the survival information.

From the analysis of our patient dataset, we found that the sensitivity and specificity of both tests, which used only clinical and pathological criteria, were smaller than 0.8. A more accurate diagnostic test using the molecular criteria should be developed in the future, as pointed out by Huang et al. [8]. Our model will enable clinicians to make better-informed decisions about which diagnostic test to use and have better knowledge in identifying and quantifying the covariate effects on the probability of IBTR being NP and on the hazards. In addition, the model-fitting results from the original dataset can be used to provide new patients who develop IBTR the subject-specific prediction of some useful prognostic information such as the probability of the IBTR being NP and the median survival time from IBTR to death. This prognostic information is valuable for efficiently developing, targeting, and evaluating intervention, thus helping clinicians provide more suitable therapy for their patients, which in turn will improve patient outcomes. Our proposed method can be broadly applied to many studies with a similar data structure consisting of imperfectly classified binary outcomes and survival information that is correlated with the outcomes. For example, tumor grade is an important prognostic indicator of pancreatic cancer survival after pancreatic resection [42, 43, 44, 45, 46, 47], as higher tumor grade (III vs. I/II) is generally associated with poor survival [48]. Another example is that higher expression level of the chemokine CXCL12 (high vs. low/moderate) is an important predictor of poor survival in ovarian cancer [49]. However, the classification of tumor grade and CXCL12 expression level are subject to errors and there is no gold standard available.

Adjustment for potential bias due to misclassification requires information on the misclassification structure to make the model identifiable [50]. The covariates in x in modeling IBTR status are instrumental variables and they make the reduced model identifiable when their number of different possible realizations is sufficient [51]. In addition, the survival information included in the proposed model is an important determinant of IBTR status. This is manifested by the clear dichotomy in the Kaplan-Meier curves displayed in Figure 2. As pointed out by one of the reviewers, when there is no correlated survival data and the probability of IBTR being NP is independent of covariate, i.e., π(x) ≡ π, the proposed model reduces to the scenario of two conditionally independent tests and one population and hence lacks identifiability. The detailed discussion of the identifiability, modeling, and parameter estimation of multiple conditional dependent diagnostic tests can be found in some recent literature, e.g., Dendukuri and Joseph [52], Georgiadis et al [53], and Jones et al [54].

Bayesian inference using MCMC simulation described in this article produces reliable results. However, the model fitting was computationally intensive. For example, it took approximately 8 and 6 hours for piecewise constant and Weibull baseline hazard function models, respectively, to get 50, 000 samples for a single MCMC chain on a PC (Dell workstation Optiplex 960, Intel quad CPU at 3GHz, 8 GB RAM). In contrast, it took only about 30 minutes and a few seconds, using the reduced model and the logistic regression method, respectively, on the same PC. Even though our implementation was slower, our proposed method improved the parameter estimation in bias and efficiency and produced subject-level predictions. It has been previously discussed that the improvement on parameter estimation is important and necessary [55].

Our modeling strategy had some limitations that we will address in our future research endeavors. One limitation was that both sensitivity and specificity were assumed to be non-differential, i.e., that they did not depend on the covariates. In reality, there may be a subgroup of patients whose disease is less likely than that of other patients to be misclassified under both diagnostic tests. For example, most previously published studies assumed that the IBTR that occurred at the same location and with the same histology as the primary tumor was TR. Thus the classification of patients with no change in tumor location and histology into the TR group is less prone to errors than the classification of other patients into the NP group.

Appendix A: Likelihood derivation of model (1)

The likelihood of observing outcomes y₁ and y₂ for one patient is

$$\begin{array}{ll}& f(y_1,y_2|\mathit{x})\hfill \\ =\hfill & p{(y_1=1,y_2=1|\mathit{x})}^{y_1{y}_2}p{(y_1=0,y_2=1|\mathit{x})}^{{\overline{y}}_1{y}_2}p{(y_1=1,y_2=0|\mathit{x})}^{y_1{\overline{y}}_2}p{(y_1=0,y_2=0|\mathit{x})}^{{\overline{y}}_1{\overline{y}}_2}\hfill \\ =\hfill & {[p(y_1=1,y_2=1|y=1,\mathit{x})p(y=1|\mathit{x})+p(y_1=1,y_2=1|y=0,\mathit{x})p(y=0|\mathit{x})]}^{y_1{y}_2}\hfill \\ \cdot \hfill & {[p(y_1=0,y_2=1|y=1,\mathit{x})p(y=1|\mathit{x})+p(y_1=0,y_2=1|y=0,\mathit{x})p(y=0|\mathit{x})]}^{{\overline{y}}_1{y}_2}\hfill \\ \cdot \hfill & {[p(y_1=1,y_2=0|y=1,\mathit{x})p(y=1|\mathit{x})+p(y_1=1,y_2=0|y=0,\mathit{x})p(y=0|\mathit{x})]}^{y_1{\overline{y}}_2}\hfill \\ \cdot \hfill & {[p(y_1=0,y_2=0|y=1,\mathit{x})p(y=1|\mathit{x})+p(y_1=0,y_2=0|y=0,\mathit{x})p(y=0|\mathit{x})]}^{{\overline{y}}_1{\overline{y}}_2}\hfill \\ =\hfill & {[\pi (\mathit{x})p_1{p}_2+\overline{\pi }(\mathit{x}){\overline{q}}_1{\overline{q}}_2]}^{y_1{y}_2}{[\pi (\mathit{x}){\overline{p}}_1{p}_2+\overline{\pi }(\mathit{x})q_1{\overline{q}}_2]}^{{\overline{y}}_1{y}_2}{[\pi (\mathit{x})p_1{\overline{p}}_2+\overline{\pi }(\mathit{x}){\overline{q}}_1{q}_2]}^{y_1{\overline{y}}_2}{[\pi (\mathit{x}){\overline{p}}_1{\overline{p}}_2+\overline{\pi }(\mathit{x})q_1{q}_2]}^{{\overline{y}}_1{\overline{y}}_2},\hfill \end{array}$$ (7)

The second equality is derived from the law of total probability and the last equality holds because we assume that two diagnostic tests are independent conditional on the true IBTR status (conditional independence assumption).

Appendix B: Formulation of Weibull distribution as baseline hazard function

We assume that baseline hazard function λ_0j for survival time t_j follows Weibull distribution ${\lambda }_{0j}(t_j)={\lambda }_j{t}_j^{{\upsilon }_j}$, where λ_j is the scale parameter and υ_j is the shape parameter. The hazard function of survival time t_j for NP patients is ${\lambda }_j^N(t_j)={\lambda }_{0j}(t_j)exp(\mathit{x}{\mathit{\gamma }}_j+b)$, where the superscript N denotes NP status. The survival function is: $S_j^N(t_j)=exp\left\{-\frac{{\lambda }_j}{{\upsilon }_j+1}{t}_j^{{\upsilon }_j+1}exp(\mathit{x}{\mathit{\gamma }}_j+b)\right\}$. To solve for t_j, we have $t_j^N={\left[-\frac{({\upsilon }_j+1)log{S}_j^N}{{\lambda }_{j}exp(\mathit{x}{\mathit{\gamma }}_j+b)}\right]}^{\frac{1}{{\upsilon }_j+1}}$. The likelihood of observing t_j is $L_j^N={[{\lambda }_j^N(t_j)]}^{{\delta }_j}{S}_j^N(t_j)$. The hazard function for TR patients is ${\lambda }_j^T(t_j)={\lambda }_j^N(t_j)e^{{\alpha }_j}={\lambda }_{j0}(t_j)exp(\mathit{x}{\mathit{\gamma }}_j+b+{\alpha }_j)$, where α_j describes the additional hazards of being TR patients comparing to NP patients, the superscript T denotes TR status. We can derive $S_j^T(t_j)=exp\left\{-\frac{{\lambda }_j}{{\upsilon }_j+1}{t}_j^{{\upsilon }_j+1}exp(\mathit{x}{\mathit{\gamma }}_j+{\alpha }_j+b)\right\}$, $t_j^T={\left[-\frac{({\upsilon }_j+1)log{S}_j^T}{{\lambda }_{j}exp(\mathit{x}{\mathit{\gamma }}_j+{\alpha }_j+b)}\right]}^{\frac{1}{{\upsilon }_j+1}}$, and the likelihood $L_j^T={[{\lambda }_j^T(t_j)]}^{{\delta }_j}{S}_j^T(t_j)$.

Appendix C: Likelihood derivation of model (5)

Under conditional dependence assumption, we have

$$\begin{array}{ll}\hfill & P(y_1=1,y_2=1)=P(y_1=1)=\pi (\mathit{x})p_1+\overline{\pi }(\mathit{x}){\overline{q}}_1\hfill \\ \hfill & P(y_1=0,y_2=1)=P(y_1=0,I_E=1)\hfill \\ =\hfill & P(y_1=0,I_E=1|y=1)P(y=1)+P(y_1=0,I_E=1|y=0)P(y=0)\hfill \\ =\hfill & P(y_1=0|y=1)P(I_E=1|y=1)P(y=1)+P(y_1=0|y=0)P(I_E=1|y=0)P(y=0)\hfill \\ =\hfill & \pi (\mathit{x}){\overline{p}}_1{p}_E+\overline{\pi }(\mathit{x})q_1{\overline{q}}_E\hfill \end{array}$$

$$\begin{array}{ll}\hfill & P(y_1=1,y_2=0)=0\hfill \\ \hfill & P(y_1=0,y_2=0)=P(y_1=0,I_E=0)\hfill \\ =\hfill & P(y_1=0,I_E=0|y=1)P(y=1)+P(y_1=0,I_E=0|y=0)P(y=0)\hfill \\ =\hfill & P(y_1=0|y=1)P(I_E=0|y=1)P(y=1)+P(y_1=0|y=0)P(I_E=0|y=0)P(y=0)\hfill \\ =\hfill & \pi (\mathit{x}){\overline{p}}_1{\overline{p}}_E+\overline{\pi }(\mathit{x})q_1{q}_E.\hfill \end{array}$$

Note that P(y₁ = 1, y₂ = 0) is a null event because of the inherent relationship between the two diagnostic tests explained in Section 1.2.

The likelihood of observing outcomes y₁ and y₂ for one patient is

$$\begin{array}{ll}& f(y_1,y_2|\mathit{x})\hfill \\ =\hfill & p{(y_1=1,y_2=1|\mathit{x})}^{y_1{y}_2}p{(y_1=0,y_2=1|\mathit{x})}^{{\overline{y}}_1{y}_2}p{(y_1=1,y_2=0|\mathit{x})}^{y_1{\overline{y}}_2}p{(y_1=0,y_2=0|\mathit{x})}^{{\overline{y}}_1{\overline{y}}_2}\hfill \\ =\hfill & {[\pi (\mathit{x})p_1+\overline{\pi }(\mathit{x}){\overline{q}}_1]}^{y_1{y}_2}{[\pi (\mathit{x}){\overline{p}}_1{p}_E+\overline{\pi }(\mathit{x})q_1{\overline{q}}_E]}^{{\overline{y}}_1{y}_2}{[\pi (\mathit{x}){\overline{p}}_1{\overline{p}}_E+\overline{\pi }(\mathit{x})q_1{q}_E]}^{{\overline{y}}_1{\overline{y}}_2}.\hfill \end{array}$$ (8)